Benford’s Law in Electric Distribution Network

Abstract

Benford’s law can be used as a method to detect non-natural changes in data sets with certain properties; in our case, the dataset was collected from electricity metering devices. In this paper, we present a theoretical background behind this law. We applied Benford’s law first digit probability distribution test for electricity metering data sets acquired from smart electricity meters, i.e., the natural data of electricity consumption acquired during a specific time interval. We present the results of Benford’s law distribution for an original measured dataset with no artificial intervention and a set of results for different kinds of affected datasets created by simulated artificial intervention. Comparing these two dataset types with each other and with the theoretical probability distribution provided us the proof that with this kind of data, Benford’s law can be applied and that it can extract the dataset’s artificial manipulation markers. As presented in the results part of the article, non-affected datasets mostly have a deviation from BL theoretical probability values below 10%, rarely between 10% and 20%. On the other side, simulated affected datasets show deviations mostly above 20%, often approximately 70%, but rarely lower than 20%, and this only in the case of affecting a small part of the original dataset (10%), which represents only a small magnitude of intervention.

1. Introduction

In electricity distribution networks, the consumption values measured at certain network nodes follow natural, authentic value distribution when no special conditions are present. However, in cases when special conditions occur in the consumption situation, e.g., some kind of artificial intervention due to macro-economic or micro-economic requirements, or non-technical losses occur due to electricity theft, the character of the consumption values change and the dataset value become unauthentic and unnatural.

Macroeconomic or micro-economic requirements and their effects are important for electricity production planning. Thus, detecting their presence could be a useful tool in helping electricity production planning [1,2].

Technical and non-technical losses make up an important part of costs for electricity distribution. Electricity theft is a significant challenge for companies, utilities, and distributors, where attackers alter usage measurement data collected by conventional and smart meters in a non-natural way. Detecting this kind of loss could provide a useful tool for theft prevention actions [2,3,4,5].

Benford’s law provides a tool for one of the methods to detect such a non-natural change in data sets collected from electricity metering devices. However, Benford’s law, in short BL, has a much wider implementation portfolio, helping fraud detection, e.g., in accounting, bank transaction register, etc. The contribution of this paper is the verification of BL validity for electricity metering data sets (the consumption of the electric power), as well as the verification of first digit distribution deviation when comparing BL first digit distribution in natural and affected datasets [1,3,6,7,8,9,10,11,12,13,14,15].

Within the references survey, we can make some statements:

Smart electricity meters are gradually being installed by distribution companies, and a deeper analysis of the data using Benford’s law has not yet been conducted. However, the application of Benford’s law is in various areas and branches of science, as can be read in some publications [16,17,18].

In [6], the authors describe how Benford’s law can be applied to datasets acquired from different energy systems. Their research results indicate that Benford’s law can be used to detect malicious data injected by hackers into the supervisory control and data acquisition (SCADA) system of a transmission network. The relative square deviation index returns values lower than 0.05 in all tested cases in this study [19,20,21,22,23].

In another paper [10], the authors focused on analyzing electricity consumption data in a company in Fujian Province. They applied Benford’s law to consumption data because the record of electricity consumption data is often uncomprehensive and inaccurate. The proposed algorithm effectively identifies problematic data and estimates overall electricity consumption through limited data, with the deviation rate within an acceptable range [20,21,22,23,24].

In the paper [2], the authors proposed a Distributed Intelligent Framework for Electricity Theft Detection, equipped with Benford’s Analysis for initial diagnostics on smart meter big data. Various samples of data, both normal and manipulated by attackers, were compared. The results indicate that Benford’s law works well for analyzing normal data. However, when manipulated data were subjected to Benford’s law analysis, significant deviations from normal data were observed. This demonstrates the power of Benford’s analysis in detecting potentially manipulated data.

Furthermore, in papers [24,25,26,27,28,29,30,31,32], Benford’s law was applied to:

-

determine whether lists of COVID-19 infection numbers, claiming to be measurements of real events or sizes, were manipulated,

-

analyze lightning data and assess the negative effects with precise parameters of lightning in kA unit,

-

detect image forgery during resizing and compression,

-

detect anomalies in the number of publications per researcher and the number of researchers per publication,

-

analyze the distribution of starting letters in novels and similar studies,

-

evaluate the quality of economic data in companies.

Our motivation for performing our experiments in a described way was to incorporate BL deviation detection in electricity theft methods in opposition to the methods presented in other articles and cited in Section 4 of this article. We also wanted to verify the BL deviation detection sensitivity by affecting different amounts of data in the recorded dataset.

After studying these publications, we assumed that Benford’s law can be verified and applied to analyze data in various directions, but it encounters the issue of reduced accuracy when we have insufficient data amount recorded.

Thus, BL is valid for datasets across different science branches, e.g., sociology, geology, mathematics, geography, economy, medicine, electric power enginnering and many others, one of the aims of this article was to experimentally verify the acquired dataset’s suitability for BL tests. The first part of the experimental phase focused on first digit probability distribution. We found that the acquired datasets comply with BL distribution as shown in graphs and tables with experimental results. It is the task of future studies to extend the experiments for datasets from smart electrometers in larger areas and acquired during longer periods (although presented datasets can be considered as sufficient and relevant).

As a result of the reference survey, we formulated a research gap by the following points:

• using BL for electricity theft detection methods,
• verifying the detection sensitivity by affecting different amounts of the original dataset,
• examining the dataset behavior according to BL by applying different kinds of intervention operations.

The research gap points mirror our contribution in this research field by using the BL electricity theft detection method verified by different simulated intervention operators at different levels of dataset affection.

As stated in [33], one of the basic requirements for datasets to comply with Benford’s Law is the value of the order of magnitude is higher than 3. However, in our experiments, the datasets had this value lower than 3. Despite this fact, the datasets complied with BL in most of our cases. We think that this is an interesting contribution to formerly published facts regarding BL.

However, after we have made a survey of the references available in the world, we have realized that there are only a few articles dealing with datasets acquired in electricity distribution networks. So, we had only limited possibilities to make comparisons with other study cases in this scientific field.

In addition, due to the amount of recorded data, it was impossible to do perform experiments for method sensitivity testing by choosing more levels of affected data amount.

In our article, we first take a look at the basic theory behind the BL with some limitations for datasets under examination and operations used for theft simulation and dataset intervention in general; then, we describe the BL usage in electric power engineering. In Section 5, we describe our experimental datasets; in Section 6, our experimental method is presented. Section 7 presents the results from experimental calculations in tabular and graphical ways. Section 8 and Section 9 include our discussion regarding the presented results and some conclusions.

2. The Theory behind Benford’s Law

Simon Newcomb first observed the effects of BL in 1881; however, Frank Benford reinvented and published the BL effects in 1938. Benford elaborated this statistical law in more depth, and he named it “Law of Anomalous Numbers”. Newcomb and Benford discovered this law by observing the wear and tear of logarithmic, square root, and trigonometric table letter pages, where the first pages were worn much more than the latter ones. (assuming the first pages in these tables contained numbers beginning with digits 1, 2, …, etc. digit), i.e., the users of these tables searched corresponding information mostly on first pages [1,9].

Because of these observations, a first significant digit probability can be constructed. Benford also observed various datasets and their behavior. He found a few dataset properties, which made the dataset best suited according to BL.

Intuitively, the probability that the numbers begin with a significant digit is equal for all (decimal) digits. However, a large number of datasets fulfilling requirements described later in this section have this probability unequal, and this probability distribution follows BL; the probability is skewed towards smaller digits.

First, we have to define the term “significant number” [17]: every real number excluding zero and denoting it as x, the first significant decimal number of the real number x, denoted as D₁(x), is the unique integer j ∈ {1, 2, …, 9} satisfying conditions [1]

10^kj ≤ |x| < 10^k(j + 1)

(1)

for some (unique) k ∈ Z. Additionally, for every number m ≥ 2, m ∈ N, the m-th significant decimal digit of x is denoted as D_m(x). Ths is defined inductively as a unique integer number j ∈ {0, 1, …, 9} in the following formula [1]:

$${10}^{\mathrm{k}}\left({\sum }_{\mathrm{i}=1}^{\mathrm{m}-1}{\mathrm{D}}_{\mathrm{i}}\left(\mathrm{x}\right){10}^{\mathrm{m}-1}+\mathrm{j}\right)\le \left|\mathrm{x}\right|<{10}^{\mathrm{k}}\left({\sum }_{\mathrm{i}=1}^{\mathrm{m}-1}{\mathrm{D}}_{\mathrm{i}}\left(\mathrm{x}\right){10}^{\mathrm{m}-1}+\mathrm{j}+1\right)$$

(2)

for some unique number k ∈ Z; for convenience, D_m(0): = 0 for all m ∈ N. By definition, the first significant digit D₁(x) of x! = 0 is never zero. However, when considering the second, third, fourth and so on, these significant digits may be any integers including zeros, i.e., they are defined by the set of {0, 1, …, 9} decimal numbers.

Benford’s law is a statistical law describing what is the probability that a specific digit becomes the first significant digit of the number from a dataset. However, the dataset that follows BL must fulfill the following basic requirements:

• The dataset must not be radically restricted in value range (e.g., the dataset of people’s height or IQ is a radical restriction because of a very small range of possible values).
• The dataset must not be influenced by any kind of artificial effects caused by human actions aiming to change the values intentionally.
• The value range in the dataset must be large enough, e.g., [14]:

F_diff > 3, according to F_diff = log(max) − log(min)

(3)

where max and min stand for maximal and minimal dataset values, respectively.

4.

The dataset should be large enough.

The Formula (2) describes the calculation of the first significant digit probability according to BL [14]:

F_d = log₁₀(d + 1/d)

(4)

where F_d is the probability value. (In the case of decimal numbers, we have to use decimal logarithm), and

d ∈ D = (1, 2… 9)

(5)

Then, for digit 1:

F₁ = log₁₀(1 + 1/1) = 0.30103

(6)

i.e., the probability that the decimal digit 1 is the first significant digit in approximately 30,103% of cases. The sum of all probabilities is 1, i.e., 100% probability for all decimal digits d ∈ D = (1, 2… 9), the digit 0 cannot be the first significant digit, and dataset samples having the value 0 (e.g., 0 or 0.000) are excluded from the dataset because they do not contain a significant digit.

From calculations, we can observe a descending trend of the probability.

The probability distribution mentioned above is valid for decimal number systems; however, BL is not restricted to this system, and it is also applicable for other numeric systems, e.g., octal or hexadecimal numeric systems. Then, we can write the first significant digit probability equation in more general form, assuming that the difference between 2 logarithms equals to the logarithm of the ratio:

F_d = log_n(d + 1) − log_n(d)

(7)

where d denotes a particular digit from a particular numeric system, and n denotes the particular numeric system.

3. Other Observations Regarding Benford’s Law and Operations Performed on Datasets Following This Law

The mathematical operations performed on the datasets can be divided into two groups: operations that do not break the BL validity on a dataset and operations that do break this validity.

• Conversion from one numeric system into another (base-invariance) means only changing the base of the logarithm.
• Scale invariance means that the significant digit distribution should be invariant under changes of scale and thus must comply with Benford distribution according to the following definition:

  -

  A probability measure P on (R+, A) with A ⊃ S has scale-invariant significant digits if and only if P(A) = B(A) for every A ∈ S, i.e., if and only if P follows Benford’s law (proof can be found in [17]).

• Furthermore, the sum-invariance term says that the first digit probability distribution has sum-invariant digits if, in a set of numbers with that distribution, the sums of all entries with the first digit 1 has the same value as each other of the sums for all entries with the remaining first digits. For example, the sum of all the entries with the first two significant digits 1 and 3, respectively, has the same value as the sum of all remaining entries with any other combination of the first two significant digits, etc.

By definition, a random variable X has sum-invariant significant digits if, for every m ∈ N, the value of Exact sum-invariance ESd₁, …, d_m(X) is independent of d₁, …, d_m [1,15].

4. Benford Law in Electric Power Engineering

Electricity theft is one of the major contributors to non-technical losses in distribution networks. When this network fulfills the parameters of a smart network, smart electrometers are used for measuring electricity consumption at different points and distribution levels. These smart electrometers are installed not only at the customer’s site but also at higher network levels. From such a network, data can be obtained at different points, and we can obtain an overall image of electricity consumption and losses at a particular locality. However, in the case of traditional networks without smart devices, it is much harder to detect electricity theft. The customer data is also an important issue in this case. Therefore, BL is a promising option for electricity theft detection.

Another typical utilization of BL is electricity consumption prediction and monitoring. Some outer objective factors can influence BL distribution in particular time intervals, e.g., weather, holidays, working schedule during the day, etc. BL can help detect the irregularities in standard prediction of electricity consumption, problems in monitoring. As BL results from mathematical statistics, it can help to predict and future consumption in order to improve planning and managements of electricity production. [2].

BL can also monitor the electricity production process and check the stability or dropouts during these processes. Comparing actual production with expected BL distribution, the electricity production companies can identify places where analysis and data acquisition improvement are needed. This contributes to minimizing energy loss [2].

However, there are a few restrictions using BL in electric power engineering [2,5,11]:

• Small data sets—In case we have only small data sets as the input of the comparison, these data sets are not statistically significant,
• Specific data distribution—BL distribution can fail in cases when the first digits of the data are symmetrically distributed around zero, or the first digit probability is distributed evenly by the nature of the data,
• Data manipulation—This manipulation can be considered natural, and usually, it is introduced by companies intentionally in order to fulfill specific production or distribution process requirements,
• Deviations from normal processes—In case of irregular and exceptional situations, e.g., electricity supply dropouts, the dataset is influenced.

These restrictions have to be considered when using BL in electric power engineering.

In fact, there are only a few articles dealing with datasets acquired in electricity distribution networks, so we had only limited possibility to compare our methods with methods published so far. There are a few references dealing with other types of datasets, but due to some special aspects of the data from the distribution network (e.g., seasonal character of electricity consumption, electricity theft performed physically or by changing the data after acquisition), the methods in these references cannot be directly compared.

In [34], the theft of electricity detection method was presented based on the electricity network model. Our experiments do not assume any special electricity distribution model because we tried to make our method more general and not related to any grid model or grid extent.

In [33], a novel method for electricity theft is presented based on three three-phase state estimators based on phasor measurement units. This requires extensive changes in the distribution grid. However, the authors do not assume the usage of BL, which does not require any changes in the grid at all.

In [35], a theft detection method is presented, which uses comprehensive features in time and frequency domains with deep neural network-based classification. Again, the BL is not assumed by the authors.

As stated above, approaches including the BL method presented in our paper do not assume any physical changes in the electricity distribution grid nor assume any special measures before data recording because the dataset is ready to use for this method already in the phase of the electricity consumption billing.

In our references survey, we did not encounter any paper dealing with BL deviation experiments by affecting different amounts of the data in the original dataset. We did not find any reference making similar intervention operation tests as we did.

5. Dataset for Our Experiments

Let us summarize the requirements for dataset collection for which first digit probability distribution should follow BL distribution [15,16,17]:

• The data in the dataset must come from the same situation/effect or should describe the same parameter,
• There should be no limits on minimum and maximum values,
• The dataset should be statistically random; the data must not be generated according to pre-defined rules or equations (serial or telephone number, any identification numbers, etc.),
• The dataset should include smaller than bigger values, the mean value should be smaller than the median, and the dataset should have positive skewness,
• The values in the dataset should be on the same scale,
• The values should have at least two orders.

In our experiments, we have collected a dataset of electricity consumption values in cooperation with a local electricity distribution company in east Slovakia-Východoslovenská distribučná a.s. The measuring points were placed in the Košice–Pereš locality, in the low-voltage distribution grid. We have used 48 “smart”.

The values were measured remotely and stored in a local database on the server. The measurements were made in the time range from 1 January 2021 0:15:00 until 1 April 2022 0:00:00, while the data were measured and stored each 15 min. The overall number of measured and stored values in our experimental dataset is 43,676.

Each record in the database has the same attributes: the date and time of the data acquisition, the place of the electrometer (a node in the distribution grid), the consumption value, and the identification number of the electrometer.

The original datasets came from real-world measurements and were recorded during normal electricity distribution grid operation. As the dataset owner stated, the electricity theft in this part of the grid during the acquisition period was very unlike due to the measures that the company made in the last years. This was also the reason why we chose this locality for our experimental data acquisition. The data deviation due to electricity theft is hard to characterize in a general way, especially when the theft is made by a physical attack on the distribution grid. These events can have very random characters and affect different amounts of data in a dataset. However, we assume that the illegally connected electricity consumption node behaves in a non-natural way. When we assume a non-physical attack to the grid made by accounting data falsification, this causes the injection of non-natural dataset parts into the original dataset. This is, of course, the target case for BL.

We assumed the original dataset affection at different magnitudes to better model real-world electricity theft cases and also due to the comparison with different affection magnitude levels.

6. The Methods Used in Our Experiment

One part of the experiments focused on BL deviation detection sensitivity. Therefore, we have chosen different levels of false data injection magnitude into the original dataset. By assumption, a higher magnitude of the injection should cause higher values of the first digit probability deviation compared to theoretical values of BL.

In addition, in the real world, the magnitude of a dataset attack is unknown and cannot be predicted, though it can be limited to maximal magnitude. E.g., we do not assume 100% of affected values in the dataset. We decided to choose relatively evenly distributed levels of data affection magnitude to cover the whole magnitude spectrum.

We have prepared a validation method for BL distribution for first digit probability in the dataset and for the violation of this distribution due to artificial intervention simulated by the following operations:

• Adding +1 to dataset values,
• Division of the dataset values by 2,
• Multiplication of the dataset value by 2.

In addition, supplementary violation operations were performed on the dataset, where:

• 75% of the overall dataset values were affected (32,757 values were replaced by pseudo-random numbers),
• 50% of the overall dataset values were affected (21,838 values were replaced by pseudo-random numbers),
• 25% of the overall dataset values were affected (10,919 values were replaced by pseudo-random numbers),
• and 10% of the overall dataset values were affected (4367 values were replaced by pseudo-random numbers).

Before performing the violation operations, we multiplied all the values in the dataset by 1000 to perform data scaling and in order to obtain all the values greater than 1. BL distribution is not affected by scaling operation.

Modeling errors have various aspects in our experiments. First, there are errors influencing the grid from which we acquired the original dataset. This error can be divided into several parts:

• Environmental and social errors, which means that the dataset can be influenced by seasonal factors, e.g., weather in general, outside temperature, etc., and the social behavior of electricity consumers. All these aspects of course change the original dataset in unnatural way, causing its corruption and deviation from BL distribution. This aspect was significantly canceled by proper selection of data recording interval.
• Data quality includes measurement accuracy and completeness.
• A single recording method can be another source of inaccuracies in data values.

Then, the simulation of false data can introduce further errors in the experimental results. We have tried to partially avoid this by choosing different levels and kinds of original data intervention.

In summary, we can draw the following methodology flowchart (Figure 1):

The methodology flowchart above begins with electricity consumption value acquisition from smart electrometers. Then, the original dataset BL distribution calculation is performed and we obtain the deviations of probabilities. For considering the particular dataset as capable of further experiments, the deviations in this step must as minimal as possible, otherwise the dataset does not follow BL distribution. The original dataset is affected by particular simulated intervention operations at different dataset amounts. As a result, we obtain again the BL distribution deviations. In the last step we compare the unaffected and affected dataset deviation from BL distribution. High values of these differences are markers of successful simulated intervention detection, i.e., (a) the intervention simulation model is detectable by BL, (b) the dataset and similar dataset types naturally follow BL distribution, (c) BL can be used for false data detection for such kind of datasets.

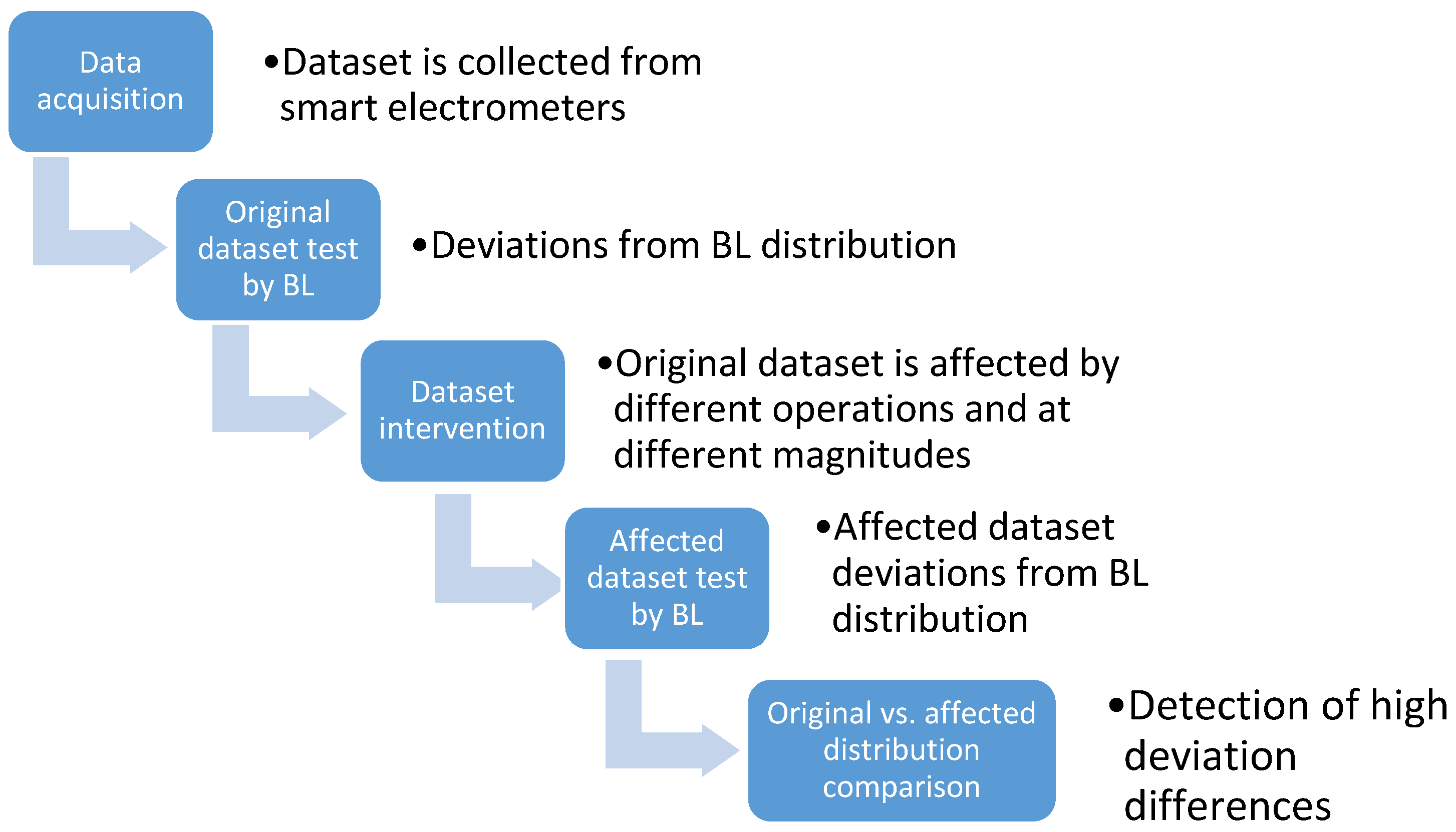
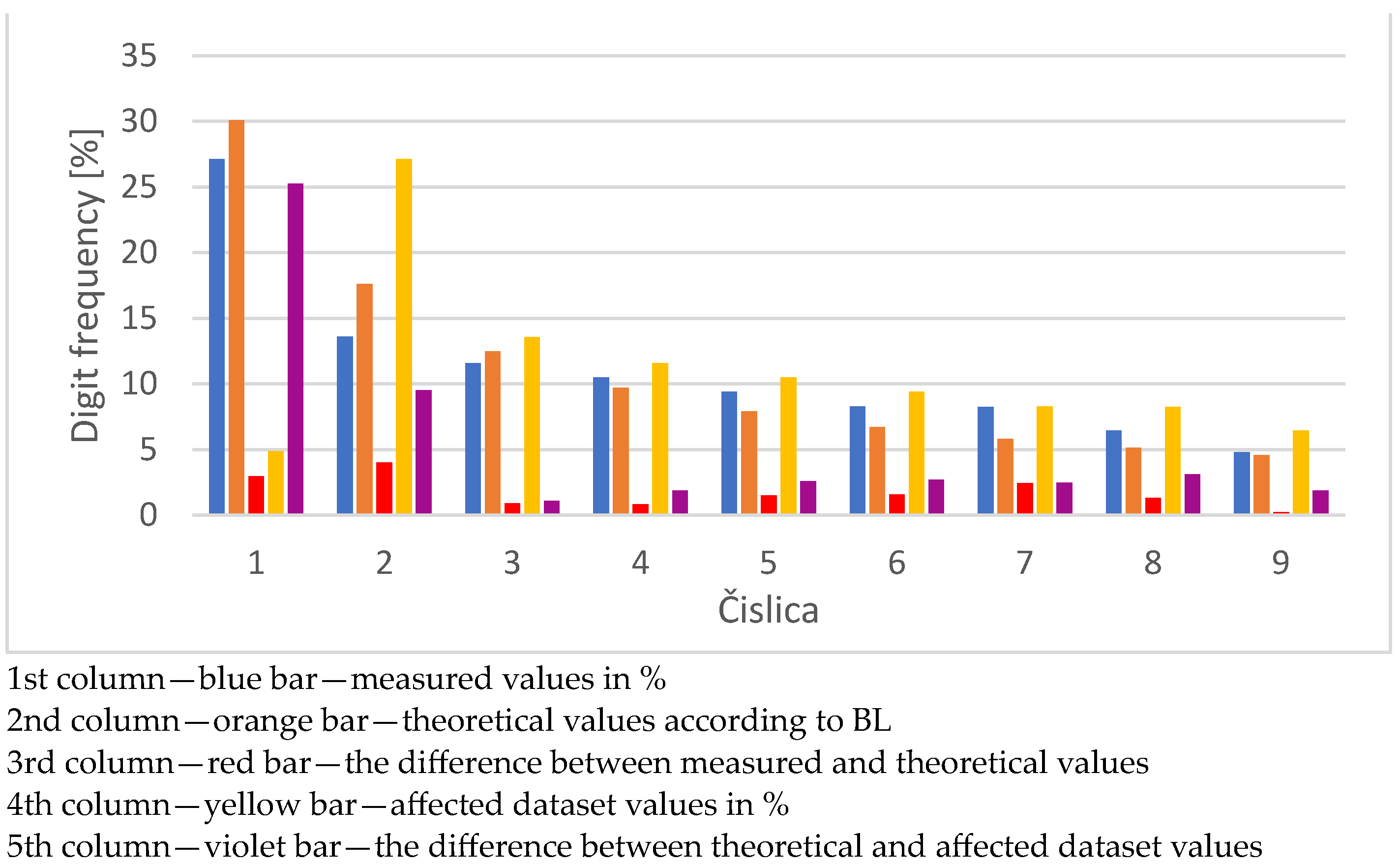
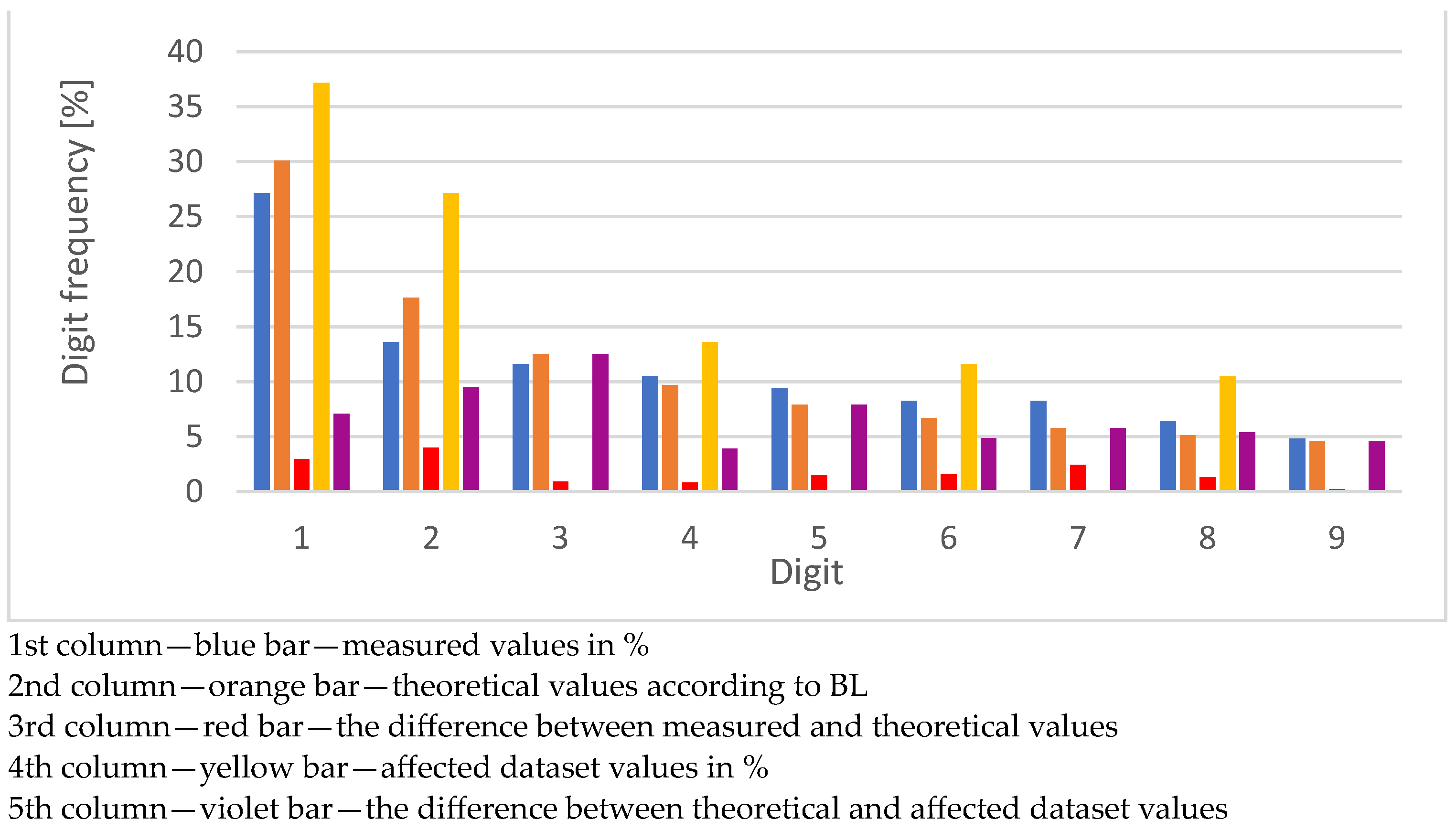
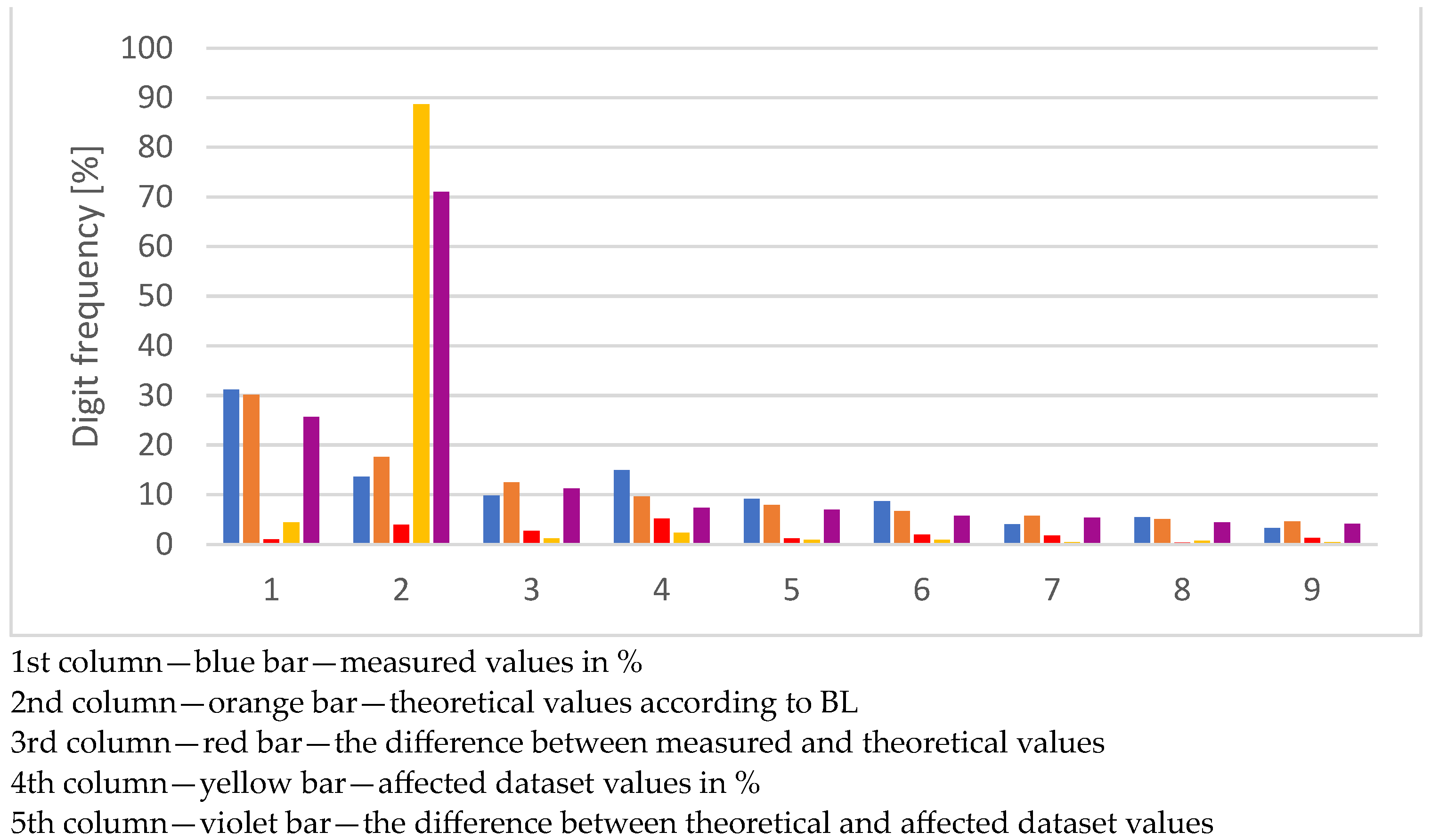
7. The Results of the Experiments

The following figures and tables demonstrate the results of our experimental calculations of the first digit probability distribution according to BL and affected probability distribution as described above. Each graph (figure) and table pair show the results for five different electrometers, i.e., five different nodes in the electricity distribution grid in combination with the above-described different dataset violation operations. Appropriate node and operation combination describes the caption of the figure and the table and the accompanying description.

7.1. Violation Operation–Division by Two

This section shows the results for the violation operation–two divide the whole dataset of values.

Table 1. Node No. 1 without and with violation operations.

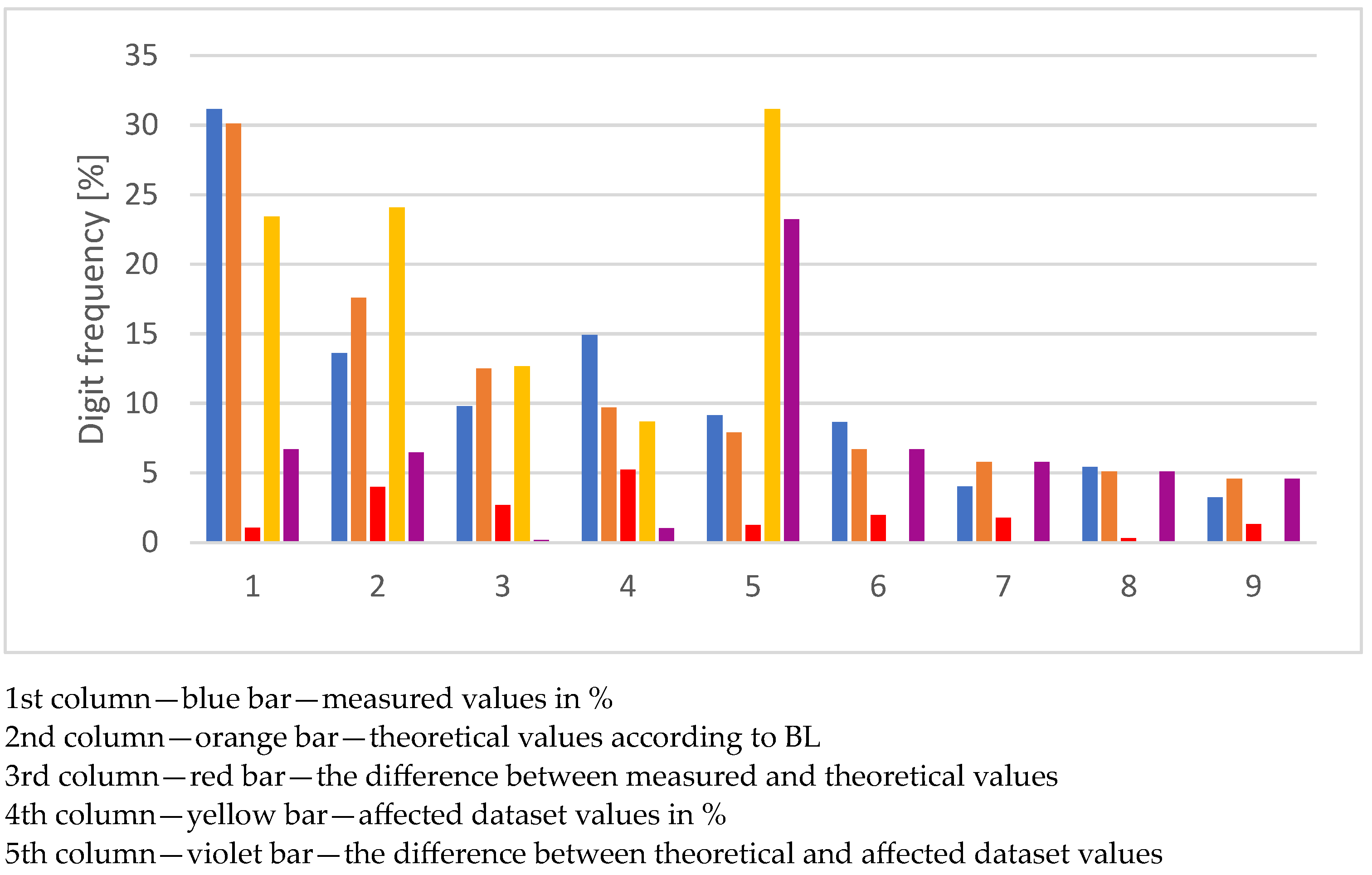
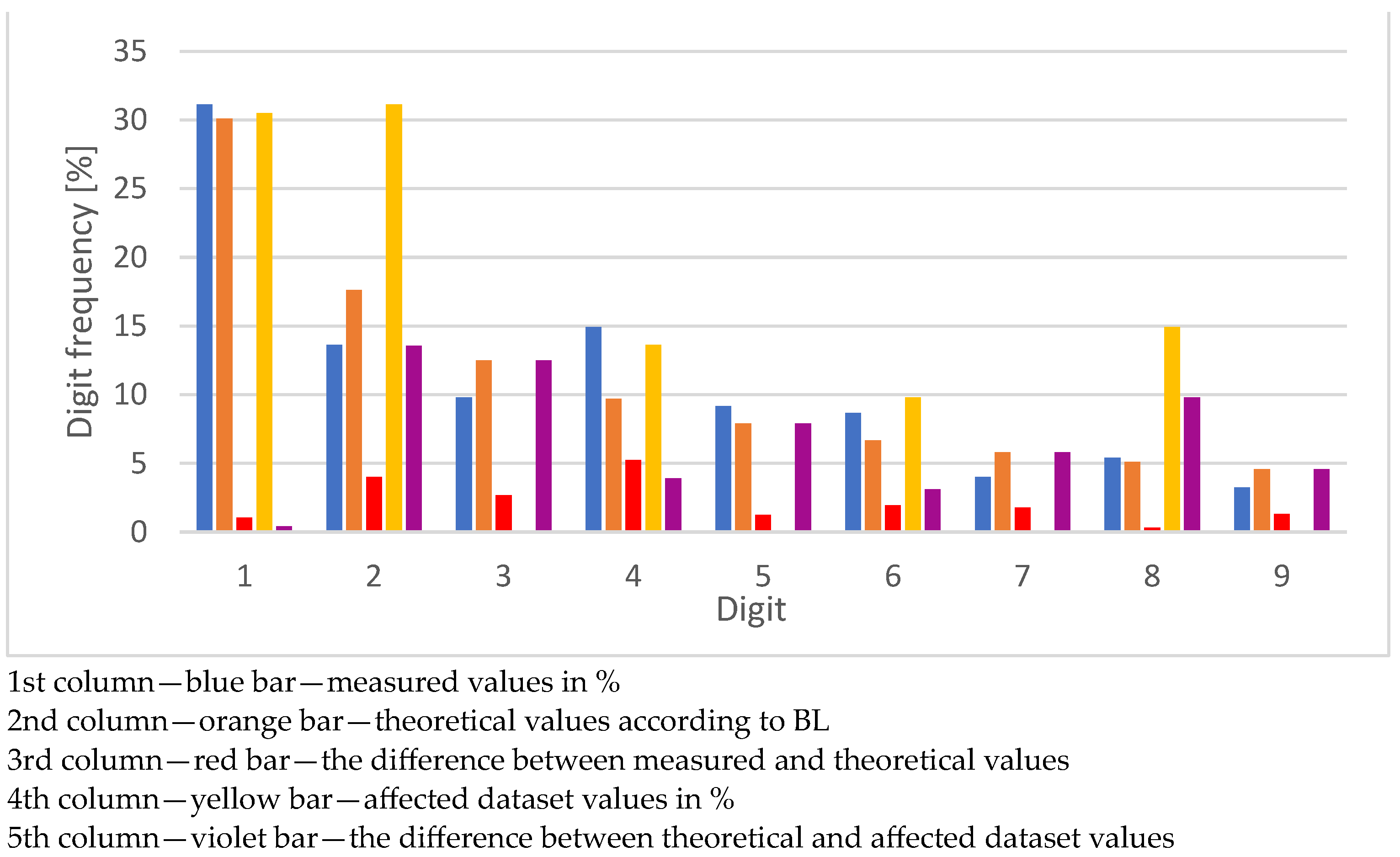
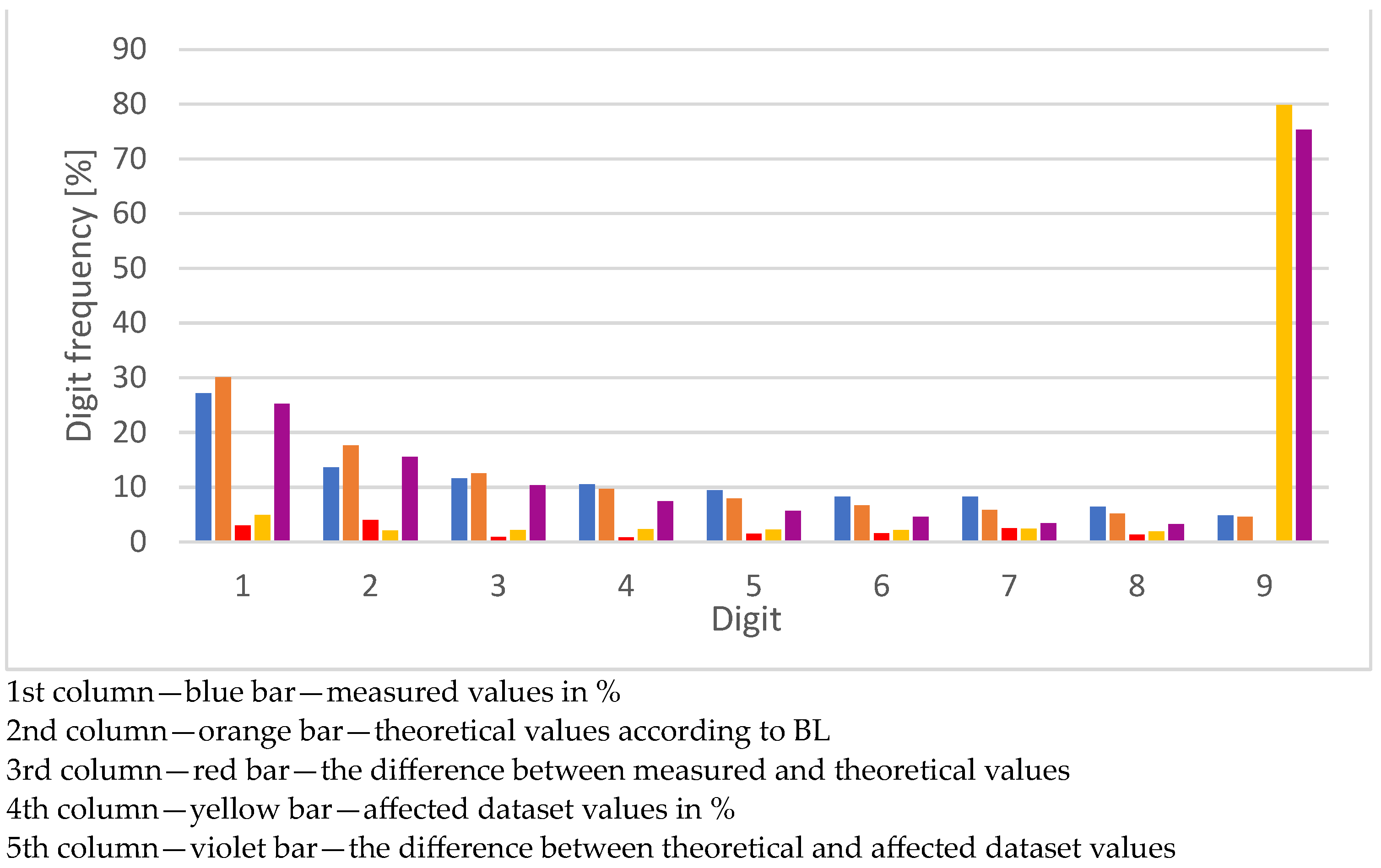
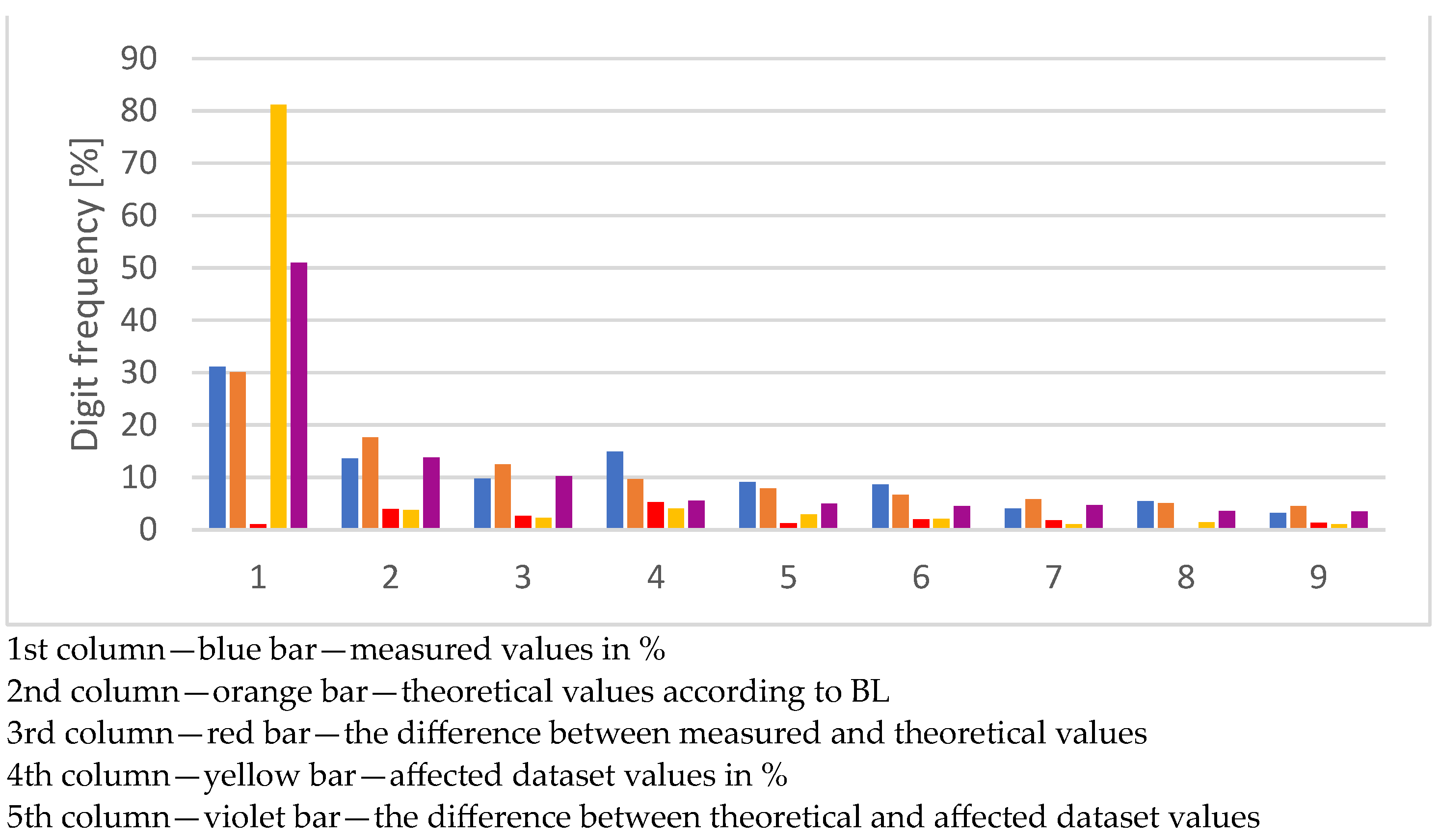
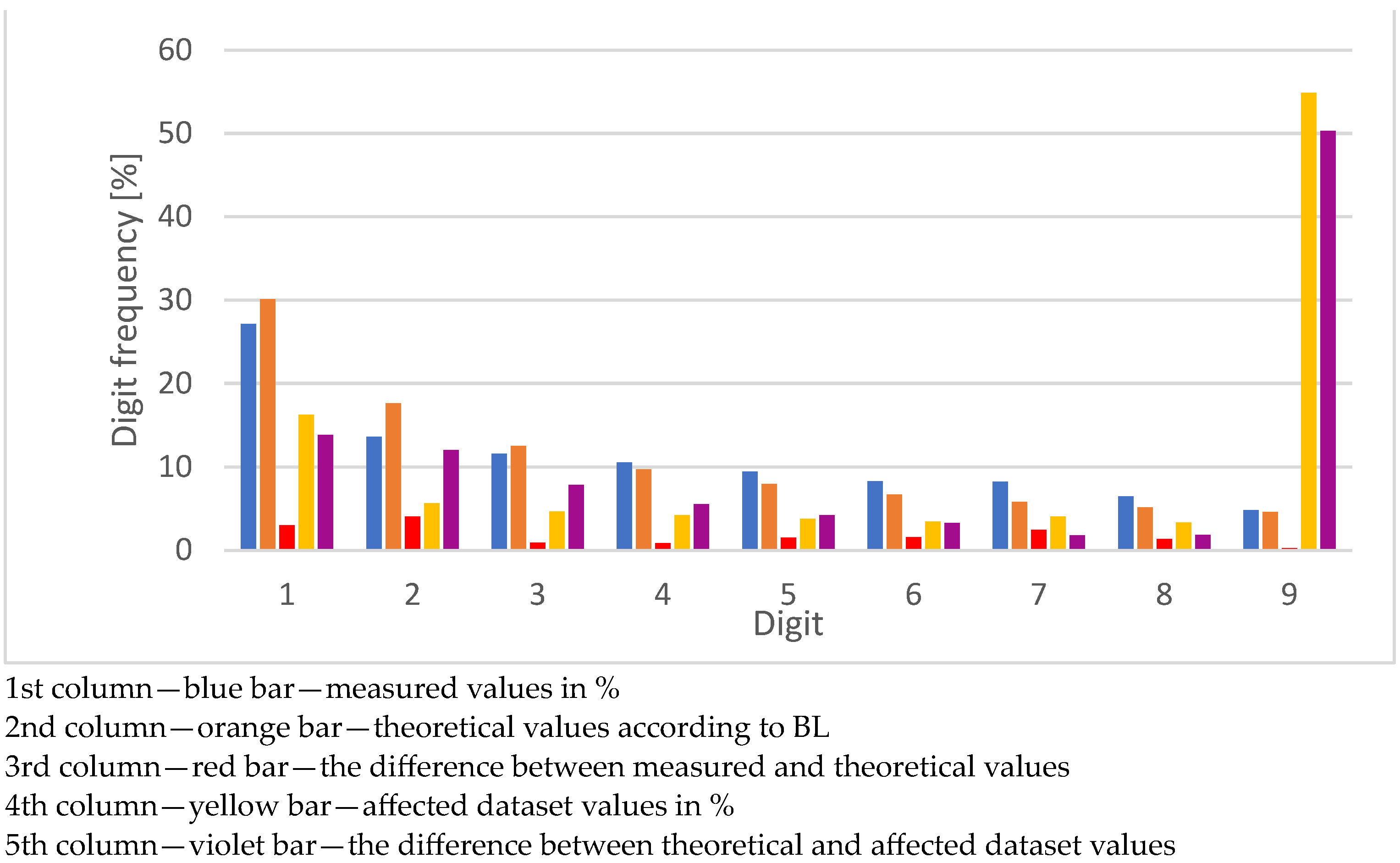
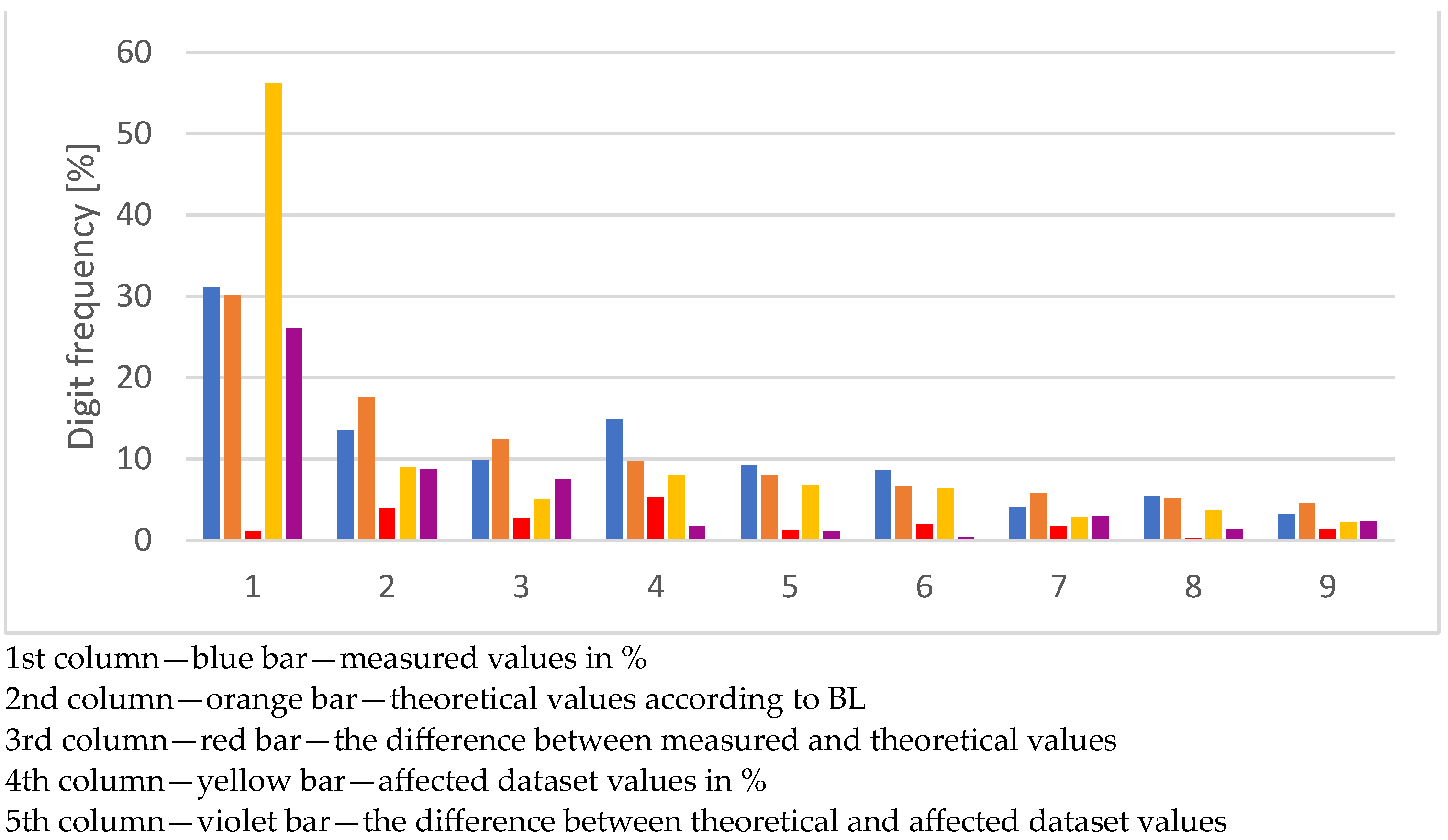
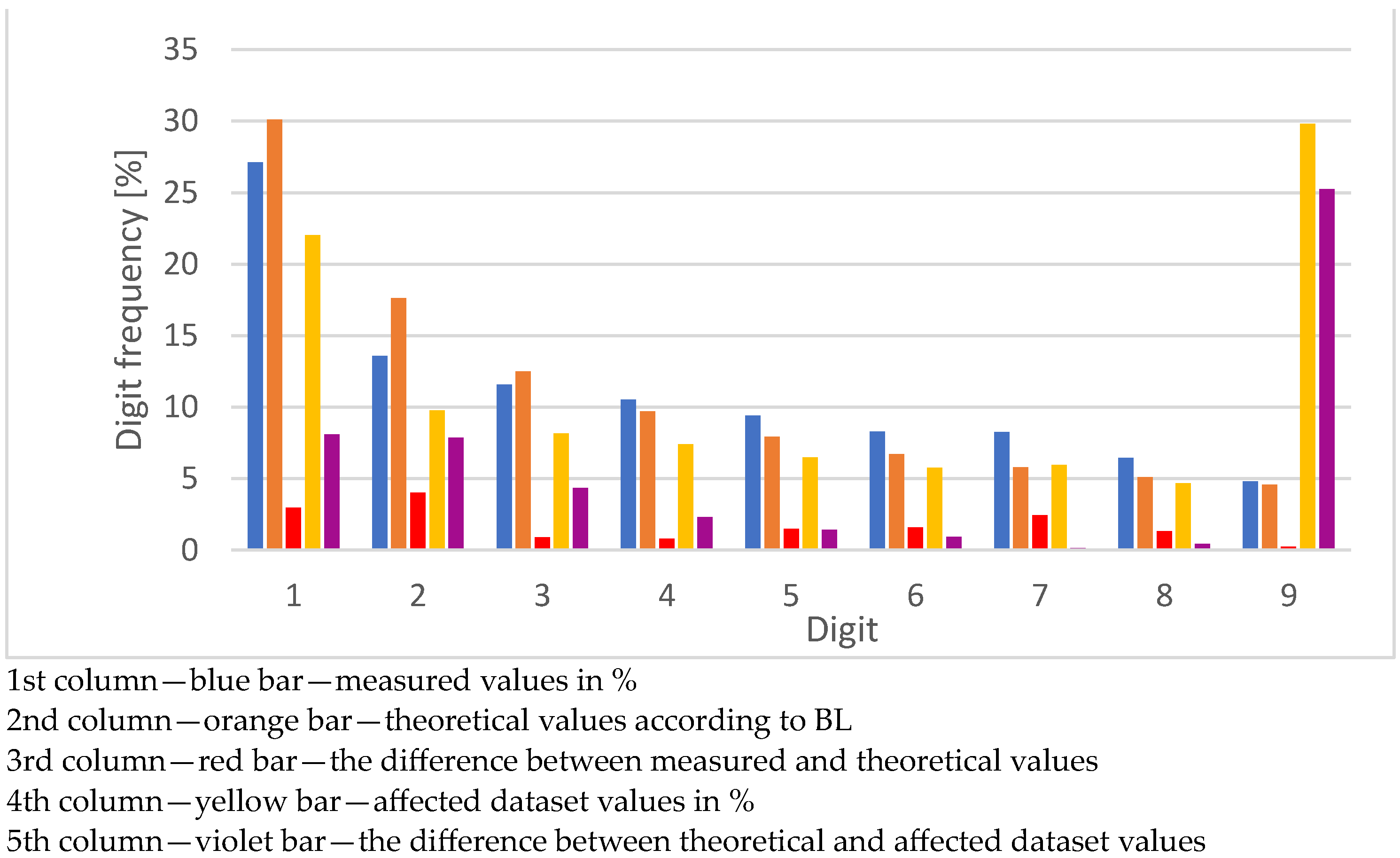
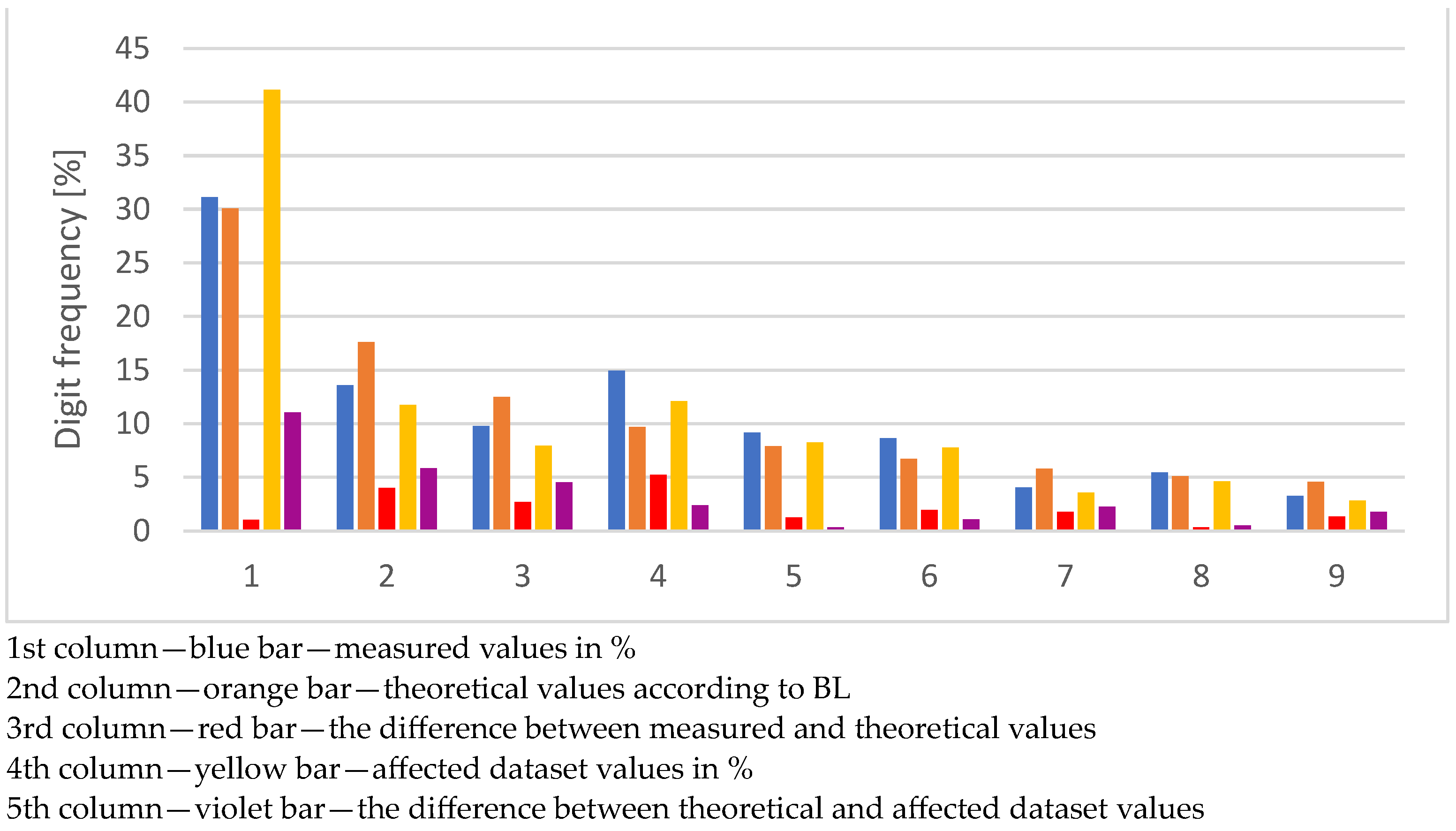
Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	23.4075	6.6955
2	5943	13.6076	17.6091	4.0015	24.0830	6.4739
3	4280	9.7999	12.4939	2.6940	12.6826	0.1887
4	6518	14.9242	9.6910	5.2332	8.6756	1.0154
5	4000	9.1588	7.9181	1.2406	31.1513	23.2331
6	3780	8.6550	6.6947	1.9604	0.0000	6.6947
7	1759	4.0276	5.7992	1.7716	0.0000	5.7992
8	2370	5.4266	5.1153	0.3113	0.0000	5.1153
9	1419	3.2491	4.5757	1.3267	0.0000	4.5757

and

Table 2. Node No. 2 without and with violation operations.

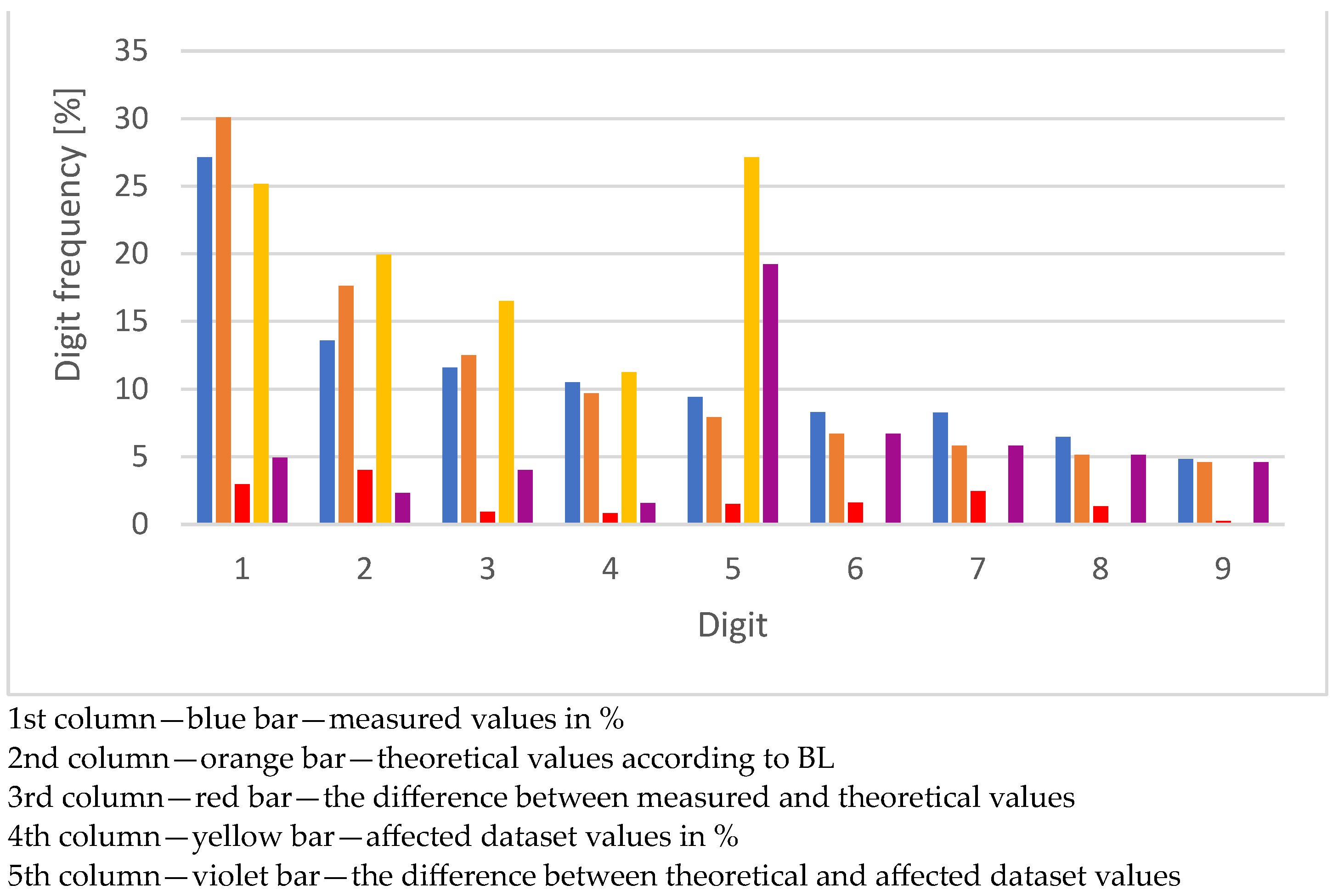
Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	4.8585	25.2445
2	5932	13.5884	17.6091	4.0208	27.1247	9.5156
3	5054	11.5771	12.4939	0.9167	13.5818	1.0880
4	4587	10.5074	9.6910	0.8164	11.5716	1.8806
5	4108	9.4101	7.9181	1.4920	10.5023	2.5842
6	3614	8.2785	6.6947	1.5839	9.4056	2.7109
7	3598	8.2419	5.7992	2.4427	25.1655	4.9375
8	2814	6.4460	5.1153	1.3307	19.9175	2.3084
9	2101	4.8127	4.5757	0.2370	16.5204	4.0266

and Figure 2 and Figure 3 show the results of the experiment in tabular and graphical form. The 1st column and the x-axis in the graph represent the first significant digit under examination. The 2nd columns represent the number of samples in the dataset with the corresponding first significant digit. The 3rd column and the blue bar in the graph represent the same number of values in the dataset expressed in percentage. We have inserted also 4th column and orange as the theoretical values of the probability distribution according to the BL. To make comparison possible, we have calculated the difference between theoretical and calculated distribution (5th columns and the red bar) expressed in percentage. This column values show the suitability of the input dataset for the verification experiment, because the lower the values in this column, the more the input dataset follows the BL probability distribution. If the values were too high, the input dataset does not fulfill the requirements for BL datasets.

The 6th column and yellow bar represent values for probability distribution after violation operation in percentage. This column indicates the violation operation effect, which is also expressed in the last tabular column and violet bar.

High values in these last two columns (violation indicator columns) indicate the presence of the violation in comparison to the original unaffected dataset.

As we can see, the violation indication columns include relatively high differences, especially for the fifth digit. We can consider this as the original dataset violation marker.

In

Table 3. Nodes No. 3, No. 4, and No. 5—the difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	3.3158	1.8701	1.8937
2	7.3884	0.8683	7.4681
3	5.7579	8.3941	0.6547
4	2.5972	2.1109	0.6062
5	29.4182	29.4699	16.5620
6	6.6947	6.6947	6.6947
7	5.7992	5.7992	5.7992
8	5.1153	5.1153	5.1153
9	4.5757	4.5757	4.5757

and Figure 4, we can see the dataset violation markers, e.g., for digit 5.

As for measuring node No. 1 in the electricity distribution network, the original dataset values follow the BL first digit probability distribution according to the theoretical probability distribution. The highest deviations are 4–5% for digits 2 and 4.

We can say that for node No. 2, the original dataset values also follow the BL first digit probability distribution according to the theoretical probability distribution. The highest deviations are 2–4% for digits 1, 2 and 7.

However, despite these deviations, we can consider the dataset from both nodes as capable of fraud detection by BL because of quite a good match of the probability distribution to the theoretical distribution values.

In Table 3, the experimental results for the other three nodes can be found; however, we have aggregated these results in one table. The differences between theoretical probability distribution values and measured original dataset value first digit probability distribution values were slightly higher than for nodes No. 1 and No. 2. The particular differences were up to 7%. For none of our dataset values, however, this difference was higher than 10%.

7.2. Violation Operation–Adding Integer Number to the Dataset Values

This section shows the results for the violation operation–adding an integer number (in our case, adding one value) to the whole dataset.

In

Table 4. Node No. 1 without and with violation operations.

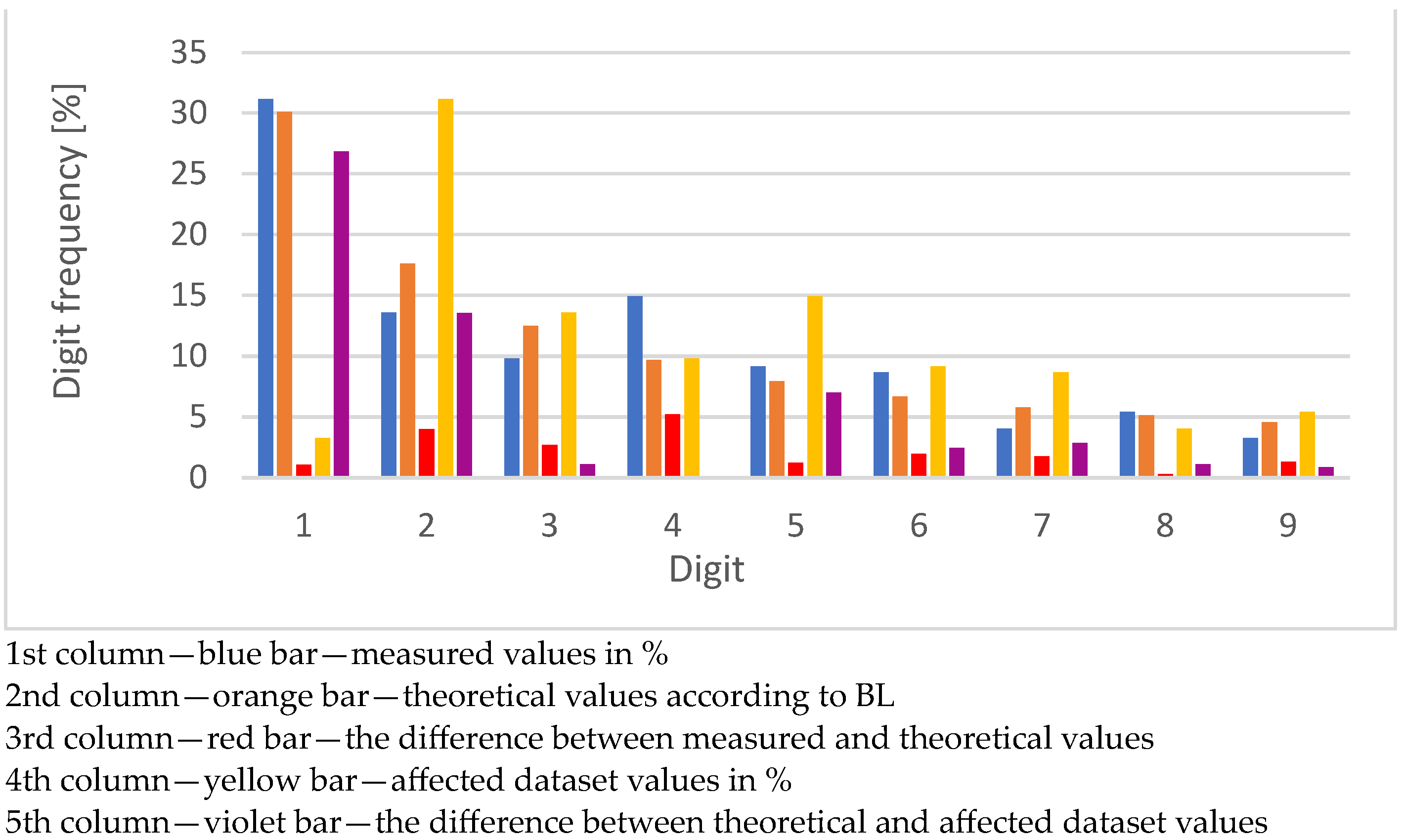
Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	3.2535	26.8495
2	5943	13.6076	17.6091	4.0015	31.1498	13.5407
3	4280	9.7999	12.4939	2.6940	13.6070	1.1131
4	6518	14.9242	9.6910	5.2332	9.7994	0.1084
5	4000	9.1588	7.9181	1.2406	14.9235	7.0054
6	3780	8.6550	6.6947	1.9604	9.1583	2.4637
7	1759	4.0276	5.7992	1.7716	8.6546	2.8554
8	2370	5.4266	5.1153	0.3113	4.0274	1.0879
9	1419	3.2491	4.5757	1.3267	5.4263	0.8506

and Figure 4, we can see the results for measuring node No. 1.

In

Table 5. Node No. 2 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	4.8585	25.2445
2	5932	13.5884	17.6091	4.0208	27.1247	9.5156
3	5054	11.5771	12.4939	0.9167	13.5818	1.0880
4	4587	10.5074	9.6910	0.8164	11.5716	1.8806
5	4108	9.4101	7.9181	1.4920	10.5023	2.5842
6	3614	8.2785	6.6947	1.5839	9.4056	2.7109
7	3598	8.2419	5.7992	2.4427	8.2746	2.4754
8	2814	6.4460	5.1153	1.3307	8.2379	3.1227
9	2101	4.8127	4.5757	0.2370	6.4429	1.8671

and Figure 5, node No. 2 results are depicted.

Table 4 and Table 5 and Figure 4 and Figure 5 show the results of the experiment for adding integer value one to the whole original dataset. The columns in the table and graph follow the same meaning as described in Section 7.1. High values in these last two columns (violation indicator columns) indicate the presence of the violation in comparison to the original unaffected dataset.

As we can see, the violation indication columns include relatively high differences, especially for lower digits as one or two. We can consider this as the original dataset violation marker.

In

Table 6. Nodes No. 3, No. 4, and No. 5—difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	27.6509	28.2553	25.5353
2	19.7272	19.7455	6.5140
3	11.8925	6.0953	4.5017
4	0.6586	0.0724	1.1113
5	0.9921	7.7999	9.1095
6	3.4000	3.9518	0.9892
7	1.5886	3.2600	2.2304
8	2.5898	3.5583	0.1881
9	5.2603	5.4572	1.2673

, we can see aggregated violation operation results for nodes 3, 4, and 5. Again, the difference in the probability distribution compared to the BL can be seen, especially for lower digits, so we can reliably identify the violation markers.

7.3. Violation Operation–Multiplying the Dataset Values by Integer Number

This section represents the results in the case of multiplication of the dataset values by integer number. All the values in the dataset are affected. The

Table 7. Node No. 1 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	30.517	0.414
2	5943	13.6076	17.6091	4.0015	31.151	13.542
3	4280	9.7999	12.4939	2.6940	0.000	12.494
4	6518	14.9242	9.6910	5.2332	13.608	3.917
5	4000	9.1588	7.9181	1.2406	0.000	7.918
6	3780	8.6550	6.6947	1.9604	9.800	3.105
7	1759	4.0276	5.7992	1.7716	0.000	5.799
8	2370	5.4266	5.1153	0.3113	14.924	9.809
9	1419	3.2491	4.5757	1.3267	0.000	4.576

and Figure 6 above show the results for the measuring node No. 1.

Table 7 and

Table 8. Node No. 2 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	37.1893	7.0863
2	5932	13.5884	17.6091	4.0208	27.1378	9.5287
3	5054	11.5771	12.4939	0.9167	0.0000	12.4939
4	4587	10.5074	9.6910	0.8164	13.5884	3.8974
5	4108	9.4101	7.9181	1.4920	0.0000	7.9181
6	3614	8.2785	6.6947	1.5839	11.5771	4.8825
7	3598	8.2419	5.7992	2.4427	0.0000	5.7992
8	2814	6.4460	5.1153	1.3307	10.5074	5.3921
9	2101	4.8127	4.5757	0.2370	0.0000	4.5757

and Figure 6 and Figure 7 show the results of the experiment for multiplying by integer value two the complete original dataset. The columns in the table and graph follow the same meaning as described in Section 7.1. High values in these last two columns (violation indicator columns) indicate the presence of the violation in comparison to the original unaffected dataset.

As we can see, the violation indication columns include relatively high differences, especially for almost all digits except the digit 1. We can consider this as the original dataset violation marker.

In

Table 9. Nodes No. 3, No. 4, and No. 5—difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	27.6509	28.2553	25.5353
2	19.7272	19.7455	6.5140
3	11.8925	6.0953	4.5017
4	0.6586	0.0724	1.1113
5	0.9921	7.7999	9.1095
6	3.4000	3.9518	0.9892
7	1.5886	3.2600	2.2304
8	2.5898	3.5583	0.1881
9	5.2603	5.4572	1.2673

, the experimental results for nodes 3, 4, and 5 can be found. As in previous cases, we can find violation markers especially for lower digits and they correspond to the markers for nodes 1 and 2.

The Table 8 and Figure 7 show the results for the measuring node No. 2.

7.4. Violation Operation–Affection 75% of Dataset Values

This section represents the results when a data violation affects only 75% of the original dataset values. The data violation operation is made by setting the affected values to an integer number; in our case, it was the value of 2.

The

Table 10. Node No. 1 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	4.4120	25.6910
2	5943	13.6076	17.6091	4.0015	88.6070	70.9979
3	4280	9.7999	12.4939	2.6940	1.2364	11.2575
4	6518	14.9242	9.6910	5.2332	2.3331	7.3579
5	4000	9.1588	7.9181	1.2406	0.8952	7.0229
6	3780	8.6550	6.6947	1.9604	0.9364	5.7582
7	1759	4.0276	5.7992	1.7716	0.4236	5.3756
8	2370	5.4266	5.1153	0.3113	0.6983	4.4169
9	1419	3.2491	4.5757	1.3267	0.4579	4.1178

and Figure 8 below show the results for the measuring node No. 1.

In the

Table 11. Node No. 2 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	4.8928	25.2102
2	5932	13.5884	17.6091	4.0208	2.0547	15.5544
3	5054	11.5771	12.4939	0.9167	2.1715	10.3224
4	4587	10.5074	9.6910	0.8164	2.3181	7.3729
5	4108	9.4101	7.9181	1.4920	2.2609	5.6573
6	3614	8.2785	6.6947	1.5839	2.1692	4.5254
7	3598	8.2419	5.7992	2.4427	2.3891	3.4101
8	2814	6.4460	5.1153	1.3307	1.8966	3.2186
9	2101	4.8127	4.5757	0.2370	79.8470	75.2712

and Figure 9, the results for measuring node No. 2 are depicted. In

Table 12. Nodes No. 3, No. 4, and No. 5—difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	22.7603	20.6101	25.4483
2	12.7094	13.9494	14.2320
3	9.8494	10.4716	9.9227
4	7.6441	6.1961	4.2807
5	6.8145	7.1005	6.1391
6	5.3507	5.9229	5.0050
7	5.0253	5.2702	4.6887
8	2.7226	2.6830	3.8171
9	5.2603	5.4572	73.5335

, the aggregated results can be found for nodes 3, 4, and 5.

Table 10 and Table 11 and Figure 8 and Figure 9 show the results of the experiment, which affected the original dataset only partially, which is a first approximation of the real-world case. In this experiment, we have changed 75% of the original dataset values to a fixed integer number 2. However, 75% is a high percentage when talking about fraud, but we have chosen this percentage for comparison reasons. The columns in the table and graph follow the same meaning as described in Section 7.1. The selected integer number for dataset violation operation also explains the high difference between theoretical probability distribution and calculated probability values especially in the case of the 2 digit. This indicates the presence of the violation in comparison to the original unaffected dataset. We can consider this as the original dataset violation marker. However, assuming other value for partial replacement in the original dataset, the high difference markers could shift to these other value/values.

7.5. Violation Operation–Affection 50% of Dataset Values

This section represents the results when a data violation affects only 50% of the original dataset values. The data violation operation is made by setting the affected values to an integer number; in our case, it was the value of 1.

The

Table 13. Node No. 1 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	81.1498	51.0468
2	5943	13.6076	17.6091	4.0015	3.8053	13.8038
3	4280	9.7999	12.4939	2.6940	2.2781	10.2157
4	6518	14.9242	9.6910	5.2332	4.0846	5.6064
5	4000	9.1588	7.9181	1.2406	2.9559	4.9623
6	3780	8.6550	6.6947	1.9604	2.1339	4.5608
7	1759	4.0276	5.7992	1.7716	1.0578	4.7414
8	2370	5.4266	5.1153	0.3113	1.4768	3.6385
9	1419	3.2491	4.5757	1.3267	1.0578	3.5180

and Figure 10 below show the results for measuring node No. 1. Additionally, in the

Table 14. Node No. 2 without and with violation operations.

Digit	Number of values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	16.2501	13.8529
2	5932	13.5884	17.6091	4.0208	5.6053	12.0038
3	5054	11.5771	12.4939	0.9167	4.6455	7.8484
4	4587	10.5074	9.6910	0.8164	4.1805	5.5105
5	4108	9.4101	7.9181	1.4920	3.7430	4.1751
6	3614	8.2785	6.6947	1.5839	3.4315	3.2632
7	3598	8.2419	5.7992	2.4427	4.0133	1.7859
8	2814	6.4460	5.1153	1.3307	3.2940	1.8212
9	2101	4.8127	4.5757	0.2370	54.8368	50.2610

and Figure 11 the results for the measuring node No. 2 are depicted. In

Table 15. Nodes No. 3, No. 4, and No. 5—difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	13.1326	12.3648	17.8697
2	5.4377	9.1112	9.5223
3	7.6193	8.3125	7.5072
4	6.0322	0.6180	0.4777
5	6.2078	6.5136	4.4013
6	4.5951	5.3704	2.8734
7	4.6223	4.9034	3.4798
8	0.2293	0.0243	2.4021
9	47.8764	47.2182	48.5335

, the aggregated results can be found for nodes 3, 4, and 5.

Table 13 and Table 14 and Figure 10 and Figure 11 depict the results of the experiment, which affected the original dataset only partially, which simulates the real-world case (assuming a fraud attempt, the original set would be affected only partially). In this experiment, we have changed 50% of the original dataset values to a fixed integer number 1. We have chosen other integer numbers in order to verify the probability difference shift to a particular digit. The columns in the table and graph follow the same meaning as described in Section 7.1. The selected integer number for dataset violation operation also explains the high difference between theoretical probability distribution and calculated probability values especially in the case of the 1 digit. This indicates the presence of the violation in comparison to the original unaffected dataset. We can consider this as the original dataset violation marker. However, the difference is not as high as in the case when 75% of values have changed.

7.6. Violation Operation–Affection 25% of Dataset Values

This section represents the results when a data violation affects only 25% of the original dataset values. The data violation operation is made by setting the affected values to an integer number; in our case, it was the value of 1.

Table 16. Node No. 1 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	56.1524	26.0494
2	5943	13.6076	17.6091	4.0015	8.9206	8.6885
3	4280	9.7999	12.4939	2.6940	5.0190	7.4749
4	6518	14.9242	9.6910	5.2332	8.0093	1.6817
5	4000	9.1588	7.9181	1.2406	6.7729	1.1452
6	3780	8.6550	6.6947	1.9604	6.3218	0.3728
7	1759	4.0276	5.7992	1.7716	2.8323	2.9668
8	2370	5.4266	5.1153	0.3113	3.7253	1.3899
9	1419	3.2491	4.5757	1.3267	2.2462	2.3296

and

Table 17. Node No. 2 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	22.0250	8.0780
2	5932	13.5884	17.6091	4.0208	9.7492	7.8600
3	5054	11.5771	12.4939	0.9167	8.1549	4.3390
4	4587	10.5074	9.6910	0.8164	7.3852	2.3058
5	4108	9.4101	7.9181	1.4920	6.4826	1.4355
6	3614	8.2785	6.6947	1.5839	5.7611	0.9336
7	3598	8.2419	5.7992	2.4427	5.9375	0.1383
8	2814	6.4460	5.1153	1.3307	4.6799	0.4354
9	2101	4.8127	4.5757	0.2370	29.8248	25.2490

, and Figure 12 and Figure 13 depict the results of the experiment, which affected the original dataset only partially, which simulates the real-world case (assuming a fraud attempt, the original set would be affected only partially). In this experiment, we have changed 25% of the original dataset values to a fixed integer number 1. We have chosen other integer numbers in order to verify the probability difference shift to a particular digit. The columns in the table and graph follow the same meaning as described in Section 7.1. The selected integer number for dataset violation operation also explains the high difference between theoretical probability distribution and calculated probability values especially in the case of the 1 digit. This indicates the presence of the violation in comparison to the original unaffected dataset. We can consider this as the original dataset violation marker. However, the difference is not as high (see

Table 18. Nodes No. 3, No. 4, and No. 5—difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	3.8964	2.3330	11.6512
2	0.4006	5.2549	5.8590
3	5.5656	6.6433	5.1832
4	3.8915	4.1230	3.6184
5	5.2599	5.8075	1.9560
6	3.3679	4.7285	0.0984
7	3.9286	4.6167	1.9344
8	3.4341	3.0544	0.4697
9	22.8764	22.2066	23.5335

) as in the case when 75% of values have changed.

7.7. Violation Operation–Affect Only 10% of Dataset Values

This section represents the results when a data violation affects only 10% of the original dataset values. The data violation operation is made by setting the affected values to an integer number; in our case, it was the value of 1.

Table 19. Node No. 1 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	13,605	31.1513	30.1030	1.0483	41.1503	11.0473
2	5943	13.6076	17.6091	4.0015	11.7690	5.8401
3	4280	9.7999	12.4939	2.6940	7.9521	4.5418
4	6518	14.9242	9.6910	5.2332	12.0942	2.4032
5	4000	9.1588	7.9181	1.2406	8.2658	0.3477
6	3780	8.6550	6.6947	1.9604	7.7781	1.0834
7	1759	4.0276	5.7992	1.7716	3.5536	2.2456
8	2370	5.4266	5.1153	0.3113	4.6252	0.4901
9	1419	3.2491	4.5757	1.3267	2.8117	1.7640

and

Table 20. Node No. 2 without and with violation operations.

Digit	Number of Values	Number of Values in %	BL	Delta %	Violation %	Violation Delta %
1	11,847	27.1378	30.1030	2.9652	24.9364	5.1666
2	5932	13.5884	17.6091	4.0208	11.7856	5.8235
3	5054	11.5771	12.4939	0.9167	10.2760	2.2178
4	4587	10.5074	9.6910	0.8164	9.3643	0.3267
5	4108	9.4101	7.9181	1.4920	8.2671	0.3490
6	3614	8.2785	6.6947	1.5839	7.3966	0.7020
7	3598	8.2419	5.7992	2.4427	7.4058	1.6066
8	2814	6.4460	5.1153	1.3307	5.7519	0.6367
9	2101	4.8127	4.5757	0.2370	14.8162	10.2404

and Figure 14 and Figure 15 depict the results of the experiment, which affected the original dataset only partially, which simulates the real-world case (assuming a fraud attempt, the original set would be affected only partially). In this experiment, we have changed 10% of the original dataset values to a fixed integer number 1. We have chosen other integer numbers in order to verify the probability difference shift to a particular digit. The columns in the table and graph follow the same meaning as described in Section 7.1. The selected integer number for dataset violation operation also explains the high difference between theoretical probability distribution and calculated probability values especially in the case of the 1 digit. This indicates the presence of the violation in comparison to the original unaffected dataset (see

Table 21. Nodes No. 3, No. 4, and No. 5—difference between original and affected dataset.

Digit	Node. No. 3 Violation Delta %	Node. No. 4 Violation Delta %	Node. No. 5 Violation Delta %
1	3.1670	2.8851	8.6377
2	4.3526	1.3317	2.5374
3	4.4414	3.9575	2.6322
4	3.4656	5.2436	6.1621
5	4.9760	5.3859	0.6718
6	2.9375	4.3022	0.8825
7	3.5806	4.3234	1.3039
8	4.0065	3.9802	0.1569
9	7.8750	7.1918	8.5815

). We can consider this as the original dataset violation marker. However, the difference is not as high as in the case when 75% of values have changed.

The raw measured data from electrometers are subject to secrecy due to the legal reasons valid in the Slovak Republic. In addition, the datasets are huge (they have a magnitude of more than 40,000 data samples for each of the 10 nodes under examination), and it is not possible to share the data even from one node acquired during one measurement time interval in such a limited extent within the article. However, we can provide an anonymized sample of these data in the table below—

Table 22. Anonymized sample of the raw power consumption data in node No. 1—a distributing transformer 22/0.4 kV.

Timestamp	Power [kW]
1 January 2021 00:15:00	142.800
1 January 2021 00:30:00	150.400
1 January 2021 00:45:00	146.000
1 January 2021 01:00:00	129.600
1 January 2021 01:15:00	138.000
1 January 2021 01:30:00	126.400
1 January 2021 01:45:00	124.800
1 January 2021 02:00:00	123.600
1 January 2021 02:15:00	119.600

.

8. Discussion

For all of the randomly selected datasets of real-world values, we can say that they follow the first-digit probability distribution according to the BL. If there were high differences compared to the theoretical values, that particular dataset could not be used in our verification experiments because it would probably be already affected by some artificial effect. From this point of view, the random dataset selection proved that the nature of our datasets predicts the effective application of BL for fraud detection.

The data violation experiments involving some kind of arithmetic operation presented us with relatively high difference values for the first digit probability distribution, especially with peaks in distribution graphs for some of the datasets. This can be considered as a particular influence on the arithmetical operation.

For the experiment series with changing only a part of the dataset, we wanted to prove and compare the effectiveness of fraud detection by BL. We have chosen a whole range of changed dataset sizes, and we have gradually lowered this size to the most probable fraud scenario when only smaller parts of the dataset are changed. However, the larger sizes were applied for comparison reasons. Especially for 10% changed dataset values, the violation markers are not so prominent, and the marker detection algorithm should be more sensitive.

The presented experimental work can be extended in almost any direction. The random dataset selection should be given with particular rules on how to decide if the scenario is capable of fraud detection by BL. A much wider range of arithmetic operations and operands could be used. Some of these operations indicated special violation markers, and any further work could explore the possibility of detecting the violation operation given the different markers.

The partially changed dataset could involve a more refined examination of the changed dataset difference markers’ dependency on the changed dataset size. This could have a high profit for the fraud detection process, and this detection algorithm could be refined.

Finally, the application of machine learning algorithms could be useful for the fraud detection process. This possibility is discussed, e.g., in [36]. Detecting the deviations from BL distribution is a typical task for supervised kind of machine learning. During training phase, the artificial intelligence agent is trained to recognize BL and non-BL distribution datasets. Then, a pattern recognition process takes place and as a result we find the decision if the provided unknown dataset complies with BL first digit distribution.

9. Conclusions

Benford’s law is one of the methods to detect non-natural changes in data sets collected from electricity metering devices. In this paper, we tried to verify BL’s first digit probability distribution for electricity metering data sets, i.e., the data of electricity consumption. We have presented BL distribution for original dataset with no artificial intervention and a set of results for different kinds of affected datasets with artificial intervention. We also proposed further investigation directions and ideas.

We found out that, surprisingly, the datasets with a lower order of magnitude also comply with BL distribution. We also verified the datasets acquired in electricity distribution grids against BL’s first-digit probability distribution according to BL. There are some references focusing on this kind of dataset, but we have not found any that deal with this dataset’s origin to this extent. We also used specific models of original dataset intervention, as discussed in the experimental part of the article, that were never published.

The results of our research indicate that Benford’s Law (BL) can be applied for detecting data anomalies compared to the original unaffected dataset. Similar to previous studies [22,23,24,25,26,27,28,29,30,31,32,33,34], our research also confirms that the more data is manipulated, the more accurate the results become. Therefore, using BL for minor data changes is not recommended. The outcomes, as seen in previous research, would be distorted and imprecise. In previous studies, the authors also recommended augmenting the results of data analysis using BL with additional conditions that would more effectively reveal potential discrepancies with the unaltered data.

The published article and research gap are summarized below in

Table 23. Contributions and research gaps.

Published Article Contributions	Research Gap
BL is a suitable method for original dataset unnatural alteration	Only a minimal amount of research was performed to validate BL for electricity consumption data
Articles propose algorithms that identify problematic data and estimate overall electricity consumption through limited datasets	Dataset magnitude determination for applicability of BL
BL validity for datasets in different science areas	Experimental research gap for electricity theft detection methods. The lack of sensitivity verification affects different amounts of data in the recorded dataset. The lack of BL validity verification affects different types of alteration operators.
One of the basic requirements for datasets to comply with Benford’s Law is the value of the order of magnitude is higher than 3	Verification gap for this requirement in electricity consumption data, where this order of magnitude is often lower than 3.
References provide some simulation tests for altered datasets and the detection of these alterations	No reference tests the sensitivity and alteration detection threshold in combination with different alteration operations.

:

In conclusion, it is important to focus on facts that have not yet been examined in the publications [24,25,26,27,28,29,30,31,32,33,34], as mentioned in the introduction. We have also performed an investigation focusing on the gaps identified in the reviewed references:

-

The data examined in this manuscript are unique as they come from an operation distribution system. Because this kind of data is not always freely accessible, they have not been extensively explored in other publications. Therefore, one of the contributions of our study is the validation of Benford’s law in this specific domain. Publication [2] focuses on the analysis of electric meter data, but it uses different methods for detecting electricity theft. However, the model presented in [2] is highly sensitive to changes in input data, whereas our results are more accurate. The accuracy of error detection can be further enhanced by additional conditions defined by the distribution company and by further investigation of the method sensitivity and accurate detection threshold determination.

-

Previous research did not focus on the impact of data sensitivity as it is in our paper. We also examined the quantity of pseudo-random numbers within the overall dataset, gradually altering 10%, 25%, 50%, and 75% of the overall dataset values. Our research results demonstrate whether and how the quantity of altered data affects the overall dataset values.

-

We also artificially modified the data in several ways, including 1. Adding +1 to dataset values; 2. Division of the dataset values by 2, 3; Multiplication of the dataset value by 2. Such diversity of changes in previous research references in the field of electricity consumption data has not yet been explored nor verified.

-

The data in our study did not always have a range of values for orders of magnitude that exceeded three. After studying various publications, the authors recommended an order of magnitude for datasets exceeding 3. In our case, this value was not always higher than three, which is again an area that has not been explored. Our research shows the possibility of using Benford’s law even with a dataset order of magnitude slightly lower than three.