Abstract
The production of monoclonal antibodies (mAbs) plays a pivotal role in therapeutic treatments, and optimizing their production is crucial for minimizing costs and improving their accessibility to patients. One way of improving the production process is to improve model accuracy through the correct estimation of its states and parameters. The contributions of this paper lie in the provision of guidelines for sensor selection in the upstream production process of mAbs to enhance the accuracy of state estimation. Furthermore, this paper applies an effective variable selection technique for simultaneous state and parameter estimations for enhanced estimation results in the biomanufacturing processes of mAbs. An estimation framework of MHE is designed for three different case studies to demonstrate the efficiency of the proposed approach. The estimation performance is compared and assessed using the Root Mean Squared Error (RMSE) as an evaluation criterion.
MSC:
49M37
1. Introduction
Monoclonal antibodies (mAbs) are monospecific and homogeneous antibodies that are developed in a laboratory to enhance the body’s natural immune response against pathogens [1]. Due to their unique properties, they serve as powerful tools in the advancement of therapeutic treatments [2]. Over the years, they have become vital in the field of medicine, and have been applied in the treatment of diverse diseases including cancer and infectious diseases such as COVID-19 [1,3,4,5]. However, the cost of treatments involving mAbs can be significantly high due to the necessity for high doses and the expensive production process [6]. Consequently, optimizing the production of mAbs has become imperative in order to minimize expenses and to make these treatments more accessible.
Most of the processes for mAb production rely on batch or fed-batch operation, which involves using a batch or fed-batch bioreactor to provide nutrients for cells in order to facilitate antibody production. This is followed by several batch purification steps [3]. Batch processes, however, present several challenges, including difficulties in scaling up, limited adaptability to meet dynamic market demands, poor yield, and the additional expenses associated with storing and handling intermediate products. As a result of these drawbacks, there has been a growing interest in the continuous production of mAbs, which has the potential to eliminate time-consuming and labor-intensive procedures, enhance product quality, and improve overall profitability [3,7,8]. The continuous production of mAbs can be divided into two primary stages: the upstream and downstream processes. The upstream process entails antibody production within a perfusion bioreactor, where a continuous supply of nutrients is introduced. The downstream process involves purifying the produced antibodies through a number of chromatography steps [9].
In the context of control, buffer tanks play a critical role by serving as an intermediary step between the continuous operation units of the upstream and downstream processes. They help regulate and manage fluctuations in flow rates, pressure, and other state variables [10]. The application of advanced sensor technologies, such as mass and Raman spectroscopy, allows for online or at-line measurements of cell characteristics, substrate concentrations, and metabolic byproduct concentrations, thereby enabling effective control strategies [11,12].
Feedback control in different scenarios can be achieved using either a proportional integral derivative (PID) controller or a model predictive controller (MPC), depending on the specific requirements. The implementation of the PID controller is relatively simple, widespread, and faster in terms of computational time, while MPC offers more advanced capabilities for complex processes; in addition, MPC utilizes process models and optimization tools to forecast the response of manipulated variables, albeit at the cost of increased computational time. Despite the remarkable technological advancements in control and automation that have been facilitated by high-performance computing, these developments have primarily occurred outside the pharmaceutical industry, and biomanufacturing processes predominantly rely on classical control systems [8] as evidenced in studies such as [13], which is where a PID controller was utilized to regulate dissolved oxygen in vaccine production. However, there is a rising interest in implementing advanced process control (APC) strategies, such as model predictive control (MPC), within continuous biomanufacturing [14,15]. For instance, in [16], MPC was formulated to maximize the production of monoclonal antibodies and to showcase its superiority over the utilization of a PID controller. Krausch et al. [17] have also applied a multi-stage MPC strategy that builds a scenario tree to account for parameter uncertainties. It provides a strategy for accelerating bioprocess development through advanced control techniques, thus addressing challenges related to parameter uncertainties and constrained optimization. Other controller designs have also been applied to cell cultures. For instance, Abbate et al. [18] have explored a multivariable robust control framework for perfusion animal cell cultures. In their work, this control structure adopts a cascade configuration. It employs a feedback controller with linearization capabilities in the inner loop and linear controllers in the outer loops, all of these are aimed at the concurrent regulation of cell concentration and glucose concentration within the bioreactor.
Through the accurate estimation of state variables, processes can be efficiently monitored and controlled to achieve desired yield and product quality, while also minimizing resource utilization. A number of studies have documented the application of the Extended Kalman Filter (EKF) in the field of biotechnological processes for state estimation. For instance, in the work by Tuveri et al. [18], an EKF and an Unscented Kalman Filter (UKF) were utilized for estimation in a fed-batch bacterial cultivation process. Similarly, Narayanan et al. [19] also employed an EKF for real-time monitoring and control in mammalian cell culture processing. Dewasme et al. [20] provided an experimental validation of a full-horizon interval observer, which was applied to monitor the concentration of mAbs produced by hybridoma cell cultures, where the observer was based on a data-driven model and involved in the solution of a nonlinear programming problem at each sampling time. Bogaerts et al. [21] also applied a nonlinear and linearized full-horizon-state observer to a bioprocess involving animal cell culture. Moving Horizon Estimation (MHE) has also been applied to bioprocesses in the work by Tebbani et al. [22], Rodríguez et al. [23], and Raïssi et al. [24]. MHE presents the capacity to effectively handle nonlinear dynamics and incorporate constraints [25]. Considering the nonlinear nature of this system, as well as constraints in state and parameter variables, MHE will be employed in this work; nevertheless, alternative estimation methods remain viable options.
Achieving accurate state estimation also relies on the concept of observability. By placing the sensors strategically, it is possible to obtain measurements from which we can extract sufficient information to reconstruct the entire state information of a system. Joubert et al. [26] presented an approach for sensor selection in which sensitivity-based calculations were employed together with SVD analysis to determine unidentifiable parameters. The authors then subsequently proceeded with the re-parametrization of structurally unidentifiable ordinary differential equation (ODE) models. Similarly, in the work by Liu et al. [27], a sensitivity-based approach was introduced for determining the optimal sensor combination for state estimation problems. The algorithm seeks to determine an optimal sensor subset that ensures that the entire state information can be reconstructed. The algorithm involves several steps, including the construction of a sensitivity matrix, the use of successive orthogonalization, and the application of the degree of observability to identify the optimal sensor subset that satisfies the full rank condition.
Given that MHE is a model-based technique, enhancing the accuracy of the model is important, and parameter estimation is one way through which to enhance model accuracy. In [28], a particle swarm optimization (PSO) algorithm was developed and used for parameter estimation in the mAb production process. One drawback of this algorithm is its associated high search complexity. As the search space increases, the computational effort required to find the optimal solution also grows, impacting the efficiency of the algorithm [29,30]. A common approach is to estimate the states and parameters simultaneously. This often involves augmenting the parameters as additional states of the system. However, this augmentation can introduce challenges as it may lead to a loss of observability in the system, even with the use of the optimally-selected sensors. The augmented system may have more variables than can be accurately estimated, making it necessary to select a subset of variables for estimation. In [31], an algorithm for variable selection in augmented systems was proposed. The study identified the subset of variables that can be accurately estimated by effectively extracting information from the measured output. The selected variables were then estimated using MHE.
In this work, the objective is to estimate the states of the upstream process of mAb production. To achieve this, we begin by addressing sensor placement, aiming to determine the minimum sensor combination and their optimal locations. Additionally, we focus on estimating a selected set of parameters within the model to maximize the information extracted from the available measurements. Since the evaluation of each possible sensor combination would not be practical for a system with a large number of states, such as the system under consideration, the sensor selection algorithm developed in the work by Liu et al. [27] was applied. Furthermore, simultaneous state and parameter estimations were performed by first augmenting the parameters of the system as additional states and then employing the variable selection technique used in [31] to select the variables to be estimated. This paper offers contributions in the following areas:
- 1
- A detailed consideration of sensor placement for continuous mAb production processes. The results provide guidelines for the sensor selection of similar continuous mAb production processes.
- 2
- Maximizing estimation accuracy in continuous mAb production processes through variable selection and simultaneous state and parameter estimations. The findings not only offer valuable insights into optimal variable selections for estimation, but also underscore the improvement in estimation accuracy achieved through simultaneous state and parameter estimations.
- 3
- A state estimation design in the framework of MHE for continuous mAb production processes that can extract the maximum information from the measurements.
2. System Description and Problem Formulation
2.1. System Description
The diagram presented in Figure 1 illustrates the upstream system of a continuous mAb production process, which is a modified version from [9]. The system primarily consists of a well-stirred bioreactor and a microfiltration unit/cell retention device. The buffer tank, introduced for smoother operation [32], is located between the upstream and downstream process components, and it is considered in this work alongside the upstream components.
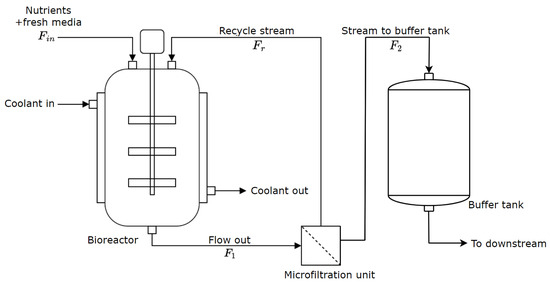
Figure 1.
A schematic diagram of the upstream process for mAb production.
In this setup, the bioreactor employs perfusion culture, where nutrients such as glucose and glutamine are continuously supplied with a flow rate represented by to create an optimal environment for mAb production with a mammalian cell culture in the bioreactor. Specifically, the GS- NSOcell culture system, as described in [33], is considered here. During the production of the desired mAbs, the cell culture undergoes metabolic activities that lead to the production of the key metabolites: lactate and ammonia.
The effluent stream, comprising the cells, mAbs, and metabolites, exits the bioreactor into the microfiltration unit at a flow rate denoted as . The microfiltration unit recycles the cells back into the bioreactor through the recycle stream with a flow rate of . This recycling process ensures the maintenance of a high cell density within the bioreactor. The remaining content of the stream is allowed to pass on into the buffer tank with a flow rate denoted as . A cooling jacket is used around the bioreactor to regulate the temperature of the bioreactor components [9]. Finally, the stream from the buffer tank, which contains the product, metabolites, and any toxic by-products, is directed downstream for product purification. The mathematical model of the upstream process is based on the work by [9,34,35].
2.1.1. Bioreactor Modeling
The bioreactor model encompasses three key aspects: cell growth and death, cell metabolism, and mAb production. To describe cell growth and death, as well as cell metabolism, the Monod kinetics model from [33] was employed, and the dynamic model for the upstream system was developed under the following assumptions:
- 1
- The content within the bioreactor is homogeneously mixed.
- 2
- The enthalpy change resulting from cell death is negligible.
- 3
- The dilution effect is negligible.
- 4
- No heat is lost to the external environment.
- 5
- The temperature of the recycled stream and the reaction mixture are equivalent.
- 6
- The buffer tank level, volume of the bioreactor, and volume of the cell retention device remain constant throughout the process.
To describe the growth and death of cells, Equations (1) and (2) were used [33].
They represent the conversion of viable cells and total cells within the culture [9], where X is the cell concentration in cells/L, is the specific growth rate in min, and is the specific death rate in min. The subscripts v and t signify viable and total cells, and the subscript 1 represents the bioreactor throughout the paper. represents the bioreactor volume in L, is the volumetric flow rate of nutrients into the bioreactor, is volumetric flow rate of the recycle stream, and is the volumetric flow rate out of the bioreactor in L/min.
The specific cell growth rate depends on temperature, the concentrations of glucose and glutamine, as well as the metabolites lactate and ammonia. It can be calculated using the following Monod kinetic equations [33]:
where is the maximum specific growth rate in min, and and are the nutrient limitation function and the product inhibition function, respectively. The concentrations of glucose, glutamine, lactate, and ammonia, which are measured in mM, are represented by , , , and , respectively. The Monod constant in for glucose, glutamine, lactate, and ammonia are also denoted as , , , and , respectively. The specific death rate is given by Equation (6), which operates under the assumption that cell death is only a function of the accumulation of ammonia and that n is assumed to be greater than 1 so as to give a sharper increase in the specific death of cells with increasing ammonia concentration. The maximum cell death rate, , was also fixed as a constant.
In [9], a linear regression analysis was performed utilizing data sourced from [36] to establish a linear correlation between temperature and the maximum cell growth rate. This relationship is expressed by Equation (7), where T denotes the temperature of the bioreactor contents in C. The dataset used for this analysis was obtained at the temperatures of 33 C and 37 C. The heat balance equation for the bioreactor is given by [9]
where is the temperature of media entering the bioreactor in C, is the heat of reaction due to cell growth in J/mol, is the density of the reaction mixture in g/L, is the specific heat capacity of the reaction in J/(g C), U is the overall heat transfer coefficient in J/(h C), and is the temperature of coolant in the cooling jacket in C. The first term in Equation (8) accounts for the heat transfer resulting from the inflow of the feed into the bioreactor. It takes into consideration the temperature difference between the incoming feed and the current temperature of the bioreactor contents. The second term represents the heat consumption due to cell growth, and the last term represents the external heat transfer due to the cooling jacket.
As the cells in the bioreactor consume nutrients, undergo growth, and engage in metabolic activities, they generate two main metabolites, namely lactate and ammonia. The mass balance equations for the nutrients glucose and glutamine in the bioreactor can be described using Equations (9)–(13):
where and are the yield of cells, in cell/mmol, on glucose and glutamine, respectively, is the constant for glutamine degradation in min, and is the maintenance coefficient of glucose. and are the constants of the glutamine maintenance coefficient. The mass balance equations for lactate and ammonia in the bioreactor can also be described using Equations (14)–(17):
where and are the yield of lactate from glucose and the yield of ammonia from glutamine, in mmol/mmol, respectively.
The production rate of the mAbs in the bioreactor is described using Equations (18) and (19):
where denotes the maximum specific productivity measured in mg/cell/h. denotes the pH-dependent productivity constant, and denotes the optimal culture pH, as shown in [37]. The pH value in Equation (19) is assumed to be a function of a state, and its model is given by Equations (20) and (21):
where the constants and were obtained from nonlinear regression [9].
2.1.2. Mircofiltration
As the stream leaving the bioreactor enters the cell retention device, the cells are separated from the remaining contents of the stream. It is assumed that, in the separation process, no reactions occur. The concentration of each variable in the recycle stream is given as follows [9]:
where () is the cell recycle rate and () is the retention rate of glucose, glutamine, lactate, ammonia, and mAb [38]. The mass balance for glucose, glutamine, lactate, ammonia, and mAb concentrations around the cell retention device can be expressed by Equations (29)–(35):
where the subscript 2 denotes the cell retention device. It is assumed that the volume of the contents in the cell retention device, , is constant. Additionally, and are the concentrations of viable cells and total cells in the cell retention device, respectively.
2.1.3. Buffer Tank Model
Following the retention of cells by the microfiltration unit, the remaining contents of the stream, which had a high mAb concentration, flow into the buffer tank. The rate of change in mAb concentration in the buffer tank can be described by Equations (36) and (37):
where represents the inlet flow rate of the buffer tank in L/min, h represents the buffer tank level (which is assumed to be constant), and represents the inlet concentration of mAb in mg/L. denotes the concentration of mAb in the buffer tank in mg/L, and D represents the diameter of the buffer tank (which is fixed).
The parameters used in the model are described by Equations (1)–(37), which are listed in Table 1. The values are obtained from the literature or calculated via a steady-state design. For instance, the constant buffer tank level used, as well as the fixed volumes of the bioreactor and cell retention device, were obtained via a steady-state operation. Furthermore, the parameters used in the equations describing mAb synthesis, as well as cell growth, death, and metabolism in the bioreactor were obtained from the works by Papathanasiou et al. [33] and Villiger et al. [37]. The cell recycle rate and the retention rates of the mAbs, nutrients, and metabolites around the cell retention device were also obtained from the work by Clincke et al. [38]. Table 1 also provides a list of the inputs utilized in the simulations conducted in the subsequent sections.

Table 1.
Inputs under the nominal conditions and parameters of the model [9].
2.2. Problem Formulation
The continuous-time model in Section 2.1 was discretized using the fourth-order Runge–Kutta method with a sampling time of min. This sampling time was chosen because it was sufficient to capture the dynamics of the process. The discrete-time system was represented by Equations (38) and (39) for simplicity.
In Equation (38), the system state vector comprises 16 elements, and these represent the state variables listed in Table 2. The input vector consists of 8 elements and represents the inputs to the system. The parameter vector has 27 elements, the process noise vector accounts for disturbances in the system, and the nonlinear state equation is denoted by F. Equation (39) describes the measured output vector , which comprises the measurements obtained through the sensor selection process. The measurement noise vector represents the errors associated with the measurement process, and H represents the output equation that relates the system states to the measured outputs. In this work, the process and measurement noise are assumed to be Gaussian noise.

Table 2.
States for the upstream process model.
The main objective of this work is to estimate the states of the system described in Equations (38) and (39). To achieve this, the sensor placement problem is first considered with the aim of determining the minimum number of sensors for which the system is observable, as well as the optimal sensor locations. The following section provides a comprehensive overview of the selection process for the optimal set of sensors for state estimation. We present the algorithm used for sensor selection and reveal the sensors that are ultimately chosen.
3. Sensor Selection for State Estimation
The problem of optimal sensor selection is encountered in various areas such as robotics, healthcare, and industrial process control. While an exhaustive search of all possible sensor combinations may be feasible for small-scale systems, it becomes computationally inefficient for large-scale systems, which is where the complexity grows exponentially with the number of candidate sensors. Addressing this issue requires a reliable sensor selection scheme that offers improved performance and lower computational complexity [39,40]. In this paper, we apply a sensitivity-based approach for optimal sensor selection to the upstream process of mAb production. This approach, developed by Liu et al. [27], was utilized to determine the optimal number and placement of sensors in a wastewater treatment plant. The algorithm involves constructing the sensitivity matrix, as well as employing orthogonalization and a degree of observability for sensor selection. To begin, we take a look at the construction of the sensitivity matrix and the sensor placement process.
3.1. Construction of the Sensitivity Matrix
Observability plays a crucial role in state estimation as it determines the possibility of deducing the internal states of a system based on the measurements of a subset of those states. The sensitivity matrix, in the context of nonlinear systems, is a valuable tool for assessing observability. The work presented in [31] sheds light on the relation between the sensitivity matrix and the observability of dynamical nonlinear systems. Moreover, it elucidates the correlation between the observability matrix and observability in linear systems. Through these insights, a deeper understanding of the relationship between observability and the sensitivity matrix can be gained. Here, we delve into the use of the sensitivity matrix for evaluating the observability of a discrete-time nonlinear system. Considering the discrete-time nonlinear system described by Equations (38) and (39), the sensitivity matrix, , at sampling time k can be constructed as shown in Equation (40):
where each column represents the sensitivity of the different outputs to a specific state element. The individual entries of the matrix, which can be denoted as , can be calculated using Equation (41a). Furthermore, Equation (41b) expresses the sensitivity of the state with respect to the initial state , as mentioned in [27].
The normalized sensitivity matrix from sampling time 0 to k can be constructed as Equation (42). If the observability matrix, , is a full rank along the entire trajectory from sampling time 0 to k, then the nonlinear system is locally observable along the trajectory. This implies that the current states can be fully estimated using input and output data [26,31].
3.2. Procedure to Determine Minimum Number and Optimal Placement of Sensors
The sensitivity matrix is normalized to ensure that the magnitudes of its elements are on a consistent scale. The norm of each column of the sensitivity matrix is used as a measure of the degree of observability. Larger norms indicate a greater sensitivity of the output to the corresponding state. However, the direct use of the norms is limited by the potential linear dependence among some columns. To address this, successive orthogonalization is applied to identify the strongly linearly independent columns. Starting with the sensor corresponding to the column with the smallest norm, sensors are successively removed for states that contribute the least to the overall system observability. The process continues until removing another sensor would render the system unobservable. The orthogonalization procedure used to rank the columns by magnitude, and the final algorithm used to obtain the minimum sensor set were detailed in [27].
To derive the ultimate minimum sensor set, the procedure in Figure 2 was implemented. Given the initial sensor set containing all the sensors, the sensors were removed one at a time. For each sensor removed from the set, the rank of the normalized sensitivity matrix was checked to ensure that the system was still observable. If the matrix was rank-deficient, the degree of observability was set to zero. If the matrix was full rank, the total degree of observability was calculated based on the remaining sensors in the set. This ensures that the algorithm considers only observable systems moving forward. The total degree of observability is the sum of the norms of the columns of the normalized sensitivity matrix, which is where the norms of the matrix were obtained and ordered using orthogonalization to eliminate linear dependence. The sensor, which when removed from the set results in the highest degree of observability, is chosen and removed permanently from the set. This is because that sensor contributes the least to the overall observability of the system. This process continues until the further removal of any sensor would cause the system to lose observability. Consequently, the algorithm terminates at the step where, for all the remaining sensors, the degree of observability is set to zero due to rank deficiency.
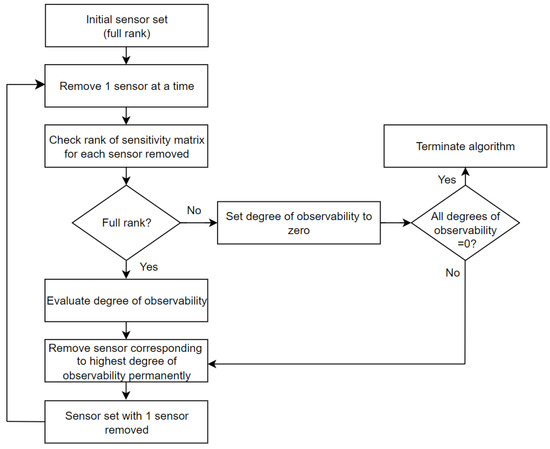
Figure 2.
A schematic flow diagram of the sensor selection process.
3.3. Minimum Sensor Set Selection
Consider the mAb process described in Section 2.1 and its compact representation given by Equations (38) and (39). We assume the presence of commercially available sensors, as discussed in [41,42,43], which are capable of measuring all of the 16 states that represent temperature and the concentrations of the nutrients, metabolites, and mAbs. To initiate the sensor selection process, we begin with the original full sensor set denoted as , which comprises all 16 sensors. The initial set is defined as {, , , , , , , , , , , , , , T, c}, which can be simplified as for convenience.
Table 3 illustrates the step-by-step removal of sensors using the sensor selection algorithm to determine the final optimal minimum sensor set. Following the algorithm, for each sensor removed, the degree of observability for the remaining set is calculated and the corresponding sensor for the set with the highest degree of observability is removed. This removal is performed because the removed sensor contributes the least to the overall observability of the system. In Table 3, m represents the number of sensors remaining in the sensor set, denotes the set of removed sensors, is the rank of the sensitivity matrix (which is constructed based on the current sensor set combination). degree is the maximum degree of observability at each step of the removal process and for which the corresponding sensor is permanently removed; sensor indicates the sensor corresponding to the maximum degree of observability, which is removed permanently at the current step. also represents the degree of observability for a particular sensor that is taken out.

Table 3.
Sensor selection process for the mAb process.
We initiate the sensor selection algorithm with the full sensor set , which exhibits a total degree of observability of 64.025 and a full-rank sensitivity matrix. The algorithm proceeds sequentially by removing one sensor at a time from the set of 16 sensors. For each iteration, the sensitivity matrix is reconstructed and its rank is assessed. If the rank of the sensitivity matrix is less than 16, indicating rank deficiency, the degree of observability is set to zero. Conversely, if the rank is 16, the degree of observability remains effective. Through analyzing the degrees of observability for each sensor removal, we find that removing Sensor 2 yields the highest degree of observability at 61.994. Hence, Sensor 2 is permanently eliminated from the set as it contributes the least to the overall observability of the system.
Moving forward, we proceed to the next step of the algorithm with a sensor set of 15 sensors. The objective is to remove one more sensor to obtain an optimal set containing 14 sensors. After evaluating the degrees of observability for each sensor removal, it is observed that removing Sensor 1 leads to the maximum degree of observability. Consequently, Sensor 1 is removed permanently from the set. Following a similar procedure, Sensors 3, 7, 14, 6, 15, 5, and 4 were subsequently removed permanently from the set—one after another.
After the removal of Sensor 4, the remaining set consists of Sensors . Upon removing Sensor 8, the sensitivity matrix was rank-deficient; therefore, the degree of observability, , was set to 0 and Sensor 8 was not permanently removed. Similar observations were made for Sensors 9, 10, 11, 12, 13, and 16; therefore, none of these sensors were removed permanently as the removal of any of these sensors resulted in a rank-deficient sensitivity matrix. Thus, the algorithm terminated at , and the final optimal minimum sensor set was , which corresponds to .
4. State Estimation Method
The sensors selected in Section 3.3 play a crucial role in obtaining measurements, which, when combined with the process model, enable the reconstruction of the system’s states. However, relying solely on state estimation may not capture all the valuable information embedded within the measurements. To fully exploit the available information, it is advantageous to also estimate some parameters. This approach enhances the algorithm’s resilience to model uncertainty and improves overall estimation performance. Simultaneous state and parameter estimation has garnered significant attention as it offers the capability to achieve better estimation outcomes [31,44,45].
Estimating parameters in complex systems usually presents a challenge as there are often more parameters than can be reliably estimated. Consequently, it becomes crucial to determine a subset of parameters that can be accurately estimated. How to select the appropriate subset of parameters becomes a significant question to address [46]. To determine which parameters should be included for estimation, variable selection was employed. First, the parameters were augmented as extra states of the original system. Next, the sensitivity matrix for the augmented system, , was constructed and normalized. Subsequently, the rank of the normalized sensitivity matrix was checked. If the sensitivity matrix was not full rank, it indicated that not all the elements of the augmented system could be uniquely estimated, and it then becomes important to identify the subset of elements that can be estimated accurately.
Using orthogonalization, the norms of the columns of were evaluated and the column with the largest norm was selected and denoted as . Next, the residual information matrix is calculated. The column of , which corresponds to the largest norm in the residual matrix, is taken and added to to form . The cut-off criterion for algorithm termination is the rank of the sensitivity matrix. Columns are added successively in this order until the rank of is equal to the rank of , and the algorithm is then terminated. The variables corresponding to the columns of were identified as the most estimable variables, and they corresponded to the strongly linearly independent columns of the sensitivity matrix. The variable selection procedure used can be found in [31], where it is illustrated with an example.
Here, the variable selection process considers a total of 18 parameters, which are the parameters of interest and are listed as follows: {, , , , , , n, , , , , , , , , , , , U}. To estimate the states and parameters simultaneously, the parameters are augmented as extra states by combining Equation (43) with Equation (44).
Equation (43) represents the state equation, and the parameters of interest (which are represented by the vector ) are considered. Equation (44) represents the parameter equation, where is a vector representing process noise and contains 18 elements. The parameters, represented by the vector p, are assumed to be constant. The augmented state vector is represented by X, where . The discrete-time representation of the augmented system is shown in Equations (45) and (46):
where the subscript ‘a’ represents the augmented system. In Equation (45), represents the augmented system state vector, represents the input vector, and represents the process noise vector. Equation (46) describes the measured output vector , which contains the measurements obtained from the 7 selected sensors. The measurement noise vector is represented by .
Through Singular Value Decomposition (SVD) analysis, the rank of the normalized sensitivity matrix of the augmented system was determined to be 21. Therefore, the variable selection algorithm terminates after the selection of the first 21 most estimable variables. The selected variables consist of all 16 states and 5 of the parameters. The chosen parameters were as follows: . The 21 selected variables were estimated using MHE, which is an estimation technique in which the estimation problem is formulated as an optimization problem [23,47,48,49]. The MHE formulation at sampling time k for the simultaneous state and parameter estimation of the augmented system is given by Equations (47a)–(47f):
The objective of MHE optimization is to minimize the mismatch between the predicted and actual measurements, which is represented by the term in Equation (47a). The term is defined in Equation (47c), and the caret sign indicates an estimated variable. The process disturbance is also accounted for by the term in Equation (47a), and is defined in Equation (47f). The arrival cost, which represents the information from the initial state of the model to the beginning of the estimation window, is given by . Here, N denotes the length of the estimation window, and and are the decision variables of the optimization problem. represents the estimated variable and is defined in Equation (47e). represents the estimated state, , at time instant , and is given by Equation (47d). The matrices P, Q, and R are the covariance matrices for state uncertainty, process noise, and measurement noise, respectively. Furthermore, MHE incorporates constraints on the states, parameters, and model uncertainties in Equations (47e) and (47f).
5. State Estimation Results
In this section, the focus is on performing state estimation with the selected sensors that were determined by the sensor placement algorithm described in Section 3. The MHE technique is employed to estimate all 16 states of the system using the nominal parameter values provided in Table 1. The estimation results are then examined by comparing the estimated state trajectories with the actual state trajectories.
Furthermore, to investigate the effect of estimating some parameters in addition to the states, three different cases were analyzed. In Case 1, state estimation alone was conducted; in Case 2, all 16 states and 18 parameters were estimated simultaneously. In Case 3, only the selected variables (16 states and 5 parameters) obtained through the variable selection algorithm described in Section 4 were estimated, thus representing the proposed approach. In all three cases, some bias was added to the parameters of the plant model, whereas the nominal parameters were used for the estimator. The initial parameter guess for MHE were the nominal parameter values. The evaluation of the estimation results in all three cases involved comparing the Root Mean Squared Errors (RMSEs) and plotting the estimated and actual values. Additionally, the error evolution for all three cases was analyzed to assess the estimation performance comprehensively.
Simulation Settings
To begin, state estimation is performed. For the MHE estimator, the weighting matrices are diagonal matrices where the state covariance matrix, , and the process covariance matrix and measurement covariance matrix are given by Q and R, respectively:
,
. The covariance matrices were obtained by first making rough assumptions on a realistic magnitude of state noise and then modifying the matrices to achieve a satisfying MHE performance in the simulations. Using a moving horizon length of 40 for the MHE, the results obtained were plotted in Figure 3, where the red line represents the actual state trajectories and the blue line represents the estimates. Since the estimated states are able to closely track the actual state trajectory, it can be concluded that the sensor selection algorithm was effective in selecting the minimum number of sensors, as well as their optimal locations for estimation.
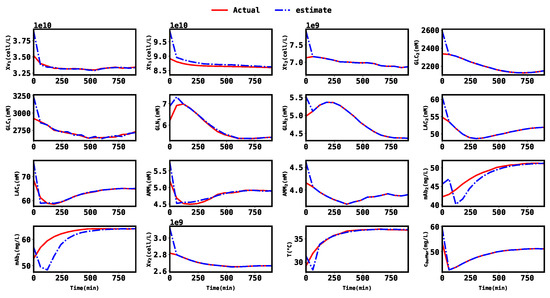
Figure 3.
Plot of the actual states and their estimates based on the minimum sensor set.
Furthermore, to assess the benefit of estimating some additional parameters, estimation was performed for the three cases mentioned above, the state trajectories of which are compared in Figure 4. In the plots, the red line represents the actual state trajectories, the blue line represents the estimates from Case 1, the black line represents the estimates from Case 2, and the green line represents the estimates from Case 3. The estimated parameters were also plotted and compared in Figure 5. The average RMSE for all three cases over time, from to , was calculated using Equations (48a) and (48b). These are compared in Table 4.
Equation (48a) represents the RMSE for the states. Equation (48b) represents the RMSE for the parameters, where represents the total number of simulation steps, represents the total number of states, denotes the actual states, and denotes the estimated states. Similarly, represents the total number of parameters, denotes the true parameters, and denotes the estimated parameters.
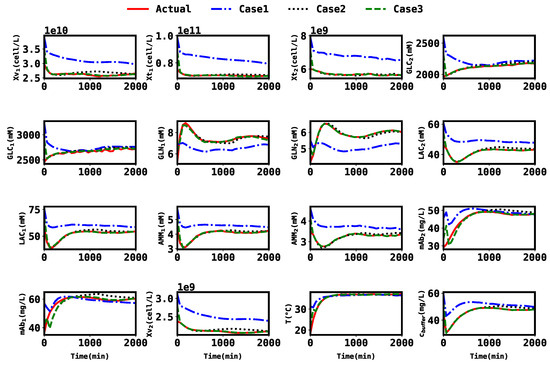
Figure 4.
Plot of the actual states and estimates for all three cases.
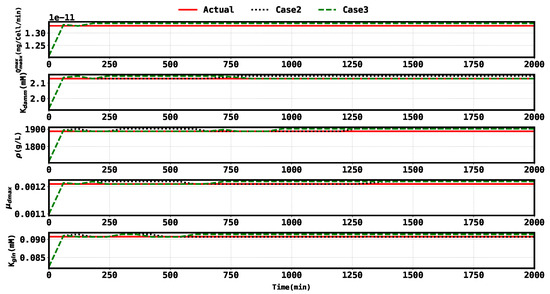
Figure 5.
Plot of the true parameters and estimates for Case 2 and Case 3.

Table 4.
Average RMSE considering different initial states in all three cases.
From Table 4, we can see that estimating parameters in addition to the states (Case 2 and Case 3) leads to better estimation performance. This is evident from the fact that Case 1 exhibits the poorest performance. The better performance of the proposed approach, Case 3, compared to Case 2 shows that estimating more than the selected variables of the augmented system leads to a degradation in state estimation performance. Table 4 clearly demonstrates that the proposed approach, Case 3, yields the most favorable outcome as evidenced by its lowest RMSE values for both the states and parameters. The parameter RMSE recorded in Case 1 is constant. This is because, in Case 1, no parameters are estimated, and the RMSE calculation is based on the true parameters used in the plant and the nominal parameters used in the estimator. The true parameters are represented as follows:
To quantify the improvement percentage of the state RMSE for Case 3 compared to Case 1 and Case 2, we utilize Equations (50a) and (50b):
Considering the average state RMSE, Case 3 shows a and improvement over Case 1 and Case 2, respectively. Similarly, considering the average parameter RMSE, Case 3 shows a improvement over Case 2. The error evolution for the states and parameters were also plotted and compared in Figure 6 and Figure 7, respectively.
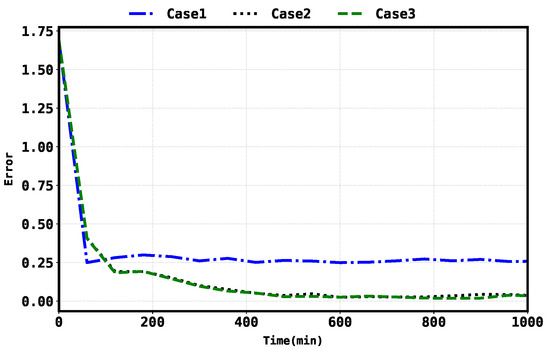
Figure 6.
State error evolution in all three cases.
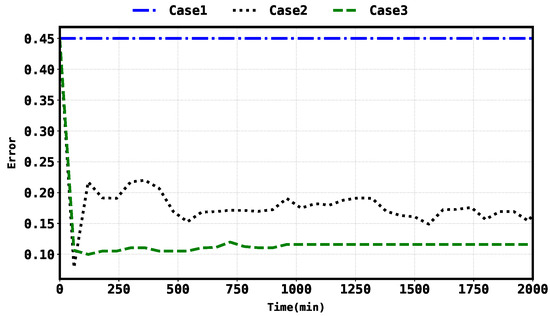
Figure 7.
Parameter error evolution in Case 2 and Case 3.
6. Conclusions
In conclusion, the results presented in Table 4 exhibit the superiority of the proposed approach, Case 3, in terms of estimation performance. Case 3 consistently exhibits the lowest RMSE values for both the states and parameters, indicating the benefit of estimating the additional parameters selected through the variable selection procedure.
Conversely, Case 1, which solely focuses on state estimation without considering parameter estimation, demonstrates the poorest performance, as reflected by the highest RMSE. This emphasizes the importance of including parameter estimation in achieving improved estimation results.
Furthermore, comparing Case 3 to Case 2, in which all variables of the augmented system were estimated, we see that estimating all of the parameters alongside the states can lead to a degradation in estimation performance. The average RMSE of Case 3 was found to be lower than that of Case 2, indicating the potential adverse effect of estimating unobservable parameters.
Through quantifying the improvement percentage of Case 3 over Case 1 and Case 2 in terms of state RMSE, we observe an impressive improvement over Case 1 and a modest improvement over Case 2. Similarly, comparing the parameter RMSE of Case 3 to Case 2, Case 3 exhibits a noteworthy improvement. The plotted error evolution for the states and parameters, as shown in Figure 6 and Figure 7, respectively, further supports the findings and provides a visual representation of the performance differences between the cases.
In summary, the inclusion of parameter estimation, as demonstrated in Case 3, enhances the overall estimation performance. By leveraging a selective approach that considers both state and parameter estimation, more accurate and reliable estimation results can be obtained, thus enabling a better understanding and control of the system under consideration.
Author Contributions
Conceptualization, S.A.O. and J.L.; methodology, S.A.O., B.T.A., S.D., S.L. and J.L.; software, S.A.O.; validation, S.A.O.; investigation, S.A.O.; data curation, S.A.O.; writing—original draft preparation, S.A.O.; writing—review and editing, J.L.; supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from the National Sciences and Engineering Research Council of Canada (NSERC) is greatly acknowledged.
Data Availability Statement
The data used in this study are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lloyd, E.C.; Gandhi, T.N.; Petty, L.A. Monoclonal antibodies for COVID-19. JAMA 2021, 325, 1015. [Google Scholar] [CrossRef] [PubMed]
- Breedveld, F. Therapeutic monoclonal antibodies. Lancet 2000, 355, 735–740. [Google Scholar] [CrossRef] [PubMed]
- Gomis-Fons, J.; Schwarz, H.; Zhang, L.; Andersson, N.; Nilsson, B.; Castan, A.; Solbrand, A.; Stevenson, J.; Chotteau, V. Model-based design and control of a small-scale integrated continuous end-to-end mAb platform. Biotechnol. Prog. 2020, 36, e2995. [Google Scholar] [CrossRef] [PubMed]
- Keizer, R.J.; Huitema, A.D.; Schellens, J.H.; Beijnen, J.H. Clinical pharmacokinetics of therapeutic monoclonal antibodies. Clin. Pharmacokinet. 2010, 49, 493–507. [Google Scholar] [CrossRef]
- Rodrigues, M.E.; Costa, A.R.; Henriques, M.; Azeredo, J.; Oliveira, R. Technological progresses in monoclonal antibody production systems. Biotechnol. Prog. 2010, 26, 332–351. [Google Scholar] [CrossRef]
- Farid, S.S. Process economics of industrial monoclonal antibody manufacture. J. Chromatogr. B 2007, 848, 8–18. [Google Scholar] [CrossRef]
- Plumb, K. Continuous processing in the pharmaceutical industry: Changing the mind set. Chem. Eng. Res. Des. 2005, 83, 730–738. [Google Scholar] [CrossRef]
- Chopda, V.; Gyorgypal, A.; Yang, O.; Singh, R.; Ramachandran, R.; Zhang, H.; Tsilomelekis, G.; Chundawat, S.P.; Ierapetritou, M.G. Recent advances in integrated process analytical techniques, modeling, and control strategies to enable continuous biomanufacturing of monoclonal antibodies. J. Chem. Technol. Biotechnol. 2022, 97, 2317–2335. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Decardi-Nelson, B.; Song, B.; Zhang, A.; Liu, J.; Tao, S.; Cheng, J.; Liu, X.; Yu, D.; et al. SMPL: Simulated Industrial Manufacturing and Process Control Learning Environments. arXiv 2022, arXiv:2206.08851. [Google Scholar]
- Thakur, G.; Nikita, S.; Tiwari, A.; Rathore, A.S. Control of surge tanks for continuous manufacturing of monoclonal antibodies. Biotechnol. Bioeng. 2021, 118, 1913–1931. [Google Scholar] [CrossRef]
- Craven, S.; Whelan, J.; Glennon, B. Glucose concentration control of a fed-batch mammalian cell bioprocess using a nonlinear model predictive controller. J. Process Control 2014, 24, 344–357. [Google Scholar] [CrossRef]
- Lopes, J.A.; Costa, P.F.; Alves, T.P.; Menezes, J.C. Chemometrics in bioprocess engineering: Process analytical technology (PAT) applications. Chemom. Intell. Lab. Syst. 2004, 74, 269–275. [Google Scholar] [CrossRef]
- Khan, O.; Madhuranthakam, C.M.R.; Douglas, P.; Lau, H.; Sun, J.; Farrell, P. Optimized PID controller for an industrial biological fermentation process. J. Process Control 2018, 71, 75–89. [Google Scholar] [CrossRef]
- Bhaskar, A.; Barros, F.N.; Singh, R. Development and implementation of an advanced model predictive control system into continuous pharmaceutical tablet compaction process. Int. J. Pharm. 2017, 534, 159–178. [Google Scholar] [CrossRef]
- Singh, R.; Ierapetritou, M.; Ramachandran, R. System-wide hybrid MPC–PID control of a continuous pharmaceutical tablet manufacturing process via direct compaction. Eur. J. Pharm. Biopharm. 2013, 85, 1164–1182. [Google Scholar] [CrossRef]
- Sarna, S.; Patel, N.; Corbett, B.; McCready, C.; Mhaskar, P. Process-aware data-driven modelling and model predictive control of bioreactor for the production of monoclonal antibodies. Can. J. Chem. Eng. 2023, 101, 2677–2692. [Google Scholar] [CrossRef]
- Krausch, N.; Kim, J.W.; Lucia, S.; Groß, S.; Barz, T.; Neubauer, P.; Bournazou, M.N.C. Optimal operation of parallel mini-bioreactors in bioprocess development using multi-stage MPC. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2022; Volume 51, pp. 1069–1074. [Google Scholar]
- Abbate, T.; Sbarciog, M.; Dewasme, L.; Vande Wouwer, A. Experimental validation of a cascade control strategy for continuously perfused animal cell cultures. Processes 2020, 8, 413. [Google Scholar] [CrossRef]
- Narayanan, H.; Behle, L.; Luna, M.F.; Sokolov, M.; Guillén-Gosálbez, G.; Morbidelli, M.; Butté, A. Hybrid-ekf: Hybrid model coupled with extended Kalman filter for real-time monitoring and control of mammalian cell culture. Biotechnol. Bioeng. 2020, 117, 2703–2714. [Google Scholar] [CrossRef]
- Dewasme, L.; Vande Wouwer, A. Experimental validation of a full-horizon interval observer applied to hybridoma cell cultures. Int. J. Control 2020, 93, 2719–2728. [Google Scholar] [CrossRef]
- Bogaerts, P.; Hanus, R. Nonlinear and linearized full horizon state observers-application to bioprocesses. IFAC Proc. Vol. 2000, 33, 371–376. [Google Scholar] [CrossRef]
- Tebbani, S.; Le Brusquet, L.; Petre, E.; Selisteanu, D. Robust moving horizon state estimation: Application to bioprocesses. In Proceedings of the 2013 17th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 11–13 October 2013; pp. 539–544. [Google Scholar]
- Hernández Rodríguez, T.; Posch, C.; Pörtner, R.; Frahm, B. Dynamic parameter estimation and prediction over consecutive scales, based on moving horizon estimation: Applied to an industrial cell culture seed train. Bioprocess Biosyst. Eng. 2021, 44, 793–808. [Google Scholar] [CrossRef]
- Raïssi, T.; Ramdani, N.; Candau, Y. Bounded error moving horizon state estimator for non-linear continuous-time systems: Application to a bioprocess system. J. Process Control 2005, 15, 537–545. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B. Constrained process monitoring: Moving-horizon approach. AIChE J. 2002, 48, 97–109. [Google Scholar] [CrossRef]
- Joubert, D.; Stigter, J.; Molenaar, J. An efficient procedure to assist in the re-parametrization of structurally unidentifiable models. Math. Biosci. 2020, 323, 108328. [Google Scholar] [CrossRef]
- Liu, S.; Yin, X.; Pan, Z.; Liu, J. A sensitivity-based approach to optimal sensor selection for process networks. arXiv 2022, arXiv:2208.00584. [Google Scholar]
- Selişteanu, D.; Șendrescu, D.; Georgeanu, V.; Roman, M. Mammalian cell culture process for monoclonal antibody production: Nonlinear modelling and parameter estimation. BioMed Res. Int. 2015, 2015, 598721. [Google Scholar] [CrossRef]
- Juneja, M.; Nagar, S. Particle swarm optimization algorithm and its parameters: A review. In Proceedings of the 2016 International Conference on Control, Computing, Communication and Materials (ICCCCM), Allahabad, India, 21–22 October 2016; pp. 1–5. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Liu, J.; Gnanasekar, A.; Zhang, Y.; Bo, S.; Liu, J.; Hu, J.; Zou, T. Simultaneous state and parameter estimation: The role of sensitivity analysis. Ind. Eng. Chem. Res. 2021, 60, 2971–2982. [Google Scholar] [CrossRef]
- Faanes, A.; Skogestad, S. Buffer tank design for acceptable control performance. Ind. Eng. Chem. Res. 2003, 42, 2198–2208. [Google Scholar] [CrossRef]
- Papathanasiou, M.M.; Quiroga-Campano, A.L.; Steinebach, F.; Elviro, M.; Mantalaris, A.; Pistikopoulos, E.N. Advanced model-based control strategies for the intensification of upstream and downstream processing in mAb production. Biotechnol. Prog. 2017, 33, 966–988. [Google Scholar] [CrossRef] [PubMed]
- Kontoravdi, C.; Asprey, S.P.; Pistikopoulos, E.N.; Mantalaris, A. Application of global sensitivity analysis to determine goals for design of experiments: An example study on antibody-producing cell cultures. Biotechnol. Prog. 2005, 21, 1128–1135. [Google Scholar] [CrossRef]
- Kontoravdi, C.; Pistikopoulos, E.N.; Mantalaris, A. Systematic development of predictive mathematical models for animal cell cultures. Comput. Chem. Eng. 2010, 34, 1192–1198. [Google Scholar] [CrossRef]
- Jimenez del Val, I.; Fan, Y.; Weilguny, D. Dynamics of immature mAb glycoform secretion during CHO cell culture: An integrated modelling framework. Biotechnol. J. 2016, 11, 610–623. [Google Scholar] [CrossRef]
- Villiger, T.K.; Scibona, E.; Stettler, M.; Broly, H.; Morbidelli, M.; Soos, M. Controlling the time evolution of mAb N-linked glycosylation-Part II: Model-based predictions. Biotechnol. Prog. 2016, 32, 1135–1148. [Google Scholar] [CrossRef] [PubMed]
- Clincke, M.F.; Mölleryd, C.; Samani, P.K.; Lindskog, E.; Fäldt, E.; Walsh, K.; Chotteau, V. Very high density of Chinese hamster ovary cells in perfusion by alternating tangential flow or tangential flow filtration in WAVE bioreactor™—Part II: Applications for antibody production and cryopreservation. Biotechnol. Prog. 2013, 29, 768–777. [Google Scholar] [CrossRef]
- Contreras, S.; Kachroo, P.; Agarwal, S. Observability and sensor placement problem on highway segments: A traffic dynamics-based approach. IEEE Trans. Intell. Transp. Syst. 2015, 17, 848–858. [Google Scholar] [CrossRef]
- Naeem, M.; Xue, S.; Lee, D. Cross-entropy optimization for sensor selection problems. In Proceedings of the 2009 9th International Symposium on Communications and Information Technology, Bellevue, WA, USA, 20–24 July 2009; pp. 396–401. [Google Scholar]
- Renneberg, R.; Trott-Kriegeskorte, G.; Lietz, M.; Jäger, V.; Pawlowa, M.; Kaiser, G.; Wollenberger, U.; Schubert, F.; Wagner, R.; Schmid, R.; et al. Enzyme sensor-FIA-system for on-line monitoring of glucose, lactate and glutamine in animal cell cultures. J. Biotechnol. 1991, 21, 173–185. [Google Scholar] [CrossRef]
- Li, F.; Vijayasankaran, N.; Shen, A.; Kiss, R.; Amanullah, A. Cell culture processes for monoclonal antibody production. In mAbs; Taylor & Francis: Abingdon, UK, 2010; Volume 2, pp. 466–479. [Google Scholar]
- Maruthamuthu, M.K.; Rudge, S.R.; Ardekani, A.M.; Ladisch, M.R.; Verma, M.S. Process analytical technologies and data analytics for the manufacture of monoclonal antibodies. Trends Biotechnol. 2020, 38, 1169–1186. [Google Scholar] [CrossRef] [PubMed]
- Ibrir, S. Joint state and parameter estimation of non-linearly parameterized discrete-time nonlinear systems. Automatica 2018, 97, 226–233. [Google Scholar] [CrossRef]
- Stroud, J.R.; Katzfuss, M.; Wikle, C.K. A Bayesian adaptive ensemble Kalman filter for sequential state and parameter estimation. Mon. Weather Rev. 2018, 146, 373–386. [Google Scholar] [CrossRef]
- Kravaris, C.; Hahn, J.; Chu, Y. Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng. 2013, 51, 111–123. [Google Scholar] [CrossRef]
- Allgöwer, F.; Badgwell, T.A.; Qin, J.S.; Rawlings, J.B.; Wright, S.J. Nonlinear predictive control and moving horizon estimation—An introductory overview. In Advances in Control; Springer: London, UK, 1999; pp. 391–449. [Google Scholar]
- Bo, S.; Sahoo, S.R.; Yin, X.; Liu, J.; Shah, S.L. Parameter and state estimation of one-dimensional infiltration processes: A simultaneous approach. Mathematics 2020, 8, 134. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Event-triggered state estimation of linear systems using moving horizon estimation. IEEE Trans. Control Syst. Technol. 2020, 29, 901–909. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).