Discriminating among Generalized Exponential, Weighted Exponential and Weibull Distributions
Abstract
1. Introduction
2. Methodology
2.1. The Ratio of Maximized Likelihood Method
2.2. The Minimum Kolmogorov Distance Method
2.3. The SPRT Method
2.4. Algorithm
- (i)
- Generating a sample with sample size n follows the null hypothesis.
- (ii)
- Using the sample to compute the corresponding MLE of the distribution follows , , .
- (iii)
- (iv)
- Select the correct distribution according to the criteria from each procedure.
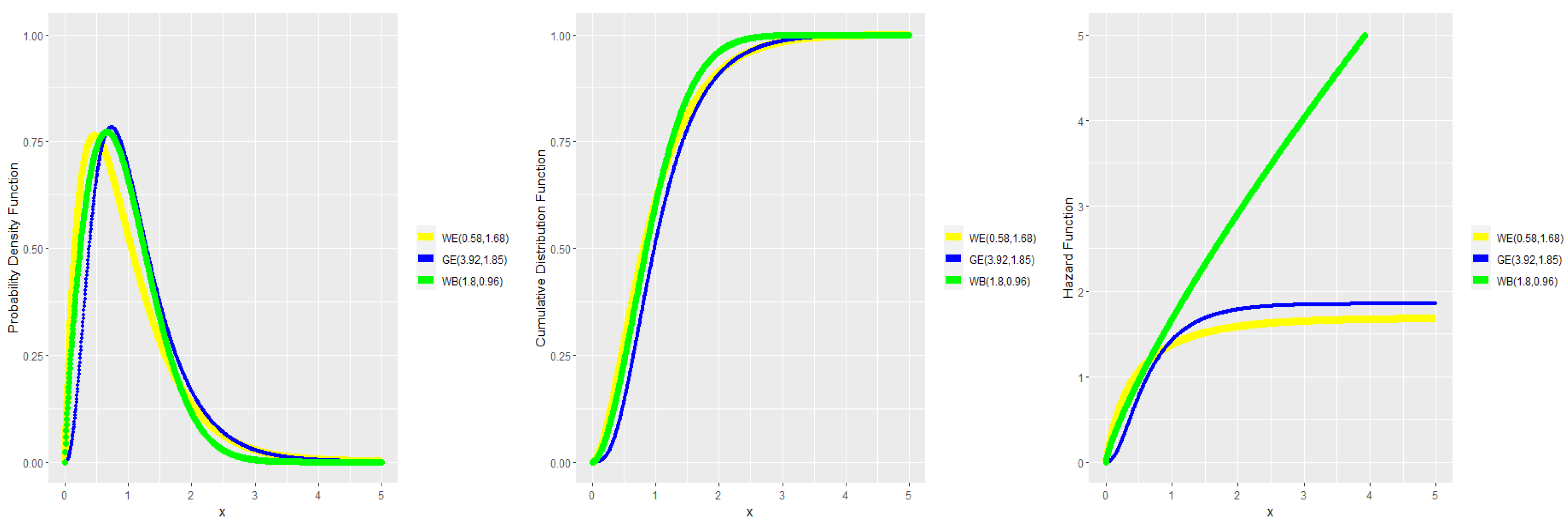
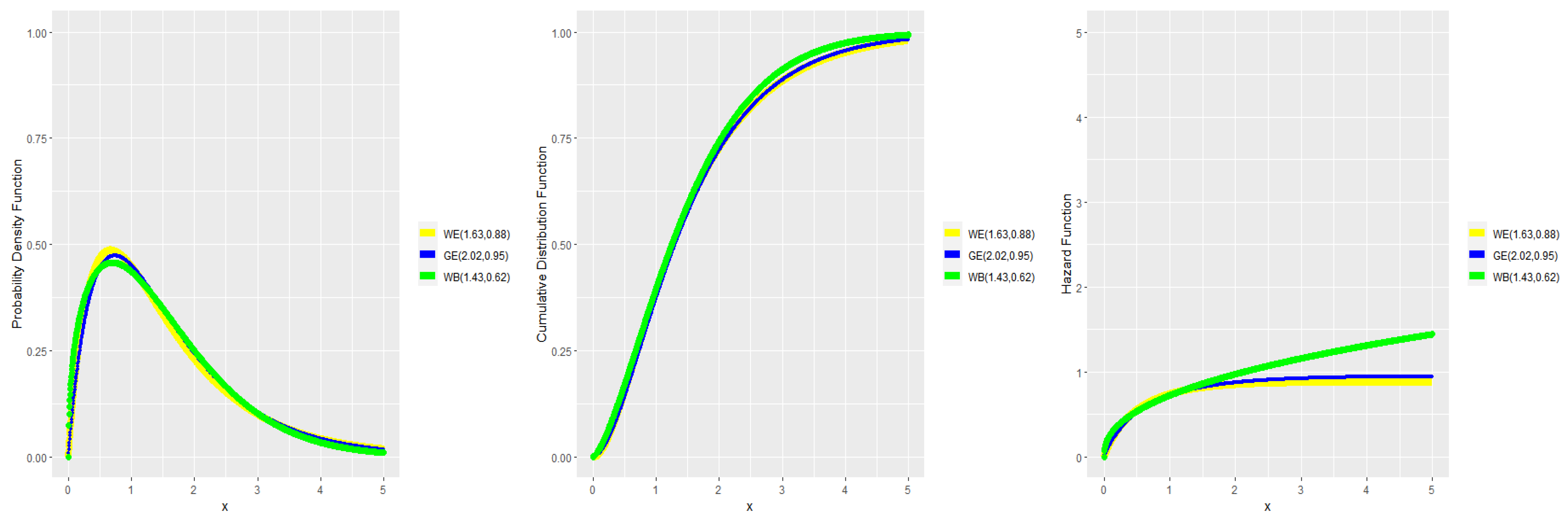
3. Numerical Results
- I:
- The data come from the WE distribution. In this case, we set η = 5.0, 5.2, 5.4, 5.8 and λ = 0.5, 1.0, 1.5. We compute and as defined in (8) and the can be written as follows,
- II:
- The data come from the GE distribution. We set γ = 2.5, 2.7, 2.9, 3.3 and θ = 0.5, 1, 1.5, and the can be obtained as follows,
- III:
- The data come from the WB distribution. We set the parameters β = 2.5, 2.7, 2.9, 3.3 and ξ = 0.5, 1, 1.5, and the can be calculated as follows,
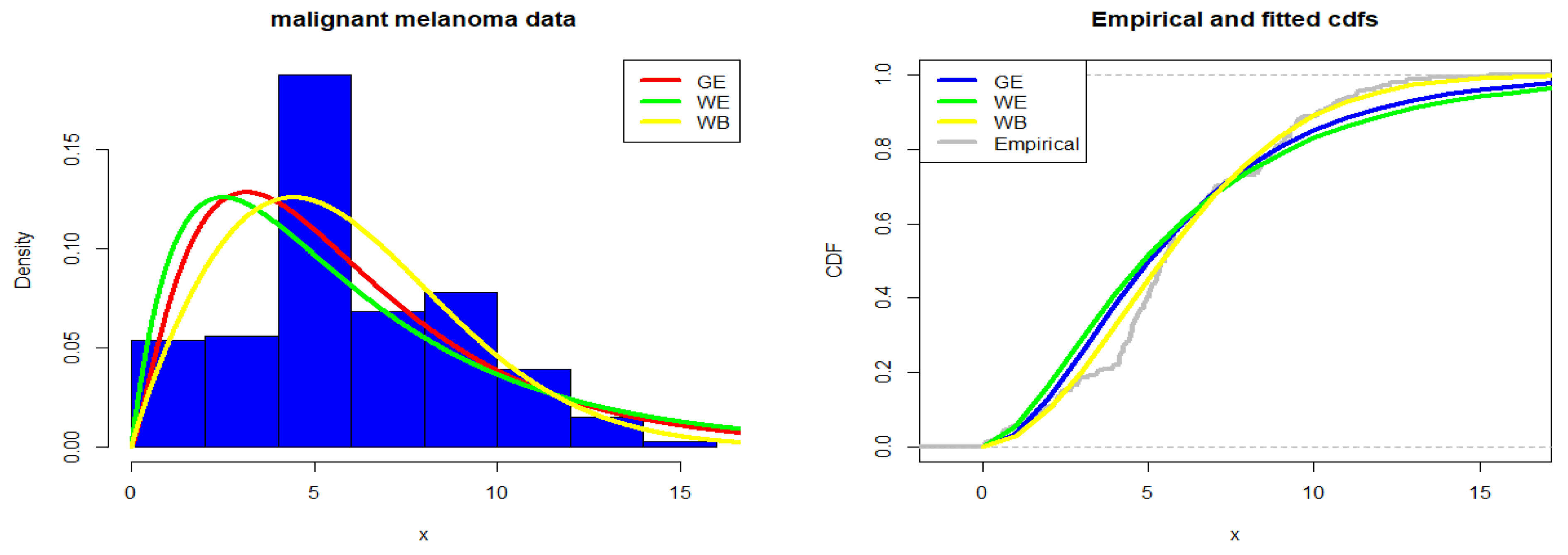
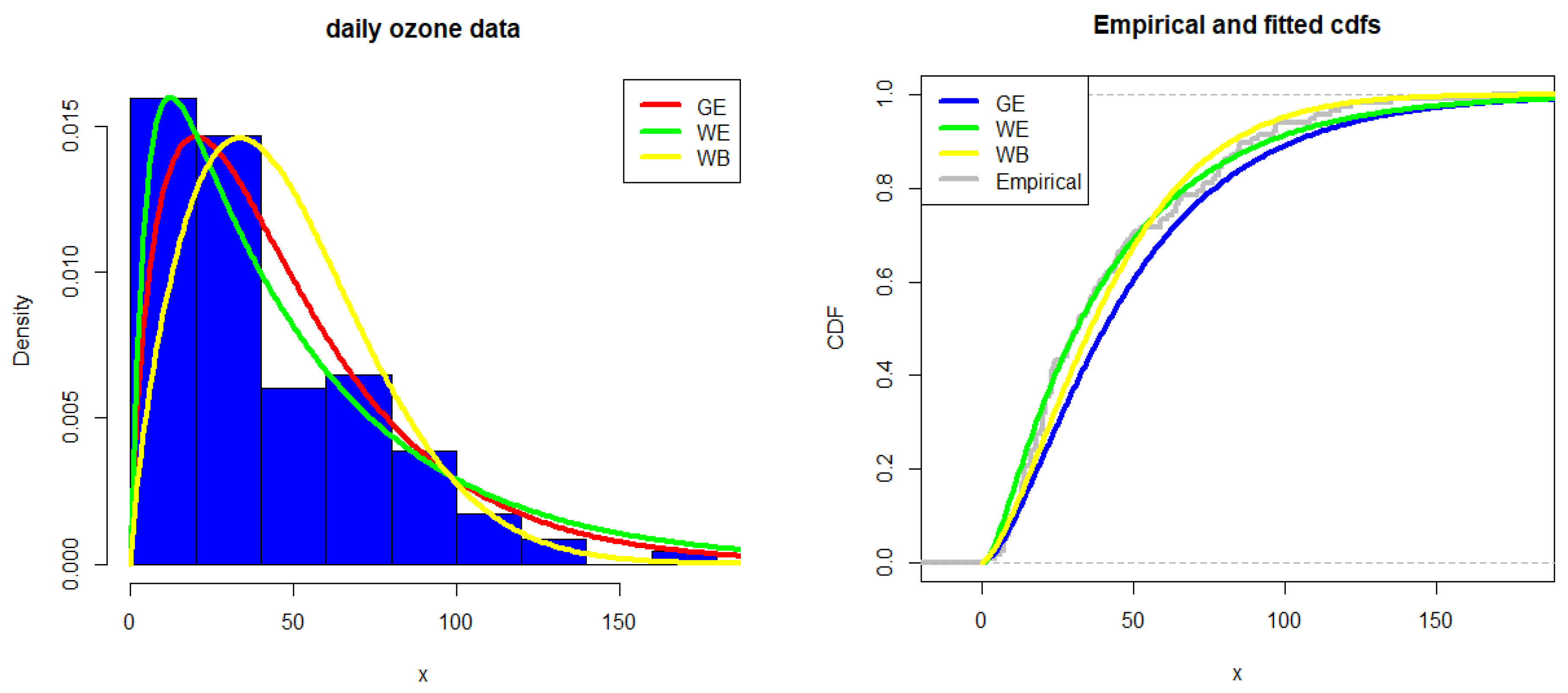
4. Data Analysis
4.1. Malignant Melanoma Data
4.2. Daily Ozone Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Malignant Melanoma Data
Appendix A.2. Daily Ozone Data
Appendix B
References
- Atkinson, A.C. A test for discriminating between models. Biometrika 1969, 56, 337–347. [Google Scholar] [CrossRef]
- Atkinson, A.C. A method for discriminating between models. J. R. Stat. Soc. Ser. B Methodol. 1970, 32, 323–345. [Google Scholar] [CrossRef]
- Chen, W. On the tests of separate families of hypotheses with small sample size. J. Stat. Comput. Simul. 1980, 11, 183–187. [Google Scholar] [CrossRef]
- Chambers, E.A.; Cox, D.R. Discrimination between alternative binary response models. Biometrika 1967, 54, 573–578. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.R. Tests of separate families of hypotheses. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Statistical Laboratory of the University of California: Berkeley, CA, USA, 1961; Volume 1, pp. 105–123. [Google Scholar]
- Cox, D.R. Further results on tests of separate families of hypotheses. J. R. Stat. Soc. Ser. B Methodol. 1962, 24, 406–424. [Google Scholar] [CrossRef]
- Dyer, A.R. Discrimination procedures for separate families of hypotheses. J. Am. Stat. Assoc. 1973, 68, 970–974. [Google Scholar] [CrossRef]
- Weibull, W. A statistical theory of the strength of materials. R. Swed. Inst. Eng. Res. 1939, 151, 7. [Google Scholar]
- Gupta, R.D.; Kundu, D. Theory & methods: Generalized exponential distributions. Aust. N. Z. J. Stat. 1999, 41, 173–188. [Google Scholar]
- Gupta, R.D.; Kundu, D. A new class of weighted exponential distributions. Statistics 2009, 43, 621–634. [Google Scholar] [CrossRef]
- Makhdoom, I. Estimation of r = p[y<x] for weighted exponential distribution. J. Appl. Sci. 2012, 12, 1384–1389. [Google Scholar]
- Dey, S.; Ali, S.; Park, C. Weighted exponential distribution: Properties and different methods of estimation. J. Stat. Comput. Simul. 2015, 85, 3641–3661. [Google Scholar] [CrossRef]
- Tian, W.; Yang, Y. Change point analysis for weighted exponential distribution. Commun. Stat.-Simul. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Closeness of gamma and generalized exponential distribution. Commun. Stat.-Theory Methods 2003, 32, 705–721. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Discriminating between Weibull and generalized exponential distributions. Comput. Stat. Data Anal. 2003, 43, 179–196. [Google Scholar] [CrossRef]
- Pakyari, R. Discriminating between generalized exponential, geometric extreme exponential and Weibull distributions. J. Stat. Comput. Simul. 2010, 80, 1403–1412. [Google Scholar] [CrossRef]
- Raqab, M.Z. Discriminating between the generalized Rayleigh and Weibull distributions. J. Appl. Stat. 2013, 40, 1480–1493. [Google Scholar] [CrossRef]
- Elsherpieny, E.A.; Muhammed, H.Z.; Radwan, N.U.M.M. On discriminating between gamma and log-logistic distributions in case of progressive type II censoring. Pak. J. Stat. Oper. Res. 2017, 13, 157–183. [Google Scholar] [CrossRef][Green Version]
- Ahmad, M.A.; Raqab, M.Z.; Kundu, D. Discriminating between the generalized Rayleigh and Weibull distributions: Some comparative studies. Commun. Stat.-Simul. Comput. 2017, 46, 4880–4895. [Google Scholar] [CrossRef]
- Raqab, M.Z.; Al-Awadhi, S.A.; Kundu, D. Discriminating among Weibull, log-normal, and log-logistic distributions. Commun. Stat.-Simul. Comput. 2018, 47, 1397–1419. [Google Scholar] [CrossRef]
- Vaidyanathan, V.S.; Varghese, A.S. Discriminating Between Exponential and Lindley Distributions. J. Stat. Theory Appl. 2019, 18, 295–302. [Google Scholar] [CrossRef]
- Paul, B.; De, S.K.; Kundu, D. A sequential sampling approach for discriminating log-normal, Weibull, and log-logistic distributions. Commun. Stat.-Simul. Comput. 2021, 1–23. [Google Scholar] [CrossRef]
- Wald, A. Sequential tests of statistical hypotheses. Annu. Math. Stat. 1945, 16, 117–186. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Andersen, P.K.; Borgan, O.; Gill, R.D.; Keiding, N. Statistical Models Based on Counting Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Scheike, T.H.; Zhang, M.J. Analyzing competing risk data using the R timereg package. J. Stat. Softw. 2011, 38, i02. [Google Scholar] [CrossRef] [PubMed]
- Nadarajah, S. A truncated inverted beta distribution with application to air pollution data. Stoch. Environ. Res. Risk Assess. 2008, 22, 285–289. [Google Scholar] [CrossRef]
| () | PCS | 20 | 40 | 60 | 80 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| (5, 0.5) | RML | 0.5072 | 0.5956 | 0.6446 | 0.6700 | 0.6976 | 0.7527 | 0.8570 |
| MKD | 0.3992 | 0.4562 | 0.5012 | 0.5563 | 0.6112 | 0.7002 | 0.7882 | |
| (5.2, 0.5) | RML | 0.5216 | 0.6102 | 0.6522 | 0.6862 | 0.6990 | 0.7642 | 0.8552 |
| MKD | 0.4002 | 0.4577 | 0.5032 | 0.5575 | 0.6155 | 0.7156 | 0.7889 | |
| (5.4, 0.5) | RML | 0.5288 | 0.6136 | 0.6544 | 0.6844 | 0.7114 | 0.7654 | 0.8628 |
| MKD | 0.4132 | 0.4585 | 0.5045 | 0.5584 | 0.6225 | 0.7226 | 0.7995 | |
| (5.8, 0.5) | RML | 0.5364 | 0.6264 | 0.6630 | 0.6950 | 0.7152 | 0.7770 | 0.8702 |
| MKD | 0.4235 | 0.4598 | 0.5112 | 0.5598 | 0.6310 | 0.7250 | 0.8002 | |
| (5, 1) | RML | 0.5152 | 0.6066 | 0.6486 | 0.6760 | 0.6966 | 0.7582 | 0.8588 |
| MKD | 0.4005 | 0.4587 | 0.5022 | 0.5589 | 0.6136 | 0.7125 | 0.7902 | |
| (5.2, 1) | RML | 0.5236 | 0.6192 | 0.6540 | 0.6872 | 0.6996 | 0.7666 | 0.8564 |
| MKD | 0.4050 | 0.4592 | 0.5044 | 0.5591 | 0.6162 | 0.7163 | 0.7905 | |
| (5.4, 1) | RML | 0.5340 | 0.6216 | 0.6594 | 0.6896 | 0.7132 | 0.7692 | 0.8666 |
| MKD | 0.4138 | 0.4598 | 0.5199 | 0.5589 | 0.6255 | 0.7320 | 0.8002 | |
| (5.8, 1) | RML | 0.5386 | 0.6348 | 0.6740 | 0.6972 | 0.7158 | 0.7802 | 0.8744 |
| MKD | 0.4244 | 0.4608 | 0.5220 | 0.5623 | 0.6332 | 0.7365 | 0.8115 | |
| (5, 1.5) | RML | 0.5176 | 0.6072 | 0.6584 | 0.6856 | 0.7030 | 0.7602 | 0.8596 |
| MKD | 0.4010 | 0.4599 | 0.5056 | 0.5623 | 0.6188 | 0.7223 | 0.7956 | |
| (5.2, 1.5) | RML | 0.5312 | 0.6224 | 0.6562 | 0.6918 | 0.7094 | 0.7690 | 0.8654 |
| MKD | 0.4112 | 0.4602 | 0.5089 | 0.5633 | 0.6220 | 0.7228 | 0.7998 | |
| (5.4, 1.5) | RML | 0.5422 | 0.6240 | 0.6622 | 0.6914 | 0.7164 | 0.7728 | 0.8710 |
| MKD | 0.4189 | 0.4625 | 0.5232 | 0.5662 | 0.6305 | 0.7335 | 0.8156 | |
| (5.8, 1.5) | RML | 0.5454 | 0.6358 | 0.6694 | 0.7006 | 0.7188 | 0.7830 | 0.8774 |
| MKD | 0.4256 | 0.4668 | 0.5238 | 0.5671 | 0.6354 | 0.7399 | 0.8226 |
| () | PCS | 20 | 40 | 60 | 80 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| (2.5, 0.5) | RML | 0.4690 | 0.5460 | 0.6124 | 0.6612 | 0.7070 | 0.8168 | 0.9482 |
| MKD | 0.3746 | 0.4156 | 0.4620 | 0.5042 | 0.5218 | 0.6410 | 0.8226 | |
| (2.7, 0.5) | RML | 0.5056 | 0.6176 | 0.6698 | 0.7276 | 0.7706 | 0.8874 | 0.9808 |
| MKD | 0.4098 | 0.4758 | 0.5040 | 0.5554 | 0.5934 | 0.7382 | 0.9170 | |
| (2.9, 0.5) | RML | 0.5560 | 0.6578 | 0.7252 | 0.7774 | 0.8094 | 0.9200 | 0.9866 |
| MKD | 0.4116 | 0.4889 | 0.5051 | 0.5561 | 0.5955 | 0.7392 | 0.9188 | |
| (3.3, 0.5) | RML | 0.5930 | 0.7102 | 0.7728 | 0.8180 | 0.8512 | 0.9370 | 0.9932 |
| MKD | 0.4225 | 0.4902 | 0.5066 | 0.5575 | 0.5965 | 0.7399 | 0.9192 | |
| (2.5, 1) | RML | 0.4862 | 0.5596 | 0.6182 | 0.6648 | 0.7082 | 0.8192 | 0.9504 |
| MKD | 0.3756 | 0.4174 | 0.4648 | 0.5052 | 0.5240 | 0.6468 | 0.8304 | |
| (2.7, 1) | RML | 0.5138 | 0.6184 | 0.6706 | 0.7334 | 0.7788 | 0.8878 | 0.9812 |
| MKD | 0.4105 | 0.4768 | 0.5063 | 0.5559 | 0.5996 | 0.7388 | 0.9220 | |
| (2.9, 1) | RML | 0.5576 | 0.6620 | 0.7276 | 0.7812 | 0.8112 | 0.9212 | 0.9896 |
| MKD | 0.4220 | 0.4992 | 0.5065 | 0.5602 | 0.5998 | 0.7401 | 0.9232 | |
| (3.3, 1) | RML | 0.6006 | 0.7136 | 0.7766 | 0.8186 | 0.8532 | 0.9376 | 0.9936 |
| MKD | 0.4236 | 0.4933 | 0.5074 | 0.5678 | 0.6002 | 0.7411 | 0.9235 | |
| (2.5, 1.5) | RML | 0.4894 | 0.5604 | 0.6224 | 0.6696 | 0.7188 | 0.8254 | 0.9510 |
| MKD | 0.3804 | 0.4238 | 0.4690 | 0.5070 | 0.5260 | 0.6514 | 0.8322 | |
| (2.7, 1.5) | RML | 0.5154 | 0.6278 | 0.6790 | 0.7354 | 0.7830 | 0.8892 | 0.9842 |
| MKD | 0.4188 | 0.4777 | 0.5077 | 0.5613 | 0.6005 | 0.7416 | 0.9235 | |
| (2.9, 1.5) | RML | 0.5592 | 0.6716 | 0.7326 | 0.7848 | 0.8128 | 0.9238 | 0.9910 |
| MKD | 0.4222 | 0.5009 | 0.5112 | 0.5622 | 0.6015 | 0.7554 | 0.9245 | |
| (3.3, 1.5) | RML | 0.6098 | 0.7208 | 0.7820 | 0.8246 | 0.8536 | 0.9398 | 0.9954 |
| MKD | 0.4288 | 0.4955 | 0.5142 | 0.5688 | 0.6116 | 0.7623 | 0.9255 |
| () | PCS | 20 | 40 | 60 | 80 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| (2.5, 0.5) | RML | 0.7356 | 0.8264 | 0.8894 | 0.9264 | 0.9458 | 0.9888 | 1 |
| MKD | 0.4326 | 0.6158 | 0.7206 | 0.7882 | 0.8324 | 0.9418 | 0.9956 | |
| (2.7, 0.5) | RML | 0.7660 | 0.8600 | 0.9058 | 0.9368 | 0.9532 | 0.9944 | 1 |
| MKD | 0.4628 | 0.6406 | 0.7564 | 0.8106 | 0.8590 | 0.9576 | 0.9978 | |
| (2.9, 0.5) | RML | 0.7698 | 0.8642 | 0.9214 | 0.9452 | 0.9682 | 0.9954 | 1 |
| MKD | 0.4816 | 0.6566 | 0.7652 | 0.8250 | 0.8688 | 0.9630 | 0.9990 | |
| (3.3, 0.5) | RML | 0.7946 | 0.8850 | 0.9348 | 0.9634 | 0.9782 | 0.9984 | 1 |
| MKD | 0.5260 | 0.6880 | 0.8044 | 0.8604 | 0.9074 | 0.9782 | 0.9996 | |
| (2.5, 1) | RML | 0.7406 | 0.8284 | 0.8968 | 0.9294 | 0.9480 | 0.9914 | 1 |
| MKD | 0.4450 | 0.6214 | 0.7232 | 0.7912 | 0.8416 | 0.9442 | 0.9958 | |
| (2.7, 1) | RML | 0.7628 | 0.8610 | 0.9084 | 0.9396 | 0.9588 | 0.9948 | 1 |
| MKD | 0.4633 | 0.6423 | 0.7612 | 0.8226 | 0.8599 | 0.9662 | 0.9981 | |
| (2.9, 1) | RML | 0.7746 | 0.8680 | 0.9228 | 0.9462 | 0.9696 | 0.9966 | 1 |
| MKD | 0.4822 | 0.6589 | 0.7668 | 0.8288 | 0.8696 | 0.9676 | 0.9995 | |
| (3.3, 1) | RML | 0.7996 | 0.8868 | 0.9350 | 0.9664 | 0.9784 | 0.9986 | 1 |
| MKD | 0.5311 | 0.6885 | 0.8123 | 0.8698 | 0.9122 | 0.9881 | 0.9998 | |
| (2.5, 1.5) | RML | 0.7468 | 0.8456 | 0.8990 | 0.9302 | 0.9522 | 0.9922 | 1 |
| MKD | 0.4466 | 0.6234 | 0.7252 | 0.7930 | 0.8426 | 0.9464 | 0.9970 | |
| (2.7, 1.5) | RML | 0.7672 | 0.8694 | 0.9088 | 0.9442 | 0.9604 | 0.9954 | 1 |
| MKD | 0.4665 | 0.6466 | 0.7655 | 0.8239 | 0.8623 | 0.9702 | 0.9985 | |
| (2.9, 1.5) | RML | 0.7778 | 0.8768 | 0.9266 | 0.9520 | 0.9714 | 0.9974 | 1 |
| MKD | 0.4836 | 0.6612 | 0.7670 | 0.8295 | 0.8702 | 0.9702 | 0.9998 | |
| (3.3, 1.5) | RML | 0.8002 | 0.8912 | 0.9384 | 0.9678 | 0.9804 | 0.9992 | 1 |
| MKD | 0.5326 | 0.6892 | 0.8133 | 0.8706 | 0.9222 | 0.9905 | 1 |
| True Distribution | Boundaries | Savings % | ||||
|---|---|---|---|---|---|---|
| WE (5, 0.5) | 2.9957 | 0.9662 | 0.9605 | 521.33 | 800 | 34.83 |
| 2.3026 | 0.9009 | 0.9025 | 483.66 | 700 | 30.91 | |
| WE (5.2, 0.5) | 2.9957 | 0.9447 | 0.9436 | 506.66 | 750 | 32.45 |
| 2.3026 | 0.9118 | 0.9156 | 452.22 | 660 | 34.63 | |
| WE (5.4, 0.5) | 2.9957 | 0.9502 | 0.9500 | 485.99 | 690 | 29.57 |
| 2.3026 | 0.9100 | 0.9164 | 421.20 | 610 | 30.95 | |
| WE (5.8, 0.5) | 2.9957 | 0.9409 | 0.9438 | 458.66 | 640 | 28.33 |
| 2.3026 | 0.9009 | 0.9066 | 396.88 | 560 | 29.13 |
| True Distribution | Boundaries | Savings % | ||||
|---|---|---|---|---|---|---|
| GE (2.5, 0.5) | 2.9957 | 0.9420 | 0.9446 | 452.22 | 780 | 42.02 |
| 2.3026 | 0.9002 | 0.9056 | 411.32 | 660 | 37.68 | |
| GE (2.7, 0.5) | 2.9957 | 0.9500 | 0.9588 | 422.60 | 710 | 40.48 |
| 2.3026 | 0.9118 | 0.9156 | 395.66 | 620 | 36.18 | |
| GE (2.9, 0.5) | 2.9957 | 0.9444 | 0.9494 | 400.22 | 650 | 38.43 |
| 2.3026 | 0.9103 | 0.9111 | 378.60 | 580 | 34.72 | |
| GE (3.3, 0.5) | 2.9957 | 0.9599 | 0.9556 | 385.89 | 600 | 35.69 |
| 2.3026 | 0.9101 | 0.9119 | 346.22 | 550 | 37.05 |
| True Distribution | Boundaries | Savings % | ||||
|---|---|---|---|---|---|---|
| WB (2.5, 0.5) | 2.9957 | 0.9433 | 0.9450 | 243.22 | 500 | 51.36 |
| 2.3026 | 0.9006 | 0.9063 | 205.12 | 380 | 46.02 | |
| WB (2.7, 0.5) | 2.9957 | 0.9336 | 0.9380 | 228.62 | 450 | 49.20 |
| 2.3026 | 0.9112 | 0.9156 | 186.23 | 340 | 45.23 | |
| WB (2.9, 0.5) | 2.9957 | 0.9503 | 0.9551 | 206.88 | 410 | 49.54 |
| 2.3026 | 0.9050 | 0.9066 | 206.88 | 320 | 35.35 | |
| WB (3.3, 0.5) | 2.9957 | 0.9333 | 0.9368 | 206.88 | 380 | 45.56 |
| 2.3026 | 0.9034 | 0.9067 | 126.33 | 290 | 56.44 |
| Model | GE | WE | WB |
|---|---|---|---|
| shape parameters’ estimation | = 2.3371 | = 2.1321 | = 1.8895 |
| scale parameters’ estimation | = 0.2712 | = 0.2152 | = 0.1521 |
| −6.6095 | |||
| 23.4740 | |||
| 16.8645 | |||
| 2.1162 | |||
| −2.3319 | |||
| −2.3102 | |||
| AIC | 1081.2700 | 1094.4870 | 1047.5400 |
| BIC | 1087.9160 | 1101.1330 | 1054.1860 |
| MKD | 0.1700 | 0.1813 | 0.1127 |
| Model | GE | WE | WB |
|---|---|---|---|
| shape parameters’ estimation | = 1.7960 | = 9.4201 | = 1.3402 |
| scale parameters’ estimation | = 0.0337 | = 0.0205 | = 0.0217 |
| 0.4501 | |||
| −1.6644 | |||
| −1.2143 | |||
| −2.3088 | |||
| 2.3112 | |||
| 2.0036 | |||
| AIC | 1086.7920 | 1085.8920 | 1089.2210 |
| BIC | 1092.2990 | 1091.3990 | 1094.7280 |
| MKD | 0.0846 | 0.0564 | 0.0900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, R.; Tian, W.; Zhang, Y. Discriminating among Generalized Exponential, Weighted Exponential and Weibull Distributions. Mathematics 2023, 11, 3847. https://doi.org/10.3390/math11183847
Niu R, Tian W, Zhang Y. Discriminating among Generalized Exponential, Weighted Exponential and Weibull Distributions. Mathematics. 2023; 11(18):3847. https://doi.org/10.3390/math11183847
Chicago/Turabian StyleNiu, Ruizheng, Weizhong Tian, and Yunchu Zhang. 2023. "Discriminating among Generalized Exponential, Weighted Exponential and Weibull Distributions" Mathematics 11, no. 18: 3847. https://doi.org/10.3390/math11183847
APA StyleNiu, R., Tian, W., & Zhang, Y. (2023). Discriminating among Generalized Exponential, Weighted Exponential and Weibull Distributions. Mathematics, 11(18), 3847. https://doi.org/10.3390/math11183847







