Controlling COVID-19 Spreading: A Three-Level Algorithm
Abstract
:1. Introduction
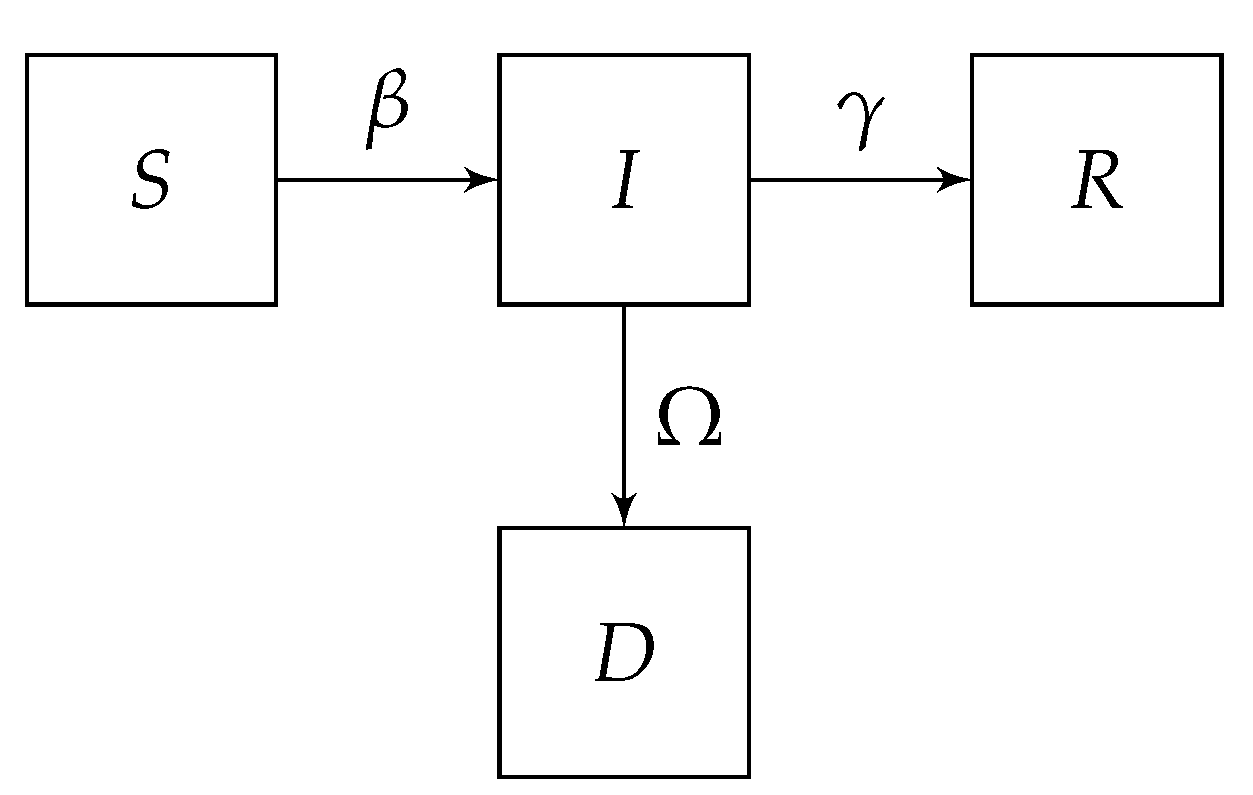
2. Model Formulation
- A recovered individual should acquire immunity and does not return to the susceptible compartment. Hence, they become “Removed” (“R” from SIRD);
- Parameters , and are considered to be constants, despite depending on individual behavior, healthcare availability and age.
3. System Dynamics Analysis
3.1. Equilibrium Conditions
3.2. Equilibrium Points Classification
- If 0 ⇒ these fixed points are unstable [62]; so, there will be a growth in cases for a small perturbation.
- If ⇒ the center manifold theorem must be applied in order to classify the stability condition.
- .
3.3. Basic Reproduction Rate
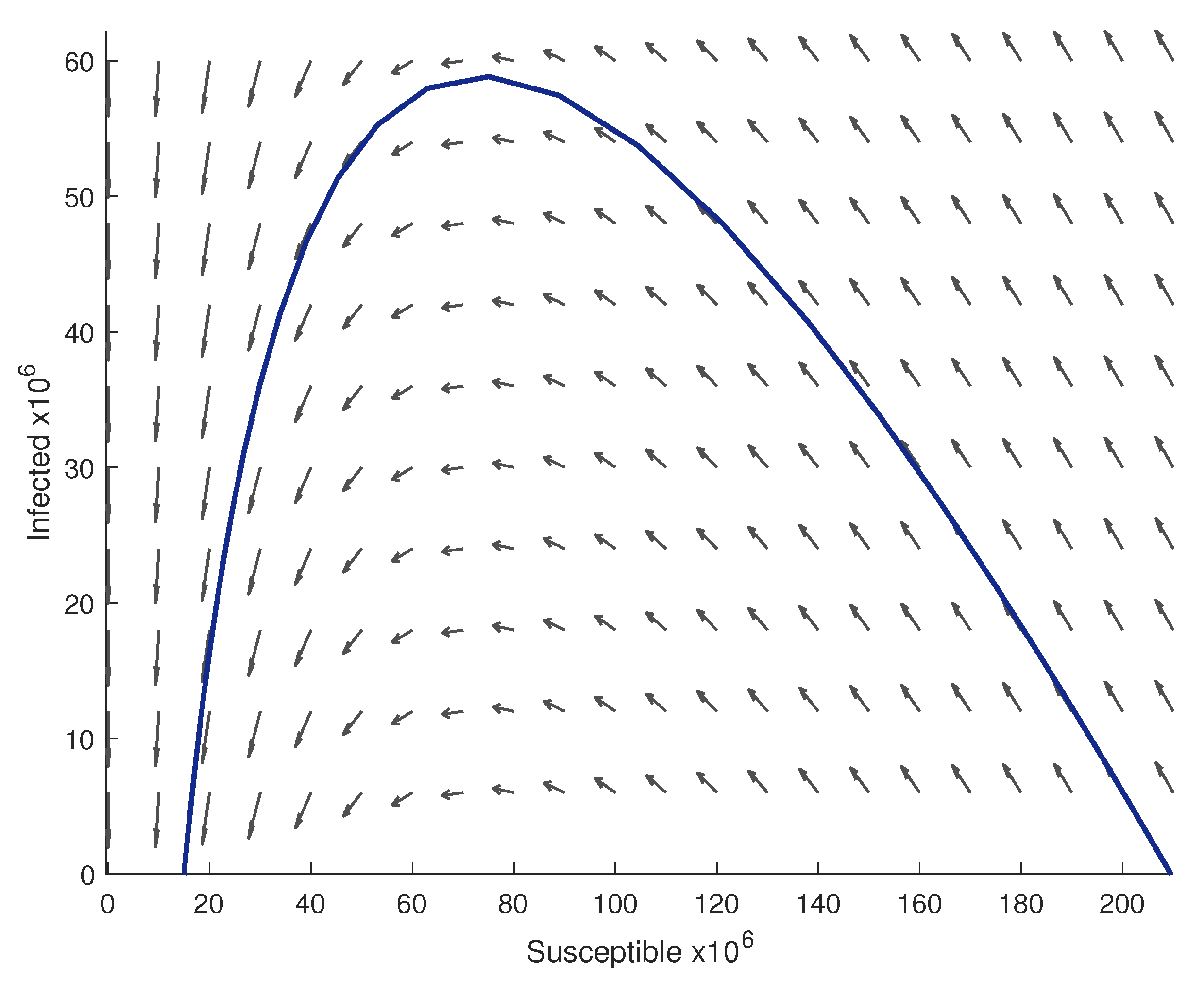
3.4. Phase Portrait for Different Values of
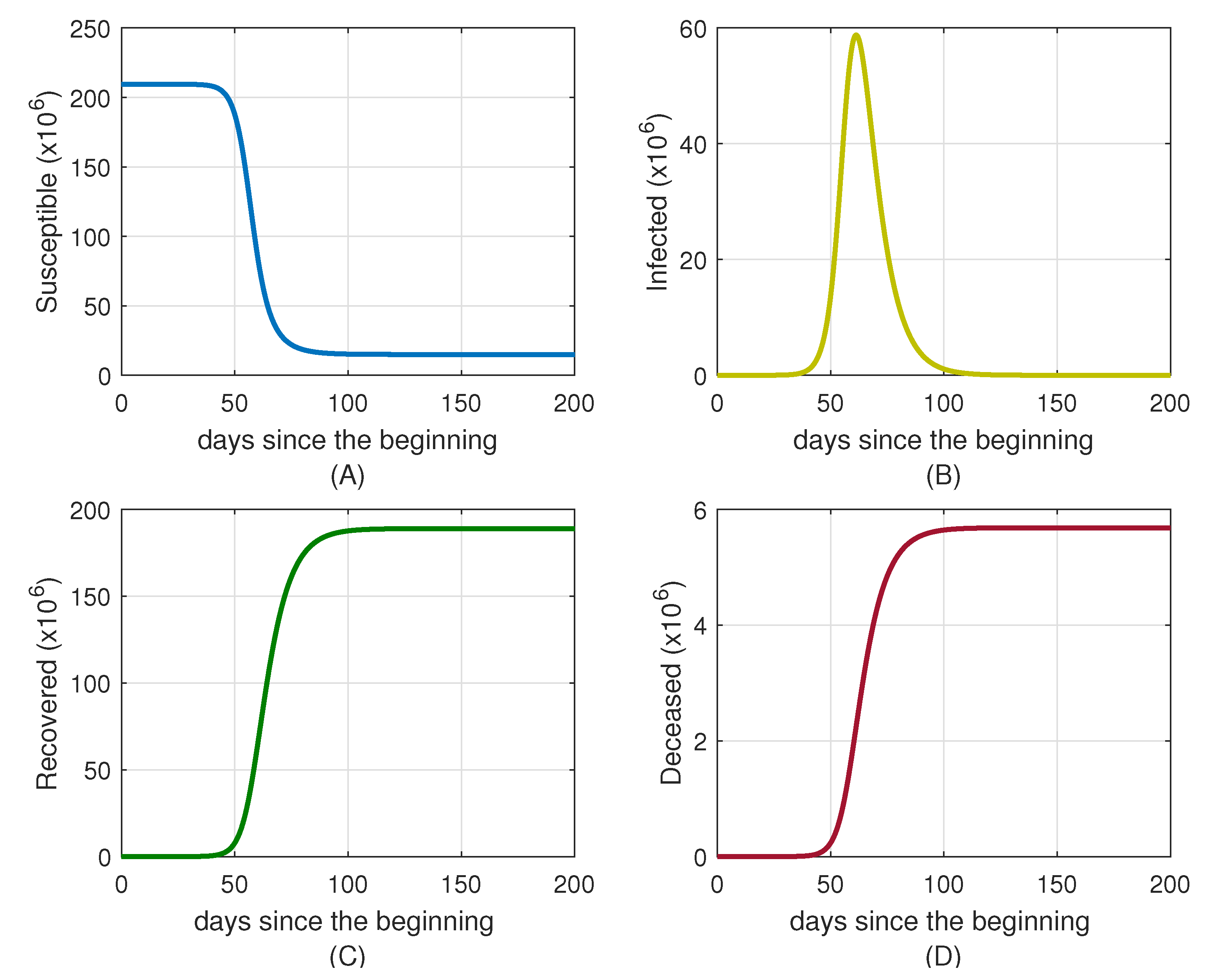
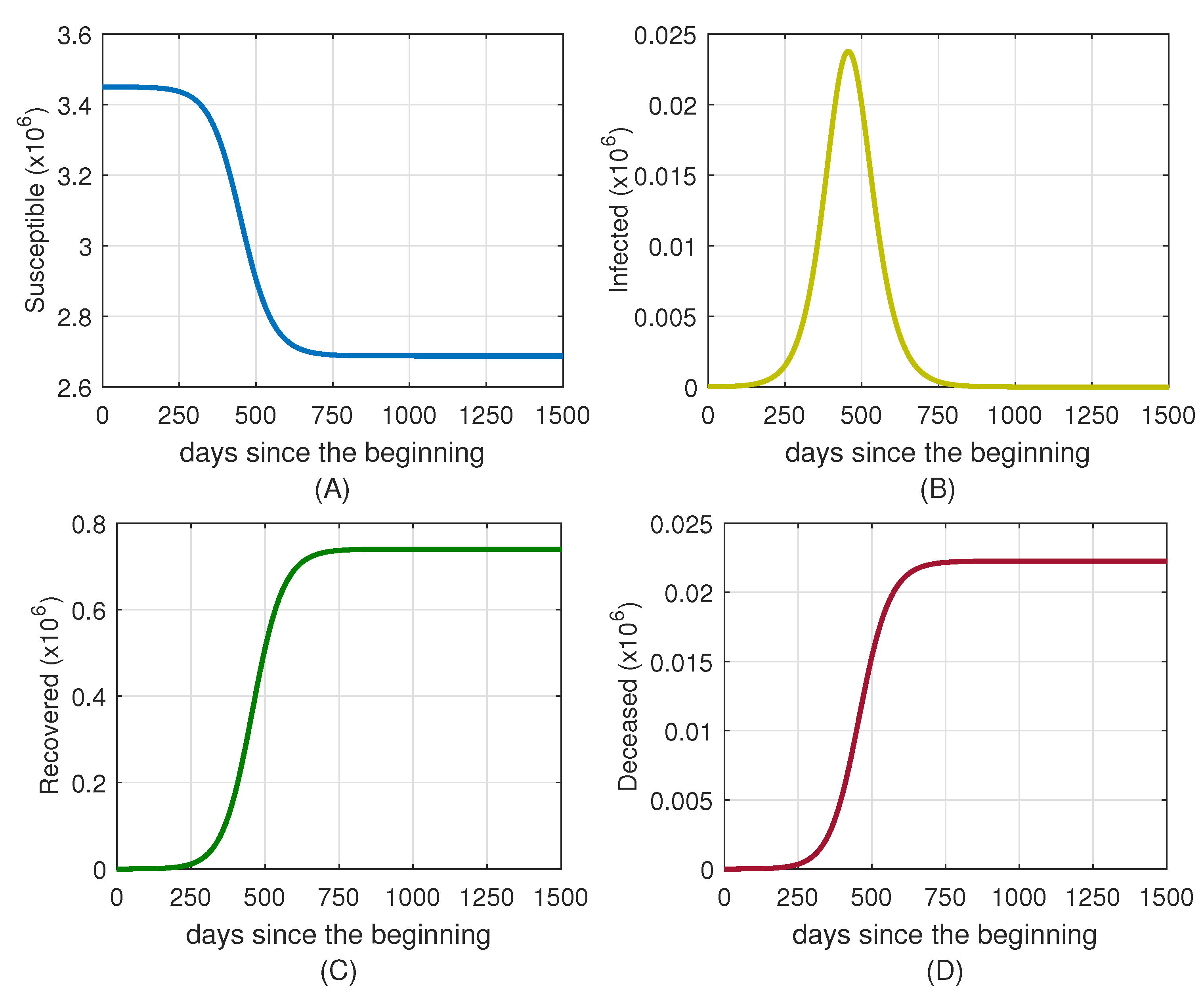
4. Case Studies and Numerical Simulations
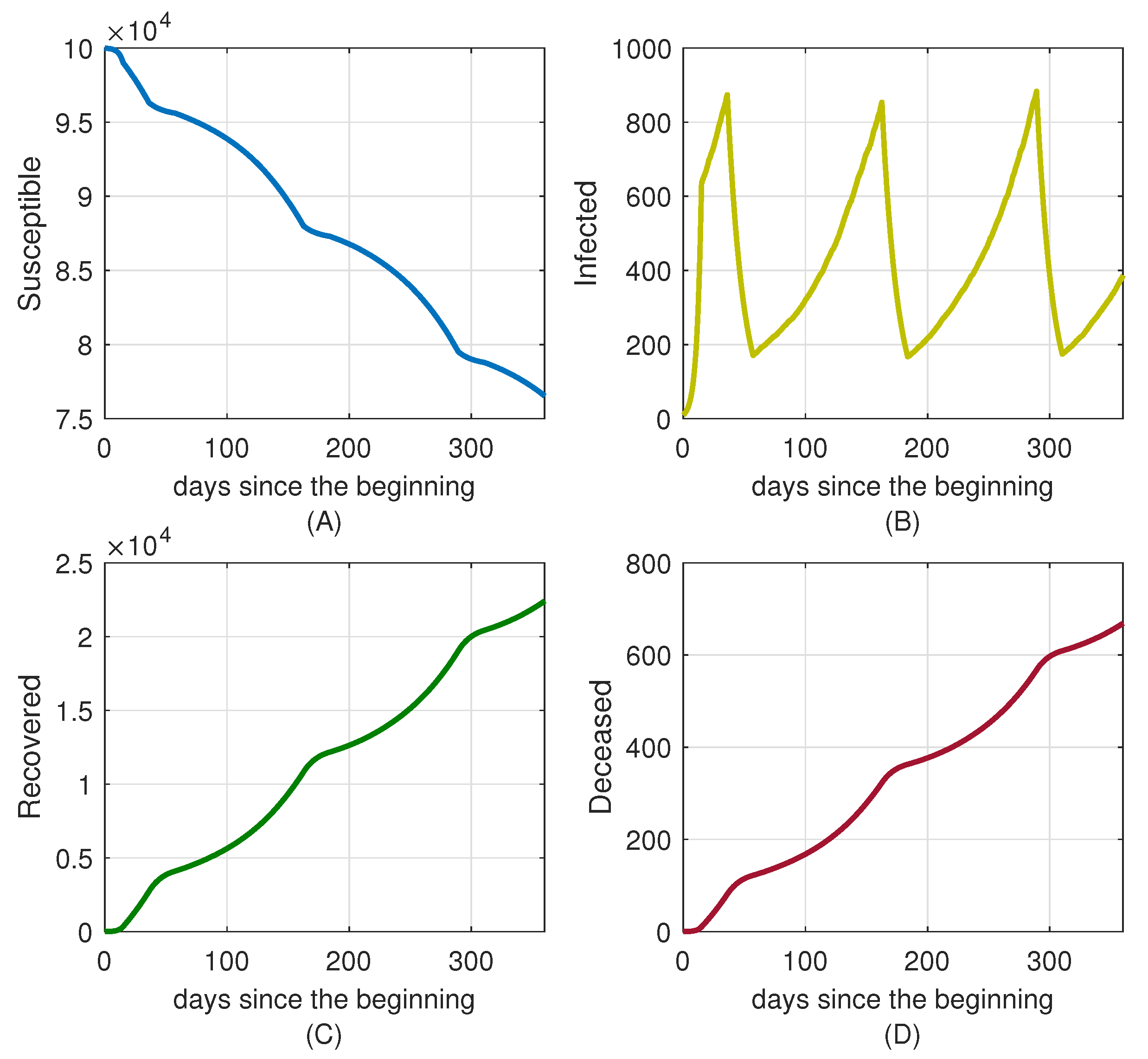
4.1. Simulation for Brazil
4.2. Simulation for Uruguay
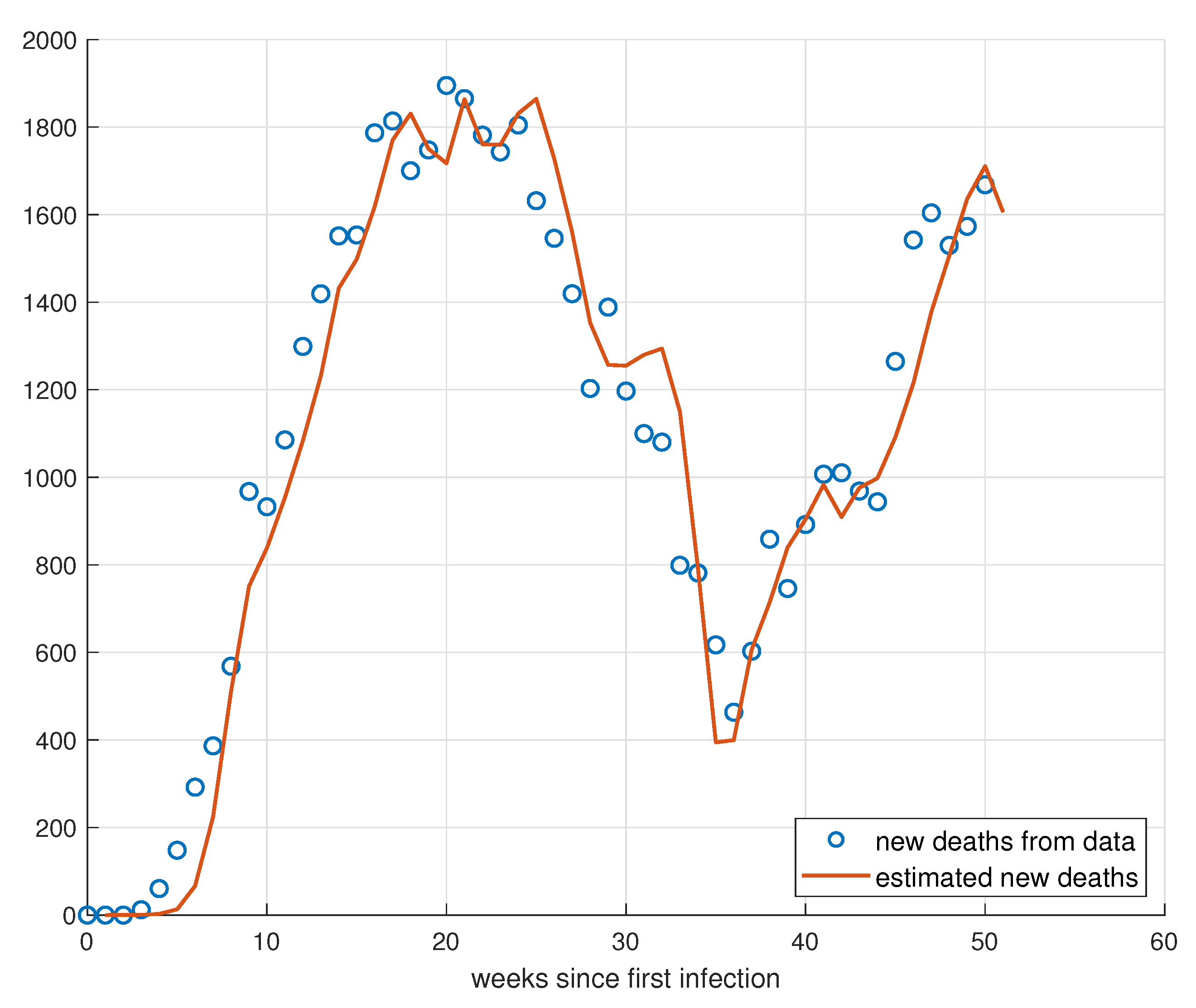
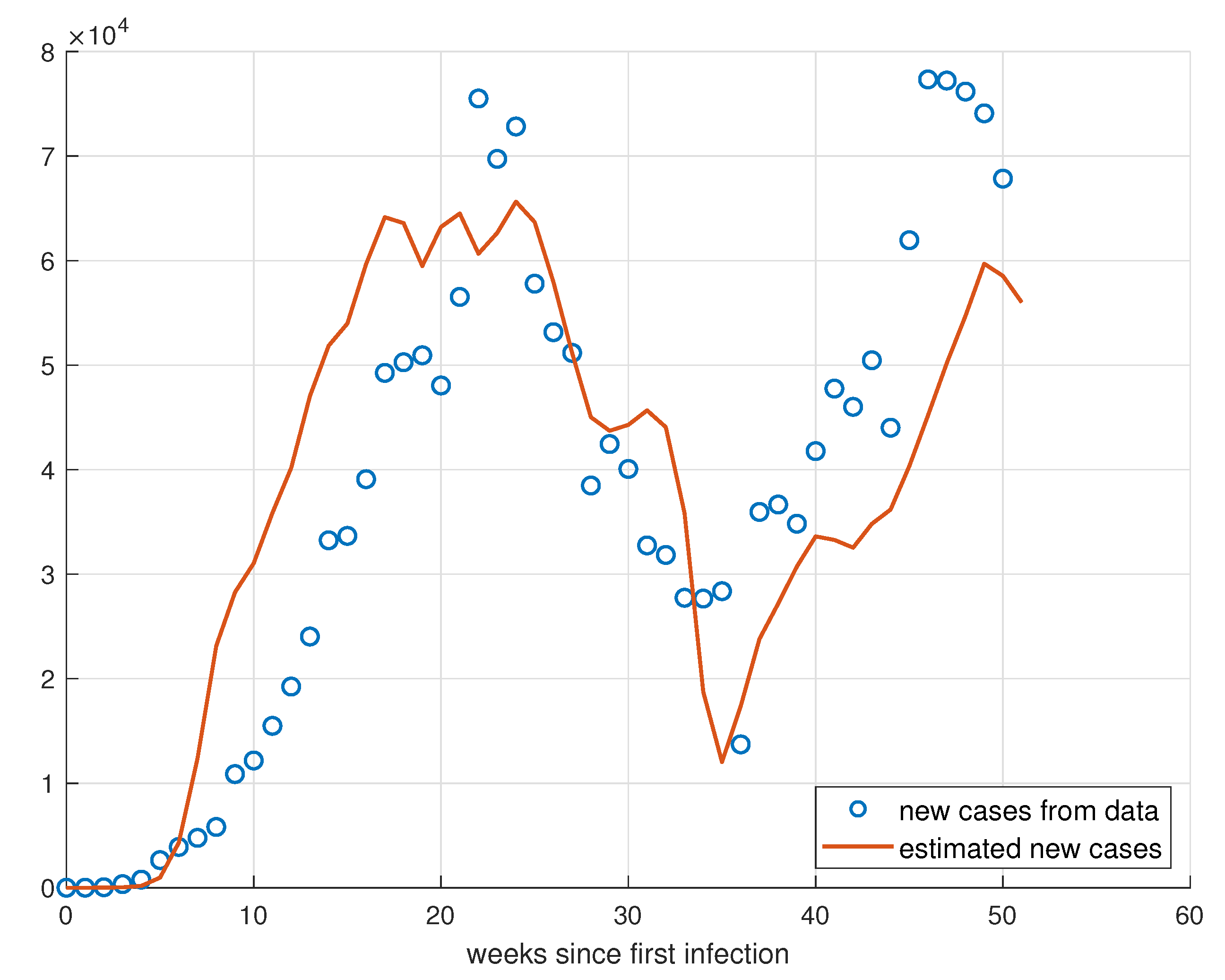
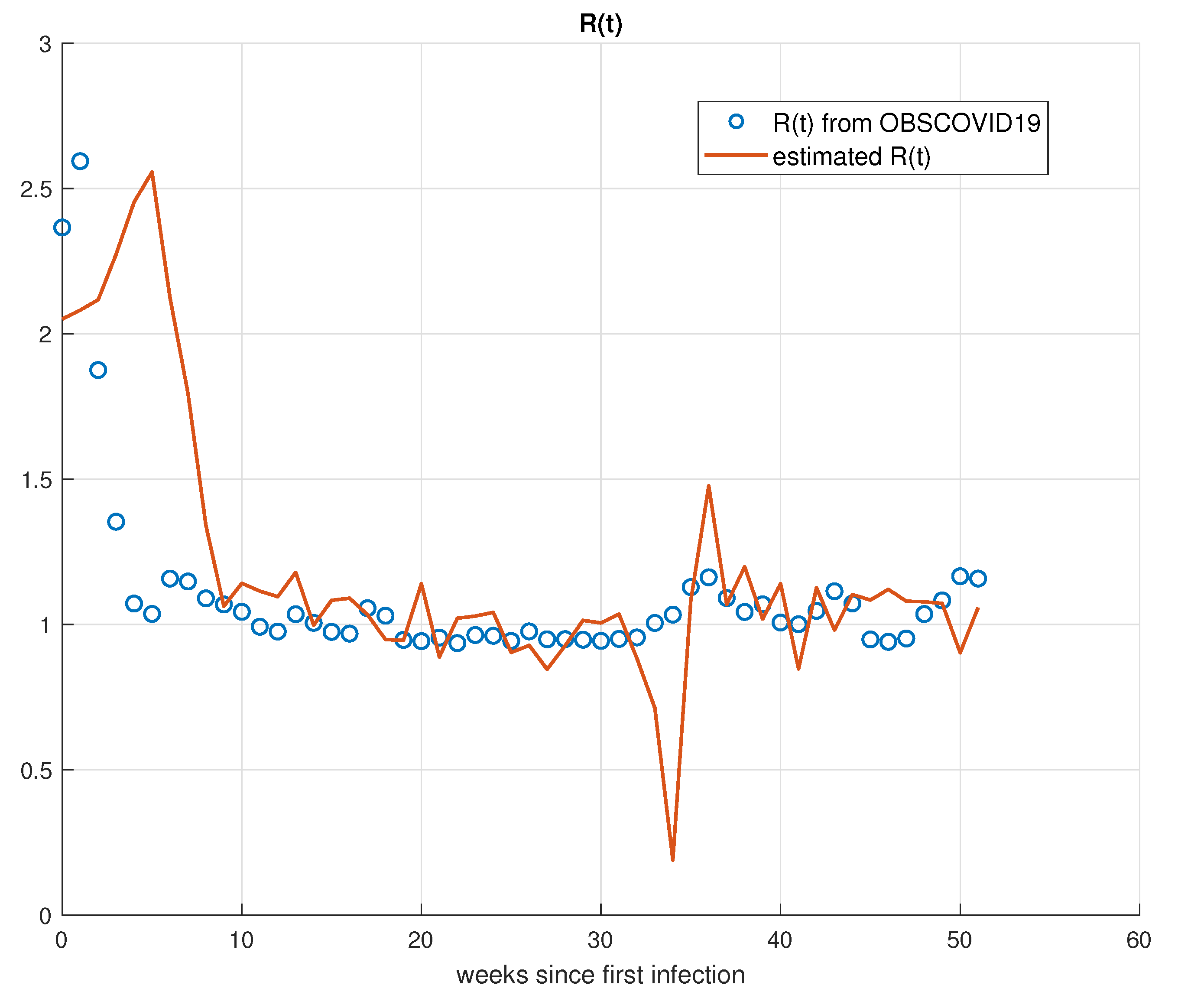
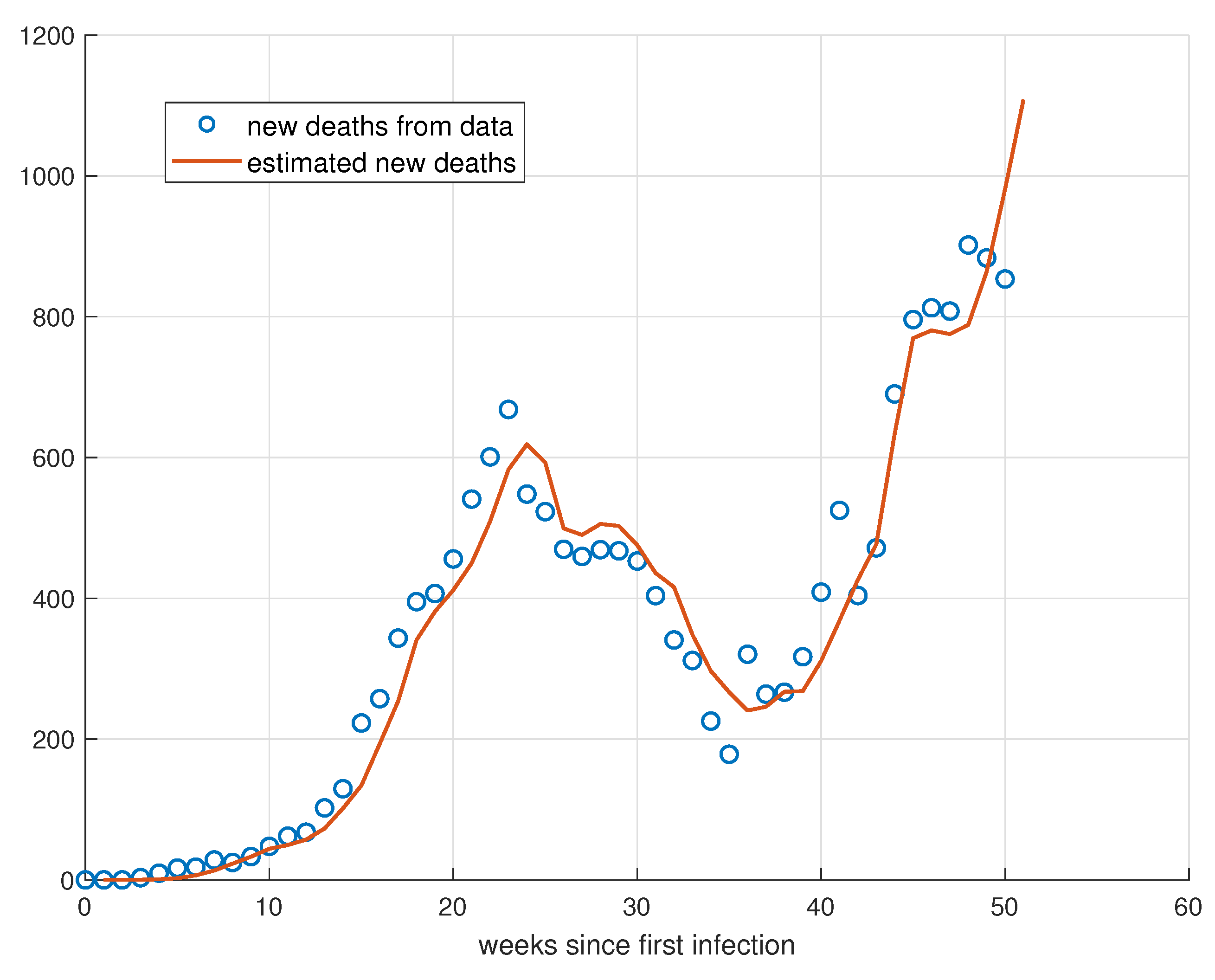
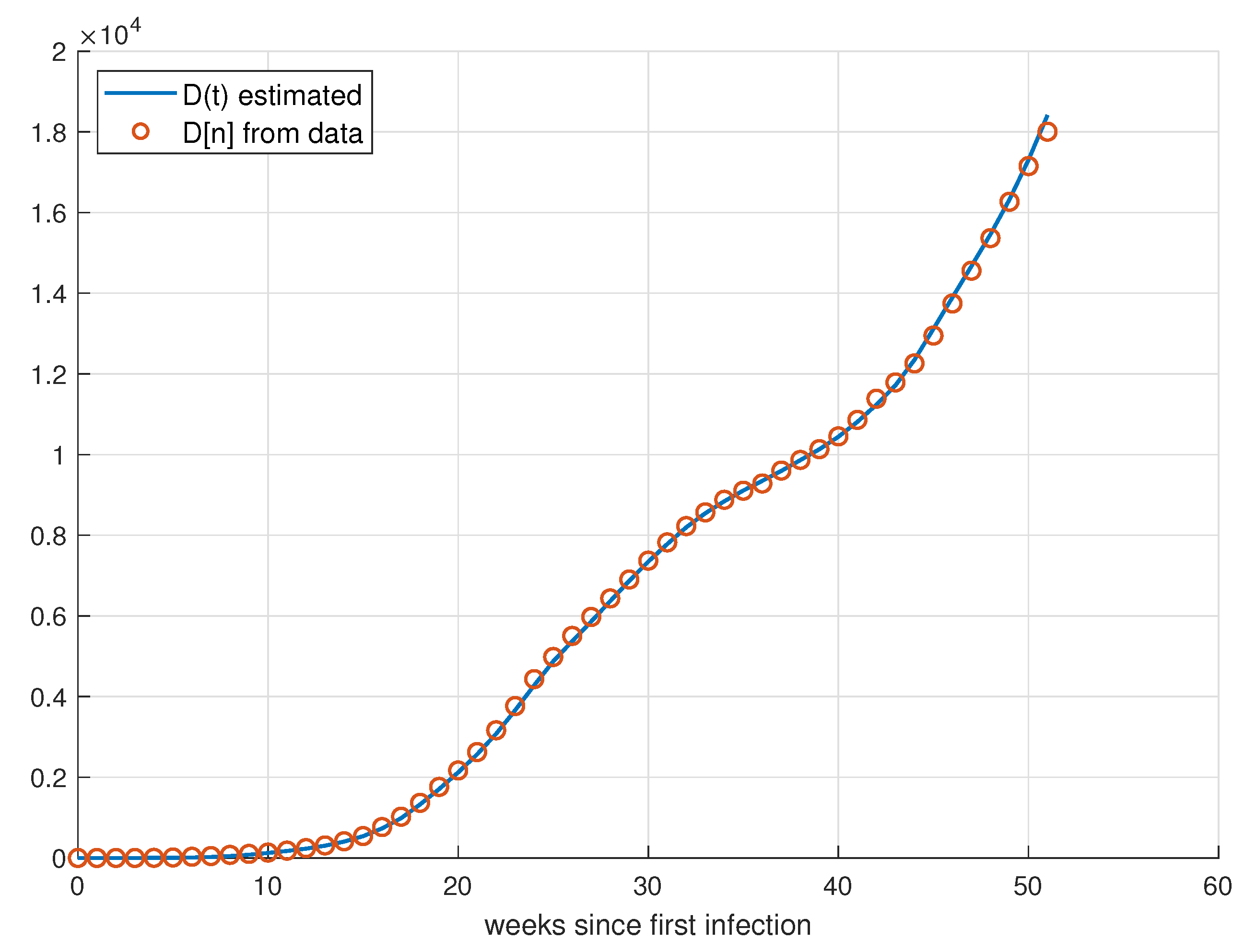
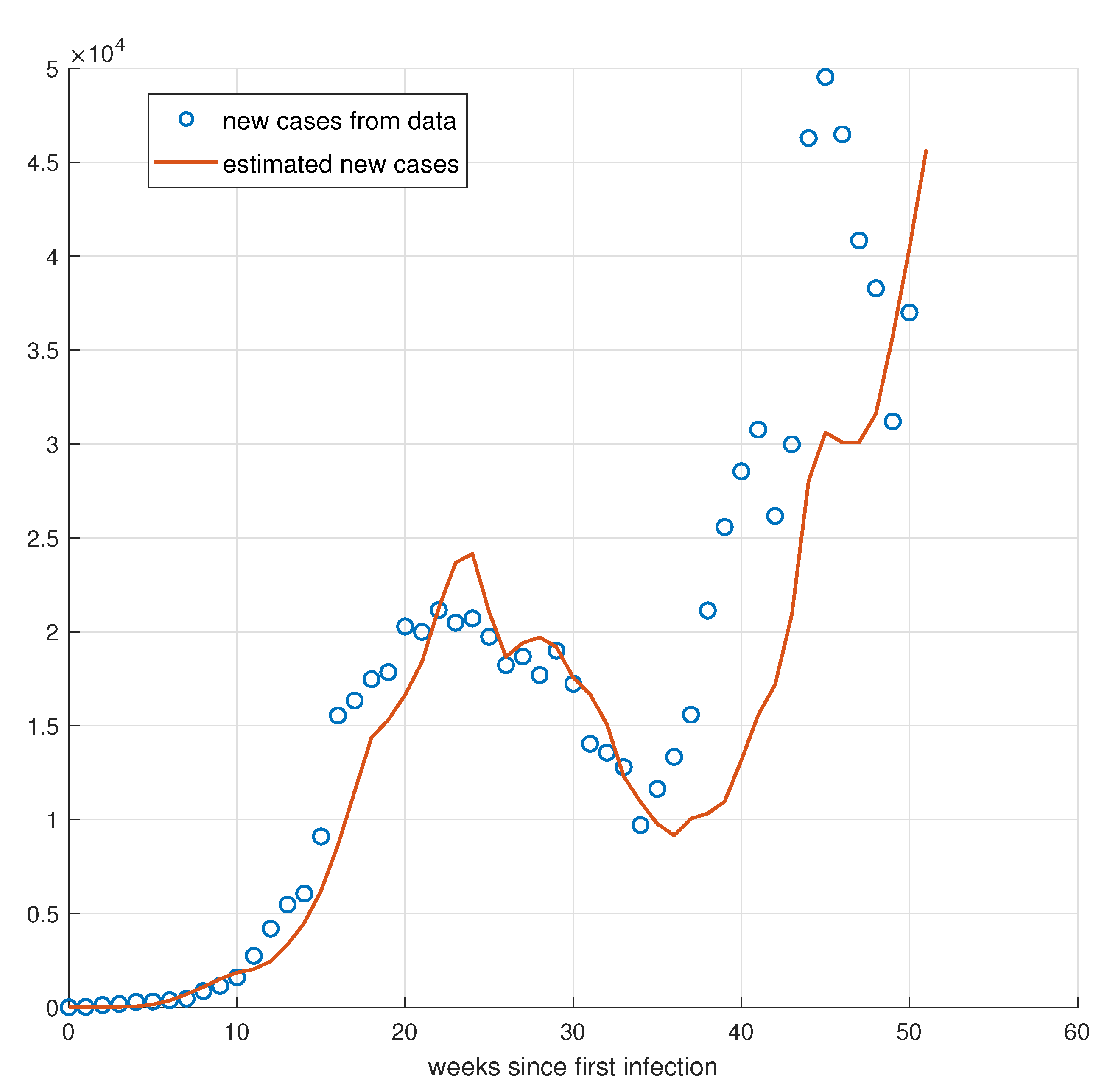
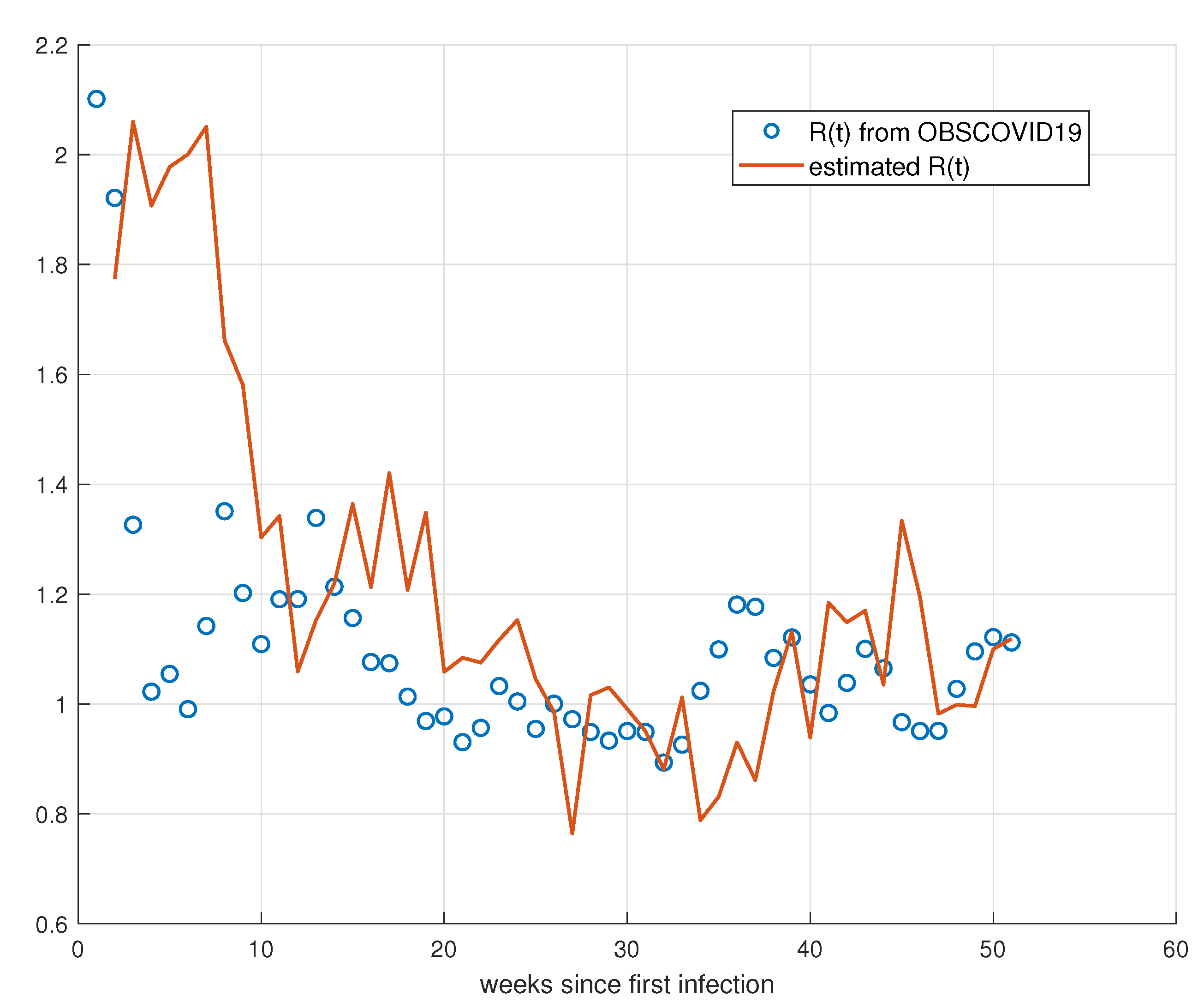
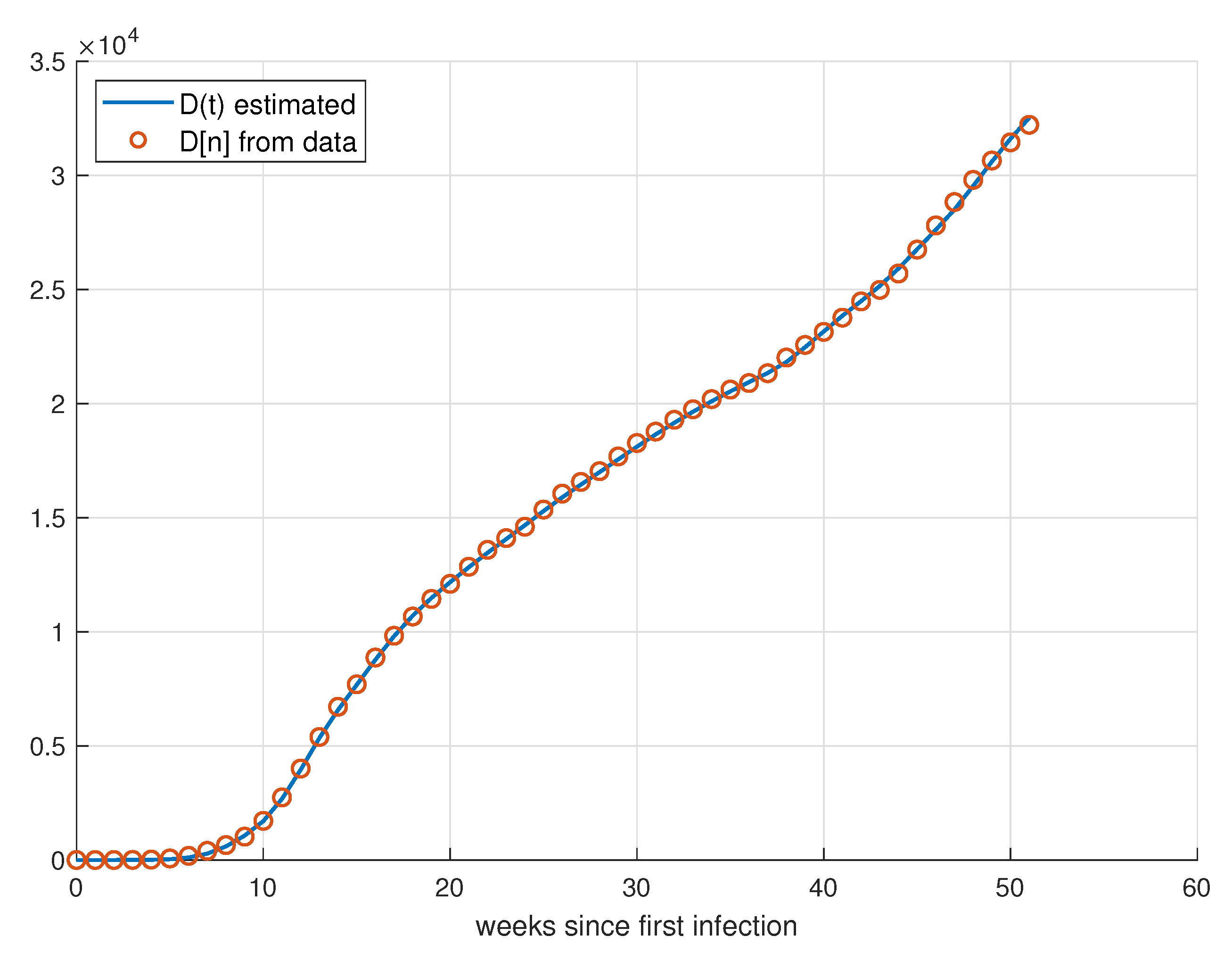
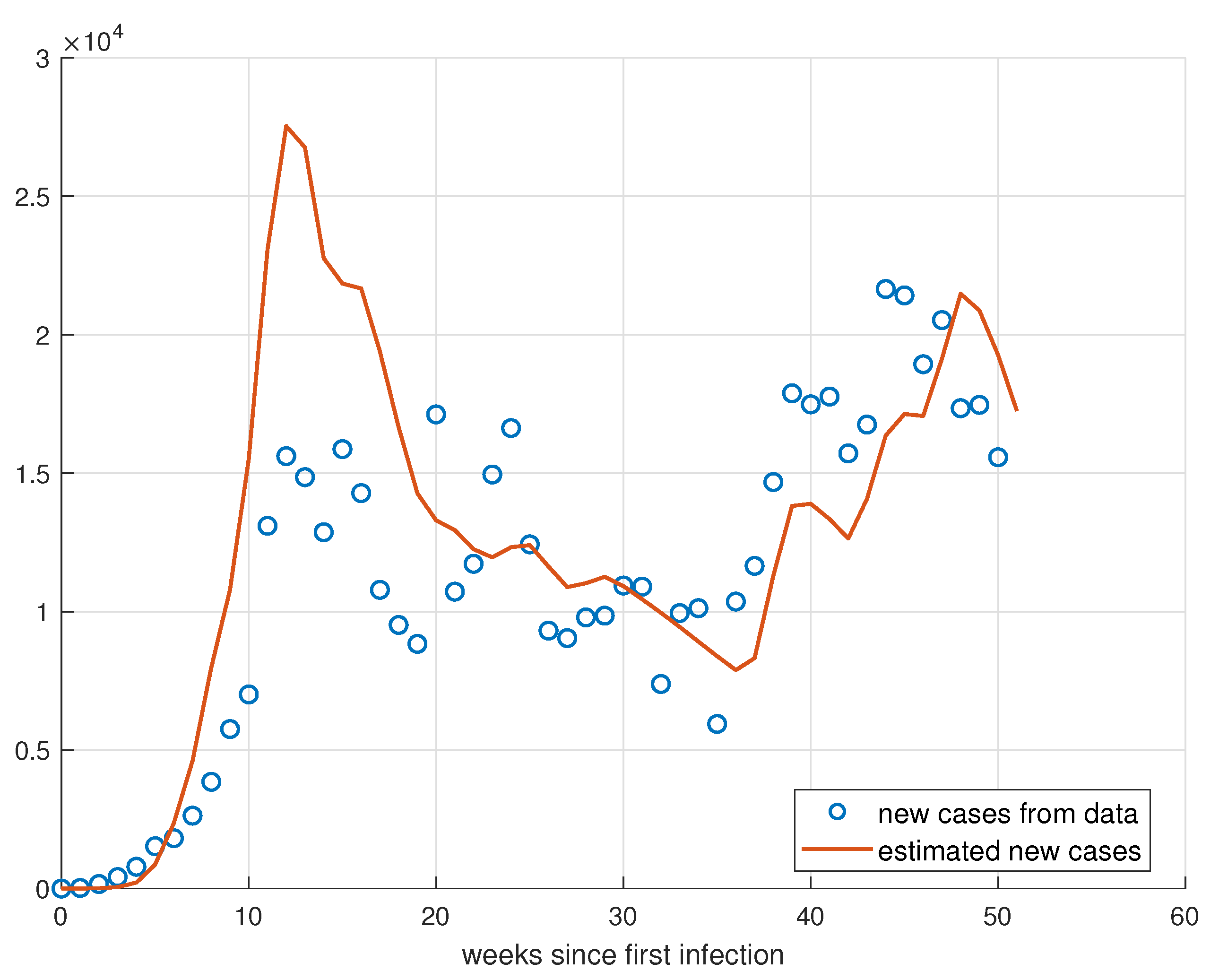
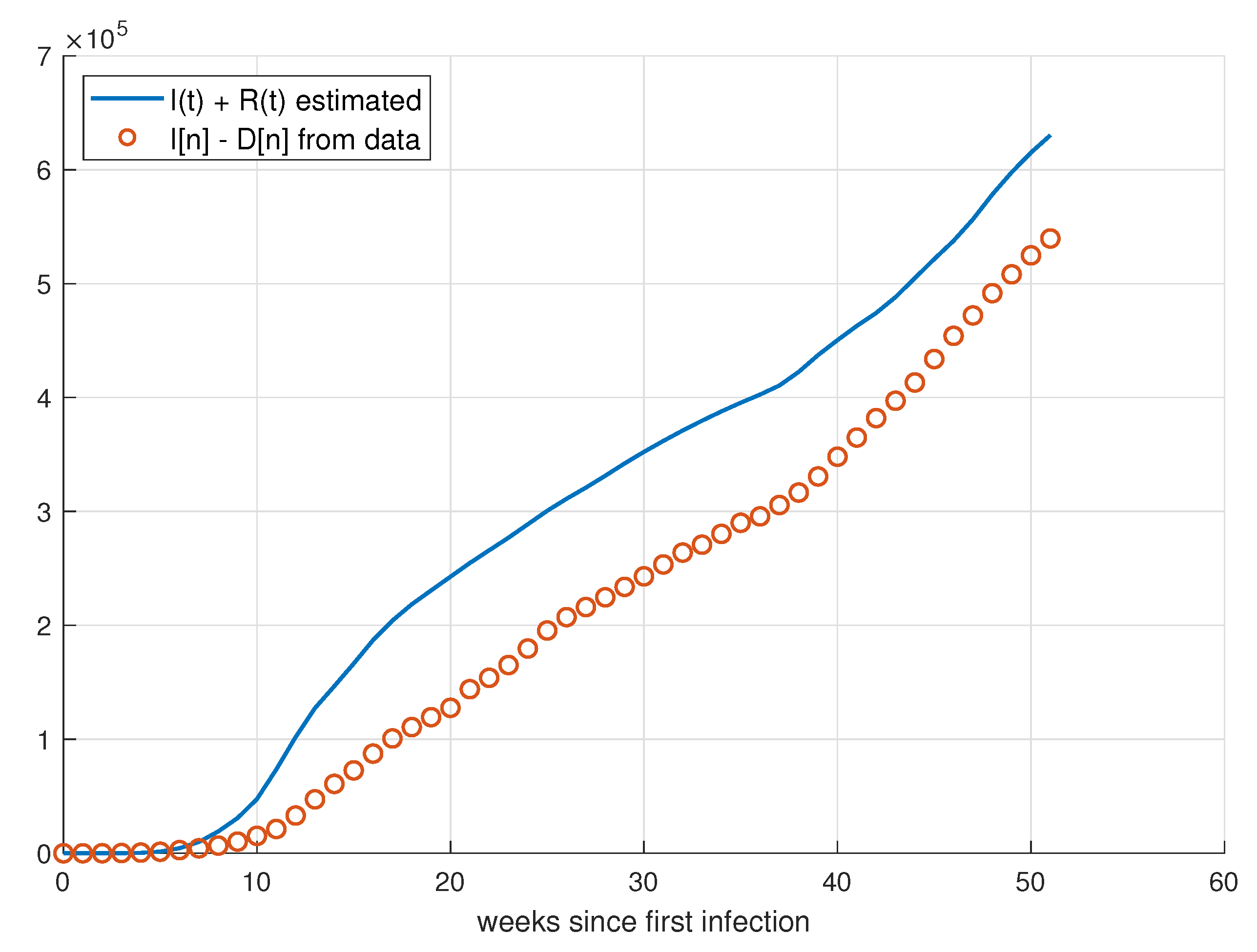
5. Validation for the SIRD Model
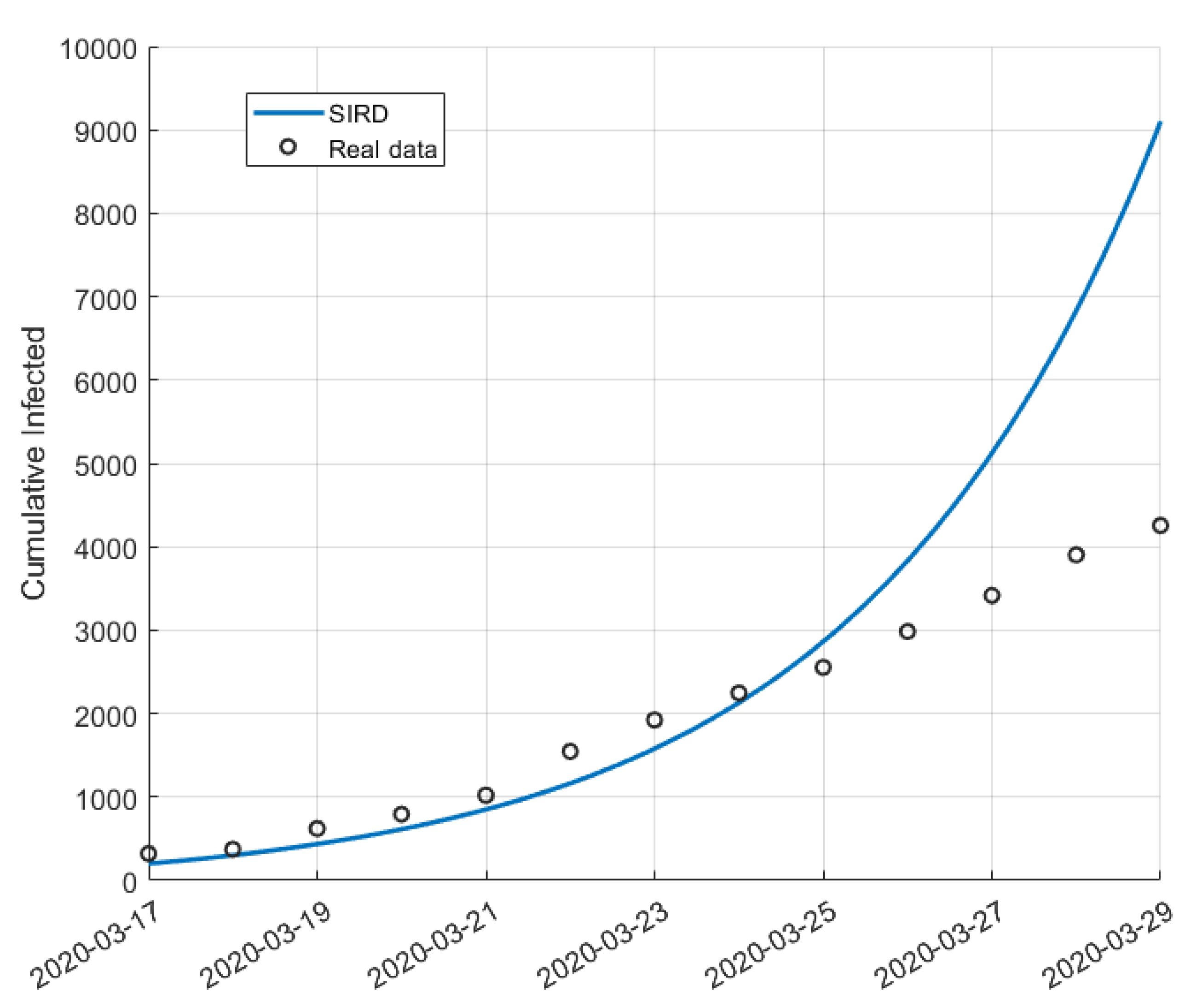
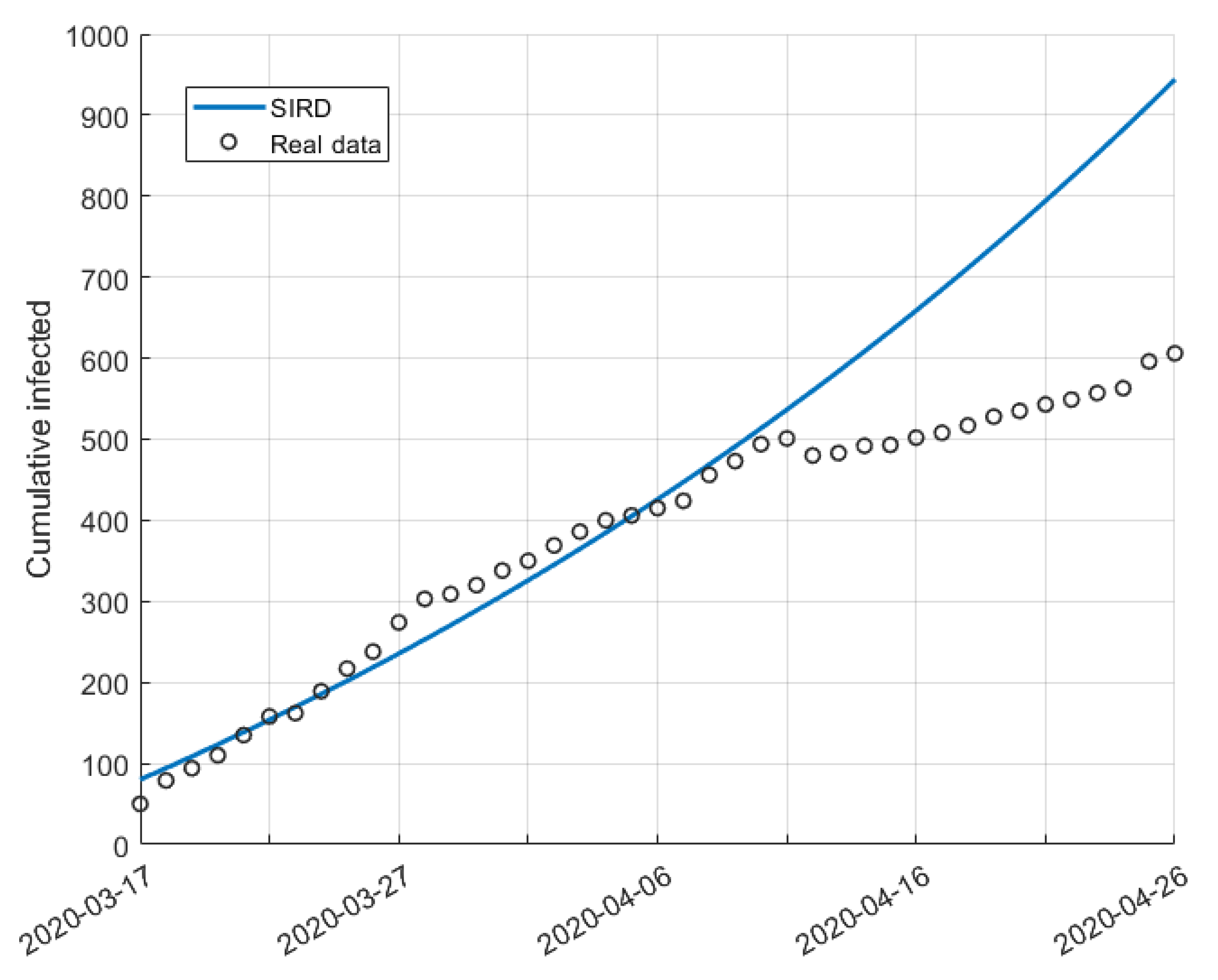
5.1. Validation for São Paulo
5.2. Validation for Minas Gerais
5.3. Validation for Rio de Janeiro
6. Spread Control
Algorithm Implementation
7. Control Strategy Results
7.1. No Attempt to Control the Spread of the Disease
7.2. Updating Every 30 Days
7.3. Updating Every 21 Days
8. Epidemic Control
8.1. Control by Social Distancing
Results for Social Distancing Control
8.2. Vaccination Control
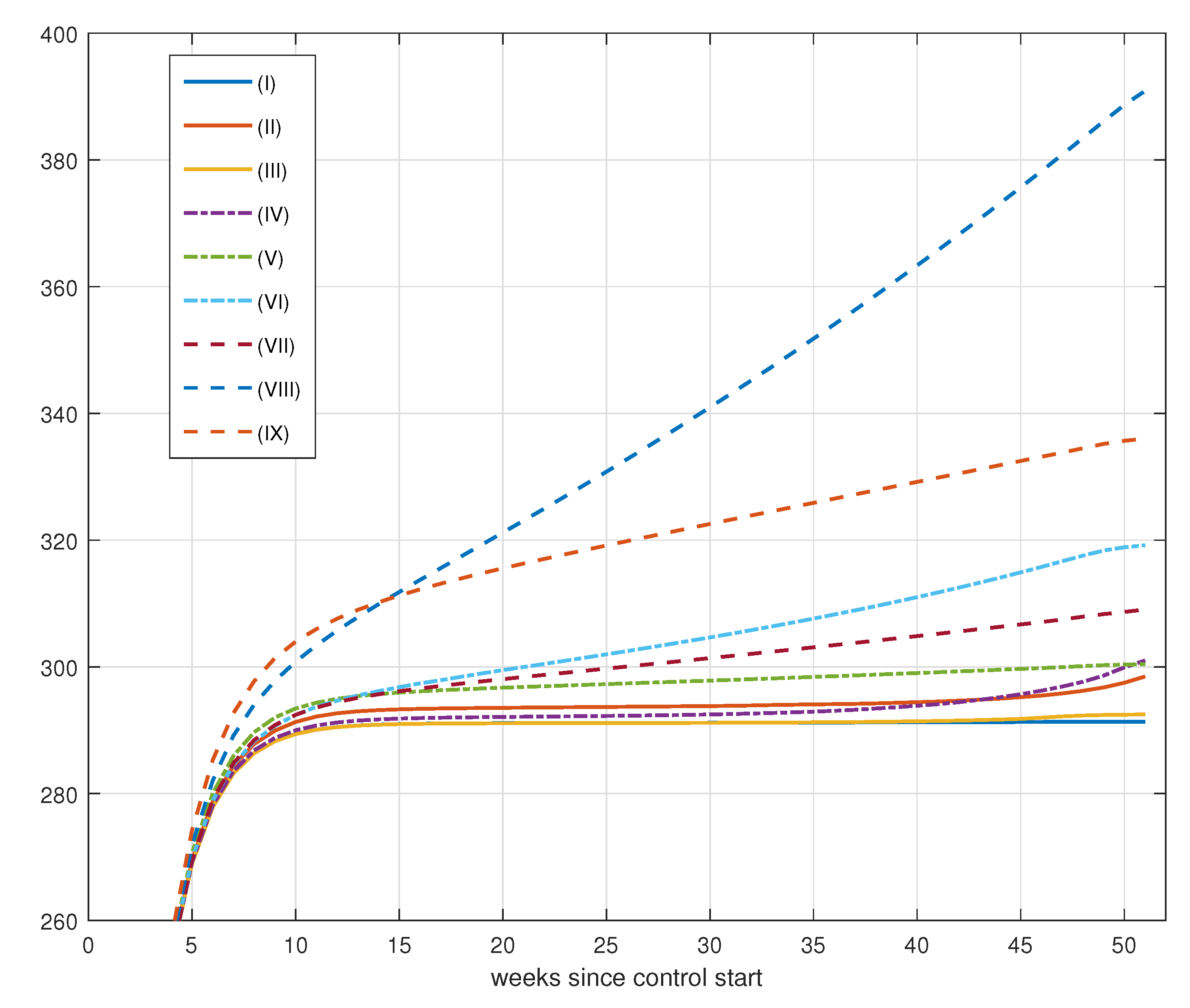
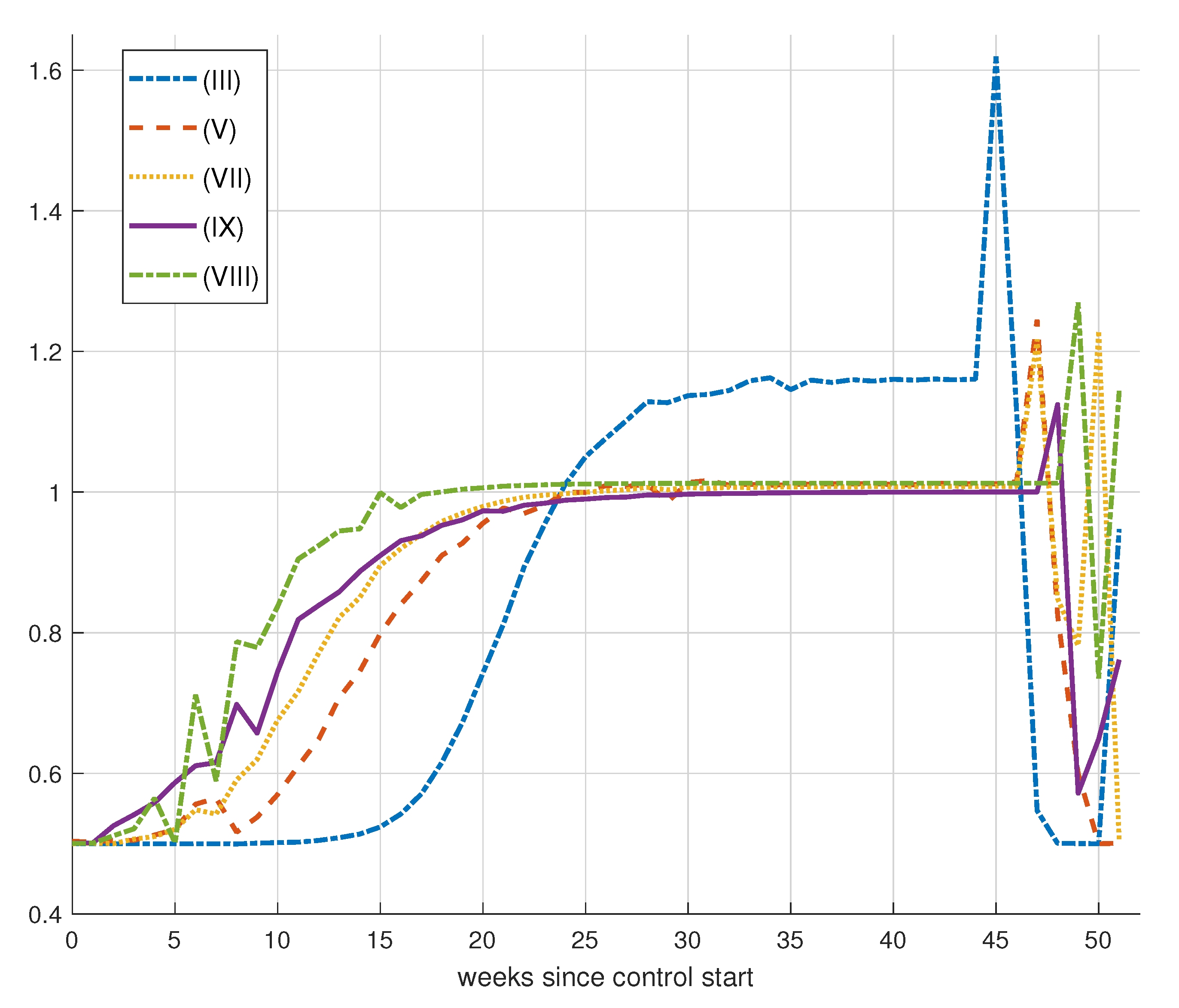
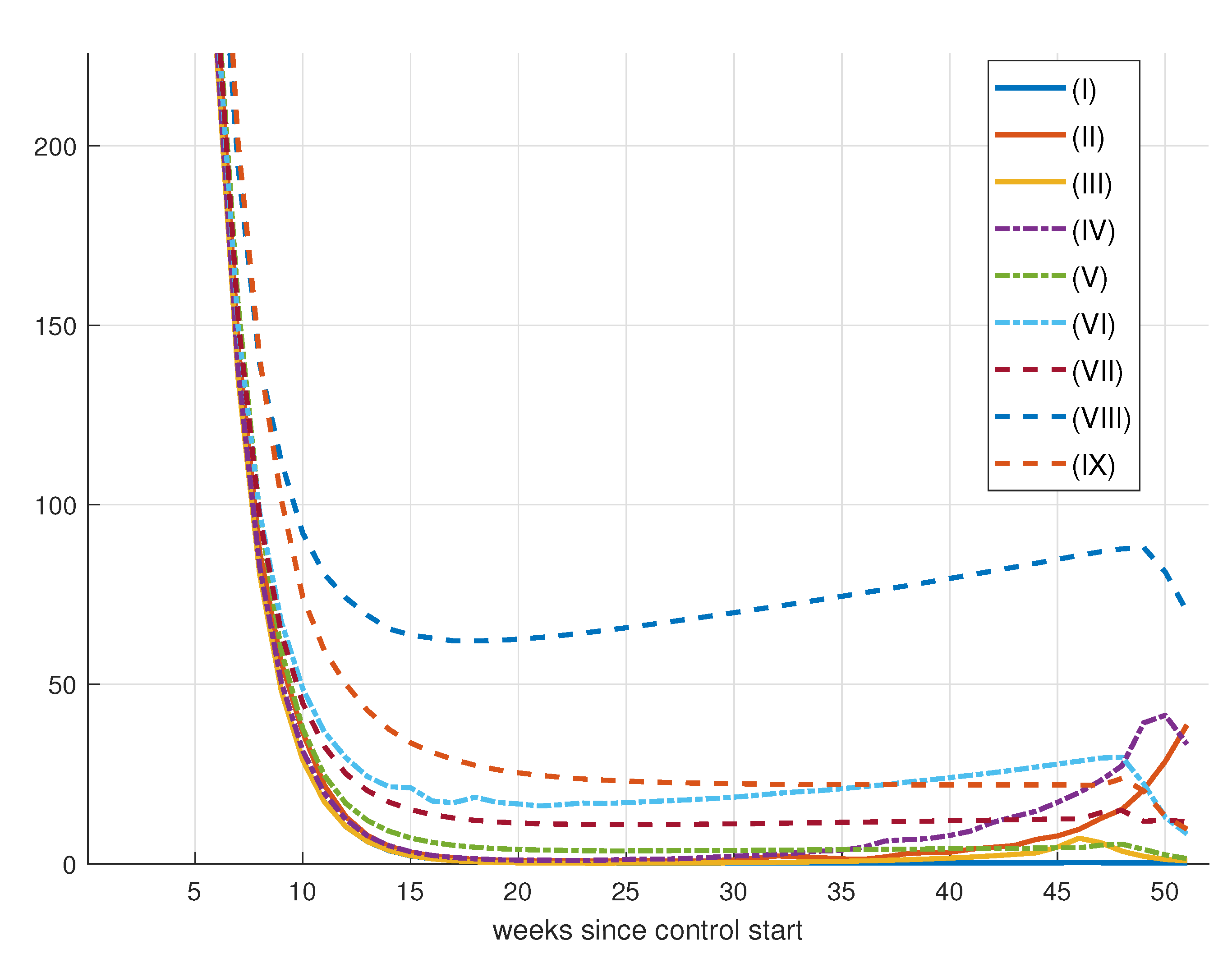
8.2.1. Results for Vaccination Control
8.2.2. Effect of Increase in Weekly Vaccination
8.2.3. Effects of Changes in Vaccination Campaign Prioritization
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Velavan, T.P.; Meyer, C.G. The COVID-19 epidemic. Trop. Med. Int. Health 2020, 25, 278–280. [Google Scholar] [CrossRef]
- Wu, Z.; McGoogan, J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: Summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef]
- World Health Organization. WHO Timeline-Covid-19; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Van Doremalen, N.; Bushmaker, T.; Morris, D.H.; Holbrook, M.G.; Gamble, A.; Williamson, B.N.; Tamin, A.; Harcourt, J.L.; Thornburg, N.J.; Gerber, S.I.; et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 2020, 382, 1564–1567. [Google Scholar] [CrossRef]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.Y.; Chen, L.; Wang, M. Presumed asymptomatic carrier transmission of COVID-19. JAMA 2020, 323, 1406–1407. [Google Scholar] [CrossRef]
- Sohrabi, C.; Alsafi, Z.; O’Neill, N.; Khan, M.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, R. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19). Int. J. Surg. 2020, 76, 71–76. [Google Scholar] [CrossRef]
- Singh, S.; Parmar, K.S.; Kumar, J.; Makkhan, S.J.S. Development of new hybrid model of discrete wavelet decomposition and autoregressive integrated moving average (ARIMA) models in application to one month forecast the casualties cases of COVID-19. Chaos Solitons Fractals 2020, 135, 109866. [Google Scholar] [CrossRef]
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 2020, 5, e261–e270. [Google Scholar] [CrossRef]
- Colbourn, T. COVID-19: Extending or relaxing distancing control measures. Lancet Public Health 2020, 5, e236–e237. [Google Scholar] [CrossRef]
- Mishra, B.K.; Keshri, A.K.; Rao, Y.S.; Mishra, B.K.; Mahato, B.; Ayesha, S.; Rukhaiyyar, B.P.; Saini, D.K.; Singh, A.K. COVID-19 created chaos across the globe: Three novel quarantine epidemic models. Chaos Solitons Fractals 2020, 138, 109928. [Google Scholar] [CrossRef]
- Rai, R.K.; Khajanchi, S.; Tiwari, P.K.; Venturini, E.; Misra, A.K. Impact of social media advertisements on the transmission dynamics of COVID-19 pandemic in India. J. Appl. Math. Comput. 2020, 68, 19–44. [Google Scholar] [CrossRef]
- Tiwari, P.K.; Rai, R.K.; Khajanchi, S.; Gupta, R.K.; Misra, A.K. Dynamics of coronavirus pandemic: Effects of community awareness and global information campaigns. Eur. Phys. J. Plus 2021, 136, 994. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. Siam Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Dietz, K. The first epidemic model: A historical note on PD En’ko. Aust. J. Stattistic 1998, 30, 56–65. [Google Scholar] [CrossRef]
- Laarabi, H.; Abta, A.; Hattaf, K. Optimal control of a delayed SIRS epidemic model with vaccination and treatment. Acta Biotheor. 2015, 63, 87–97. [Google Scholar] [CrossRef]
- Aldila, D.; Götz, T.; Soewono, E. An optimal control problem arising from a dengue disease transmission model. Math. Biosci. 2013, 242, 9–16. [Google Scholar] [CrossRef]
- Ruan, S.; Xiao, D.; Beier, J.C. On the delayed Ross-Macdonald model for malaria transmission. Bull. Math. Biololgy 2008, 70, 1098–1114. [Google Scholar] [CrossRef]
- Nwankwo, A.; Okuonghae, D. A mathematical model for the population dynamics of malaria with a temperature dependent control. Differ. Equations Dyn. Syst. 2019, 30, 719–748. [Google Scholar] [CrossRef]
- Egonmwan, A.O.; Okuonghae, D. Mathematical analysis of a tuberculosis model with imperfect vaccine. Int. J. Biomath. 2019, 12, 1950073. [Google Scholar] [CrossRef]
- Omame, A.; Okuonghae, D.; Umana, A.R.; Inyama, S.C. Analysis of a co-infection model for HPV-TB. Appl. Math. Model. 2020, 77, 881–901. [Google Scholar] [CrossRef]
- Omame, A.; Okuonghae, D.; Inyama, S.C. A Mathematical Study of a Model for HPV with Two High-Risk Strains. In Mathematical Modelling in Health, Social and Applied Sciences; Springer: Singapore, 2020; pp. 107–149. [Google Scholar]
- Hattaf, K.; Yousfi, N. Optimal control of a delayed HIV infection model with immune response using an efficient numerical method. Int. Sch. Res. Not. 2012, 2012, 215124. [Google Scholar] [CrossRef]
- Al-Khaled, K.; Yousef, M. An analytic study of the fractional order model of HIV-1 virus and CD4 + T-cells using adomian method. Int. J. Electr. Comput. Eng. 2021, 11, 1460–1468. [Google Scholar] [CrossRef]
- Khan, M.I.; Al-Khaled, K.; Raza, A.; Khan, S.U.; Omar, J.; Galal, A.M. Mathematical and numerical model for the malaria transmission: Euler method scheme for a malarial model. Int. J. Mod. Phys. B 2023, 37, 2350158. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London Ser. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. II.—The problem of endemicity. Proc. R. Soc. London Ser. A 1932, 138, 55–83. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. III.—Further studies of the problem of endemicity. Proc. R. Soc. London Ser. A 1933, 141, 94–122. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, K.; Mondal, J.; Nisar, K.S.; Abdelwahab, S.F. Mathematical modeling of the COVID-19 pandemic with intervention strategies. Results Phys. 2021, 25, 104285. [Google Scholar] [CrossRef]
- Cantó, B.; Coll, C.; Sánchez, E. Estimation of parameters in a structured SIR mode. Adv. Differ. Equ. 2017, 2017, 33. [Google Scholar] [CrossRef]
- Ng, T.W.; Turinici, G.; Danchin, A. A double epidemic model for the SARS propagation. BMC Infect. Dis. 2003, 3, 19. [Google Scholar] [CrossRef]
- Danca, M.F.; Kuznetsov, N. Matlab code for Lyapunov exponents of fractional-order systems. Int. J. Bifurc. Chaos 2018, 28, 1850067. [Google Scholar] [CrossRef]
- Godio, A.; Pace, F.; Vergnano, A. SEIR modeling of the Italian epidemic of SARS-CoV-2 using computational swarm intelligence. Int. J. Environ. Res. Public Health 2020, 17, 3535. [Google Scholar] [CrossRef]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Piqueira, J.R.C.; Araujo, V.O. A modified epidemiological model for computer viruses. Appl. Math. Comput. 2009, 213, 355–360. [Google Scholar] [CrossRef]
- Piqueira, J.R.C.; Batistela, C.M. Considering quarantine in the SIRA malware propagation model. Math. Probl. Eng. 2019, 2019, 6467104. [Google Scholar] [CrossRef]
- Khajanchi, S.; Das, D.K.; Kar, T.K. Dynamics of tuberculosis transmission with exogenous reinfections and endogenous reactivation. Phys. A Stat. Mech. Its Appl. 2018, 497, 52–71. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, S.; Banerjee, S. Modeling the dynamics of COVID-19 pandemic with implementation of intervention strategies. Eur. Phys. J. Plus 2022, 137, 129. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Rai, R.K.; Tiwari, P.K.; Khajanchi, S. Modeling the influence of vaccination coverage on the dynamics of COVID-19 pandemic with the effect of environmental contamination. Math. Methods Appl. Sci. 2023, 46, 12425–12453. [Google Scholar] [CrossRef]
- Mizumoto, K.; Chowell, G. Transmission potential of the novel coronavirus (COVID-19) onboard the diamond Princess Cruises Ship. Infect. Dis. Model. 2020, 5, 264–270. [Google Scholar] [CrossRef]
- Atangana, A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals 2020, 136, 109860. [Google Scholar] [CrossRef]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef]
- Ivorra, B.; Ferrández, M.R.; Vela-Pérez, M.; Ramos, A.M. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Commun. Nonlinear Sci. Numer. Simul. 2020, 88, 105303. [Google Scholar] [CrossRef]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef]
- Samui, P.; Mondal, J.; Khajanchi, S. A mathematical model for COVID-19 transmission dynamics with a case study of India. Chaos Solitons Fractals 2020, 140, 110173. [Google Scholar] [CrossRef]
- Batistela, C.M.; Correa, D.P.; Bueno, A.M.; Piqueira, J.R.C. SIRSi compartmental model for COVID-19 pandemic with immunity loss. Chaos Solitons Fractals 2021, 142, 110388. [Google Scholar] [CrossRef]
- Batistela, C.M.; Correa, D.P.; Bueno, A.M.; Piqueira, J.R.C. SIRSi-vaccine dynamical model for the Covid-19 pandemic. ISA Trans. 2023, 139, 391–405. [Google Scholar] [CrossRef]
- Malki, Z.; Atlam, E.S.; Ewis, A.; Dagnew, G.; Ghoneim, O.A.; Mohamed, A.A.; Abdel-Daim, M.M.; Gad, I. The COVID-19 pandemic: Prediction study based on machine learning models. Environ. Sci. Pollut. Reserach 2021, 28, 40496–40506. [Google Scholar] [CrossRef]
- Wieczorek, M.; Siłka, J.; Połap, D.; Woźniak, M.; Damaševičius, R. Real-time neural network based predictor for cov19 virus spread. PLoS ONE 2020, 15, e0243189. [Google Scholar] [CrossRef]
- Braga, M.B.; Fernandes, R.D.S.; Souza, G.N., Jr.; Rocha, J.E.C.D.; Dolácio, C.J.F.; Tavares, I.D.S., Jr.; Pinheiro, R.R.; Noronha, F.N.; Rodrigues, L.L.S.; Ramos, R.T.J.; et al. Artificial neural networks for short-term forecasting of cases, deaths, and hospital beds occupancy in the COVID-19 pandemic at the Brazilian Amazon. PLoS ONE 2021, 16, e0248161. [Google Scholar] [CrossRef]
- Iwendi, C.; Mahboob, K.; Khalid, Z.; Javed, A.R.; Rizwan, M.; Ghosh, U. Classification of COVID-19 individuals using adaptive neuro-fuzzy inference system. Multimed. Syst. 2021, 28, 1223–1237. [Google Scholar] [CrossRef]
- Iwendi, C.; Bashir, A.K.; Peshkar, A.; Sujatha, R.; Chatterjee, J.M.; Pasupuleti, S.; Mishra, R.; Pillai, S.; Jo, O. COVID-19 Patient health prediction using boosted random forest algorithm. Front. Public Health 2020, 8, 357. [Google Scholar] [CrossRef]
- Stewart, G.; Heusden, K.; Dumont, G.A. How control theory can help us control COVID-19. IEEE Spectr. 2020, 57, 22–29. [Google Scholar] [CrossRef]
- Moler, C.B. Numerical Computing with MATLAB; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Murray, J.D. Mathematical Biology I. An Introduction; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Bastos, S.B.; Cajueiro, D.O. Modeling and forecasting the early evolution of the COVID-19 pandemic in Brazil. Sci. Rep. 2020, 10, 19457. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F.; Van den Driessche, P.; Wu, J.; Allen, L.J. Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar] [CrossRef]
- Andronov, A.A.; Vitt, A.A.; Khaikin, S.E. Theory of Oscillators; Elsevier Ltd.: Pergamon, Turkey, 1966. [Google Scholar] [CrossRef]
- Khajanchi, S.; Bera, S.; Roy, T.K. Mathematical analysis of the global dynamics of a HTLV-I infection model, considering the role of cytotoxic T-lymphocytes. Math. Comput. Simul. 2021, 180, 354–378. [Google Scholar] [CrossRef]
- Dutra, C. Estimate of the basic number of reproduction R0 of COVID-19 in South American countries. Interam. J. Med. Health 2020, 3, 1–7. [Google Scholar] [CrossRef]
- Our World in Data. Coronavirus (COVID-19) Cases. 2021. Available online: https://ourworldindata.org/covid-cases (accessed on 7 September 2021).
- Bai, Y.; Peng, Z.; Wei, F.; Jin, Z.; Wang, J.; Xu, X.; Zhang, X.; Xu, J.; Ren, Z.; Lu, B.; et al. Study on the COVID-19 epidemic in mainland China between November 2022 and January 2023, with prediction of its tendency. J. Biosaf. Biosegurance 2023, 5, 39–44. [Google Scholar] [CrossRef]
- Wei, F.; Peng, Z.; Jin, Z.; Wang, J.; Xu, X.; Zhang, X.; Xu, J.; Ren, Z.; Bai, Y.; Wang, X.; et al. Study and prediction of the 2022 global monkeypox epidemic. J. Biosaf. Biosegurance 2022, 4, 158–162. [Google Scholar] [CrossRef]
- Observatório COVID-19 BR. 2021. Available online: https://covid19br.github.io/ (accessed on 28 September 2021).
- Kruse, T.; Strack, P. Optimal Control of an Epidemic Through Social Distancing. Cowles Found Discuss. 2020, 3581295, 2229. [Google Scholar] [CrossRef]
- Jaberi-Douraki, M.; Moghadas, S.M. Optimal control of vaccination dynamics during an influenza epidemic. Math. Biosci. Eng. 2014, 11, 1045–1063. [Google Scholar] [CrossRef]
- Hansen, E.; Day, T. Optimal control of epidemics with limited resources. J. Math. Biol. 2011, 62, 423–451. [Google Scholar] [CrossRef] [PubMed]
- Morato, M.M.; Bastos, S.B.; Cajueiro, D.O.; Normey-Rico, J.E. An optimal predictive control strategy for COVID-19 (SARS-CoV-2) social distancing policies in Brazil. Annu. Rev. Control 2020, 50, 417–431. [Google Scholar] [CrossRef] [PubMed]
- Köhler, J.; Schwenkel, L.; Koch, A.; Berberich, J.; Pauli, P.; Allgöwer, F. Robust and optimal predictive control of the COVID-19 outbreak. Annu. Rev. Control 2020, 51, 525–539. [Google Scholar] [CrossRef]
- Köhler, J.; Enyioha, C.; Allgöwer, F. Dynamic resource allocation to control epidemic outbreaks a model predictive control approach. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 1546–1551. [Google Scholar] [CrossRef]
- Bin, M.; Cheung, P.Y.; Crisostomi, E.; Ferraro, P.; Lhachemi, H.; Murray-Smith, R.; Myant, C.; Parisini, T.; Shorten, R.; Stein, S.; et al. Post-lockdown abatement of COVID-19 by fast periodic switching. PLoS Comput. Biol. 2021, 17, e1008604. [Google Scholar] [CrossRef]
- Meidan, D.; Schulmann, N.; Cohen, R.; Haber, S.; Yaniv, E.; Sarid, R.; Barzel, B. Alternating quarantine for sustainable epidemic mitigation. Nat. Commun. 2021, 12, 220. [Google Scholar] [CrossRef] [PubMed]
- Khailaie, S.; Mitra, T.; Bandyopadhyay, A.; Schips, M.; Mascheroni, P.; Vanella, P.; Lange, B.; Binder, S.C.; Meyer-Hermann, M. Development of the reproduction number from coronavirus SARS-CoV-2 case data in Germany and implications for political measures. BMC Med. 2021, 19, 32. [Google Scholar] [CrossRef] [PubMed]
- Garnett, G.P. Role of herd immunity in determining the effect of vaccines against sexually transmitted disease. J. Infect. Dis. 2005, 191, S97–S106. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. Information for Clinicians on Investigational Therapeutics for Patients with COVID-19. 2020. Available online: https://www.cdc.gov/coronavirus/2019-ncov/hcp/therapeutic-options.html (accessed on 13 March 2021).
- Johns Hopkins Medicine. Is the Coronavirus Treatable? 2020. Available online: https://www.hopkinsmedicine.org/health/conditions-and-diseases/coronavirus/coronavirus-treatment-whats-in-development (accessed on 5 April 2021).
- FDA. Coronavirus (COVID-19) Update: FDA Authorizes Monoclonal Antibodies for Treatment of COVID-19. 2020. Available online: https://www.fda.gov/news-events/press-announcements/coronavirus-covid-19-update-fda-authorizes-monoclonal-antibodies-treatment-covid-19 (accessed on 7 September 2021).
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.L.; Hui, D.S.; et al. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef]
- COVID-19 to Slash Global Economic Output by $8.5 Trillion over Next Two Years. 2020. Available online: https://www.un.org/en/desa/covid-19-slash-global-economic-output-85-trillion-over-next-two-years (accessed on 9 September 2021).
- Global Economy Could Lose over $4 Trillion Due to COVID-19 Impact on Tourism. 2021. Available online: https://unctad.org/news/global-economy-could-lose-over-4-trillion-due-covid-19-impact-tourism (accessed on 9 September 2021).
- Global Economic Effects of COVID-19 (CRS Report No. R46270). Retrieved from Congressional Research Service Website. 2021. Available online: https://crsreports.congress.gov/ (accessed on 8 September 2021).
- Gupta, A.G.; Moyer, C.A.; Stern, D.T. The economic impact of quarantine: SARS in Toronto as a case study. J. Infect. 2005, 50, 386–393. [Google Scholar] [CrossRef]
- Demirgüç-Kunt, A.; Lokshin, M.; Torre, I. The Sooner, the Better: The Early Economic Impact of Non-Pharmaceutical Interventions During the COVID-19 Pandemic. World Bank Policy Res. Work. Pap. 2020, 26, 9257. [Google Scholar] [CrossRef]
- Chen, S.; Igan, D.O.; Pierri, N.; Presbitero, A.F.; Soledad, M.; Peria, M. Tracking the economic impact of COVID-19 and mitigation policies in Europe and the United States. IMF Work. Pap. 2020, 125, 25. [Google Scholar] [CrossRef]
- Aum, S.; Lee, S.Y.; Shin, Y. COVID-19 doesn’t need lockdowns to destroy jobs: The effect of local outbreaks in Korea. Labour Econ. 2021, 70, 101993. [Google Scholar] [CrossRef]
- Imperial College London. Report 9—Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. 2020. Available online: https://www.imperial.ac.uk/media/imperial-college/%5Cmedicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf (accessed on 8 April 2021).
- Teslya, A.; Pham, T.M.; Godijk, N.G.; Kretzschmar, M.E.; Bootsma, M.C.J.; Rozhnova, G. Impact of self-imposed prevention measures and short-term government-imposed social distancing on mitigating and delaying a COVID-19 epidemic: A modelling study. PLoS Med. 2020, 17, e1003166. [Google Scholar] [CrossRef] [PubMed]
- G1. Governo de SP Avança 6 Regiões Para a Fase Amarela da Quarentena, Que Permite Funcionamento de Restaurantes até 22h. 2021. Available online: https://g1.globo.com/sp/sao-paulo/noticia/2021/02/05/governo-de-sp-avanca-6-regioes-para-a-fase-amarela-que-permite-funcionamento-do-comercio-ate-22h.ghtml (accessed on 28 March 2021).
- Hyafil, A.; Moriña, D. Analysis of the impact of lockdown on the reproduction number of the SARS-Cov-2 in Spain. Gac. Sanit. 2022, 35, 453–458. [Google Scholar] [CrossRef] [PubMed]
- Conselho Federal de Medicina. Medicina Intensiva no Brasil. 2018. Available online: https://portal.cfm.org.br/images/PDF/leitosdeuticapitais2018.pdf (accessed on 25 March 2021).
- Cleve, M.I. The lightning-fast quest for COVID vaccines and what it means for other diseases. Nature 2021, 589, 16–18. [Google Scholar] [CrossRef]
- CNN. UK Becomes First Country to Authorize Pfizer/BioNTech’s COVID-19 Vaccine, First Shots Roll Out Next Week. 2020. Available online: https://edition.cnn.com/2020/12/02/uk/pfizer-coronavirus-vaccine-uk-intl-hnk/index.html (accessed on 17 April 2021).
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: New York, NY, USA, 1990. [Google Scholar]




















| Parameter | Parameter Description |
|---|---|
| Average contact rate. | |
| Mean infectious period. | |
| Mortality rate. |
| Parameter | Parameter Description | Value |
|---|---|---|
| recovery rate | 1.071 | |
| lethality of virus (mortality rate) | 0.0285 | |
| N | population size | 46,289,333 |
| Parameter | Parameter Description | Value |
|---|---|---|
| recovery rate | 0.9973 | |
| lethality of virus (mortality rate) | 0.0258 | |
| N | population size | 21,292,666 |
| Parameter | Parameter Description | Value |
|---|---|---|
| recovery rate | 0.9431 | |
| lethality of virus (mortality rate) | 0.0500 | |
| N | population size | 17,366,189 |
| Level | Measures Taken | Value Source | When | |
|---|---|---|---|---|
| A | 2 | Self-imposed measures are stimulated in order to accelerate awareness spread. Prevention measures such as mask wearing, hand washing and self-imposed social distancing can be described as reductions in infectious output, susceptibility and contact rate, respectively [92]. | As such measures stack up additively [92], a 10% efficacy for each one reduces the effective contact rate by 30%. | Intensive care unit demand is lower than 10% of the total amount available. 5 |
| B | 1.1 | Government implements social distancing measures such as reduced business hours and occupation or public spaces restrictions. | A similar is obtained for the state of Sao Paulo in March 2021, when such measures where adopted [93]. | Intensive care unit demand is between 10–80% of the total amount available. 40 |
| C | 0.5 | Mandatory home confinement except for vital sectors workers. | Very close to the obtained by Spain during adoption of lock down [94]. | Intensive care unit demand is higher than 80% of the total amount available. 40 |
| Parameter | Parameter Description | Value |
|---|---|---|
| recovery rate | 1 | |
| lethality of virus (mortality rate) | 0.03 | |
| N | population size | 10,000,000 |
| L | number of hospital beds available | 5000 |
| T | simulation period | 52 weeks |
| initial number of infected | 5000 | |
| minimum value for effective reproduction number | 0.5 |
| Simulation | D() | |||||
|---|---|---|---|---|---|---|
| (I) | 1 | 1 | 1 | 291.3530 | 6.2783 | 0.5796 |
| (II) | 1 | 10 | 1 | 298.4825 | 7.1895 | 2.0587 |
| (III) | 1 | 10 | 10 | 292.4858 | 6.6241 | 1.0437 |
| (IV) | 1 | 50 | 10 | 300.9959 | 7.0514 | 1.1845 |
| (V) | 1 | 50 | 50 | 300.4231 | 6.4384 | 0.5781 |
| (VI) | 1 | 100 | 50 | 319.1812 | 6.6833 | 0.9307 |
| (VII) | 1 | 100 | 100 | 309.0499 | 6.6805 | 0.9949 |
| (VIII) | 1 | 250 | 100 | 390.8686 | 6.9906 | 0.8825 |
| (IX) | 1 | 250 | 150 | 336.0118 | 6.6467 | 0.6248 |
| Parameter | Parameter Description | Value |
|---|---|---|
| average number of contacts | 2.06 | |
| recovery rate | 1 | |
| lethality of virus (mortality rate) | 0.03 | |
| N | population size | 10,000,000 |
| L | number of hospital beds available | 5000 |
| T | simulation period | 52 weeks |
| initial number of infected | 1 | |
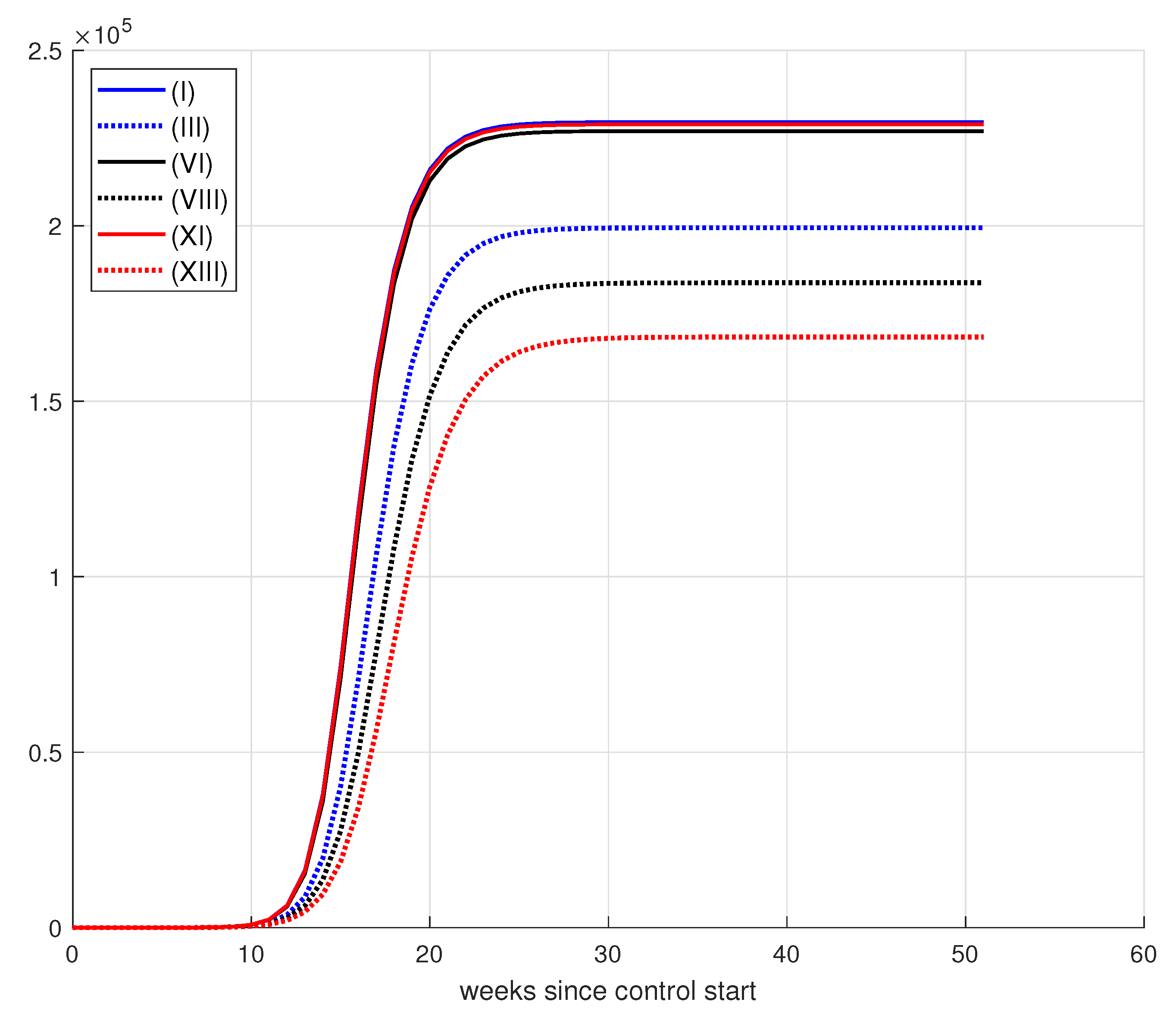
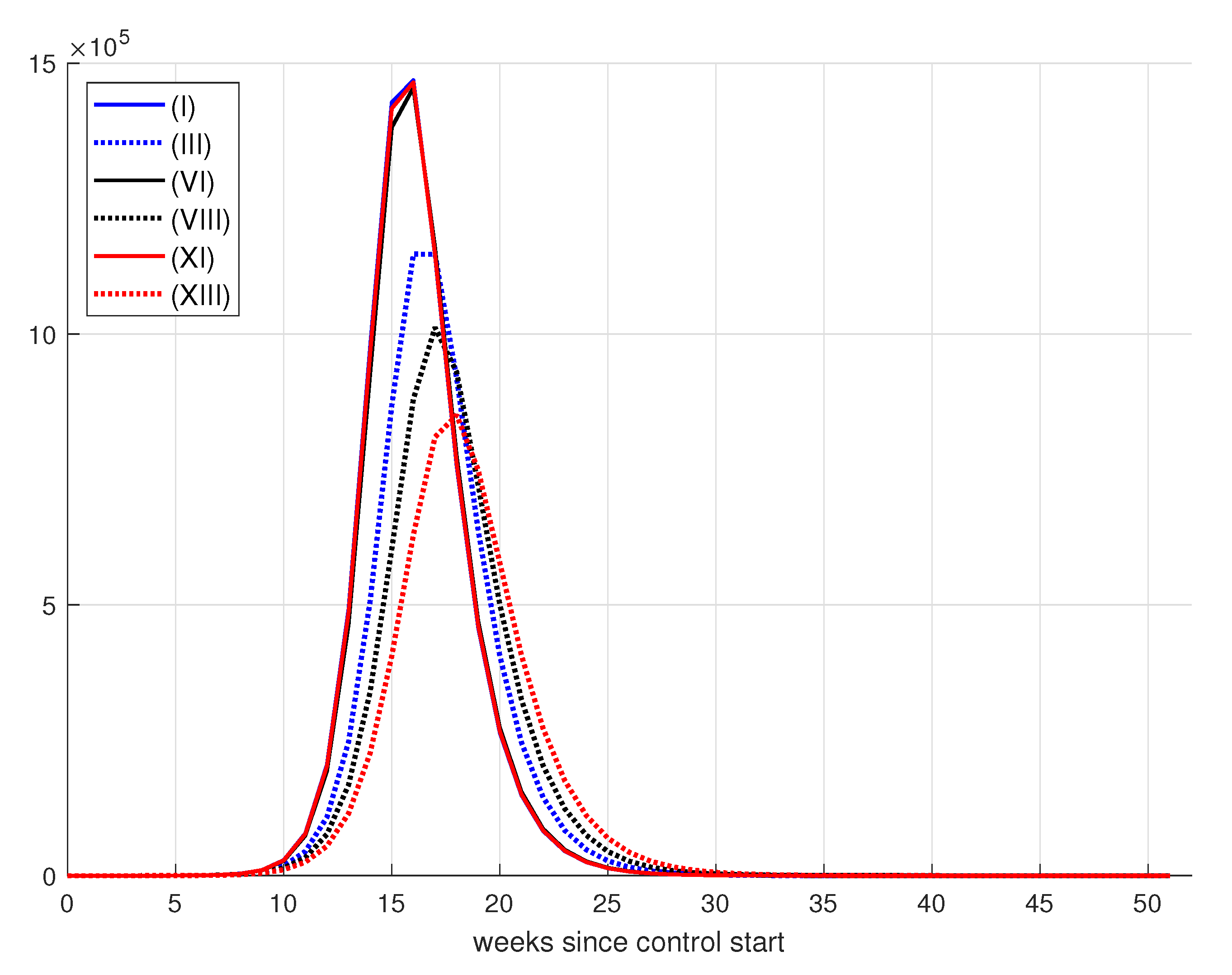
| Maximum vaccination value per instant of time | variable |
| Simulation | D() | ||||||
|---|---|---|---|---|---|---|---|
| (I) | 50,000 | 1 | 1 | 1 | 229,543 | 15,987 | 3943 |
| (II) | 50,000 | 10 | 1 | 1 | 198,924 | 210,293 | 14,770 |
| (III) | 50,000 | 50 | 1 | 1 | 199,421 | 209,570 | 18,477 |
| (IV) | 50,000 | 50 | 10 | 1 | 218,448 | 86,979 | 24,296 |
| (V) | 50,000 | 50 | 10 | 5 | 217,986 | 90,980 | 9120 |
| (VI) | 75,000 | 1 | 1 | 1 | 226,986 | 34,343 | 15,489 |
| (VII) | 75,000 | 10 | 1 | 1 | 189,715 | 259,974 | 24,880 |
| (VIII) | 75,000 | 50 | 1 | 1 | 183,758 | 294,083 | 40,017 |
| (IX) | 75,000 | 50 | 10 | 1 | 216,815 | 96,340 | 10,545 |
| (X) | 75,000 | 50 | 10 | 5 | 211,212 | 132,180 | 14,563 |
| (XI) | 100,000 | 1 | 1 | 1 | 228,907 | 21,677 | 7933 |
| (XII) | 100,000 | 10 | 1 | 1 | 170,477 | 368,702 | 45,626 |
| (XIII) | 100,000 | 50 | 1 | 1 | 168,307 | 386,925 | 86,353 |
| (XIV) | 100,000 | 50 | 10 | 1 | 218,549 | 86,186 | 12,683 |
| (XV) | 100,000 | 50 | 10 | 1 | 211,336 | 131,626 | 13,796 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dieguez, G.; Batistela, C.; Piqueira, J.R.C. Controlling COVID-19 Spreading: A Three-Level Algorithm. Mathematics 2023, 11, 3766. https://doi.org/10.3390/math11173766
Dieguez G, Batistela C, Piqueira JRC. Controlling COVID-19 Spreading: A Three-Level Algorithm. Mathematics. 2023; 11(17):3766. https://doi.org/10.3390/math11173766
Chicago/Turabian StyleDieguez, Giovanni, Cristiane Batistela, and José R. C. Piqueira. 2023. "Controlling COVID-19 Spreading: A Three-Level Algorithm" Mathematics 11, no. 17: 3766. https://doi.org/10.3390/math11173766
APA StyleDieguez, G., Batistela, C., & Piqueira, J. R. C. (2023). Controlling COVID-19 Spreading: A Three-Level Algorithm. Mathematics, 11(17), 3766. https://doi.org/10.3390/math11173766







