A Novel Two-Step Inertial Viscosity Algorithm for Bilevel Optimization Problems Applied to Image Recovery
Abstract
1. Introduction
2. Preliminaries
- (i)
- ;
- (ii)
- ;
- (iii)
- .
3. Main Results
| Algorithm 1 Modified Two-Step Inertial Viscosity Algorithm (MTIVA) |
| Initialization: Let , , and let , be bounded sequences. Take arbitrarily. For . |
| Step 1. Compute the inertial step:
|
| Step 2. Compute the viscosity step:
|
| Step 3. Compute :
|
- (C1)
- (C2)
- for some ,
- (C3)
- , and .
- (A1)
- is a convex and differentiable function such that is Lipschitz continuous with constant and are proper lower semi-continuous and convex functions;
- (A2)
- is strongly convex with parameter such that is -Lipschitz continuous and .
| Algorithm 2 Two-Step Inertial Forward–Backward Bilevel Gradient Method (TIFB-BiGM) |
| Initialization: Let , , , and let , be bounded sequences. Take arbitrarily. |
| Let with as , where . For . |
| Step 1. Compute the inertial step:
|
| Step 2. Compute:
|
4. Application to Image Recovery
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franceschi, L.; Frasconi, P.; Salzo, S.; Grazzi, R.; Pontil, M. Bilevel programming for hyperparameter optimization and meta-learning. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1568–1577. [Google Scholar]
- Shaban, A.; Cheng, C.-A.; Hatch, N.; Boots, B. Truncated back-propagation for bilevel optimization. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Okinawa, Japan, 16–18 April 2019; pp. 1723–1732. [Google Scholar]
- Kunapuli, G.; Bennett, K.P.; Hu, J.; Pang, J.-S. Classification model selection via bilevel programming. Optim. Methods Softw. 2008, 23, 475–489. [Google Scholar] [CrossRef]
- Flamary, R.; Rakotomamonjy, A.; Gasso, G. Learning constrained task similarities in graph regularized multitask learning. In Regularization, Optimization, Kernels, and Support Vector Machines; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014; Volume 103, ISBN 978-0367658984. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Denver, CO, USA, 30 November–2 December 1999; pp. 1008–1014. [Google Scholar]
- Bruck, R.E., Jr. On the weak convergence of an ergodic iteration for the solution of variational inequalities for monotone operators in Hilbert space. J. Math. Anal. Appl. 1977, 61, 159–164. [Google Scholar] [CrossRef]
- Lions, P.L.; Mercier, B. Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 1979, 16, 964–979. [Google Scholar] [CrossRef]
- Janngam, K.; Suantai, S. An inertial modified S-Algorithm for convex minimization problems with directed graphs and their applications in classification problems. Mathematics 2022, 10, 4442. [Google Scholar] [CrossRef]
- Cabot, A. Proximal point algorithm controlled by a slowly vanishing term: Applications to hierarchial minimization. SIAM J. Optim. 2005, 15, 555–572. [Google Scholar] [CrossRef]
- Xu, H.K. Averaged mappings and the gradient-projection algorithm. J. Optim. Theory Appl. 2011, 150, 360–378. [Google Scholar] [CrossRef]
- Passty, G.B. Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 1979, 72, 383–390. [Google Scholar] [CrossRef]
- Beck, A.; Sabach, S. A first order method for finding minimal norm-like solutions of convex optimization problems. Math. Program. 2014, 147, 25–46. [Google Scholar] [CrossRef]
- Sabach, S.; Shtern, S. A first order method for solving convex bilevel optimization problems. SIAM J. Optim. 2017, 27, 640–660. [Google Scholar] [CrossRef]
- Nesterov, Y.E. A method for solving the convex programming problem with convergence rate O(1/k2). Sov. Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Shehu, Y.; Vuong, P.T.; Zemkoho, A. An inertial extrapolation method for convex simple bilevel optimization. Optim. Methods Softw. 2019, 36, 1–19. [Google Scholar] [CrossRef]
- Moudafi, A. Viscosity approximation method for fixed-points problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef]
- Xu, H.K. Viscosity approximation methods for nonexpansive mappings. J. Math. Anal. Appl. 2004, 298, 279–291. [Google Scholar] [CrossRef]
- Takahashi, W. Viscosity approximation methods for countable families of nonexpansive mappings in Banach spaces. Nonlinear Anal. 2009, 70, 719–734. [Google Scholar] [CrossRef]
- Jailoka, P.; Suantai, S.; Hanjing, A. A fast viscosity forward–backward algorithm for convex minimization problems with an application in image recovery. Carpathian J. Math. 2021, 37, 449–461. [Google Scholar] [CrossRef]
- Janngam, K.; Suantai, S.; Cho, Y.J.; Kaewkhao, A.; Wattanataweekul, R. A Novel Inertial Viscosity Algorithm for Bilevel Optimization Problems Applied to Classification Problems. Mathematics 2023, 11, 3241. [Google Scholar] [CrossRef]
- Poon, C.; Liang, J. Geometry of First-order Methods and Adaptive Acceleration. arXiv 2020, arXiv:2003.03910. [Google Scholar]
- Liang, J. Convergence Rates of First-Order Operator Splitting Methods. Ph.D. Thesis, Normandie Universit’e, Normaundie, France, 2016. [Google Scholar]
- Poon, C.; Liang, J. Trajectory of Alternating Direction Method of Multiplier and Adaptive Acceleration. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Polyak, B.T. Introduction to Optimization; Optimization Software, Publication Division: New York, NY, USA, 1987. [Google Scholar]
- Combettes, P.L.; Glaudin, L. Quasi-Nonexpansive Iterations on the Affine Hull of Orbits: From Mann’s Mean Value Algorithm to Inertial Methods. SIAM J. Optim. 2017, 27, 2356–2380. [Google Scholar] [CrossRef]
- Nakajo, K.; Shimoji, K.; Takahashi, W. On strong convergence by the hybrid method for families of mappings in Hilbert spaces. Nonlinear Anal. 2009, 71, 112–119. [Google Scholar] [CrossRef]
- Aoyama, K.; Kimura, Y. Strong convergence theorems for strongly nonexpansive sequences. Appl. Math. Comput. 2011, 217, 7537–7545. [Google Scholar] [CrossRef]
- Aoyama, K.; Kohsaka, F.; Takahashi, W. Strong convergence theorems by shrinking and hybrid projection methods for relatively nonexpansive mappings in Banach spaces. Nonlinear Anal. Convex Anal. 2009, 10, 7–26. [Google Scholar]
- Moreau, J.J. Fonctions convexes duales et points proximaux dans un espace hilbertien. Comptes Rendus Acad. Sci. Paris Ser. A Math. 1962, 255, 2897–2899. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: New York, NY, USA, 2011. [Google Scholar]
- Bussaban, L.; Suantai, S.; Kaewkhao, A. A parallel inertial S-iteration forward–backward algorithm for regression and classification problems. Carpathian J. Math. 2020, 36, 35–44. [Google Scholar] [CrossRef]
- Takahashi, W. Introduction to Nonlinear and Convex Analysis; Yokohama Publishers: Yokohama, Japan, 2009. [Google Scholar]
- Saejung, S.; Yotkaew, P. Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Anal. 2012, 75, 724–750. [Google Scholar] [CrossRef]
- Maurya, A.; Tiwari, R. A Novel Method of Image Restoration by using Different Types of Filtering Techniques. Int. J. Eng. Sci. Innov. Technol. 2014, 3, 124–129. [Google Scholar]
- Suseela, G.; Basha, S.A.; Babu, K.P. Image Restoration Using Lucy Richardson Algorithm For X-Ray Images. IJISET Int. J. Innov.Sci. Eng. Technol. 2016, 3, 280–285. [Google Scholar]
- Vogel, C.R. Computational Methods for Inverse Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Eldén, L. Algorithms for the Regularization of Ill-Conditioned Least Squares Problems. BIT Numer. Math. 1977, 17, 134–145. [Google Scholar] [CrossRef]
- Hansen, P.C.; Nagy, J.G.; O’Leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering (Fundamentals of Algorithms 3) (Fundamentals of Algorithms); SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Yatakoat, P.; Suantai, S.; Hanjing, A. On Some Accelerated Optimization Algorithms Based on Fixed Point and Linesearch Techniques for Convex Minimization Problems with Applications. Adv. Cont. Discr. Mod. 2022, 2022, 43:1–43:13. [Google Scholar] [CrossRef]
- Thung, K.; Raveendran, P. A survey of image quality measures. In Proceedings of the 2009 International Conference for Technical Postgraduates (TECHPOS), Kuala Lumpur, Malaysia, 14–15 December 2009; pp. 1–4. [Google Scholar]
- Chen, D.Q.; Zhang, H.; Cheng, L.Z. A fast fixed-point algorithmfixed-point algorithmfixed-point algorithmfixed-point algorithm for total variation deblurring and segmentation. J. Math. Imaging Vis. 2012, 43, 167–179. [Google Scholar] [CrossRef]

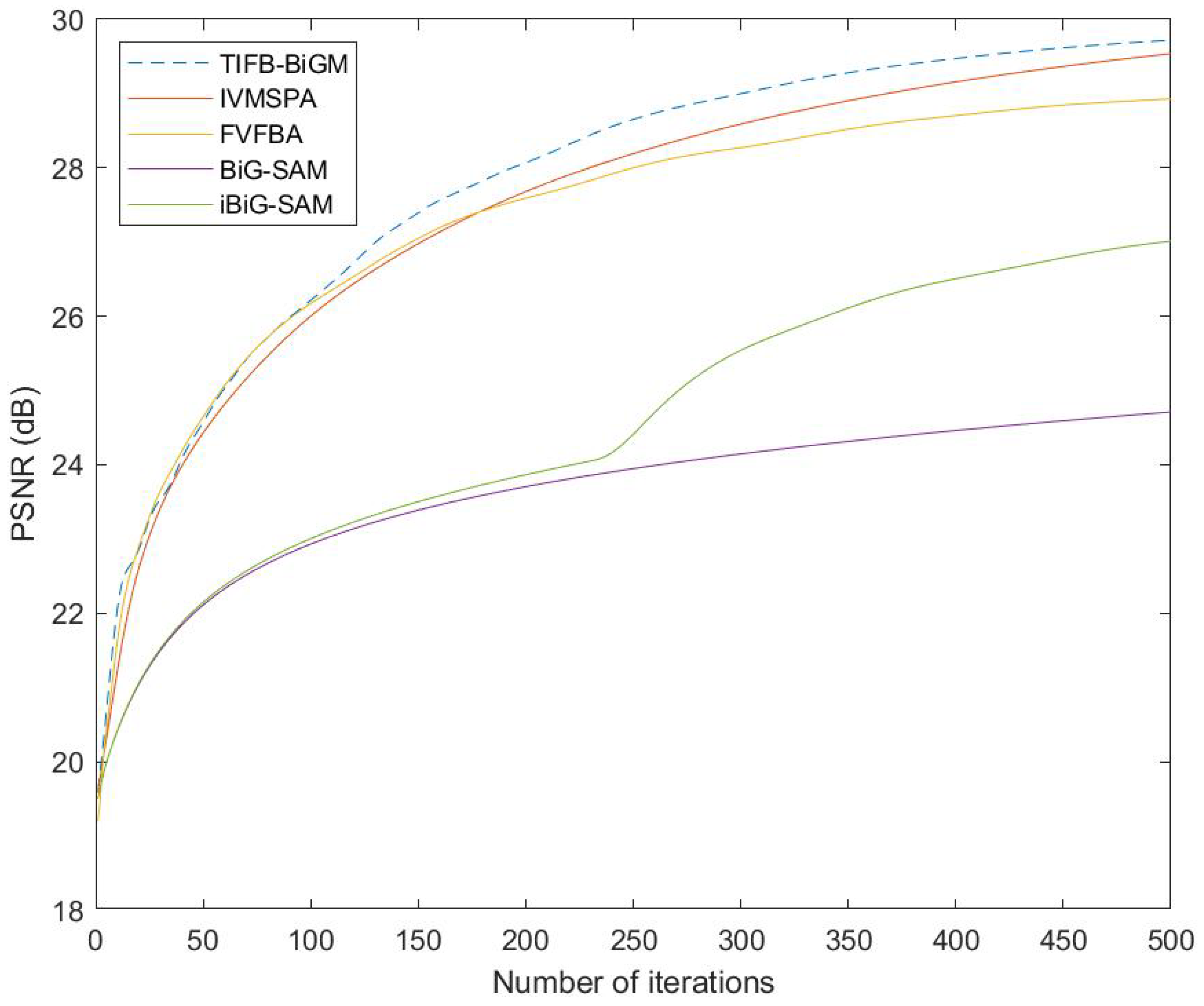
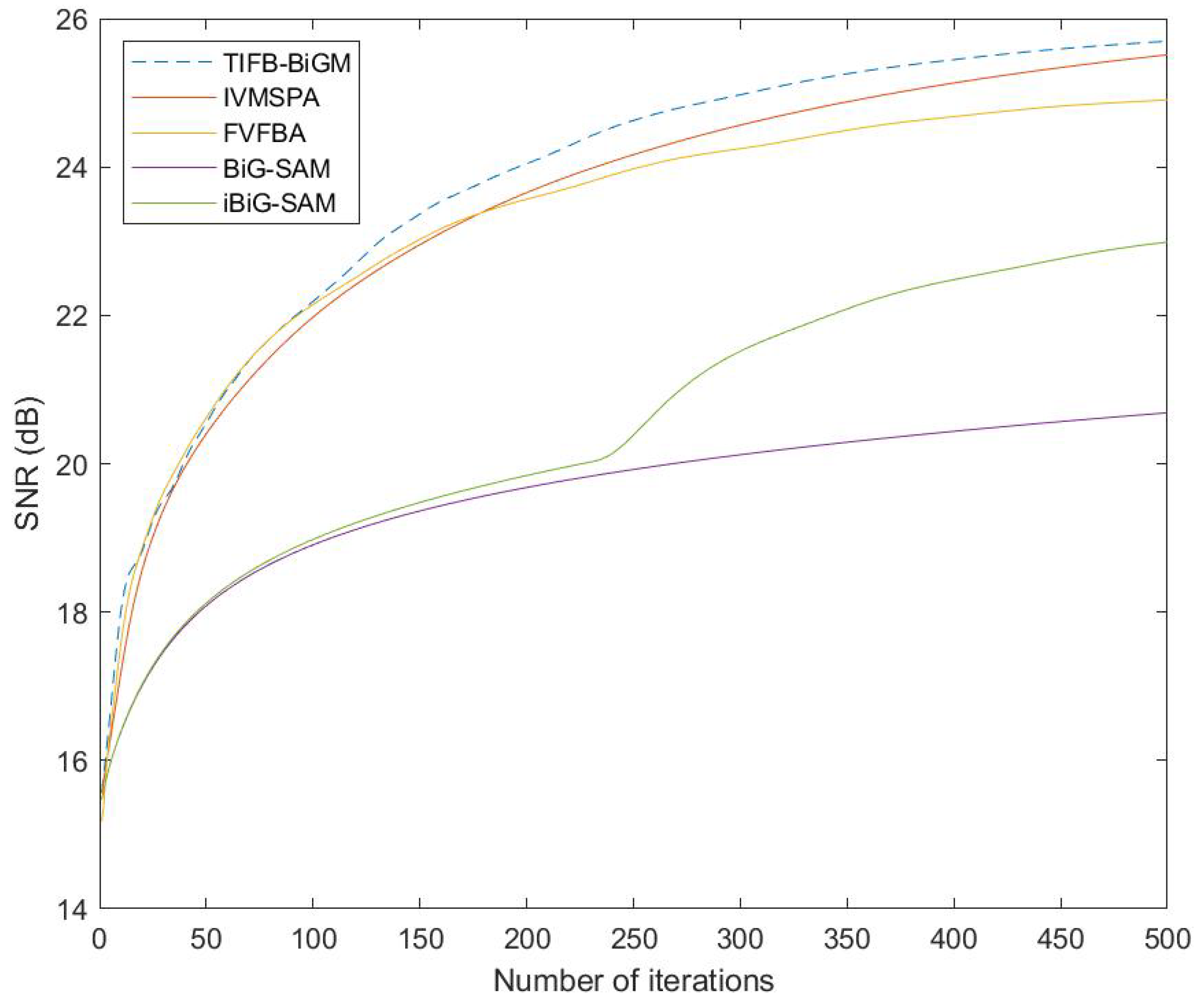
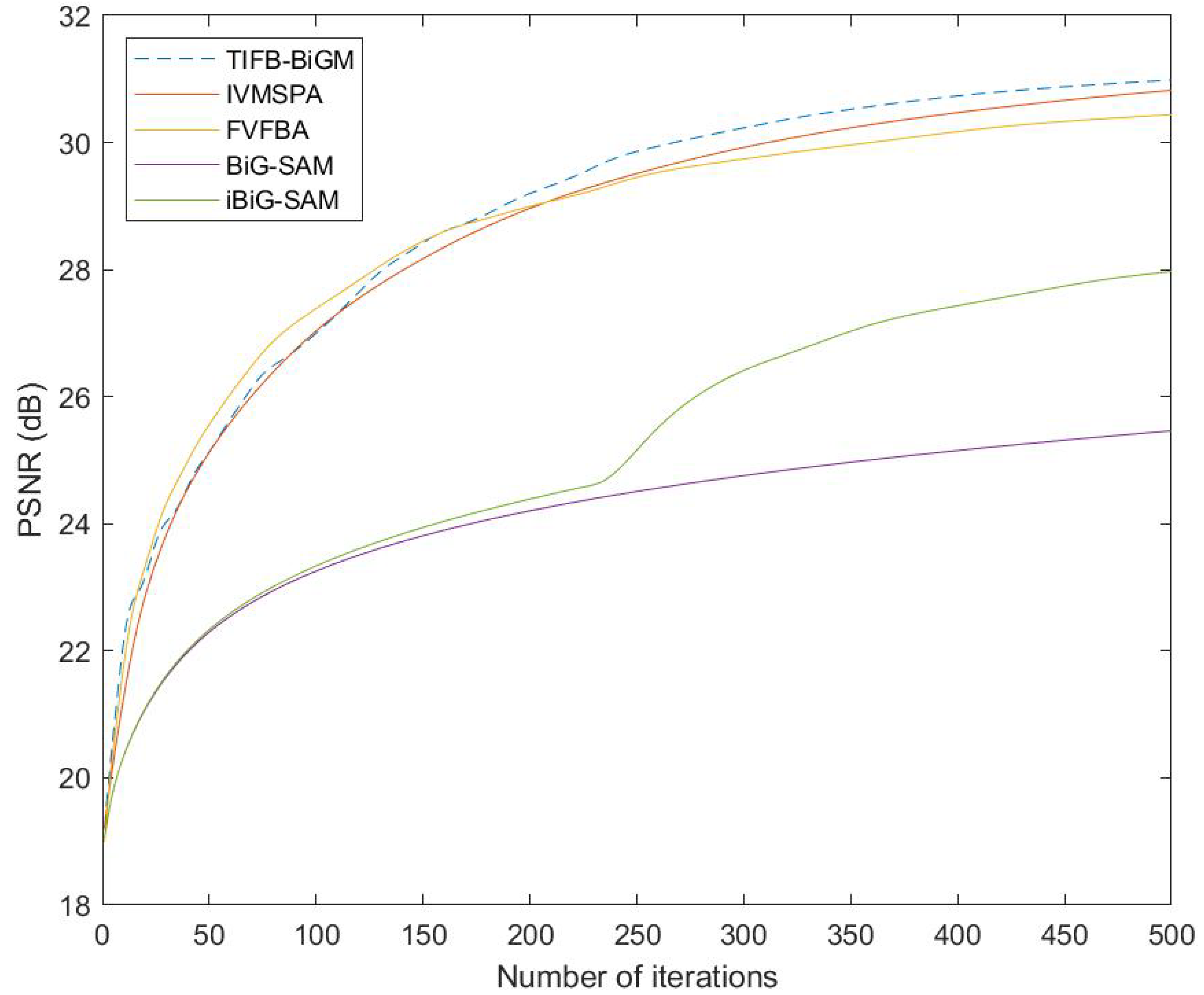
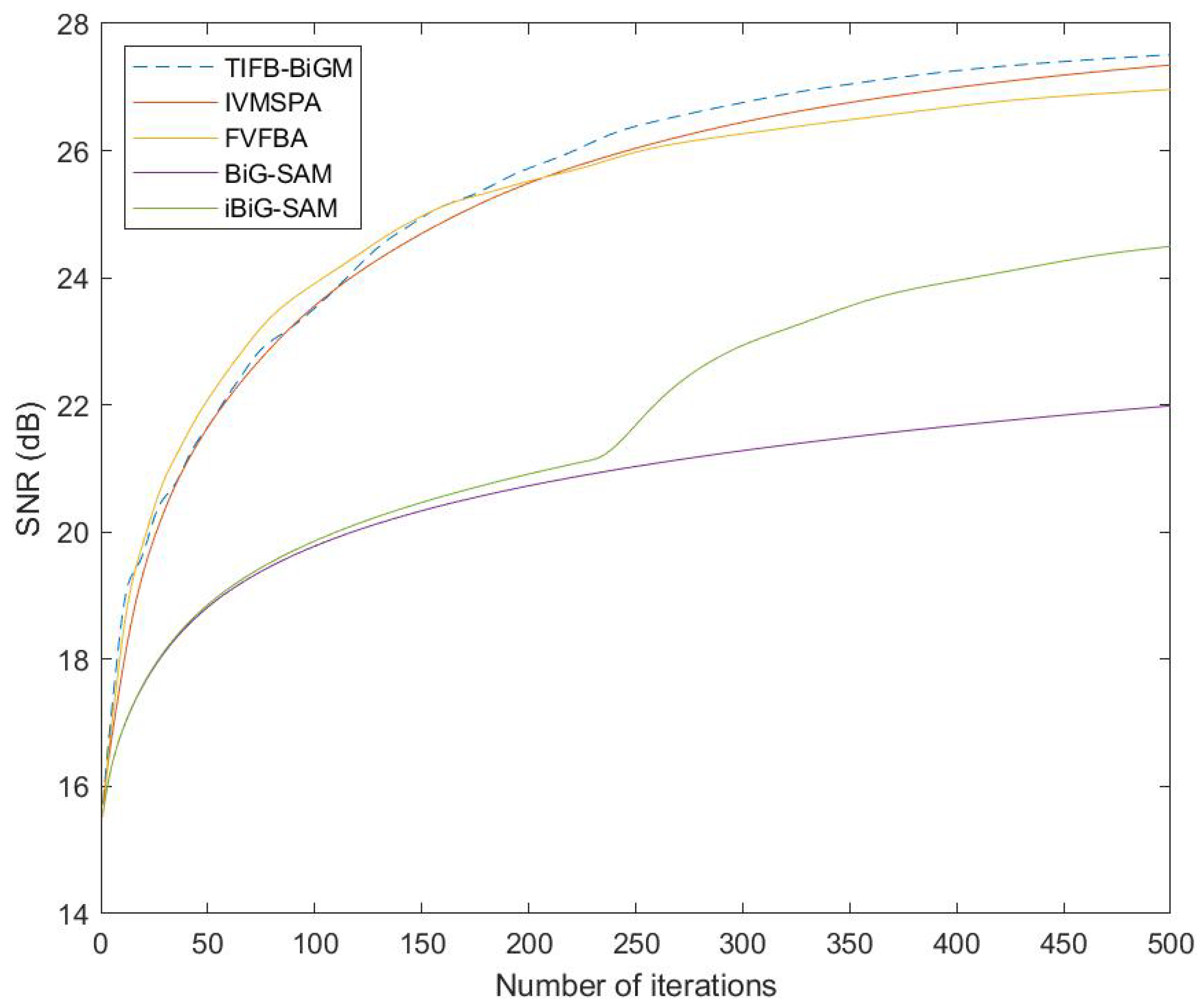




| 0.1 | 0.3 | 0.5 | 0.9 | 1 | ||
|---|---|---|---|---|---|---|
| 0.1 | 22.9755 | 23.2143 | 23.5185 | 24.6769 | 25.3398 | 25.4489 |
| 0.3 | 22.7791 | 22.9764 | 23.2154 | 23.9454 | 24.2129 | 24.2479 |
| 0.5 | 22.6116 | 22.7799 | 22.9773 | 23.5215 | 23.6923 | 23.7133 |
| 0.9 | 22.3362 | 22.4662 | 22.6129 | 22.9789 | 23.0805 | 23.0924 |
| 23.0847 | 23.3513 | 23.7038 | 25.4271 | 26.2116 | 24.9267 |
| 0.1 | 0.3 | 0.5 | 0.9 | 1 | ||
|---|---|---|---|---|---|---|
| 0.1 | 18.9503 | 19.1890 | 19.4932 | 20.6516 | 21.3144 | 21.4236 |
| 0.3 | 18.7539 | 18.9510 | 19.1901 | 19.9200 | 20.1876 | 20.2225 |
| 0.5 | 18.5864 | 18.7545 | 18.9519 | 19.4961 | 19.6670 | 19.6879 |
| 0.9 | 18.3110 | 18.4408 | 18.5875 | 18.9536 | 19.0551 | 19.0670 |
| 19.0595 | 18.3260 | 19.6784 | 21.4018 | 22.1913 | 20.9014 |
| Methods | Setting |
|---|---|
| TIFB-BiGM | , , , , , , |
| IVMSPA | , , , , where and |
| FVFBA | , , , |
| BiG-SAM | , , |
| iBiG-SAM | , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wattanataweekul, R.; Janngam, K.; Suantai, S. A Novel Two-Step Inertial Viscosity Algorithm for Bilevel Optimization Problems Applied to Image Recovery. Mathematics 2023, 11, 3518. https://doi.org/10.3390/math11163518
Wattanataweekul R, Janngam K, Suantai S. A Novel Two-Step Inertial Viscosity Algorithm for Bilevel Optimization Problems Applied to Image Recovery. Mathematics. 2023; 11(16):3518. https://doi.org/10.3390/math11163518
Chicago/Turabian StyleWattanataweekul, Rattanakorn, Kobkoon Janngam, and Suthep Suantai. 2023. "A Novel Two-Step Inertial Viscosity Algorithm for Bilevel Optimization Problems Applied to Image Recovery" Mathematics 11, no. 16: 3518. https://doi.org/10.3390/math11163518
APA StyleWattanataweekul, R., Janngam, K., & Suantai, S. (2023). A Novel Two-Step Inertial Viscosity Algorithm for Bilevel Optimization Problems Applied to Image Recovery. Mathematics, 11(16), 3518. https://doi.org/10.3390/math11163518





