Abstract
Predicting lithium-ion batteries’ state of charge (SOC) is essential to electric vehicle battery management systems. Traditional lithium-ion battery models mainly include equivalent circuit models (ECMs) and electrochemical models (EMs). ECMs are based on integer-order component modeling, which cannot characterize the internal electrochemical reaction mechanism of the battery, resulting in lower SOC prediction accuracy. In contrast, due to their complex structure, EMs are limited in their application. This study takes lithium batteries as the research object and proposes a fractional-order impedance model (FOIM) that characterizes the dynamic properties of the internal behavior of lithium-ion batteries using fractional-order elements. Considering the highly nonlinear characteristics of lithium-ion batteries, this study introduces the theory of fractional-order calculus into the extended Kalman filter (EKF) algorithm, and proposes the fractional-order extended Kalman filter (FEKF) algorithm applied to the prediction of battery charge state. Comparative analysis of simulation and experimental results shows that the accuracy of the FOIM, compared to ECMs, is significantly improved. The FEKF algorithm has good robustness in estimating the SOC, and the SOC prediction accuracy achieved with the algorithm is also improved compared with that obtained using the EKF algorithm of the integer-order model.
Keywords:
state of charge; lithium-ion battery; fractional-order impedance model; fractional-order extended Kalman filter; fractional-order calculus theory MSC:
03C98
1. Introduction
The development of electric vehicles (EVs) should be vigorously promoted to protect the deteriorating environment and cope with the energy crisis [1]. As one of the primary power sources of electric vehicles or hybrid electric vehicles, the safety and reliability of lithium-ion batteries are vital issues affecting the development of electric vehicles. The battery management system (BMS), as one of the most critical systems of EVs, has the functionality of improving the efficiency of battery use, preventing battery overcharge and discharge and prolonging battery life [2,3,4]. In BMSs, state of charge (SOC) estimation is the most basic and essential component [5]. However, the equipment cannot directly measure SOC; it must be calculated. Additionally, due to complex electrochemical reactions inside the battery, the system has strong nonlinear characteristics, increasing the difficulty of SOC estimation [6]. Therefore, finding an accurate method to estimate SOC for the safe use and popularization of EVs is significant.
Lithium-ion battery models mainly include EMs and ECMs [7]. Based on the porous electrode theory and the concentrated solution theory, EMs describe the charge and discharge behavior of lithium-ion batteries from the perspective of the electrochemical mechanism by numerically quantifying the internal electrochemical reaction kinetics, mass transfer, heat transfer, and other microscopic reaction processes.
Therefore, the electrochemical mechanism model has been widely used to optimize lithium-ion batteries, simulate charge and discharge behavior, and diagnose charge, health, and thermal states [8]. For example, Gopaluni et al. used the original pseudo-two-dimensional model to build a model and developed a particle filter algorithm independent of time and space coordinates to estimate the state of charge [9]. Bizeray et al. integrated the Chebyshev orthogonal configuration method into the partial differential equation of the pseudo-two-dimensional model for spatial discretization and then combined it with the extended Kalman filter (EKF) algorithm for battery state estimation [10]. Domenico Di et al. established an average electrode model and used the EKF to estimate the state of charge and critical surface charge [11]. Gao et al. disassembled the same kind of estimated target battery, measured the structural parameters of the battery via scanning electron microscopy, identified other unknown electrochemical model parameters using a genetic algorithm, and established a calculation rule of positive electrode capacity based on the stoichiometric ratio [12]. However, its complex governing equations and significant calculation result in a high computational load, which limits the application and development of EMs in practical engineering.
An ECM does not need to consider the complex chemical reactions inside the battery but only uses electrical components to simulate its characteristics. ECMs are the most commonly used methods in modeling, simulation, and engineering applications, which often combine filtering algorithms to estimate the battery’s SOC. Xie et al. established a second-order RC equivalent circuit model and used the unsent-particle filter to estimate SOC, and the results show that its estimation accuracy and real-time performance are relatively good [13]. Li et al. took lithium iron phosphate batteries as the research object, established the PNGV equivalent circuit model of batteries, and used the EKF algorithm to estimate the SOC of lithium-ion batteries. The results show that the PNGV model combined with the EKF method improved the SOC estimation accuracy [14]. Wang et al. first established the second-order RC equivalent circuit model of lithium-ion batteries and identified the model’s parameters. Second, given the shortcomings of the untracked Kalman filter algorithm, the convergence criterion of the general filter was introduced, and the SOC method of estimating the state of charge of lithium-ion batteries based on the adaptive untracked Kalman filter was formed [15]. Zhang et al. established a dual-polarization equivalent circuit model, integrated AEKF and PF algorithms, and developed an adaptive extended Kalman particle filter algorithm (AEKPF) [16]. Qiao et al. took the Thevenin equivalent circuit model as the initial model and improved it to form a dynamic migration model. In addition, a chaotic firefly particle filter method was proposed to realize the collaborative estimation of SOC and SOH for lithium-ion batteries [17]. However, the traditional method of modeling the ECM of lithium-ion batteries is usually based on integer-order modeling. There is an anomalous diffusion phenomenon based on the fractal medium between electrodes inside lithium-ion batteries, and its diffusion coefficient is directly related to the fractional order [18]. Moreover, in the application process of the integer-order equivalent model, although the increase in RC parallel links will improve the accuracy of the model to a certain extent, it will also lead to a significant increase in the complexity and calculation of the model, which seriously affects the application of the equivalent model. However, the application of fractional-order derivatives is becoming more and more widespread. In particular, this mathematical device has been successfully used to describe processes of an anomalous nature [19,20]. Examples of such systems in different scientific fields, including problems related to electrochemical reactions, are discussed in detail in [21]. As a result, the transition from an ECM to the fractional-order impedance model (FOIM) becomes possible.
As seen above, the structure of an EM is complex, and the amount of computation required is large. However, an ECM cannot describe the dynamic characteristics of the battery, and the model’s accuracy needs to be improved. Therefore, a new modeling method needs to make up for the shortcomings of the above models.
In this paper, a fractional-order modeling approach for power batteries based on the Grunwald–Letnikov (G-L) fractional-order calculus definition is used. The fractional-order electrical component structure is used to establish an FOIM for lithium-ion batteries. Compared with the existing electrochemical models, this model is more accurate than the integer-order modeling method, simplifying the model structure and reducing the amount of calculation required without lowering the model’s accuracy.
In addition, this study introduces the theory of fractional-order calculus into the EKF algorithm, forming the fractional-order extended Kalman filter (FEKF) algorithm to estimate the SOC of the battery. The simulation experiments, including the DST (dynamic stress test) and FUDS (federal urban dynamic schedule) conditions, are compared with the EKF algorithm. We further verify the robustness and accuracy of the algorithm.
2. Fractional-Order Modeling of Lithium-Ion Batteries
2.1. Thevenin Equivalent Circuit Model
In the Thevenin equivalent circuit model in the Rint equivalent circuit model based on the addition of a parallel RC network, the nature of the RC network coincides with the internal polarization phenomenon of the battery, which can be a good reflection of the internal dynamic and static characteristics of the battery. The structure of the Thevenin equivalent circuit model is shown in Figure 1, which mainly consists of three parts: the open-circuit voltage , the ohmic resistance , the polarization resistance , and the polarization capacitance . The parallel link composed of and is used to describe the polarization phenomenon of the battery.
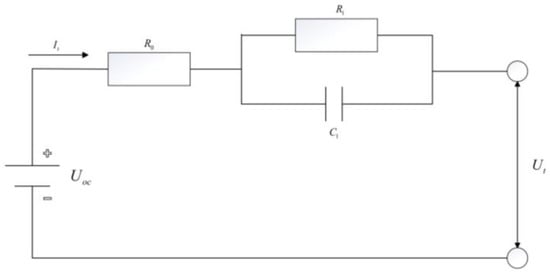
Figure 1.
Schematic diagram of Thevenin equivalent circuit model.
2.2. Fractional Calculus Modeling
2.2.1. Fractional-Order Calculus Definition
As early as 1695, Leibnitz’s letter to L’Hospital mentioned the concept of fractional-order calculus theory (fractional-order calculus, FOC). FOC is a generalization of the traditional integral calculus theory, which is widely used in physics, fluid mechanics, chemistry, biophysics, signal processing, aerodynamics, economics, control theory, and other scientific and engineering fields [22,23]. At present, there are many definition forms of fractional calculus, among which three standard definition forms are Grunwald–Letnikov (G-L) definition, Riemann–Liouville (R-L) definition, and Caputo definition [24]. The G-L definition form is often used in calculating fractional-order differentiation because it can discretize calculus directly. The definition form of G-L fractional calculus for any function is shown in Equation (1):
where Δ represents the differential operator; is the upper bound of calculus; stands for fractional order; means sampling time; is Newton’s binomial coefficient with the expansion as below, and its development is
Here is the Gamma function, = 0, 1, 2, …. Generally, a coefficient calculation is inevitable in the fractional calculus operation. In order to simplify the calculation process, a recursive method is adopted, as shown in Equation (3):
where stands for .
2.2.2. Fractional-Order Impedance Model
Electrochemical Impedance Spectroscopy (EIS) is a method of electrochemical measurement using small-amplitude sine wave potential (current) as the disturbance signal, which can be used for nondestructive measurement of parameters and effective measurement of battery dynamics. The shape of the electrochemical impedance spectra of lithium-ion batteries under different SOC states is almost consistent, as shown in Figure 2. In the figure below, the abscissa represents the impedance of the real part, and the ordinate represents the impedance of the imaginary part. The impedance spectrum is divided into high-, middle-, and low-frequency bands.
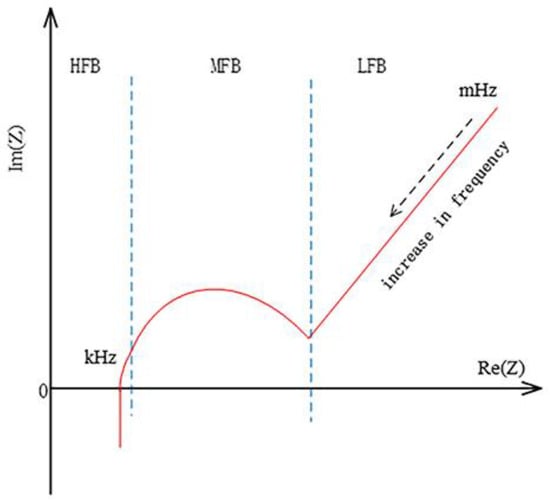
Figure 2.
Typical electrochemical impedance spectra of lithium-ion batteries.
As can be seen from Figure 2, the low-frequency part is a straight line with a constant slope, which characterizes the ion diffusion phenomenon (concentration polarization) in the electrochemical reaction of lithium-ion batteries. This part can be represented by a constant-phase element, usually called the element.
Let be the open-circuit voltage, which is a function of ; is the voltage of element in parallel with resistance ; is the voltage of element ; is terminal voltage; is ohmic resistance; the lithium-ion battery FOIM is shown in Figure 3. In terms of architecture, it is similar to an ECM, and its ability to reflect the electrochemical mechanism is better than that of an ECM, while it overcomes the shortcoming of the complexity of an EM.
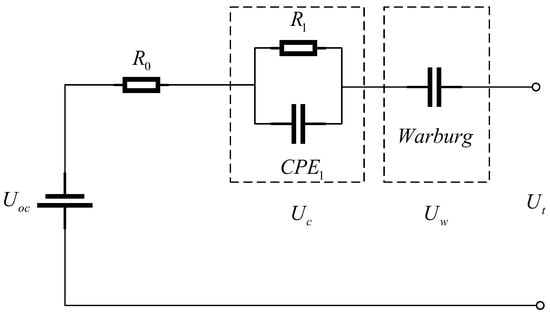
Figure 3.
Fractional-order impedance model of lithium-ion batteries.
Among them, the two constant components of and are fractional components formed in the frequency domain, so that they can be defined in the following formula [25]:
where and are the fractional order of element and element respectively; is the sampling frequency; represents imaginary units; and are constants.
According to Kirchhoff’s laws, the mathematical expression of FOIM is
The mathematical expression of terminal voltage is
where is the battery’s rated capacity; is the current flowing through the battery at the time ; is the Coulomb efficiency, which generally ranges from 0.92 to 0.98, where .
According to Equations (6) and (7), let state vector , input vector , and output vector ; then, the state transition equation and measurement equation of FOIM of lithium-ion batteries can be obtained as follows:
where ; ; ; ; ; , , , C1, , and are the parameters to be identified.
2.3. Parameter Identification
Accurate identification of the six parameters of FOIM in lithium-ion batteries is a prerequisite for accurate and predictive SOC.
- (1)
- Identification of parameters , , , ,
The FOIM of lithium-ion batteries involves several parameters that need to be identified. A genetic algorithm (GA) is selected to identify the model parameters to obtain the optimal solution. This is an efficient and parallel global search method that can automatically acquire and accumulate knowledge about search space in the search process and control the search process adaptively, so it can overcome the disadvantage of falling into a local minimum in the general iterative method. GAs have been widely applied and developed for parameter identification [26]. They are available for parameter identification of the Thevenin equivalent circuit model and FOIM. After determining the model parameters to be identified, a starting population that meets the requirements is randomly generated. The value of the fitness function is calculated for the initial population, and then new candidate populations are created using genetic operators (selection, crossover, and mutation). The value of the fitness function for the new population is iteratively calculated. The fitness function value of the new population is calculated repeatedly until the fitness function value of an individual is less than the specified precision. The iteration ends at this moment, and the individual is the best possible individual output. Otherwise, the iteration continues.
The purpose of parameter identification is to minimize the error of terminal voltage, so the fitness function of the genetic algorithm can be set as follows:
where is the length of terminal voltage ; represents the estimated value of terminal voltage, which can be calculated using Equation (8).
- (2)
- Identification of parameter
The change curve of the battery terminal voltage under the known pulse discharge current [27] is shown in Figure 4. When the discharge/charge current is executed or stopped, the battery’s terminal voltage will rise or fall suddenly, mainly due to ohmic polarization.
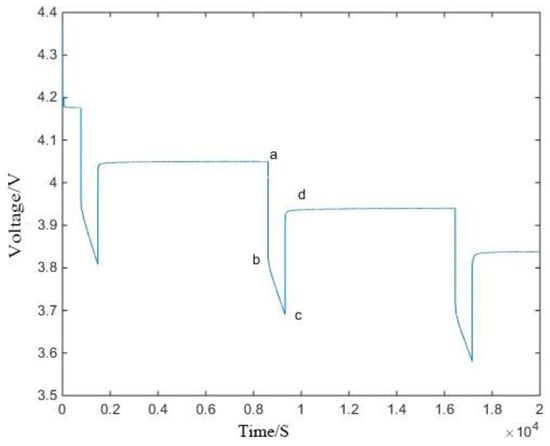
Figure 4.
Current pulse excitation voltage response curve of lithium-ion batteries.
Therefore, the two curves can be used to calculate the value of the ohm internal resistance of the battery. The calculation formula is as follows:
3. SOC Prediction Based on the Fractional-Order Extended Kalman Filter
The EKF algorithm is the extension of the traditional Kalman filter algorithm, which is widely used in engineering because of its simplicity and ease of use. This paper introduces the fractional calculus theory based on the EKF algorithm, and the SOC prediction is based on it.
Equation (8) can be discretized to obtain
In the above Equation, ; ; ; ; is the current flowing through the battery at the time ; is the terminal voltage of the battery at the time ; and are process noise and measurement noise, respectively; and are state variables corresponding to time and time , respectively.
Equation (11) is transformed by the G-L calculus definition to give the discrete equations of the system as:
where represents sampling time; the coefficient .
The FEKF algorithm was used to predict the SOC of lithium-ion batteries. The flowchart of the FEKF algorithm is shown in Figure 5, and the process is as follows:
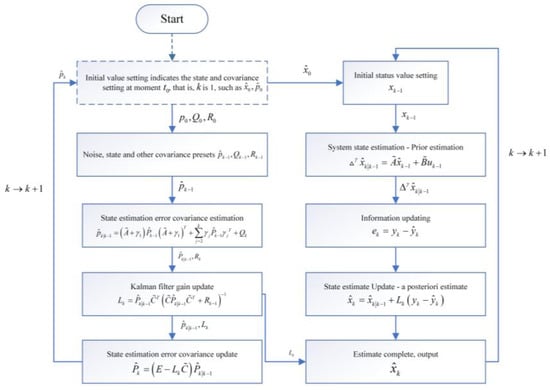
Figure 5.
Flow chart of the fractional-order extended Kalman filter.
- (1)
- Initialization
Suppose the estimated value of the initial state is and the error covariance matrix of the initial state is , then:
In the above Equation, is the expected value.
- (2)
- Time update
The prior estimation of the state and error covariance matrix at the time is obtained through the posterior estimation of the state matrix and error covariance matrix at the time , namely:
where is the covariance matrix for measuring noise .
- (3)
- Measurement update
Posteriori estimate of the state and error covariance matrix at the time can be obtained by updating the prior estimate of the state matrix and error covariance matrix at the time , namely:
where ; is the estimated SOC value at the time ; is the estimated value of the terminal voltage at the time ; Lk is the gain matrix of Kalman filter; is the covariance matrix of process noise ; is the identity matrix of .
4. Experiment Results
4.1. Data Acquisition
These data used here were obtained from the experimental data provided openly by the laboratory of the University of Maryland [27]. The battery model used in the experiment is the INR18650-20R power battery, whose rated capacity is 2 Ah and cut-off voltage is 4.2 V. Under the constant temperature conditions of 0 °C, 25 °C, and 45 °C, pulse current charge and discharge, constant current charge and discharge, and multi-condition dynamic test experiments were carried out. All three test experiments could be used to verify the model, and the pulse discharge test data were selected to verify the model.
4.2. Battery Model Verification
Model parameters were identified using the aforementioned parameter identification method and compared with the first-order fractional impedance model (IM) and integer Thevenin equivalent circuit model in the literature [28].
The parameter identification results for the FOIM, IM, and Thevenin models are shown in Table 1.

Table 1.
Parameter identification results.
Further, a terminal voltage comparison diagram of the FOIM, IM, and Thevenin model and its error comparison diagram under pulse discharge conditions could be obtained, as shown in Figure 6 and Figure 7.
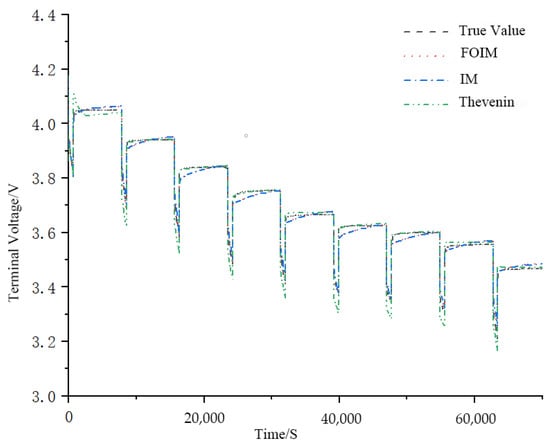
Figure 6.
Voltage comparison of FOIM, IM, and Thevenin model under pulse discharge.
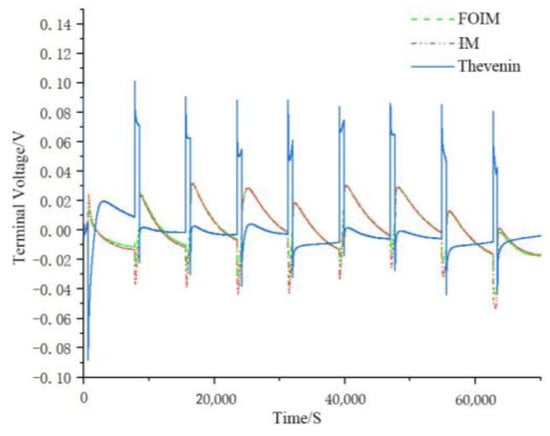
Figure 7.
Voltage error comparison of FOIM, IM, and Thevenin model under pulse discharge.
It can be seen from Figure 7 that the FOIM had a certain degree of improvement in accuracy compared with the IM and the integer-order Thevenin model, which can better track the actual measurements.
The error analysis results show that significant errors occurred at the beginning and end of the operating condition test, which were caused by the battery model error. The terminal voltage error of the FOIM constantly fluctuated within ±0.02 V and decreased with time, while the terminal voltage error of the integer Thevenin model increased with time. The root mean square error (RMSE) calculation results for the FOIM, IM, and Thevenin terminal voltage models are shown in Table 2.

Table 2.
FOIM, IM, and Thevenin model terminal voltage root mean square error.
As seen in Table 2, the root mean square error of the terminal voltage of the FOIM was 0.0139 V, which is 0.013 V and 0.056 V less than the RMSE of the IM and Thevenin model, respectively.
The above analysis shows that the FOIM is effective. Its accuracy was significantly improved compared with the IM and Thevenin model. This is because, on the one hand, the ECM usually contains one or more RC links, and RC links can only describe the physical characteristics of batteries, while the CPE components in the FOIM can explain the diffusion phenomenon inside batteries, which not only accords with the electrochemical mechanism inside the battery but also dramatically improves the accuracy of the model; on the other hand, compared with the IM, the FOIM increases the description of the low-frequency part of the electrochemical impedance spectrum, thus improving the accuracy of the model. In addition, based on integer-order equivalent circuit modeling, an FOIM for lithium-ion batteries is proposed. If compared with the Thevenin equivalent circuit model, the second- or third-order models are more accurate. As a matter of fact, these higher-order models can result in a significant increase in the complexity and calculation of the model, which seriously affects the application of the equivalent model. In addition, the accuracy of the model does not considerably increase when the order of the RC network increases to the third order or higher, and a significant amount of computation has to be considered [29,30]. Apparently, the Thevenin equivalent circuit model satisfies a better balance between accuracy and computational efficiency [31]. The transition from the Thevenin equivalent circuit model to the FOIM is justified. In a word, the Thevenin equivalent circuit model is more advantageous according to the results.
4.3. SOC Prediction and Analysis of Lithium-Ion Batteries
The complex driving conditions of electric vehicles lead to frequent and irregular charging and discharging behaviors of lithium-ion batteries during the driving process. Therefore, verifying the effectiveness and reliability of SOC estimation algorithms under different driving conditions is necessary.
Here, two commonly used test conditions, DST and FUDS, are selected; the FOIM is combined with the FEKF algorithm; the SOC estimation strategy is established; parameters are substituted into the algorithm; and the FEKF algorithm calculates the SOC value. The SOC predicted value is compared with the SOC predicted value of the traditional EFK algorithm and SOC reference value. The SOC reference value can be calculated using Equation (20):
where is the value of the charge status at the initial time; indicates the battery’s rated capacity; represents the current flowing through the battery.
4.3.1. DST Working Condition Simulation Verification
The DST condition is a widely used dynamic driving test condition which can be used to evaluate a vehicle’s performance and verify the accuracy of the battery model or algorithm efficiency. To verify the FEKF algorithm, DST operating condition test data were obtained from the University of Maryland at 25 °C. The experimental results show that the working range of SOC was reduced from 80% to 10%, including over multiple DST operating cycles. The DST test operating current and terminal voltage curves are shown in Figure 8 and Figure 9, respectively. In order to verify the accuracy and robustness of the FEKF algorithm under the DST condition, the initial SOC value was set as 70% and compared with the EKF algorithm of the integer-order model.
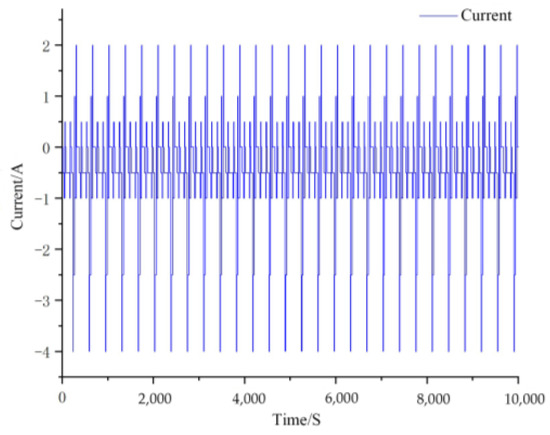
Figure 8.
The current diagram under the DST test condition.
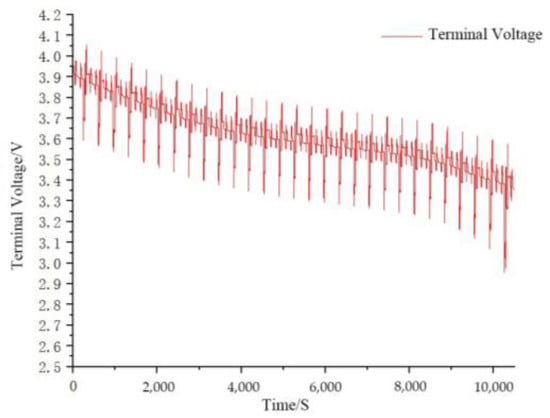
Figure 9.
Terminal voltage curve under the DST test condition.
Here, the SOC value calculated using Equation (20) was used as the reference value, compared with the SOC predicted value calculated using the FEKF algorithm and the one calculated using the integer-order EKF; then, the error analysis was carried out further. The results are shown in Figure 10 and Figure 11.
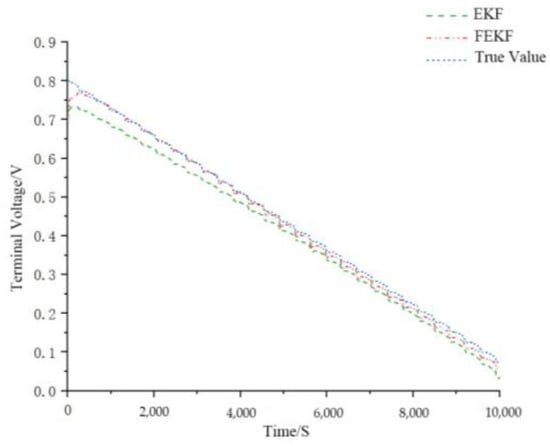
Figure 10.
Comparison of SOC estimation between FEKF and EKF under the DST test condition.
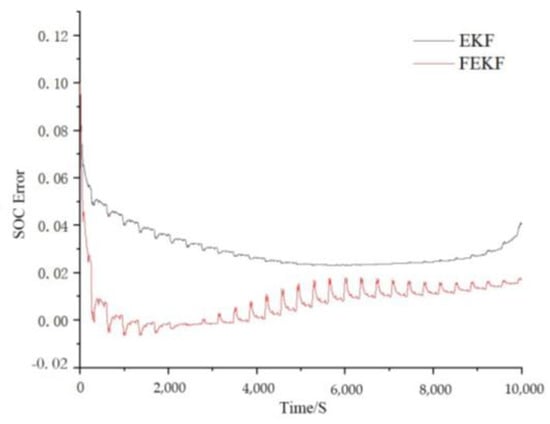
Figure 11.
The SOC estimation errors comparison of FEKF and EKF under the DST test condition.
Figure 10 shows that the SOC curves of the FEKF and EKF algorithms could converge to the true SOC value despite different initial SOC values, indicating that both algorithms have good robustness. Figure 11 shows that the SOC convergence error of the FEKF algorithm was within ±0.02, which is significantly less than the SOC convergence error of the EFK algorithm. Meanwhile, the time taken for the error of the FEFK algorithm to reach convergence was considerably less than the convergence time of the EKF algorithm. This indicates that the FEKF algorithm has higher accuracy and efficiency than the EFK algorithm under the DST test condition.
4.3.2. FUDS Working Condition Simulation Verification
The FUDS condition is another typical dynamic driving cycle test condition which can be used to verify the model’s and algorithm’s effectiveness. Similar to the DST test condition, after several FUDS charging and discharging cycles, the SOC operating range was reduced from 80% to 10%. The current and terminal voltage curves of the FUDS test condition are shown in Figure 12 and Figure 13. In order to verify the accuracy and robustness of the FEKF algorithm under the FUDS condition, the initial SOC value was set to 70%, and the predicted SOC value of the FEKF algorithm was compared with that of the EKF algorithm of the integer-order model. The comparison results and error diagrams are shown in Figure 14 and Figure 15.
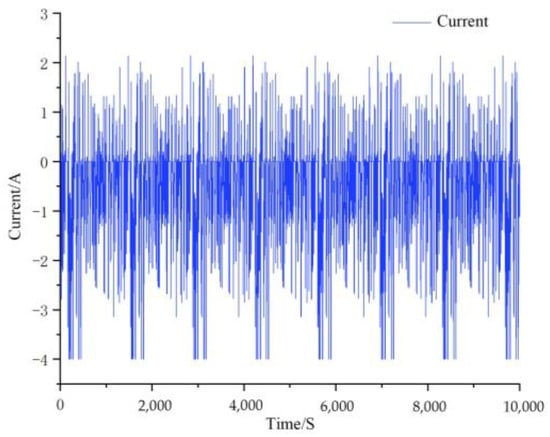
Figure 12.
The current diagram under the FUDS test condition.
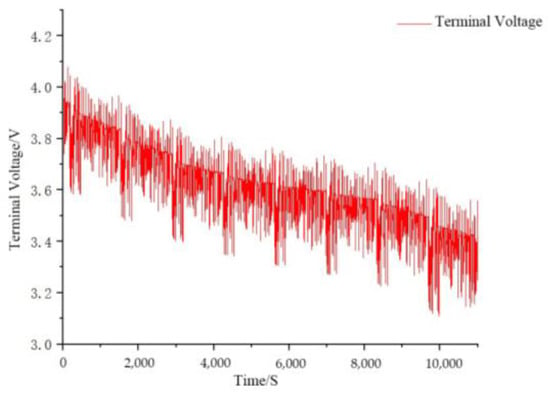
Figure 13.
Terminal voltage diagram under the FUDS test condition.
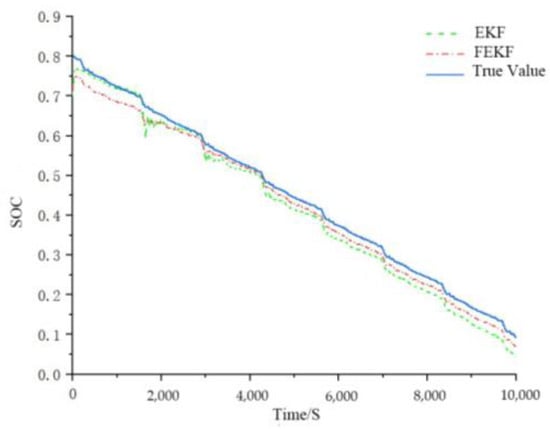
Figure 14.
Comparison of SOC chart of FEKF and EKF under the FUDS test condition.
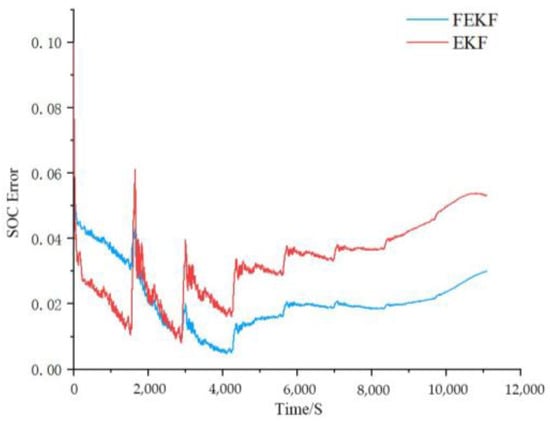
Figure 15.
The SOC error comparison of FEKF and EFK under the FUDS test condition.
It can be seen from Figure 14 that the FEKF algorithm had good robustness under the FUDS test condition. The SOC error diagram in Figure 15 shows that the SOC error predicted by the FEKF algorithm converged to 0.02, while the SOC error predicted by the EKF algorithm converged to 0.035 under the FUDS condition, which indicates that the accuracy of the former is significantly better than that of the EKF algorithm. According to the SOC error diagram, under DST and FUDS test conditions, when the SOC is in a low or high range, there is an increase in the error in SOC prediction. The increased SOC error under the FEKF algorithm is less than that under the EKF algorithm because the battery parameters change when the SOC is in the lower or higher range. This leads to the phenomenon wherein the predicted value deviates from the real value, but the FEKF algorithm can inhibit this phenomenon.
In order to quantify the accuracy of the proposed algorithm, error analysis of the predicted SOC of the FEKF algorithm and EKF under DST and FUDS test conditions was carried out. The statistical results for the root mean square error and maximum error of SOC estimation are shown in Table 3 and Table 4.

Table 3.
Comparison of the RMSE between FEKF and EKF for the SOC estimation.

Table 4.
Comparison of max SOC estimation error between FEKF and EKF.
It can be seen from Table 3 and Table 4 that under DST and FUDS test conditions, the SOC estimation RMSE of the FEKF algorithm was 0.0121 and 0.0233, respectively, being reduced by 0.0231 and 0.0115 compared with the EKF estimation effect, respectively. In the DST and FUDS tests, the maximum estimation error of SOC estimated by the FEKF algorithm was 0.042 and 0.020, respectively, being significantly reduced compared with the maximum error of SOC estimated using the EKF. Noted that modeling error is the main factor affecting SOC estimation, and the accuracy of SOC estimation of the FEKF algorithm was better than that of the EKF due to the use of fractional models to reduce modeling error. Therefore, the FEKF algorithm used in the fractional-order model had good robustness to the SOC estimation, and the SOC prediction accuracy was improved compared with the EKF algorithm of the integer-order model.
5. Conclusions
This paper introduces the fractional calculus theory into lithium-ion battery modeling and state prediction. A fractional-order battery modeling and SOC prediction methods based on the FEKF are also proposed. Compared with the traditional ECM, the FOIM can accurately describe the electrochemical mechanism of the battery. Simulation experiments and calculations were carried out to verify the accuracy of the FOIM, and the RMSE error of the FOIM was reduced by 0.013 V and 0.058 V compared with the IM and Thevenin model, respectively. Based on the fractional impedance model, the FEKF algorithm was used to predict the SOC of the battery, and compared with the EKF algorithm, the root mean square errors of the FEKF algorithm were reduced by 0.0231 and 0.0115 under DST and FUNDS working conditions, respectively; the maximum errors were reduced by 0.022 and 0.015, respectively. The FEKF algorithm has the characteristics of good robustness, high accuracy, and high efficiency in predicting SOC. Therefore, the FOIM proposed in this paper can accurately simulate battery characteristics, and the FEKF algorithm used to predict the battery SOC provides an effective way to improve the accuracy of state estimation in the battery management system of electric vehicles.
Author Contributions
Conceptualization, X.Z.; methodology, X.L.; writing—original draft preparation, Z.W.; writing—review and editing, K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Program of Shaanxi, grant number 2022GY-303, and in part by the Xi’an Science and Technology Planning Project under grant numbers 2022GXFW0152 and 2022GXFW0116.
Data Availability Statement
The data presented in this research are available in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martinez, C.M.; Hu, X.S.; Cao, D.P.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef]
- Liu, F.; Ma, J.; Su, W.; Dou, R.; Lin, H. Estimation method of charging state of electric vehicle power battery in full life cycle based on adaptive regression Extended Kalman filter. Trans. China Electrotech. Soc. 2020, 35, 698–707. [Google Scholar]
- Lv, J.; Song, W.; Feng, Z. Design and implementation of battery management system. Batteries 2019, 49, 499–501. [Google Scholar]
- Wang, Z.; Wang, Q.; Liu, P.; Zhang, Z. A review of power battery health state estimation methods driven by Big data. J. Mech. Eng. 2023, 59, 151–168. [Google Scholar]
- Wang, Y.; Zuo, X. Estimation methods of state of charge of lithium-ion batteries and their application scenarios. Autom. Electr. Power Syst. 2022, 46, 193–207. [Google Scholar]
- Tian, Y.; Li, D.; Tian, J.D.; Xia, B.Z. State of charge estimation of lithium-ion batteries using an optimal adaptive gain nonlinear observer. Electrochim. Acta 2017, 225, 225–234. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium-Sulphur. Renew. Sust. Energy. Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Yang, J.; Wang, T.; Du, C.; Min, F.; Lu, T.; Zhang, Y.; Yan, L.; Xie, J.; Yin, G. A review of lithium-ion battery models. Energy Storage Sci. Technol. 2019, 8, 58–64. [Google Scholar]
- Gopaluni, R.B.; Braatz, R.D. State of Charge Estimation in Li-ion Batteries Using an Isothermal Pseudo Two-Dimensional Model. IFAC Proc. Vol. 2013, 46, 135–140. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Zhao, S.; Duncan, S.R.; Howey, D.A. Lithium-ion battery thermal-electrochemical model-based state estimation using orthogonal collocation and a modified extended Kalman filter. J. Power Sources 2015, 296, 400–412. [Google Scholar] [CrossRef]
- Di Domenico, D.; Stefanopoulou, A.; Fiengo, G. Lithium-Ion Battery State of Charge and Critical Surface Charge Estimation Using an Electrochemical Model-Based Extended Kalman Filter. J. Dyn. Syst. Meas. Control 2010, 132, 061302. [Google Scholar] [CrossRef]
- Gao, R.; Lv, Z.; Zhao, S.; Huang, X. Estimation of lithium-ion battery health status based on electrochemical model. J. Beijing Univ. Technol. 2022, 42, 791–797. [Google Scholar]
- Xie, C.; Fei, Y.; Zeng, C.; Fang, W. State estimation of vehicle-mounted lithium ion batteries based on untracked particle filter. Trans. China Electrotech. Soc. 2018, 33, 3958–3964. [Google Scholar]
- Li, W.; Liu, W.; Deng, Y. Estimation of charged state of lithium-ion batteries based on Extended Kalman filter. China Mech. Eng. 2020, 31, 321–327+343. [Google Scholar]
- Wang, P.; Gong, Q.; Cheng, Z.; Zhang, J. SOC Estimation method for lithium-ion batteries based on AUKF. Automot. Eng. 2022, 44, 1080–1087. [Google Scholar]
- Zhang, X.; Yao, M.; Song, R.; Cui, J. Joint estimation of SOC and SOH for lithium-ion batteries based on AEKPF algorithm. J. Jiangsu Univ. (Nat. Sci. Ed.) 2022, 43, 24–31. [Google Scholar]
- Qiao, J.L.; Wang, S.L.; Yu, C.M.; Yang, X.; Fernandez, C. A chaotic firefly-Particle filtering method of dynamic migration modeling for the state-of-charge and state-of-health co-estimation of a lithium-ion battery performance. Energy 2023, 263, 126164. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers: Volume I Background and Theory Volume II Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zelenyi, L.M.; Milovanov, A.V. Fractal topology and strange kinetics: From percolation theory to problems in cosmic electrodynamics. Phys. Uspekhi 2004, 47, 749–788. [Google Scholar] [CrossRef]
- Metzler, R.J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A. Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations [electronic resource]: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 2013, 2013, 553–563. [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. Higher Education Press: Beijing, China, 2011. [Google Scholar]
- Wang, B. Modeling and State Estimation of Lithium-Ion Batteries Based on Fractional Order Theory. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Sun, G.; Ren, J.; Cheng, L.; Zhu, Y.; Wei, Z.; Zang, H. Estimation of charged state of lithium iron phosphate batteries based on fractional impedance model. Autom. Electr. Power Syst. 2018, 42, 57–63. [Google Scholar]
- Center for Advanced Life Cycle Engineering, University of Maryland. Battery Research Data. Available online: https://calce.umd.edu/data (accessed on 10 March 2021).
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Xu, J.; Pei, L.; Xu, B.; Wu, G.; Zhu, C. Battery equivalent circuit model analysis based on simulation comparison. Electr. Meas. Instrum. 2017, 54, 6. [Google Scholar]
- Wang, Y.; Zhao, Y.; Hua, D.; An, R. State estimation method of lithium battery based on second-order equivalent circuit model. Energy Sav. 2022, 41, 38–42. [Google Scholar]
- Guo, X.; Gao, Y.; Si, Y.; Liu, Z.; Xu, X. Research on equivalent circuit model of power battery. Sens. Microsyst. 2022, 41, 4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).