A Proposed Application of Fractional Calculus on Time Dilation in Special Theory of Relativity
Abstract
1. Introduction
2. Concepts of the FC
3. Derivation of Standard TD Formula via Integral Technique
4. The TD in FC (FTD)
5. Derivation of Standard TD Formula as a Special Case:
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Narahari Achar, B.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Dynamics of the fractional oscillator. Physica A 2001, 297, 361–367. [Google Scholar] [CrossRef]
- Sebaa, N.; Fellah, Z.E.A.; Lauriks, W.; Depollier, C. Application of fractional calculus to ultrasonic wave propagation in human cancellous bone. Signal Process. 2006, 86, 2668–2677. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Heisenberg equation. Phys. Lett. A 2008, 372, 2984–2988. [Google Scholar] [CrossRef]
- Ding, Y.; Yea, H. A fractional-order differential equation model of HIV infection of CD4+T-cells. Math. Comput. Model. 2009, 50, 386–392. [Google Scholar] [CrossRef]
- Wang, S.; Xu, M.; Li, X. Green’s function of time fractional diffusion equation and its applications in fractional quantum mechanics. Nonlinear Anal. Real World Appl. 2009, 10, 1081–1086. [Google Scholar] [CrossRef]
- Song, L.; Xu, S.; Yang, J. Dynamical models of happiness with fractional order. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 616–628. [Google Scholar] [CrossRef]
- Gómez-Aguilara, J.F.; Rosales-García, J.J.; Bernal-Alvarado, J.J. Fractional mechanical oscillators. Rev. Mex. Física 2012, 58, 348–352. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Garcia, J.J.R.; Calderon, M.G.; Ortiz, J.M.; Baleanu, D. Motion of a particle in a resisting medium using fractional calculus approach. Proc. Rom. Acad. Ser. A 2013, 14, 42–47. [Google Scholar]
- Machado, J.T. A fractional approach to the Fermi-Pasta-Ulam problem. Eur. Phys. J. Spec. Top. 2013, 222, 1795–1803. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Akgül, A.; De la Sen, M.; Bayram, M. Approximate and Exact Solutions in the Sense of Conformable Derivatives of Quantum Mechanics Models Using a Novel Algorithm. Symmetry 2023, 15, 744. [Google Scholar] [CrossRef]
- Ebaid, A. Analysis of projectile motion in view of the fractional calculus. Appl. Math. Model. 2011, 35, 1231–1239. [Google Scholar] [CrossRef]
- Ebaid, A.; El-Zahar, E.R.; Aljohani, A.F.; Salah, B.; Krid, M.; Machado, J.T. Analysis of the two-dimensional fractional projectile motion in view of the experimental data. Nonlinear Dyn. 2019, 97, 1711–1720. [Google Scholar] [CrossRef]
- Ahmad, B.; Batarfi, H.; Nieto, J.J.; Oscar, O.-Z.; Shammakh, W. Projectile motion via Riemann-Liouville calculus. Adv. Differ. Equ. 2015, 63. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 2018, 133, 133–259. [Google Scholar] [CrossRef]
- Ebaid, A.; Cattani, C.; Al Juhani, A.S.; El-Zahar, E.R. A novel exact solution for the fractional Ambartsumian equation. Adv. Differ. Equ. 2021, 2021, 88. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Alotaibi, A.M.; Ebaid, A.; Aljohani, A.F.; Gómez Aguilar, J.F. The Riemann-Liouville fractional derivative for Ambartsumian equation. Results Phys. 2020, 19, 103551. [Google Scholar] [CrossRef]
- Ebaid, A.; Masaedeh, B.; El-Zahar, E. A new fractional model for the falling body problem. Chin. Phys. Lett. 2017, 34, 020201. [Google Scholar] [CrossRef]
- Khaled, S.M.; El-Zahar, E.R.; Ebaid, A. Solution of Ambartsumian delay differential equation with conformable derivative. Mathematics 2019, 7, 425. [Google Scholar] [CrossRef]
- Kaur, D.; Agarwal, P.; Rakshit, M.; Chand, M. Fractional Calculus involving (p,q)-Mathieu Type Series. Appl. Math. Nonlinear Sci. 2020, 5, 15–34. [Google Scholar] [CrossRef]
- Iqbal, Z.; Rehman, M.A.-U.; Imran, M.; Ahmed, N.; Fatima, U.; Akgül, A.; Rafiq, M.; Raza, A.; Djuraev, A.A.; Jarad, F. A finite difference scheme to solve a fractional order epidemic model of computer virus. AIMS Math. 2023, 8, 2337–2359. [Google Scholar] [CrossRef]
- Agarwal, P.; Singh, R. Modelling of transmission dynamics of Nipah virus (Niv): A fractional order approach. Phys. A Stat. Mech. Its Appl. 2020, 547, 124243. [Google Scholar] [CrossRef]
- Feng, Y.-Y.; Yang, X.-J.; Liu, J.-G. On overall behavior of Maxwell mechanical model by the combined Caputo fractional derivative. Chin. J. Phys. 2020, 66, 269–276. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana-Baleanu-Caputo fractional derivative. Adv. Differ. Equ. 2020, 2020, 334. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Mathematical Modeling of an Autonomous Nonlinear Dynamical System for Malaria Transmission Using Caputo Derivative. In Fractional Order Analysis: Theory, Methods and Applications; John Wiley & Sons: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Fang, J.; Nadeem, M.; Habib, M.; Akgül, A. Numerical Investigation of Nonlinear Shock Wave Equations with Fractional Order in Propagating Disturbance. Symmetry 2022, 14, 1179. [Google Scholar] [CrossRef]
- Aljohani, A.F.; Ebaid, A.; Algehyne, E.A.; Mahrous, Y.M.; Cattani, C.; Al-Jeaid, H.K. The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis. Fractal Fract. 2022, 6, 125. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. The Mittag–Leffler Functions for a Class of First-Order Fractional Initial Value Problems: Dual Solution via Riemann–Liouville Fractional Derivative. Fractal Fract. 2022, 6, 85. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Korper. Ann. Der Phys. 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Forshaw, J.R.; Smith, A.G. Dynamics and Relativity; Wiley: Chichester, UK, 2009. [Google Scholar]
- Behroozi, F. A Simple Derivation of Time Dilation and Length Contraction in Special Relativity. Phys. Teach. 2014, 52, 410–412. [Google Scholar] [CrossRef]
- Bailey, J.; Borer, K.; Combley, F.; Drumm, H.; Krienen, F.; Lange, F.; Picasso, E.; Von Ruden, W.; Farley, F.J.M.; Field, J.H.; et al. Measurements of relativistic time dilatation for positive and negative muons in a circular orbit. Nature 1977, 268, 301–305. [Google Scholar] [CrossRef]

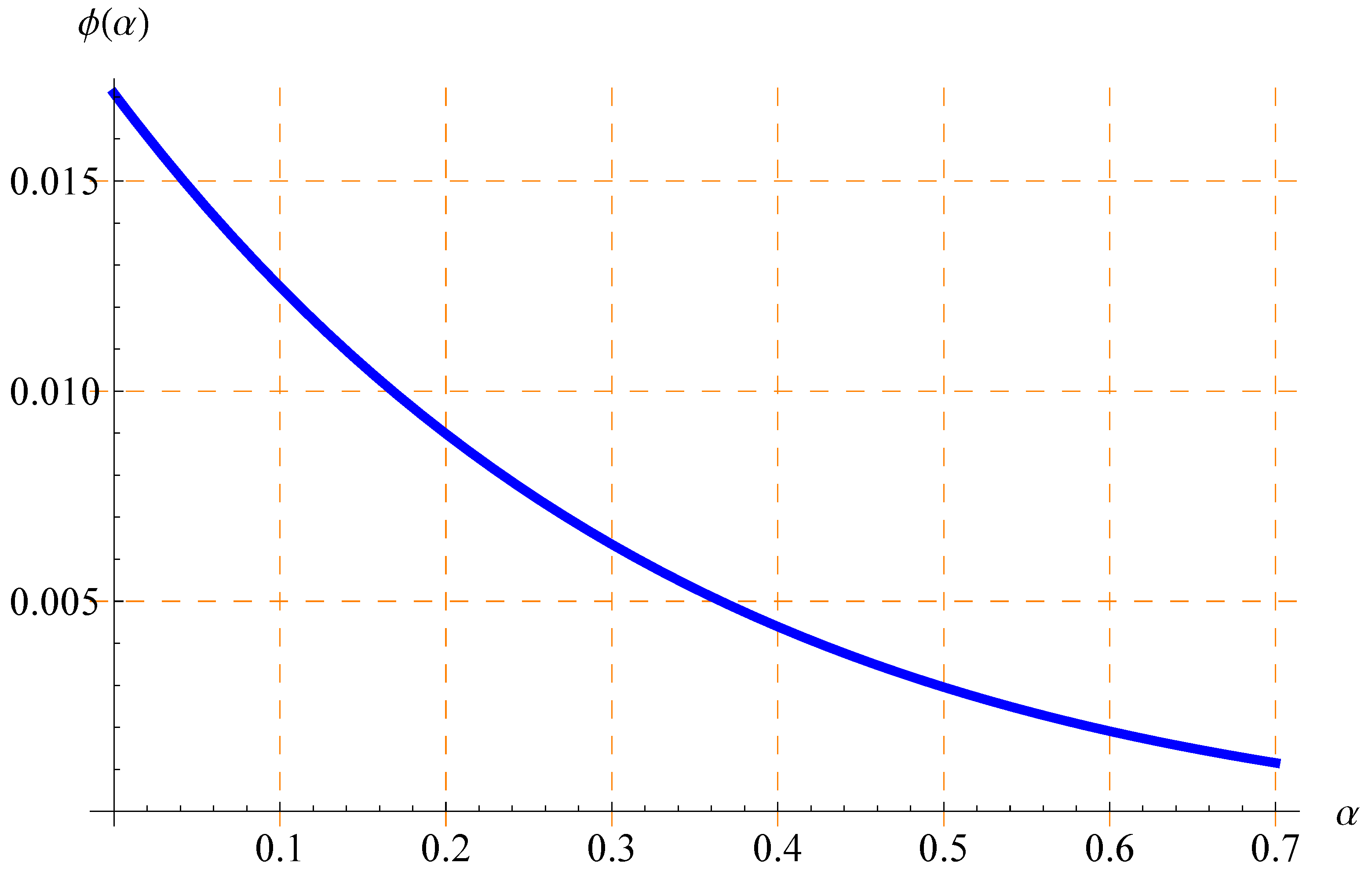
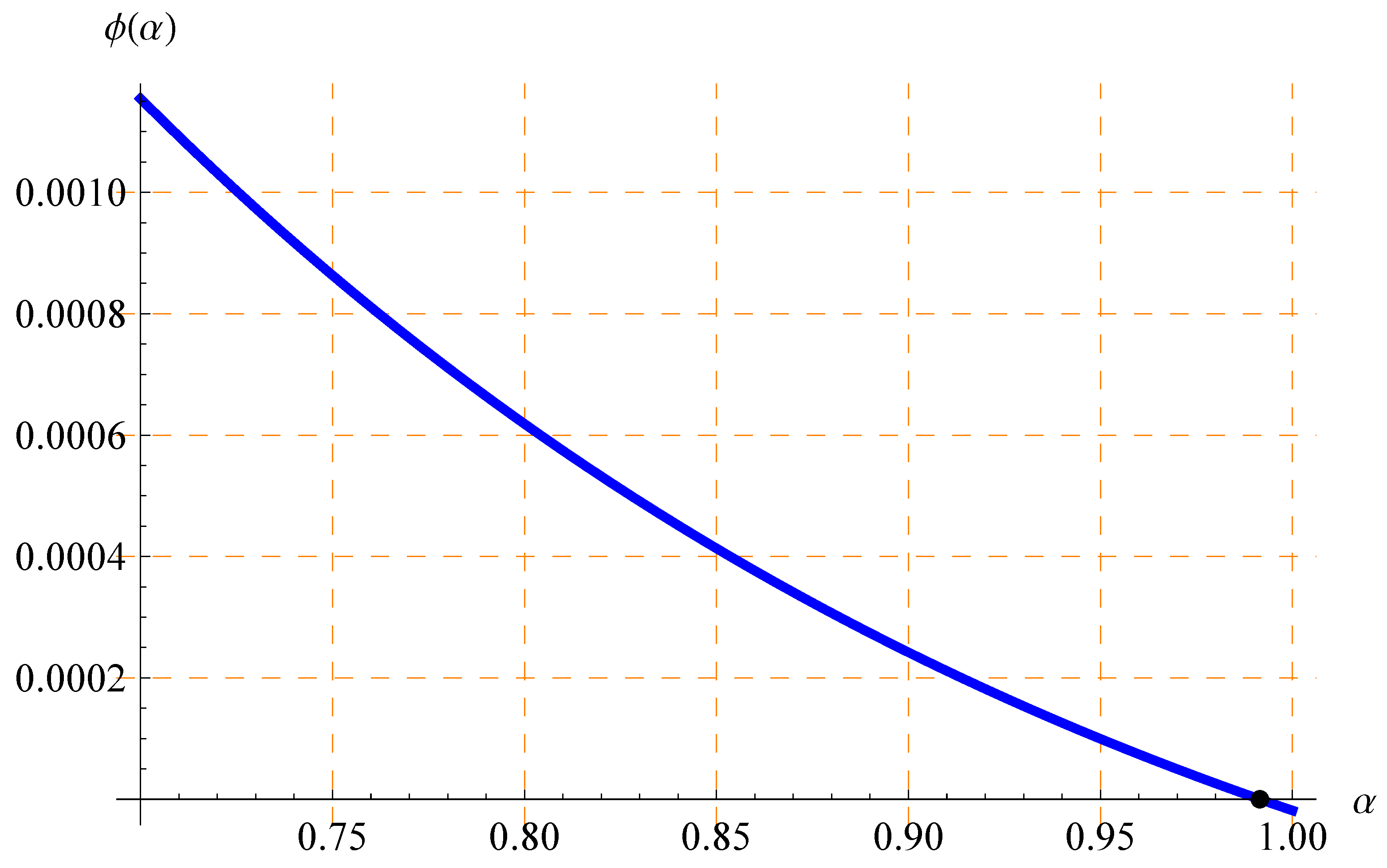
| Values of t at [s] | Values of t at [s] | |
|---|---|---|
| 1/8 | 0.001250 | 488.270 |
| 1/4 | 0.062417 | 39.0105 |
| 3/8 | 0.225690 | 16.4981 |
| 1/2 | 0.422998 | 10.5750 |
| 5/8 | 0.609126 | 7.99943 |
| 3/4 | 0.768356 | 6.56935 |
| 7/8 | 0.897999 | 5.65066 |
| 9/10 | 0.920515 | 5.04528 |
| 99/100 | 0.992784 | 5.03833 |
| Values of t at [s] | Values of t at [s] | |
|---|---|---|
| 1/8 | 0.159996 | 1049.74 |
| 1/4 | 0.499334 | 40.4461 |
| 3/8 | 0.716522 | 13.4138 |
| 1/2 | 0.845997 | 7.61397 |
| 5/8 | 0.923262 | 5.35450 |
| 3/4 | 0.968067 | 4.18858 |
| 7/8 | 0.991472 | 3.47986 |
| 9/10 | 0.994211 | 3.36987 |
| 99/100 | 0.999759 | 3.03275 |
| Present Values of t [s] | The Experimental Value of t [s] | |
|---|---|---|
| 1/8 | 11.1279 | |
| 1/4 | ||
| 3/8 | ||
| 1/2 | ||
| 5/8 | ||
| 3/4 | ||
| 7/8 | ||
| 9/10 | ||
| 99/100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algehyne, E.A.; Aldhabani, M.S.; Areshi, M.; El-Zahar, E.R.; Ebaid, A.; Al-Jeaid, H.K. A Proposed Application of Fractional Calculus on Time Dilation in Special Theory of Relativity. Mathematics 2023, 11, 3343. https://doi.org/10.3390/math11153343
Algehyne EA, Aldhabani MS, Areshi M, El-Zahar ER, Ebaid A, Al-Jeaid HK. A Proposed Application of Fractional Calculus on Time Dilation in Special Theory of Relativity. Mathematics. 2023; 11(15):3343. https://doi.org/10.3390/math11153343
Chicago/Turabian StyleAlgehyne, Ebrahem A., Musaad S. Aldhabani, Mounirah Areshi, Essam R. El-Zahar, Abdelhalim Ebaid, and Hind K. Al-Jeaid. 2023. "A Proposed Application of Fractional Calculus on Time Dilation in Special Theory of Relativity" Mathematics 11, no. 15: 3343. https://doi.org/10.3390/math11153343
APA StyleAlgehyne, E. A., Aldhabani, M. S., Areshi, M., El-Zahar, E. R., Ebaid, A., & Al-Jeaid, H. K. (2023). A Proposed Application of Fractional Calculus on Time Dilation in Special Theory of Relativity. Mathematics, 11(15), 3343. https://doi.org/10.3390/math11153343









