Simultaneous Exact Controllability of Mean and Variance of an Insurance Policy

Abstract

We explore the simultaneous exact controllability of mean and variance of an insurance policy by utilizing the benefit $S_t$ and premium $P_t$ as control inputs to manage the policy value ${}_{t}V$ and the variance ${}^2{\sigma }_t$ of future losses. The goal is to determine whether there exist control inputs that can steer the mean and variance from a prescribed initial state at $t=0$ to a prescribed final state at $t=T$, where the initial–terminal pair of states $({}_{0}V,{}_{T}V)$ and $({}^2{\sigma }_0,{}^2{\sigma }_T)$ represent the mean and variance of future losses at times $t=0$ and $t=T$, respectively. The mean ${}_{t}V$ and variance ${}^2{\sigma }_t$ are governed by Thiele’s and Hattendorff’s differential equations in continuous time and recursive equations in discrete time. Our study focuses on solving the problem of exact controllability in both continuous and discrete time. We show that our result can be used to devise control inputs $S_t,P_t$ in the interval $[0,T]$ so that the mean and variance partially track a specified curve ${}_{t}V=a\left(t\right)$ and ${}^2{\sigma }_t=b\left(t\right)$, respectively, i.e., at a fine sampling of points in the time interval $[0,T]$.

1. Introduction

The expected present value denoted by ${}_{t}V$, of future losses of an insurance policy at time t, in continuous time, is well known to follow Thiele’s differential equation. In discrete time, a corresponding recursion is also well known [1]. Similarly, the variance ${}^2{\sigma }_t$ of future losses of an insurance policy in continuous time is governed by the Hattendorff differential equation [2,3] and in discrete time there exists a similar recursive equation that is well known [1].

Stochastic processes play a crucial role in modeling various aspects of insurance policies. Several types of stochastic processes are commonly used in insurance modeling, including the following:

• Poisson Processes: Poisson processes are widely employed to model the occurrence of rare events, such as insurance claims or policyholder arrivals. They are characterized by independent and stationary increments, making them suitable for modeling the arrival rate of events over time.
• Markov Processes: Markov processes, specifically Markov chains and Markov jump processes, are utilized to model insurance policies with discrete states or transitions between different states. Markov processes assume that the future state depends only on the current state, making them valuable for modeling policy durations, policyholder behavior, or other discrete phenomena.
• Brownian Motion: Brownian motion, also known as a continuous-time random walk, is a fundamental process used in finance and insurance. It is employed to model continuous and random fluctuations, such as stock prices or interest rates. Brownian motion exhibits continuous paths and has independent and normally distributed increments, making it suitable for modeling continuous-time phenomena.
• Levy Processes: Levy processes are generalizations of Brownian motion that include both continuous and discontinuous components. They are employed to model complex phenomena in insurance, such as extreme events or jumps in asset prices. Levy processes offer flexibility in capturing various types of stochastic behavior.
• Geometric Brownian Motion (GBM): Geometric Brownian motion is a specific type of stochastic process commonly used to model the dynamics of financial variables like asset prices. It incorporates constant drift and volatility, making it suitable for modeling investment returns or the growth of policy values over time.

We refer the reader to [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] for a detailed overview of the processes mentioned above. These are just a few examples of the stochastic processes commonly employed in insurance modeling. The choice of the appropriate process depends on the specific characteristics of the insurance policy and the phenomena being modeled. In this paper, however, the differential and difference equations (Thiele and Hattendorff) that we consider are born out of the Markovian assumption for policy values from one state to the other. This framework is widely used in the literature as seen in [1]. We note that the notation used in this paper is the standard actuarial notation employed by actuarial societies and bears a lot of similarity to the notation used in some of the stochastic processes such as Geometric Brownian Motion [19] mentioned above.

In this paper, we are interested in analyzing a simultaneous exact controllability problem for the mean ${}_{t}V$ and variance ${}^2{\sigma }_t$ of future losses of an insurance policy. More specifically, we are interested in the following question: Do there exist control inputs in the form of premiums $P_t$ and benefits $S_t$, that can steer the mean and variance from a prescribed initial state $({}_{0}V,{}^2{\sigma }_0)$ at $t=0$ to a prescribed final state $({}_{T}V,{}^2{\sigma }_T)$ at $t=T$, where the mean ${}_{t}V$ and variance ${}^2{\sigma }_t$ evolve according to Thiele’s and Hattendorff’s differential equations (or recursions), respectively. We refer the reader to Appendix C for a list of symbols from actuarial mathematics that we have used in this paper. We consider both discrete and continuous cases with variable interest rate $i_t$ as a function of time. At the outset, we note that while a typical actuarial setting involves specifying the benefits, computing premiums using a given principle (such as the equivalence premium principle), and computing the policy value and variance, in the exact controllability setting it is the opposite. In other words, we are specifying the mean and the variance of the policy at the initial and final time instants, and we are interested in computing premiums and benefits (the structure of the policy) so that the specified mean and variance are achieved at the given time instants.

The main reasons to study the simultaneus exact controllability problem for the mean and variance of an insurance policy is as follows:

• Most insurance problems, in general, involve the computation of the mean and variance given an insurance structure. However, the formulation of the simultaneous exact controllability problem allows us to design the structure of the insurance policy by choosing premiums and benefits so that the mean and variance of the present value of the policy at time $t=0$ satisfies prescribed values. For example, an insurance company might be interested in exactly controlling the mean and variance of the present value of future losses in order to maintain the said mean and variance within prescribed bounds to reduce losses in the long run.
• The formulation also allows the insurance company to partially track the mean and variance of present value of future losses to follow prescribed curves. We call this problem the patchwork problem and solve this completely later on in this paper.
• Lastly, the Thiele and Hattendorff equations that govern the mean and the variance of present values of future losses are legitimate differential/difference equations that have been studied by the actuarial mathematics community for decades. In general, given that differential equations govern the evolution of the state of a variety of real life problems, the question of exact controllability is a very important one, as it allows the state of the differential equation to be controlled to achieve a variety of objectives such as disturbance rejection and tracking. Given that the simultaneous exact controllability problem stated in this paper has not been studied before, the solution of said problem is an important result that adds to the literature of both differential equations and actuarial mathematics.

This paper solves the simultaneous exact controllability problem stated above by explicitly computing control inputs in the form of premium $P_t$ and benefit $S_t$ for both the continuous and discrete time cases. In other words, we show explicit formulae for the said control input that satisfies the control objective of starting from the prescribed initial state at $t=0$ and ending at the prescribed terminal state at $t=T$ for both mean and variance.

There have been several papers on the topic of optimal control of insurance policy such as [20,21,22]. The idea in [23] comes close to our work, where the authors use the interest rate as the control input to solve an optimal control problem. However, to our knowledge the problem of exact controllability of the mean and variance has not been considered. Our result can be used to solve a partial tracking problem (which we call the patchwork problem later on in the paper) for ${}_{t}V$ and ${}^2{\sigma }_t$, where curves of evolution $a\left(t\right)$ and $b\left(t\right)$ for the mean and variance are given, and the problem is to design control inputs $(S_t,P_t)$ so that the solution of Thiele’s and Hattendorff’s equations in given by ${}_{t}V$ and ${}^2{\sigma }_t$ satisfy ${}_{t}V=a\left(t\right)$ and ${}^2{\sigma }_t=b\left(t\right)$, respectively, in the time interval $[0,T]$. The tracking is partial in the sense that the values match at a fine sampling of time instants in the interval $[0,T]$ i.e., the policy value and standard deviation on the specified curves $a\left(t\right)$ and $b\left(t\right)$ will both be achieved for a given sampling of points ${\left\{lh\right\}}_{l=0}^N$ of the interval $[0,T]$. The study of controllability of the evolution of ${}_{t}V$ and ${}^2{\sigma }_t$ in the time interval $[0,T]$ is reminiscent of the time-averaged displacements of GBM and generalized GBM that were studied in [24].

The main goals of this paper are as follows:

• In Section 2, we tackle the problem of exact controllability of Thiele’s equation governing the policy value ${}_{t}V$ in the continuous case. As we will see, the solution is not unique as the control input is a linear combination of the premium $P_t$ and the benefit $S_t$.
• In Section 3, we state and solve the exact controllability of the policy value ${}_{t}V$ in the discrete case, where the ${}_{t}V$ evolves according to a discrete recursion equation. We assume a time step of h. In both the continuous and discrete case problems of exact controllability of the policy value ${}_{t}V$, we assume a variable interest rate $i_t$.
• In Section 4 we state and solve the simultaneous exact controllability problem for the coupled Thiele–Hattendorff system of differential equations.
• In Section 5, we tackle the problem of simultaneous exact controllabilty of the coupled system of the recursion equation for the mean ${}_{t}V$ and variance ${}^2{\sigma }_t$.
• In Section 6, we show some examples where the exact controllability is achieved.
• In Section 7, we end the paper with our conclusions.

2. Exact Controllability of Thiele’s Equation in Continuous Time

In this section, we consider the problem of exactly controlling the mean ${}_{t}V$ in time T. We start by stating and proving an exact controllability result for Thiele’s equation.

Theorem 1.

The following Thiele’s differential equation governing the evolution of the policy value ${}_{t}V$ in continuous time is exactly controllable in a time interval $[0,T]$ i.e., given an initial–terminal state pair $({}_{0}V,{}_{T}V)$, there exist functions $P_t,S_t$ denoting premiums and benefits at time t such that the solution of the differential Equation (1) below will evolve from ${}_t{V|}_{t=0}={}_{0}V$ to ${}_t{V|}_{t=T}={}_{T}V$.

$$\begin{array}{ccc}\hfill {}_t{V}^{\prime }& =& {\delta }_t·{}_{t}V+P_t-{\mu }_{\left[x\right]+t}(S_t-{}_{t}V),\hfill \\ \hfill & =& ({\delta }_t+{\mu }_{\left[x\right]+t})·{}_{t}V+\underset{u\left(t\right)}{\underbrace{(P_t-{\mu }_{\left[x\right]+t}{S}_t)}}\hfill \end{array}$$

(1)

Proof. 

In Equation (1), we will first solve for $u\left(t\right)$ so that the mean ${}_{t}V$ evolves from the initial value ${}_t{V|}_{t=0}=V_0$ to the final value ${}_t{V|}_{t=T}=V_T$ in time T. Here the pair ${(}_{0}V{,}_{T}V)$ is known apriori, and the goal is to devise a control input $u\left(t\right)$. Once we solve for $u\left(t\right)$ explicitly, then there are multiple possibilities for $P_t$ and $S_t$ that might work to exactly control ${}_{t}V$. However, as we will see later, simultaneously controlling the variance ${}^2{\sigma }_t$ as well, will fix $P_t$ and $S_t$ to an extent. We first write the variation of constants formula for Equation (1) as follows:

$${}_{t}V=e^{{\int }_0^t({\mu }_{\left[x\right]+s}+{\delta }_s)ds}{}_{0}V+{\int }_0^t{e}^{{\int }_s^t({\mu }_{\left[x\right]+s}+{\delta }_s)ds)}u\left(s\right)ds$$

We define the control input as

$$\begin{array}{cc}\hfill u\left(t\right)& =\frac{e^{-{\int }_t^T({\mu }_{\left[x\right]+t}+{\delta }_t)dt}}{T}\left({}_{T}V-e^{{\int }_0^T({\mu }_{\left[x\right]+t}+{\delta }_t)dt}·{}_{0}V\right)\hfill \\ \hfill & =\frac{{}_{(T-t)}{E}_{\left[x\right]+t}}{T}\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right).\hfill \end{array}$$

(2)

We note that once $u\left(t\right)$ is known from Equation (2), ${}_{t}V$ is also completely known for all $t\in [0,T]$.

Then,

$$\begin{array}{cc}\hfill {\left.{}_{t}V\right|}_{t=T}& =e^{{\int }_0^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}{}_{0}V\hfill \\ & +\frac{1}{T}{\int }_0^T{e}^{{\int }_s^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}·e^{-{\int }_s^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds)}·\underset{\mathrm{constant}}{\underbrace{\left\{{}_{T}V-e^{{\int }_0^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}·{}_{0}V\right\}}}\hfill \\ \hfill & =e^{{\int }_0^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}{}_{0}V+\frac{1}{T}\left({}_{T}V-e^{{\int }_0^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}·{}_{0}V\right)·{\int }_0^{T}1ds\hfill \\ \hfill & =e^{{\int }_0^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}{}_{0}V+\frac{1}{T}\left({}_{T}V-e^{{\int }_0^T({\mu }_{\left[x\right]+s}+{\delta }_s)ds}·{}_{0}V\right)·T\hfill \\ \hfill & ={}_{T}V.\hfill \end{array}$$

We also have the following:

$$u\left(t\right)=P_t-{\mu }_{\left[x\right]+t}·S_t,$$

where we emphasize that $u\left(t\right)$ is completely known. We could fix the premium $P_t$ and solve for $S_t$ or vice versa. Note that there are two degrees of freedom in this case. Thus, $P_t$ and $S_t$ could be used to our advantage in controlling ${}_{t}V$ and ${\sigma }_t$ (or Var($L_T$)), as we shall see later. However, this proves the theorem. □

Remark 1.

The form of $u\left(t\right)$ in the proof of this theorem is obtained from the controllability Grammian, which is used to solve the general exact controllability problem for linear differential equations.

Remark 2.

We note that the expression $V_{av}=\frac{1}{T}\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right)$ is an average rate of change between the initial and final values ${}_{0}V$ and ${}_{T}V$, respectively, (with the initial value ${}_{0}V$ adjusted with the actuarial discount factor). Hence, $u\left(t\right)$ is the actuarial present value of $V_{av}$ at the time instant $(T-t)$.

3. Discrete Case

In this section, we solve the problem of exactly controlling ${}_{t}V$ in the discrete case described by the following recursion.

$${(}_{t}V+P_t){(1+i_t)}^{1/m}{=}_{t+1/m}V{+}_{1/m}{q}_{\left[x\right]+t}\left(S_{t+1/m}{-}_{t+1/m}V\right)$$

Let $h=1/m$. Then, we can rewrite the above (see Appendix A) as follows:

$$\begin{array}{cc}\hfill {}_{t+h}V& =\frac{{}_{t}V}{{}_t{E}_{\left[x\right]+t}}+u(t+h),\hfill \end{array}$$

(3)

where

$${}_t{E}_{\left[x\right]+t}=\frac{{(1+i_t)}^h}{{}_h{p}_{[x+t]}}, \mathrm{and} u(t+h)=P_t\frac{{(1+i_t)}^h}{{}_h{p}_{[x+t]}}-\frac{{}_h{q}_{\left[x\right]+t}·S_{t+h}}{{}_h{p}_{[x+t]}}.$$

Theorem 2.

The discrete recursion (A1) and (3) given above is exactly controllable on the time interval $[0,T]$, i.e., given an initial–terminal state pair $({}_{0}V,{}_{T}V)$, there exist functions $P_t,S_t$ denoting premiums and benefits at time t such that the solution of the differential Equation (1) below will evolve from ${}_t{V|}_{t=0}={}_{0}V$ to ${}_t{V|}_{t=T}={}_{T}V$.

Proof. 

Proceeding as we did before,

$$\begin{array}{cc}\hfill {}_{t+h}V& {=}_{t}V\frac{{(1+i_t)}^h}{{}_h{p}_{[x+t]}}+u(t+h),\mathrm{where}a\left(kh\right)={\Pi }_{l=0}^{(k-1)}{(1+i_l)}^h\hfill \\ \hfill {}_{h}V& {=}_{0}V\frac{{(1+i_0)}^h}{{}_h{p}_{\left[x\right]}}+u\left(h\right)\hfill \\ \hfill {}_{2h}V& {=}_{h}V\frac{{(1+i_1)}^h}{{}_h{p}_{[x+h]}}+u\left(2h\right)=\frac{\stackrel{a\left(2h\right)}{\overbrace{{(1+i_1)}^h{(1+i_0)}^h}}}{{}_{2h}{p}_{\left[x\right]}}{}_{0}V+\frac{\stackrel{\frac{a\left(2h\right)}{a\left(h\right)}}{\overbrace{{(1+i_1)}^h}}}{{}_h{p}_{\left[x\right]+h}}u\left(h\right)+u\left(2h\right)\hfill \\ \hfill {}_{3h}V& {=}_{2h}V\frac{{(1+i_2)}^h}{{}_h{p}_{[x+2h]}}+u\left(3h\right)=\frac{\stackrel{a\left(3h\right)}{\overbrace{{(1+i_2)}^h{(1+i_1)}^h{(1+i_0)}^h}}}{{}_{3h}{p}_{\left[x\right]}}{}_{0}V+\frac{\stackrel{\frac{a\left(3h\right)}{a\left(h\right)}}{\overbrace{{(1+i_1)}^h{(1+i_0)}^h}}}{{}_{2h}{p}_{[x+h]}}u\left(h\right)\hfill \\ \hfill & +\frac{\stackrel{\frac{a\left(3h\right)}{a\left(2h\right)}}{\overbrace{{(1+i_2)}^h}}}{{}_h{p}_{\left[x\right]+2h}}u\left(2h\right)+u\left(3h\right)\hfill \\ \hfill & ⋮\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill {}_{kh}V& =\underset{{}_{kh}{E}_{\left[x\right]}}{\underbrace{\frac{a\left(kh\right)}{{}_{kh}{p}_{\left[x\right]}}}}{}_{0}V+\sum _{l=1}^{\left(k\right)}\frac{a\left(kh\right)}{a\left(lh\right)}·\frac{u\left(lh\right)}{{}_{(k-l)h}{p}_{\left[x\right]+lh}}\hfill \\ \hfill & =\frac{{}_{0}V}{{}_{kh}{E}_{\left[x\right]}}+\sum _{l=1}^k\frac{u\left(lh\right)}{{}_{(k-l)h}{E}_{\left[x\right]+lh}}.\hfill \end{array}$$

Now, for a particular function $u\left(t\right)$, which solves

$${}_{t+h}V{=}_{t}V\frac{{(1+i_t)}^h}{{}_h{p}_{\left[x\right]+t}}+u\left(t\right);\mathrm{when}{}_{0}V\mathrm{and}{}_{T}V\mathrm{are}\mathrm{given}$$

Let $T=Nh$. Choosing

$$u\left(lh\right)=\frac{1}{N}{·}_{(N-l)h}{E}_{\left[x\right]+lh}·\left\{{}_{Nh}V-\frac{1}{{}_{Nh}{E}_{\left[x\right]}}{}_{0}V\right\},\mathrm{for}l=0,1,2,\dots ,(N-1),$$

(4)

then, by a similar calculation as in the continuous case, we have:

$${\left.{}_{t}V\right|}_{t=T=Nh}{=}_{Nh}V,$$

as prescribed. We recall that

$$u\left(lh\right)=P_{(l-1)h}\frac{{(1+i_{(l-1)h})}^h}{{}_h{p}_{[x+(l-1\left)h\right]}}-\frac{{}_h{q}_{\left[x\right]+(l-1)h}·S_{lh}}{{}_h{p}_{[x+(l-1\left)h\right]}}.$$

Hence, given $S_{lh}$, we can solve for $P_{lh}$ or vice versa since $u\left(lh\right)$ is completely known from Equation (4). This proves the theorem. □

Remark 3.

We note that the units for $u\left(lh\right)$ in the discrete case is in dollars, whereas the units for $u\left(t\right)$ in the continuous case is in dollars per unit time.

Remark 4.

In the discrete case, the control action happens at the right end point of each sub-interval $\left(\right(l-1)h,lh)$ where $l=1,2,3,\dots ,N$. We also note that the control input $u\left(lh\right)$ is uniquely determined but there might be various choices of $P_{lh}$ and $S_{(l+1)h}$ that might lead to the same $u\left(lh\right)$. We will see in later sections that this non-uniqueness can somewhat be alleviated by requiring that the variance ${}^2{\sigma }_t$ also be exactly controlled.

We next consider the problem of simultaneously controlling the mean and variance of an insurance policy.

4. Hattendorff(scalar): Controlling ${}_{\mathit{t}}\mathit{V}$ and ${}^{\mathbf{2}}{\mathit{\sigma }}_{\mathit{t}}$ for the Continuous Case

In this section, we will prove a simultaneous exact controllability result for the mean and variance of an insurance policy in continuous time. We know that

$$\begin{array}{cc}\hfill {}_t{V}^{\prime }& ={({\delta }_t+{\mu }_{\left[x\right]+t})}_{t}V+\stackrel{u\left(t\right)}{\overbrace{(P_t-{\mu }_{\left[x\right]+t}{S}_t)}}\hfill \\ \hfill {}^2{\sigma }_t^{\prime }& =(2{\delta }_t+{\mu }_{\left[x\right]+t})·{}^2{\sigma }_t\underset{v\left(t\right)}{\underbrace{-{\mu }_{\left[x\right]+t}{\left(S_t{-}_{t}V\right)}^2}}.\hfill \end{array}$$

(5)

So, we have

$$\begin{array}{cc}\hfill {}_t{V}^{\prime }=& {({\delta }_t+{\mu }_{\left[x\right]+t})}_{t}V+u\left(t\right)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {}^2{\sigma }_t^{\prime }=& (2{\delta }_t+{\mu }_{\left[x\right]+t})·{}^2{\sigma }_t+v\left(t\right).\hfill \end{array}$$

(7)

Remark 5.

The function $v\left(t\right)$ has ${}_{t}V$ hidden in it. However, (6) is decoupled from (7) and devoid of any ${}^2{\sigma }_t$ terms.

We state the two main problems inthis section here:

• Problem 1: Given ${\left.{}_{t}V\right|}_{t=T}{=}_{T}V$, ${\left.{}_{t}V\right|}_{t=0}{=}_{0}V$, ${\left.{}^2{\sigma }_t\right|}_{t=T}{=}^2{\sigma }_T$ and ${\left.{}^2{\sigma }_t\right|}_{t=0}{=}^2{\sigma }_0$, design $u\left(t\right)$ and $v\left(t\right)$ so that a solution of (6) and (7) above, goes from the corresponding prescribed initial states to prescribed final states.
• Problem 2: Once $u\left(t\right)$ and $v\left(t\right)$ have been identified, then use these functions to determine $P_t$ and $S_t$ to achieve the same objective of exact controllability as in Problem 1.

We state and prove a theorem that answers both problems above in the affirmative.

Theorem 3.

The coupled set of differential equations given by Equation (5) above is exactly controllable on the time interval $[0,T]$, i.e., given an initial–terminal state pair $({}_{0}V,{}_{T}V)$ and $({}^2{\sigma }_0,{}^2{\sigma }_T)$, respectively, for the mean and variance, there exist functions $P_t,S_t$ denoting premiums and benefits at time t such that the solution of the differential Equation (5) above will evolve from the initial states ${}_{t}V{{|}_{t=0}={}_{0}V,{}_t{}^2\sigma |}_{t=0}={}^2{\sigma }_0$ at time $t=0$ to the final states ${}_{t}V{{|}_{t=T}={}_{T}V,{}^2\sigma |}_{t=T}={}^2{\sigma }_T$ at time $t=T$.

Proof. 

We have already solved explicitly for $u\left(t\right)$ so that the following is true:

$${}_{t}V{{|}_{t=T}{=}_{T}V{,}_{t}V|}_{t=0}{=}_{0}V \mathrm{in} \mathrm{time} T.$$

That is, if we choose

$$u\left(t\right)=\underset{\mathrm{We}\mathrm{completely}\mathrm{know}.}{\underbrace{\frac{{}_{T-t}{E}_{\left[x\right]+t}}{T}\left[{}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right]}}=\underset{P_t\mathrm{and}{S}_t\mathrm{unknown}\mathrm{at}\mathrm{this}\mathrm{point}.}{\underbrace{P_t-{\mu }_{\left[x\right]+t}{S}_t.}}$$

With the function $u\left(t\right)$ defined as above, we can completely solve for ${}_{t}V$ in (6). Hence, the ${}_{t}V$ inside $v\left(t\right)=-{\mu }_{\left[x\right]+t}{\left(S_t{-}_{t}V\right)}^2$ is known completely. Now, we look at (7). We have the following variation of constants solution formula:

$$\begin{array}{cc}\hfill {}^2{\sigma }_t^{\prime }=& (2{\delta }_t+{\mu }_{\left[x\right]+t})·{}^2{\sigma }_t+v\left(t\right)\hfill \\ \hfill {\left.{}^2{\sigma }_t\right|}_{t=T}=& e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}·{}^2{\sigma }_0+{\int }_0^T{e}^{{\int }_s^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}v\left(s\right)ds.\hfill \end{array}$$

Now, choose

$$\begin{array}{cc}\hfill v\left(s\right)& =\frac{e^{-{\int }_s^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}}{T}·\left\{{}^2{\sigma }_T-e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}v\left(s\right)ds{·}^2{\sigma }_0\right\}\hfill \\ \hfill & =\frac{{}_{T-s}{}^2{E}_{\left[x\right]+s}}{T}\left\{{}^2{\sigma }_T-\frac{{}^2{\sigma }_0}{{}_T^{2}E\left[x\right]}\right\}.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill & {\left.{}^2{\sigma }_t\right|}_{t=T}\hfill \\ & =e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}·{}^2{\sigma }_0\hfill \\ \hfill & +{\int }_0^T{e}^{{\int }_s^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}\frac{e^{-{\int }_s^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}}{T}ds\left\{{}^2{\sigma }_T-e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}·{}^2{\sigma }_0\right\}ds\hfill \\ \hfill & =e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}·{\sigma }_0+\frac{1}{T}{\int }_0^T{(}^2{\sigma }_T-e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}{}^2{\sigma }_0)ds\hfill \\ \hfill & =e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}·{}^2{\sigma }_0+\frac{1}{T}T{(}^2{\sigma }_T-e^{{\int }_0^T(2{\delta }_s+{\mu }_{\left[x\right]+s})ds}{}^2{\sigma }_0)\hfill \\ \hfill & ={}^2{\sigma }_T.\hfill \end{array}$$

Putting this all together, we have functions $u\left(t\right)$ and $v\left(t\right)$ that are completely known. That is,

$$\begin{array}{cc}\hfill u\left(t\right)& =\frac{{}_{(T-t)}{E}_{\left[x\right]+t}}{T}·\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right)\hfill \\ \hfill v\left(t\right)& =\frac{{}_{(T-t)}^2{E}_{\left[x\right]+t}}{T}\left({}^2{\sigma }_T-\frac{{}^2{\sigma }_0}{{}_T^{2}E\left[x\right]}\right),\hfill \end{array}$$

where ${}_{(T-t)}^2{E}_{\left[x\right]+t}$ is the actuarial discount factor for second moments. Next, we try to solve for $P_t$ and $S_t$ from $u\left(t\right)$ and $v\left(t\right)$ as follows:

$$P_t-{\mu }_{\left[x\right]+t}{S}_t=u\left(t\right)$$

(8)

and

$$-{\mu }_{\left[x\right]+t}{\left(S_t{-}_{t}V\right)}^2=v\left(t\right).$$

(9)

We note that $u\left(t\right)$ and $v\left(t\right)$ in Equations (8) and (9) are completely known. We solve for $S_t$ in Equation (9) first and then solve for $P_t$. In other words we first can find,

$$S_t{=}_{t}V\pm \sqrt{\frac{-v\left(t\right)}{{\mu }_{\left[x\right]+t}}}.$$

Assuming that the death strain at risk (DSAR) is always positive, we can ignore the negative sign in the above equation, so we have:

$$S_t{=}_{t}V+\sqrt{\frac{-v\left(t\right)}{{\mu }_{\left[x\right]+t}}}.$$

Then, we use $S_t$ in Equation (8) to determine $P_t$. That is,

$$\begin{array}{cc}\hfill P_t-{\mu }_{\left[x\right]+t}{S}_t=& u\left(t\right)\hfill \\ \hfill P_t=& u\left(t\right)+{\mu }_{\left[x\right]+t}·S_t\hfill \\ \hfill =& u\left(t\right)+{\mu }_{\left[x\right]+t}\left({}_{t}V+\sqrt{\frac{-v\left(t\right)}{{\mu }_{\left[x\right]+t}}}\right).\hfill \end{array}$$

To make sure that the term inside the square root is positive, we note the following:

$${}^2{\sigma }_t=\frac{{}^2{\sigma }_0}{{}_t^2{E}_{\left[x\right]}}-\int \frac{\stackrel{>0}{\overbrace{{\mu }_{\left[x\right]+s}}}\stackrel{>0}{\overbrace{{\left(S_s{-}_{s}V\right)}^2}}}{\underset{>0}{\underbrace{{}_{(t-s)}{E}_{\left[x\right]+s}}}}ds.$$

Hence,

$${}^2{\sigma }_t-\frac{{}^2{\sigma }_0}{{}_t^2{E}_{\left[x\right]}}<0\mathrm{for} \mathrm{all} t,$$

and hence $v\left(t\right)<0\mathrm{for} \mathrm{all} t>0$. Thus, there are no issues mathematically to compute both $S_t$ and $P_t$ explicitly. If we choose ${}_{T}V$ and ${}_{0}V$ so that $\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right)>0$, then we have that $u\left(t\right)>0$ and hence $P_t$ is also guaranteed to be positive. This proves the theorem. □

Remark 6.

In the proof of this theorem, we can satisfy $\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right)>0$ by choosing ${}_{0}V=0$ (Equivalence Premium Principle condition at $t=0$) always. Alternatively for cases of endowment insurance, we can choose a large endowment value ${}_{T}V$ to meet this condition. When the initial state ${}_{0}V$ is chosen to be zero, such a controllability problem is called a reachability problem. Exact controllability (which is the result that we have proved in this paper) is a much more general result for arbitrary prescribed initial and terminal states, and hence implies reachability. In general, as we will see later in the patchwork example, this condition means that the time value of the initial policy value ${}_{0}V$ at the final time instant $t=T$ (obtained by dividing by the discount factor ${}_T{E}_{\left[x\right]}$, which is equivalent to multiplying by the accumulation factor) is less than the terminal policy value ${}_{T}V$. This means that the terminal policy value ${}_{T}V$ at $t=T$ exceeds the growth of the initial policy value ${}_{0}V$ at $t=0$ over the time period $[0,T]$.

5. Hattendorff(scalar): Controlling ${}_{\mathit{t}}\mathit{V}$ and ${}^{\mathbf{2}}{\mathit{\sigma }}_{\mathit{t}}$ for the Discrete Case

In this section, we tackle the discrete control problem of the variance ${}^2{\sigma }_t$. From the Hattendorff theorem we know that

$$\begin{array}{cc}\hfill {}^2{\sigma }_t& =v_h^{2h}{·}_h{p}_{\left[x\right]+t}{}^2{\sigma }_{t+h}+v_h^{2h}{p}_{\left[x\right]+t}{·}_h{q}_{\left[x\right]+t}{\left(S_{t+h}{-}_{t+h}V\right)}^2,\hfill \\ \hfill \mathrm{where} v_h^{2h}{}_h{p}_{\left[x\right]+t}& {=}_h^2{E}_{\left[x\right]+t}.\hfill \end{array}$$

Now,

$${}^2{\sigma }_{t+h}=\frac{{}^2{\sigma }_t}{{}_h^2{E}_{\left[x\right]+t}}+v(t+h) \mathrm{where} v(t+h)={-}_h{q}_{\left[x\right]+t}{\left(S_{t+h}{-}_{t+h}V\right)}^2.$$

We can use recursion to show the following (see Appendix B):

$${}^2{\sigma }_{kh}=\frac{{}^2{\sigma }_0}{{}_{kh}^2{E}_{\left[x\right]}}+\sum _{l=1}^k\frac{v\left(lh\right)}{{}_{(k-l)h}^2{E}_{\left[x\right]+lh}}.$$

Now, we attack the combined problem.

$$\begin{array}{cc}\hfill {}_{t+h}V=& \frac{{}_{t}V}{{}_h{E}_{\left[x\right]+t}}+u(t+h);u(t+h)=\frac{P_t}{{}_h{E}_{\left[x\right]+t}}-\frac{{}_h{q}_{\left[x\right]+t}}{{}_h{p}_{\left[x\right]+t}}·S_{t+h}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {}^2{\sigma }_{t+h}=& \frac{{}^2{\sigma }_t}{{}_h^2{E}_{\left[x\right]+t}}+v(t+h);v(t+h)={-}_h{q}_{\left[x\right]+t}{\left(S_{t+h}{-}_{t+h}V\right)}^2\hfill \end{array}$$

(11)

The same questions arise in this case.

• Problem 3: Given ${\left.{}_{t}V\right|}_{t=T}{=}_{T}V$, ${\left.{}_{t}V\right|}_{t=0}{=}_{0}V$, ${\left.{}^2{\sigma }_t\right|}_{t=T}{=}^2{\sigma }_T$ and ${\left.{}^2{\sigma }_t\right|}_{t=0}{=}^2{\sigma }_0$, design $u\left(t\right)$ and $v\left(t\right)$ so that the corresponding initial states for ${(}_{t}V{,}^2{\sigma }_t)$ are driven to the corresponding prescribed final states in time T.
• Problem 4: Once $u\left(t\right)$ and $v\left(t\right)$ have been identified, then use these functions to determine $P_t$ and $S_t$ to achieve the same objective of exact controllability as in Problem 3.

We state and prove a theorem that answers both questions above in the affirmative.

Theorem 4.

The coupled set of differential equations given by (10) and (11) is exactly controllable on the time interval $[0,T]$, i.e., given an initial–terminal state pair $({}_{0}V,{}_{T}V)$ and $({}^2{\sigma }_0,{}^2{\sigma }_T)$, respectively, for the mean and variance, there exist functions $P_t,S_t$ denoting premiums and benefits at time t such that the solution of the differential Equations (10) and (11) above will evolve from the initial states ${}_{t}V{{|}_{t=0}={}_{0}V,{}_t{}^2\sigma |}_{t=0}={}^2{\sigma }_0$ at time $t=0$ to the final states ${}_{t}V{{|}_{t=T}={}_{T}V,{}^2\sigma |}_{t=T}={}^2{\sigma }_T$ at time $t=T$.

Proof. 

We already know that in the discrete case,

$$u\left(lh\right)=\frac{1}{N}{·}_{(N-l)h}{E}_{\left[x\right]+lh}·\left\{{}_{T}V-\frac{{}_{0}V}{{}_{Nh}{E}_{\left[x\right]}}\right\};l=1,2,\dots N,\mathrm{with}T=Nh,$$

(12)

which is completely known, will guarantee that ${}_{0}V$ goes to ${}_{T}V$ in time T. This also means that ${}_{t}V$ is known for $t=0$ to $t=T$. We can do this independently of the ${}^2{\sigma }_t$ equation since the ${}_{t}V$ equation does not have any ${}^2{\sigma }_t$ terms (uncoupled). Now,

$${}^2{\sigma }_{kh}=\frac{{}^2{\sigma }_0}{{}_{kh}^2{E}_{\left[x\right]}}+\sum _{l=1}^k\frac{v\left(lh\right)}{{}_{(k-l)h}^2{E}_{\left[x\right]+lh}}.$$

(13)

Choose,

$$v\left(lh\right)=\frac{1}{N}{·}_{(N-l)h}^2{E}_{\left[x\right]+lh}\left\{{}^2{\sigma }_{Nh}-\frac{{}^2{\sigma }_0}{{}_{Nh}^2{E}_{\left[x\right]}}\right\}l=1,2,\dots N,\mathrm{with}T=Nh.$$

(14)

Then, we are guaranteed that ${}^2{\sigma }_{Nh}$ in Equation (3) satisfies ${\left.{}^2{\sigma }_{kh}\right|}_{k=N}{=}^2{\sigma }_{Nh}$. That is,

$$\begin{array}{cc}\hfill {\left.{}^2{\sigma }_{kh}\right|}_{k=N}& =\frac{{}^2{\sigma }_0}{{}_{Nh}^2{E}_{\left[x\right]}}+\sum _{l=1}^N\frac{1}{N}\frac{{}_{(N-l)h}^2{E}_{\left[x\right]+lh}}{{}_{(N-l)h}^2{E}_{\left[x\right]+lh}}·\left\{{}^2{\sigma }_{Nh}-\frac{{}^2{\sigma }_0}{{}_{Nh}^2{E}_{\left[x\right]}}\right\}\hfill \\ \hfill & ={}^2{\sigma }_{Nh}\hfill \\ \hfill & ={}^2{\sigma }_T.\hfill \end{array}$$

Now we have

$$\begin{array}{cc}\hfill u\left(lh\right)& =\frac{P_{(l-1)h}}{{}_h{E}_{\left[x\right]+(l-1)h}}-\frac{{}_h{q}_{\left[x\right]+(l-1)h}}{{}_h{p}_{\left[x\right]+(l-1)h)}}·S_{lh}\hfill \\ \hfill v\left(lh\right)& ={-}_h{q}_{\left[x\right]+(l-1)h}{\left(S_{lh}{-}_{lh}V\right)}^2.\hfill \end{array}$$

Note:

$$\begin{array}{cc}\hfill {}^2{\sigma }_{kh}-\frac{{}^2{\sigma }_0}{{}_{kh}^2{E}_{\left[x\right]}}& =-\sum _{l=1}^k\frac{q_{\left[x\right]+(l-1)h}}{{}_{(k-l)h}^2{E}_{\left[x\right]+lh}}·\left\{S_{lh}{-}_{lh}{V)}^2\right\}\hfill \\ \hfill & <0\mathrm{for}\mathrm{all}k.\hfill \end{array}$$

This means that our solution

$$\begin{array}{cc}\hfill v\left(lh\right)& ={\frac{1}{N}}_{(k-l)h}^2{E}_{\left[x\right]+lh}\left\{{}^2{\sigma }_{Nh}-\frac{{}^2{\sigma }_0}{{}_{Nh}^2{E}_{\left[x\right]}}\right\}<0,\hfill \end{array}$$

as well. So, as in the continuous case, we first solve for $S_{lh}$ from

$$v\left(lh\right)={-}_h{q}_{\left[x\right]+(l-1)h}{\left(S_{lh}{-}_{lh}V\right)}^2.$$

That is,

$$S_{lh}{=}_{lh}V+\sqrt{\frac{-v\left(lh\right)}{{}_h{q}_{\left[x\right]+(l-1)h}}};l=1,2,\dots ,N,$$

(15)

which is completely known. We choose the plus sign for the second term above, assuming that the death strain at risk $\left(S_{lh}{-}_{lh}V\right)$ is positive. Next, we solve for $P_{lh}$ using $S_{lh}$ calculated previously and by recalling that

$$u\left(lh\right)=\frac{P_{(l-1)h}}{{}_h{E}_{\left(\right[x]+(l-1\left)h\right)}}-\frac{{}_h{q}_{\left[x\right]+(l-1)h}}{{}_h{p}_{\left[x\right]+(l-1)h}}·S_{lh},l=1,2,\dots ,N,$$

which implies that

$$P_{(l-1)h}{=}_h{E}_{\left[x\right]+(l-1)h}\left\{u\left(lh\right)+\frac{{}_h{q}_{\left[x\right]+(l-1)h}{S}_{lh}}{{}_h{p}_{\left[x\right]+(l-1)h}}\right\};l=1,2,\dots ,N.$$

(16)

Like in the continuous case, if we choose ${}_{T}V$ and ${}_{0}V$ so that $\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right)>0$, then we have that $u\left(lh\right)>0$ and hence $P_{(l-1)h}$ is also guaranteed to be positive. This proves the theorem. □

Remark 7.

We clarify here that $u\left(lh\right)$ and $v\left(lh\right)$ are completely known in terms of the prescribed initial and terminal states as shown in Equations (12) and (14). We also note that the premium $P_{lh}$ and the benefit $S_{lh}$ are explicitly related to the policy value $V_{lh}$ through Equations (15) and (16).

6. Examples

6.1. Constant Coefficients in Thiele’s Equation

Suppose that $\mu$ and $\delta$ are constants. Thus, Thiele’s Equation reduces to

$$\begin{array}{cc}\hfill {}_t{V}^{\prime }& =(\delta +\mu )·{}_{t}V+P_t-\mu S_t\hfill \\ \hfill & =(\delta +\mu )·{}_{t}V+u\left(t\right),\hfill \end{array}$$

where

$$u\left(t\right)=\underset{\mathrm{We}\mathrm{completely}\mathrm{know}.}{\underbrace{\frac{e^{-(\mu +\delta )\ast (T-t)}}{T}\left[{}_{T}V-{}_{0}V·e^{(\mu +\delta )\ast T}\right]}}=\underset{P_t\mathrm{and}{S}_t\mathrm{unknown}\mathrm{at}\mathrm{this}\mathrm{point}.}{\underbrace{P_t-{\mu }_{\left[x\right]+t}{S}_t.}}$$

This is a differential equation can be solved numerically, or in for some strategies solved analytically. Thus, we can use a preferred premium strategy, $P_t$, and benefit plan $S_t$ to develop a value stream for ${}_{t}V$. In fact, given that $u\left(t\right)$ is completely known, if we choose $P_t$, then we can calculate $S_t$ and vice versa.

6.2. Constant $\mu$ and $\delta$ When Controlling ${}_{t}V$ and ${}^2{\sigma }_t$ for the Continuous Case

Suppose that $\mu$ and $\delta$ are constants. Thus, we have

$$\begin{array}{cc}\hfill {}_t{V}^{\prime }=& {(\delta +\mu )}_{t}V+u\left(t\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {}^2{\sigma }_t^{\prime }=& (2\delta +\mu )·{}^2{\sigma }_t+v\left(t\right),\hfill \end{array}$$

(18)

where ${\left.{}_{t}V\right|}_{t=T}{=}_{T}V$, ${\left.{}_{t}V\right|}_{t=0}{=}_{0}V$, ${\left.{}^2{\sigma }_t\right|}_{t=T}{=}^2{\sigma }_T$ and ${\left.{}^2{\sigma }_t\right|}_{t=0}={}^2{\sigma }_0$, with

$$\begin{array}{cc}\hfill u\left(t\right)& =\frac{e^{-(\delta +\mu )\ast (T-t)}}{T}·\left({}_{T}V{-}_{0}V·e^{-(\delta +\mu )T}\right)\hfill \\ \hfill v\left(t\right)& =\frac{e^{-(2\ast \delta +\mu )\ast (T-t)}}{T}\left({}^2{\sigma }_T{-}^2{\sigma }_0·e^{-(2\ast \delta +\mu )\ast T}\right).\hfill \end{array}$$

Thus,

$$S_t{=}_{t}V+\sqrt{\frac{-v\left(t\right)}{\mu }}.$$

Then use $S_t$ in Equation (8) to determine $P_t$. That is,

$$\begin{array}{cc}\hfill P_t=& u\left(t\right)+\mu ·S_t\hfill \\ \hfill =& u\left(t\right)+\mu \left({}_{t}V+\sqrt{\frac{-v\left(t\right)}{\mu }}\right).\hfill \end{array}$$

We now substitute $u\left(t\right)$ and $v\left(t\right)$ into the equations and have

$$\begin{array}{cc}\hfill S_t& {=}_{t}V+\sqrt{-\frac{e^{-(2\delta +\mu )\ast (T-t)}·\left({}^2{\sigma }_T{-}^2{\sigma }_0·e^{-(2\delta +\mu )T}\right)}{\mu T}}\hfill \\ \hfill P_t& =\frac{e^{-(\delta +\mu )\ast (T-t)}}{T}·\left({}_{T}V{-}_{0}V·e^{-(\delta +\mu )T}\right)+\hfill \\ & \mu \left({}_{t}V+\sqrt{-\frac{e^{-(2\delta +\mu )\ast (T-t)}·\left({}^2{\sigma }_T{-}^2{\sigma }_0·e^{-(2\delta +\mu )T}\right)}{\mu T}}\right)\hfill \end{array}$$

Thus, we have readily available expressions for the premiums and the benefits that drive the solution from initial states through terminal states.

6.3. Constant $\mu$ and $\delta$ When Controlling ${}_{t}V$ and ${}^2{\sigma }_t$ for the Discrete Case

We can use constant $\mu$ and $\delta$ into our analysis for the discrete case:

$$\begin{array}{cc}\hfill {}_{kh}V& =\frac{{}_{0}V}{{}_{kh}{E}_{\left[x\right]}}+\sum _{l=1}^k\frac{u\left(lh\right)}{{}_{(k-l)h}{E}_{\left[x\right]+lh}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {}_{kh}V& =\frac{{}_{0}V}{e^{-(\delta +\mu )kh}}+\sum _{l=1}^k\frac{u\left(lh\right)}{e^{-(\delta +\mu )(k-l)h}},\hfill \end{array}$$

where $u\left(lh\right)$ is given by the following, respectively:

$$u\left(lh\right)=\frac{1}{N}{·}_{(N-l)h}{E}_{\left[x\right]+h}·\left\{{}_{T}V-\frac{{}_{0}V}{{}_{Nh}{E}_{\left[x\right]}}\right\};l=1,2,\dots N,\mathrm{with}T=Nh.$$

$$u\left(lh\right)=\frac{1}{N}·e^{-(\delta +\mu )(N-l)h}·\left\{{}_{T}V-\frac{{}_{0}V}{e^{-(\delta +\mu )Nh}}\right\};l=1,2,\dots N.$$

Again, this is completely known and will guarantee that ${}_{0}V$ goes to ${}_{T}V$ in time T. This also means that ${}_{t}V$ is known for $t=0$ to $t=T$. Now, we also know the ${}^2{\sigma }_t$ equation since the ${}_{t}V$ equation does not have any ${}^2{\sigma }_t$ terms (uncoupled). Thus,

$${}^2{\sigma }_{kh}=\frac{{}^2{\sigma }_0}{e^{-(2\delta +\mu )\left(kh\right)}}+\sum _{l=1}^k\frac{v\left(lh\right)}{e_{-(2\delta +\mu )(k-l)h}},$$

(19)

with

$$v\left(lh\right)=\frac{1}{N}{·}_{(k-l)h}^2{E}_{\left[x\right]+lh}\left\{{}^2{\sigma }_{Nh}-\frac{{}^2{\sigma }_0}{{}_{Nh}{}^2{E}_{\left[x\right]}}\right\},$$

which reduces to

$$v\left(lh\right)=\frac{1}{N}·e^{-(2\delta +\mu )(k-l)h}\left\{{}^2{\sigma }_{Nh}-\frac{{}^2{\sigma }_0}{e^{-(2\delta +\mu )\left(Nh\right)}}\right\}.$$

Again, these expressions are easily calculable for constant coefficients.

6.4. Patchwork Example—Controlling Sub-Intervals for the Discrete Case

We are faced with the problem of guaranteeing that a prescribed set of means and variances at the time instants ${\left\{lh\right\}}_{l=0}^{N-1}$ can be exactly achieved when we choose a set of premiums ${\left\{P_{lh}\right\}}_{l=0}^{N-1}$ and benefits ${\left\{S_{lh}\right\}}_{l=1}^N$. From Section 5, we know that

$$\begin{array}{cc}\hfill {}_{t+h}V=& {}_{t}V·\frac{{(1+i_t)}^h}{{}_h{p}_{\left[x\right]+t}}+u(t+h);u(t+h)=P_t·\frac{{(1+i_t)}^h}{{}_h{p}_{\left[x\right]x+t}}-\frac{{}_h{q}_{\left[x\right]+t}}{{}_h{p}_{\left[x\right]+t}}·S_{t+h}\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {}^2{\sigma }_{t+h}=& \frac{{}^2{\sigma }_t}{{}_h^2{E}_{\left[x\right]+t}}+v(t+h);v(t+h)={-}_h{q}_{\left[x\right]+t}{\left(S_{t+h}{-}_{t+h}V\right)}^2.\hfill \end{array}$$

(21)

In particular, for the interval $[0,Nh]$ the definitions above imply that

$$\begin{array}{cc}\hfill u\left(lh\right)& ={\frac{1}{N}}_{(N-l)h}{E}_{\left[x\right]+lh}\left\{{}_{Nh}V-\frac{{}_{0}V}{{}_{Nh}{E}_{\left[x\right]}}\right\}\hfill \\ \hfill v\left(lh\right)& ={\frac{1}{N}}_{(N-l)h}^2{E}_{\left[x\right]+lh}·\left\{{}^2{\sigma }_{Nh}=\frac{{}^2{\sigma }_0}{{}_{Nh}^2{E}_{\left[x\right]}}\right\},\hfill \end{array}$$

solves the exact controllability problem on $[0,Nh]$. A little algebra implies that for $l=1,2,3,\dots ,N$

$$\begin{array}{cc}\hfill S_{lh}& {=}_{lh}V+\sqrt{-\frac{v\left(lh\right)}{{}_h{q}_{\left[x\right]+(l-1)h}}}\hfill \\ \hfill P_{(l-1)h}& {=}_h{E}_{\left[x\right]+(l-1)h}\left\{u\left(lh\right)+\frac{{}_h{q}_{\left[x\right]+(l-1)h}}{{}_h{p}_{\left[x\right]+(l-1)h}}·S_{lh}\right\}.\hfill \end{array}$$

We now rewrite the above for the interval $\left[\right(l-1)h,lh]$, where $N=1$, with ${(}_{(l-1)h}V{,}_{lh}V)$ and ${(}^2{\sigma }_{\left(\right(l-1\left)h\right)}{,}^2{\sigma }_{(lh})$ pre-specified. We need to determine $P_l\left((l-1)h\right)$ and $S_l\left(lh\right)$ so that the initial and terminal states above are exactly achieved in $\left[\right(l-1)h,lh]$. We attack this problem by re-solving the problem above on the interval $\left[\right(l-1)h,lh]$. That is, our previous work gives us both u and v. That is,

$$\begin{array}{cc}\hfill u\left(lh\right)& {=}_{lh}V-\frac{{}_{(l-1)h}V}{{}_h{E}_{\left[x\right]}}\hfill \\ \hfill v\left(lh\right)& {=}^2{\sigma }_{lh}-\frac{{}^2{\sigma }_{(l-1)h}}{{}_h^2{E}_{\left[x\right]}}.\hfill \end{array}$$

Now, $S_{lh}$ and $P_{(l-1)h}$ are the benefit and premium, respectively, at $t=lh$ and $t=(l-1)h$ on the interval $\left[\right(l-1)h,lh]$. Therefore,

$$\begin{array}{cc}\hfill S_{lh}& {=}_{lh}V+\sqrt{-\frac{v_l\left(lh\right)}{{}_h{q}_{\left[x\right]+(l-1)h}}}\hfill \\ \hfill P_{(l-1)h}& {=}_h{E}_{\left[x\right]+(l-1)h}\left\{u\left(lh\right)+\frac{{}_h{q}_{\left[x\right]+(l-1)h}{S}_{lh}}{{}_h{p}_{\left[x\right]+(l-1)h}}\right\};l=1,2,\dots ,N.\hfill \end{array}$$

So, the above is the solution to the exact controllability problem on $\left[\right(l-1)h,lh]$ Now, we can patch together the solution on $\left[\right(l-1)h,lh]$ for $l=1,2,3,\dots ,N$ as the following figure indicates for each prescribed premium and benefit.

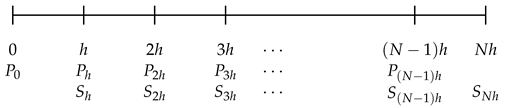
Then, given the sequence of prescribed states ${\left\{{}_{lh}V\right\}}_{l=0}^N$ and ${\left\{{}^2{\sigma }_{lh}\right\}}_{l=0}^N$ the sequence of premiums ${\left\{P_{lh}\right\}}_{l=0}^{N-1}$ and benefits ${\left\{S_{lh}\right\}}_{l=1}^N$ shown above will guarantee that:

$${\left.{}_{t}V\right|}_{t=lh}{=}_{lh}V\mathrm{and}{\left.{}^2{\sigma }_t\right|}_{t=lh}{=}^2{\sigma }_{lh}\mathrm{for}l=0,1,2,\dots ,N.$$

In other words, we can guarantee that that the prescribed set of means and variances at the time instants ${\left\{lh\right\}}_{l=0}^{N-1}$ are exactly achieved by choosing the premiums ${\left\{P_{lh}\right\}}_{l=0}^{N-1}$ and benefits ${\left\{S_{lh}\right\}}_{l=1}^N$. This solves the objective of exactly controlling the means and variances at the time instants ${\left\{lh\right\}}_{l=0}^{N-1}$.

Remark 8.

We note that by choosing a growing sequence of policy values satisfying ${}_{lh}V-\frac{{}_{(l-1)h}V}{{}_h{E}_{\left[x\right]}}>0$, we are guaranteed that the benefits $S_{lh}$ and premiums $P_{lh}$ are both positive.

7. Conclusions

We start this section by outlining the broad ideas of this paper. The main problem that is considered in this paper is one of simultaneous exact controllability of the mean and variance of the present value of future losses of an insurance policy with the premium and benefit considered as control inputs. This is an important problem to consider because it allows for the re-design on the structure of the insurance policy by choosing premiums and benefits in order to make sure that the mean and variance of the policy are within prescribed bounds in general. The specific formulation of the problem considered in this paper allows for the mean and variance to assume exact prescribed initial and final state values at time instants $t=0$ and $t=T$, respectively. Such a problem has not been considered before in the literature, and hence the formulation and the solution shown in this paper are novel. The main result is that both the Thiele and Hattendorff equations, which govern the evolution of the mean and variance of the present value of the future losses of an insurance policy, in both continuous and discrete time, are exactly controllable. The premium and benefit, which are our control inputs, have explicit expressions in terms of the policy value and other parameters of the Thiele and Hattendorff equations. We now summarize the specifics of the results proven in this paper.

In this paper we have considered the problem of exactly controlling the mean ${}_{t}V$ and the variance ${}^2{\sigma }_t$ of an insurance policy on a finite time interval $[0,T]$. In other words, we have shown that there exist control inputs in the form of premiums $P_t$ and benefits $S_t$, that can steer the mean and variance from a prescribed initial state $({}_{0}V,{}^2{\sigma }_0)$ at $t=0$ to a prescribed final state $({}_{T}V,{}^2{\sigma }_T)$ at $t=T$, where the mean ${}_{t}V$ and variance ${}^2{\sigma }_t$ evolve according to Thiele’s and Hattendorff’s differential equations (or recursions), respectively. This is, in a sense, quite opposite to the situations considered in a normal actuarial setting, where the benefits or premiums are specified and the policy value ${}_{t}V$ and the variance ${}^2{\sigma }_t$ are calculated at various instants of time.

We have shown both the Thiele’s and Hattendorff’s equations (and their respective discrete counterparts) are exactly controllable in time T. We first computed control inputs in the form of $u\left(t\right)$ and $v\left(t\right)$ explicitly in terms of the specified initial and terminal states $({}_{0}V,{}_{T}V)$ and $({}^2{\sigma }_0,{}^2{\sigma }_T)$ for mean and variance, respectively. We then used these known control inputs to work our way to explicit expressions for the premium $P_t$ and benefit $S_t$. We saw that the condition $\left({}_{T}V-\frac{{}_{0}V}{{}_T{E}_{\left[x\right]}}\right)>0$ guarantees that the premiums $P_t$ are positive. The benefit $S_t$ is positive as well.

We note that Thiele’s equation for the mean has no terms involving the variance, while the Hattendorff’s equation for the variance is actually coupled to Thiele’s equation through a ${}_{t}V$ term. Hence, Thiele’s equation can be separately exactly controlled (if we are not interested in controlling the variance), through two degrees of freedom $S_t$ and $P_t$ as seen in Theorems 1 and 2. If we choose a form for the premiums $P_t$, then the benefits $S_t$ can be computed in terms of $P_t$ or vice versa. However, we lose this degree of freedom if we want to control both the mean and the variance simulataneously as seen in Theorems 3 and 4.

We derived explicit expressions for the constant $\mu$ and $\delta$ case in Section 6.1, Section 6.2 and Section 6.3. Finally, we showed an example in Section 6.4 where a given discrete trajectory of mean and variance at sampled time instants ${\left\{lh\right\}}_{l=0}^N$ is exactly achieved by premiums ${\left\{P_{lh}\right\}}_{l=0}^{N-1}$ and ${\left\{S_{lh}\right\}}_{l=1}^N$. Choosing a growing sequence of specified policy values ${\left\{{}_{l}hV\right\}}_{l=1}^N$ satisfying ${}_{lh}V-\frac{{}_{(l-1)h}V}{{}_h{E}_{\left[x\right]}}>0$ will guarantee a positive value for the premiums ${\left\{P_{lh}\right\}}_{l=0}^{N-1}$ whereas the benefits ${\left\{S_{lh}\right\}}_{l=1}^N$ are positive automatically (assuming the DSAR is positive in each of the sub-intervals).

Classical formulations in the literature of actuarial mathematics typically deal with the reverse problem, i.e., given the premium and benefit structure of an insurance policy, compute the mean and the variance of the insurance policy at time t. The main novelty of our result is that for the first time, we are considering the premium $P_t$ and the benefit $S_t$ as the unknowns and want to exactly control the evolution of the mean ${}_{t}V$ and the variance ${}^2{\sigma }_t$ of an insurance policy. Like we mentioned before, this allows the insurance company to think about the design of the insurance product, i.e., premium and benefit, in order to achieve a certain value of mean and variance for the present value of future losses. The mean $V_t$ is an indication of an average amount of reserve that the company needs to have at time t and the variance ${}^2{\sigma }_t$ is an indication of how much the reserve at time t can vary. Based on historical data, an insurance company can have an idea of what the mean and variance of reserves should be at time t in order for the company to be profitable, thereby, allowing the company to specify ${}_{t}V$ and ${}^2{\sigma }_t$ at the initial and final time instants $t=0$ and $t=T$. Then the question becomes, how should the premiums and benefits at time t be designed in order to satisfy the condition that the specified ${}_{t}V$ and ${}^2{\sigma }_t$ are achieved at times $t=0$ and $t=T$. To our knowledge, this is the first time such a formulation has been stated and solved in the form of a simultaneous exact controllability problem of the mean ${}_{t}V$ and the variance ${}^2{\sigma }_t$ of an insurance policy. Using our approach, we can precisely calculate the premium $P_t$ and the benefit $S_t$ that needs to be specified apriori, that will achieve exact controllability of the mean ${}_{t}V$ and the variance ${}^2{\sigma }_t$ of an insurance policy in a time interval $[0,T]$. To our knowledge the problem of simultaneous exact controllability of the mean and variance of an insurance policy has not been considered before and hence, this work fills an important gap in the literature. In our future work, we will consider the same simultaneous exact controllability problem for multi-state Markov insurance models.