Analysis of Evolving Hazard Overflows and Construction of an Alert System in the Chinese Finance Industry Using Statistical Learning Methods
Abstract
1. Introduction
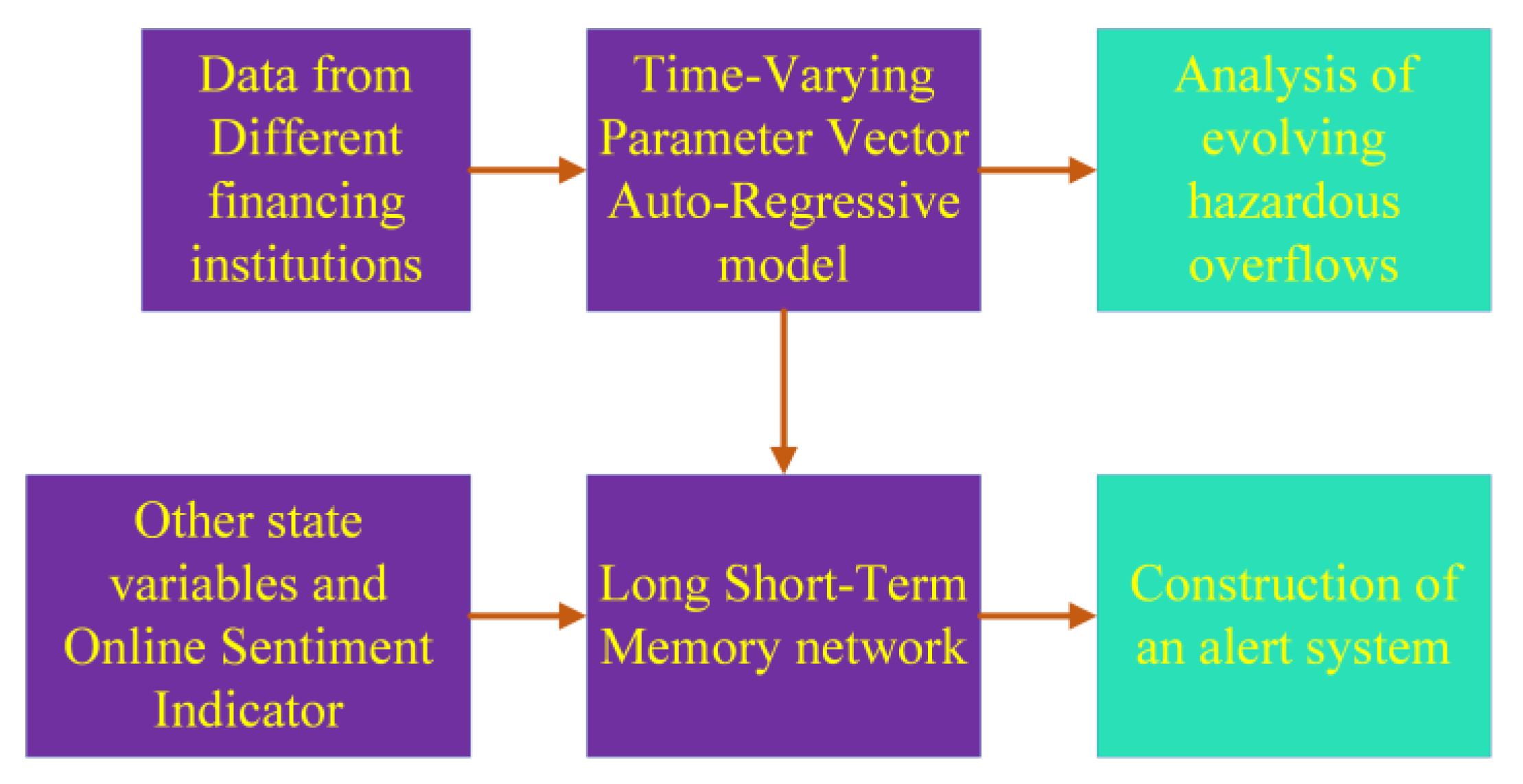
2. Materials and Methods
2.1. Analysis of Evolving Hazard Overflows Using TVP-VAR
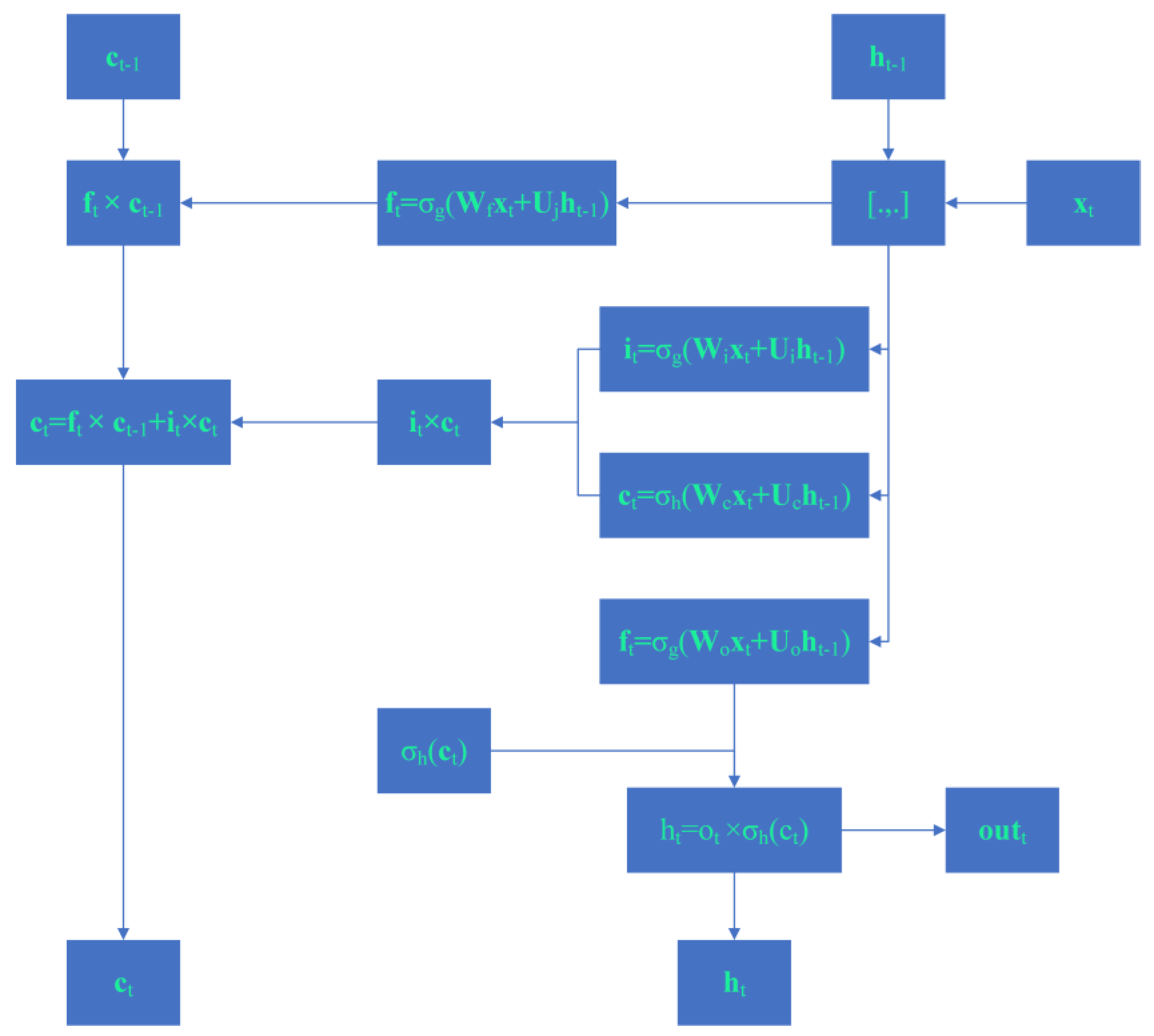
2.2. Construction of an Hazard Alert System Using LSTM
3. Research and Analysis
3.1. Analysis about Evolving Hazard Overflows
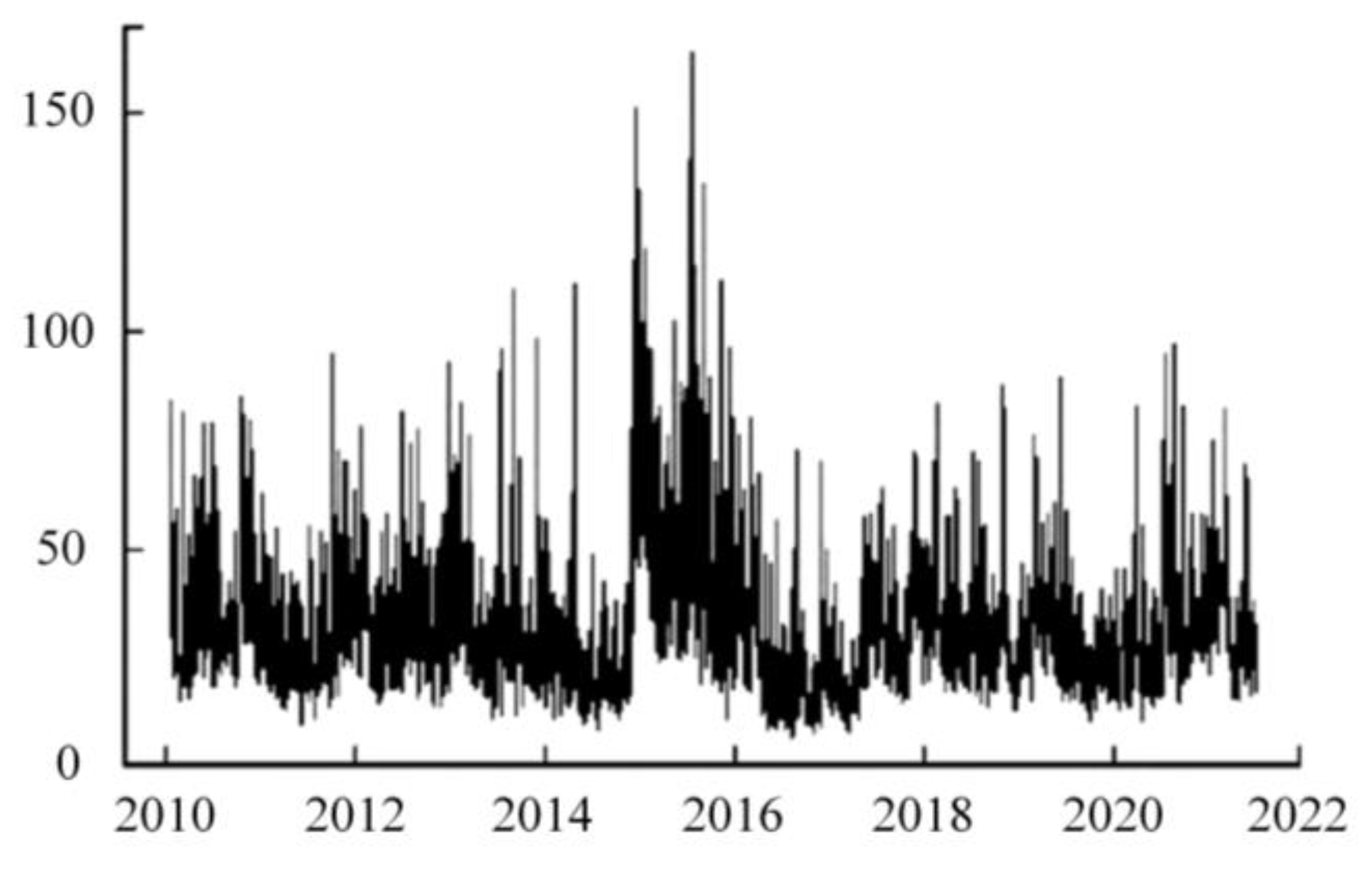
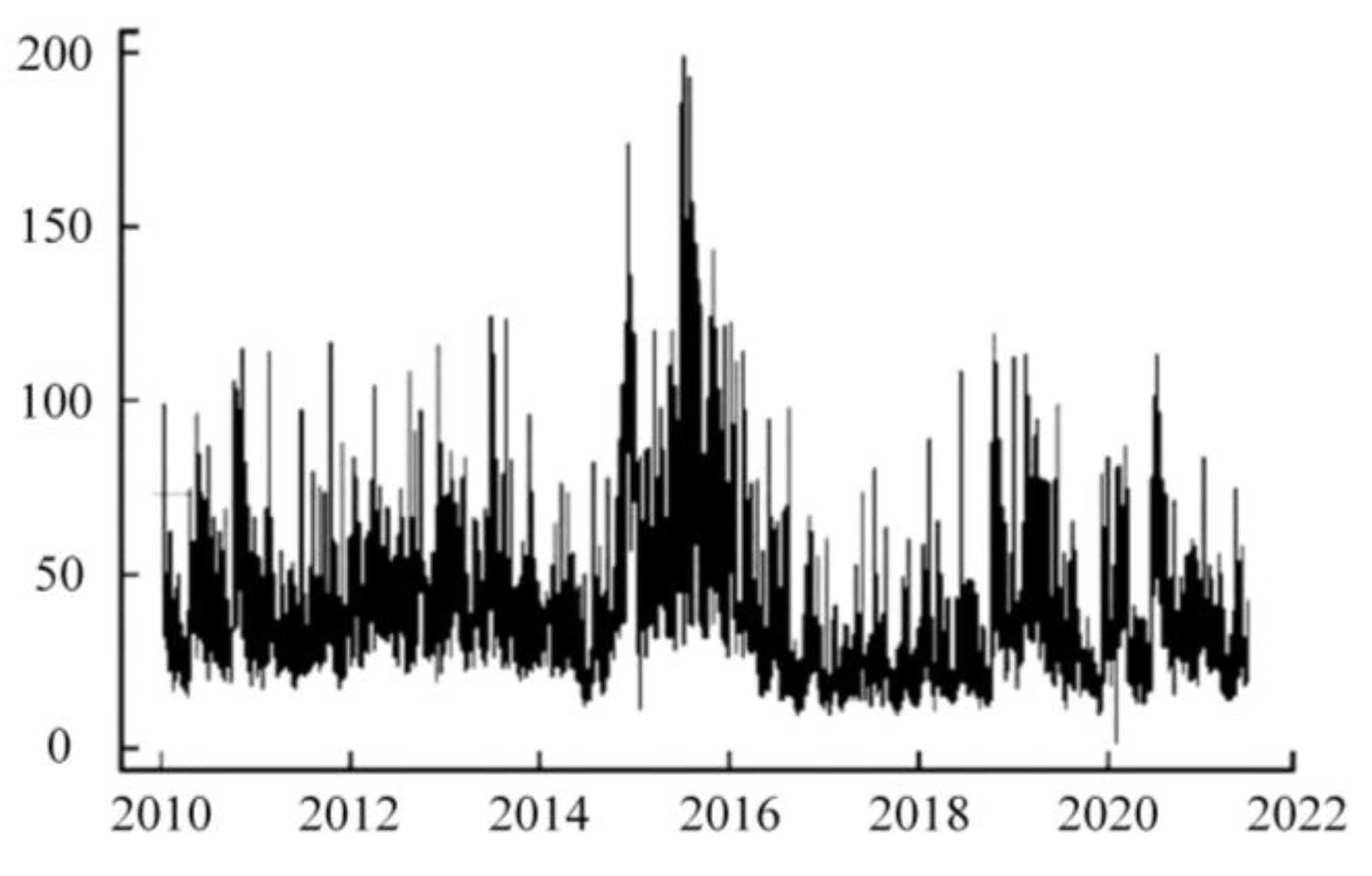
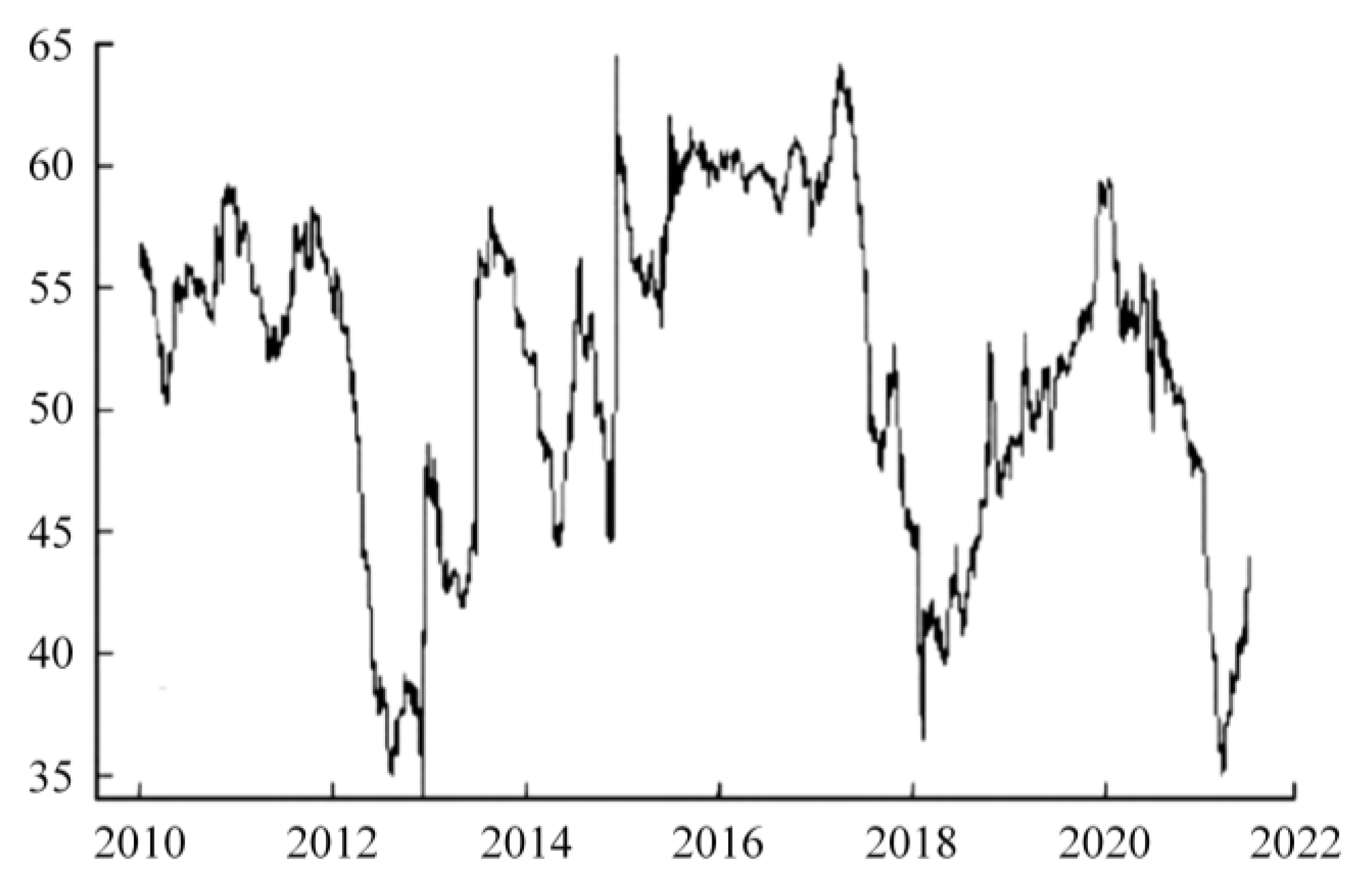
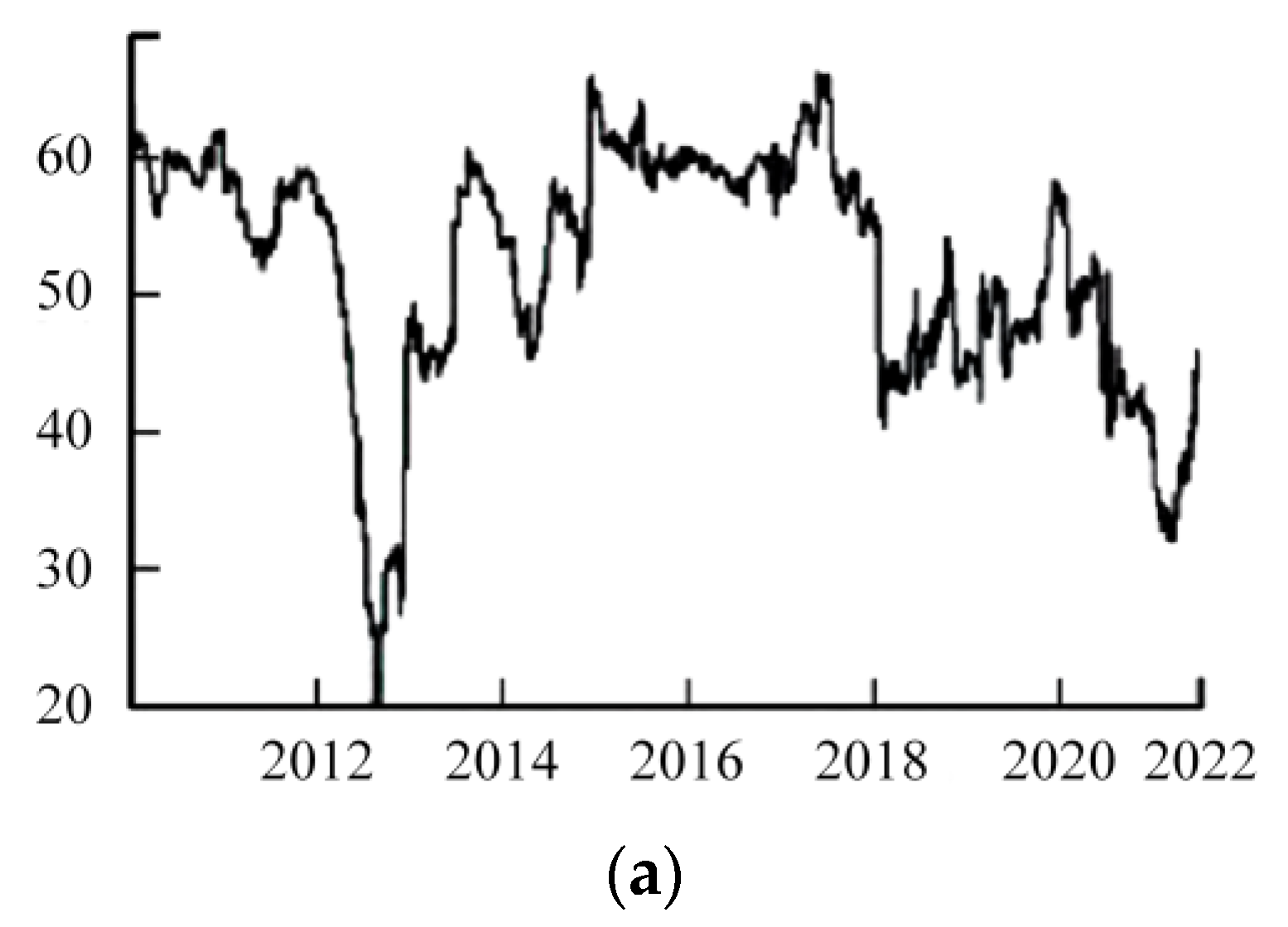
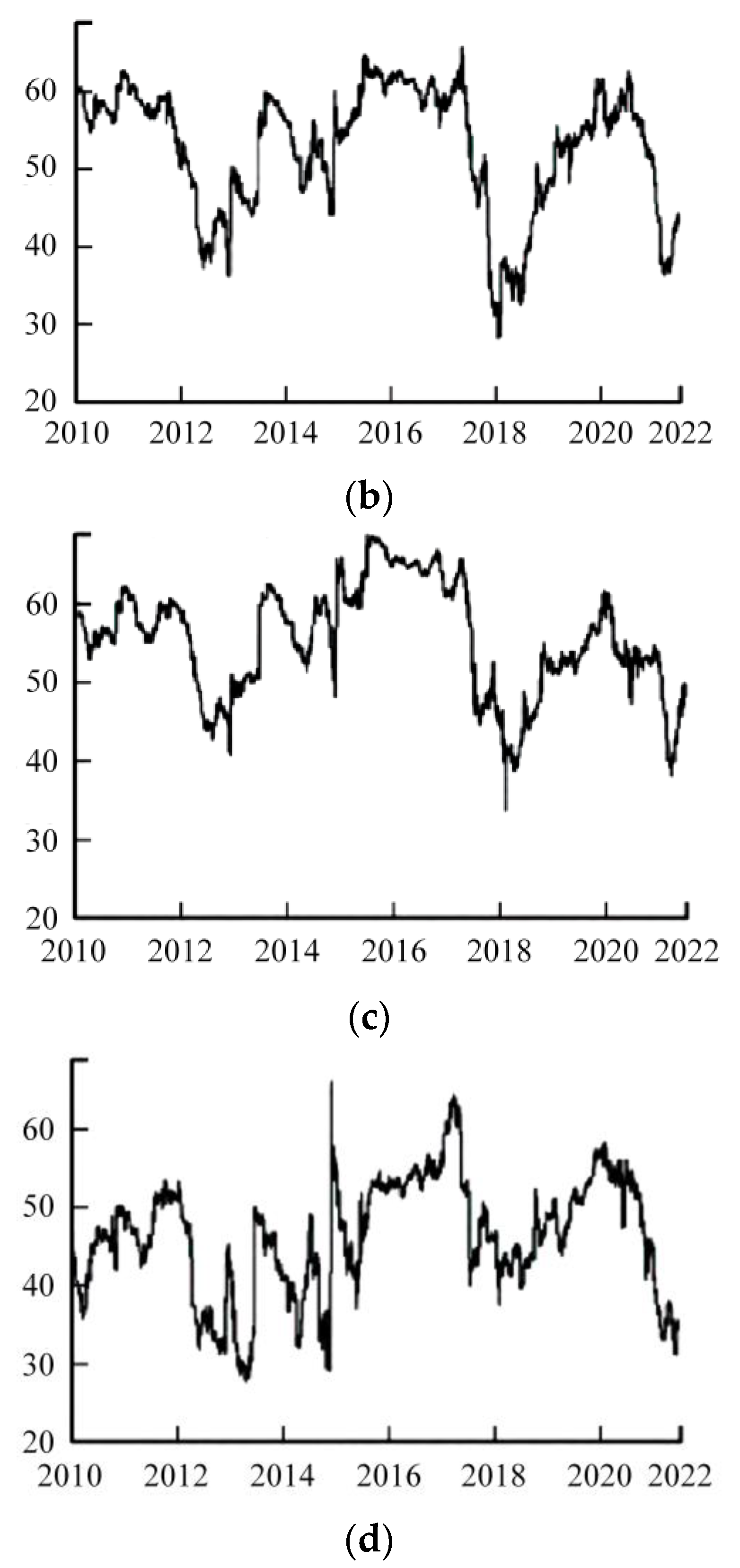
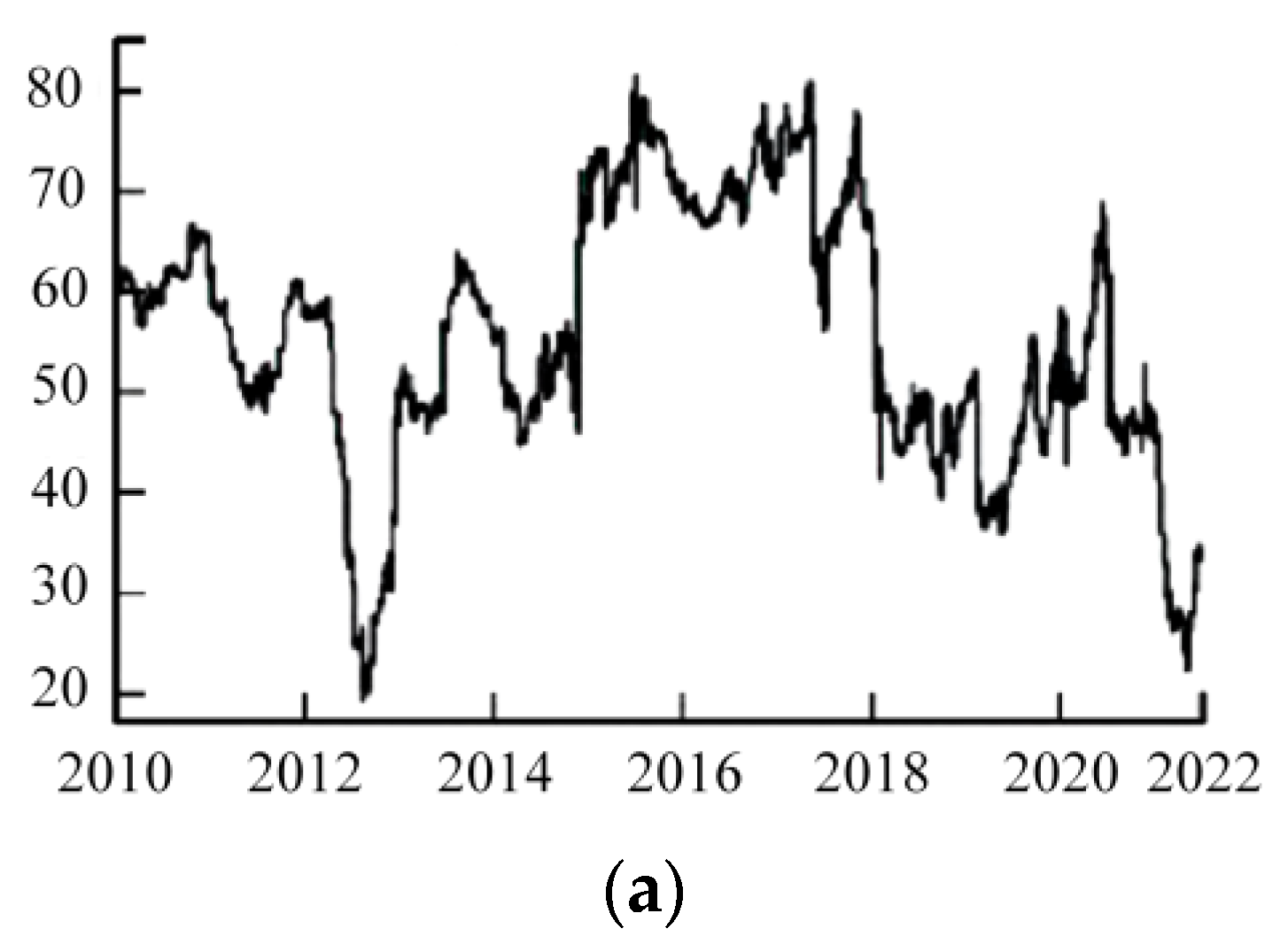
3.1.1. Data Source and Analysis
3.1.2. Analysis of Evolving Hazard Overflows
3.2. Analysis of Hazard Alert
3.2.1. Construction of Financial Hazard Alert Indexes and Experiment Settings
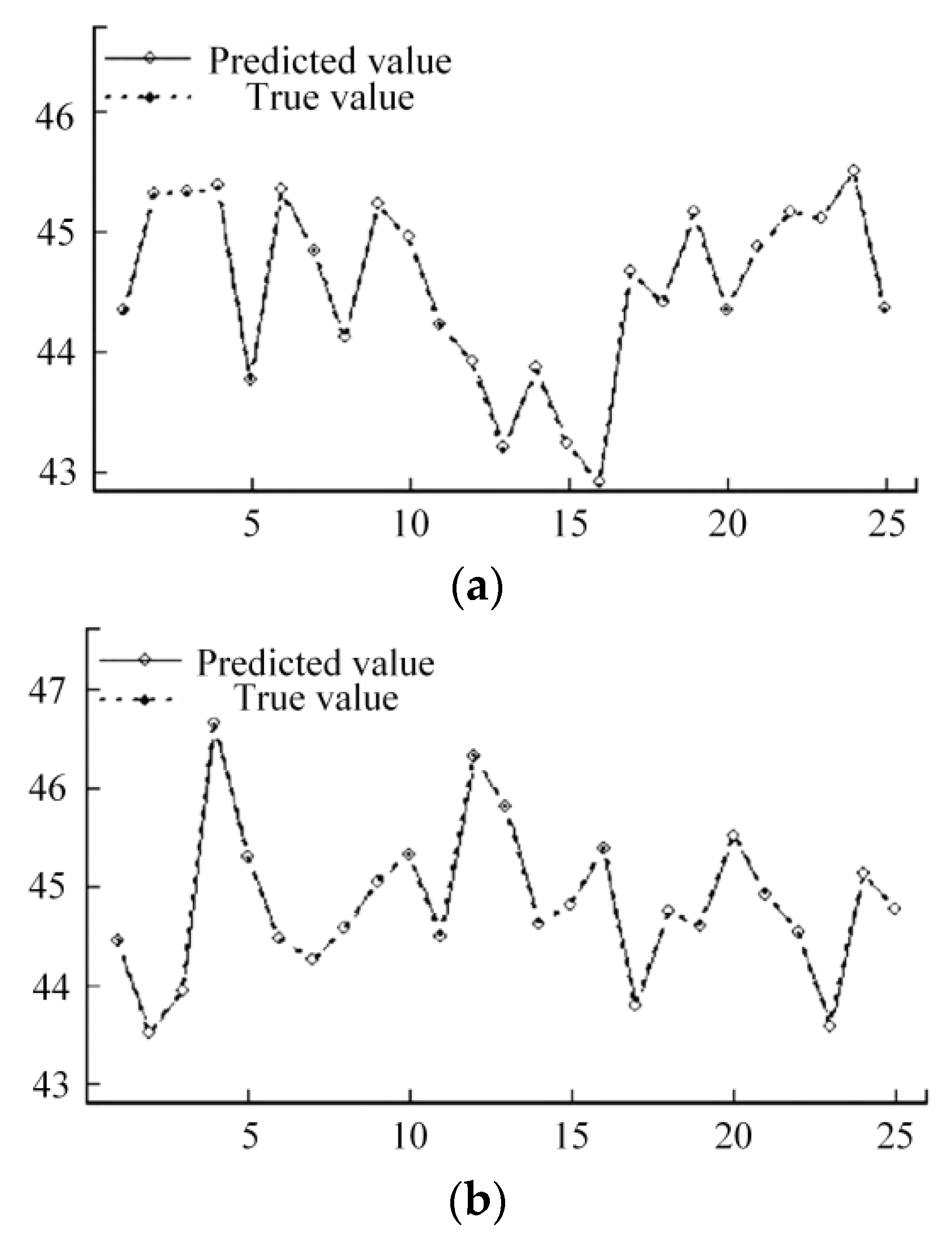
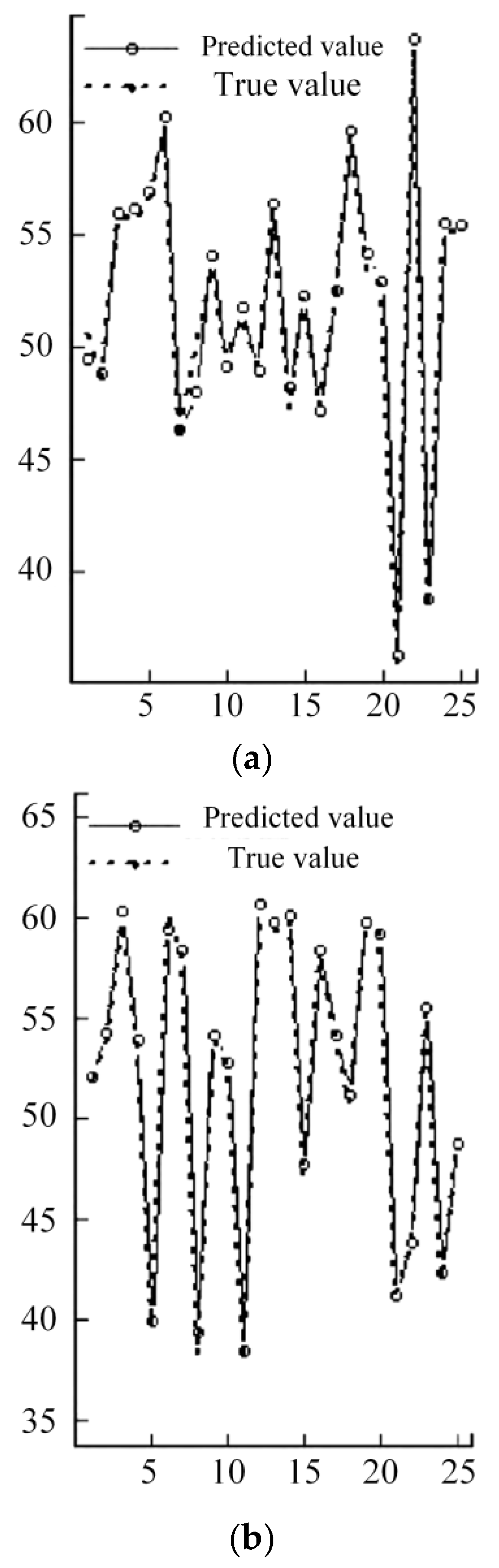
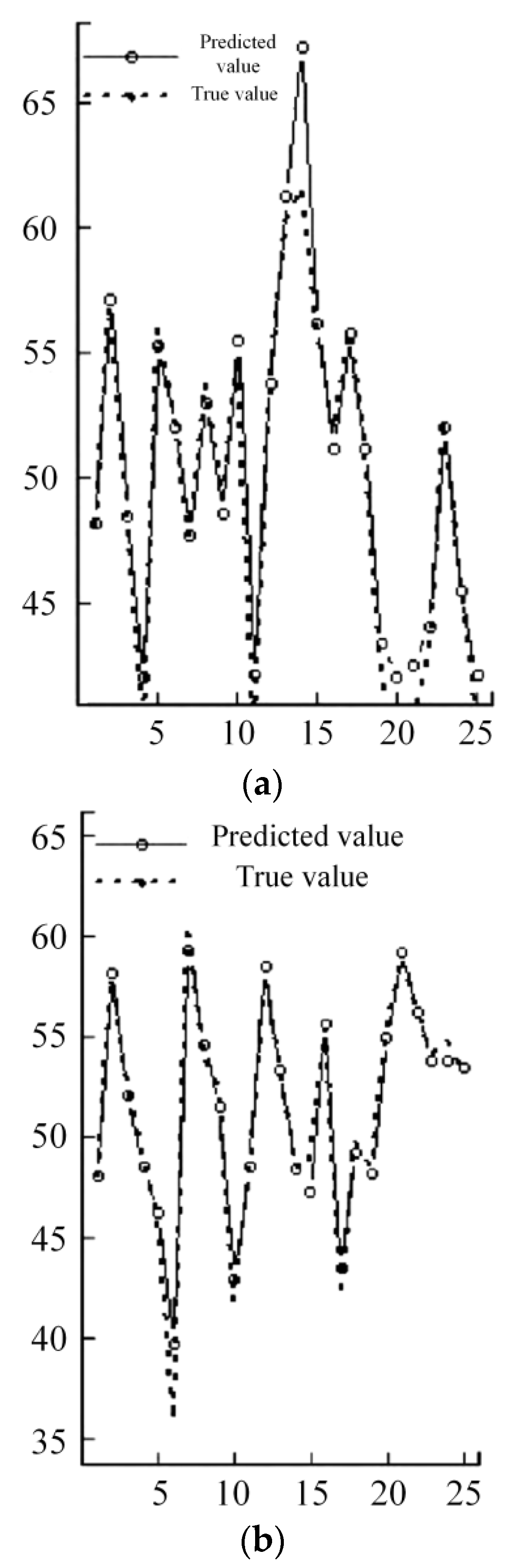
3.2.2. Construction of the Hazard Alert System
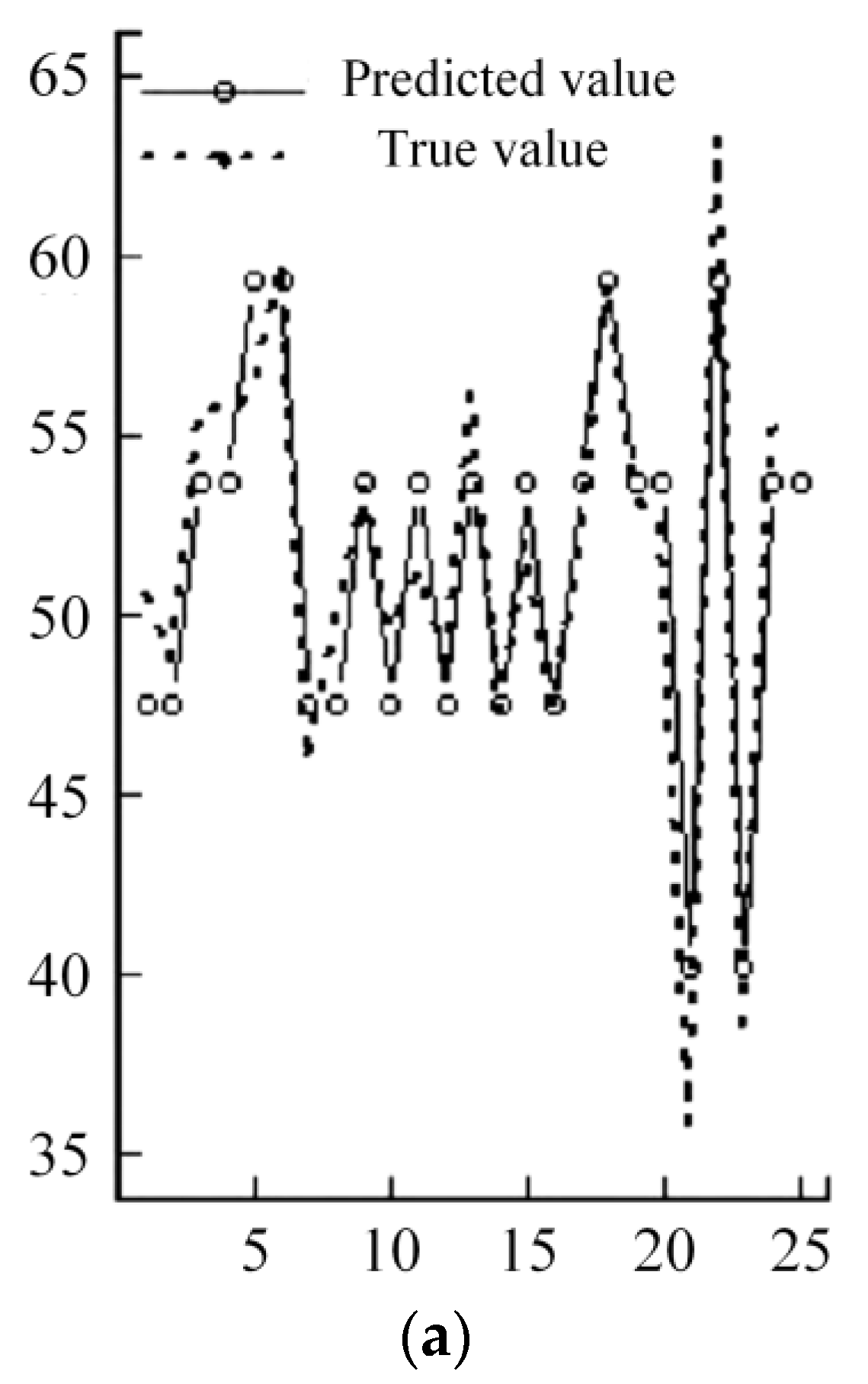
3.2.3. Further Analysis—Research on Financial Hazard Alert Incorporating OSI
4. Conclusions
5. Managerial Insights
Funding
Data Availability Statement
Conflicts of Interest
References
- López-Espinosa, G.; Moreno, A.; Rubia, A.; Valderrama, L. Short-term wholesale funding and systemic risk: A global CoVaR approach. J. Bank. Financ. 2012, 36, 3150–3162. [Google Scholar] [CrossRef]
- Derbali, A.; Hallara, S. Systemic risk of European financial institutions: Estimation and ranking by the Marginal Expected Shortfall. Res. Int. Bus. Financ. 2016, 37, 113–134. [Google Scholar] [CrossRef]
- Engle, R. Systemic risk 10 years later. Annu. Rev. Financ. Econ. 2018, 10, 125–152. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, Z.; Zhang, D.; Ji, Q. Identifying systemically important financial institutions in China: New evidence from a dynamic copula-CoVaR approach. Ann. Oper. Res. 2021, 1–35. [Google Scholar] [CrossRef]
- Cao, J.; Lei, L.; Zhang, R.; Lei, Q. Risk of spillovers between the Chinese and international crude oil futures’ markets: A dynamic Copula-CoES approach. J. Phys. Conf. Ser. 2021, 1941, 012059. [Google Scholar] [CrossRef]
- Aslam, F.; Ferreira, P.; Mughal, K.S.; Bashir, B. Intraday volatility spillovers among European financial markets during COVID-19. Int. J. Financ. Stud. 2021, 9, 5. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, S.; Guo, Y.; Yang, Q.; Li, Q.; Zhuang, F.; Liu, J.; Kou, G. Bankruptcy Prediction via Mixing Intra-Risk and Spillover-Risk. arXiv 2022, arXiv:2202.03874. [Google Scholar]
- Ni, Z.X.; Lu, X.; Xue, W.J. Can the belt and road strategy solve the problem of iron and steel production overcapacity in China? A study based on TVP-VAR-DMA. J. Int. Trade 2016, 3, 161–174. [Google Scholar]
- Yang, X.; Chen, S.; Liu, Z.; Yang, X.; Huang, C. Systemically important financial institutions in China: From view of tail risk spillover network. Appl. Econ. Lett. 2022, 29, 1833–1839. [Google Scholar] [CrossRef]
- Ma, X.; Sun, S.; Ding, C.; Wang, Y. A coupling analysis of multimodal transportation demands based on TVP-VAR models. Beijing Hangkong Hangtian Daxue Xuebao/J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 18–26. [Google Scholar]
- Wang, C.; Wei, Y. Simulation of financial risk spillover effect based on ARMA-GARCH and fuzzy calculation model. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2021, 40, 6555–6566. [Google Scholar] [CrossRef]
- Tan, L.; Tang, Q.G. Study on the risk spillover effect of Internet financial products. In Proceedings of the 2019 16th International Conference on Service Systems and Service Management (ICSSSM), Shenzhen, China, 13–15 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Moșteanu, N.R. International Financial Markets face to face with Artificial Intelligence and Digital Era. Theor. Appl. Econ. 2019, 26, 123–134. [Google Scholar]
- Pervin, M.; Roy, S.K.; Sannyashi, P.; Weber, G.W. Sustainable inventory model with environmental impact for non-instantaneous deteriorating items with composite demand. RAIRO-Oper. Res. 2023, 57, 237–261. [Google Scholar] [CrossRef]
- Chong, X. Hybrid PSO-SVM for Financial Early-Warning Model of Small and Medium-Sized Enterprises. In Proceedings of the 6th International Conference on Financial Innovation and Economic Development (ICFIED 2021), Sanya, China, 29–31 January 2021; Atlantis Press: Amsterdam, The Netherlands, 2021; pp. 107–114. [Google Scholar]
- Shi, Y.; Dai, W.; Long, W.; Li, B. Improved ACD-based financial trade durations prediction leveraging LSTM networks and Attention Mechanism. Math. Probl. Eng. 2021, 2021, 7854512. [Google Scholar] [CrossRef]
- Foglia, M.; Addi, A.; Angelini, E. The Eurozone banking sector in the time of COVID-19: Measuring volatility connectedness. Glob. Financ. J. 2022, 51, 100677. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Hou, W. Asymmetric risk spillover networks and risk contagion driver in Chinese financial markets: The perspective of economic policy uncertainty. Complexity 2021, 2021, 3169534. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, D.; Ji, Q. Systemic risk and financial contagion across top global energy companies. Energy Econ. 2021, 97, 105221. [Google Scholar] [CrossRef]
- Jiménez, A.; Rodríguez, G.; Arellano, M.A. Time-varying impact of fiscal shocks over GDP growth in Peru: An empirical application using hybrid TVP-VAR-SV models. Struct. Change Econ. Dyn. 2023, 64, 314–332. [Google Scholar] [CrossRef]
- Adjei AN, K.; Tweneboah, G.; Junior, P.O. Nonlinear causal relationship between economic policy uncertainty and macroeconomic variables in selected emerging market economies. Ann. Financ. Econ. 2023, 18, 2240002. [Google Scholar] [CrossRef]
- Alizadeh, S.; Brandt, M.W.; Diebold, F.X. High- and Low-Frequency Exchange Rate Volatility Dynamics: Range-Based Estimation of Stochastic Volatility Models. J. Financ. 2002, 57, 1047–1091. [Google Scholar] [CrossRef]
- Antonakakis, N.; Chatziantoniou, I.; Gabauer, D. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. J. Risk Financ. Manag. 2020, 13, 84. [Google Scholar] [CrossRef]
- Available online: https://www.gtarsc.com/ (accessed on 29 March 2023).
- Available online: https://www.wind.com.cn/ (accessed on 1 April 2023).
- Markham, A.; Das, R.; Grosse-Wentrup, M. A distance covariance-based kernel for nonlinear causal clustering in heterogeneous populations. In Proceedings of the First Conference on Causal Learning and Reasoning, Eureka, CA, USA, 11–13 April 2022; pp. 542–558. [Google Scholar]
- Lv, Y.; Piao, J.; Li, B.; Yang, M. Does online investor sentiment impact stock returns? Evidence from the Chinese stock market. Appl. Econ. Lett. 2022, 29, 1434–1438. [Google Scholar] [CrossRef]
- Solairaj, A.; Sugitha, G.; Kavitha, G. Enhanced Elman spike neural network based sentiment analysis of online product recommendation. Appl. Soft Comput. 2023, 132, 109789. [Google Scholar]
- Lin, P.; Ma, S.; Fildes, R. The Value of the Online Sentiment Proxies in Realized Volatility Forecasting: A Large scale Longitudinal Evaluation. 2021. Available online: http://dx.doi.org/10.2139/ssrn.4460034 (accessed on 1 April 2023).


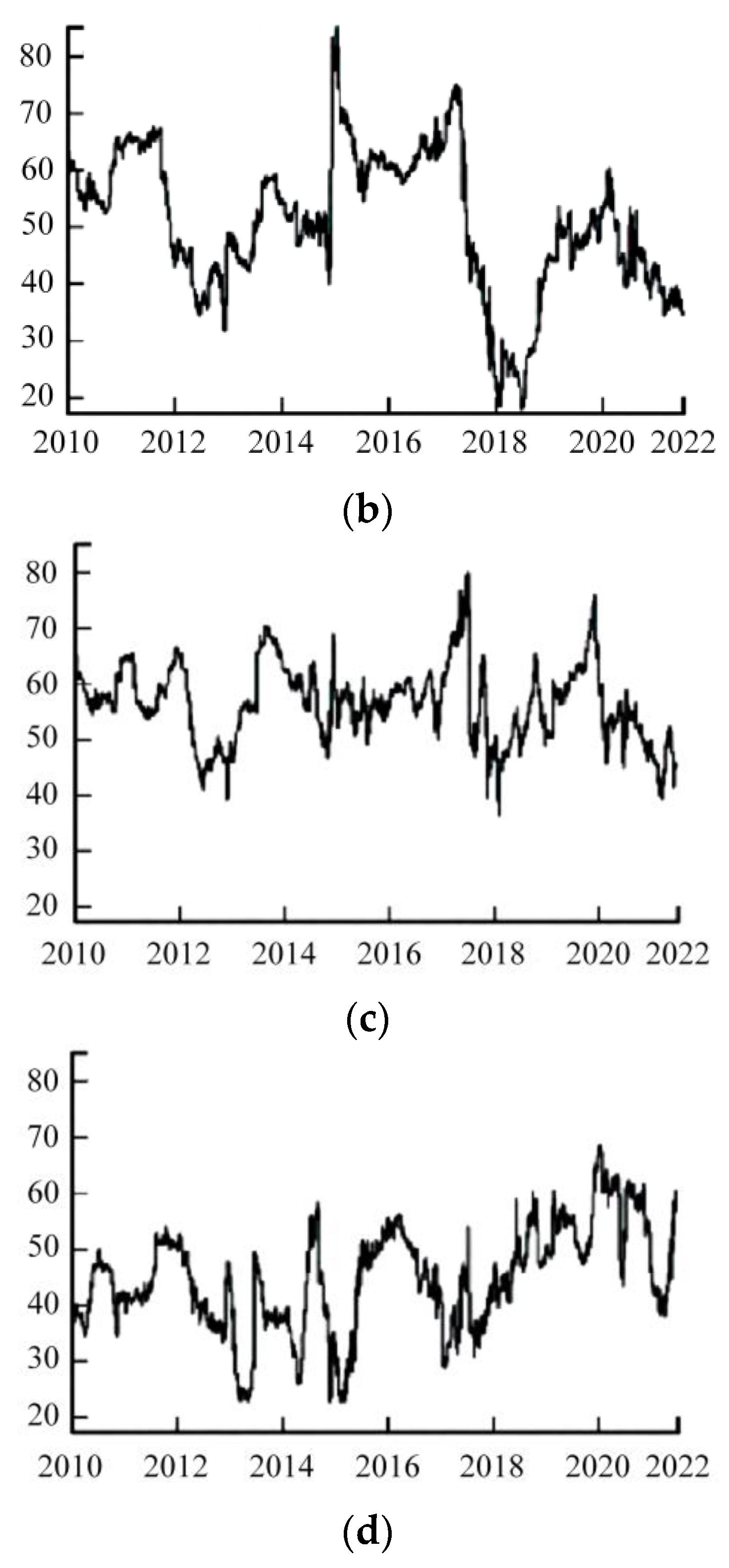
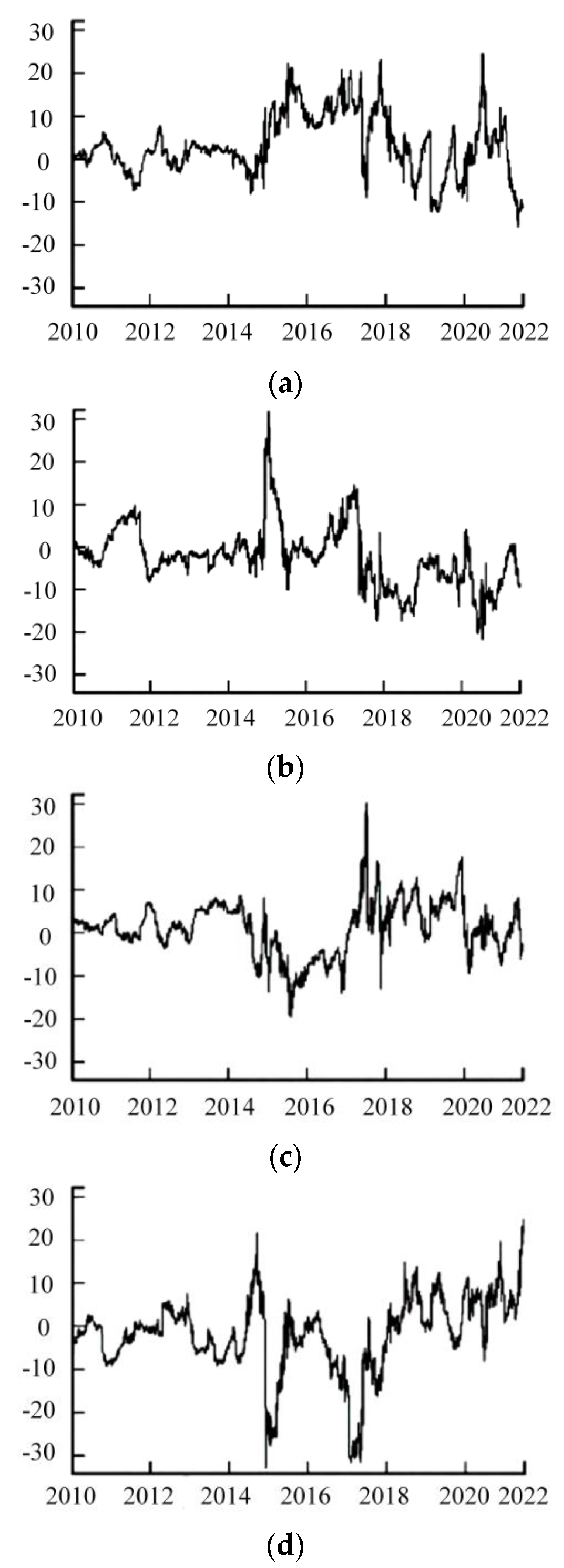
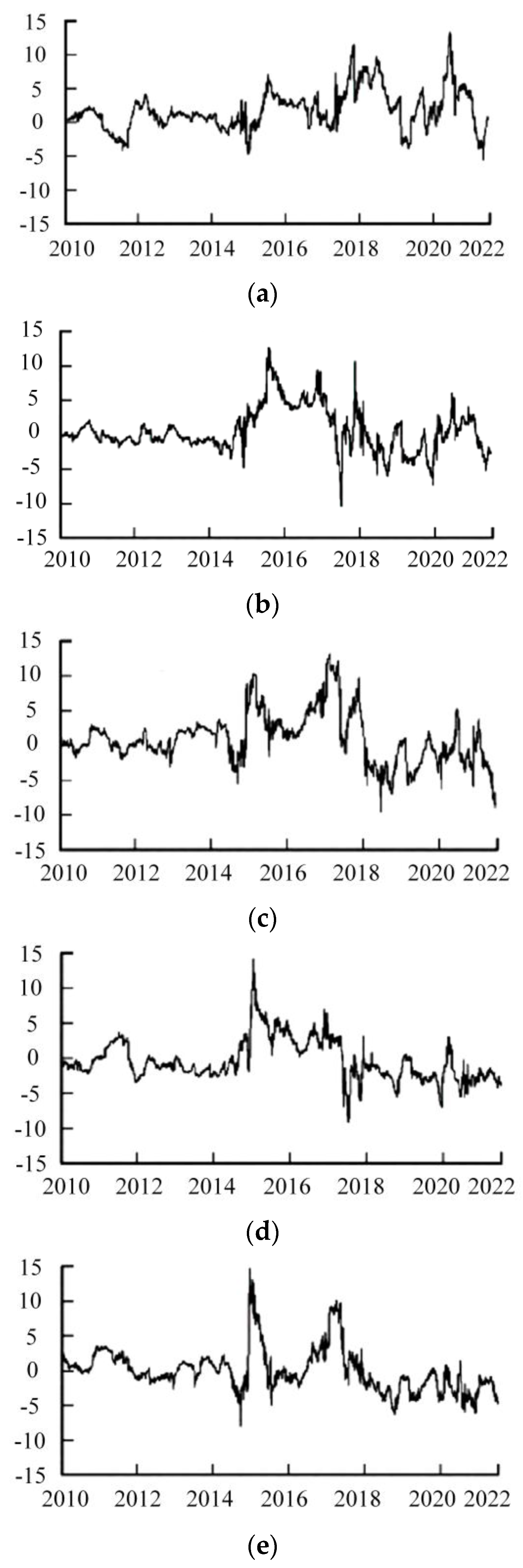
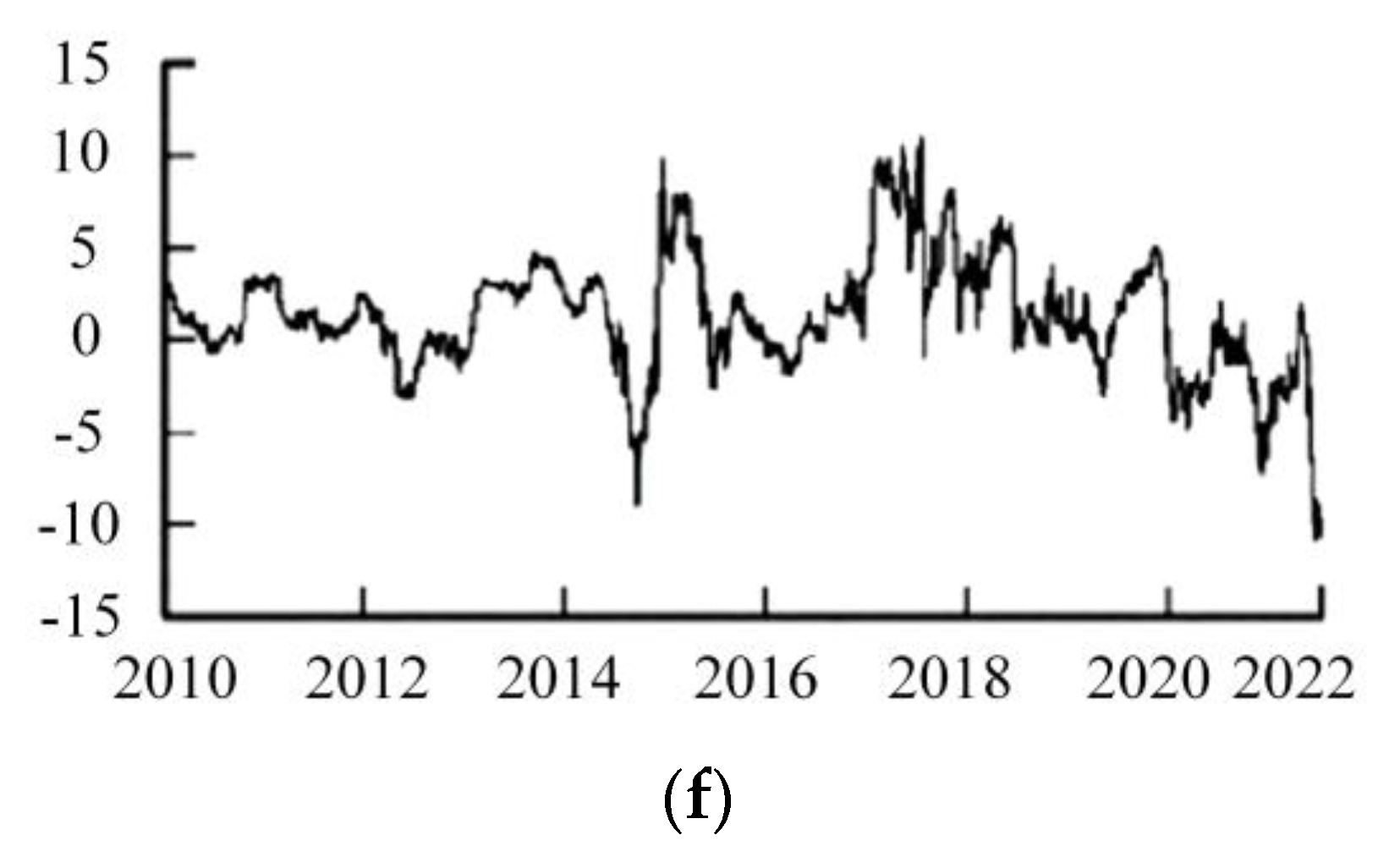

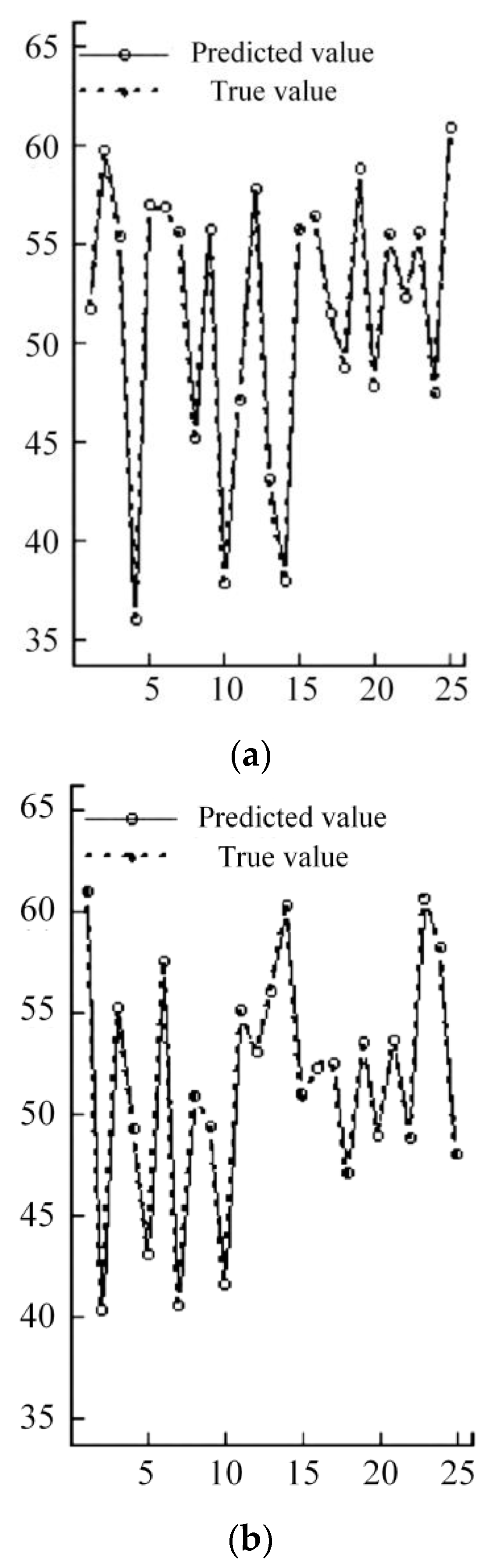
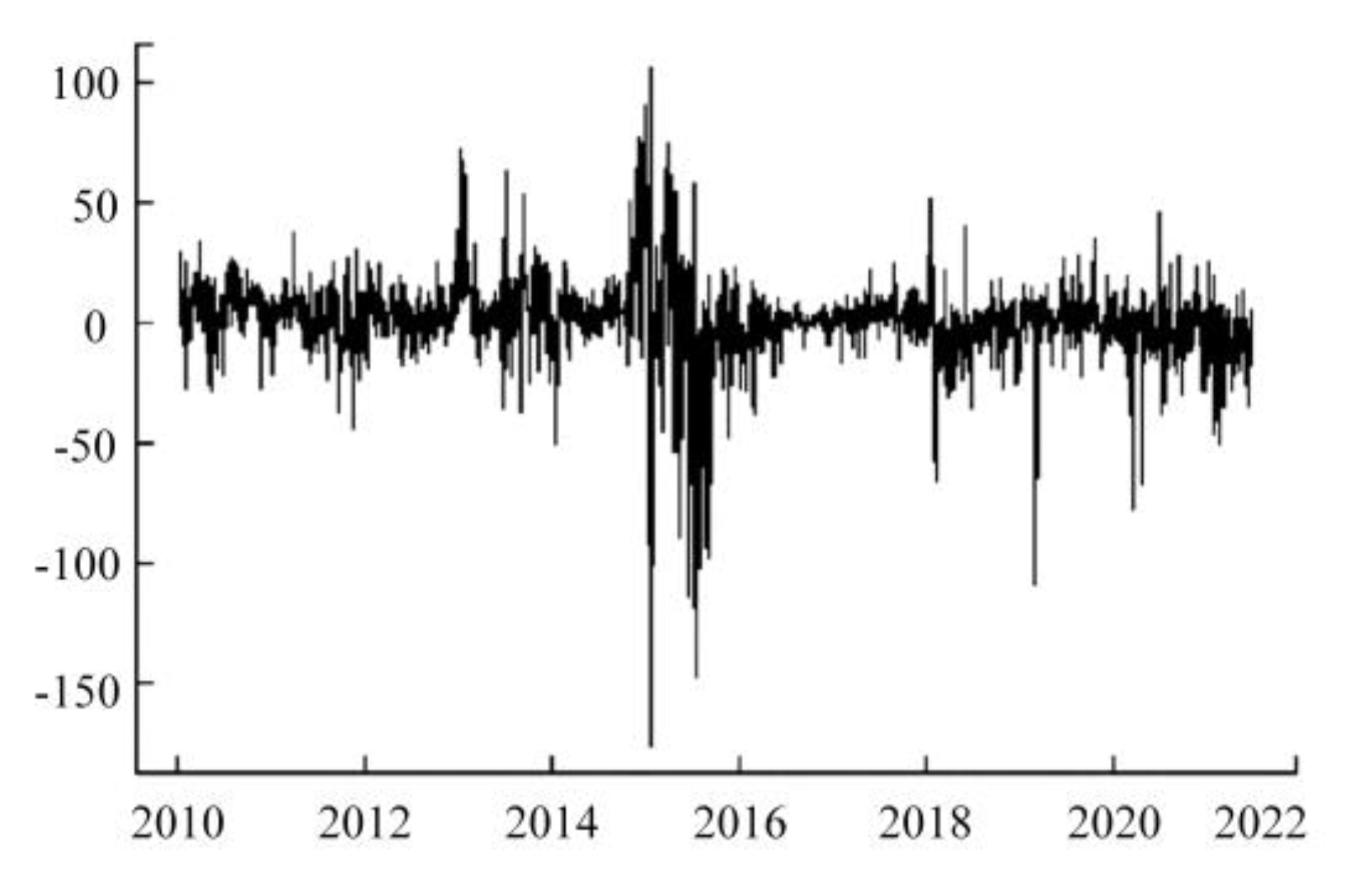
| Literature | Baseline | State | Hazardous Overflow | Hazardous Alert |
|---|---|---|---|---|
| López et al. [1] | Conditional value-at-risk | Failure to consider the interdependence and volatility characteristics between financial relevant time-series data | √ | × |
| Derbali et al. [2] | Marginal expected shortfall | Ditto | √ | × |
| Engle et al. [3] | Coefficient of systemic financial hazard | Ditto | √ | × |
| Wu et al. [4] | Time-varying generalized auto-regressive conditional heteroscedasticity model | N/A | √ | × |
| Wu et al. [4] | Rolling window dynamic Copula method | N/A | √ | × |
| Cao et al. [5] | Variance decomposition & Rolling window | Information loss | √ | × |
| Zhao et al. [7] | Time-varying parameter vector auto-regressive | Information loss | √ | × |
| Ni et al. [8] | Weighted network | N/A | √ | × |
| Yang et al. [9] | TENET | N/A | √ | √ |
| Wang et al. [11] | Factor hazard model | Lack of interpretability for financial time-series data | × | √ |
| Wang et al. [11] | Stochastic time-varying model | Ditto | × | √ |
| Wang et al. [16] | Machine learning | Poor generalization | × | √ |
| Zhang et al. [18,19] | Average stochastic gradient descent and weight-dropped LSTM | N/A | × | √ |
| Industries & Indicators | 1 | 2 | … | m | In-Degree |
|---|---|---|---|---|---|
| 1 | … | ||||
| 2 | … | ||||
| … | … | … | … | … | … |
| m | … | ||||
| Out-degree | … | ||||
| Net overflow | Net1,t | Net2,t | … | Netm,t | FHOt |
| IDs | Institutions | Industries |
|---|---|---|
| 1 | Ping An Bank | Banking |
| 2 | Bank of Ningbo | Banking |
| 3 | Pudong Development Bank | Banking |
| 4 | Hua Xia Bank | Banking |
| 5 | Minsheng Bank | Banking |
| 6 | Merchants Bank | Banking |
| 7 | Bank of Nanjing | Banking |
| 8 | Industrial Bank | Banking |
| 9 | Bank of beijing | Banking |
| 10 | Bank of Communications | Banking |
| 11 | Industrial and Commercial Bank | Banking |
| 12 | China Construction Bank | Banking |
| 13 | Bank of China | Banking |
| 14 | China Citic Bank | Banking |
| 15 | China Pacific Insurance | Insurance |
| 16 | China Life Insurance | Insurance |
| 17 | Ping An Insurance | Insurance |
| 18 | Northeast Securities | Securities |
| 19 | Guoyuan Securities | Securities |
| 20 | Changjiang Securities | Securities |
| 21 | Citic Securities | Securities |
| 22 | Sinolink Securities | Securities |
| 23 | Southwest Securities | Securities |
| 24 | Sunny Loan Top | Securities |
| 25 | Everbright Securities | Securities |
| 26 | Shaanxi International Trust A | Diversified finance |
| 27 | New huangpu | Diversified finance |
| 28 | Henan Zhongyuan expressway | Diversified finance |
| 29 | Haide Limited | Diversified finance |
| 30 | Tianmao Group | Diversified finance |
| Statistics | Banking | Insurance | Securities | Diversified Finance |
|---|---|---|---|---|
| Sample size | 2792 | 2792 | 2792 | 2792 |
| Mean | 26.09 | 32.75 | 38.97 | 40.52 |
| Standard deviation | 15.60 | 17.63 | 22.44 | 18.95 |
| Median | 21.84 | 28.35 | 32.85 | 35.75 |
| Maximum | 7.28 | 6.63 | 1.42 | 6.88 |
| Minimum | 177.14 | 163.97 | 197.82 | 187.50 |
| Indexes | Descriptions |
|---|---|
| Financial hazard overflow (FHO) | The financial industry’s own hazard overflow indicator |
| Logarithmic return of the Shanghai Composite Index (LR) | The daily closing price logarithmic return |
| Volatility of the Shanghai Composite Index (VO) | The difference between the daily highest price and the daily lowest price |
| Short-term liquidity spread (SLS) | The spread between the 6-month SHIBOR(Shanghai Interbank Offered Rate) and the 6-month government bond yield |
| Interest rate hazard (IRH) | The spread between the pre- and post-maturity yields of the 6-month government bonds. |
| Interest rate term structure (IRTS) | The difference between the 6-month government bond yield and the 10-year government bond yield at time period t, minus the difference between the 6-month government bond yield and the 10-year government bond yield at time period t − 1 |
| Real estate yield (REY) | Daily closing price logarithmic return |
| Structure | Parameters | |
|---|---|---|
| Input | Time step | 5 |
| → LSTM layer | Prediction step | 1 |
| → LSTM Layer | Number of iterations | 600 |
| → Dropout layer | Optimizer | Adam |
| → Full Connection layer | Dropout rate | 0.01 |
| → Output | Loss function | MSE |
| Activation function | Tanh | |
| Batch_size | 30 | |
| Number of hidden layer neurons | 50 | |
| Proportion of test set | 0.25 | |
| Null Hypothesis | Statistics |
|---|---|
| FHO is not the cause of LR | 1.699 ** |
| LR is not the cause of FHO | 1.483 * |
| FHO is not the cause of VO | 0.781 |
| VO is not the cause of FHO | 1.480 * |
| FHO is not the cause of SLS | 1.743 ** |
| SLS is not the cause of FHO | 1.780 * |
| FHO is not the cause of IRH | 1.311 * |
| IRH is not the cause of FHO | 1.407 * |
| FHO is not the cause of IRTS | 1.460 * |
| IRTS is not the cause of FHO | 0.041 |
| FHO is not the cause of REY | 2.490 *** |
| REY is not the cause of FHO | 1.778 ** |
| Error | Training Set | Testing Set |
|---|---|---|
| MAE | 0.0895 | 0.0957 |
| MSE | 0.0086 | 0.0230 |
| Models | Metrics | Training Set | Testing Set |
|---|---|---|---|
| ANN | MAE | 0.3302 | 0.3422 |
| MSE | 0.3041 | 0.3465 | |
| SVM | MAE | 0.8047 | 0.8366 |
| MSE | 1.3993 | 1.4089 | |
| RF | MAE | 0.1266 | 0.3431 |
| MSE | 0.0478 | 0.3346 | |
| DT | MAE | 1.5751 | 1.5377 |
| MSE | 3.6723 | 3.5053 |
| Models | Metrics | Training Set | Testing Set |
|---|---|---|---|
| LSTM | MAEa | 0.0895 | 0.0957 |
| MAEb | 0.0572 | 0.0865 | |
| MSEa | 0.0086 | 0.0230 | |
| MSEb | 0.0039 | 0.0256 | |
| ANN | MAEa | 0.3302 | 0.3422 |
| MAEb | 0.2991 | 0.3106 | |
| MSEa | 0.3041 | 0.3465 | |
| MSEb | 0.2716 | 0.3200 | |
| SVM | MAEa | 0.8047 | 0.8366 |
| MAEb | 0.7963 | 0.8345 | |
| MSEa | 1.3993 | 1.4089 | |
| MSEb | 1.3867 | 1.4146 | |
| RF | MAEa | 0.1266 | 0.3431 |
| MAEb | 0.1256 | 0.3350 | |
| MSEa | 0.0478 | 0.3346 | |
| MSEb | 0.0466 | 0.3389 | |
| DT | MAEa | 1.5751 | 1.5377 |
| MAEb | 1.5751 | 1.5377 | |
| MSEa | 3.6723 | 3.5053 | |
| MSEb | 3.6723 | 3.5053 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J. Analysis of Evolving Hazard Overflows and Construction of an Alert System in the Chinese Finance Industry Using Statistical Learning Methods. Mathematics 2023, 11, 3279. https://doi.org/10.3390/math11153279
Li J. Analysis of Evolving Hazard Overflows and Construction of an Alert System in the Chinese Finance Industry Using Statistical Learning Methods. Mathematics. 2023; 11(15):3279. https://doi.org/10.3390/math11153279
Chicago/Turabian StyleLi, Jin. 2023. "Analysis of Evolving Hazard Overflows and Construction of an Alert System in the Chinese Finance Industry Using Statistical Learning Methods" Mathematics 11, no. 15: 3279. https://doi.org/10.3390/math11153279
APA StyleLi, J. (2023). Analysis of Evolving Hazard Overflows and Construction of an Alert System in the Chinese Finance Industry Using Statistical Learning Methods. Mathematics, 11(15), 3279. https://doi.org/10.3390/math11153279







