LPGRI: A Global Relevance-Based Link Prediction Approach for Multiplex Networks
Abstract
1. Introduction
2. Methodology
2.1. Measurement of Interlayer Correlation in Multiplex Networks
2.2. Probability Estimation of Potential Links in Multiplex Networks
3. Data Description and Evaluation Metric
3.1. Datasets
- Lazega [43]: The dataset consists of a multiplex network representing corporate law partnerships among employees. It contains three kinds of relationships, namely advice, co-work, and friendship. There are a total of 71 nodes, with the number of active nodes in each layer being 71, 70, and 69, respectively.
- C. elegans [44]: The Caenorhabditis elegans dataset comprises three layers that correspond to different synaptic junctions, namely electric links, chemical monadic links, and chemical polyadic links. The multiplex network consists of 279 nodes in total. Each layer has a different number of active nodes, with 253, 260, and 278 nodes, respectively.
- Kapferer [45]: The Kapferer tailor shop dataset describes the interactions in a tailor shop in Zambia over a period of ten months. The four layers of the network are generated by two different types of interaction. The first two layers, TS1 and TS2, represent “sociational” interactions, specifically friendship and socioemotional connections. The last two layers, TI1 and TI2, record “instrumental” interactions related to work and assistance at two different time points. The multiplex network consists of 39 nodes, with the number of active nodes in each layer being 39, 39, 35, and 37, respectively.
- Vicker [46]: This dataset is a multiplex social network depicting the relationships between 29 Grade 7 students in a school in Victoria, Australia. It consists of three layers, with each layer corresponding to different types of relationships, namely getting on, best friends, and preferring working together. There are 29 nodes in total. The number of active nodes in each layer is also 29.
- CKM [47]: This dataset constitutes a multiplex network that captures the interaction among physicians during the adoption of a new drug. It consists of three layers that represent different types of relationships: friendship, discussion, and asking for advice. There are 245 nodes in total. The number of active nodes in each layer is 215, 231, and 227, respectively.
- Rattus [48]: This dataset provides a multiplex network of genetic and protein interactions in Rattus Norvegicus. The raw data comprise 2640 nodes and 6 layers. In order to remove uninformative layers, we exclude those with only a few dozen edges. Within the paper, the multiplex network is analyzed using three layers: physical association, direct interaction, and colocalization. There are a total of 2538 nodes, with 1948, 979, and 149 active nodes in each layer, respectively.
3.2. Evaluation Metric
4. Experimental Analysis
4.1. Correlation Between Layers in Real Datasets
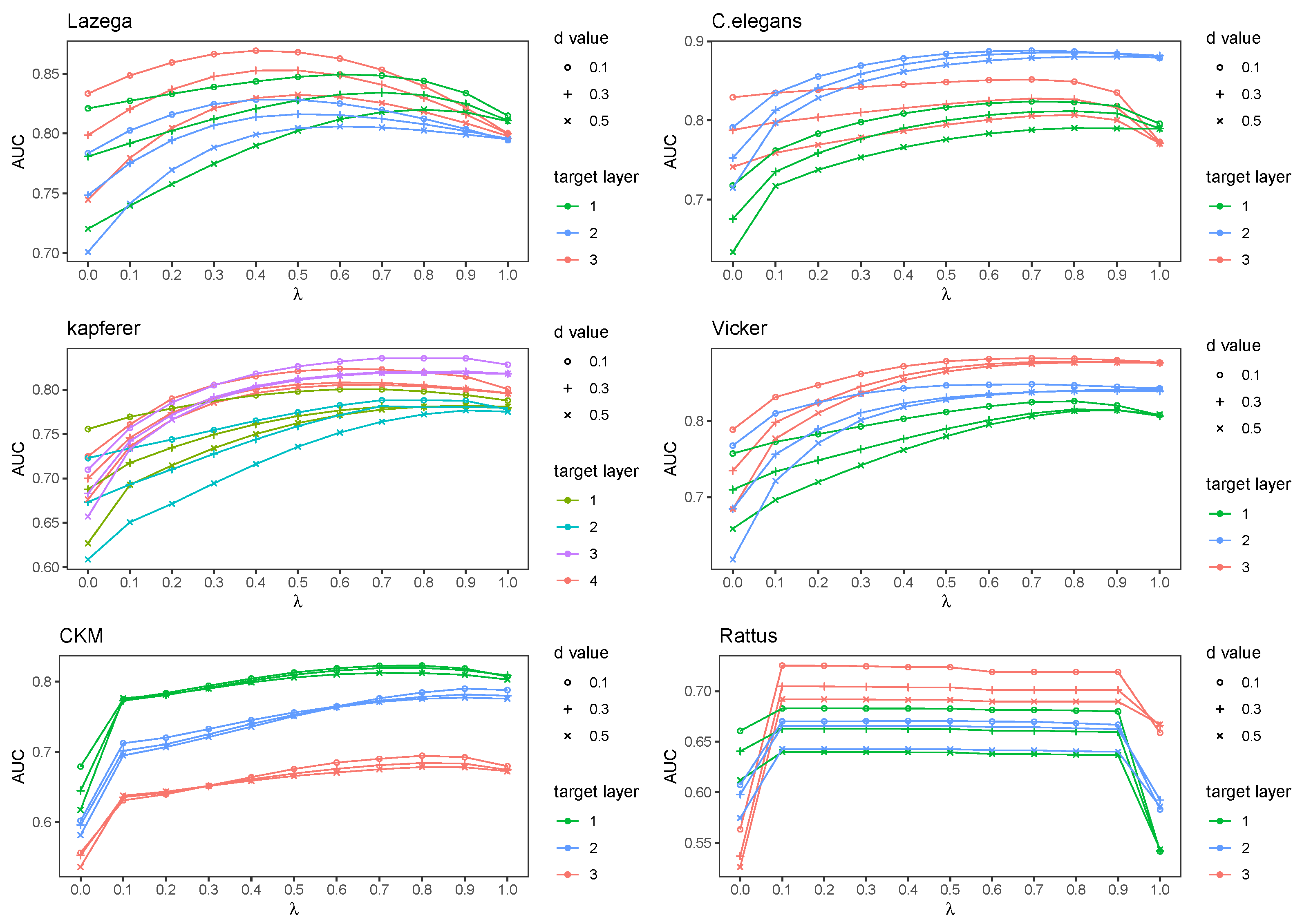
4.2. Tunable Parameter Analysis
4.3. Analysis of the Influence of Auxiliary Layers on Prediction Performance
4.4. Comparison of LPGRI with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LPGRI | Link Prediction based on Global Relevance of Interlayer |
| GR | Global Relevance |
| AUC | Area Under the Curve |
| RI | Ratio of Improvement |
References
- Cardillo, A.; Gómez-Gardeñes, J.; Zanin, M.; Romance, M.; Papo, D.; del Pozo, F.; Boccaletti, S. Emergence of network features from multiplexity. Sci. Rep. 2013, 3, 1344. [Google Scholar] [CrossRef] [PubMed]
- Nicosia, V.; Bianconi, G.; Latora, V.; Barthelemy, M. Growing multiplex networks. Phys. Rev. Lett. 2013, 111, 058701. [Google Scholar] [CrossRef] [PubMed]
- Szell, M.; Lambiotte, R.; Thurner, S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 2010, 107, 13636–13641. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Tang, F.; Wang, C.; Wang, Y.; Su, J. Link prediction for multilayer networks using interlayer structural information. Int. J. Mod. Phys. C 2022, 33, 2250003. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Albert, R.; Barabasi, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Kleinberg, J. The link prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Physica A 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Wang, P.; Xu, B.; Wu, Y.; Zhou, X. Link prediction in social networks:the state-of-the-art. Sci. China Inf. Sci. 2015, 58, 1–38. [Google Scholar]
- Ji, P.; Ye, J.; Mu, Y.; Lin, W.; Tian, Y.; Hens, C.; Perc, M.; Tang, Y.; Sun, J.; Kurths, J. Signal propagation in complex networks. Phys. Rep. 2023, 1017, 1–96. [Google Scholar] [CrossRef]
- Martínez, V.; Berzal, F.; Cubero, J.C. A survey of link prediction in complex networks. ACM. Comput. Surv. 2016, 49, 69.1–69.33. [Google Scholar] [CrossRef]
- Lorrain, F.; White, H.C. Structural equivalence of individuals in social networks. J. Math. Sociol. 1971, 1, 49–80. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the Web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.; Zhang, Y. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
- Martinčić-Ipšić, S.; Močibob, E.; Perc, M. Link prediction on Twitter. PLoS ONE 2017, 12, e0181079. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Jeh, G.; Widom, J. Simrank: A measure of structural-context similarity. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; ACM Press: New York, NY, USA, 2002; pp. 271–279. [Google Scholar]
- Clauset, A.; Moore, C.; Newman, M.E.J. Hierarchical structure and the prediction of missing links in networks. Nature 2008, 453, 98–101. [Google Scholar] [CrossRef]
- Holland, P.W.; Laskey, K.B.; Leinhardt, S. Stochastic blockmodels: First steps. Soc. Netw. 1983, 5, 109–137. [Google Scholar] [CrossRef]
- Friedman, N.; Getoor, L.; Koller, D.; Pfeffer, A. Learning Probabilistic Relational Models; Springer: Berlin, Germany, 2000. [Google Scholar]
- Heckerman, D.; Meek, C.; Koller, D. Probabilistic entity-relationship models, PRMs, and plate models. In Proceedings of the 21st International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; pp. 55–60. [Google Scholar]
- Yu, K.; Chu, W.; Yu, S.; Tresp, V.; Xu, Z. Stochastic relational models for discriminative link prediction. Adv. Neural Inf. Process. Syst. 2006, 19, 1553–1560. [Google Scholar]
- Zhou, T. Progresses and challenges in link prediction. iScience 2021, 24, 103217. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Physica A 2020, 553, 124289. [Google Scholar] [CrossRef]
- Jafari, S.H.; Abdolhosseini-Qomi, A.M.; Asadpour, M.; Rahgozar, M.; Yazdani, N. An information theoretic approach to link prediction in multiplex networks. Sci. Rep. 2021, 11, 13242. [Google Scholar] [CrossRef]
- Davis, D.; Lichtenwalter, R.; Chawla, N.V. Multi-relational link prediction in heterogeneous information networks. In Proceedings of the 2011 International Conference on Advances in Social Networks Analysis and Mining, ASONAM, Kaohsiung, Taiwan, 25–27 July 2011; pp. 281–288. [Google Scholar]
- Hristova, D.; Noulas, A.; Bown, C.; Musolesi, M.; Mascolo, C. A multilayer approach to multiplexity and link prediction in online geo-social networks. EPJ Data Sci. 2016, 5, 1–17. [Google Scholar] [CrossRef]
- Li, W.; Li, T.; Berahmand, K. An effective link prediction method in multiplex social networks using local random walk towards dependable pathways. J. Comb. Optim. 2023, 45, 31. [Google Scholar] [CrossRef]
- Cao, J.; Lei, T.; Li, J.; Jiang, J. A Novel Link Prediction Method for Social Multiplex Networks Based on Deep Learning. Mathematics 2023, 11, 1705. [Google Scholar] [CrossRef]
- Jalili, M.; Orouskhani, Y.; Asgari, M.; Alipourfard, N.; Perc, M. Link prediction in multiplex online social networks. R. Soc. Open Sci. 2017, 4, 160863. [Google Scholar] [CrossRef]
- Bacco, C.D.; Power, E.A.; Larremore, D.B.; Moore, C. Community detection, link prediction, and layer interdependence in multilayer networks. Phys. Rev. E 2017, 95, 042317. [Google Scholar] [CrossRef]
- Yang, Y.; Chawla, N.; Sun, Y.; Hani, J. Predicting links in multi-relational and heterogeneous networks. In Proceedings of the 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 755–764. [Google Scholar]
- Sharma, S.; Singh, A. An efficient method for link prediction in complex multiplex Networks. In Proceedings of the 11th Signal-Image Technology and Internet-Based Systems (SITIS), Bangkok, Thailand, 23–27 November 2015; pp. 453–459. [Google Scholar]
- Sharma, S.; Singh, A. An efficient method for link prediction in weighted multiplex networks. Comput. Soc. Netw. 2016, 3, 1–17. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yao, Y.; Zhang, R.; Yang, F.; Yuan, Y.; Sun, Q.; Qiu, Y.; Hu, R. Link prediction via layer relevance of multiplex networks. Int. J. Mod. Phys. C 2017, 28, 1750101. [Google Scholar] [CrossRef]
- Najari, S.; Salehi, M.; Ranjbar, V.; Jalili, M. Link prediction in multiplex networks based on interlayer similarity. Physica A 2019, 536, 120978. [Google Scholar] [CrossRef]
- Abdolhosseini-Qomi, A.M.; Jafari, S.H.; Taghizadeh, A.; Yazdani, N.; Asadpour, M.; Rahgozar, M. Link prediction in real-world multiplex networks via layer reconstruction method. R. Soc. Open Sci. 2020, 7, 191928. [Google Scholar] [CrossRef]
- Liao, H.; Zeng, A.; Zhang, Y.C. Predicting missing links via correlation between nodes. Physica A 2015, 436, 216–223. [Google Scholar] [CrossRef]
- Zhang, Y.; Elizaveta, L.; Zhu, J. Estimating network edge probabilities by neighborhood smoothing. Biometrika 2017, 104, 771–783. [Google Scholar] [CrossRef]
- Lazega, E. The Collegial Phenomenon: The Social Mechanisms of Cooperation among Peers in a Corporate Law Partnership; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Chen, B.L.; Hall, D.H.; Chklovskii, D.B. Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. USA 2006, 103, 4723–4728. [Google Scholar] [CrossRef]
- Kapferer, B. Strategy and Transaction in an African Factory; Manchester University Press: Manchester, UK, 1972. [Google Scholar]
- Vickers, M.; Chan, S. Representing Classroom Social Structure; Victoria Institute of Secondary Education: Melbourne, Australia, 1981. [Google Scholar]
- Coleman, J.; Katz, E.; Menzel., H. The diffusion of an innovation among physicians. Sociometry 1957, 20, 253–270. [Google Scholar] [CrossRef]
- Domenico, M.D.; Nicosia, V.; Arenas, A.; Latora, V. Structural reducibility of multilayer networks. Nat. Commun. 2015, 6, 6864. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Y.J.; Levina, E.; Zhu, J. Link Prediction for Partially Observed Networks. J. Comput. Graph. Stat. 2017, 26, 725–733. [Google Scholar] [CrossRef]


| Notations | Explanations |
|---|---|
| the set of nodes in the -th layer () | |
| the set of edges in the -th layer | |
| the layer | |
| the adjacency matrix of | |
| the target layer | |
| the i-th row of the adjacency matrix of layer | |
| the i-th column of the adjacency matrix of layer | |
| the mean value of | |
| the standard deviation of | |
| probability of potential links between node pair in the target layer |
| Network Type | Dataset | L | N | Layer Name | D | |||
|---|---|---|---|---|---|---|---|---|
| undirected | Lazega | 3 | 71 | 71 | 1 | advice | 717 | 0.298 |
| 70 | 2 | work | 378 | 0.152 | ||||
| 69 | 3 | friend | 399 | 0.161 | ||||
| C. elegans | 3 | 279 | 253 | 1 | electric | 514 | 0.013 | |
| 260 | 2 | mono | 888 | 0.023 | ||||
| 278 | 3 | poly | 1703 | 0.044 | ||||
| Kapferer | 4 | 39 | 39 | 1 | TS1 | 158 | 0.213 | |
| 39 | 2 | TS2 | 223 | 0.301 | ||||
| 35 | 3 | TI1 | 76 | 0.103 | ||||
| 37 | 4 | TI2 | 95 | 0.128 | ||||
| directed | Vicker | 3 | 29 | 29 | 1 | get on | 361 | 0.445 |
| 29 | 2 | friend | 181 | 0.223 | ||||
| 29 | 3 | co-work | 198 | 0.244 | ||||
| CKM | 3 | 245 | 215 | 1 | advice | 480 | 0.008 | |
| 231 | 2 | discussion | 565 | 0.009 | ||||
| 227 | 3 | friend | 504 | 0.008 | ||||
| Rattus | 3 | 2538 | 1948 | 1 | physical association | 2894 | 0.00052 | |
| 979 | 2 | direct interaction | 1024 | 0.00018 | ||||
| 149 | 3 | colocalization | 119 | 0.00002 |
| Type | Dataset | Layer Name | Method | RI | ||||
|---|---|---|---|---|---|---|---|---|
| LPGRI | NSILR | LPIS | NBS | LPPON | ||||
| undirected | Lazega | advice | 0.8513 | 0.8498 | 0.8417 | 0.8245 | 0.8011 | 0.18% |
| work | 0.8407 | 0.8101 | 0.7625 | 0.7983 | 0.7788 | 0.38% | ||
| friend | 0.8664 | 0.8769 | 0.8639 | 0.8245 | 0.8011 | −0.12% | ||
| C. elegans | electric | 0.8141 | 0.8522 | 0.7901 | 0.7011 | 0.7441 | −4.47% | |
| mono | 0.8880 | 0.8648 | 0.8047 | 0.7585 | 0.8139 | 2.68% | ||
| poly | 0.8527 | 0.8493 | 0.8571 | 0.8292 | 0.7952 | −0.51% | ||
| Kapferer | TS1 | 0.7922 | 0.7875 | 0.7289 | 0.7540 | 0.7212 | 0.60% | |
| TS2 | 0.7899 | 0.7786 | 0.7554 | 0.7391 | 0.7148 | 1.45% | ||
| TI1 | 0.8042 | 0.7914 | 0.7561 | 0.7096 | 0.7072 | 1.62% | ||
| TI2 | 0.8225 | 0.8225 | 0.7685 | 0.7330 | 0.7517 | 0.00% | ||
| directed | Vicker | get on | 0.8253 | 0.7755 | 0.8046 | 0.7576 | 0.7256 | 2.57% |
| friend | 0.8448 | 0.8026 | 0.8208 | 0.7585 | 0.7889 | 2.92% | ||
| co-work | 0.8906 | 0.7924 | 0.8443 | 0.7741 | 0.7926 | 5.48% | ||
| CKM | advice | 0.8225 | 0.7117 | 0.5913 | 0.6792 | 0.7006 | 15.57% | |
| discussion | 0.7816 | 0.7667 | 0.5791 | 0.6022 | 0.6848 | 1.94% | ||
| friend | 0.6897 | 0.7397 | 0.5875 | 0.5442 | 0.5971 | −6.76% | ||
| Rattus | physical association | 0.6830 | 0.5458 | 0.5464 | 0.6647 | 0.5872 | 2.75% | |
| direct interaction | 0.6702 | 0.5175 | 0.5601 | 0.6229 | 0.5923 | 7.59% | ||
| colocalization | 0.7252 | 0.5742 | 0.5938 | 0.5588 | 0.5757 | 22.13% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Tang, F.; Zhao, X. LPGRI: A Global Relevance-Based Link Prediction Approach for Multiplex Networks. Mathematics 2023, 11, 3256. https://doi.org/10.3390/math11143256
Wang C, Tang F, Zhao X. LPGRI: A Global Relevance-Based Link Prediction Approach for Multiplex Networks. Mathematics. 2023; 11(14):3256. https://doi.org/10.3390/math11143256
Chicago/Turabian StyleWang, Chunning, Fengqin Tang, and Xuejing Zhao. 2023. "LPGRI: A Global Relevance-Based Link Prediction Approach for Multiplex Networks" Mathematics 11, no. 14: 3256. https://doi.org/10.3390/math11143256
APA StyleWang, C., Tang, F., & Zhao, X. (2023). LPGRI: A Global Relevance-Based Link Prediction Approach for Multiplex Networks. Mathematics, 11(14), 3256. https://doi.org/10.3390/math11143256






