Mathematical Modeling and Analysis Using Nondimensionalization Technique of the Solidification of a Splat of Variable Section
Abstract
1. Introduction
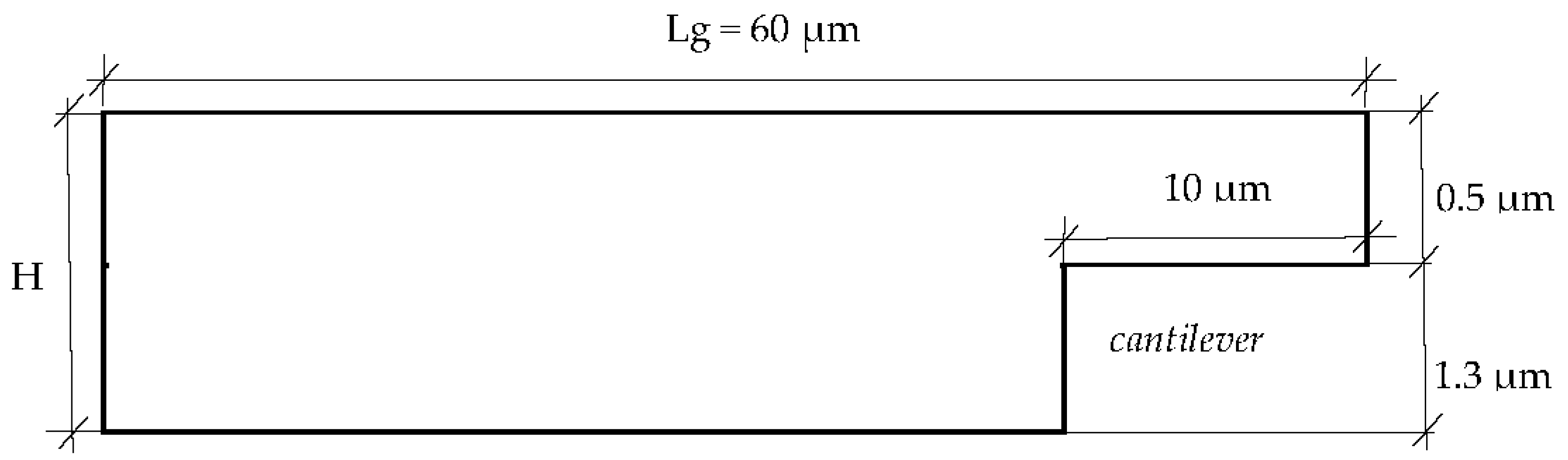
2. Splat Morphology
3. Mathematical Model
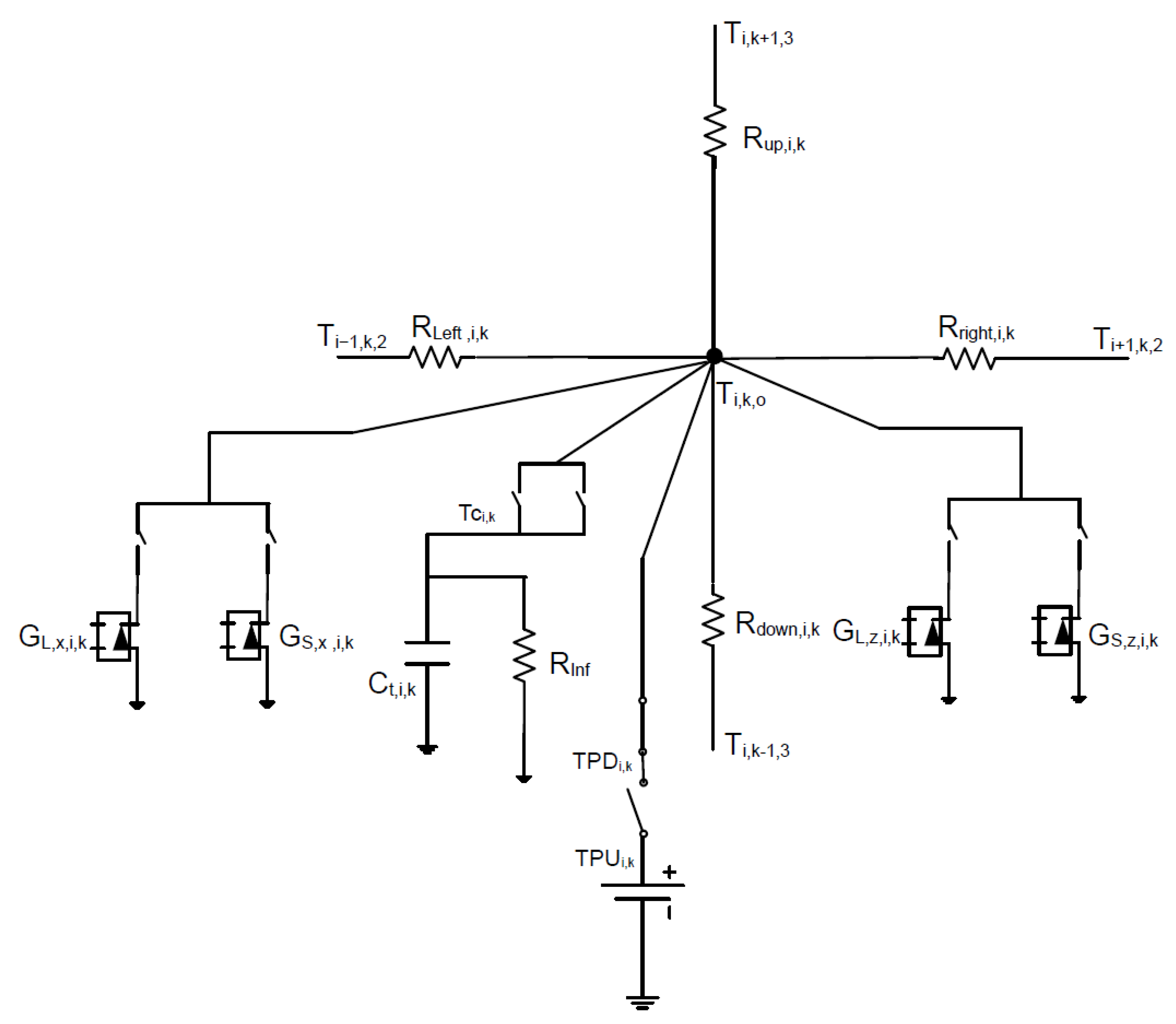
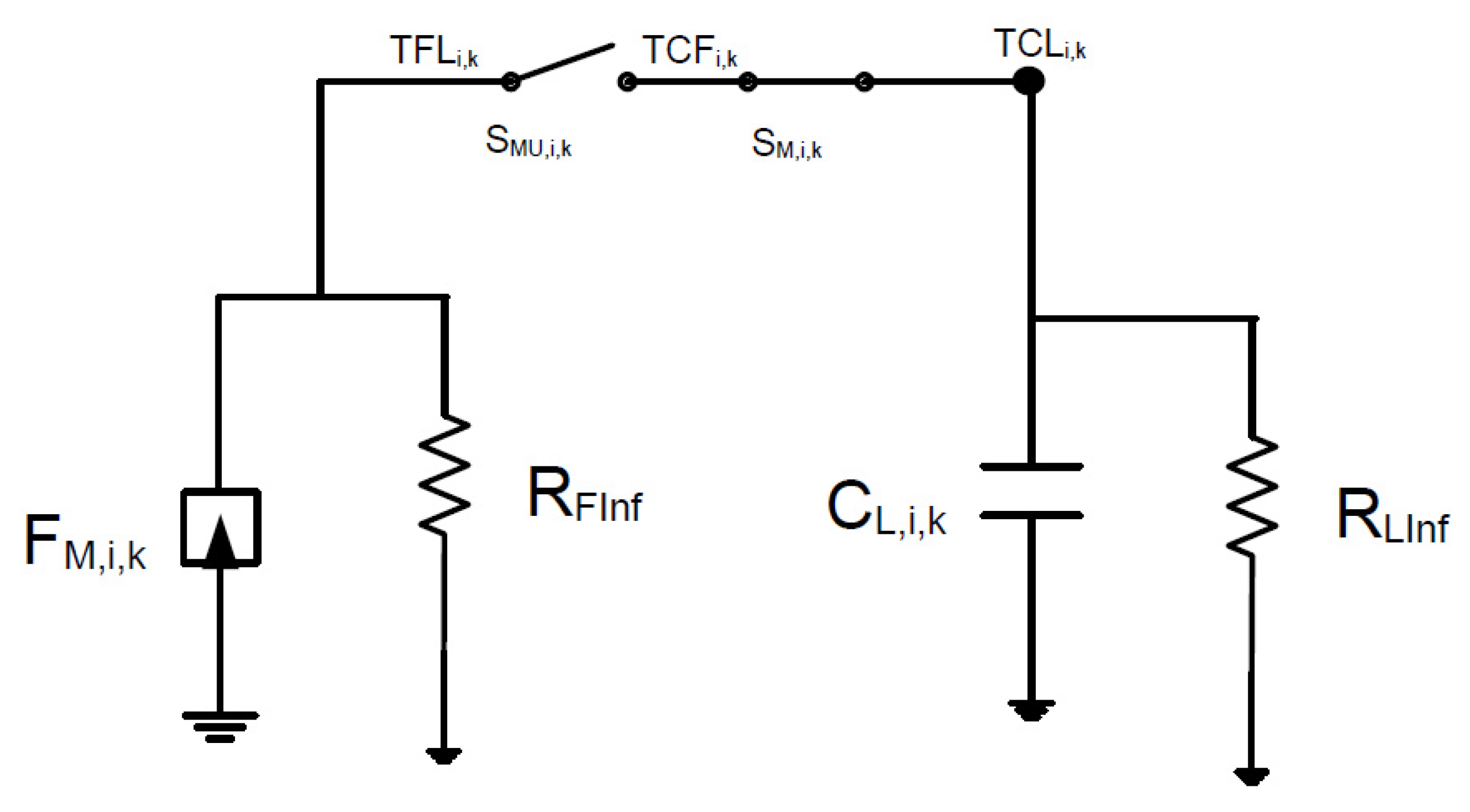
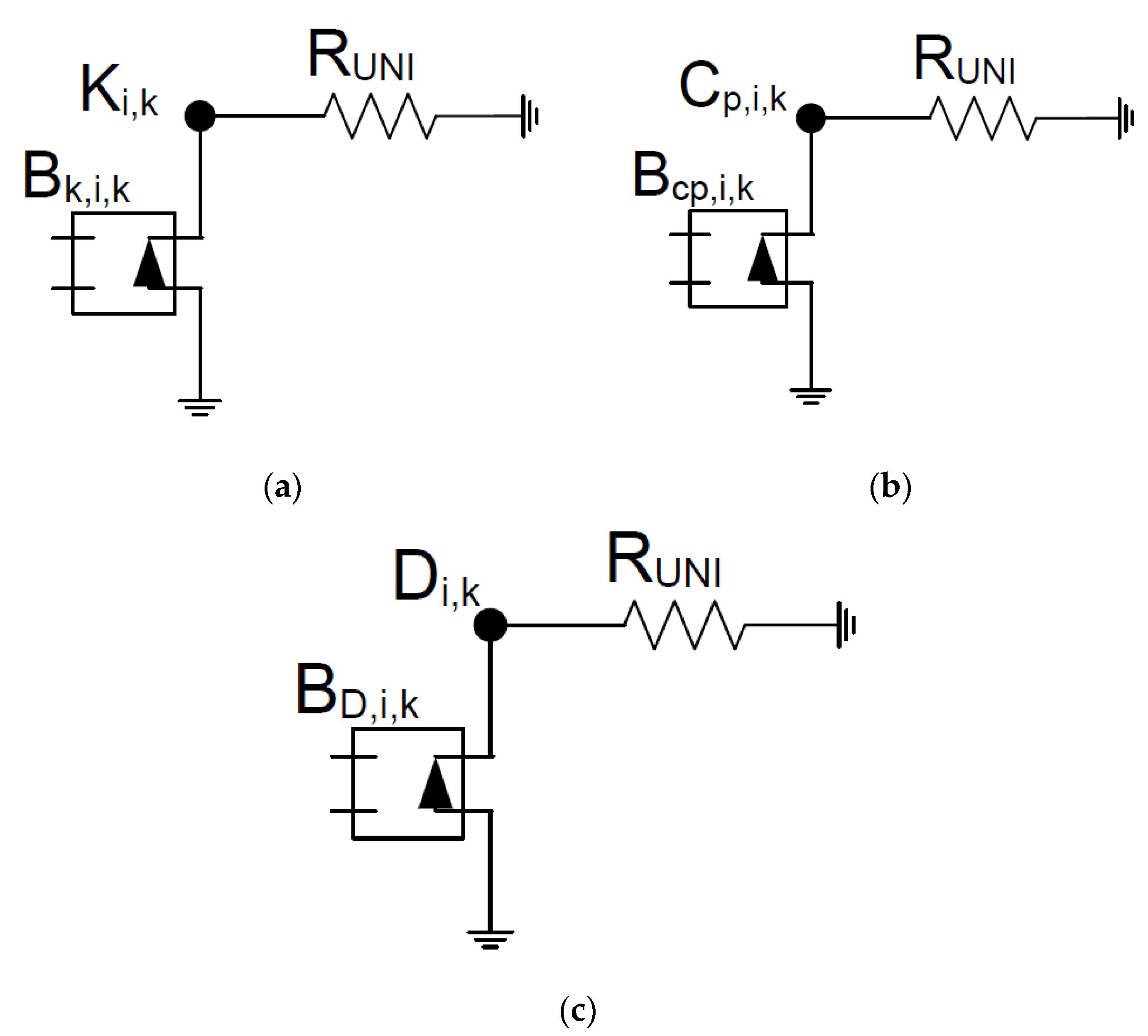
4. Network Model
- In the first place, the relationship between the voltage in the central node and the variable to be studied is established;
- Each sum of the equations is implemented by means of currents that are balanced in a central node. For this, there are different electrical devices with which to implement the addend, such as resistors, current generators, capacitors, batteries, etc.;
- The circuit created must comply with Kirchhoff’s laws.
5. Nondimensionalization
6. Material Properties
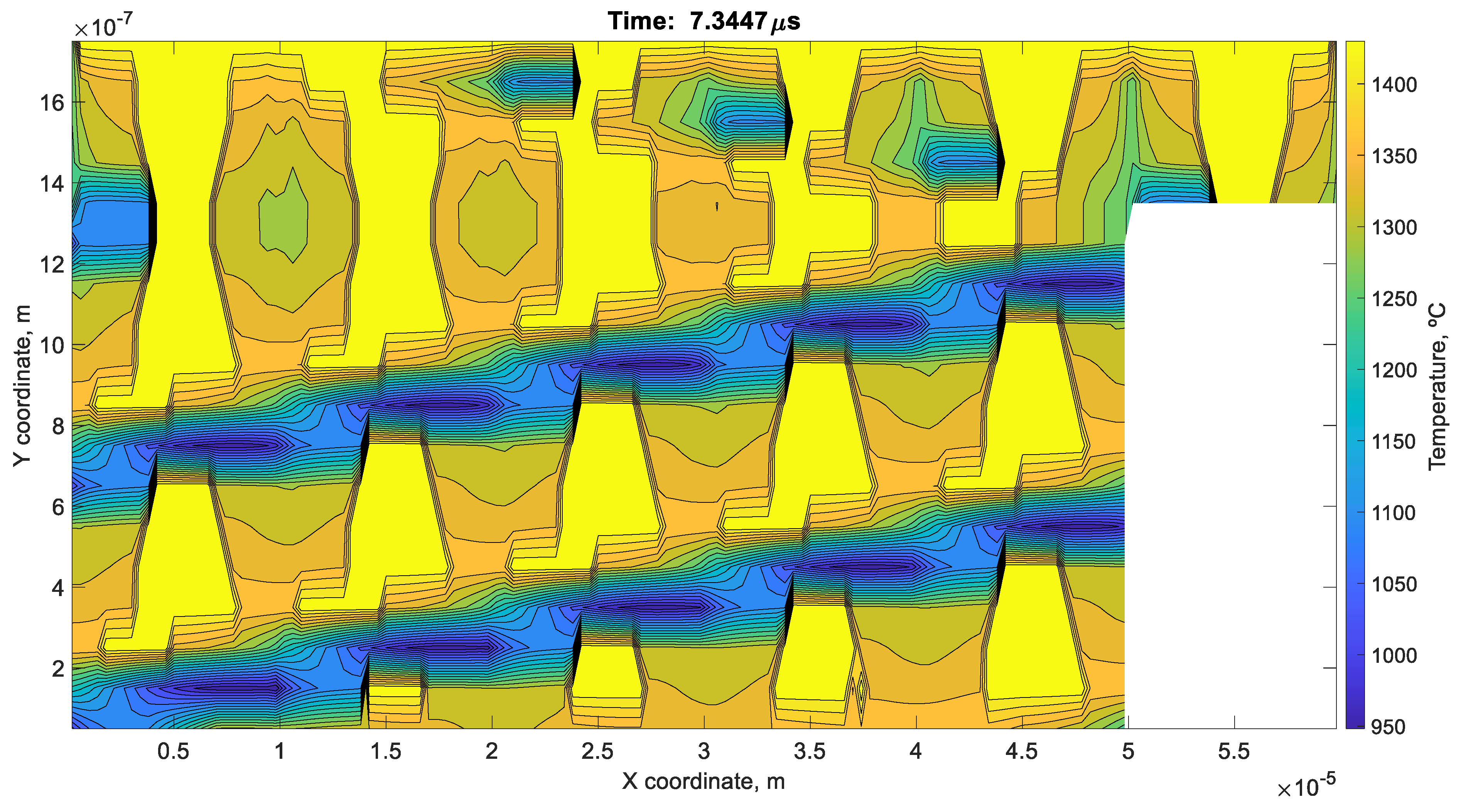
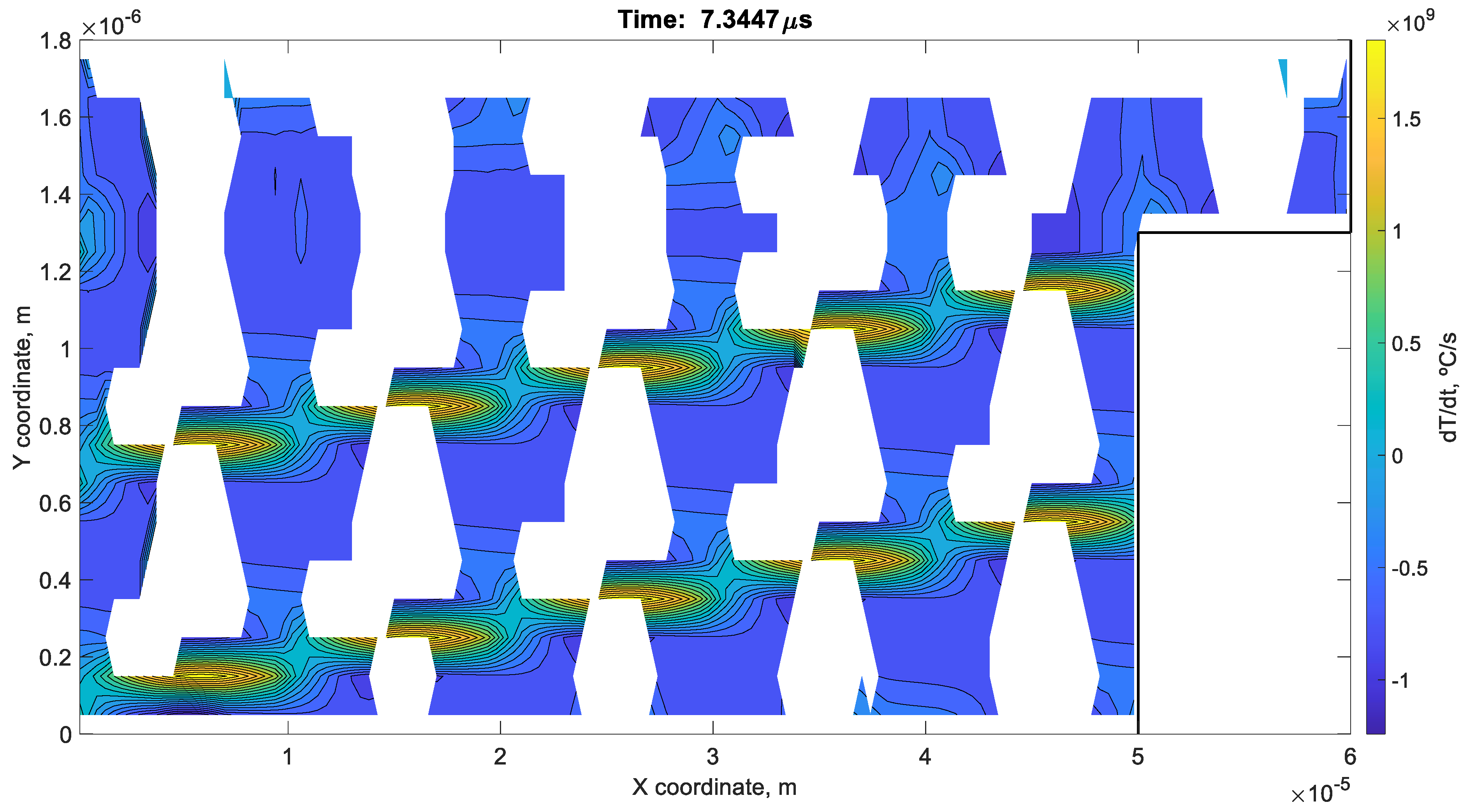
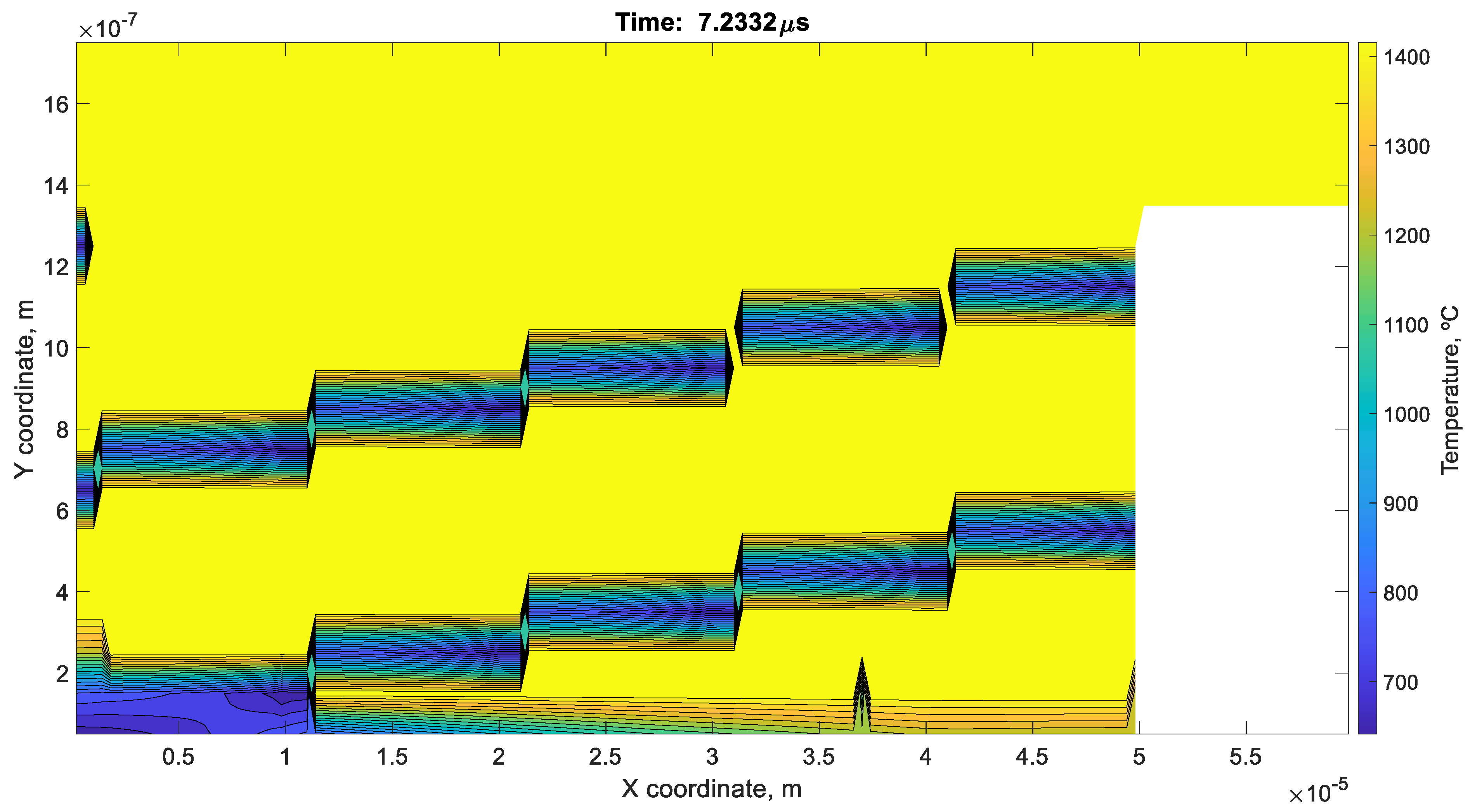
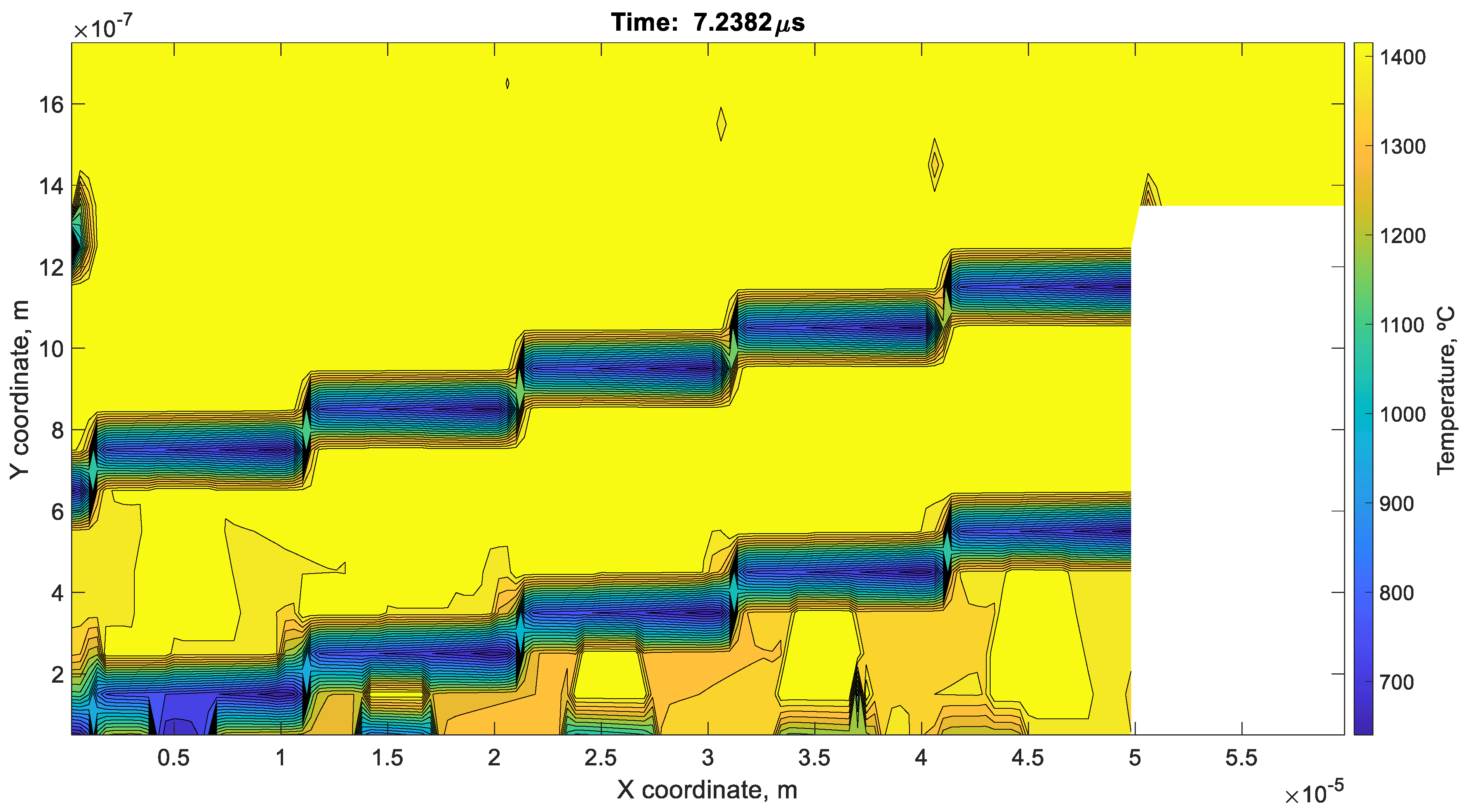
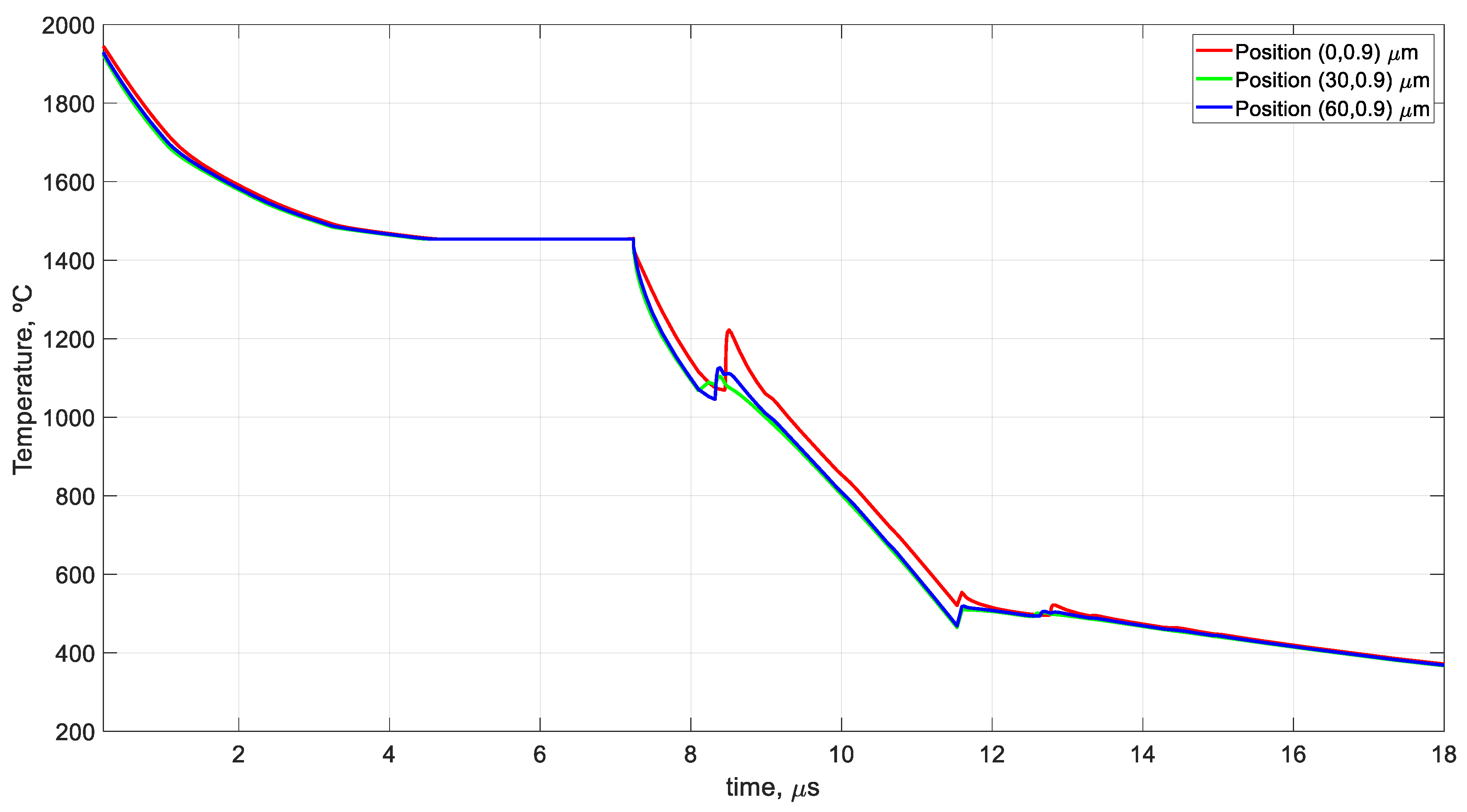
7. Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morales, N.G.; Sánchez-Pérez, J.F.; Nicolás, J.A.M.; Killinger, A. Modelling of Alumina Splat Solidification on Preheated Steel Substrate Using the Network Simulation Method. Mathematics 2020, 8, 1568. [Google Scholar] [CrossRef]
- Fauchais, P.; Vardelle, M.; Goutier, S. Atmospheric Plasma Spraying Evolution Since the Sixties through Modeling, Measurements and Sensors. Plasma Chem. Plasma Process. 2017, 37, 601–626. [Google Scholar] [CrossRef]
- Dhiman, R.; McDonald, A.G.; Chandra, S. Predicting splat morphology in a thermal spray process. Surf. Coat. Technol. 2007, 201, 7789–7801. [Google Scholar] [CrossRef]
- Chandra, S.; Fauchais, P. Formation of Solid Splats During Thermal Spray Deposition. J. Therm. Spray Technol. 2009, 18, 148–180. [Google Scholar] [CrossRef]
- Tanaka, Y.; Fukumoto, M. Investigation of dominating factors on flattening behavior of plasma sprayed ceramic particles. Surf. Coatings Technol. 1999, 120–121, 124–130. [Google Scholar] [CrossRef]
- Jiang, X.; Wan, Y.; Herman, H.; Sampath, S. Role of condensates and adsorbates on substrate surface on fragmentation of impinging molten droplets during thermal spray. Thin Solid Films 2001, 385, 132–141. [Google Scholar] [CrossRef]
- McDonald, A.; Moreau, C.; Chandra, S. Thermal contact resistance between plasma-sprayed particles and flat surfaces. Int. J. Heat Mass Transf. 2007, 50, 1737–1749. [Google Scholar] [CrossRef]
- Fukumoto, M.; Huang, Y. Flattening Mechanism in Thermal Sprayed Nickel Particle Impinging on Flat Substrate Surface. J. Therm. Spray Technol. 1999, 8, 427–432. [Google Scholar] [CrossRef]
- Pershin, V.; Lufitha, M.; Chandra, S.; Mostaghimi, J. Effect of Substrate Temperature on Adhesion Strength of Plasma-Sprayed Nickel Coatings. J. Therm. Spray Technol. 2003, 12, 370–376. [Google Scholar] [CrossRef]
- Mantry, S.; Jha, B.; Mandal, A.; Mishra, D.; Mishra, B.; Chakraborty, M. Influence of in-flight particle state diagnostics on properties of plasma sprayed YSZ-CeO2 nanocomposite coatings. Int. J. Smart Nano Mater. 2014, 5, 207–216. [Google Scholar] [CrossRef]
- Zhang, C.; Kanta, A.-F.; Li, C.-X.; Li, C.-J.; Planche, M.-P.; Liao, H.; Coddet, C. Effect of in-flight particle characteristics on the coating properties of atmospheric plasma-sprayed 8mol% Y2O3–ZrO2 electrolyte coating studying by artificial neural networks. Surf. Coat. Technol. 2009, 204, 463–469. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.J.; Liao, H.; Planche, M.P.; Li, C.X.; Coddet, C. Effect of in-flight particle velocity on the performance of plasma-sprayed YSZ electrolyte coating for solid oxide fuel cells. Surf. Coat. Technol. 2008, 202, 2654–2660. [Google Scholar] [CrossRef]
- Yin, Z.; Tao, S.; Zhou, X.; Ding, C. Particle in-flight behavior and its influence on the microstructure and mechanical properties of plasma-sprayed Al2O3 coatings. J. Eur. Ceram. Soc. 2008, 28, 1143–1148. [Google Scholar] [CrossRef]
- Syed, A.; Denoirjean, A.; Hannoyer, B.; Fauchais, P.; Denoirjean, P.; Khan, A.; Labbe, J. Influence of substrate surface conditions on the plasma sprayed ceramic and metallic particles flattening. Surf. Coat. Technol. 2005, 200, 2317–2331. [Google Scholar] [CrossRef]
- Okumus, S.C. Microstructural and mechanical characterization of plasma sprayed Al2O3–TiO2 composite ceramic coating on Mo/cast iron substrates. Mater. Lett. 2005, 59, 3214–3220. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Zheng, L.; Jiang, X. Studies of splat morphology and rapid solidification during thermal spraying. Int. J. Heat Mass Transf. 2001, 44, 4579–4592. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Pershin, V.; Chandra, S.; Mostaghimi, J. Splat Shapes in a Thermal Spray Coating Process: Simulations and Experiments. J. Therm. Spray Technol. 2002, 11, 206–217. [Google Scholar] [CrossRef]
- Robert, C.; Denoirjean, A.; Vardelle, A.; Wang, G.-X.; Sampath, S. Nucleation and Phase Selection in Plasma-Sprayed Alumina: Modeling and Experiment. In Proceedings of the International Thermal Spray Conference, Nice, France, 25–29 May 1998; pp. 407–412. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Bhola, R.; Chandra, S.; Mostaghimi, J. Deposition of tin droplets on a steel plate: Simulations and experiments. Int. J. Heat Mass Transf. 1998, 41, 2929–2945. [Google Scholar] [CrossRef]
- Fauchais, P.; Vardelle, M.; Vardelle, A.; Bianchi, L.; Léger, A.C. Parameters controlling the generation and properties of plasma sprayed zirconia coatings. Plasma Chem. Plasma Process. 1995, 16, S99–S125. [Google Scholar] [CrossRef]
- Levi, C.G.; Jayaram, V.; Valencia, J.J.; Mehrabian, R. Phase selection in electrohydrodynamic atomization of alumina. J. Mater. Res. 1988, 3, 969–983. [Google Scholar] [CrossRef]
- Wang, S.P.; Wang, G.X.; Matthys, E.F. Melting and resolidification of a substrate in contact with a molten metal: Operational maps. Int. J. Heat Mass Transf. 1998, 41, 1177–1188. [Google Scholar] [CrossRef]
- Vardelle, M.; Vardelle, A.; Fauchais, P.; Moreau, C. Pyrometer system for monitoring the particle impact on a substrate during a plasma spray process. Meas. Sci. Technol. 1994, 5, 205–212. [Google Scholar] [CrossRef]
- Allen, R.F. The role of surface tension in splashing. J. Colloid Interface Sci. 1975, 51, 350–351. [Google Scholar] [CrossRef]
- Fukumoto, M.; Suzuki, D.; Maeda, N.; Jinbo, M. The splat formation issue in thermal spray processes. WIT Trans. Eng. Sci. 2017, 116, 181–185. [Google Scholar] [CrossRef]
- Yang, E.J.; Luo, X.T.; Yang, G.J.; Li, C.X.; Li, C.J.; Takahashi, M. Epitaxial grain growth during 8YSZ splat formation on polycrystalline YSZ substrates by plasma spraying. Surf. Coat. Technol. 2015, 274, 37–43. [Google Scholar] [CrossRef]
- Pech, J.; Hannoyer, B.; Denoirjean, A.; Fauchais, P. Influence of Substrate Preheating Monitoring on Alumina Splat Formation in DC Plasma Process. In Proceedings of the International Thermal Spray Conference, Montreal, QC, Canada, 8–11 May 2000; pp. 759–765. [Google Scholar] [CrossRef]
- Espie, G.; Fauchais, P.; Hannoyer, B.; Labbe, J.C.; Vardelle, A. Effect of metal particles oxidation during the APS on the wettability. Ann. N. Y. Acad. Sci. 1999, 891, 143–151. [Google Scholar] [CrossRef]
- Pech, J.; Hannoyer, B.; Lagnoux, O.; Denoirjean, A.; Fauchais, P. Influence of preheating parameters on the plasma-jet oxidation of a low-carbon steel. High Temp. Mater. Process. 2011, 15, 51–60. [Google Scholar] [CrossRef]
- Valette, S.; Denoirjean, A.; Lefort, P.; Fauchais, P. Influence of dc plasma preheating on oxide layers formed by furnace heating on low carbon steel substrates and resulting adhesion/cohesion of alumina coatings. High Temp. Mater. Process. 2003, 7, 11–215. [Google Scholar] [CrossRef]
- Maitre, A.; Denoirjean, A.; Fauchais, P.; Lefort, P. Plasma-jet coating of preoxidized XC38 steel: Influence of the nature of the oxide layer. Phys. Chem. Chem. Phys. 2002, 4, 3887–3893. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M. Flattening of Droplets and Formation of Splats in Thermal Spraying: A Review of Recent Work—Part 2. J. Therm. Spray Technol. 1999, 8, 301–314. [Google Scholar] [CrossRef]
- Sobolev, V.V.; Guilemany, J.M. Flattening of Droplets and Formation of Splats in Thermal Spraying: A Review of Recent Work—Part 1. J. Therm. Spray Technol. 1999, 8, 87–101. [Google Scholar] [CrossRef]
- Vogt, H.; Atkinson, G.; Nenzi, P.; Warning, D.; Ngspice Contributors Team. NgSpice. 2023. Available online: https://ngspice.sourceforge.io/docs/ngspice-html-manual/manual.xhtml (accessed on 26 May 2023).
- Jin, T.; Li, F.; Peng, H.; Li, B.; Jiang, D. Uncertain barrier swaption pricing problem based on the fractional differential equation in Caputo sense. Soft Comput. 2023, 27, 11587–11602. [Google Scholar] [CrossRef]
- Dutt, N.; Hedau, A.J.; Kumar, A.; Awasthi, M.K.; Singh, V.P.; Dwivedi, G. Thermo-hydraulic performance of solar air heater having discrete D-shaped ribs as artificial roughness. Environ. Sci. Pollut. Res. 2023, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Liu, X.; Song, Y. Analysis of the Steady-Stream Active Flow Control for the Blended-Winged-Body Underwater Glider. J. Mar. Sci. Eng. 2023, 11, 1344. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I. Computation of the Exact Forms of Waves for a Set of Differential Equations Associated with the SEIR Model of Epidemics. Computation 2023, 11, 129. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, D.; Tian, C.; Jin, T.; Song, F. Adopting improved Adam optimizer to train dendritic neuron model for water quality prediction. Math. Biosci. Eng. 2023, 20, 9489–9510. [Google Scholar] [CrossRef]
- Yadav, H.; Roy, A.K.; Kumar, A. The influence of interactions between two high-rise buildings on the wind-induced moment. Asian J. Civ. Eng. 2023, 1–13. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Marin, F.; Morales, J.L.; Cánovas, M.; Alhama, F. Modeling and simulation of different and representative engineering problems using Network Simulation Method. PLoS ONE 2018, 13, e0193828. [Google Scholar] [CrossRef]
- García-Ros, G.; Alhama, I.; Cánovas, M. Use of discriminated nondimensionalization in the search of universal solutions for 2-D rectangular and cylindrical consolidation problems. Open Geosci. 2018, 10, 209–221. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Alhama, I. Universal curves for the solution of chlorides penetration in reinforced concrete, water-saturated structures with bound chloride. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105201. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; García-Ros, G.; Conesa, M.; Castro, E.; Cánovas, M. Methodology to Obtain Universal Solutions for Systems of Coupled Ordinary Differential Equations: Examples of a Continuous Flow Chemical Reactor and a Coupled Oscillator. Mathematics 2023, 11, 2303. [Google Scholar] [CrossRef]
- González, N.; Zapata, J.; Martínez, V.; Gadow, R.; García, J. Manufacturing parameter analysis for alumina coating on steel substrate by automated image processing of isolated splats samples. PLoS ONE 2020, 15, e0240928. [Google Scholar] [CrossRef]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Sánchez-Pérez, J.F.; Mascaraque-Ramírez, C.; Nicolás, J.A.M.; Castro, E.; Cánovas, M. Study of the application of PCM to thermal insulation of UUV hulls using Network Simulation Method. Alex. Eng. J. 2021, 60, 4627–4637. [Google Scholar] [CrossRef]
- Fernández, C.F.G.; Alhama, F.; Sánchez, J.F.L.; Horno, J. Application of the network method to heat conduction processes with polynomial and potential-exponentially varying thermal properties. Numer. Heat Transf. Part A Appl. 1998, 33, 549–559. [Google Scholar] [CrossRef]
- Perez, J.F.S.; Conesa, M.; Alhama, I. Solving ordinary differential equations by electrical analogy: A multidisciplinary teaching tool. Eur. J. Phys. 2016, 37, 065703. [Google Scholar] [CrossRef]
- Zueco, J.; Alhama, F.; Fernández, C.F.G. Inverse determination of heat generation sources in two-dimensional homogeneous solids: Application to orthotropic medium. Int. Commun. Heat Mass Transf. 2006, 33, 49–55. [Google Scholar] [CrossRef]
- Fernández, M.; Sánchez-Pérez, J.F.; del Cerro, F.; Conesa, M. Mathematical Model to Calculate Heat Transfer in Cylindrical Vessels with Temperature-Dependent Materials. Axioms 2023, 12, 335. [Google Scholar] [CrossRef]
- Kreith, F.; Manglik, R.M.; Bohn, M.S. Principles of Heat Transfer, SI Edition, 7th ed.; Global Engineering: Tokyo, Japan, 1999; Volume 2. [Google Scholar]
- Vuik, C. Some Historical Notes about the Stefan Problem. Unknown. 1993. Available online: https://www.researchgate.net/publication/2764813_Some_historical_notes_about_the_Stefan_problem (accessed on 29 May 2023).
- Lock, G.S.H. On the Use of Asymptotic Solutions to Plane Ice—Water Problems. J. Glaciol. 1969, 8, 285–300. [Google Scholar] [CrossRef]
- Valencia, J.J.; Quested, P.N. Thermophysical Properties, ASM Handbook; ASM: Almelle, The Netherlands, 2008; Volume 15. [Google Scholar]




| Solid Density (kg/m3) | Liquid Density (kg/m3) | Melting Temperature (°C) | Latent Heat (J/kg) | Emissivity | Heat Transfer Coefficient (W/m2K) | Initial Temperature (°C) |
|---|---|---|---|---|---|---|
| 8700 | 6853 | 1454 | 293,000 | 0.2 | 100 | 2000 |
| T (°C) | 0 | 200 | 400 | 600 | 800 | 1000 |
| Cp (J/kg·K) | 220 | 129.03 | 132.43 | 135.84 | 139.25 | 142.66 |
| T (°C) | 1200 | 1400 | 1454 | 1500 | 3000 | |
| Cp (J/kg·K) | 146.06 | 149.47 | 156.75 | 156.75 | 156.75 |
| T (°C) | 0 | 200 | 400 | 600 | 800 | 1000 |
| k (W/m2) | 70 | 70 | 70 | 70 | 70 | 70 |
| T (°C) | 1200 | 1400 | 1454 | 1500 | 3000 | |
| k (W/m2) | 70 | 70 | 60 | 60 | 60 |
| Solid Density (kg/m3) | Emissivity | Heat Transfer Coefficient (W/m2K) | Initial Temperature (°C) |
|---|---|---|---|
| 7870 | 0.3 | 100 | 27 |
| T (°C) | 0 | 200 | 400 | 600 | 800 | 1000 |
| Cp (J/kg·K) | 510 | 600 | 725 | 900 | 562 | 600 |
| T (°C) | 1200 | 1400 | 1454 | 1500 | 3000 | |
| Cp (J/kg·K) | 618 | 637 | 637 | 637 | 637 |
| T (°C) | 0 | 200 | 400 | 600 | 800 | 1000 |
| k (W/m2) | 45 | 41 | 36 | 32 | 27 | 23 |
| T (°C) | 1200 | 1400 | 1454 | 1500 | 3000 | |
| k (W/m2) | 18 | 13 | 13 | 13 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Pérez, J.F.; Jorde-Cerezo, G.; Fernández-Roiz, A.; Moreno-Nicolás, J.A. Mathematical Modeling and Analysis Using Nondimensionalization Technique of the Solidification of a Splat of Variable Section. Mathematics 2023, 11, 3174. https://doi.org/10.3390/math11143174
Sánchez-Pérez JF, Jorde-Cerezo G, Fernández-Roiz A, Moreno-Nicolás JA. Mathematical Modeling and Analysis Using Nondimensionalization Technique of the Solidification of a Splat of Variable Section. Mathematics. 2023; 11(14):3174. https://doi.org/10.3390/math11143174
Chicago/Turabian StyleSánchez-Pérez, Juan Francisco, Guillermo Jorde-Cerezo, Adrián Fernández-Roiz, and José Andrés Moreno-Nicolás. 2023. "Mathematical Modeling and Analysis Using Nondimensionalization Technique of the Solidification of a Splat of Variable Section" Mathematics 11, no. 14: 3174. https://doi.org/10.3390/math11143174
APA StyleSánchez-Pérez, J. F., Jorde-Cerezo, G., Fernández-Roiz, A., & Moreno-Nicolás, J. A. (2023). Mathematical Modeling and Analysis Using Nondimensionalization Technique of the Solidification of a Splat of Variable Section. Mathematics, 11(14), 3174. https://doi.org/10.3390/math11143174








