Properties of GA-h-Convex Functions in Connection to the Hermite–Hadamard–Fejér-Type Inequalities

Abstract

In this study, the Hermite–Hadamard–Fejér inequalities for $GA$-h-convex are proved, and the results for particular classes of functions are highlighted. In addition, several generalizations of the Hermite–Hadamard inequalities are presented. Some features of functions $\mathcal{H}$ and $\mathcal{F}$ that are naturally linked to the Hermite–Hadamard–Fejér-type inequalities for $GA$-h-convex have also been discussed. Finally, we obtain applications of the results related to the p-logarithmic mean and the mean of order p.

1. Introduction

The subject of mathematical inequalities has become a very important topic due to its rich geometrical interpretations and a number of applications in diverse areas of the mathematical, physical, engineering, and statistical sciences. Mathematicians have obtained novel results in the field of mathematical inequalities and used them in solving problems in differential equations, optimization problems, numerical quadrature rules, and probability theory. The following definition of convex functions has an important role in establishing a number of novel results in the theory of inequalities.

Definition 1.

Let $\mathcal{K}$ be an interval of real numbers. The function $\phi :\mathcal{K}\to \mathcal{R}$ is said to be convex on $\mathcal{K}$ if, for all $\sigma ,\nu \in \mathcal{K}$, and $\vartheta \in [0,1]$, one has the inequality:

$$\phi (\vartheta \sigma +(1-\vartheta \left)\nu \right)\le \vartheta \phi \left(\sigma \right)+(1-\vartheta )\phi \left(\nu \right)$$

Let $\phi :\mathcal{K}\subseteq \mathcal{R}\to \mathcal{R}$ be a convex function and ${\kappa }_1,{\kappa }_2\in \mathcal{K}$ with ${\kappa }_1<{\kappa }_2$. Then the following double inequality [1,2]:

$$\phi \left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)\le \frac{1}{{\kappa }_2-{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\phi \left(\sigma \right)d\sigma \le \frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{2}.$$

(1)

holds for convex mapping, this is known as Hermite–Hadamard inequality. If $\phi$ is a concave function, the inequalities in (1) apply in reverse. The inequalities (1) have a number of extensions and generalizations. The interested reader is encouraged to see the references [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40] and the studies mentioned in them for a variety of results related to (1). In [41], Hudzik and Maligranda considered that some properties of two classes of s-convex real valued functions already exist in the literature.

Definition 2

([41]). A function $\phi :[0,\infty )\to \mathcal{R}$ is said to be s-convex in the first sense if

$$\phi (\vartheta \sigma +(1-\vartheta )\nu )\le {\vartheta }^s\phi \left(\sigma \right)+(1-{\vartheta }^s)\phi \left(\nu \right)$$

for all $\sigma ,\nu \in [0,\infty )$ and all $\vartheta \in [0,1]$. The class $K_s^1$ contains all the s-convex in the first.

Definition 3

([41]). A function $\phi :[0,\infty )\to \mathcal{R}$ is said to be s-convex in the second sense if

$$\phi (\vartheta \sigma +(1-\vartheta )\nu )\le {\vartheta }^s\phi \left(\sigma \right)+{(1-\vartheta )}^s\phi \left(\nu \right)$$

for all $\sigma ,\nu \in [0,\infty )$ and all $\vartheta \in [0,1]$. The class $K_s^2$ contains all the s-convex in the second.

Remark 1.

It is clear that s-convexity in the first sense and second sense means just the convexity when $s=1$.

Dragomir and Fitzpatrick demonstrated in [42] the following form of Hermite–Hadamard’s inequality for s-convex functions in the second sense:

Theorem 1

([42]). For an s-convex function in the second sense $\phi :[0,\infty )\to [0,\infty )$, where $s\in (0,1)$, and let ${\kappa }_1,{\kappa }_2\in [0,\infty )$, ${\kappa }_1<{\kappa }_2$. If $\phi \in {\mathcal{L}}_1\left([{\kappa }_1,{\kappa }_2]\right)$, the following inequalities hold:

$$2^{s-1}\phi \left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)\le \frac{1}{{\kappa }_2-{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\phi \left(\sigma \right)d\sigma \le \frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{s+1}$$

(2)

The constant $\frac{1}{s+1}$ is the best possible in the second inequality in (2).

Varošanec investigated a broader family of non-negative functions known as h-convex functions in his study [43]. This class includes well-known functions, such as non-negative convex functions, s-convex in the second sense, Godunova–Levin functions, and P-functions.

Definition 4

([43]). A function $\phi :\mathcal{K}\subseteq \mathcal{R}\to \mathcal{R}$ is said to be h-convex, or φ is said to belong to the class $SX(h,\mathcal{K})$, if φ is non-negative and

$$\phi (\vartheta \sigma +(1-\vartheta \left)\nu \right)\le h\left(\vartheta \right)\phi \left(\sigma \right)+h(1-\vartheta )\phi \left(\nu \right)$$

for all $\sigma ,\nu \in \mathcal{K}$ and $\vartheta \in (0,1)$ we have, where $h:\mathcal{J}\subseteq \mathcal{R}\to \mathcal{R}$, $(0,1)\subseteq \mathcal{J}$ is a positive function. In any case, if the inequality is everted, the function φ is claimed to be h-concave and we say that φ belongs to the class $SV(h,\mathcal{K})$.

Fejér [44] established the following double inequality as a weighted generalization of (1):

$$\begin{array}{c}\hfill \phi \left(\frac{{\kappa }_1+{\kappa }_2}{2}\right){\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}w\left(\sigma \right)d\sigma \le {\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\phi \left(\sigma \right)w\left(\sigma \right)d\sigma \le \frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}w\left(\sigma \right)d\sigma ,\end{array}$$

(3)

where $\phi :\mathcal{K}⟶\mathcal{R},$ $Ø\ne \mathcal{K}\subseteq \mathcal{R}$, ${\kappa }_1,{\kappa }_2\in \mathcal{K}$ with ${\kappa }_1<{\kappa }_2$ is any convex function and $w:\left[{\kappa }_1,{\kappa }_2\right]\to \mathcal{R}$ is non-negative integrable and symmetric about $\sigma =\frac{{\kappa }_1+{\kappa }_2}{2}$.

In [45], Bombardelli and Varošanec showed that extending the class of convex functions to the class of h-convex functions has no effect on the features associated with the integral mean of the function f. The authors also demonstrated Hermite–Hadamard–Fejér inequality for an h-convex function and, in some situations, other kinds of functions, such as convex and s-convex functions. In this study, it was also discovered that the left-hand side of the inequality in their finding is stronger than the right-hand side of the inequality in that result. This research also includes various features of functions:

$$H\left(\tau \right)=\frac{1}{{\kappa }_2-{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\phi \left(\tau \sigma +\left(1-\tau \right)\frac{{\kappa }_1+{\kappa }_2}{2}\right)d\sigma$$

and

$$F\left(\tau \right)=\frac{1}{{\left({\kappa }_2-{\kappa }_1\right)}^2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\phi \left(\tau \sigma +\left(1-\tau \right)\nu \right)d\nu d\sigma$$

that arise when the function $\phi$ is an h-convex function.

We recall that notable generalizations of the convex functions are geometrically arithmetically convex functions also known GA-convex functions stated below:

Definition 5

([46]). A function $\phi :$$\mathcal{K}\subseteq \left(0,\infty \right)\to \mathcal{R}$ is considered to be GA-convex if

$$\phi \left({\sigma }^{\vartheta }{\nu }^{1-\vartheta }\right)\le \vartheta \phi \left(\sigma \right)+\left(1-\vartheta \right)\phi \left(\nu \right)$$

(4)

for all $\sigma ,\nu \in \mathcal{K}$ and $\vartheta \in \left(0,1\right)$. The function $\phi :$$\mathcal{K}\to \mathcal{R}$ is $GA$-concave if the inequality in (4) reversed.

We state some key facts about $GA$-convex and convex functions and utilize them to demonstrate the essential points.

Theorem 2

([46]). Let $h:\mathcal{J}\subseteq \mathcal{R}\to \mathcal{R}$, where $(0,1)\subseteq \mathcal{J}$, be a positive function. If $[{\kappa }_1,{\kappa }_2]\subset (0,\infty )$ and the function $\mathcal{G}:[ln{\kappa }_1,ln{\kappa }_2]\to \mathcal{R}$ is convex (concave) on $[ln{\kappa }_1,ln{\kappa }_2]$, then the function $\phi :[{\kappa }_1,{\kappa }_2]\to \mathcal{R},\phi \left(\tau \right)=\mathcal{G}(ln\tau )$ is $GA$-convex ($GA$-concave) on $[{\kappa }_1,{\kappa }_2]$.

Theorem 2 can easily be generalized as follows:

Theorem 3.

If $[{\kappa }_1,{\kappa }_2]\subset (0,\infty )$ and the function $\mathcal{G}:[ln{\kappa }_1,ln{\kappa }_2]\to \mathcal{R}$ is h-convex (h-concave) on $[ln{\kappa }_1,ln{\kappa }_2]$, then the function $\phi :[{\kappa }_1,{\kappa }_2]\to \mathcal{R},\phi \left(\tau \right)=\mathcal{G}(ln\tau )$ is $GA$-h-convex ($GA$-h-concave) on $[{\kappa }_1,{\kappa }_2]$.

Remark 2

([46]). It is obvious from Theorem 2 that if $\phi :[{\kappa }_1,{\kappa }_2]\to \mathcal{R}$ is GA-convex on $[{\kappa }_1,{\kappa }_2]\subset (0,\infty )$, then $\phi \circ exp$ is convex on $[ln{\kappa }_1,ln{\kappa }_2]$. It follows that $\phi \circ exp$ has finite lateral derivatives on $(ln{\kappa }_1,ln{\kappa }_2)$, and by gradient inequality for convex functions, we have

$$\phi \circ exp\left(\sigma \right)-\phi \circ exp\left(\nu \right)(\sigma -\nu )\ge \phi (exp\nu )exp\left(\nu \right),$$

where $\phi (exp\nu )\in \left[{\phi }_{-}^{{}^{\prime }}\left(exp\nu \right),{\phi }_{+}^{{}^{\prime }}\left(exp\nu \right)\right]$ for any $\sigma ,\nu \in \left(ln{\kappa }_1,ln{\kappa }_2\right)$.

With regard to $GA$-convex functions, the following inequality of Hermite–Hadamard type is true (for an extension to $GA$-h-convex functions, see [47]):

Theorem 4

([47]). Let $\phi :\mathcal{K}\subseteq \left(0,\infty \right)\to \mathcal{R}$ be a $GA$-convex function and ${\kappa }_1,{\kappa }_2\in \mathcal{K}$ with ${\kappa }_1<{\kappa }_2$. If $\phi \in \mathcal{L}\left(\left[{\kappa }_1,{\kappa }_2\right]\right)$, then the following inequalities hold:

$$\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le \frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \le \frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{2}.$$

(5)

The notion of geometrically symmetric functions was proposed in [48].

Definition 6

([48]). A function $w:\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)\to \mathcal{R}$ is geometrically symmetric with respect to $\left(0,\infty \right)$ if

$$w\left(\sigma \right)=w\left(\frac{{\kappa }_1{\kappa }_2}{\sigma }\right)$$

holds for all $\sigma \in \left[{\kappa }_1,{\kappa }_2\right]$.

Fejér-type inequalities using GA-convex functions using geometric symmetric functions were presented in Latif et al. [48].

Theorem 5

([48]). Let $\phi :\mathcal{K}\subseteq \left(0,\infty \right)\to \mathcal{R}$ be a $GA$-convex function and ${\kappa }_1,{\kappa }_2\in \mathcal{K}$ with ${\kappa }_1<{\kappa }_2$. If $\phi \in \mathcal{L}\left(\left[{\kappa }_1,{\kappa }_2\right]\right)$ and $w:\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)\to \mathcal{R}$ is non-negative, integrable, and geometrically symmetric with respect to $\sqrt{{\kappa }_1{\kappa }_2}$, then

$$\begin{array}{c}\hfill \phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right){\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma \le {\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma \le \frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma .\end{array}$$

(6)

A wider class of $GA$-convex functions known as the class of $GA$-h-convex functions was taken into account by Noor et al. [47]. Numerous functional classes, including non-negative GA-convex functions, $GA$-s-convex in the second sense, $GA$-Godunova-Levin functions, and $GA$-P-functions, are included in this class.

Definition 7.

Let $h:\left[0,1\right]\to \left[0,\infty \right)$ be a non-negative function. A function $\phi :$$\mathcal{K}\subseteq \left(0,\infty \right)\to \mathcal{R}$ is said to be $GA$-h-convex if

$$\phi \left({\sigma }^{\vartheta }{\nu }^{1-\vartheta }\right)\le h\left(\vartheta \right)\phi \left(\sigma \right)+h\left(1-\vartheta \right)\phi \left(\nu \right)$$

(7)

for all $\sigma ,\nu \in \mathcal{K}$ and $\vartheta \in \left(0,1\right)$. The function $\phi :$$\mathcal{K}\to \mathcal{R}$ is $GA$-h-concave if the inequality in (7) reversed.

The interested readers are referred to [47] for integral inequalities for the class of $GA$-h-convex functions.

The main motivation of this research is the study conducted by Bombardelli and Varošanec [45]. In the next section, we will prove that there will be no change in the properties of $\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma$ if the class of $GA$-convex functions is extended to the class of $GA$-h-convex functions. We will also show Hermite–Hadamard–Fejér-type inequalities for a $GA$-h-convex function and discuss some particular cases for other kinds of functions, such as $GA$-convex and $GA$-s-convex functions. In this paper, we will show that the left-hand side of the Hermite–Hadamard-type inequalities is stronger than the right-hand side of the inequalities shown in [47] for $GA$-h-convex functions. Lastly, some properties of the mappings $\mathcal{H},\mathcal{F}:[0,1]\to \mathcal{R}$ can be defined by

$$\mathcal{H}\left(\tau \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma }\phi \left({\sigma }^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }\right)d\sigma ,$$

$$\mathcal{F}\left(\tau \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left({\sigma }^{\tau }{\nu }^{1-\tau }\right)d\sigma d\nu ,$$

where $\phi :\mathcal{K}\subseteq (0,\infty )\to \mathcal{R}$ is $GA$-convex on $\mathcal{K}$ and ${\kappa }_1,{\kappa }_2\in \mathcal{K}$ will be observed as well.

2. The Hermite–Hadamard–Fejér Inequalities for a $\mathbf{GA}$-$\mathbf{h}$-Convex Function

We begin this section with the following Hermite–Hadamard–Fejér inequality for a $GA$-h-convex function.

Theorem 6.

Let $\phi :$$\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)\to \mathcal{R}$ be a $GA$-h-convex function and $w:\left[{\kappa }_1,{\kappa }_2\right]\to \mathcal{R}$ be non-negative, integrable, and symmetric with respect to $\sqrt{{\kappa }_1{\kappa }_2}$. Then

$$\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma \le \left[\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)\right]{\mathit{\int }}_0^{1}h\left(\tau \right)w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)d\tau .$$

(8)

If $\phi :$$\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)\to \mathcal{R}$ is a $GA$-h-concave function, then the inequality in (8) is reversed.

Proof. 

For $\sigma \in \left({\kappa }_1,{\kappa }_2\right)$, there exists $\vartheta \in \left(0,1\right)$ such that $\sigma ={\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }$, where $\vartheta =1-\vartheta$. Since $\phi$ is a $GA$-h-convex function, we have

$$\phi \left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)\le \left[h\left(\vartheta \right)\phi \left({\kappa }_1\right)+h\left(\vartheta \right)\phi \left({\kappa }_2\right)\right]w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)$$

(9)

and

$$\phi \left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)\le \left[h\left(\vartheta \right)\phi \left({\kappa }_1\right)+h\left(\vartheta \right)\phi \left({\kappa }_2\right)\right]w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right).$$

(10)

Adding (9) and (10) and integrating with respect to $\vartheta$ over the interval $\left[0,1\right]$, we obtain

$$\begin{array}{c}{\mathit{\int }}_0^1\phi \left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)d\vartheta +{\mathit{\int }}_0^1\phi \left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)d\vartheta \hfill \\ \le \phi \left({\kappa }_1\right){\mathit{\int }}_0^{1}h\left(\vartheta \right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)d\vartheta +\phi \left({\kappa }_1\right){\mathit{\int }}_0^{1}h\left(\vartheta \right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)d\vartheta \\ \hfill +\phi \left({\kappa }_2\right){\mathit{\int }}_0^{1}h\left(\vartheta \right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)d\vartheta +\phi \left({\kappa }_2\right){\mathit{\int }}_0^{1}h\left(\vartheta \right)w\left({\kappa }_1^{\vartheta }{\kappa }_2^{\vartheta }\right)d\vartheta .\end{array}$$

(11)

By making use of the substitution $\vartheta =\tau$ in (11) and using the assumption that w is symmetric with respect to $\sqrt{{\kappa }_1{\kappa }_2}$, we have

$$\begin{array}{c}{\mathit{\int }}_0^1\phi \left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)w\left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)d\tau +{\mathit{\int }}_0^1\phi \left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)d\tau \hfill \\ \le 2\phi \left({\kappa }_1\right){\mathit{\int }}_0^{1}h\left(\tau \right)w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)d\tau +2\phi \left({\kappa }_2\right){\mathit{\int }}_0^{1}h\left(\tau \right)w\left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)d\tau \\ =2\left[\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)\right]{\mathit{\int }}_0^{1}h\left(\tau \right)w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)d\tau .\hfill \end{array}$$

(12)

By using the change of variable techniques, we observe that each integral on the right-hand side of (12) is equal to $\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma$. Hence, the theorem is established.   □

Remark 3.

If in Theorem 6

(i) 

The function φ is convex, that is, if $h\left(\tau \right)=\tau$, then

$${\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma \le \left[\frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{ln{\kappa }_2-ln{\kappa }_1}\right]{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}ln\left(\frac{{\kappa }_2}{\sigma }\right)\frac{w\left(\sigma \right)}{\sigma }d\sigma .$$

(13)

(ii) 

The function φ is s-convex, that is, if $h\left(\tau \right)={\tau }^s$, $s\in \left(0,1\right)$, then

$${\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma \le \left[\frac{\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)}{ln{\kappa }_2-ln{\kappa }_1}\right]{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\left[ln\left(\frac{{\kappa }_2}{\sigma }\right)\right]}^s\frac{w\left(\sigma \right)}{\sigma }d\sigma .$$

(14)

Theorem 7.

Let h be defined over the interval $\left[1,max\left\{1,\frac{{\kappa }_2}{{\kappa }_1}\right\}\right]$ and $\phi :$$\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)\to \mathcal{R}$ be a $GA$-h-convex function and $w:\left[{\kappa }_1,{\kappa }_2\right]\to \mathcal{R}$ be non-negative, integrable, and symmetric with respect to $\sqrt{{\kappa }_1{\kappa }_2}$ with ${\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\tau \right)}{\tau }d\tau >0$. Then

$$\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le \mathcal{C}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma ,$$

(15)

where $\mathcal{C}=\frac{2h\left(\frac{1}{2}\right)}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma }.$

Furthermore, if ${\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{h\left(ln\nu -ln\sigma \right)w\left(\nu \right)w\left(\sigma \right)}{\sigma \nu }d\nu d\sigma \ne 0$, $h\left(\sigma \right)\ne 0$ for $\sigma \ne 0$ and

(i) 

If h is multiplicative or

(ii) 

If h is supermultiplicative and φ is non-negative

and if φ is a $GA$-h-convex function, then inequality (15) holds for

$$\mathcal{C}=min\left\{\frac{2h\left(\frac{1}{2}\right)}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma },\frac{{\mathit{\int }}_1^{\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}}\frac{h\left(ln\sigma \right)w\left(\sigma \sqrt{{\kappa }_1{\kappa }_2}\right)}{\sigma }d\sigma }{{\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{h\left(ln\nu -ln\sigma \right)w\left(\nu \right)w\left(\sigma \right)}{\sigma \nu }d\nu d\sigma }\right\}.$$

Proof. 

Since $\phi$ is a $GA$-h-convex function, then for $\vartheta =\frac{1}{2}$, $\sigma ={\kappa }_1^{\tau }{\kappa }_2^{1-\tau }$, and $\sigma ={\kappa }_1^{1-\tau }{\kappa }_2^{\tau }$, from the definition of a $GA$-h-convex function, we have the following inequality:

$$\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le h\left(\frac{1}{2}\right)\left[\phi \left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)+\phi \left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)\right].$$

Now we multiply it by $w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)=w\left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)$ and integrate with respect to $\tau$ over $\left[0,1\right]$ to obtain

$$\begin{array}{c}\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right){\mathit{\int }}_0^{1}w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)d\tau \hfill \\ \le h\left(\frac{1}{2}\right)\left[{\mathit{\int }}_0^1\phi \left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)w\left({\kappa }_1^{\tau }{\kappa }_2^{1-\tau }\right)d\tau \right.\\ \left.+{\mathit{\int }}_0^1\phi \left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)w\left({\kappa }_1^{1-\tau }{\kappa }_2^{\tau }\right)d\tau \right].\hfill \end{array}$$

(16)

Making a suitable substitution, we get that

$$\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le \frac{2h\left(\frac{1}{2}\right)}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma }{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma .$$

The equality (15) is thus established.

We observe due to the h-convexity $\phi \circ exp$ that

$$\begin{array}{cc}\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\hfill & =\phi \circ exp\left(ln\left(\sqrt{{\kappa }_1{\kappa }_2}\right)\right)\hfill \\ & =\phi \circ exp\left(\left(\frac{ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}}{ln\nu -ln\sigma }\right)ln\sigma +\left(\frac{\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma }{ln\nu -ln\sigma }\right)ln\nu \right)\hfill \\ & \le h\left(\frac{ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}}{ln\nu -ln\sigma }\right)\phi \circ exp\left(ln\sigma \right)+h\left(\frac{\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma }{ln\nu -ln\sigma }\right)\phi \circ exp\left(\nu \right)\hfill \\ & =h\left(\frac{ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}}{ln\nu -ln\sigma }\right)\phi \left(\sigma \right)+h\left(\frac{\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma }{ln\nu -ln\sigma }\right)\phi \left(\nu \right).\hfill \end{array}$$

(17)

Let $\vartheta =\frac{ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}}{ln\nu -ln\sigma }$ and $\vartheta =1-\vartheta =\frac{\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma }{ln\nu -ln\sigma }$l; hence, (17) takes the form

$$\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le h\left(\vartheta \right)\phi \left(\sigma \right)+h\left(\vartheta \right)\phi \left(\nu \right).$$

(18)

Since h is supermultiplicative, we have

$$h\left(\vartheta \right)=h\left(\frac{ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}}{ln\nu -ln\sigma }\right)\le \frac{h\left(ln\sigma -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)}{h\left(ln\nu -ln\sigma \right)}$$

and

$$h\left(\vartheta \right)=h\left(\frac{\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma }{ln\nu -ln\sigma }\right)\le \frac{h\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma \right)}{h\left(ln\nu -ln\sigma \right)}.$$

Thus, from (18), we have

$$\begin{array}{c}h\left(ln\nu -ln\sigma \right)\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\hfill \\ \le h\left(ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\phi \left(\sigma \right)+h\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma \right)\phi \left(\nu \right).\hfill \end{array}$$

(19)

Multiplying (19) with $\frac{w\left(\sigma \right)}{\sigma }$ and integrating over interval $\left[{\kappa }_1,\sqrt{{\kappa }_1{\kappa }_2}\right]$ with respect to $\sigma$ and then multiplying with $\frac{w\left(\nu \right)}{\nu }$ and integrating over interval $\left[\sqrt{{\kappa }_1{\kappa }_2},{\kappa }_2\right]$ with respect to $\nu$, we have

$$\begin{array}{c}\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right){\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}h\left(ln\nu -ln\sigma \right)d\nu d\sigma \hfill \\ \le {\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma {\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}h\left(ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\frac{w\left(\nu \right)}{\nu }d\nu \hfill \\ +{\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}h\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma \right)\frac{w\left(\sigma \right)}{\sigma }d\sigma {\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{\phi \left(\nu \right)w\left(\nu \right)}{\nu }d\nu .\hfill \end{array}$$

(20)

Substituting $ln\tau =ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}$ in the first integral and substituting $ln\tau =\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma$ in the second integral on the right-hand side of (20), we have

$$\begin{array}{l}\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right){\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}h\left(ln\nu -ln\sigma \right)d\nu d\sigma \\ \le {\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma {\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}h\left(ln\nu -\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\frac{w\left(\nu \right)}{\nu }d\nu \\ +{\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}h\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}-ln\sigma \right)\frac{w\left(\sigma \right)}{\sigma }d\sigma {\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\phi \left(\nu \right)\frac{w\left(\nu \right)}{\nu }d\nu \\ ={\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma {\mathit{\int }}_1^{\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}}h\left(ln\tau \right)\frac{w\left(\tau \sqrt{{\kappa }_1{\kappa }_2}\right)}{\tau }d\tau \\ +{\mathit{\int }}_1^{\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}}h\left(ln\tau \right)w\left(\frac{\sqrt{{\kappa }_1{\kappa }_2}}{\tau }\right)\frac{d\tau }{\tau }{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma .\end{array}$$

(21)

Since the mapping w is geometrically symmetric with respect to $\sqrt{{\kappa }_1{\kappa }_2}$, $w\left(\frac{\sqrt{{\kappa }_1{\kappa }_2}}{\tau }\right)=w\left(\tau \sqrt{{\kappa }_1{\kappa }_2}\right)$ for all $\tau \in \left[1,\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}\right]$. Thus, from (21), we have

$$\begin{array}{c}\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right){\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}h\left(ln\nu -ln\sigma \right)d\nu d\sigma \hfill \\ \le {\mathit{\int }}_1^{\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}}h\left(ln\tau \right)\frac{w\left(\tau \sqrt{{\kappa }_1{\kappa }_2}\right)}{\tau }d\tau {\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)w\left(\sigma \right)}{\sigma }d\sigma .\hfill \end{array}$$

Hence, (15) is established.   □

Remark 4.

Suppose that the conditions of Theorem 7 are satisfied and

(i) 

If φ is a $GA$-h-concave function, then the inequality in (15) is reversed.

(ii) 

If h is submultiplicative with ${\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}h\left(ln\nu -ln\sigma \right)w\left(\nu \right)w\left(\sigma \right)d\nu d\sigma \ne 0$, $h>0$, and if φ is a $GA$-h-concave function, then the inequality in (15) is reversed with constant $\mathcal{C}$ as given in Theorem 7 by changing min to max.

Remark 5.

In Theorem 7,

(a) 

If φ is $GA$-convex, i.e., $h\left(\tau \right)=\tau$, then inequality (15) holds for $\mathcal{C}=\frac{1}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\tau \right)}{\tau }d\tau }$.

Furthermore, if ${\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{\left(ln\nu -ln\sigma \right)w\left(\nu \right)w\left(\sigma \right)}{\sigma \nu }d\nu d\sigma \ne 0$, $h\left(\sigma \right)\ne 0$ for $\sigma \ne 0$ and if h is multiplicative or if h is supermultiplicative and φ is non-negative, then inequality (15) holds for

$$\mathcal{C}=min\left\{\frac{1}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma },\frac{{\mathit{\int }}_1^{\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}}\frac{\left(ln\sigma \right)w\left(\sigma \sqrt{{\kappa }_1{\kappa }_2}\right)}{\sigma }d\sigma }{{\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{\left(ln\nu -ln\sigma \right)w\left(\nu \right)w\left(\sigma \right)}{\sigma \nu }d\nu d\sigma }\right\}.$$

(b) 

If φ is $GA$-s-convex, i.e., $h\left(\tau \right)={\tau }^s$, then inequality (15) holds for $\mathcal{C}=\frac{2^{1-s}}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma }$.

Furthermore, if ${\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{{\left(ln\nu -ln\sigma \right)}^{s}w\left(\nu \right)w\left(\sigma \right)}{\sigma \nu }d\nu d\sigma \ne 0$, $h\left(\sigma \right)\ne 0$ for $\sigma \ne 0$ and if h is multiplicative or if h is supermultiplicative and φ is non-negative, then inequality (15) holds for

$$\mathcal{C}=min\left\{\frac{2^{1-s}}{{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{w\left(\sigma \right)}{\sigma }d\sigma },\frac{{\mathit{\int }}_1^{\sqrt{\frac{{\kappa }_2}{{\kappa }_1}}}\frac{{\left(ln\sigma \right)}^{s}w\left(\sigma \sqrt{{\kappa }_1{\kappa }_2}\right)}{\sigma }d\sigma }{{\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1{\kappa }_2}}{\mathit{\int }}_{\sqrt{{\kappa }_1{\kappa }_2}}^{{\kappa }_2}\frac{{\left(ln\nu -ln\sigma \right)}^{s}w\left(\nu \right)w\left(\sigma \right)}{\sigma \nu }d\nu d\sigma }\right\}.$$

Remark 6.

In Theorem 7,

(a) 

If φ is $GA$-convex, i.e., $h\left(\tau \right)=\tau$ and $w\left(\sigma \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}$, $\sigma \in \left[{\kappa }_1,{\kappa }_2\right]$, then inequality (15) becomes the first inequality in (5).

(b) 

If φ is $GA$-s-convex, i.e., $h\left(\tau \right)={\tau }^s$ and $w\left(\sigma \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}$, $\sigma \in \left[{\kappa }_1,{\kappa }_2\right]$, then inequality (15) becomes the first inequality proved in [47] (Corollary 2.1, page 93).

Let us now consider nonweighted Hermite–Hadamard inequalities for a $GA$-h-convex function from [47] (Theorem 2.2, page 92):

$$\begin{array}{c}\hfill \frac{1}{2h\left(\frac{1}{2}\right)}\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le \frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \le \left[\phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)\right]{\mathit{\int }}_0^{1}h\left(\tau \right)d\tau ,\end{array}$$

(22)

where $h\left(\frac{1}{2}\right)>0$.

Now we define $\mathcal{L}:\left[{\kappa }_1,{\kappa }_2\right]\to \mathcal{R}$ and $P:\left[{\kappa }_1,{\kappa }_2\right]\to \mathcal{R}$ by

$$\mathcal{L}\left(\nu \right)=\left[\phi \left({\kappa }_1\right)+\phi \left(\nu \right)\right]\left(ln\nu -ln{\kappa }_1\right){\mathit{\int }}_0^{1}h\left(\tau \right)d\tau -{\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma$$

and

$$P\left(\nu \right)={\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma -\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\frac{\left(ln\nu -ln{\kappa }_1\right)}{2h\left(\frac{1}{2}\right)}$$

respectively.

Theorem 8.

If the function φ is $GA$-h-convex, $\phi \ge 0$, $h\left(\frac{1}{2}\right)>0$ and $\frac{1}{4h\left(\frac{1}{2}\right)}\ge {\mathit{\int }}_0^{1}h\left(\tau \right)d\tau$, then

$$\mathcal{L}\left(\nu \right)\ge P\left(\nu \right)\ge 0,\nu \in \left[{\kappa }_1,{\kappa }_2\right].$$

(23)

Proof. 

Applying the second Hermite–Hadamard-type inequalities over the intervals $\left[{\kappa }_1,\sqrt{{\kappa }_1\nu }\right]$ and $\left[\sqrt{{\kappa }_1\nu },\nu \right]$, we obtain

$${\mathit{\int }}_{{\kappa }_1}^{\sqrt{{\kappa }_1\nu }}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \le \left[\frac{\phi \left({\kappa }_1\right)+\phi \left(\sqrt{{\kappa }_1\nu }\right)}{2}\right]\left(ln\nu -ln{\kappa }_1\right){\mathit{\int }}_0^{1}h\left(\tau \right)d\tau$$

(24)

and

$${\mathit{\int }}_{\sqrt{{\kappa }_1\nu }}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \le \left[\frac{\phi \left(\sqrt{{\kappa }_1\nu }\right)+\phi \left(\nu \right)}{2}\right]\left(ln\nu -ln{\kappa }_1\right){\mathit{\int }}_0^{1}h\left(\tau \right)d\tau .$$

(25)

Adding (24) and (25), we obtain

$${\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \le \left(ln\nu -ln{\kappa }_1\right)\left[\phi \left(\sqrt{{\kappa }_1\nu }\right)+\frac{\phi \left({\kappa }_1\right)+\phi \left(\nu \right)}{2}\right]{\mathit{\int }}_0^{1}h\left(\tau \right)d\tau .$$

(26)

Multiplying both sides of (26), we obtain

$$\begin{array}{c}{\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma -\left(ln\nu -ln{\kappa }_1\right)\left[\phi \left({\kappa }_1\right)+\phi \left(\nu \right)\right]{\mathit{\int }}_0^{1}h\left(\tau \right)d\tau \hfill \\ \le 2\left(ln\nu -ln{\kappa }_1\right)\phi \left(\sqrt{{\kappa }_1\nu }\right){\mathit{\int }}_0^{1}h\left(\tau \right)d\tau -{\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma .\hfill \end{array}$$

(27)

We can observe now that

$$\begin{array}{c}P\left(\nu \right)={\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma -\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\frac{\left(ln\nu -ln{\kappa }_1\right)}{2h\left(\frac{1}{2}\right)}\hfill \\ \le {\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma -2\left(ln\nu -ln{\kappa }_1\right)\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right){\mathit{\int }}_0^{1}h\left(\tau \right)d\tau \hfill \\ \le \left(ln\nu -ln{\kappa }_1\right)\left[\phi \left({\kappa }_1\right)+\phi \left(\nu \right)\right]{\mathit{\int }}_0^{1}h\left(\tau \right)d\tau -{\mathit{\int }}_{{\kappa }_1}^{\nu }\frac{\phi \left(\sigma \right)}{\sigma }d\sigma =\mathcal{L}\left(\nu \right).\hfill \end{array}$$

Hence, the first inequality in (23) is proved. The second inequality in (23) follows from the first inequality in (22). The proof is thus accomplished.   □

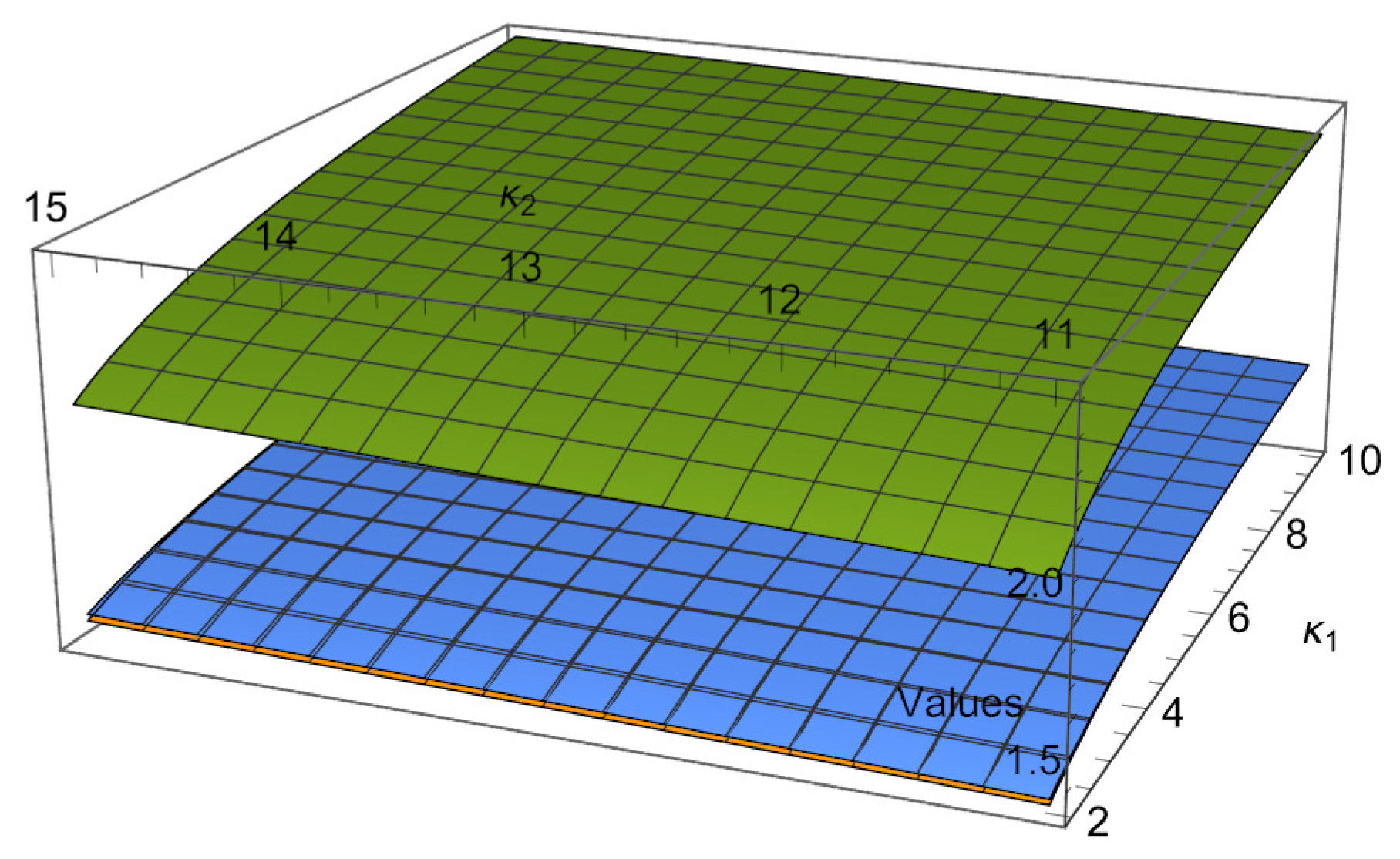
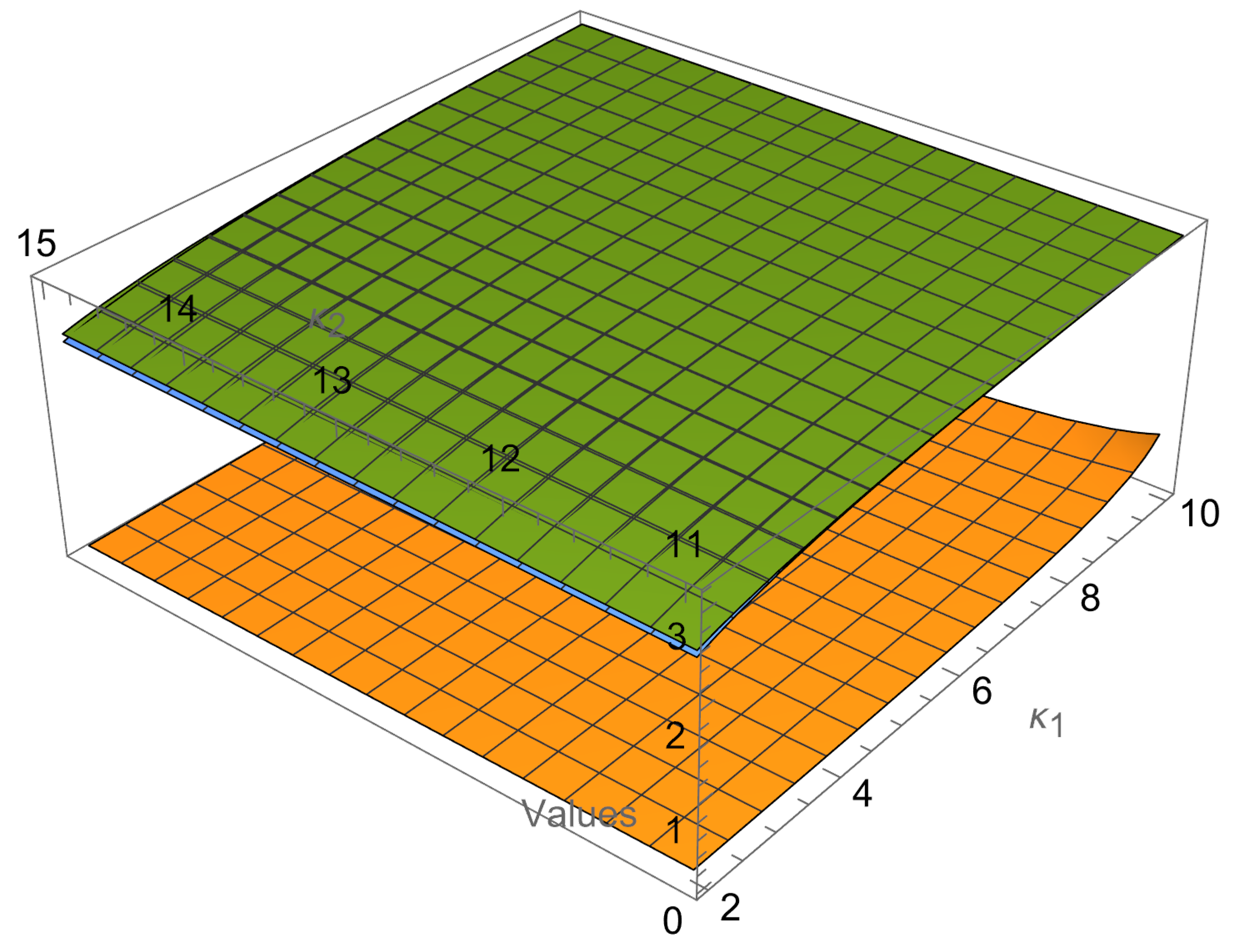
3. Mappings Connected with the Hermite–Hadamard-Type Inequalities for $\mathbf{GA}$-Convex Functions

Consider the mappings $\mathcal{H},\mathcal{F}:[0,1]\to \mathcal{R}$ defined by

$$\mathcal{H}\left(\tau \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma }\phi \left({\sigma }^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }\right)d\sigma$$

and

$$\mathcal{F}\left(\tau \right)=\frac{1}{{\left(ln{\kappa }_2-ln{\kappa }_1\right)}^2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left({\sigma }^{\tau }{\nu }^{1-\tau }\right)d\nu d\sigma ,$$

where $\phi :\mathcal{K}\subseteq (0,\infty )\to \mathcal{R}$ is $GA$-convex on $\mathcal{K}$ and ${\kappa }_1,{\kappa }_2\in \mathcal{K}$.

Latif et al. [49] proved that $\mathcal{H}\left(0\right)=\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)$ and $\mathcal{H}\left(1\right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma$. Latif et al. [49] also discussed some properties for $GA$-convex functions, and now we investigate which of those properties of the mappings $\mathcal{H}$ and $\mathcal{F}$ are for $GA$-h-convex mappings.

Theorem 9.

Let φ be $GA$-h-convex on $\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)$ and $h:\mathcal{J}\to \mathcal{R}$, $\left[0,1\right]\subseteq \mathcal{J}$. Then the mapping $\mathcal{H}$ is $GA$-h-convex on $\left(0,1\right]$ for $\tau \in \left(0,1\right]$

$$\mathcal{H}\left(0\right)\le \tau {\mathcal{C}}_1\mathcal{H}\left(\tau \right),$$

where

$$\tau {\mathcal{C}}_1=\left\{\begin{array}{cc}2h\left(\frac{1}{2}\right)\hfill & \mathrm{in}\mathrm{a}\mathrm{general}\mathrm{case},\hfill \\ & \\ min\left\{2h\left(\frac{1}{2}\right),\frac{{\mathit{\int }}_1^{e}h\left(\frac{ln{\kappa }_2-ln{\kappa }_1}{2}\tau ln\sigma \right)\frac{d\sigma }{\sigma }}{{\mathit{\int }}_1^e{\mathit{\int }}_1^{e}h\left(\frac{ln{\kappa }_2-ln{\kappa }_1}{2}\tau \left(ln\nu +ln\sigma \right)\right)\frac{d\nu d\sigma }{\sigma \nu }}\right\},\hfill \end{array}\right.$$

where h satisfies (i) or (ii) of Theorem 7.

Proof. 

We know that if $\phi :[{\kappa }_1,{\kappa }_2]\to \mathcal{R}$ is $GA$-h-convex on $[{\kappa }_1,{\kappa }_2]\subset (0,\infty )$, then $\phi \circ exp$ is h-convex on $[ln{\kappa }_1,ln{\kappa }_2]$. In order to show that $\mathcal{H}$ is $GA$-h-convex on $\left(0,1\right]$, it suffices to prove that the mapping $\overline{\mathcal{H}}:\left[0,1\right]\to \mathcal{R}$ defined by

$$\overline{\mathcal{H}}\left(\tau \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{ln{\kappa }_1}^{ln{\kappa }_2}\phi \circ exp\left(\tau ln\sigma +\left(1-\tau \right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right)d\sigma$$

is h-convex on $\left(0,1\right]$. Let $\vartheta$, $\beta \in \left[0,1\right]$ with $\vartheta +\beta =1$ and ${\tau }_1$, ${\tau }_2\in \left(0,1\right]$, then

$$\begin{array}{l}\overline{\mathcal{H}}\left(\vartheta {\tau }_1+{\tau }_2\beta \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{ln{\kappa }_1}^{ln{\kappa }_2}\phi \circ exp\left(\left(\vartheta {\tau }_1+{\tau }_2\beta \right)ln\sigma \right.\\ \left.+\left(1-\left(\vartheta {\tau }_1+{\tau }_2\beta \right)\right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right)d\sigma =\frac{1}{ln{\kappa }_2-ln{\kappa }_1}\\ \times {\mathit{\int }}_{ln{\kappa }_1}^{ln{\kappa }_2}\phi \circ exp\left(\left(\vartheta {\tau }_1+{\tau }_2\beta \right)ln\sigma +\left(\vartheta +\beta -\left(\vartheta {\tau }_1+{\tau }_2\beta \right)\right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right)d\sigma \\ =\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{ln{\kappa }_1}^{ln{\kappa }_2}\phi \circ exp\left(\vartheta \left[{\tau }_{1}ln\sigma +\left(1-{\tau }_1\right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right]\right.\\ \left.+\beta \left[{\tau }_{2}ln\sigma +\left(1-{\tau }_2\right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right]\right)d\sigma .\end{array}$$

Since $\phi \circ exp$ is h-convex, we obtain

$$\begin{array}{l}\overline{\mathcal{H}}\left(\vartheta {\tau }_1+{\tau }_2\beta \right)\\ \le \vartheta \left[\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{ln{\kappa }_1}^{ln{\kappa }_2}\phi \circ exp\left({\tau }_{1}ln\sigma +\left(1-{\tau }_1\right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right)d\sigma \right]\\ +\beta \left[\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{ln{\kappa }_1}^{ln{\kappa }_2}\phi \circ exp\left({\tau }_{2}ln\sigma +\left(1-{\tau }_2\right)\left(\frac{ln{\kappa }_1+ln{\kappa }_2}{2}\right)\right)d\sigma \right]\\ =\vartheta \overline{\mathcal{H}}\left({\tau }_1\right)+\beta \overline{\mathcal{H}}\left({\tau }_2\right).\hfill \end{array}$$

By making the substitution $u={\sigma }^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }$, we obtain

$$\begin{array}{c}\mathcal{H}\left(\tau \right)=\frac{1}{\tau \left(ln{\kappa }_2-ln{\kappa }_1\right)}{\mathit{\int }}_{{\kappa }_1^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }}^{{\kappa }_2^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }}\frac{\phi \left(u\right)}{u}du\hfill \\ =\frac{1}{ln\left({\kappa }_2^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }\right)-ln\left({\kappa }_1^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }\right)}{\mathit{\int }}_{{\kappa }_1^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }}^{{\kappa }_2^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }}\frac{\phi \left(u\right)}{u}du\\ =\frac{1}{ln{u}_U-ln{u}_{\mathcal{L}}}{\mathit{\int }}_{u_{\mathcal{L}}}^{u_U}\frac{\phi \left(u\right)}{u}du.\hfill \end{array}$$

(28)

Multiplying both sides of (28) by ${\mathcal{C}}_1$, we obtain

$${\mathcal{C}}_1\mathcal{H}\left(\tau \right)=\frac{{\mathcal{C}}_1}{ln{u}_U-ln{u}_{\mathcal{L}}}{\mathit{\int }}_{u_{\mathcal{L}}}^{u_U}\frac{\phi \left(u\right)}{u}du\ge \phi \left(\sqrt{u_{\mathcal{L}}{u}_U}\right)=\phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right),$$

(29)

where ${\mathcal{C}}_1$ is a constant defined in Theorem 7 over the interval $\left[u_{\mathcal{L}},u_U\right]$, where $u_{\mathcal{L}}={\kappa }_1^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }$ and $u_U={\kappa }_2^{\tau }{\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{1-\tau }$ and $w\left(u\right)=\frac{1}{ln{u}_U-ln{u}_{\mathcal{L}}}$, $u\in \left[u_{\mathcal{L}},u_U\right]$.   □

Remark 7.

If φ is a $GA$-convex function, then we obtain

$$\mathcal{H}\left(0\right)\le \mathcal{H}\left(\tau \right),$$

(30)

for all $\tau \in \left[0,1\right]$. The inequality (30) is a known result for a $GA$-convex function proved in [49]. If φ is a $GA$-s-convex function in the second sense, then $\tau {\mathcal{C}}_1=\frac{s+2}{2^{s+2}-2}$, so we have

$$\mathcal{H}\left(0\right)\le \frac{s+2}{2^{s+2}-2}\mathcal{H}\left(\tau \right).$$

(31)

Theorem 10.

Let φ be $GA$-h-convex on $\left[{\kappa }_1,{\kappa }_2\right]\subseteq \left(0,\infty \right)$ and $h:\mathcal{J}\to \mathcal{R}$, $\left[0,1\right]\subseteq \mathcal{J}$. Then the mapping $\mathcal{F}$ is symmetric with respect to $\frac{1}{2}$ and $GA$-h-convex on $\left(0,1\right]$. Furthermore, the following inequalities hold:

$$2h\left(\frac{1}{2}\right)\mathcal{F}\left(\tau \right)\ge \mathcal{F}\left(\frac{1}{2}\right)\mathrm{and}\tau {\mathcal{C}}_1\mathcal{F}\left(\tau \right)\ge \mathcal{H}\left(1-\tau \right)$$

(32)

for $\tau \in \left(0,1\right]$, where ${\mathcal{C}}_1$ is defined as in Theorem 9.

Proof. 

We observe that the following equality holds for all $\sigma$, $\nu \in \left[{\kappa }_1,{\kappa }_2\right]$ and $\tau \in \left(0,1\right]$:

$$\sqrt{\sigma \nu }=\sqrt{{\sigma }^{\tau }{\nu }^{1-\tau }}\sqrt{{\sigma }^{1-\tau }{\nu }^{\tau }}.$$

Since $\phi$ is $GA$-h-convex on $\left[{\kappa }_1,{\kappa }_2\right]$, we have

$$\phi \left(\sqrt{\sigma \nu }\right)=\phi \left(\sqrt{{\sigma }^{\tau }{\nu }^{1-\tau }}\sqrt{{\sigma }^{1-\tau }{\nu }^{\tau }}\right)\le h\left(\frac{1}{2}\right)\phi \left({\sigma }^{\tau }{\nu }^{1-\tau }\right)+h\left(\frac{1}{2}\right)\phi \left({\sigma }^{1-\tau }{\nu }^{\tau }\right).$$

(33)

Multiplying the inequality (33) by $\frac{1}{\sigma \nu }$, integrating with respect to $\sigma$ over $\left[{\kappa }_1,{\kappa }_2\right]$, with respect to $\nu$ over $\left[{\kappa }_1,{\kappa }_2\right]$, and using the fact that

$${\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left({\sigma }^{\tau }{\nu }^{1-\tau }\right)d\nu d\sigma ={\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left({\sigma }^{1-\tau }{\nu }^{\tau }\right)d\nu d\sigma$$

we obtain the inequality

$$\begin{array}{l}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left(\sqrt{\sigma \nu }\right)d\nu d\sigma \le 2h\left(\frac{1}{2}\right){\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left({\sigma }^{1-\tau }{\nu }^{\tau }\right)d\nu d\sigma \\ =2h\left(\frac{1}{2}\right){\left(ln{\kappa }_2-ln{\kappa }_1\right)}^2·\frac{1}{{\left(ln{\kappa }_2-ln{\kappa }_1\right)}^2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma \nu }\phi \left({\sigma }^{1-\tau }{\nu }^{\tau }\right)d\nu d\sigma \\ =2{\left(ln{\kappa }_2-ln{\kappa }_1\right)}^{2}h\left(\frac{1}{2}\right)\mathcal{F}\left(\tau \right).\end{array}$$

(34)

Thus, the first inequality in (32) is proved.

Let us consider the mapping

$${\mathcal{H}}_{\nu }\left(\tau \right)=\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{1}{\sigma }\phi \left({\sigma }^{\tau }{\nu }^{1-\tau }\right)d\sigma$$

for a fixed $\nu$.

By making use of the substitution $u={\sigma }^{\tau }{\nu }^{1-\tau }$, we obtain

$${\mathcal{H}}_{\nu }\left(\tau \right)=\frac{1}{\tau \left(ln{\kappa }_2-ln{\kappa }_1\right)}{\mathit{\int }}_{{\kappa }_1^{\tau }{\nu }^{1-\tau }}^{{\kappa }_2^{\tau }{\nu }^{1-\tau }}\frac{\phi \left(u\right)}{u}du=\frac{1}{ln{u}_U-ln{u}_{\mathcal{L}}}{\mathit{\int }}_{u_{\mathcal{L}}}^{u_U}\frac{\phi \left(u\right)}{u}du,$$

where $u_{\mathcal{L}}={\kappa }_1^{\tau }{\nu }^{1-\tau }$ and $u_U={\kappa }_2^{\tau }{\nu }^{1-\tau }$.

Using the result from Theorem 7, we obtain

$${\mathcal{C}}_1{\mathcal{H}}_{\nu }\left(\tau \right)={\mathcal{C}}_1{\mathit{\int }}_{u_{\mathcal{L}}}^{u_U}\frac{\phi \left(u\right)}{u}\frac{1}{ln{u}_U-ln{u}_{\mathcal{L}}}du\ge \phi \left({\left(\sqrt{{\kappa }_1{\kappa }_2}\right)}^{\tau }{\nu }^{1-\tau }\right)$$

(35)

Multiplying both sides of the inequality (35) by $\frac{1}{\nu }$, integrating with respect to $\nu$ over $\left[{\kappa }_1,{\kappa }_2\right]$ and dividing both sides by $ln{u}_U-ln{u}_{\mathcal{L}}$, we obtain

$$\tau {\mathcal{C}}_1\mathcal{F}\left(\tau \right)\ge \mathcal{H}(1-\tau ).$$

Hence, the second inequality in (32) is also established, where ${\mathcal{C}}_1$ is given in Theorem 9.   □

Remark 8.

If $\tau {\mathcal{C}}_1>0$, then we have

$$\mathcal{F}\left(\tau \right)\ge \frac{1}{\tau {\mathcal{C}}_1}\mathcal{H}(1-\tau )$$

(36)

for all $\tau \in \left(0,1\right]$. Replacing τ with $1-\tau$ in (36), we have

$$\mathcal{F}(1-\tau )\ge \frac{1}{\left(1-\tau \right){\mathcal{C}}_1}\mathcal{H}\left(\tau \right)$$

(37)

for all $\tau \in \left(0,1\right]$.

Since $\mathcal{F}$ is symmetric with respect to $\frac{1}{2}$, we have

$$\mathcal{F}\left(\tau \right)\ge max\left\{\frac{1}{\tau {\mathcal{C}}_1}\mathcal{H}(1-\tau ),\frac{1}{\left(1-\tau \right){\mathcal{C}}_1}\mathcal{H}\left(\tau \right)\right\}.$$

(38)

If φ is a $GA$-convex function, then we obtain the following result:

$$\mathcal{F}\left(\tau \right)\ge max\left\{\mathcal{H}(1-\tau ),\mathcal{H}\left(\tau \right)\right\}.$$

(39)

If h is a multiplicative function, then $\tau {\mathcal{C}}_1=\left(1-\tau \right){\mathcal{C}}_1$. Thus, we obtain

$$\mathcal{F}\left(\tau \right)\ge \frac{1}{\tau {\mathcal{C}}_1}max\left\{\mathcal{H}(1-\tau ),\mathcal{H}\left(\tau \right)\right\}.$$

(40)

If φ is a $GA$-s-convex function, then $h\left(\tau \right)={\tau }^s$ and we obtain the following result:

$$\mathcal{F}\left(\tau \right)\ge \frac{2^{s+2}-2}{s+2}max\left\{\mathcal{H}(1-\tau ),\mathcal{H}\left(\tau \right)\right\}.$$

(41)

4. Applications to Special Means

Suppose that $\phi$ is $GA$-concave and $GA$-h-convex simultaneously, or vice versa, when $\phi$ is $GA$-convex and $GA$-h-concave. If $\phi$ is a $GA$-concave and $GA$-h-convex function with ${\mathit{\int }}_0^{1}h\left(\tau \right)d\tau >0$, then the Hermite–Hadamard-type inequalities of Theorems 4, 6, and 7 lead us to the following inequalities:

$$\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \le \phi \left(\sqrt{{\kappa }_1{\kappa }_2}\right)\le \mathcal{C}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma$$

(42)

and

$$\begin{array}{c}\frac{1}{\left(ln{\kappa }_2-ln{\kappa }_1\right){\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}h\left(\tau \right)d\tau }{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma \hfill \\ \le \phi \left({\kappa }_1\right)+\phi \left({\kappa }_2\right)\le \frac{2}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma .\hfill \end{array}$$

(43)

If $\phi$ is a $GA$-convex and $GA$-h-concave function simultaneously, then the inequalities (42) and (43) hold in reversed directions.

Let ${\kappa }_1$ and ${\kappa }_2$ be two non-negative real numbers; then the $\alpha$-logarithmic mean ${\mathcal{L}}_{\alpha }$ and geometric mean of the order $\alpha$ are defined as

$${\mathcal{L}}_{\alpha }\left({\kappa }_1,{\kappa }_2\right)={\left[\frac{{\kappa }_2^{\alpha +1}-{\kappa }_1^{\alpha +1}}{\left(\alpha +1\right)\left({\kappa }_2-{\kappa }_1\right)}\right]}^{\frac{1}{\alpha }},\alpha \in \mathcal{R}\setminus \left\{0,-1\right\}$$

and

$${\mathcal{M}}_{\alpha }\left({\kappa }_1,{\kappa }_2\right)={\left(\frac{{\kappa }_1^{\alpha }+{\kappa }_2^{\alpha }}{2}\right)}^{\frac{1}{\alpha }}.$$

It has been shown in [43] that for the functions $\phi$ and $h_k$ defined as $h_k\left(\sigma \right)={\sigma }^k$, $\phi \left(\sigma \right)={\sigma }^{\alpha }$, $\sigma >0$, k, $\alpha \in \mathcal{R}$, we have the following facts:

(i)

The function $\phi$ is $h_k$-convex if

(a)

$\alpha \in \left(-\infty ,0\right]\cup \left[1,\infty \right)$ and $k\le 1$;

(b)

$\alpha \in \left(0,1\right)$ and $k\le \alpha$.

(ii)

The function $\phi$ is $h_k$-concave if

(a)

$\alpha \in \left(0,1\right)$ and $k\ge 1$;

(b)

$\alpha >1$ and $k\ge \alpha$.

According to Theorem 3 for the functions $h_k\left(\sigma \right)={\sigma }^k$, $\phi \left(\sigma \right)={\sigma }^{\alpha }$, $\sigma >1$, k, $\alpha \in \mathcal{R}$, we have that

(i)

The function $\phi \left(ln\sigma \right)$ is $GA$-$h_k$-convex if

(a)

$\alpha \in \left(-\infty ,0\right]\cup \left[1,\infty \right)$ and $k\le 1$;

(b)

$\alpha \in \left(0,1\right)$ and $k\le \alpha$.

(ii)

The function $\phi \left(ln\sigma \right)$ is $GA$-$h_k$-concave if

(a)

$\alpha \in \left(0,1\right)$ and $k\ge 1$;

(b)

$\alpha >1$ and $k\ge \alpha$.

Let $\alpha \in \left(0,1\right)$ and $0\le k\le \alpha$; then we have the following inequalities:

$${\mathcal{L}}_{\alpha }^{\alpha }\left(ln{\kappa }_1,ln{\kappa }_2\right)\le {\mathcal{M}}_1^{\alpha }\left(ln{\kappa }_1,ln{\kappa }_2\right)\le \left(\frac{k+2}{2^{k+1}-1}\right){\mathcal{L}}_{\alpha }^{\alpha }\left(ln{\kappa }_1,ln{\kappa }_2\right)$$

(44)

and

$$\frac{{\mathcal{L}}_{\alpha }^{\alpha }\left(ln{\kappa }_1,ln{\kappa }_2\right)}{\left({\kappa }_2-{\kappa }_1\right){\mathcal{L}}_k^k\left({\kappa }_1,{\kappa }_2\right)}\le 2{\mathcal{M}}_1\left({\left(ln{\kappa }_1\right)}^{\alpha },{\left(ln{\kappa }_2\right)}^{\alpha }\right)\le 2{\mathcal{L}}_{\alpha }^{\alpha }\left(ln{\kappa }_1,ln{\kappa }_2\right).$$

(45)

The graphical representations of inequalities (44) and (45) for $\alpha =\frac{1}{2}$ and $k=\frac{1}{3}$ with $2\le {\kappa }_1\le 10$, $11\le {\kappa }_2\le 15$ (Figure 1).

The graphical representations of inequalities (44) and (45) for $\alpha =\frac{1}{2}$ and $k=\frac{1}{3}$ with $2\le {\kappa }_1\le 10$, $11\le {\kappa }_2\le 15$ (Figure 2).

5. Conclusions

This study contains new Hermite–Hadamard–Fejér-type inequalities for one of the generalizations of usual convexity, known as $GA$-convexity. We have also discussed in this research that there is no change in the properties associated with $\frac{1}{ln{\kappa }_2-ln{\kappa }_1}{\mathit{\int }}_{{\kappa }_1}^{{\kappa }_2}\frac{\phi \left(\sigma \right)}{\sigma }d\sigma$ even if the class of $GA$-convex functions is extended to the class of $GA$-h-convex functions. We also proved Hermite–Hadamard–Fejér inequality for a $GA$-h-convex function and looked at specific examples for other types of functions including $GA$-convex functions and $GA$-s-convex functions. In this study, it was also discovered that the left-hand-side Hermite–Hadamard–Fejér-type inequalities for $GA$-convex functions of the result are stronger than the right-hand-side inequality. This manuscript’s study can serve as an inspiration for mathematicians working on the topic of mathematical inequalities.