Exact Solutions of Reaction–Diffusion PDEs with Anisotropic Time Delay

Abstract

This study is devoted to reaction–diffusion equations with spatially anisotropic time delay. Reaction–diffusion PDEs with either constant or variable transfer coefficients are considered. Nonlinear equations of a fairly general form containing one, two, or more arbitrary functions and free parameters are analyzed. For the first time, reductions and exact solutions for such complex delay PDEs are constructed. Additive, multiplicative, generalized, and functional separable solutions and some other exact solutions are presented. In addition to reaction–diffusion equations, wave-type PDEs with spatially anisotropic time delay are considered. Overall, more than twenty new exact solutions to reaction–diffusion and wave-type equations with anisotropic time delay are found. The described nonlinear delay PDEs and their solutions can be used to formulate test problems applicable to the verification of approximate analytical and numerical methods for solving complex PDEs with variable delay.

Contents

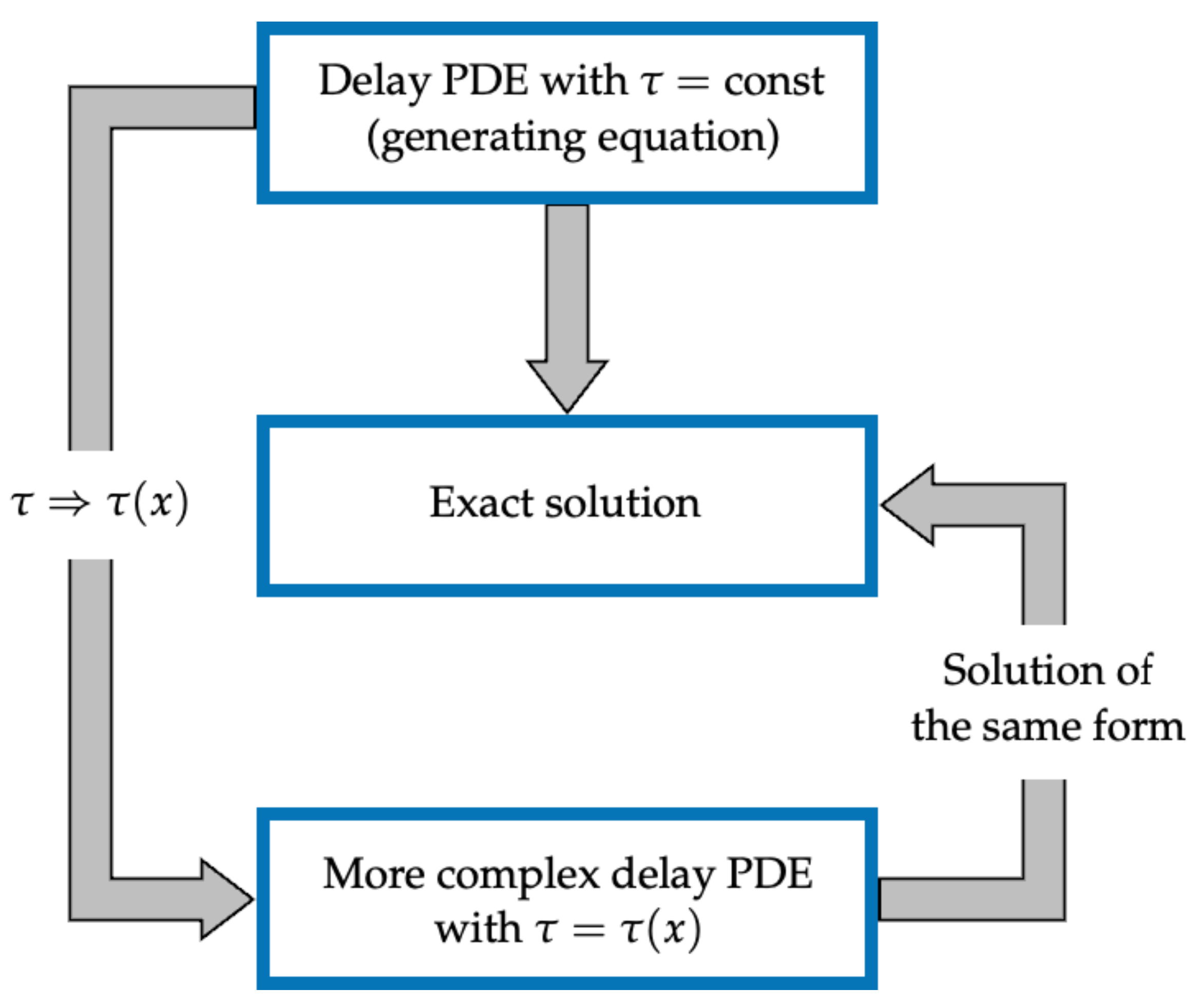
1. Introduction 1.1. Differential Equations with Delay: Brief Overview 1.2. PDEs with Spatially Anisotropic Time Delay. Reductions. Term ‘Exact Solution’   2. Approaches to Constructing Exact Solutions 2.1. Constructing Solutions to Complex Equations Using Solutions of Simpler Equations 2.2. PDEs with Anisotropic Time Delay Allowing Solutions of a Special Form   3. Exact Solutions of Reaction–Diffusion Type PDEs 3.1. Reaction–Diffusion Equations with Spatially Anisotropic Time Delay 3.2. Reaction–Diffusion Equations with Proportional Anisotropic Time Delay   4. Exact Solutions of Wave-Type PDEs 4.1. Wave-Type Equations with Spatially Anisotropic Time Delay 4.2. Wave-Type Equations with Proportional Anisotropic Time Delay   5. Table of Generating PDEs with Constant or Proportional Delay   6. Brief Conclusions  References

1. Introduction

1.1. Differential Equations with Delay: Brief Overview

Hereditary systems are characterized by the dependence of the state of the system on a period or a certain moment in the past. Such systems are often modeled by introducing functions with delayed arguments into partial differential equations (PDEs). Let $u=u(x,t)$ be the unknown function and w be the function with time delay. Then, we have several different possibilities:

(i)

PDEs with constant delay (or, usually, PDEs with delay) contain a function w of the form $w=u(x,t-\tau )$, where $\tau >0$ is the constant delay time;

(ii)

PDEs with proportional delay contain a function w of the form $w=u(x,qt)$, where q is the scaling parameter, $0<q<1$;

(iii)

PDEs with variable delay contain a function w of the form $w=u(x,t-\tau (t\left)\right)$, where $\tau \left(t\right)>0$ is the variable delay.

Remark 1.

Delays of types (i), (ii), or (iii) can also occur in the argument x.

Remark 2.

If there is no dependence on x, one can easily have similar items for delay ordinary differential equations (ODEs).

In more complex cases, the variable delay can depend either on the spatial coordinate, i.e., be spatially anisotropic, $\tau =\tau \left(x\right)$, or on both spatial and time arguments, $\tau =\tau (x,t)$, or even on both arguments and the desired solution, $\tau =\tau (x,t,u)$. In this article, for the first time, we study exact solutions and reductions of PDEs with spatially anisotropic time delay $\tau =\tau \left(x\right)$.

Table 1. Some functional differential equations (ODEs and PDEs) with delays of different types.

Type of Equation	Form of Equation	References/Comments
First-order ODE with delay	$u_t^{\prime }=f(u,w)$, $w=u(t-\tau )$	[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
Second-order ODE with delay	$u_{tt}^{″}+c{u}_t^{\prime }=f(u,w)$, $w=u(x,t-\tau )$	[21]
First-order ODE with proportional argument	$u_t^{\prime }=au+bw$, $w=u\left(qt\right)$	$0<q<1:$ [22] $q>1:$ [23,24]
First-order ODE with variable delay	$u_t^{\prime }=f(u,w)$, $w=u(x,t-\tau (t\left)\right)$	[25]
First-order PDE with delay	$u_t+u_x=f(x,t,u,w)$, $w=u(x,t-\tau )$	[26]
First-order Hopf-type PDE with delay	$u_t+u{u}_x=f(u,w)$, $w=u(x,t-\tau )$	[27]
First-order PDE with proportional argument	$u_t+u_x=au+bw$, $w=u(px,t)$	$p>1$: [28]
First-order PDE with delay and proportional argument	$u_t+c{u}_x=f(x,t,u,w)$, $w=u(px,t-\tau )$	$0<p<1$: [29]
First-order PDE with constant time delay and variable space delay	$u_t+g\left(x\right)u_x=f(t,u,w)$, $w=u\left(\xi \right(x),t-\tau )$	[30]
Reaction–diffusion PDE with delay	$u_t=a{u}_{xx}+f(u,w)$, $w=u(x,t-\tau )$	Exact solutions construction: [31,32,33,34] Traveling waves analysis: [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] Other topics: [17,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77]
Reaction–diffusion PDE with delay and variable transfer coefficient	$u_t={\left[g\left(u\right)u_x\right]}_x+f(u,w)$, $w=u(x,t-\tau )$	[78,79,80,81]
Reaction–diffusion PDE with proportional argument	$u_t=a{u}_{xx}+f(u,w)$, $w=u(x,qt)$	[82,83]
Reaction–diffusion PDE with proportional argument	$u_t=a{u}_{xx}+f(u,w)$, $w=u(px,t)$	[83]
Reaction–diffusion PDE with proportional arguments	$u_t=a{u}_{xx}+f(u,w)$, $w=u(px,qt)$	[83,84]
Reaction–diffusion PDE with variable delay	$u_t=a{u}_{xx}+f(u,w)$, $w=u(x,t-\tau (t\left)\right)$	[31,33,84,85,86,87,88,89]
Fokker–Planck type PDE with proportional argument	$u_t+c{u}_x=a{u}_{xx}+bu+kw$, $w=u(px,t)$	$p>1$: [90]
Wave-type PDE with delay	$u_{tt}=a{u}_{xx}+f(u,w)$, $w=u(x,t-\tau )$	[91,92,93]
Wave-type PDE with variable delay	$u_{tt}=a{u}_{xx}+f(u,w)$, $w=u(x,t-\tau (t\left)\right)$	[94]
Telegraph type PDE with delay	$u_{tt}+u_t=a{u}_{xx}+f(u,w)$, $w=u(x,t-\tau )$	[95]
Telegraph type PDE with proportional argument	$u_{tt}+c{u}_t=a{u}_{xx}+f(u,w)$, $w=u(x,qt)$	$0<q<1$: [96]
Wave-type PDE with proportional argument	$u_{tt}=a{u}_{xx}+f(u,w)$, $w=u(x,qt)$	[97]
Wave-type PDE with nonlinear speed and proportional arguments	$u_{tt}={\left[g\left(u\right)u_x\right]}_x+f(u,w)$, $w=u(px,qt)$	[97]

presents some common and specific differential equations with delay found in the literature. These equations arise in population theory, medicine, economics, epidemiology, biology, chemistry, control theory, theory of artificial neural networks, and many other fields. In the column “References/Comments”, there are publications devoted to applications of differential equations with delay, exact solutions, numerical methods, etc. Note that in Table 1, for brevity and uniformity, we use the term “proportional argument” regardless of the values of the scaling parameters $p>0$ or $q>0$ (although if $0<p<1$ or $0<q<1$, the term “proportional delay” is usually used); and “with delay” means “with constant delay”.

Some specific mathematical models with delay can be found in [14,34,98,99]. Symmetries, linearizations, and some exact solutions of complex first- and second-order ODEs with delay are studied in [100,101,102]. Exact solutions to nonlinear time-fractional PDEs with delay are considered in [103,104].

The monograph [105] gathers the latest results on exact solutions, provides some fundamental theory, and describes certain models and numerical methods for delay ODEs and PDEs. Many of the equations listed in Table 1 are also considered in [105].

PDEs with two independent variables, x and t, and constant delay generally admit traveling-wave solutions, $u=u\left(z\right)$, where $z=kx+\lambda t$ [55,106,107,108], and do not have self-similar solutions, $u=t^{\alpha }U\left(y\right)$, where $y=x{t}^{\beta }$. Additive, multiplicative, and generalized separable solutions and more complex solutions of PDEs with constant or varying delays are obtained in [27,31,32,33,78,79,91,92,93,94,95,97,109,110,111,112,113,114,115,116,117] (for a brief overview of publications on exact solutions, see [97,99]). In contrast, PDEs with one proportional delay do not have traveling-wave solutions but can admit self-similar ones. These and more complex solutions are constructed in [83,84,97,118].

Note that for finding exact solutions to nonlinear PDEs with constant or variable delay, most of the analytical methods that are effective for nonlinear PDEs without delay are either inapplicable or their applicability is very limited.

1.2. PDEs with Spatially Anisotropic Time Delay. Reductions. Exact Solutions

In this article, by saying a PDE with spatially anisotropic time delay (briefly, a PDE with anisotropic time delay) we mean a functional-differential equation that, in addition to the desired function $u(x,t)$, also contains a delayed function of the form $u(x,t-\tau (x\left)\right)$, where $\tau \left(x\right)$ is a given positive function, and partial derivatives of u with respect to x and t. PDEs with an anisotropic time delay can model delay systems in anisotropic and inhomogeneous media, in which the signal propagation speed depends on the chosen direction or varies at different points of the medium. For example, in medicine, this can be differences in the rate of transmission of a nerve impulse in “healthy” and “sick” tissues of the human body.

Approaches to constructing solutions to a mathematical equation based on solutions to simpler equations are usually called reductions. One-dimensional reductions are the most important for nonlinear PDEs; using them, one can obtain solutions for these PDEs in terms of much simpler solutions to ODEs. Furthermore, reductions of various differential and functional-differential equations play a key role in constructing their exact solutions.

By exact solutions of a nonlinear PDE with anisotropic time delay, we understand solutions that can be expressed via elementary functions, functions included in the PDE under consideration, indefinite integrals, or/and solutions of some ODEs without delay (systems of such ODEs). It is important to note that the exact solutions to nonlinear equations of mathematical physics and related PDEs (both with and without delay) play an essential role in ’mathematical standards’, which are widely used to assess the accuracy, verify, and develop various numerical, asymptotic, and approximate analytical methods.

Reductions and exact solutions for nonlinear PDEs with constant, proportional, or variable time delay of the form $\tau =\tau \left(t\right)$ are usually constructed using the method of separation of variables [119,120,121], modifications of the method of functional constraints [31,79], the principle of analogy of solutions [80,81,83,84,97,118], or combinations of these methods. As a result, many reductions and exact solutions have been obtained.

2. Approaches to Constructing Exact Solutions

2.1. Constructing Solutions to Complex Equations Using Solutions of Simpler Equations

It should be noted that at present, there are no methods for constructing exact solutions to nonlinear PDEs with spatially anisotropic time delay and related functional PDEs (the methods mentioned at the end of Section 1.2 are not applicable to such equations).

In this article, to construct exact solutions to such equations, we use a simple but very important proposition, namely, exact solutions of certain PDEs with constant delay can serve as the basis for constructing solutions to more complex PDEs with variable anisotropic delay (a somewhat similar approach was used in [80,81,83,84,118] to construct solutions to nonlinear PDEs with constant or proportional delay using solutions of simpler nondelay PDEs and was referred to as the principle of analogy of solutions). This approach to constructing exact solutions, using the principle “from simple to complex”, is illustrated below with specific examples.

Example 1.

Consider a delay reaction–diffusion equation with power-law nonlinearity,

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+b{(u-w)}^k,w=u(x,t-\tau ),\end{array}$$

(1)

where the time delay $\tau >0$ is a constant.

It is easy to verify that Equation (1) admits an additive separable solution of the form

$$\begin{array}{c}\hfill u=ct+\psi \left(x\right),\end{array}$$

(2)

where c is an arbitrary constant and the function $\psi =\psi \left(x\right)$ satisfies the second-order linear ODE

$$a{\psi }_{xx}^{″}+b{\left(c\tau \right)}^k-c=0.$$

Its general solution is written as:

$$\psi =\frac{1}{2a}[c-b{\left(c\tau \right)}^k]x^2+C_{1}x+C_2,$$

where $C_1$ and $C_2$ are arbitrary constants.

A more complex reaction–diffusion equation with anisotropic delay obtained from (1) by formally replacing the constant τ with an arbitrary function $\tau \left(x\right)$ (using the principle “from simple to complex”), namely:

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+b{(u-w)}^k,w=u\left(x,t-\tau \left(x\right)\right),\end{array}$$

(3)

admits an exact solution of the same form (2) with the function $\psi =\psi \left(x\right)$ satisfying the second-order linear ODE:

$$a{\psi }_{xx}^{″}+b{\left[c\tau \left(x\right)\right]}^k-c=0,$$

which is easily integrated.

Thus, in this case, we can say that a solution of the simpler PDE (1) generates a solution to the more complex PDE (3).

A reaction–diffusion equation with spatially anisotropic time delay, more general than (3), is considered below (see Equation (12)).

For clarity, the procedure for constructing exact solutions to PDEs with anisotropic delay based on exact solutions of simpler PDEs with constant delay, which was used in Example 1 and will be used further, is schematically shown in Figure 1.

2.2. PDEs with Anisotropic Time Delay Allowing Solutions of a Special Form

Functional PDEs with anisotropic time delay and their exact solutions in some cases can be found by analogy from simpler PDEs with a constant delay that allow solutions of the form:

$$\begin{array}{c}\hfill F\left(u\right)=kt+\theta \left(x\right)\mathrm{or}F\left(u\right)=e^{kt}\theta \left(x\right),\end{array}$$

(4)

and satisfy the following two conditions:

(i)

The original simpler PDEs with constant delay (similar equations are called generating equations later) are reduced to ODEs depending only on the spatial argument x;

(ii)

Parameters and functional coefficients of original PDEs with constant delay do not explicitly depend on $\tau$.

In the simplest cases, in solutions (4), we have $F\left(u\right)=u$. Forms of exact solutions other than (4) are also considered.

In the following section, we present new exact solutions and reductions to linear and nonlinear PDEs with anisotropic time delay. We describe complex delay PDEs that admit additive, multiplicative, functional, and generalized separable solutions [120,121]. Special attention is paid to nonlinear PDEs of a rather general form involving arbitrary functions. Exact solutions of such equations are of primary interest because they can be used as test problems for the verification of various approximate analytical and numerical methods.

We give only the final results without intermediate calculations (the generating equations used will be given later in Section 5). The obtained solutions are easily verified by direct substitutions into the considered equations.

Remark 3.

This article does not consider both the simplest solutions of the form $u=const$ and degenerate solutions with only one of the two independent variables.

Remark 4.

Notably, any PDEs with anisotropic time delay admit neither traveling-wave solutions nor self-similar solutions.

Remark 5.

In all the equations discussed in this article, it is assumed that the anisotropic time delay $\tau \left(x\right)$ is an arbitrary positive function.

3. Exact Solutions of Reaction–Diffusion Type PDEs

3.1. Reaction–Diffusion Equations with Spatially Anisotropic Time Delay

Equation (1). Consider a linear reaction–diffusion equation with anisotropic time delay of the form:

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+bu+cw,w=u(x,t-\tau \left(x\right)),\end{array}$$

(5)

where b and c are free parameters.

$1^{\circ }$. Equation (5) admits a multiplicative separable exact solution,

$$\begin{array}{c}\hfill u=e^{\lambda t}\phi \left(x\right),\end{array}$$

(6)

where $\lambda$ is an arbitrary constant and the function $\phi =\phi \left(x\right)$ satisfies the linear ODE:

$$\begin{array}{c}\hfill a{\phi }_{xx}^{″}+(b-\lambda +c{e}^{-\lambda \tau \left(x\right)})\phi =0.\end{array}$$

Solution (6) and other solutions below are obtained by analogy from a corresponding simpler generating PDE. It has the form of (5) with a constant delay $\tau \left(x\right)\equiv \tau =\mathrm{const}$.

$2^{\circ }$. Equation (5) also admits a generalized separable exact solution, periodic in t,

$$\begin{array}{c}\hfill u=\phi \left(x\right)cos\left(\lambda t\right)+\psi \left(x\right)sin\left(\lambda t\right),\end{array}$$

(7)

where the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ are described by the linear system of ODEs:

$$\begin{array}{cc}\hfill & a{\phi }_{xx}^{″}+[b+ccos\left(\lambda \tau \right)]\phi -[\lambda +csin\left(\lambda \tau \right)]\psi =0,\tau =\tau \left(x\right),\hfill \\ \hfill & a{\psi }_{xx}^{″}+[b+ccos\left(\lambda \tau \right)]\psi +[\lambda +csin\left(\lambda \tau \right)]\phi =0.\hfill \end{array}$$

$3^{\circ }$.Another generalized separable solution, linear in t, has the form:

$$\begin{array}{c}\hfill u=\phi \left(x\right)t+\psi \left(x\right),\end{array}$$

(8)

where the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ are described by the linear system of ODEs:

$$\begin{array}{cc}\hfill & a{\phi }_{xx}^{″}+(b+c)\phi =0,\hfill \\ \hfill & a{\psi }_{xx}^{″}+(b+c)\psi -[c\tau \left(x\right)+1]\phi =0,\hfill \end{array}$$

which can be easily integrated sequentially (since the first ODE is homogeneous, and the second is nonhomogeneous).

$4^{\circ }$. There are also solutions of the polynomial form in t,

$$u=\sum _{k=0}^n{\phi }_k\left(x\right)t^k,$$

where n is an arbitrary positive integer and the functions ${\phi }_k\left(x\right)$ are described by a system of ODEs.

Remark 6.

For all the PDEs with anisotropic time delay, which are discussed below, the corresponding simpler generating PDEs with constant delay are listed in Section 5.

Equation (2). Consider a reaction–diffusion equation with anisotropic time delay,

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+uf(w/u),w=u(x,t-\tau \left(x\right)),\end{array}$$

(9)

where $f\left(z\right)$ is an arbitrary function that is nonlinear, in general.

Equation (9) has a multiplicative separable solution of the form (6), where the function $\phi =\phi \left(x\right)$ satisfies the second-order linear ODE:

$$\begin{array}{c}\hfill a{\phi }_{xx}^{″}-\lambda \phi +\phi f\left(e^{-\lambda \tau \left(x\right)}\right)=0.\end{array}$$

(10)

Equation (3). An equation more complex than (9),

$$\begin{array}{c}\hfill u_t={\left[a\left(x\right)u_x\right]}_x+b\left(x\right)u_x+uf(x,w/u),w=u(x,t-\tau \left(x\right)),\end{array}$$

(11)

admits a solution of the form (6) with the function $\phi =\phi \left(x\right)$ satisfying the second-order linear ODE:

$$\begin{array}{c}\hfill a\left(x\right){\phi }_{xx}^{″}+[a^{\prime }\left(x\right)+b\left(x\right)]{\phi }_x^{\prime }-\lambda \phi +\phi f(x,e^{-\lambda \tau \left(x\right)})=0.\end{array}$$

Equation (4). Consider a reaction–diffusion equation with anisotropic time delay of the form:

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+f(u-w),w=u(x,t-\tau \left(x\right)),\end{array}$$

(12)

where $f\left(z\right)$ is an arbitrary function that is nonlinear, in general.

Equation (12) admits a generalized separable solution of the form (8),

$$\begin{array}{c}\hfill u=(Ax+B)t+\psi \left(x\right),\end{array}$$

where A and B are arbitrary constants and the function $\psi =\psi \left(x\right)$ satisfies the second-order linear ODE:

$$a{\psi }_{xx}^{″}+f\left((Ax+B)\tau \left(x\right)\right)-Ax-B=0,$$

which can be easily integrated.

Equation (5). Consider a reaction–diffusion equation more complex than (12),

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+uf(u-w)+wg(u-w)+h(u-w),w=u(x,t-\tau \left(x\right)),\end{array}$$

(13)

where $f\left(z\right)$, $g\left(z\right)$, and $h\left(z\right)$ are arbitrary functions that are nonlinear, in general.

Equation (13) admits a generalized separable solution of the form (8), which is linear in t, with the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ being described by the nonlinear system of ODEs:

$$\begin{array}{cc}\hfill & a{\phi }_{xx}^{″}+\phi [f\left(\phi \tau \right)+g\left(\phi \tau \right)]=0,\tau =\tau \left(x\right),\hfill \\ \hfill & a{\psi }_{xx}^{″}+\psi [f\left(\phi \tau \right)+g\left(\phi \tau \right)]+h\left(\phi \tau \right)-\phi [1+\tau g\left(\phi \tau \right)]=0.\hfill \end{array}$$

The first equation of this system is independent.

Equation (6). The reaction–diffusion equation with anisotropic time delay (13) is further generalized by the equation:

$$\begin{array}{c}\hfill u_t={\left[a\left(x\right)u_x\right]}_x+uf(x,u-w)+wg(x,u-w)+h(x,u-w),w=u(x,t-\tau \left(x\right)).\end{array}$$

This equation admits a generalized separable solution of the form (8) with the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ satisfying the nonlinear system of ODEs:

$$\begin{array}{cc}\hfill & {\left[a\left(x\right){\phi }_x^{\prime }\right]}_x^{\prime }+\phi [f(x,\phi \tau )+g(x,\phi \tau )]=0,\tau =\tau \left(x\right),\hfill \\ \hfill & {\left[a\left(x\right){\psi }_x^{\prime }\right]}_x^{\prime }+\psi [f(x,\phi \tau )+g(x,\phi \tau )]+h(x,\phi \tau )-\phi [1+\tau g(x,\phi \tau )]=0.\hfill \end{array}$$

The first equation of this system is independent.

Equation (7). The reaction–diffusion equation with anisotropic time delay and nonlinear transfer coefficient of power-law type:

$$\begin{array}{c}\hfill u_t=a{\left(u^k{u}_x\right)}_x+bu+u^{k+1}f(w/u),w=u(x,t-\tau \left(x\right)),\end{array}$$

(14)

admits a multiplicative separable exact solution,

$$\begin{array}{c}\hfill u=e^{bt}\phi \left(x\right),\end{array}$$

where the function $\phi =\phi \left(x\right)$ satisfies the nonlinear second-order ODE:

$$a{\left({\phi }^k{\phi }_x^{\prime }\right)}_x^{\prime }+{\phi }^{k+1}f\left(e^{-b\tau \left(x\right)}\right)=0.$$

This ODE allows linearization using the substitution $\theta ={\phi }^{k+1}$.

Remark 7.

Arbitrary function f in Equation (14) can additionally depend on x.

Equation (8). The nonlinear reaction–diffusion equation with anisotropic time delay:

$$\begin{array}{c}\hfill u_t=a{\left(u^{-1/2}{u}_x\right)}_x+u^{1/2}f(u^{1/2}-w^{1/2})+g(u^{1/2}-w^{1/2}),w=u(x,t-\tau \left(x\right)),\end{array}$$

(15)

where $f\left(z\right)$ and $g\left(z\right)$ are arbitrary functions, and it has a functional separable exact solution of the form:

$$\begin{array}{c}\hfill u={[\phi \left(x\right)t+\psi \left(x\right)]}^2.\end{array}$$

(16)

To be specific, we assume that $\phi \left(x\right)>0$ and $\psi \left(x\right)>0$. Then, the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ are described by the nonlinear ODE system:

$$\begin{array}{cc}\hfill & 2a{\phi }_{xx}^{″}+\phi f\left(\phi \tau \right)-2{\phi }^2=0,\tau =\tau \left(x\right),\hfill \\ \hfill & 2a{\psi }^{″}+\psi f\left(\phi \tau \right)+g\left(\phi \tau \right)-2\phi \psi =0.\hfill \end{array}$$

Remark 8.

Arbitrary functions f and g in Equation (15) can additionally depend on x.

Equation (9). The reaction–diffusion equation with anisotropic time delay and nonlinear transfer coefficient of exponential type:

$$\begin{array}{c}\hfill u_t=a{\left(e^{\lambda u}{u}_x\right)}_x+b+e^{\lambda u}f(u-w),w=u(x,t-\tau \left(x\right)),\end{array}$$

(17)

has an additive separable solution,

$$u(x,t)=bt+\phi \left(x\right),$$

where the function $\phi =\phi \left(x\right)$ is described by the linear second-order ODE:

$$a{\left(e^{\lambda \phi }{\phi }_x^{\prime }\right)}_x^{\prime }+e^{\lambda \phi }f\left(b\tau \left(x\right)\right)=0.$$

The substitution $\theta =e^{\lambda \phi }$ reduces this equation to a linear ODE.

Remark 9.

Arbitrary function f in Equation (17) can additionally depend on x.

Equation (10). The reaction–diffusion equation with anisotropic time delay and nonlinear transfer coefficient:

$$\begin{array}{c}\hfill u_t={\left[a\left(x\right)f_u^{\prime }\left(u\right)u_x\right]}_x+\frac{b}{f_u^{\prime }\left(u\right)}+g\left(f\left(u\right)-f\left(w\right)\right),w=u(x,t-\tau \left(x\right)),\end{array}$$

(18)

where $f\left(z\right)$ and $g\left(z\right)$ are arbitrary functions, has an exact solution in implicit form,

$$\begin{array}{c}\hfill f\left(u\right)=bt+\theta \left(x\right),\end{array}$$

where the function $\theta =\theta \left(x\right)$ satisfies the linear second-order ODE:

$$\begin{array}{c}\hfill {\left[a\left(x\right){\theta }_x^{\prime }\right]}_x^{\prime }+g\left(b\tau \left(x\right)\right)=0.\end{array}$$

The general solution of this ODE is:

$$\theta =-\int \frac{1}{a\left(x\right)}\left(\int g\left(b\tau \left(x\right)\right)dx\right)dx+C_1\int \frac{dx}{a\left(x\right)}+C_2,$$

where $C_1$ and $C_2$ are arbitrary constants.

Equation (11). The reaction–diffusion equation with anisotropic time delay and nonlinear transfer coefficient:

$$\begin{array}{c}\hfill u_t=a{\left[f_u^{\prime }\left(u\right)u_x\right]}_x+b\frac{f\left(u\right)}{f_u^{\prime }\left(u\right)}+f\left(u\right)g\left(\frac{f\left(w\right)}{f\left(u\right)}\right),w=u(x,t-\tau \left(x\right)),\end{array}$$

(19)

where $f\left(z\right)$ and $g\left(z\right)$ are arbitrary functions, has an exact solution in implicit form,

$$\begin{array}{c}\hfill f\left(u\right)=e^{bt}\phi \left(x\right),\end{array}$$

where the function $\phi =\phi \left(x\right)$ satisfies the linear second-order ODE:

$$\begin{array}{c}\hfill a{\phi }_{xx}^{″}+g\left(e^{-b\tau \left(x\right)}\right)\phi =0.\end{array}$$

Remark 10.

Arbitrary function g in Equations (18) and (19) can additionally depend on x.

3.2. Reaction–Diffusion Equations with Proportional Anisotropic Time Delay

Equation (12). Consider a linear reaction–diffusion equation with proportional anisotropic time delay,

$$\begin{array}{c}\hfill u_t=a{u}_{xx}+bu+cw,w=u(x,p\left(x\right)t),\end{array}$$

(20)

where $p\left(x\right)$ is any function satisfying the condition $0<p\left(x\right)\le 1$; b and c are free parameters.

Equation (20) admits a generalized separable solution, linear in t,

$$\begin{array}{c}\hfill u=\phi \left(x\right)t+\psi \left(x\right),\end{array}$$

(21)

where the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ are described by the linear system of ODEs:

$$\begin{array}{cc}\hfill & a{\phi }_{xx}^{″}+(b+cp\left(x\right))\phi =0,\hfill \\ \hfill & a{\psi }_{xx}^{″}+(b+c)\psi -\phi =0,\hfill \end{array}$$

which can be easily integrated.

There are also solutions of the polynomial form in t,

$$\begin{array}{c}\hfill u=\sum _{k=0}^n{\phi }_k\left(x\right)t^k,\end{array}$$

(22)

where n is an arbitrary positive integer, and the functions ${\phi }_k\left(x\right)$ are described by a system of ODEs.

Solutions (21) and (22) were obtained by analogy from a corresponding simpler generating PDE. It has the form of (20) with a constant scaling parameter $p\left(x\right)\equiv p=\mathrm{const}$.

Remark 11.

For all the PDEs with proportional anisotropic time delay, which are discussed below, the corresponding simpler generating PDEs with constant scaling parameters are listed in Section 5.

Equation (13). The reaction–diffusion equation with proportional anisotropic time delay and nonlinear transfer coefficient of power-law type:

$$\begin{array}{c}\hfill u_t=a{\left(u^k{u}_x\right)}_x+u^{k+1}f(w/u),w=u(x,p\left(x\right)t),\end{array}$$

(23)

where $0<p\left(x\right)\le 1$ and $f\left(z\right)$ is an arbitrary function, admits a multiplicative separable exact solution,

$$\begin{array}{c}\hfill u=t^{-1/k}\phi \left(x\right),\end{array}$$

where the function $\phi =\phi \left(x\right)$ satisfies the nonlinear second-order ODE:

$$\begin{array}{c}\hfill a{\left({\phi }^k{\phi }_x^{\prime }\right)}_x^{\prime }+{\phi }^{k+1}f\left(p^{-1/k}\left(x\right)\right)+\frac{1}{k}\phi =0.\end{array}$$

Equation (14). The reaction–diffusion equation with proportional anisotropic time delay and nonlinear transfer coefficient of exponential type:

$$\begin{array}{c}\hfill u_t=a{\left(e^{\lambda u}{u}_x\right)}_x+e^{\lambda u}f(u-w),w=u(x,p\left(x\right)t),\end{array}$$

(24)

where $0<p\left(x\right)\le 1$ and $f\left(z\right)$ is an arbitrary function, admits an additive separable solution,

$$u=-\frac{1}{\lambda }lnt+\phi \left(x\right),$$

where the function $\phi =\phi \left(x\right)$ is described by the second-order ODE:

$$a{\left(e^{\lambda \phi }{\phi }_x^{\prime }\right)}_x^{\prime }+\frac{1}{\lambda }+e^{\lambda \phi }f\left(\frac{1}{\lambda }lnp\left(x\right)\right)=0.$$

The substitution $\theta =e^{\lambda \phi }$ reduces this equation to a linear ODE.

Remark 12.

Arbitrary function f in Equations (23) and (24) can additionally depend on x.

4. Exact Solutions of Wave-Type PDEs

4.1. Wave-Type Equations with Spatially Anisotropic Time Delay

Equation (15). Consider a linear wave-type equation with anisotropic time delay of the form:

$$\begin{array}{c}\hfill u_{tt}=a{u}_{xx}+bu+cw,w=u(x,t-\tau \left(x\right)),\end{array}$$

(25)

where b and c are free parameters.

$1^{\circ }$. Equation (25) has a multiplicative separable exact solution,

$$\begin{array}{c}\hfill u=e^{\lambda t}\phi \left(x\right),\end{array}$$

(26)

where $\lambda$ is an arbitrary constant and the function $\phi =\phi \left(x\right)$ is described by the linear second-order ODE:

$$\begin{array}{c}\hfill a{\phi }_{xx}^{″}+(b-{\lambda }^2+c{e}^{-\lambda \tau \left(x\right)})\phi =0.\end{array}$$

$2^{\circ }$. Equation (25) also has a generalized separable exact solution, periodic in t,

$$\begin{array}{c}\hfill u=\phi \left(x\right)cos\left(\lambda t\right)+\psi \left(x\right)sin\left(\lambda t\right),\end{array}$$

where the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ satisfy the linear system of ODEs:

$$\begin{array}{cc}\hfill & a{\phi }_{xx}^{″}+[b+{\lambda }^2+ccos\left(\lambda \tau \right)]\phi -csin\left(\lambda \tau \right)\psi =0,\tau =\tau \left(x\right),\hfill \\ \hfill & a{\psi }_{xx}^{″}+[b+{\lambda }^2+ccos\left(\lambda \tau \right)]\psi +csin\left(\lambda \tau \right)\phi =0.\hfill \end{array}$$

$3^{\circ }$. There are also solutions of the polynomial form in t,

$$u=\sum _{k=0}^n{\phi }_k\left(x\right)t^k,$$

where n is an arbitrary positive integer and the functions ${\phi }_k\left(x\right)$ are described by a system of ODEs.

Equation (16). The nonlinear wave-type equation with anisotropic time delay:

$$\begin{array}{c}\hfill u_{tt}=a{u}_{xx}+uf(w/u),w=u(x,t-\tau \left(x\right)),\end{array}$$

(27)

where $\tau \left(x\right)>0$ and $f\left(z\right)$ is an arbitrary function, admits the multiplicative separable exact solution (26) with the function $\phi =\phi \left(x\right)$ satisfiying the linear second-order ODE:

$$\begin{array}{c}\hfill a{\phi }_{xx}^{″}-{\lambda }^2\phi +\phi f\left(e^{-\lambda \tau \left(x\right)}\right)=0.\end{array}$$

Equation (17). A wave-type equation more complex than (27),

$$\begin{array}{c}\hfill u_{tt}={\left[a\left(x\right)u_x\right]}_x+b\left(x\right)u_x+uf(x,w/u),w=u(x,t-\tau \left(x\right)),\end{array}$$

(28)

where $f(x,z)$ is an arbitrary function, admits solution (26) with the function $\phi =\phi \left(x\right)$ satisfying the linear second-order ODE:

$$\begin{array}{c}\hfill a\left(x\right){\phi }_{xx}^{″}+[a^{\prime }\left(x\right)+b\left(x\right)]{\phi }_x^{\prime }-{\lambda }^2\phi +\phi f(x,e^{-\lambda \tau \left(x\right)})=0.\end{array}$$

Equation (18). The wave-type equation with anisotropic time delay and nonlinear speed:

$$\begin{array}{c}\hfill u_{tt}=a{\left(u^k{u}_x\right)}_x+bu+u^{k+1}f(w/u),w=u(x,t-\tau \left(x\right)),\end{array}$$

(29)

where $f\left(z\right)$ is an arbitrary function, admits a multiplicative separable exact solution of the form:

$$\begin{array}{c}\hfill u=e^{\pm \sqrt{b}t}\phi \left(x\right),\end{array}$$

where the function $\phi =\phi \left(x\right)$ satisfies the ODE:

$$a{\left({\phi }^k{\phi }_x^{\prime }\right)}_x^{\prime }+{\phi }^{k+1}f\left(e^{\mp \sqrt{b}\tau \left(x\right)}\right)=0.$$

Remark 13.

Arbitrary function f in Equation (29) can additionally depend on x.

Equation (19). The wave-type equation with anisotropic time delay and nonlinear speed:

$$\begin{array}{c}\hfill u_{tt}=a{\left(u^{-1/2}{u}_x\right)}_x+u^{1/2}f(u^{1/2}-w^{1/2})+g(u^{1/2}-w^{1/2}),w=u(x,t-\tau \left(x\right)),\end{array}$$

(30)

where $f\left(z\right)$ and $g\left(z\right)$ are arbitrary functions, admits a functional separable exact solution,

$$\begin{array}{c}\hfill u={[\phi \left(x\right)t+\psi \left(x\right)]}^2.\end{array}$$

(31)

To be specific, we assume that $\phi \left(x\right)>0$ and $\psi \left(x\right)>0$. Then, the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ are described by the nonlinear system of ODEs:

$$\begin{array}{cc}\hfill & 2a{\phi }_{xx}^{″}+\phi f\left(\phi \tau \right)=0,\tau =\tau \left(x\right),\hfill \\ \hfill & 2a{\psi }^{″}+\psi f\left(\phi \tau \right)+g\left(\phi \tau \right)-2{\phi }^2=0.\hfill \end{array}$$

The first equation is independent.

Remark 14.

Arbitrary functions f and g in Equation (30) can additionally depend on x.

Equation (20). The wave-type equation with anisotropic time delay and nonlinear speed:

$$\begin{array}{c}\hfill u_{tt}={\left[a\left(x\right)f_u^{\prime }\left(u\right)u_x\right]}_x-b^2\frac{f_{uu}^{″}}{{\left(f_u^{\prime }\right)}^3}+g\left(f\left(u\right)-f\left(w\right)\right),w=u(x,t-\tau \left(x\right)),\end{array}$$

where $f\left(z\right)$ and $g\left(z\right)$ are arbitrary functions, has an exact solution in implicit form,

$$\begin{array}{c}\hfill f\left(u\right)=bt+\theta \left(x\right),\end{array}$$

with the function $\theta =\theta \left(x\right)$ satisfying the linear second-order ODE:

$$\begin{array}{c}\hfill {\left[a\left(x\right){\theta }_x^{\prime }\right]}_x^{\prime }+g\left(b\tau \left(x\right)\right)=0.\end{array}$$

The general solution of this ODE is:

$$\theta =-\int \frac{1}{a\left(x\right)}\left(\int g\left(b\tau \left(x\right)\right)dx\right)dx+C_1\int \frac{dx}{a\left(x\right)}+C_2,$$

where $C_1$ and $C_2$ are arbitrary constants.

Equation (21). The wave-type equation with anisotropic time delay and nonlinear speed:

$$\begin{array}{c}\hfill u_{tt}={\left[a\left(x\right)f_u^{\prime }{u}_x\right]}_x+b^2\frac{f}{f_u^{\prime }}\left(1-\frac{f{f}_{uu}^{″}}{{\left(f_u^{\prime }\right)}^2}\right)+fg\left(\frac{\overline{f}}{f}\right),\overline{f}=f\left(w\right),w=u(x,t-\tau \left(x\right)),\end{array}$$

where $f\left(z\right)$ and $g\left(z\right)$ are arbitrary functions, has an exact solution in implicit form,

$$\begin{array}{c}\hfill f\left(u\right)=e^{bt}\phi \left(x\right),\end{array}$$

with the function $\phi =\phi \left(x\right)$ satisfying the linear second-order ODE:

$$\begin{array}{c}\hfill {\left[a\left(x\right){\phi }_x^{\prime }\right]}_x^{\prime }+g\left(e^{-b\tau \left(x\right)}\right)\phi =0.\end{array}$$

4.2. Wave-Type Equations with Proportional Anisotropic Time Delay

Equation (22). Consider a linear wave-type PDE with proportional anisotropic time delay,

$$\begin{array}{c}\hfill u_{tt}=a{u}_{xx}+bu+cw,w=u(x,p\left(x\right)t),\end{array}$$

(32)

where $p\left(x\right)$ is a function satisfying the condition $0<p\left(x\right)\le 1$; b and c are free parameters.

Equation (32) admits a generalized separable solution,

$$\begin{array}{c}\hfill u=\phi \left(x\right)t^2+\psi \left(x\right),\end{array}$$

where the functions $\phi =\phi \left(x\right)$ and $\psi =\psi \left(x\right)$ are described by the linear system of ODEs:

$$\begin{array}{cc}\hfill & a{\phi }_{xx}^{″}+(b+c{p}^2\left(x\right))\phi =0,\hfill \\ \hfill & a{\psi }_{xx}^{″}+(b+c)\psi -2\phi =0,\hfill \end{array}$$

which can be easily integrated sequentially.

There are also solutions of the polynomial form in t,

$$u=\sum _{k=0}^n{\phi }_k\left(x\right)t^k,$$

where n is an arbitrary positive integer and the ${\phi }_k\left(x\right)$ are described by a system of ODEs.

Equation (23). The wave PDE with proportional anisotropic time delay and nonlinear speed of power-law type:

$$\begin{array}{c}\hfill u_{tt}=a{\left(u^k{u}_x\right)}_x+u^{k+1}f(w/u),w=u(x,p\left(x\right)t),\end{array}$$

(33)

where $0<p\left(x\right)\le 1$ and $f\left(z\right)$ is an arbitrary function, admits a multiplicative separable exact solution,

$$\begin{array}{c}\hfill u=t^{-2/k}\phi \left(x\right),\end{array}$$

(34)

where the function $\phi =\phi \left(x\right)$ satisfies the nonlinear second-order ODE:

$$\begin{array}{c}\hfill a{\left({\phi }^k{\phi }_x^{\prime }\right)}_x^{\prime }+{\phi }^{k+1}f\left(p^{-2/k}\right)-\frac{2(2+k)}{k^2}\phi =0,p=p\left(x\right).\end{array}$$

(35)

Equation (24). The wave PDE with proportional anisotropic time delay and nonlinear speed of exponential type:

$$\begin{array}{c}\hfill u_{tt}=a{\left(e^{\lambda u}{u}_x\right)}_x+e^{\lambda u}f(u-w),w=u(x,p\left(x\right)t),\end{array}$$

(36)

where $0<p\left(x\right)\le 1$ and $f\left(z\right)$ is an arbitrary function, admits an additive separable solution,

$$u=-\frac{2}{\lambda }lnt+\phi \left(x\right),$$

where the function $\phi =\phi \left(x\right)$ is described by the nonlinear second-order ODE:

$$a{\left(e^{\lambda \phi }{\phi }_x^{\prime }\right)}_x^{\prime }-\frac{2}{\lambda }+e^{\lambda \phi }f\left(\frac{2}{\lambda }lnp\right)=0,p=p\left(x\right).$$

The substitution $\theta =e^{\lambda \phi }$ reduces this equation to a linear ODE.

5. Table of Generating PDEs with Constant or Proportional Delay

Table 2. Generating PDEs with constant or proportional delay.

No.	Form of Equation	References/Comments
1	$u_t=a{u}_{xx}+bu+cw,w=u(x,t-\tau )$	Equation (5) with $\tau =\mathrm{const}$
2	$u_t=a{u}_{xx}+uf(w/u),w=u(x,t-\tau )$	[31,33]
3	$u_t={\left[a\left(x\right)u_x\right]}_x+b\left(x\right)u_x+uf(x,w/u),w=u(x,t-\tau )$	[31]
4	$u_t=a{u}_{xx}+f(u-w),w=u(x,t-\tau )$	[31,33]
5	$u_t=a{u}_{xx}+uf(u-w)+wg(u-w)+h(u-w),w=u(x,t-\tau )$	[33]
6	$u_t={\left[a\left(x\right)u_x\right]}_x+uf(x,u-w)+wg(x,u-w)+h(x,u-w),w=u(x,t-\tau )$	[31]
7	$u_t=a{\left(u^k{u}_x\right)}_x+bu+u^{k+1}f(w/u),w=u(x,t-\tau )$	[79]
8	$u_t=a{\left(u^{-1/2}{u}_x\right)}_x+u^{1/2}f(u^{1/2}-w^{1/2})+g(u^{1/2}-w^{1/2}),w=u(x,t-\tau )$	[79]
9	$u_t=a{\left(e^{\lambda u}{u}_x\right)}_x+b+e^{\lambda u}f(u-w),w=u(x,t-\tau )$	[79]
10	$u_t={\left[a\left(x\right)f_u^{\prime }\left(u\right)u_x\right]}_x+\frac{b}{f_u^{\prime }\left(u\right)}+g\left(f\left(u\right)-f\left(w\right)\right),w=u(x,t-\tau )$	[79,80,81]
11	$u_t=a{\left[f_u^{\prime }\left(u\right)u_x\right]}_x+f\left(u\right)g\left(\frac{f\left(w\right)}{f\left(u\right)}\right)+b\frac{f\left(u\right)}{f_u^{\prime }\left(u\right)},w=u(x,t-\tau )$	[79,81]
12	$u_t=a{u}_{xx}+bu+cw,w=u(x,pt)$	Equation (20) with $p=\mathrm{const}$
13	$u_t=a{\left(u^k{u}_x\right)}_x+u^{k+1}f(w/u),w=u(x,pt)$	[83]
14	$u_t=a{\left(e^{\lambda u}{u}_x\right)}_x+e^{\lambda u}f(u-w),w=u(x,pt)$	[83]
15	$u_{tt}=a{u}_{xx}+bu+cw,w=u(x,t-\tau )$	Equation (25) with $\tau =\mathrm{const}$
16	$u_{tt}=a{u}_{xx}+uf(w/u),w=u(x,t-\tau )$	[91]
17	$u_{tt}={\left[a\left(x\right)u_x\right]}_x+b\left(x\right)u_x+uf(x,w/u),w=u(x,t-\tau )$	Equation (28) with $\tau =\mathrm{const}$
18	$u_{tt}=a{\left(u^k{u}_x\right)}_x+bu+u^{k+1}f(w/u),w=u(x,t-\tau )$	[81]
19	$u_{tt}=a{\left(u^{-1/2}{u}_x\right)}_x+u^{1/2}f(u^{1/2}-w^{1/2})+g(u^{1/2}-w^{1/2}),w=u(x,t-\tau )$	[114]
20	$u_{tt}={\left[a\left(x\right)f_u^{\prime }\left(u\right)u_x\right]}_x-b^2\frac{f_{uu}^{″}}{{\left(f_u^{\prime }\right)}^3}+g\left(f\left(u\right)-f\left(w\right)\right),w=u(x,t-\tau )$	[80,81,114]
21	$u_{tt}={\left[a\left(x\right)f_u^{\prime }{u}_x\right]}_x+b^2\frac{f}{f_u^{\prime }}\left(1-\frac{f{f}_{uu}^{″}}{{\left(f_u^{\prime }\right)}^2}\right)+fg\left(\frac{\overline{f}}{f}\right),\overline{f}=f\left(w\right),w=u(x,t-\tau )$	[81]
22	$u_{tt}=a{u}_{xx}+bu+cw,w=u(x,pt)$	Equation (32) with $p=\mathrm{const}$
23	$u_{tt}=a{\left(u^k{u}_x\right)}_x+u^{k+1}f(w/u),w=u(x,pt)$	[97]
24	$u_{tt}=a{\left(e^{\lambda u}{u}_x\right)}_x+e^{\lambda u}f(u-w),w=u(x,pt)$	[97]

presents generating PDEs with constant or proportional delay and references to publications that include these equations and their exact solutions. In the absence of such publications, reference is made to the equation from this article.

These equations were used to construct the more complex PDEs with anisotropic time delay described in Section 3 and Section 4.

Remark 15.

Some generating equations in Table 2 are less general than those considered in the corresponding references. For example, in [79], we have the delay PDE:

$$u_t=a{\left(u^k{u}_x\right)}_x+uf(w/u)+u^{k+1}g(w/u),w=u(x,t-\tau ),$$

which is the generating equation in row 7 with $f\left(z\right)\equiv b$.

6. Brief Conclusions

We have considered linear and nonlinear reaction–diffusion and wave-type PDEs with anisotropic (spatially variable) time delay that involve, in addition to the unknown function $u(x,t)$, functions of the form $u(x,t-\tau (x\left)\right)$, where $\tau \left(x\right)>0$ is the anisotropic time delay. Equations of a fairly general form containing one, two, or more arbitrary functions have been analyzed. Reaction–diffusion and wave-type PDEs with proportional anisotropic time delays that involve $u(x,p(x\left)t\right)$, where $0<p\left(x\right)<1$, have also been presented. Additive, multiplicative, functional, and generalized separable solutions of such equations with complicated delays have been described. The results of the article can be used for testing numerical and approximate analytical methods of solving complex PDEs with variable delay and related functional PDEs.