Abstract
The goal of this work is to build semi-analytical solutions of the Rikitake-type system by means of the optimal homotopy perturbation method (OHPM) using only two iterations. The chaotic behaviors are excepted. By taking into consideration the geometrical properties of the Rikitake-type system, the closed-form solutions can be established. The obtained solutions have a periodical behavior. These geometrical properties allow reducing the initial system to a second-order nonlinear differential equation. The latter equation is solved analytically using the OHPM procedure. The validation of the OHPM method is presented for three cases of the physical parameters. The advantages of the OHPM technique, such as the small number of iterations (the efficiency), the convergence control (in the sense that the semi-analytical solutions are approaching the exact solution), and the writing of the solutions in an effective form, are shown graphically and with tables. The accuracy of the results provides good agreement between the analytical and corresponding numerical results. Other dynamic systems with similar geometrical properties could be successfully solved using the same procedure.
Keywords:
optimal homotopy perturbation method; Rikitake system; symmetries; Hamilton–Poisson realization; periodical orbits MSC:
37B65; 37C79; 65H20; 37J06; 37J35; 65L99
1. Introduction
The first study of the Rikitake system [1] examined the behavior of two disk dynamos coupled one to another in relation to Earth’s magnetic field. These studies were continued by Steeb [2].
Some relevant dynamical and geometrical properties of the Rikitake system were examined in [3] by reporting the stability of the equilibria points, the existence of the symmetries [4], the Hamilton–Poisson realization of the Rikitake-type system with control, the existence of the periodic orbits, the Lax formulation [5,6,7], and the integrable deformations [8].
Other dynamical systems with geometrical properties are the Rabinovich system, studied in [9,10,11], the Kermack–McKendrick system, investigated in [12], and the Rossler system, explored in [13]. In addition, a Lotka–Volterra-type system was studied in [14], and a T system with an integrable deformation was examinated in [15].
Beyond the geometrical properties, many of the dynamical systems have chaotic behaviors and are found in practical applications in engineering (e.g., Chua’s circuits [16,17], the turbulence in the atmosphere and oceans [18], and plasma control systems [19]) or in medicine (e.g., multi-scale synthesis of Alzheimer’s pathogenesis [20], neuroethology [21], and a model of stress as a dynamical system [22]).
Other analytical methods for solving nonlinear differential problems were developed, namely the variational iteration method (VIM) [23,24], the multiple scales technique [25], the homotopy perturbation method (HPM) [26], the modified Laplace transform homotopy perturbation method (MLT-HPM) [27], the homotopy analysis method (HAM) [28], the least squares differential quadrature method [29], the polynomial least squares method [30], the function method [31], the optimal iteration parametrization method (OIPM) [32], the optimal variational iteration method (OVIM) [33], the optimal homotopy asymptotic method (OHAM) [34,35,36], the and optimal homotopy perturbation method (OHPM) [37,38]. The modified homotopy perturbation method (MHPM) is applied to solve sine-Gordon and coupled sine-Gordon equations [39], among other applications [40,41,42]. The modified homotopy analysis method (MHAM) is used to find appropriate solutions to Zakharov–Kuznetsov equations [43], among other uses [44]. To build some new exact solitary wave solutions for the sixth-order Boussinesq equation, which plays an important role in mathematical physics, engineering sciences and applied mathematics, the exp-function method is proposed [45], among other applications [46,47]. The modified exp-function method explores the strain wave equation in micro-structured solids, which is applied in solid physics [48], among other applications [49,50,51,52,53].
The structure of this paper is as follows. In Section 2, we present the geometrical properties and the closed-form solutions of the Rikitake-type system. Section 3 is dedicated to the basic ideas of the OHPM technique. Section 4 is focused on building semi-analytical solutions using the OHPM method. Section 5 provides the numerical results. The last section is dedicated to the conclusions.
2. The Rikitake-Type System
2.1. Global Analytic First Integrals and Hamilton–Poisson Realizations
The Rikitake-type system has the following form (see [5,6]):
where k is the tuning parameter and the state variables x, y, and z depend on and .
For the physical system describing the behavior of two disk dynamos coupled to one another in relation to Earth’s magnetic field, in agreement with [54], the state variables x, y, and z are expressed as
where and are the currents, C is moment of inertia of a dynamo about its axis, M is the mutual inductance between the dynamo circuits, L is the self-inductance, G is the torque which describes the motion of the dynamos in the report of Ohmic losses in the coils and disks, and is the angular velocity.
Remark 1.
Some geometrical properties of the system in Equation (1) are the following:
- This system admits a symmetry with respect to the axis (invariant to the transformation for , ) and symmetries with respect to all coordinate axes for and ;
- The system has a Hamilton–Poisson realization, with the Hamiltonian and the Casimir given by and , respectively, for , , , and for the special case where and ;
- The existence of the periodic orbits ensures that the solutions have periodic behaviors.
Remark 2.
Let the initial conditions be
Then, the phase curves of dynamics (1) are the intersections of the following surfaces
and
respectively.
2.2. Closed-Form Solutions
For three cases of the selected physical parameters , k, the closed-form solutions of the system in Equation (1) are obtained.
- (i)
- For , ,
The transformations
where , is an unknown smooth function, giving the closed-form solutions.
The third equation from Equation (1) yields
From Equation (1), we obtain
Remark 3.
- (ii)
- In the case , ,
The closed-form solutions can be written as
where .
Equation (1) yields
The following nonlinear problem gives the unknown function
with .
- (iii)
- A remarkable case is , .
The closed-form solutions could have the form
where . Then the third equation from Equation (1) yields
where is the solution of the following nonlinear problem
Remark 4.
An analytical approximate solution of Equation (1) is said to be a semi-analytical solution and will be denoted by , , or , , by the OHPM technique.
3. The Steps of the OHPM Technique
This section describes the ideas of the OHPM for the second-order nonlinear differential Equation [35,37,38]
with the initial/boundary conditions
where , and are the linear, nonlinear and boundary operators, respectively, and D is domain of interest and is an arbitrary continuous function.
Let be an initial approximation of the unknown function , such as
and be an embedding parameter. In the following, we consider a function in the particular form
where , are arbitrary parameters which will be determined later, is named the first approximation and is named the second approximation. Obviously, when and it holds that
respectively. Thus, as p increases from 0 to 1, the solution varies from to the solution . Consequently, the second-order approximate solution can be written as
The initial/boundary conditions become
Series expansion of the nonlinear operator with respect to the parameter p yields
where .
The homotopy relation given by Equation (23) becomes
Let , , be a number of unknown auxiliary functions that depend on the variable t and some parameters , , where is a given integer number. The following new homotopy relation is proposed:
In the following, the terms in are neglected.
Now, equating the coefficients of , and into Equation (28), it holds that is given by Equation (18), and the first approximation is obtained from the following equation:
and the second approximation is obtained from the following equation:
The nonlinear operators , , and which appear in Equations (30) and (31) may be written in the general form
where the known functions , and depend on the function and also on the nonlinear operator , m being a known integer. It is more convenient to consider the unknown function in the following forms
or
and the unknown function in the forms
or
The expression of the optimal auxiliary functions contains combinations of functions and several unknown parameters , , and n is an arbitrary integer number. There are a lot a possibility to choose the value of the integer positive n and the optimal auxiliary functions . The values of the parameters can be optimally computed via various methods: the collocation method, the least-square method, the Galerkin method, the Ritz method, and so on.
The second-order semi-analytical solutions given by Equation (21) are well-determined.
4. Approximate Analytic Solutions via OHPM
For the initial conditions and , the problem given by Equation (12) is semi-analytically solved by the OHPM technique.
Let be an unknown parameter. This problem can be rewritten as
where the linear and nonlinear operators and could be chosen in the following form:
By using Equation (40) and the initial conditions given by Equation (12), the initial approximation is the solution of the problem via Equation (18) ( = 0), namely
Choosing the auxiliary function , the solution of Equation (42) is:
If is a fixed integer number, then choosing the auxiliary functions , and , respectively, the solution of the Equation (44) has the following form:
where an arbitrary integer number depending on and the convergence-control parameters , , so will be optimally identified, such that .
Finally, the second-order approximate analytic solution is obtained from Equations (21), (41), (43) and (45) in the form
Therefore, by applying the same procedure, we obtain the second-order approximate analytic solution of nonlinear problem Equation (41) and has the form of Equation (46).
For , , from Equation (8) are obtained the linear operator and the nonlinear operator as . The nonlinear operators , and , respectively, which appear in Equations (30) and (31), become , and .
The initial approximation satisfies , with the initial conditions given by Equation (9).
In Equation (8), we can use the approximate expansions
where is an arbitrary integer number.
The expression contains a combination of the elementary functions , , . In Equation (30), choosing the auxiliary function , by a simple computation (neglecting the secular terms), the first approximation has the form
where the convergence-control parameters , , will be optimally identified.
Otherwise, contains a combination of the elementary functions , , . In Equation (31), choosing the auxiliary functions , , , by a simple computation (neglecting the secular terms), the second approximation has the form
where the convergence-control parameters , , will be optimally identified.
5. Numerical Results and Discussions
By taking into account of the second-order semi-analytical solutions given by Equations (46), (48) and (49) with the index , the effective solutions are graphically presented below and are given in Appendix A. These solutions highlighted the accuracy of the OHPM method.
The precision of the obtained results is shown in Figure 1 and Figure 2 (for , ) and Figure 3 and Figure 4 (for , ), respectively.
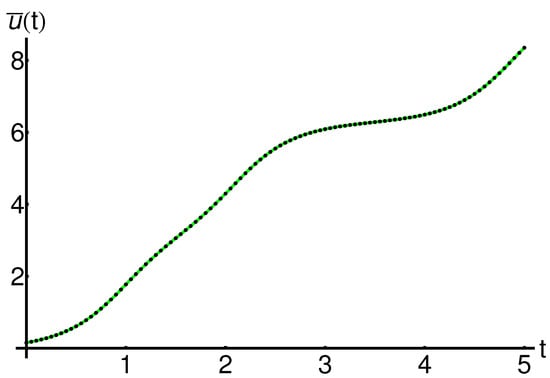
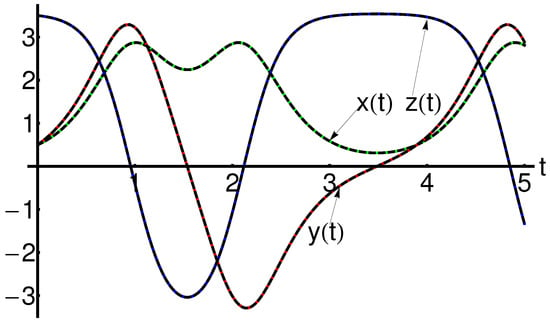
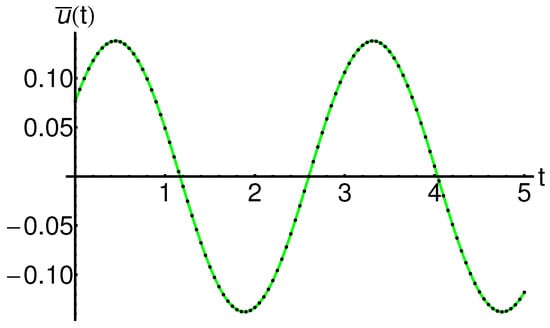
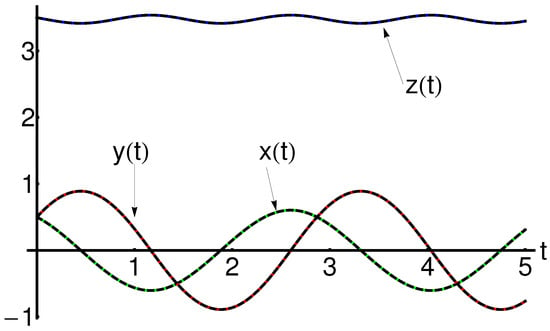
The semi-analytical solutions are in good agreement with the corresponding numerical integration results, computed by means of the fourth-order Runge–Kutta method, as shown in these figures.
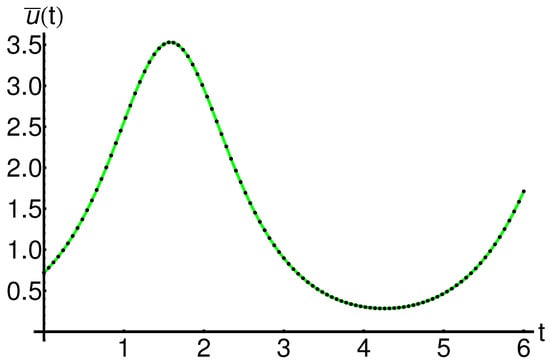
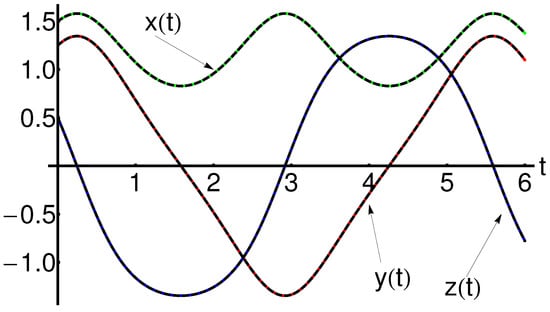
For different values of the parameter , from Equations (46)–(48), the convergence-control parameters , , , , , are optimally computed by the least square method.
The symmetry with respect to the -axis for , and the symmetry with respect to the all coordinate axes for , is highlighted in Figure 7, Figure 8 and Figure 9 (i.e., the periodic orbit of the Rikitake-type system).
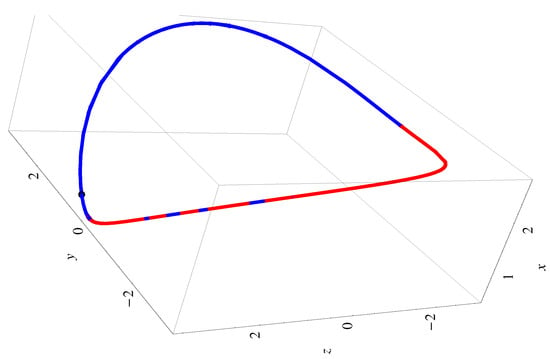
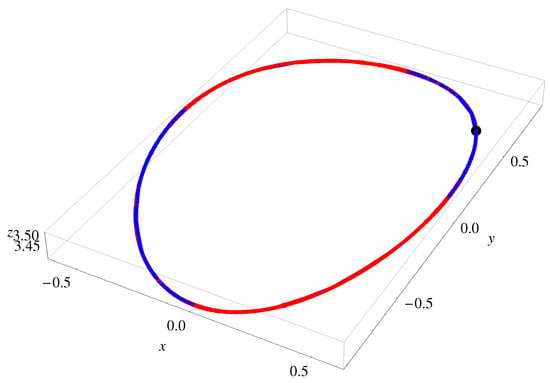
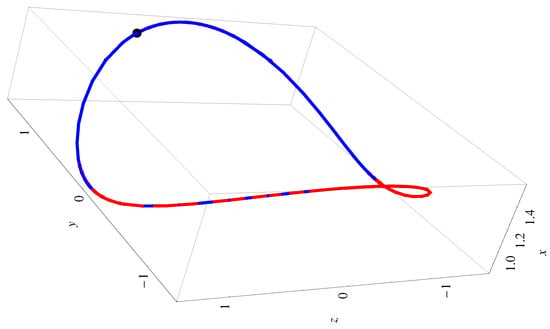
The convergence-control parameters are presented in Appendix A.
Returning to the exact solutions given by Equations (4) and (5), the approximate residuals are as follows:
and
respectively, with , , the semi-analytical solutions obtained via the OHPM method.
Figure 10 and Figure 11 show the profiles of the residuals and , given by Equation (50) in the cases where , for , , and . Figure 12 and Figure 13 show the profiles of the residuals and , given by Equation (51) in the case , for , , and . These figures emphasize the accuracy of the semi-analytical solutions obtained by the OHPM technique by an order of magnitude of of errors. Moreover, the precision of the obtained solutions increases if the index number increases. This can be seen in Table 1. Therefore, in each case, the semi-analytical solutions are approaching the exact solution.
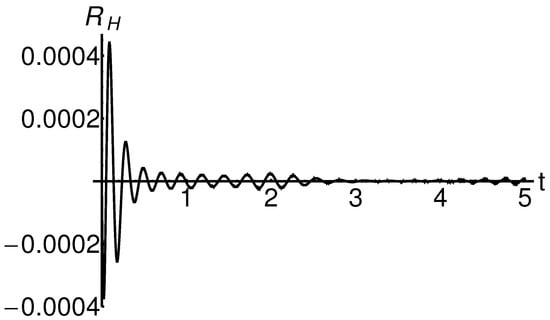
Figure 10.
Profile of the residual given by Equation (50) in the case , for , , and .
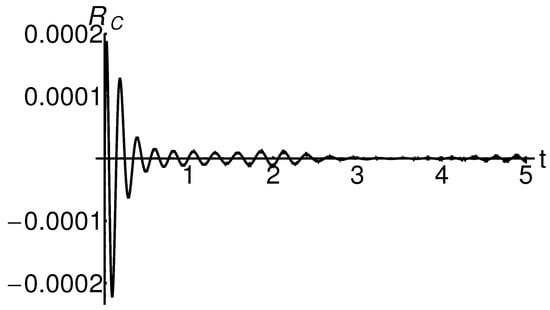
Figure 11.
Profile of the residual given by Equation (50) in the case , for , , and .
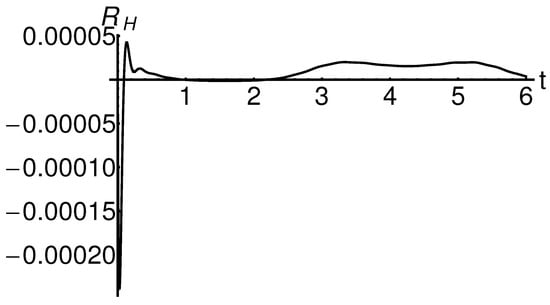
Figure 12.
Profile of the residual given by Equation (51) in the case , for , , and .
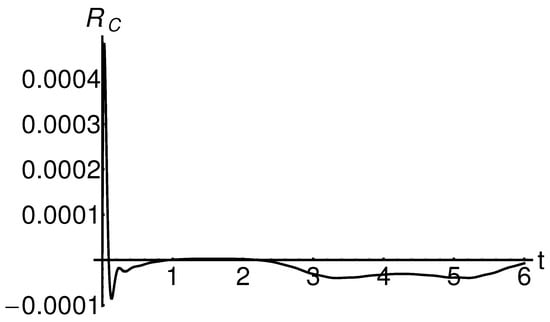
Figure 13.
Profile of the residual given by Equation (51) in the case , for , , and .

Table 1, Table 2 and Table 3 show the influence of the index number on the values of the absolute errors. The values of the better semi-analytical solutions are shown in Table 4, Table 5 and Table 6.




6. Conclusions
In the present work, the Hamilton–Poisson realization of the Rikitake-type system is emphasized and the semi-analytical solutions is established in a closed form. This 3D differential system describes the motion of the two disk dynamos coupled to one another in relation to Earth’s magnetic field. Only the periodic behaviors are taken into account, excluding chaotic ones.
The influence of the global analytic first integrals (the Hamiltonian and the Casimir functions, respectively) of the Rikitake-type system leads to a simplification to a second-order nonlinear differential equation for which the semi-analytical solutions are established.
The solution method is the optimal homotopy perturbation method (OHPM). Only two iterations are used. This method involves the presence of some auxiliary functions which depend on a set of convergence-control parameters. These parameters are optimally computed for some values of the physical parameters k and . The precision of the obtained solutions is shown by comparison with the corresponding numerical results (via the fourth-order Runge–Kutta method). This comparison highlights the effectiveness of the applied method.
The obtain semi-analytical solutions could be successfully used for the study of dynamical systems encountered in electrical engineering (the synchronization, secure communications or optimization of nonlinear system performance) or medicine.
Author Contributions
Conceptualization, R.-D.E. and N.P.; methodology, N.P.; software, R.-D.E. and N.P.; validation, R.-D.E. and N.P.; formal analysis, R.-D.E. and N.P.; investigation, R.-D.E. and N.P.; writing—original draft preparation, R.-D.E. and N.P.; writing—review and editing, R.-D.E. and N.P.; visualization, R.-D.E. and N.P.; supervision, N.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In the following, we will present just the values of the convergence-control parameters that appear in Equation (46).
Appendix A.1. The Case k>0, α>0
Appendix A.2. The Case k<0, α>0
Appendix A.3. The Remarkable Case k=1, α=0
References
- Rikitake, T. Oscillations of a system of disk dynamos. Proc. Camb. Philos. Soc. 1958, 54, 89–105. [Google Scholar] [CrossRef]
- Steeb, W.H. Continuous symmetries of the Lorenz model and the Rikitake two-disc dynamo system. J. Phys. A Math. Gen. 1982, 15, 389–390. [Google Scholar] [CrossRef]
- Braga, D.C.; Scalco, D.F.; Mello, L.F. On the stability of the equilibria of the Rikitake system. Phys. Lett. A 2010, 374, 4316–4320. [Google Scholar] [CrossRef]
- Lazureanu, C.; Binzar, T. On the symmetries of a Rikitake type system. C. R. Math. Acad. Sci. Paris 2012, 350, 529–533. [Google Scholar] [CrossRef]
- Lazureanu, C.; Binzar, T. A Rikitake type system with quadratic control. Int. J. Bifurcat. Chaos 2012, 22, 1250274. [Google Scholar] [CrossRef]
- Binzar, T.; Lazureanu, C. A Rikitake type system with one control. Discret. Contin. Dyn. Syst.-B 2013, 18, 1755–1776. [Google Scholar] [CrossRef]
- Lazureanu, C. Hamilton–Poisson realizations of the integrable deformations of the Rikitake system. Adv. Math. Phys. 2017, 2017, 4596951. [Google Scholar] [CrossRef]
- Lazureanu, C.; Petrisor, C.; Hedrea, C. On a deformed version of the two-disk dynamo system. Appl. Math. 2021, 66, 345–372. [Google Scholar] [CrossRef]
- Llibre, J.; Valls, C. Global analytic integrability of the Rabinovich system. J. Geom. Phys. 2008, 58, 1762–1771. [Google Scholar] [CrossRef]
- Xiang, Z. Integrals of motion of the Rabinovich system. J. Phys. A Math. Gen. 2000, 33, 5137. [Google Scholar] [CrossRef]
- Tudoran, R.M.; Girban, A. On the Hamiltonian dynamics and geometry of the Rabinovich system. Discret. Cont. Dyn.-B 2011, 15, 789–823. [Google Scholar] [CrossRef]
- Lazureanu, C.; Petrisor, C. Stability and energy-Casimir Mapping for integrable deformations of the Kermack-McKendrick system. Adv. Math. Phys. 2018, 2018, 5398768. [Google Scholar] [CrossRef]
- Lazureanu, C.; Binzar, T. Some symmetries of a Rossler type system. Sci. Bull. Math.-Phys. 2013, 58, 1–6. [Google Scholar]
- Lazureanu, C.; Binzar, T. Symplectic realizations and symmetries of a Lotka-Volterra type system. Regul. Chaotic Dyn. 2013, 18, 203–213. [Google Scholar] [CrossRef]
- Lazureanu, C.; Caplescu, C. Stabilization of the T system by an integrable deformation. In Proceedings of the International Conference on Applied Mathematics and Numerical Methods, Craiova, Romania, 29–31 October 2020. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Leonov, G.A.; Mokaev, T.N.; Seledzhi, S.M. Hidden attractor in the Rabinovich system, Chua circuits and PLL. AIP Conf. Proc. 2016, 1738, 210008. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H. Intelligent control of convergence rate of impulsive dynamic systems affected by nonlinear disturbances under stabilizing impulses and its application in Chua’s circuit. Chaos Solitons Fractals 2023, 169, 113289. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Raza, N.; Jhangeer, A. Dynamic study of bifurcation, chaotic behavior and multi-soliton profiles for the system of shallow water wave equations with their stability. Chaos Solitons Fractals 2023, 171, 113436. [Google Scholar] [CrossRef]
- Zheng, W.; Gan, R.; Yuan, Q.; Guo, H.; Ma, H.; Zhang, M.; Xiao, B.; Pan, Y. Design and implementation of a dynamic system simulation framework for plasma control system verification platform. Fusion Eng. Des. 2022, 182, 113249. [Google Scholar] [CrossRef]
- Rollo, J.; Crawford, J.; Hardy, J. A dynamical systems approach for multiscale synthesis of Alzheimer’s pathogenesis. Neuron. 2023; in press. [Google Scholar] [CrossRef]
- Robson, D.N.; Li, J.M. A dynamical systems view of neuroethology: Uncovering stateful computation in natural behaviors. Curr. Opin. Neurobiol. 2022, 73, 102517. [Google Scholar] [CrossRef]
- Brooks, J.; Crone, J.C.; Spangler, D.P. A physiological and dynamical systems model of stress. Int. J. Psychophysiol. 2021, 166, 83–91. [Google Scholar] [CrossRef] [PubMed]
- He, J.H.; Wu, X.H. Variational iteration method: New development and applications. Comp. Math. Appl. 2007, 54, 881–894. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Q.; Atluri, S.N. Combination of the variational iteration method and numerical algorithms for nonlinear problems. Appl. Math. Model. 2020, 79, 243–259. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Hassan, S.S.; Sherif Elbendary. The stability analysis for the motion of a nonlinear damped vibrating dynamical system with three-degrees-of-freedom. Results Phys. 2021, 28, 104561. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Kharrat, B.N.; Toma, G. Analytical Solution of Ordinary Fractional Differential Equations by Modified Homotopy Perturbation Method and Laplace Transform. J. Phys. Conf. Ser. 2019, 1366, 012037. [Google Scholar]
- Hussain, S.; Shah, A.; Ayub, S.; Ullah, A. An approximate analytical solution of the Allen-Cahn equation using homotopy perturbation method and homotopy analysis method. Heliyon 2019, 5, e03060. [Google Scholar] [CrossRef]
- Bota, C.; Caruntu, B.; Tucu, D.; Lapadat, M.; Pasca, M.S. A Least Squares Differential Quadrature Method for a Class of Nonlinear Partial Differential Equations of Fractional Order. Mathematics 2020, 8, 1336. [Google Scholar] [CrossRef]
- Caruntu, B.; Bota, C.; Lapadat, M.; Pasca, M.S. Polynomial Least Squares Method for Fractional Lane-Emden Equations. Symmetry 2019, 11, 479. [Google Scholar] [CrossRef]
- El-Rashidy, K.; Seadawy Aly, R.; Saad, A.; Makhlou, M.M. Multiwave, Kinky breathers and multi-peak soliton solutions for the nonlinear Hirota dynamical system. Results Phys. 2020, 19, 103678. [Google Scholar] [CrossRef]
- Marinca, V.; Draganescu, G.E. Construction of approximate periodic solutions to a modified van der Pol oscillator. Nonlinear Anal. Real World Appl. 2010, 11, 4355–4362. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An optimal variational iteration method. Appl. Math. Lett. 2011, 24, 762–765. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comput. Math. Appl. 2010, 60, 1607–1615. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. The Optimal Homotopy Asymptotic Method—Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Marinca, V.; Herisanu, N. An application of the optimal homotopy asymptotic method to Blasius problem. Rom. J. Tech. Sci. Appl. Mech. 2015, 60, 206–215. [Google Scholar]
- Marinca, V.; Herisanu, N. Nonlinear dynamic analysis of an electrical machine rotor-bearing system by the optimal homotopy perturbation method. Comp. Math. Appl. 2011, 61, 2019–2024. [Google Scholar] [CrossRef]
- Marinca, V.; Ene, R.D.; Marinca, B. Optimal Homotopy Perturbation Method for nonlinear problems with applications. Appl. Comp. Math. 2022, 21, 123–136. [Google Scholar]
- Darvishi, M.T.; Khani, F.; Hamedi-Nezhad, S.; Ryu, S.-W. New modification of the HPM for numerical solutions of the sine-Gordon and coupled sine-Gordon equations. Int. J. Comput. Math. 2010, 87, 908–919. [Google Scholar] [CrossRef]
- Momani, S.; Erjaee, G.H.; Alnasr, M.H. The modified homotopy perturbation method for solving strongly nonlinear oscillators. Comput. Math. Appl. 2009, 58, 2209–2220. [Google Scholar] [CrossRef]
- Kharrat, B.N.; Toma, G. Modified Homotopy Perturbation Method by Using Sumudu Transform for Solving Initial Value Problems Represented By System of Nonlinear Partial Differential Equations. World Appl. Sci. J. 2018, 36, 844–849. [Google Scholar]
- Belendez, A.; Pascual, C.; Belendez, T.; Hernandez, A. Solution of an anti-symmetric quadratic nonlinear oscillator by a modified He’s homotopy perturbation method. Nonlinear Anal.-Real. 2009, 10, 416–427. [Google Scholar] [CrossRef]
- Usman, M.; Zubair, T.; Rashid, I.; Rashid, I.; Yildirim, A.; Mohyud-Din, S.T. Modified Homotopy Analysis Method for Zakharov–Kuznetsov Equations. Walailak J. Sci. Tech. 2013, 10, 467–478. [Google Scholar]
- Yin, X.B.; Kumar, S.; Kumar, D. A modified homotopy analysis method for solution of fractional wave equations. Adv. Mech. Eng. 2015, 7, 1–8. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A.; Akbar, M.A. The exp-function method for new exact solutions of the nonlinear partial differential equations. Int. J. Phys. Sci. 2011, 6, 6706–6716. [Google Scholar]
- Misirli, E.; Gurefe, Y. Exp-function method for solving nonlinear evolution equations. Math. Comput. Appl. 2011, 16, 258–266. [Google Scholar] [CrossRef]
- Abdou, M.A.; Hendi, A.; Aaid, B. New Applications of Exp-function Method for Solving A Complex Nonlinear Evolution Equations. Stud. Nonlinear Sci. 2012, 3, 14–23. [Google Scholar]
- Shakeel, M.; Attaullah; Shah, N.A.; Chung, J.D. Application of modified exp-function method for strain wave equation for finding analytical solutions. Ain Shams Eng. J. 2023, 14, 101883. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Abdelaziz, M.A.M. The modified Exp-function method and its applications to the generalized K(n,n) and BBM equations with variable coefficient. Iran. J. Sci. Technol. Trans. A Sci. 2012, 36, 359–365. [Google Scholar]
- Shakeel, M.; Attaullah; Shah, N.A.; Chung, J.D. Modified Exp-Function Method to Find Exact Solutions of Microtubules Nonlinear Dynamics Models. Symmetry 2023, 15, 360. [Google Scholar] [CrossRef]
- Akturk, T. Modified exponential function method for nonlinear mathematical models with Atangana conformable derivative. Rev. Mex. Fis. 2021, 67, 040704. [Google Scholar] [CrossRef]
- Shakeel, M.; Mohyud-Din, S.T.; Iqbal, M.A. Modified extended exp-function method for a system of nonlinear partial differential equations defined by seismic sea waves. Pramana J. Phys. 2018, 91, 28. [Google Scholar] [CrossRef]
- Ayati, Z.; Badiepour, A. Two New Modifications of the Exp-Function Method for Solving the Fractional-Order Hirota-Satsuma Coupled KdV. Adv. Math. Phys. 2022, 2022, 6304896. [Google Scholar] [CrossRef]
- Hardy, Y.; Steeb, W.-H. The Rikitake Two-Disk Dynamo System and Domains with Periodic Orbits. Int. J. Theor. Phys. 1999, 38, 2413–2417. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).