1. Introduction
Multinomial distribution tests are a crucial statistical tool in many fields, especially when data can be categorized into multiple groups. These tests were first proposed by Karl Pearson in 1890 and have since been widely used to analyze and make inferences about the probabilities or proportions associated with each category in the multinomial distribution [
1].
Let the sample space
of a random experiment be the union of a finite number
k of mutually disjoint sets (categories)
. Assume that
,
, where
. Here
represents the probability that the outcome is an element of the set
. The random experiment is to be repeated
n independent times. Define the random variables
to be the number of times the outcome is an element of set
,
. That is,
denote the frequencies with which the outcome belongs to
, respectively. Then the joint probability mass function (pmf) of
is the multinomial with parameters
[
2]. It is desired to test the null hypothesis:
against all alternatives, where
are known constants. Within the classical frequentist framework, to test
, it is common to use the test statistic [
3]:
It is known that, under
, the limiting distribution of
is chi-squared with
degrees of freedom. When
is true,
represents the expected value of
. This implies the observed value
should not be too large if
is true. For a given significance level
, an approximate test of size
is to reject
if the observed
, where the
is the
quantile of the chi-squared distribution with
degrees of freedom; otherwise, fail to reject
. Other possible tests for
include Fisher’s exact test and likelihood ratio tests [
4].
If there are
r independent samples, then the interest is to test whether the
r samples come from the same multinomial population or that
r multinomial populations are different. Let
denote
k possible types of categories in the
ith sample,
. Let the probability that an outcome of category
will occur for the
ith population (or
ith sample) be denoted by
. Note that,
for each
. Moreover, let
be the number of times the outcome is an element of
in sample
i. Consider the completely specified hypothesis:
Under
, the test statistic in (
2) can be extended to
If
is true, then
in (
4) has an approximately chi-squared distribution with
degrees of freedom. Likewise, for a given significance level
, an approximate test of size
is to reject
if the observed
is bigger than
; otherwise, fail to reject
[
5].
A third and more common hypothesis is to test whether the
r multinomial populations are the same without specifying the values of the
. That is, we consider the null hypothesis:
The test statistics to test
are given by
where
. Here,
denotes the sample size of sample
i and
represents the total in category
. Note that
represents the pooled maximum likelihood estimator (MLE) of
under
. It is known that the limiting distribution of
in (
6) is a chi-squared distribution with
degrees of freedom. So, for a given significance level
, an approximate test of size
is to reject
if the observed
; otherwise, fail to reject
[
5]. It is worth mentioning that several other frequentist methods for testing the multinomial distribution have been proposed, utilizing different distance measures. These methods include the Euclidean distance proposed by [
6], the smooth total variation distance introduced by [
7], and
-divergences discussed by [
8]. These approaches provide alternative ways to assess the goodness-of-fit of the multinomial distribution using distance metrics.
Refs. [
9,
10,
11,
12,
13] made early advances in Bayesian methods for analyzing categorical data, focusing on smoothing proportions in contingency tables and inference about odds ratios, respectively. These methods typically employed conjugate beta and Dirichlet priors. Ref. [
14,
15] extended these methods to develop Bayesian analogs of small-sample frequentist tests for
tables, also using such priors. Ref. [
16] recommended the use of the uniform prior for predictive inference, but other priors were also suggested by discussants of his paper. The Jeffreys prior is the most commonly used prior for binomial inference, partially due to its invariance to the scale of measurement for the parameter. Reference priors (see [
17]), such as the Jeffreys prior for the binomial parameter (see [
18]), are viable options, but their specification can be computationally complex. Ref. [
10] may have been the first to utilize an empirical Bayesian approach with contingency tables, estimating parameters in gamma and log-normal priors for association factors. Empirical Bayes involves estimating the prior distribution from the observed data itself and is particularly useful when dealing with large amounts of data. Refs. [
19,
20] derived integral expressions for the posterior distributions of the difference, ratio, and odds ratio under independent beta priors. Ref. [
19] introduced Bayesian highest posterior density (HPD) confidence intervals for these measures. The HPD approach ensures that the posterior probability matches the desired confidence level, and the posterior density is higher inside the interval than outside. Ref. [
21] discussed Bayesian confidence intervals for association parameters in
tables. They argued that to achieve good coverage performance in the frequentist sense across the entire parameter space, it is advisable to use relatively diffuse priors. Even uniform priors are often too informative, and they recommended the use of the Jeffreys prior. Bayesian methods for analyzing categorical data have been extensively surveyed in the literature, including comprehensive reviews by [
22,
23] with a focus on contingency table analysis. Refs. [
24,
25,
26] proposed tests based on Bayesian nonparametric methods using Dirichlet process priors.
We build on the recent work of [
27] by extending their Bayesian approach for hypothesis testing on one-sample proportions based on Kullback–Leibler divergence and relative belief ratio, using a uniform (0, 1) prior on binomial proportions, to multinomial distributions. Our goal is to provide a comprehensive Bayesian approach for testing hypotheses
,
, and
. We derive distance formulas and use the Dirichlet distribution as a prior on probabilities. To ensure proper values of the prior’s hyperparameters, we employ the elicitation algorithm developed by [
28]. The proposed approach offers several advantages, including computational simplicity, ease of interpretation, evidence in favor of the null hypothesis, and no requirement to specify a significance level.
The paper is structured as follows.
Section 2 provides an overview of the relative belief ratio inference and KL divergence.
Section 3 details the proposed approach, including the formulas and computational algorithms. In
Section 4, several examples are presented to illustrate the approach. Finally,
Section 5 contains concluding remarks and discussions.
4. Examples
This section presents three examples that demonstrate the effectiveness of our approach in evaluating
and
. We use Algorithms 1–3, with fixed values of
,
, and
. To further investigate the efficacy of our approach, we consider three different prior distributions: uniform prior, Jeffreys prior, and an elicited prior based [
28]. Additionally, we compute the
p-values using the test statistics discussed in
Section 1 of this paper. The approach was implemented using
R (version 4.2.1), and the code is available upon request from the corresponding author.
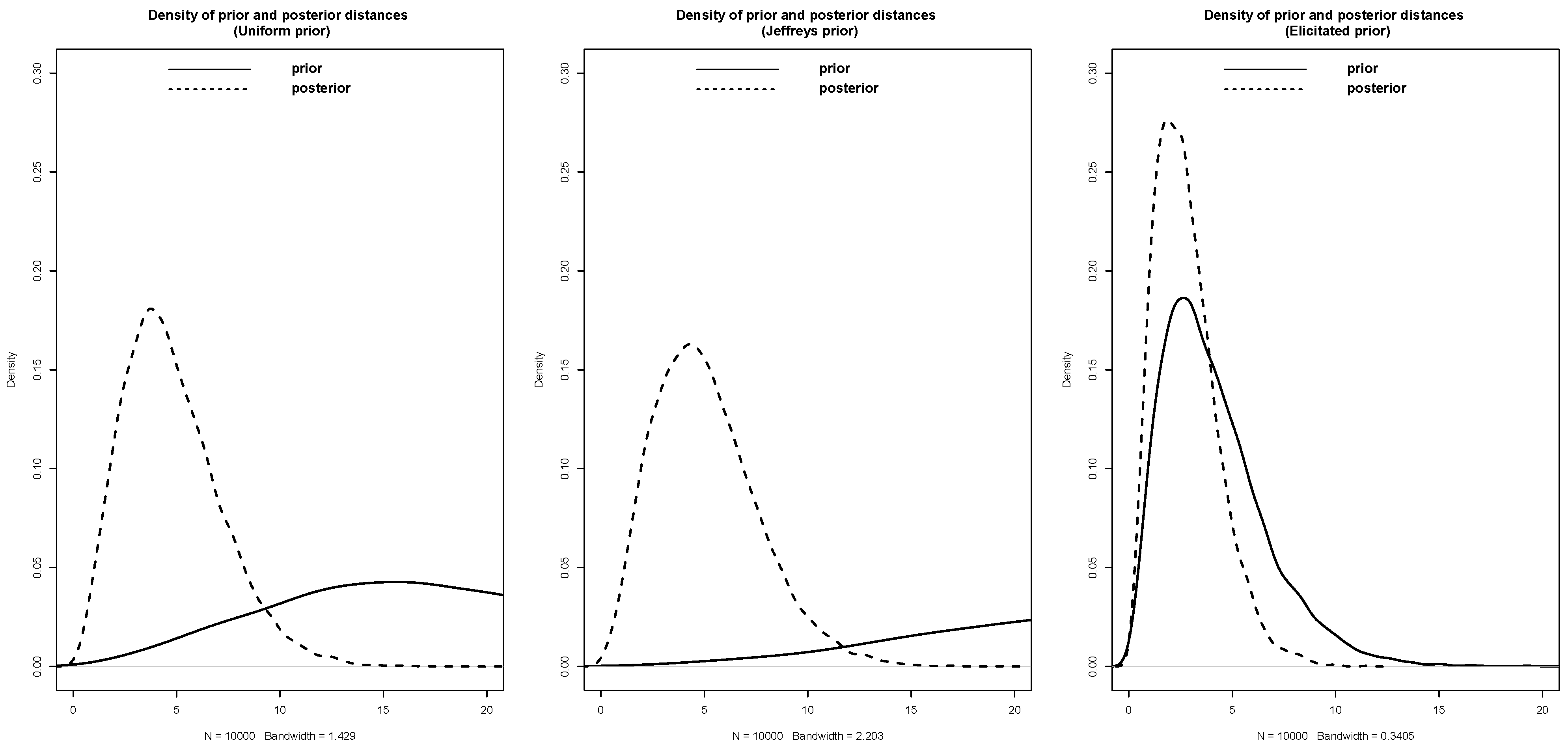
Example 1 (
Rolling Die; [
5])
. We roll a die 60 times and seek to test whether it is unbiased, that is, whether for . The Table 1 below presents the recorded data: We will use a Bayesian approach to address this problem. We employ three priors: the uniform prior represented by
, Jeffreys prior represented by
, and the elicited prior Dirichlet (5.83, 5.83, 5.83, 5.83, 5.83, 5.83) obtained using the algorithm proposed by [
28], with a lower bound of 0.05 applied to all probabilities. It is worth noting that setting the lower bound in [
28] to 0 yields the uniform prior. Additionally, we will include the
p-value for the corresponding frequentist test as a reference. The results of our analysis are presented in
Table 2. Clearly, both the proposed Bayesian approach, considering the three priors, and the frequentist approach lead to the same conclusion. It should be noted that the uniform prior and the Jefferey prior have a wider spread around zero compared to the elicited prior. As a result, they have higher relative belief ratios in this example. However, this is not practically significant in our case as we calibrate the relative belief ratio through the strength. See
Figure 1.
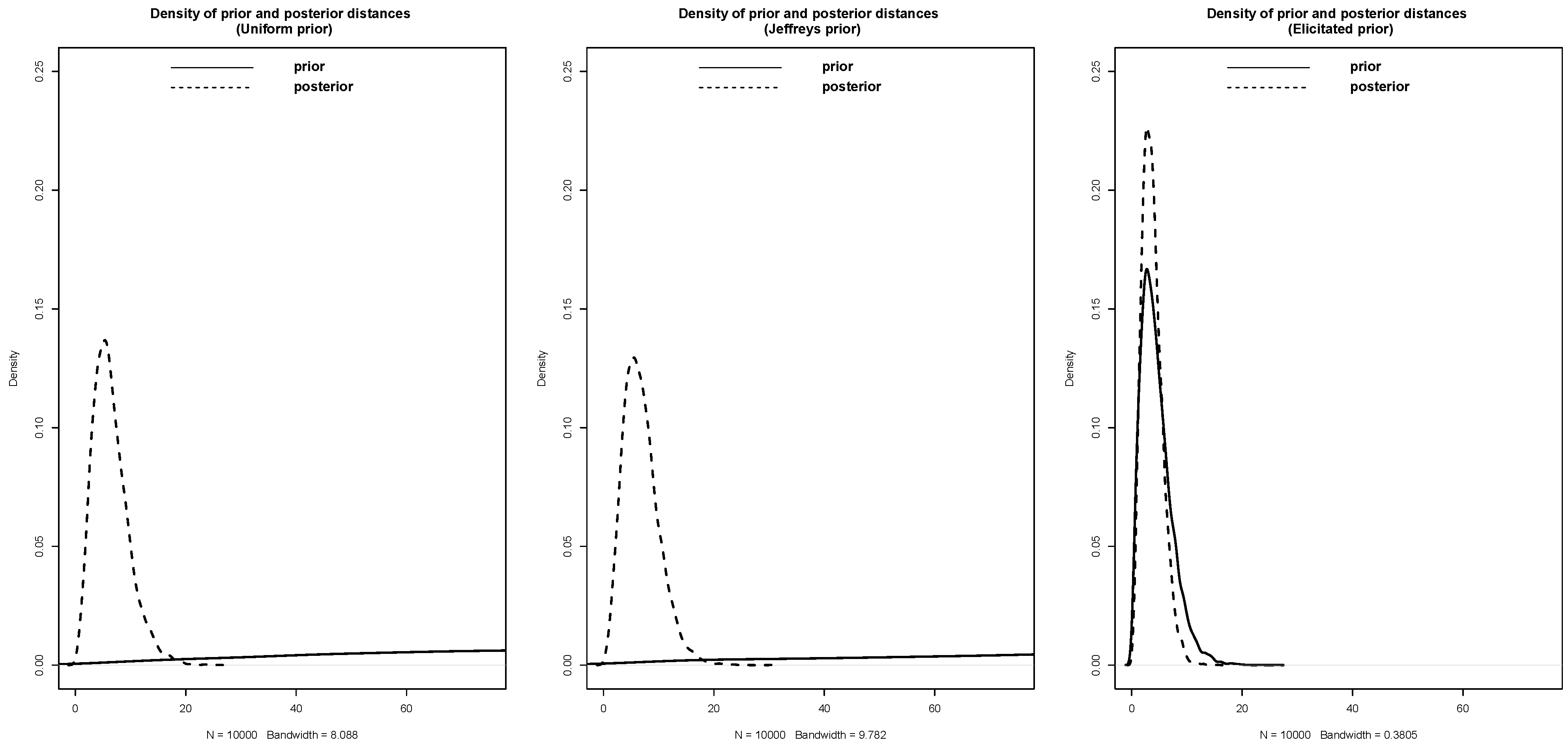
Example 2 (
Operation Trial [
5])
. In a system consisting of four independent components, let denote the probability of successful operation of the ith component, . We will test the null hypothesis ,, , , given that in 50 trials, the components operated as follows (Table 3): We use the priors:
,
, and
. We obtain the latter prior using algorithm of [
28], with lower bounds of
and
for all
.
Table 4 displays the results of our analysis. As in Example 1, both the uniform prior and the Jefferey prior exhibit less concentration around zero when compared to the elicited prior. This, in turn, leads to a notably different conclusion than that of the elicited prior and the
p-value calculated using the chi-square test. See also
Figure 2.
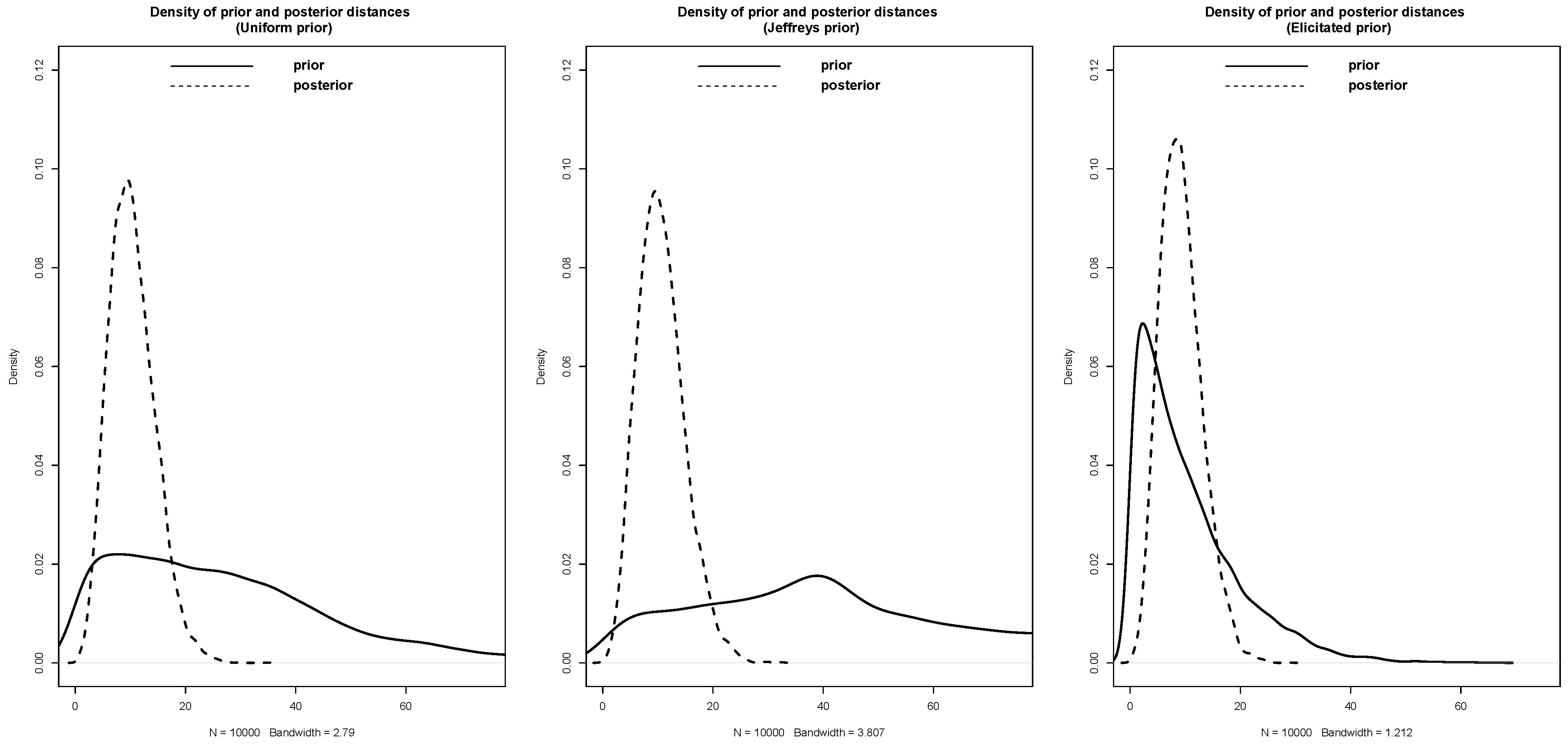
Example 3 (
Clinical Trial; [
37])
. A study was performed to determine whether the type of cancer differed between blue-collar, white-collar, and unemployed workers. A sample of 100 of each type of worker diagnosed as having cancer was categorized into one of three types of cancer. The results are shown in Table 5. See also Table 12.6 of [37]. The hypothesis to be tested is that the proportions of the three cancer types are the same for all three occupation groups. That is, for all j (types of cancer), where is the probability of occupation i having cancer type j. Similar to the previous two examples, we utilize the uniform prior
, Jeffreys prior
, and the elicited prior
. We obtained the elicited prior using the algorithm of [
28] by setting a lower bound of
for all probabilities.
Table 6 summarizes the results of our analysis. Similar to the previous examples, Jeffreys prior is not sufficiently concentrated around zero, which makes it inefficient when there is evidence against
. See
Figure 3.