A Numerical Solution and Comparative Study of the Symmetric Rossler Attractor with the Generalized Caputo Fractional Derivative via Two Different Methods
Abstract
1. Introduction
2. Basic Definitions
3. Methodology of the Apc-ABM Algorithm
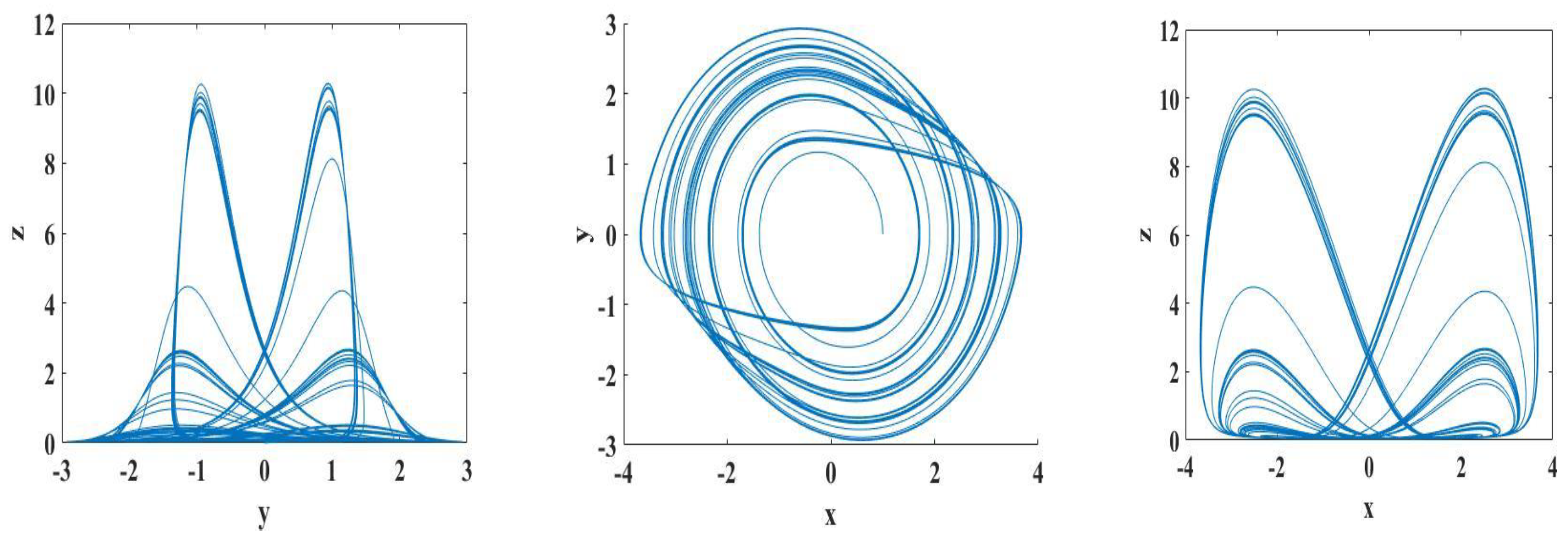
4. Applications of the Apc-ABM Algorithm
5. ρ-Laplace DM
6. Application of ρ-Laplace DM
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Wien, Austria; New York, NY, USA, 1997; pp. 277–290. [Google Scholar]
- Samko, G.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden Attractors in Dynamical Systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Xu, G.; Shekofteh, Y.; Akgül, A.; Li, C.; Panahi, S. A New Chaotic System with a Self-Excited Attractor: Entropy Measurement, Signal Encryption, and Parameter Estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- Lai, Q.; Akgul, A.; Li, C.; Xu, G.; Çavuşoğlu, Ü. A New Chaotic System with Multiple Attractors: Dynamic Analysis, Circuit Realization and S-Box Design. Entropy 2017, 20, 12. [Google Scholar] [CrossRef] [PubMed]
- Petráš, I. A Note on the Fractional-Order Chua’s System. Chaos Solitons Fractals 2006, 38, 140–147. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Hasan, F.L.; Taha, N.E. Computational Technique to Study Analytical Solutions to the Fractional Modified KDV-Zakharov-Kuznetsov Equation. Abstr. Appl. Anal. 2022, 2022, 2162356. [Google Scholar] [CrossRef]
- Abd El-Maksoud, A.J.; Abd El-Kader, A.A.; Hassan, B.G.; Rihan, N.G.; Tolba, M.F.; Said, L.A.; Radwan, A.G.; Abu-Elyazeed, M.F. FPGA Implementation of Sound Encryption System Based on Fractional-Order Chaotic Systems. Microelectronics 2019, 90, 323–335. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Elzaki, T.M.; Elbadri, M.; Mohamed, M.Z. Solution of Partial Differential Equations by New Double Integral Transform (Laplace—Sumudu Transform). Ain Shams Eng. J. 2021, 12, 4045–4049. [Google Scholar] [CrossRef]
- Sene, N. Global Asymptotic Stability of the Fractional Differential Equations. J. Nonlinear Sci. Its Appl. 2019, 13, 171–175. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A Fractional Epidemiological Model for Computer Viruses Pertaining to a New Fractional Derivative. Appl. Math. Comput. 2017, 316, 504–515. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic Behaviour of Fractional Predator-Prey Dynamical System. Chaos Solitons Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
- Hammouch, Z.; Mekkaoui, T.; Belgacem, F.B.M. Numerical Simulations for a Variable Order Fractional Schnakenberg Model. AIP Conf. Proc. 2014, 1637, 1450–1455. [Google Scholar]
- Abdoon, M.A.; Saadeh, R.; Berir, M.; Guma, F.E. Analysis, Modeling and Simulation of a Fractional-Order Influenza Model. Alex. Eng. J. 2023, 74, 231–240. [Google Scholar] [CrossRef]
- Hammouch, Z.; Mekkaoui, T. Traveling-wave solutions of the generalized Zakharov equation with time-space fractional derivatives. Math. Eng. Sci. Aerosp. 2014, 5, 489–498. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R.; Zakia, H.; Mekkaoui, T. New and Extended Applications of the Natural and Sumudu Transforms: Fractional Diffusion and Stokes Fluid Flow Realms. In Trends in Mathematics; Springer: Singapore, 2017; pp. 107–120. [Google Scholar]
- Toufik, M.; Atangana, A. New Numerical Approximation of Fractional Derivative with Non-Local and Non-Singular Kernel: Application to Chaotic Models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
- Behzad Ghanbari, D. Abdon Atangana, Some New Edge Detecting Techniques Based on Fractional Derivatives with Nonlocal and Non-Singular Kernels. Adv. Differ. Equ. 2020, 2020, 435. [Google Scholar] [CrossRef]
- Katugampola, U.N. New Approach to a Generalized Fractional Integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Katugampola, U.N. A New Approach to Generalized Fractional Derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Katugampola, U.N. Existence and Uniqueness Results for a Class of Generalized Fractional Differential Equations. arXiv 2014, arXiv:1411.5229v2, preprint. [Google Scholar]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. Fractional Differential Equations with Dependence on the Caputo–Katugampola Derivative. J. Comput. Nonlinear Dyn. 2016, 11, 061017. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 2018, 1, 88–98. [Google Scholar]
- Sene, N.; Fall, A.N. Homotopy Perturbation ρ-Laplace Transform Method and Its Application to the Fractional Diffusion Equation and the Fractional Diffusion-Reaction Equation. Fractal Fract. 2019, 3, 14. [Google Scholar] [CrossRef]
- Elbadri, M. Initial Value Problems with Generalized Fractional Derivatives and Their Solutions via Generalized Laplace Decomposition Method. Adv. Math. Phys. 2022, 2022, 3586802. [Google Scholar] [CrossRef]
- Rysak, A.; Sedlmayr, M.; Gregorczyk, M. Revealing Fractionality in the Rössler System by Recurrence Quantification Analysis. Eur. Phys. J. Spec. Top. 2023, 232, 83–98. [Google Scholar] [CrossRef]
- Qazza, A.; Abdoon, M.; Saadeh, R.; Berir, M.A. New Scheme for Solving a Fractional Differential Equation and a Chaotic System. Eur. J. Pure Appl. Math. 2023, 16, 1128–1139. [Google Scholar] [CrossRef]
- Saadeh, R.; AAbdoon, M.; Qazza, A.; Berir, M. A Numerical Solution of Generalized Caputo Fractional Initial Value Problems. Fractal Fract. 2023, 7, 332. [Google Scholar] [CrossRef]
- Elbadri, M.; Abdoon, M.A.; Berir, M.; Almutairi, D.K. A Symmetry Chaotic Model with Fractional Derivative Order via Two Different Methods. Symmetry 2023, 15, 1151. [Google Scholar] [CrossRef]
- Elbadri, M.; Ahmed, S.A.; Abdalla, Y.T.; Hdidi, W. A New Solution of Time-Fractional Coupled KdV Equation by Using Natural Decomposition Method. Abstr. Appl. Anal. 2020, 2020, 3950816. [Google Scholar] [CrossRef]
- Sene, N. Mathematical Views of the Fractional Chua’s Electrical Circuit Described by the Caputo-Liouville Derivative. Rev. Mex. Fis. 2021, 67, 91–99. [Google Scholar] [CrossRef]
- Morin, O.; Gillis, A.; Chen, J.; Aubin, M.; Bucci, M.K.; Roach, M., 3rd; Pouliot, J. Megavoltage Cone-Beam CT: System Description and Clinical Applications. Med. Dosim. Off. J. Am. Assoc. Med. Dosim. 2005, 31, 51–61. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, G. Review of Shape Representation and Description Techniques. Pattern Recognit. 2004, 37, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Yao, W.; Lin, H. Chaotic System with Bondorbital Attractors. Nonlinear Dyn. 2019, 97, 2159–2174. [Google Scholar] [CrossRef]
- Li, C.; Hu, W.; Sprott, J.C.; Wang, X. Multistability in Symmetric Chaotic Systems. Eur. Phys. J. Spec. Top. 2015, 224, 1493–1506. [Google Scholar] [CrossRef]
- Odibat, Z.; Baleanu, D. Numerical Simulation of Initial Value Problems with Generalized Caputo-Type Fractional Derivatives. Appl. Numer. Math. Trans. IMACS 2020, 156, 94–105. [Google Scholar] [CrossRef]


| 1/160 | −1.439249004245022 | 1.926879753830334 | 0.115497632553681 |
| 1/320 | −1.437027804276252 | 1.919749862274107 | 0.115546731072315 |
| 1/640 | −1.435904100808411 | 1.916191943945559 | 0.115570069443809 |
| 1/1280 | −1.435338988519151 | 1.914414758678336 | 0.115581435786859 |
| 1/2560 | −1.435055619161782 | 1.913526611637655 | 0.115587043236967 |
| 1/5120 | −1.434913731421401 | 1.913082649779714 | 0.115589828030596 |
| 1/10240 | −1.434842736816009 | 1.912860696799313 | 0.115591215694437 |
| 1/20480 | −1.434780588799649 | 1.912666503235824 | 0.115592427311921 |
| R K4 | −1.434770838159845 | 1.912637598049335 | 0.115592614892760 |
| 1/160 | 1.28921526386768 | 0.794012894194367 | 0.113077179858054 |
| 1/320 | 1.287865984843871 | 0.793856954812710 | 0.112751179833214 |
| 1/640 | 1.287192129056913 | 0.793776634317518 | 0.112588754203015 |
| 1/1280 | 1.286855399733513 | 0.793735886510549 | 0.112507684690222 |
| 1/2560 | 1.286687085043668 | 0.793715365736676 | 0.112467185722739 |
| 1/5120 | 1.286602940232841 | 0.793705068634685 | 0.112446945181642 |
| 1/10240 | 1.286560870966092 | 0.793699910905249 | 0.112436827146182 |
| 1/20480 | 1.286524062075699 | 0.793695392872633 | 0.112427975087295 |
| R K4 | 1.286518803332891 | 0.793694747080276 | 0.112426709876828 |
| 0 | 1.5 | 0.0 | 0.0 |
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 |
| - -Laplace D | - Apc-ABM | - RK4 | |
|---|---|---|---|
| 0 | 1.5 | 1.5 | 1.5 |
| 0.1 | 1.492213875 | 1.492219789642530 | 1.492218810160190 |
| 0.2 | 1.467822 | 1.467899837621127 | 1.467897787108336 |
| 0.3 | 1.4255238749999999 | 1.425901742914282 | 1.425898584622672 |
| 0.4 | 1.3643519999999998 | 1.365527369775399 | 1.365523123300982 |
| 0.5 | 1.283671875 | 1.286524062075699 | 1.286518803332891 |
| - -Laplace D | - Apc-ABM | - RK4 | |
| 0 | 0.0 | 0.0 | 0.0 |
| 0.1 | 0.15278500000000003 | 0.152780418545565 | 0.152780702318047 |
| 0.2 | 0.31024000000000007 | 0.310175637425140 | 0.310176020055442 |
| 0.3 | 0.4709250000000001 | 0.470625099220481 | 0.470625370691797 |
| 0.4 | 0.6332800000000002 | 0.632410659829444 | 0.632410592018532 |
| 0.5 | 0.7956249999999999 | 0.793695392872633 | 0.793694747080276 |
| - -Laplace D | - Apc-ABM | - RK4 | |
| 0 | 0.0 | 0.0 | 0.0 |
| 0.1 | 0.035795535625 | 0.035799537976347 | 0.035799091697084 |
| 0.2 | 0.06402089000000001 | 0.064132733630666 | 0.064131982855701 |
| 0.3 | 0.085135625625 | 0.085961681371914 | 0.085960705651558 |
| 0.4 | 0.09848848 | 0.101893186504205 | 0.101892039586943 |
| 0.5 | 0.102259765625 | 0.112427975087295 | 0.112426709876828 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elbadri, M.; Abdoon, M.A.; Berir, M.; Almutairi, D.K. A Numerical Solution and Comparative Study of the Symmetric Rossler Attractor with the Generalized Caputo Fractional Derivative via Two Different Methods. Mathematics 2023, 11, 2997. https://doi.org/10.3390/math11132997
Elbadri M, Abdoon MA, Berir M, Almutairi DK. A Numerical Solution and Comparative Study of the Symmetric Rossler Attractor with the Generalized Caputo Fractional Derivative via Two Different Methods. Mathematics. 2023; 11(13):2997. https://doi.org/10.3390/math11132997
Chicago/Turabian StyleElbadri, Mohamed, Mohamed A. Abdoon, Mohammed Berir, and Dalal Khalid Almutairi. 2023. "A Numerical Solution and Comparative Study of the Symmetric Rossler Attractor with the Generalized Caputo Fractional Derivative via Two Different Methods" Mathematics 11, no. 13: 2997. https://doi.org/10.3390/math11132997
APA StyleElbadri, M., Abdoon, M. A., Berir, M., & Almutairi, D. K. (2023). A Numerical Solution and Comparative Study of the Symmetric Rossler Attractor with the Generalized Caputo Fractional Derivative via Two Different Methods. Mathematics, 11(13), 2997. https://doi.org/10.3390/math11132997








