Exploring New Horizons: Advancing Data Analysis in Kidney Patient Infection Rates and UEFA Champions League Scores Using Bivariate Kavya–Manoharan Transformation Family of Distributions
Abstract
1. Introduction
- The new proposed bivariate family exhibits a high degree of flexibility, encompassing various well-known distributions as sub-models.
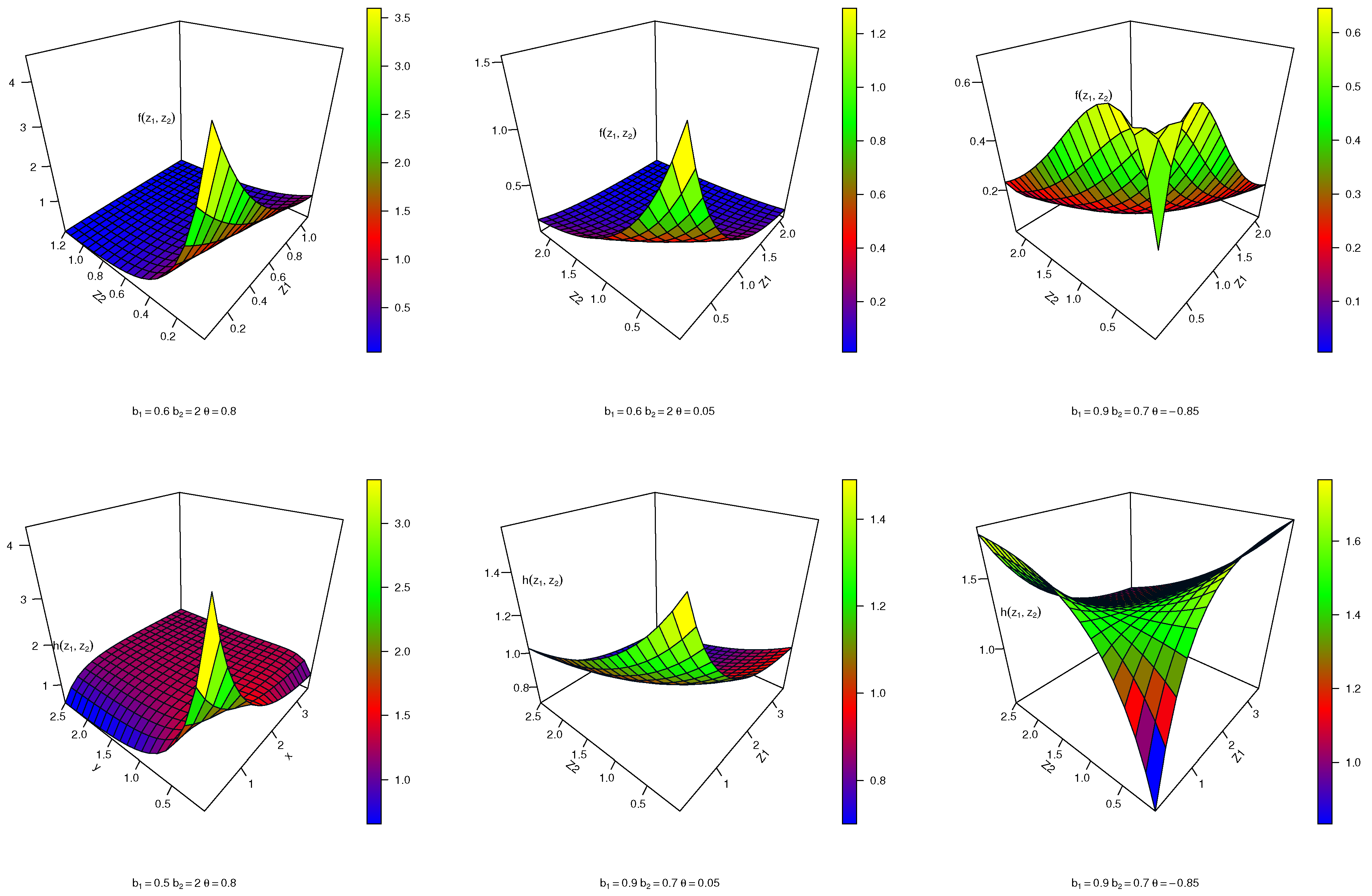
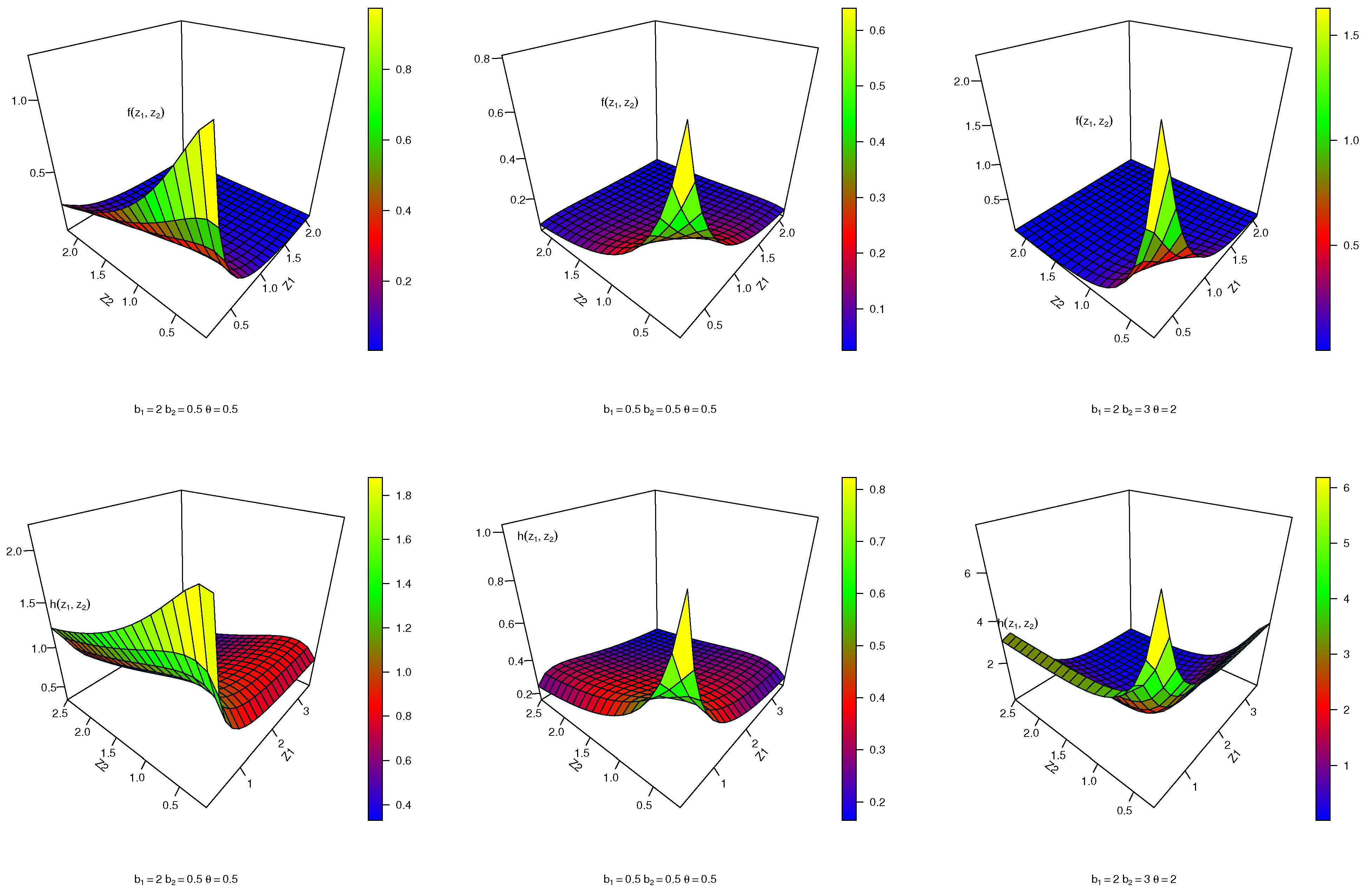
- By utilizing the bivariate Kavya–Manoharan transformation family based on the FGM copula and Clayton copula, we can generate submodels with distinct shapes. For instance, the FGMBKM-Exponential distribution’s joint hazard rate function (HRF) can exhibit bathtub-shaped, U-shaped, declining, or increasing patterns. Similarly, the CBKM-Exponential distribution can display U-shaped, declining, or increasing HRFs, as well as different tail behaviors. The FGM and Clayton copulas offer flexibility in modeling diverse types of dependence structures, further enhancing the versatility of the bivariate Kavya–Manoharan transformation family.
- Some statistical and mathematical properties of the newly proposed model are investigated.
- Additionally, unexplored mathematical properties of the univariate KM transformation family are examined, which are valuable for analyzing the bivariate KM-T family.
- A maximum likelihood estimation method and Bayesian estimation are employed to estimate the parameters of the FGMBKM-T family and the CBKM-T family.
- Three types of confidence intervals are examined for estimating the unknown parameters: asymptotic intervals, Bayesian credible intervals, and bootstrap intervals.
- The performance of the FGMBKM-T family and CBKM-T family is assessed in comparison to other copula and non-copula distributions.
2. Univariate KM-T Family
2.1. Linear Representation
2.2. Quantiles, Ordinary and Incomplete Moments
2.3. Probability Weighted Moments
3. FGM Bivariate Kavya–Manoharan Transformation (FGMBKM-T) Family
3.1. Reliability and Hazard Rate Function of FGMBKM-T Family
3.2. Special FGMBKM-T Family of Distributions
3.2.1. FGMBKM-Exponential (FGMBKM-Ex) Distribution
3.2.2. FGMBKM-Weibull (FGMBKM-W) Distribution
3.2.3. FGMBKM-Pareto (FGMBKM-Pa) Distribution
3.3. Statistical Properties of the FGMBKM-T Family
3.3.1. The Marginal Distributions
3.3.2. Conditional Distribution
- (i)
- The conditional probability distribution of given iswhere and .
- (ii)
- The conditional cdf of given is
- (iii)
- The conditional survival of given is
- (iv)
3.3.3. Generating Random Variables
- (1)
- Generate V and U independently from a uniform distribution.
- (2)
- Set .
- (3)
- in (39) to obtain using numerical analysis, such as Newton–Raphson, etc.
- (4)
- Repeat 1–3 (n) times to obtain , .
3.3.4. Moment Generating Function
3.3.5. Product Moments
4. Clayton Bivariate Kavya–Manoharan Transformation (CBKM-T) Family
4.1. Reliability and Hazard Rate Function of CBKM-T Family
4.2. Special CBKM-T Distributions
4.2.1. CBKM-Exponential (CBKM-Ex) Distribution
4.2.2. CBKM-Weibull (CBKM-W) Distribution
4.2.3. CBKM-Pareto (CBKM-Pa) Distribution
4.3. Statistical Properties of the CBKM-T Family
4.3.1. The Marginal Distributions
4.3.2. Conditional Distribution
- (i)
- The conditional probability distribution of given is
- (ii)
- The conditional cdf of given is
- (iii)
- The conditional survival of given is
4.3.3. Generating Random Variables
- (1)
- Generate V and U independently from a uniform distribution.
- (2)
- Set .
- (3)
- in (61) to obtain using numerical analysis, such as Newton–Raphson, etc.
- (4)
- Repeat 1–3 (n) times to obtain , .
5. Dependence Measures for FGMBKM-T Family and CBKM-T Family
5.1. Kendall’s Tau ()
5.2. Blomqvist’s Medial Correlation Coefficient
5.3. Spearman’s Footrule Coefficient ()
6. Parameter Estimation Methods
6.1. Maximum Likelihood Estimation
6.2. Bayesian Estimation
- Based on hyper-parameter values, they offer a variety of shapes.
- They have an adaptable disposition.
- They are reasonably simple, succinct, and might not produce a result with a complex estimate problem.
7. Confidence Intervals
7.1. Asymptotic Confidence Intervals
7.2. Bootstrap Confidence Interval
7.2.1. Percentile Bootstrap Confidence Interval
- (1)
- Determine the maximum likelihood estimator (MLE) or Bayesian estimator for the FGMBKM-T and CBKM-T distributions.
- (2)
- Use the values of and to generate a set of bootstrap samples, from which you can estimate the bootstrap values of (denoted as ) and (denoted as ).
- (3)
- Repeat step (2) B times to obtain B sets of bootstrap estimates for and .
- (4)
- Arrange the B sets of bootstrap estimates for and in ascending order and denote them as (, , …, ) and (, , …, ), respectively.
- (5)
- Compute the two-sided 100(1 − )% percentile bootstrap confidence interval for each of the unknown parameters (where ) and using the bootstrap estimates obtained in step (4). These intervals are given by [, ] and [, ], respectively.
7.2.2. Bootstrap-t Confidence Interval
- (1)
- Perform the same steps (1,2) as in the Boot-p method.
- (2)
- Calculate the t-statistic of the estimator using , where is the asymptotic variance of that can be obtained using the Fisher information matrix.
- (3)
- Repeat the above step B times and obtain ().
- (4)
- Arrange the values of T obtained in step 3 in ascending order as .
- (5)
- Compute a two-sided bootstrap confidence interval for the unknown parameters and . For , where , the interval is given by []. For , the interval is given by []. Here, is the confidence level specified by the user.
8. Simulation
- The FGMBKM-Ex and CBKM-Ex models were used to produce 1000 data-sets, each corresponding to a size of 40, 100 or 150. We generated 1000 FGMBKM-Ex and CBKM-Ex samples for different combinations. For the FGMBKM-Ex and CBKM-Ex models with varied positive and negative correlations between the four theoretical parameters, we have the following:
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
For the FGMBKM-Ex and CBKM-Ex models with varied positive correlation between the eight theoretical parameters, we have the following:- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- –
- and
- A general form to generate x from one marginal and then simulate a corresponding bivariate vector using the conditional density is . See Section 3.3.3 and Section 4.3.3.
- For each model taken into consideration, the bias, mean square error (MSE), length of confidence intervals (LCI), and coverage probability (CP) were determined.
- All necessary numerical calculations were carried out using the R 4.3.0 statistical programming language software, primarily three helpful statistical packages, namely:
- –
- “copula” for carrying out the computations of the dependency measures proposed.
- –
- “coda” for carrying out the computations of the MCMC Bayesian proposed.
- –
- “maxLik” for using the Newton–Raphson method of maximization in the computations, proposed.
- Based on their average asymptotic LCI (AALCI) and coverage percentages (CP), the interval estimates of , and were compared. To obtain Bayesian interval estimates, the HPD was used. The level of confidence intervals is 95%.
- The MSE, bias, and LCI on the estimated parameters of the FGMBKM-Ex and CBKM-Ex models decrease as the sample size grows, but the CP increases.
- Overall, the results show that the Bayesian technique outperforms the ML when accounting for the MSE in estimating positive and negative relationships (FGMBKM-Ex and CBKM-Ex).
- The MSE, bias, and LCI of each suggested estimate behave satisfactorily as n is increased.
- When increases, the MSE, bias, and LCI of each suggested estimate increases.
- When increases, the MSE, bias, and LCI of each suggested estimate increases.
- When increases, the MSE, bias, and LCI of each suggested estimate increases.
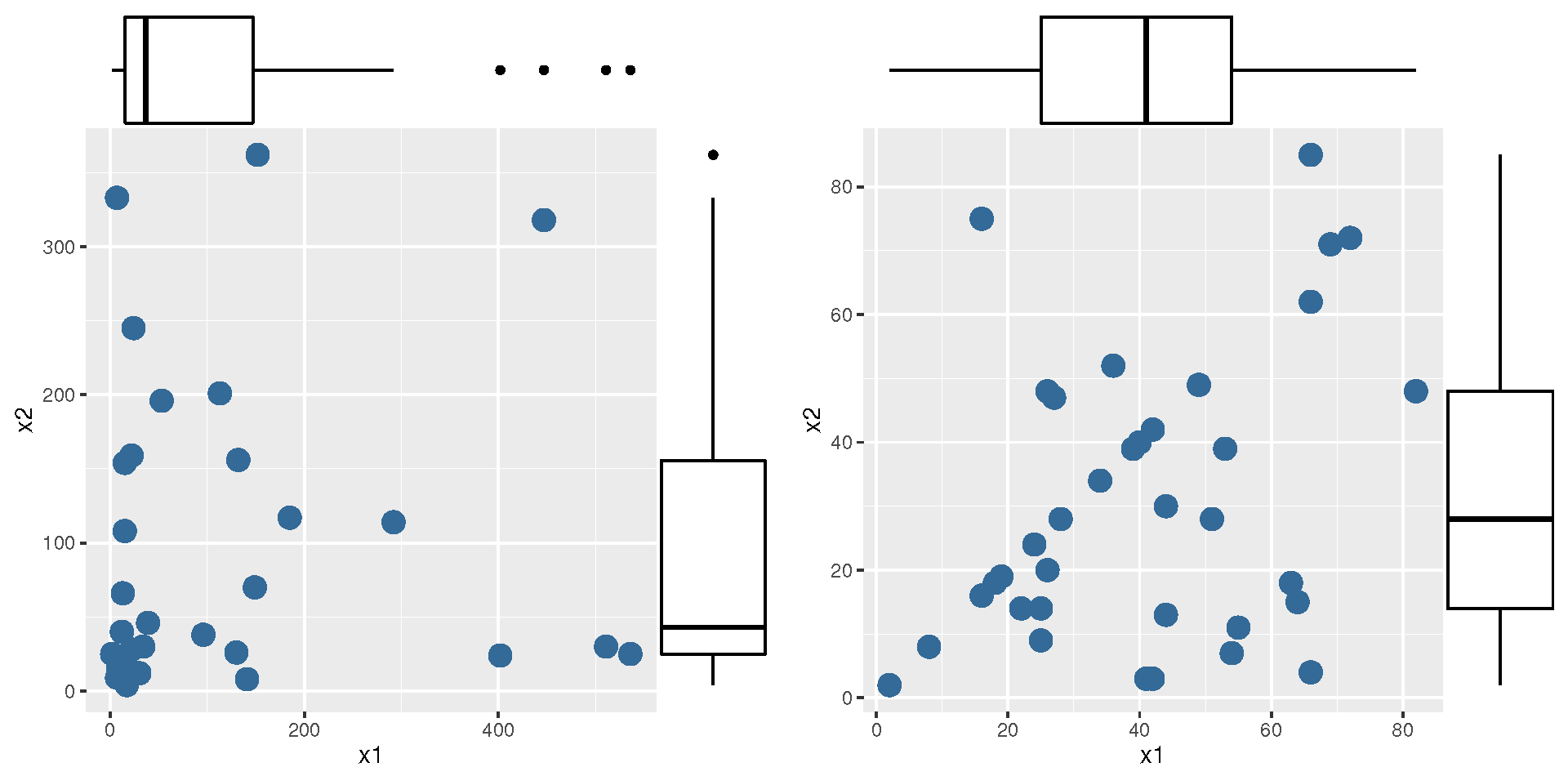
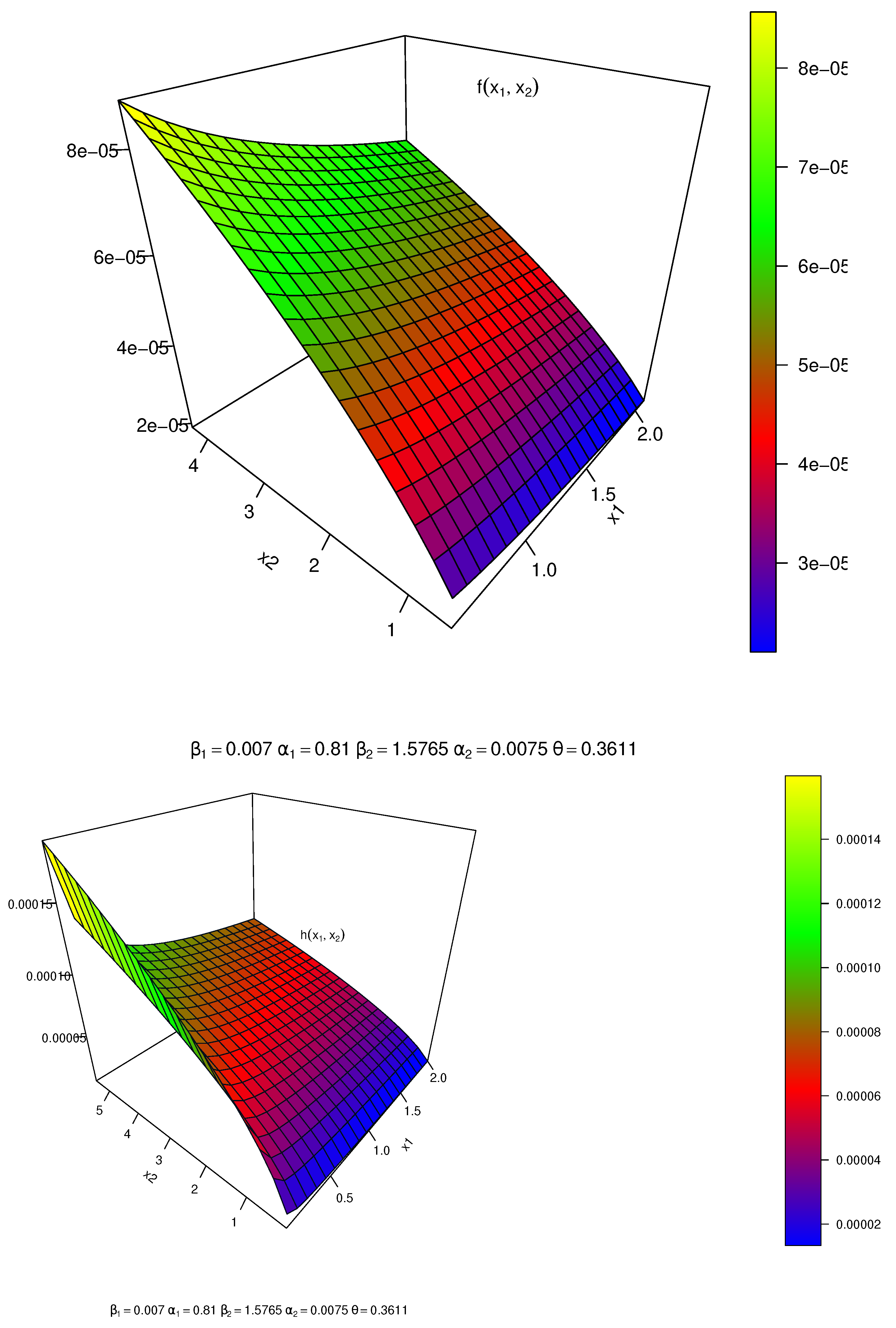
9. Application of Real Data
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| 0.6 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | Bayesian | MLE | Bayesian | |||||||||||||||
| n | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | ||
| 0.3 | 40 | 0.0084 | 0.0034 | 0.2259 | 94.00% | 0.0119 | 0.0012 | 0.1104 | 100.00% | 0.0091 | 0.0034 | 0.2254 | 95.80% | 0.0125 | 0.0012 | 0.2065 | 98.80% | |
| 0.0143 | 0.0091 | 0.3695 | 95.00% | 0.0204 | 0.0034 | 0.1983 | 99.00% | 0.0156 | 0.0093 | 0.3740 | 95.00% | 0.0206 | 0.0036 | 0.3380 | 98.50% | |||
| −0.0677 | 0.3016 | 2.1373 | 98.00% | 0.1281 | 0.1000 | 1.0427 | 93.00% | 0.0757 | 0.3257 | 2.2186 | 95.10% | −0.1778 | 0.1036 | 0.9552 | 94.10% | |||
| 100 | 0.0019 | 0.0012 | 0.1357 | 96.00% | 0.0038 | 0.0004 | 0.0685 | 99.00% | 0.0038 | 0.0012 | 0.1348 | 95.10% | 0.0049 | 0.0004 | 0.1272 | 99.60% | ||
| 0.0057 | 0.0036 | 0.2329 | 97.00% | 0.0074 | 0.0011 | 0.1220 | 100.00% | 0.0059 | 0.0033 | 0.2253 | 95.50% | 0.0082 | 0.0012 | 0.2066 | 98.90% | |||
| −0.0141 | 0.0989 | 1.2322 | 98.00% | 0.0397 | 0.0498 | 0.7989 | 82.00% | 0.0235 | 0.0944 | 1.2014 | 95.10% | −0.0479 | 0.0422 | 0.5718 | 87.50% | |||
| 150 | 0.0018 | 0.0007 | 0.1040 | 94.00% | 0.0024 | 0.0002 | 0.0543 | 98.00% | 0.0027 | 0.0007 | 0.1051 | 95.70% | 0.0030 | 0.0002 | 0.1018 | 100.00% | ||
| 0.0046 | 0.0020 | 0.1730 | 96.00% | 0.0040 | 0.0007 | 0.0977 | 99.00% | 0.0043 | 0.0023 | 0.1884 | 96.00% | 0.0042 | 0.0007 | 0.1608 | 99.30% | |||
| 0.0039 | 0.0561 | 0.9284 | 95.00% | 0.0057 | 0.0213 | 0.5614 | 85.00% | −0.0091 | 0.0485 | 0.8633 | 94.90% | −0.0128 | 0.0211 | 0.3516 | 95.60% | |||
| 0.8 | 40 | 0.0194 | 0.0232 | 0.5928 | 95.70% | 0.0286 | 0.0085 | 0.5208 | 98.70% | 0.0263 | 0.0245 | 0.6052 | 96.10% | 0.0316 | 0.0102 | 0.5219 | 98.60% | |
| 0.0183 | 0.0097 | 0.3801 | 95.60% | 0.0227 | 0.0035 | 0.3431 | 99.40% | 0.0155 | 0.0100 | 0.3874 | 96.10% | 0.0199 | 0.0039 | 0.3394 | 98.70% | |||
| −0.0898 | 0.3880 | 2.4174 | 94.80% | 0.1261 | 0.0988 | 1.0062 | 93.80% | 0.0885 | 0.3736 | 2.3720 | 95.30% | −0.1850 | 0.1105 | 1.0004 | 95.00% | |||
| 100 | 0.0121 | 0.0086 | 0.3600 | 95.00% | 0.0111 | 0.0029 | 0.3170 | 99.40% | 0.0120 | 0.0087 | 0.3621 | 94.90% | 0.0144 | 0.0032 | 0.3165 | 99.10% | ||
| 0.0016 | 0.0032 | 0.2208 | 95.00% | 0.0063 | 0.0010 | 0.2080 | 99.40% | 0.0077 | 0.0032 | 0.2195 | 95.40% | 0.0087 | 0.0011 | 0.2074 | 99.60% | |||
| −0.0210 | 0.0942 | 1.2011 | 94.50% | 0.0299 | 0.0505 | 0.6086 | 83.10% | 0.0302 | 0.0912 | 1.1784 | 94.90% | −0.0485 | 0.0474 | 0.5908 | 86.50% | |||
| 150 | 0.0070 | 0.0055 | 0.2891 | 95.10% | 0.0051 | 0.0022 | 0.2261 | 98.10% | 0.0036 | 0.0051 | 0.2793 | 95.60% | 0.0040 | 0.0021 | 0.2257 | 98.30% | ||
| 0.0021 | 0.0023 | 0.1861 | 95.00% | 0.0037 | 0.0008 | 0.1614 | 99.50% | 0.0057 | 0.0021 | 0.1787 | 95.00% | 0.0051 | 0.0007 | 0.1617 | 99.50% | |||
| 0.0021 | 0.0573 | 0.9391 | 95.20% | 0.0034 | 0.0223 | 0.3664 | 96.40% | 0.0043 | 0.0580 | 0.9443 | 95.00% | −0.0043 | 0.0222 | 0.3606 | 96.80% | |||
| 1.5 | 40 | 0.0369 | 0.0752 | 1.0659 | 95.60% | 0.0410 | 0.0343 | 0.8417 | 97.20% | 0.0421 | 0.0749 | 1.0606 | 96.70% | 0.0549 | 0.0350 | 0.8426 | 97.40% | |
| 0.0119 | 0.0089 | 0.3672 | 95.50% | 0.0188 | 0.0033 | 0.3391 | 99.10% | 0.0129 | 0.0088 | 0.3646 | 95.00% | 0.0188 | 0.0031 | 0.3404 | 99.10% | |||
| −0.0661 | 0.3152 | 2.1867 | 95.40% | 0.1394 | 0.0990 | 1.0351 | 95.10% | 0.0845 | 0.3276 | 2.2203 | 95.00% | −0.2002 | 0.1199 | 1.0064 | 93.70% | |||
| 100 | 0.0199 | 0.0308 | 0.6833 | 95.50% | 0.0133 | 0.0128 | 0.4843 | 97.00% | 0.0218 | 0.0289 | 0.6608 | 95.10% | 0.0172 | 0.0117 | 0.4874 | 97.30% | ||
| 0.0038 | 0.0032 | 0.2201 | 95.20% | 0.0066 | 0.0010 | 0.2067 | 99.60% | 0.0050 | 0.0032 | 0.2225 | 95.40% | 0.0075 | 0.0010 | 0.2077 | 99.60% | |||
| −0.0211 | 0.0913 | 1.1824 | 95.80% | 0.0310 | 0.0498 | 0.6164 | 85.00% | 0.0071 | 0.0827 | 1.1275 | 94.70% | −0.0489 | 0.0409 | 0.5942 | 90.10% | |||
| 150 | 0.0138 | 0.0186 | 0.5316 | 95.60% | 0.0043 | 0.0098 | 0.3059 | 87.70% | 0.0106 | 0.0209 | 0.5648 | 95.10% | 0.0013 | 0.0091 | 0.3052 | 88.60% | ||
| 0.0017 | 0.0022 | 0.1854 | 94.90% | 0.0036 | 0.0007 | 0.1600 | 99.50% | 0.0017 | 0.0020 | 0.1750 | 95.50% | 0.0027 | 0.0007 | 0.1590 | 99.60% | |||
| −0.0016 | 0.0588 | 0.9509 | 94.70% | 0.0031 | 0.0234 | 0.3672 | 95.30% | 0.0070 | 0.0499 | 0.8755 | 94.70% | −0.0043 | 0.0201 | 0.3562 | 97.50% | |||
| 3 | 40 | 0.0819 | 0.3144 | 2.1755 | 95.50% | 0.0389 | 0.1357 | 1.1812 | 89.90% | 0.1144 | 0.3074 | 2.1275 | 95.00% | 0.0420 | 0.1175 | 1.1718 | 93.10% | |
| 0.0198 | 0.0099 | 0.3829 | 95.00% | 0.0232 | 0.0038 | 0.3445 | 99.10% | 0.0193 | 0.0098 | 0.3814 | 95.30% | 0.0212 | 0.0036 | 0.3396 | 98.80% | |||
| −0.0127 | 0.3092 | 2.1803 | 95.50% | 0.1626 | 0.1148 | 1.0451 | 93.40% | 0.1080 | 0.4051 | 2.4600 | 96.00% | −0.1810 | 0.1109 | 1.0087 | 94.30% | |||
| 100 | 0.0121 | 0.1143 | 1.3252 | 95.70% | 0.0059 | 0.0489 | 0.6406 | 85.60% | 0.0325 | 0.1158 | 1.3285 | 95.20% | 0.0160 | 0.0517 | 0.6463 | 84.80% | ||
| 0.0045 | 0.0033 | 0.2245 | 95.30% | 0.0071 | 0.0010 | 0.2069 | 99.70% | 0.0080 | 0.0034 | 0.2281 | 95.10% | 0.0089 | 0.0011 | 0.2096 | 99.20% | |||
| 0.0000 | 0.0908 | 1.1821 | 94.60% | 0.0296 | 0.0517 | 0.6180 | 83.80% | 0.0072 | 0.0828 | 1.1283 | 95.50% | −0.0519 | 0.0439 | 0.5971 | 87.80% | |||
| 150 | 0.0140 | 0.0748 | 1.0710 | 95.10% | −0.0055 | 0.0212 | 0.3597 | 78.90% | 0.0142 | 0.0776 | 1.0911 | 94.80% | −0.0056 | 0.0194 | 0.3620 | 81.40% | ||
| 0.0031 | 0.0019 | 0.1719 | 96.00% | 0.0041 | 0.0007 | 0.1602 | 99.40% | 0.0048 | 0.0021 | 0.1804 | 94.40% | 0.0041 | 0.0007 | 0.1592 | 99.20% | |||
| −0.0115 | 0.0605 | 0.9632 | 95.50% | −0.0062 | 0.0241 | 0.3714 | 95.40% | 0.0106 | 0.0611 | 0.9683 | 94.60% | −0.0069 | 0.0218 | 0.3598 | 95.20% | |||
| 0.6 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | Bayesian | MLE | Bayesian | |||||||||||||||
| n | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | ||
| 0.3 | 40 | 0.0819 | 0.3144 | 2.1755 | 95.50% | 0.0389 | 0.1357 | 1.1812 | 89.90% | 0.0060 | 0.0030 | 0.2121 | 95.80% | 0.0110 | 0.0011 | 0.2056 | 99.10% | |
| 0.0198 | 0.0099 | 0.3829 | 95.00% | 0.0232 | 0.0038 | 0.3445 | 99.10% | 0.0507 | 0.1328 | 1.4156 | 96.00% | 0.0475 | 0.0652 | 0.9697 | 96.20% | |||
| −0.0127 | 0.3092 | 2.1803 | 95.50% | 0.1626 | 0.1148 | 1.0451 | 93.40% | −0.0346 | 0.2941 | 2.1226 | 94.60% | 0.1488 | 0.1090 | 1.0047 | 93.50% | |||
| 100 | 0.0121 | 0.1143 | 1.3252 | 95.70% | 0.0059 | 0.0489 | 0.6406 | 85.60% | 0.0033 | 0.0011 | 0.1314 | 94.80% | 0.0049 | 0.0004 | 0.1279 | 99.70% | ||
| 0.0045 | 0.0033 | 0.2245 | 95.30% | 0.0071 | 0.0010 | 0.2069 | 99.70% | 0.0308 | 0.0580 | 0.9370 | 95.30% | 0.0257 | 0.0261 | 0.5467 | 92.60% | |||
| 0.0000 | 0.0908 | 1.1821 | 94.60% | 0.0296 | 0.0517 | 0.6180 | 83.80% | −0.0073 | 0.0908 | 1.1814 | 94.40% | 0.0286 | 0.0463 | 0.5993 | 84.30% | |||
| 150 | 0.0140 | 0.0748 | 1.0710 | 95.10% | −0.0055 | 0.0212 | 0.3597 | 78.90% | 0.0031 | 0.0007 | 0.1050 | 94.70% | 0.0033 | 0.0002 | 0.1023 | 99.80% | ||
| 0.0031 | 0.0019 | 0.1719 | 96.00% | 0.0041 | 0.0007 | 0.1602 | 99.40% | 0.0127 | 0.0324 | 0.7040 | 95.00% | −0.0002 | 0.0132 | 0.3265 | 84.80% | |||
| −0.0115 | 0.0605 | 0.9632 | 95.50% | −0.0062 | 0.0241 | 0.3714 | 75.40% | −0.0163 | 0.0530 | 0.9008 | 94.60% | 0.0006 | 0.0216 | 0.3486 | 74.40% | |||
| 0.8 | 40 | 0.0158 | 0.0240 | 0.6046 | 95.10% | 0.0289 | 0.0092 | 0.5246 | 97.90% | 0.0243 | 0.0232 | 0.5896 | 95.20% | 0.0309 | 0.0087 | 0.5175 | 98.70% | |
| 0.0635 | 0.1463 | 1.4790 | 95.80% | 0.0403 | 0.0609 | 0.9960 | 95.90% | 0.0593 | 0.1475 | 1.4880 | 95.10% | 0.0473 | 0.0598 | 1.0080 | 96.50% | |||
| −0.0306 | 0.3446 | 2.2993 | 95.30% | 0.1566 | 0.1067 | 1.0625 | 95.20% | 0.1009 | 0.4341 | 2.5535 | 95.80% | −0.1952 | 0.1163 | 1.0197 | 94.50% | |||
| 100 | 0.0100 | 0.0079 | 0.3473 | 95.20% | 0.0111 | 0.0026 | 0.3167 | 99.60% | 0.0107 | 0.0084 | 0.3573 | 95.00% | 0.0114 | 0.0030 | 0.3130 | 98.80% | ||
| 0.0206 | 0.0501 | 0.8738 | 95.50% | 0.0143 | 0.0234 | 0.5663 | 93.30% | 0.0331 | 0.0528 | 0.8914 | 95.20% | 0.0246 | 0.0248 | 0.5697 | 93.80% | |||
| −0.0128 | 0.0808 | 1.1140 | 95.30% | 0.0471 | 0.0537 | 0.6312 | 84.40% | 0.0185 | 0.1041 | 1.2631 | 94.20% | −0.0451 | 0.0452 | 0.5996 | 88.20% | |||
| 150 | 0.0025 | 0.0049 | 0.2741 | 94.80% | 0.0028 | 0.0019 | 0.2270 | 98.80% | 0.0055 | 0.0054 | 0.2869 | 96.00% | 0.0036 | 0.0019 | 0.2245 | 98.70% | ||
| 0.0207 | 0.0350 | 0.7295 | 94.80% | 0.0005 | 0.0131 | 0.3293 | 84.40% | 0.0169 | 0.0335 | 0.7146 | 94.80% | 0.0045 | 0.0146 | 0.3326 | 83.80% | |||
| −0.0149 | 0.0579 | 0.9419 | 94.60% | −0.0033 | 0.0228 | 0.3716 | 97.85% | 0.0016 | 0.0555 | 0.9238 | 95.50% | −0.0090 | 0.0228 | 0.3639 | 96.50% | |||
| 1.5 | 40 | 0.0305 | 0.0729 | 1.0520 | 95.70% | 0.0402 | 0.0299 | 0.8540 | 98.30% | 0.0375 | 0.0923 | 1.1826 | 95.10% | 0.0472 | 0.0389 | 0.8510 | 96.50% | |
| 0.0545 | 0.1522 | 1.5152 | 95.20% | 0.0405 | 0.0619 | 1.0041 | 95.80% | 0.0435 | 0.1468 | 1.4931 | 95.00% | 0.0468 | 0.0601 | 0.9991 | 96.40% | |||
| −0.0617 | 0.4086 | 2.4953 | 96.90% | 0.1625 | 0.1204 | 1.0626 | 93.30% | 0.0934 | 0.4380 | 2.5697 | 96.00% | −0.2082 | 0.1211 | 1.0297 | 94.70% | |||
| 100 | 0.0135 | 0.0302 | 0.6795 | 95.30% | 0.0122 | 0.0128 | 0.4934 | 97.40% | 0.0190 | 0.0279 | 0.6511 | 94.90% | 0.0164 | 0.0122 | 0.4882 | 97.70% | ||
| 0.0219 | 0.0478 | 0.8535 | 95.30% | 0.0168 | 0.0230 | 0.5727 | 95.20% | 0.0277 | 0.0532 | 0.8983 | 95.80% | 0.0165 | 0.0225 | 0.5707 | 95.10% | |||
| −0.0198 | 0.0927 | 1.1917 | 94.80% | 0.0415 | 0.0555 | 0.6499 | 85.70% | 0.0207 | 0.0866 | 1.1512 | 94.90% | −0.0449 | 0.0432 | 0.6124 | 90.20% | |||
| 150 | 0.0091 | 0.0202 | 0.5560 | 94.70% | 0.0046 | 0.0092 | 0.3103 | 90.00% | 0.0194 | 0.0201 | 0.5501 | 94.90% | 0.0087 | 0.0087 | 0.3095 | 91.40% | ||
| 0.0214 | 0.0342 | 0.7206 | 95.70% | 0.0043 | 0.0143 | 0.3340 | 84.50% | 0.0086 | 0.0332 | 0.7139 | 94.40% | −0.0041 | 0.0132 | 0.3353 | 86.30% | |||
| −0.0056 | 0.0580 | 0.9443 | 95.20% | 0.0058 | 0.0259 | 0.3769 | 92.80% | −0.0099 | 0.0520 | 0.8931 | 94.90% | −0.0098 | 0.0210 | 0.3653 | 89.20% | |||
| 3 | 40 | 0.0639 | 0.3242 | 2.2191 | 95.10% | 0.0364 | 0.1285 | 1.2082 | 92.10% | 0.0631 | 0.3076 | 2.1612 | 95.60% | 0.0273 | 0.1329 | 1.2053 | 91.60% | |
| 0.0509 | 0.1486 | 1.4988 | 95.40% | 0.0559 | 0.0680 | 1.0163 | 95.30% | 0.0615 | 0.1578 | 1.5392 | 95.70% | 0.0482 | 0.0607 | 1.0176 | 96.90% | |||
| −0.0847 | 0.4133 | 2.4993 | 96.10% | 0.1526 | 0.1101 | 1.0601 | 94.30% | 0.0696 | 0.3794 | 2.4002 | 95.70% | −0.2135 | 0.1276 | 1.0364 | 94.20% | |||
| 100 | 0.0242 | 0.1204 | 1.3578 | 95.40% | 0.0049 | 0.0458 | 0.6597 | 87.90% | 0.0291 | 0.1179 | 1.3416 | 95.60% | 0.0085 | 0.0512 | 0.6578 | 85.50% | ||
| 0.0342 | 0.0517 | 0.8815 | 95.60% | 0.0249 | 0.0252 | 0.5763 | 93.40% | 0.0196 | 0.0515 | 0.8867 | 95.50% | 0.0159 | 0.0227 | 0.5674 | 95.00% | |||
| 0.0063 | 0.0869 | 1.1558 | 95.50% | 0.0498 | 0.0558 | 0.6578 | 84.10% | 0.0213 | 0.0970 | 1.2183 | 95.00% | −0.0486 | 0.0453 | 0.6162 | 89.00% | |||
| 150 | 0.0236 | 0.0865 | 1.1496 | 94.50% | −0.0061 | 0.0214 | 0.3752 | 81.30% | 0.0090 | 0.0774 | 1.0908 | 94.60% | −0.0103 | 0.0223 | 0.3678 | 78.90% | ||
| 0.0128 | 0.0328 | 0.7080 | 93.80% | −0.0039 | 0.0136 | 0.3452 | 86.40% | 0.0112 | 0.0339 | 0.7205 | 94.70% | −0.0012 | 0.0139 | 0.3396 | 85.60% | |||
| −0.0147 | 0.0577 | 0.9406 | 94.30% | −0.0047 | 0.0234 | 0.3727 | 95.50% | 0.0097 | 0.0576 | 0.9404 | 94.90% | −0.0084 | 0.0209 | 0.3623 | 98.20% | |||
| 0.6 | 1.5 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | Bayesian | MLE | Bayesian | |||||||||||||||
| n | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | ||
| 0.3 | 40 | 0.0005 | 0.0029 | 0.2094 | 94.90% | 0.0084 | 0.0010 | 0.2002 | 99.30% | −0.0759 | 0.0082 | 0.1917 | 94.60% | −0.0168 | 0.0007 | 0.1506 | 99.40% | |
| 0.0004 | 0.0078 | 0.3473 | 95.30% | 0.0138 | 0.0027 | 0.3246 | 99.20% | −0.1396 | 0.0268 | 0.3361 | 94.00% | −0.0353 | 0.0024 | 0.2388 | 99.20% | |||
| 0.1673 | 0.1097 | 1.1214 | 95.80% | 0.1199 | 0.0491 | 0.7839 | 98.30% | −0.9533 | 1.0225 | 1.3221 | 95.20% | −0.2660 | 0.0941 | 0.7607 | 97.20% | |||
| 100 | −0.0047 | 0.0011 | 0.1280 | 94.80% | 0.0012 | 0.0003 | 0.1232 | 99.80% | −0.0756 | 0.0082 | 0.1167 | 94.80% | −0.0248 | 0.0008 | 0.0920 | 99.90% | ||
| −0.0086 | 0.0032 | 0.2182 | 95.40% | 0.0013 | 0.0009 | 0.1996 | 99.70% | −0.1355 | 0.0267 | 0.2392 | 96.80% | −0.0348 | 0.0024 | 0.1463 | 99.70% | |||
| 0.1284 | 0.0449 | 0.6612 | 95.30% | 0.1060 | 0.0363 | 0.5226 | 90.40% | −0.8012 | 0.9506 | 0.7465 | 96.20% | −0.2724 | 0.0827 | 0.5081 | 98.70% | |||
| 150 | −0.0041 | 0.0008 | 0.1093 | 94.29% | −0.0002 | 0.0002 | 0.0997 | 99.27% | −0.0847 | 0.0078 | 0.0951 | 94.30% | −0.0246 | 0.0007 | 0.0751 | 99.90% | ||
| −0.0129 | 0.0021 | 0.1716 | 95.17% | −0.0033 | 0.0006 | 0.1545 | 99.85% | −0.1258 | 0.0266 | 0.2001 | 95.40% | −0.0346 | 0.0024 | 0.1165 | 99.30% | |||
| 0.1126 | 0.0306 | 0.5252 | 95.17% | 0.0531 | 0.0157 | 0.3232 | 83.89% | −0.7402 | 0.8068 | 0.5880 | 95.50% | −0.2075 | 0.0505 | 0.3928 | 97.80% | |||
| 0.8 | 40 | −0.0030 | 0.0206 | 0.5629 | 95.50% | 0.0200 | 0.0079 | 0.5043 | 98.60% | −0.2476 | 0.0861 | 0.6172 | 94.90% | −0.0569 | 0.0068 | 0.3660 | 98.90% | |
| 0.0015 | 0.0075 | 0.3386 | 95.20% | 0.0144 | 0.0028 | 0.3293 | 99.20% | −0.1511 | 0.0306 | 0.3455 | 95.40% | −0.0360 | 0.0025 | 0.2362 | 99.30% | |||
| 0.1489 | 0.1055 | 1.1318 | 95.00% | 0.1051 | 0.0458 | 0.7880 | 98.30% | −0.9731 | 1.0508 | 1.2637 | 95.90% | −0.2679 | 0.0954 | 0.7706 | 97.60% | |||
| 100 | −0.0151 | 0.0079 | 0.3434 | 95.00% | 0.0002 | 0.0023 | 0.3048 | 99.10% | −0.2375 | 0.0858 | 0.4329 | 97.00% | −0.0477 | 0.0047 | 0.2208 | 99.30% | ||
| −0.0089 | 0.0032 | 0.2174 | 95.80% | 0.0013 | 0.0009 | 0.2018 | 99.70% | −0.1604 | 0.0294 | 0.2361 | 96.00% | −0.0451 | 0.0025 | 0.1466 | 99.70% | |||
| 0.1164 | 0.0409 | 0.6480 | 94.80% | 0.0949 | 0.0306 | 0.5320 | 93.70% | −1.0113 | 1.0544 | 0.6993 | 94.80% | −0.2782 | 0.0848 | 0.5189 | 99.10% | |||
| 150 | −0.0173 | 0.0055 | 0.2832 | 95.90% | −0.0037 | 0.0018 | 0.2226 | 98.70% | −0.2288 | 0.0793 | 0.3807 | 97.00% | −0.0381 | 0.0038 | 0.1742 | 98.70% | ||
| −0.0130 | 0.0021 | 0.1723 | 95.00% | −0.0034 | 0.0006 | 0.1544 | 99.40% | −0.1635 | 0.0295 | 0.2050 | 96.00% | −0.0458 | 0.0025 | 0.1173 | 99.50% | |||
| 0.1086 | 0.0306 | 0.5379 | 95.80% | 0.0493 | 0.0161 | 0.3307 | 84.30% | −0.9802 | 1.0265 | 0.5857 | 95.20% | −0.2203 | 0.0558 | 0.4021 | 98.10% | |||
| 1.5 | 40 | −0.0074 | 0.0674 | 1.0178 | 96.00% | 0.0232 | 0.0246 | 0.8098 | 98.50% | −0.4875 | 0.3421 | 1.2675 | 94.50% | −0.1072 | 0.0246 | 0.6137 | 98.50% | |
| 0.0003 | 0.0082 | 0.3560 | 95.70% | 0.0131 | 0.0029 | 0.3283 | 98.90% | −0.1506 | 0.0310 | 0.3572 | 95.70% | −0.0342 | 0.0025 | 0.2411 | 99.50% | |||
| 0.1543 | 0.1090 | 1.1447 | 95.00% | 0.1135 | 0.0462 | 0.8051 | 99.20% | −0.9850 | 1.0673 | 1.2227 | 95.30% | −0.2784 | 0.0990 | 0.7766 | 98.50% | |||
| 100 | −0.0261 | 0.0280 | 0.6479 | 96.00% | −0.0010 | 0.0112 | 0.4755 | 97.20% | −0.5846 | 0.3241 | 0.9880 | 97.10% | −0.1479 | 0.0232 | 0.3633 | 97.70% | ||
| −0.0096 | 0.0035 | 0.2280 | 94.50% | 0.0005 | 0.0009 | 0.2012 | 99.30% | −0.1654 | 0.0301 | 0.2438 | 95.70% | −0.0448 | 0.0025 | 0.1465 | 99.60% | |||
| 0.1229 | 0.0465 | 0.6948 | 95.00% | 0.0970 | 0.0351 | 0.5479 | 91.40% | −0.9032 | 0.9989 | 0.7145 | 95.90% | −0.2768 | 0.0844 | 0.5185 | 99.30% | |||
| 150 | −0.0332 | 0.0174 | 0.5007 | 96.00% | −0.0079 | 0.0079 | 0.3032 | 91.30% | −0.5796 | 0.3198 | 0.8124 | 96.30% | −0.1388 | 0.0231 | 0.2822 | 96.20% | ||
| −0.0113 | 0.0021 | 0.1733 | 94.80% | −0.0028 | 0.0006 | 0.1562 | 99.50% | −0.1630 | 0.0293 | 0.2058 | 96.10% | −0.0455 | 0.0024 | 0.1169 | 99.40% | |||
| 0.1181 | 0.0333 | 0.5454 | 95.40% | 0.0580 | 0.0169 | 0.3395 | 86.30% | −0.9502 | 0.9057 | 0.5857 | 95.20% | −0.2184 | 0.0550 | 0.4088 | 99.00% | |||
| 3 | 40 | 0.0235 | 0.3092 | 2.1788 | 95.30% | 0.0366 | 0.1238 | 1.1405 | 91.10% | −1.0479 | 1.6286 | 2.8568 | 94.30% | −0.1913 | 0.1074 | 0.9301 | 93.20% | |
| 0.0006 | 0.0075 | 0.3395 | 96.10% | 0.0129 | 0.0026 | 0.3278 | 99.30% | −0.1505 | 0.0306 | 0.3500 | 94.90% | −0.0331 | 0.0023 | 0.2413 | 99.60% | |||
| 0.1402 | 0.1044 | 1.1421 | 94.90% | 0.0991 | 0.0448 | 0.7967 | 98.70% | −0.9907 | 1.0838 | 1.2547 | 95.10% | −0.2668 | 0.0952 | 0.7802 | 97.20% | |||
| 100 | −0.0599 | 0.1061 | 1.2559 | 95.10% | −0.0028 | 0.0476 | 0.6294 | 86.30% | −0.9828 | 1.1990 | 2.3418 | 98.20% | −0.2541 | 0.0937 | 0.5694 | 91.70% | ||
| −0.0103 | 0.0029 | 0.2080 | 95.10% | 0.0005 | 0.0008 | 0.2013 | 99.80% | −0.1475 | 0.0304 | 0.2531 | 96.00% | −0.0451 | 0.0020 | 0.1453 | 99.60% | |||
| 0.1149 | 0.0407 | 0.6503 | 95.10% | 0.1022 | 0.0348 | 0.5460 | 92.90% | −1.0087 | 1.0553 | 0.7632 | 95.50% | −0.2697 | 0.0810 | 0.5150 | 98.70% | |||
| 150 | −0.0670 | 0.0781 | 1.0641 | 94.10% | −0.0063 | 0.0208 | 0.3544 | 76.20% | −0.9034 | 1.0538 | 1.9738 | 97.30% | −0.1960 | 0.0582 | 0.4186 | 86.80% | ||
| −0.0120 | 0.0022 | 0.1780 | 95.40% | −0.0027 | 0.0006 | 0.1565 | 99.40% | −0.1377 | 0.0300 | 0.2183 | 95.00% | −0.0439 | 0.0019 | 0.1170 | 99.40% | |||
| 0.1127 | 0.0334 | 0.5638 | 95.20% | 0.0560 | 0.0180 | 0.3404 | 84.30% | −1.0179 | 1.0597 | 0.6037 | 95.10% | −0.2133 | 0.0524 | 0.4020 | 98.70% | |||
| 0.6 | 1.5 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | Bayesian | MLE | Bayesian | |||||||||||||||
| n | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | Bias | MSE | LACI | CP | ||
| 0.3 | 40 | −0.0181 | 0.0028 | 0.1947 | 95.90% | −0.0005 | 0.0006 | 0.1862 | 99.60% | −0.0823 | 0.0093 | 0.1977 | 94.70% | −0.0179 | 0.0008 | 0.1504 | 99.50% | |
| −0.1403 | 0.1292 | 1.2979 | 95.20% | −0.0241 | 0.0470 | 0.9058 | 96.10% | −0.6522 | 0.6298 | 1.7729 | 92.80% | −0.1464 | 0.0491 | 0.7325 | 96.50% | |||
| −0.0741 | 0.1277 | 1.3709 | 95.10% | −0.0102 | 0.0296 | 0.7549 | 96.60% | −0.9567 | 1.0380 | 1.3739 | 95.50% | −0.2595 | 0.0946 | 0.7740 | 97.10% | |||
| 100 | −0.0240 | 0.0015 | 0.1190 | 96.30% | −0.0068 | 0.0003 | 0.1151 | 99.80% | −0.0910 | 0.0094 | 0.1296 | 95.70% | −0.0245 | 0.0007 | 0.0923 | 99.50% | ||
| −0.1724 | 0.0768 | 0.8508 | 95.50% | −0.0435 | 0.0200 | 0.5179 | 94.70% | −0.5781 | 0.5735 | 1.3908 | 97.40% | −0.1385 | 0.0465 | 0.4440 | 96.00% | |||
| −0.1323 | 0.0572 | 0.7813 | 95.50% | −0.0400 | 0.0142 | 0.4511 | 96.10% | −0.9019 | 0.9766 | 0.7739 | 94.80% | −0.2672 | 0.0799 | 0.5118 | 98.90% | |||
| 150 | −0.0258 | 0.0013 | 0.0952 | 95.20% | −0.0084 | 0.0002 | 0.0922 | 99.70% | −0.0927 | 0.0093 | 0.1076 | 95.30% | −0.0244 | 0.0007 | 0.0747 | 99.90% | ||
| −0.1754 | 0.0639 | 0.7143 | 95.40% | −0.0351 | 0.0141 | 0.3195 | 84.30% | −0.4825 | 0.5078 | 1.2142 | 97.30% | −0.1707 | 0.0390 | 0.3384 | 93.90% | |||
| −0.1410 | 0.0468 | 0.6440 | 94.40% | −0.0429 | 0.0101 | 0.2973 | 91.40% | −0.8503 | 0.8013 | 0.5970 | 95.90% | −0.2137 | 0.0530 | 0.3981 | 97.80% | |||
| 0.8 | 40 | −0.0560 | 0.0224 | 0.5438 | 95.40% | −0.0052 | 0.0056 | 0.4736 | 99.10% | −0.2496 | 0.0877 | 0.6245 | 95.20% | −0.0560 | 0.0066 | 0.3692 | 99.40% | |
| −0.1378 | 0.1350 | 1.3358 | 94.80% | −0.0130 | 0.0417 | 0.9337 | 97.80% | −0.6714 | 0.6576 | 1.7835 | 93.60% | −0.1389 | 0.0492 | 0.7624 | 95.80% | |||
| −0.0848 | 0.1201 | 1.3181 | 95.40% | −0.0090 | 0.0323 | 0.7708 | 96.50% | −0.9702 | 1.0533 | 1.3122 | 95.40% | −0.2668 | 0.0940 | 0.7850 | 97.70% | |||
| 100 | −0.0665 | 0.0116 | 0.3332 | 94.50% | −0.0207 | 0.0023 | 0.2860 | 99.30% | −0.2396 | 0.0800 | 0.4370 | 95.90% | −0.0477 | 0.0061 | 0.2189 | 99.50% | ||
| −0.1625 | 0.0768 | 0.8802 | 94.90% | −0.0429 | 0.0203 | 0.5392 | 95.80% | −0.6182 | 0.6181 | 1.4034 | 97.40% | −0.1896 | 0.0476 | 0.4517 | 96.20% | |||
| −0.1188 | 0.0587 | 0.8279 | 96.50% | −0.0319 | 0.0138 | 0.4696 | 95.70% | −1.0108 | 1.0566 | 0.7330 | 95.30% | −0.2708 | 0.0809 | 0.5168 | 99.10% | |||
| 150 | −0.0723 | 0.0099 | 0.2679 | 94.60% | −0.0235 | 0.0021 | 0.2119 | 98.80% | −0.2306 | 0.0751 | 0.3863 | 96.10% | −0.0378 | 0.0060 | 0.1750 | 98.70% | ||
| −0.1827 | 0.0681 | 0.7311 | 95.70% | −0.0415 | 0.0141 | 0.3305 | 85.90% | −0.6045 | 0.6085 | 1.2282 | 97.30% | −0.1766 | 0.0403 | 0.3464 | 94.70% | |||
| −0.1475 | 0.0482 | 0.6375 | 95.80% | −0.0432 | 0.0104 | 0.3018 | 91.10% | −1.0180 | 1.0586 | 0.5860 | 95.00% | −0.2150 | 0.0532 | 0.4030 | 98.70% | |||
| 1.5 | 40 | −0.1100 | 0.0705 | 0.9482 | 95.40% | −0.0141 | 0.0218 | 0.7839 | 98.00% | −0.5083 | 0.3741 | 1.3338 | 95.00% | −0.1045 | 0.0270 | 0.6226 | 97.30% | |
| −0.1237 | 0.1294 | 1.3251 | 95.70% | −0.0119 | 0.0471 | 0.9518 | 97.10% | −0.6986 | 0.7124 | 1.8577 | 95.40% | −0.1409 | 0.0484 | 0.7573 | 96.60% | |||
| −0.0931 | 0.1282 | 1.3557 | 95.40% | −0.0144 | 0.0316 | 0.7759 | 96.40% | −0.9824 | 1.0835 | 1.3491 | 94.90% | −0.2612 | 0.0886 | 0.7882 | 98.30% | |||
| 100 | −0.1229 | 0.0409 | 0.6301 | 94.60% | −0.0316 | 0.0106 | 0.4667 | 98.00% | −0.4613 | 0.3440 | 0.9938 | 97.20% | −0.1462 | 0.0270 | 0.3655 | 97.60% | ||
| −0.1703 | 0.0763 | 0.8530 | 95.20% | −0.0453 | 0.0211 | 0.5410 | 95.50% | −0.6828 | 0.7013 | 1.3983 | 98.20% | −0.1862 | 0.0459 | 0.4565 | 96.10% | |||
| −0.1352 | 0.0585 | 0.7862 | 95.30% | −0.0403 | 0.0125 | 0.4697 | 97.50% | −0.9930 | 1.0231 | 0.7555 | 95.10% | −0.2734 | 0.0817 | 0.5267 | 99.20% | |||
| 150 | −0.1339 | 0.0347 | 0.5073 | 95.30% | −0.0396 | 0.0091 | 0.3019 | 91.00% | −0.6241 | 0.3359 | 0.8447 | 96.50% | −0.1374 | 0.0234 | 0.2856 | 96.40% | ||
| −0.1837 | 0.0657 | 0.7005 | 95.80% | −0.0428 | 0.0152 | 0.3383 | 84.90% | −0.6081 | 0.6838 | 1.2213 | 96.90% | −0.1679 | 0.0371 | 0.3486 | 95.10% | |||
| −0.1394 | 0.0457 | 0.6356 | 95.50% | −0.0434 | 0.0094 | 0.2989 | 91.40% | −0.0131 | 0.9505 | 0.5890 | 95.40% | −0.2155 | 0.0536 | 0.4058 | 98.30% | |||
| 3 | 40 | −0.1859 | 0.2764 | 1.9288 | 95.60% | −0.0241 | 0.1114 | 1.1606 | 92.30% | −1.0912 | 1.7203 | 2.8542 | 95.70% | −0.1997 | 0.1125 | 0.9716 | 94.20% | |
| −0.1378 | 0.1139 | 1.2080 | 95.30% | −0.0225 | 0.0410 | 0.9509 | 97.50% | −0.7421 | 0.7535 | 1.7660 | 96.50% | −0.1546 | 0.0471 | 0.7396 | 97.60% | |||
| −0.0620 | 0.1340 | 1.4151 | 95.10% | 0.0083 | 0.0414 | 0.7911 | 95.40% | −0.9679 | 1.0554 | 1.3504 | 95.10% | −0.2538 | 0.0892 | 0.7959 | 97.50% | |||
| 100 | −0.2643 | 0.1837 | 1.3232 | 94.90% | −0.0469 | 0.0467 | 0.6380 | 86.90% | −0.9324 | 1.6098 | 2.3031 | 98.20% | −0.2464 | 0.0907 | 0.5906 | 93.10% | ||
| −0.1781 | 0.0797 | 0.8589 | 95.90% | −0.0465 | 0.0195 | 0.5483 | 97.40% | −0.7086 | 0.7460 | 1.3956 | 96.90% | −0.1869 | 0.0455 | 0.4485 | 96.70% | |||
| −0.1409 | 0.0596 | 0.7818 | 94.90% | −0.0407 | 0.0132 | 0.4689 | 96.30% | −0.9995 | 1.0383 | 0.7780 | 94.50% | −0.2659 | 0.0780 | 0.5180 | 99.40% | |||
| 150 | −0.2736 | 0.1553 | 1.1123 | 95.50% | −0.0360 | 0.0221 | 0.3666 | 79.20% | −0.8412 | 1.5246 | 1.9721 | 97.90% | −0.1987 | 0.0584 | 0.4289 | 90.50% | ||
| −0.1893 | 0.0690 | 0.7141 | 95.50% | −0.0410 | 0.0141 | 0.3365 | 86.80% | −0.5902 | 0.6911 | 1.2270 | 96.90% | −0.1620 | 0.0352 | 0.3436 | 95.00% | |||
| −0.1413 | 0.0486 | 0.6639 | 94.80% | −0.0428 | 0.0102 | 0.3066 | 91.10% | −0.9935 | 1.0132 | 0.6337 | 94.50% | −0.2099 | 0.0516 | 0.4009 | 98.20% | |||
References
- Achcar, J.A.; Moala, F.A.; Tarumoto, M.H.; Coladello, L.F. A bivariate generalized exponential distribution derived from copula functions in the presence of censored data and covariates. Pesqui. Oper. 2015, 35, 165–186. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Misra, S.K. Some aging properties of Weibull models. Electron. J. Appl. Stat. Anal. 2016, 9, 297–307. [Google Scholar]
- Vincent Raja, A.; Gopalakrishnan, A. On the Analysis of Bivariate Lifetime Data: Some Models and Applications. Ph.D. Thesis, Cochin University of Science and Technology, Kochi, India, 2017. [Google Scholar]
- Marshall, A.W.; Olkin, I. A multivariate exponential model. J. Am. Stat. Assoc. 1967, 62, 30–44. [Google Scholar] [CrossRef]
- Pathak, A.K.; Vellaisamy, P. A bivariate generalized linear exponential distribution: Properties and estimation. Commun. Stat. Simul. Comput. 2022, 51, 5426–5446. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, D.R. Absolute continuous bivariate generalized Exponential distribution. Adv. Stat. Anal. 2011, 95, 169–185. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.C. On Bivariate Birnbaum–Saunders Distribution. Am. J. Math. Manag. Sci. 2017, 36, 21–33. [Google Scholar]
- Abd Elaal, M.K.; Jarwan, R.S. Inference of bivariate generalized exponential distribution based on copula functions. Appl. Math. Sci. 2017, 11, 1155–1186. [Google Scholar]
- Peres, M.V.D.O.; Achcar, J.A.; Martinez, E.Z. Bivariate modified Weibull distribution derived from Farlie-Gumbel-Morgenstern copula: A simulation study. Electron. J. Appl. Stat. Anal. 2018, 11, 463–488. [Google Scholar]
- Almetwally, E.M.; Muhammed, H.Z. On a bivariate Fréchet distribution. J. Stat. Appl. Probab. 2020, 9, 1–21. [Google Scholar]
- Almetwally, E.M.; Muhammed, H.Z.; El-Sherbieny, E.-S.A. Bivariate Weibull distribution: Properties and different methods of estimation. Ann. Data Sci. 2020, 7, 163–193. [Google Scholar] [CrossRef]
- Peres, M.V.D.O.; de Oliveira, R.P.; Achcar, J.A.; Martinez, E.Z. The Bivariate Defective Gompertz Distribution Based on Clayton Copula with Applications to Medical Data. Aust. J. Stat. 2020, 51, 144–168. [Google Scholar] [CrossRef]
- Samanthi, R.G.M.; Sepanski, J. On bivariate Kumaraswamy-distorted copulas. Commun. Stat. Theory Methods 2022, 51, 2477–2495. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Almetwally, E.M.; Muhammed, H.Z. Bayesian and non-bayesian estimation for the parameter of bivariate generalized Rayleigh distribution based on Clayton copula under progressive type-II censoring with random removal. Sankhya A 2021, 2021, 1–38. [Google Scholar] [CrossRef]
- Muhammed, H.Z.; El-Sherpieny, E.S.A.; Almetwally, E.M. Dependency measures for new bivariate models based on copula function. Inf. Sci. Lett. 2021, 10, 511–526. [Google Scholar]
- Abulebda, M.; Pathak, A.K.; Pandey, A.; Tyagi, S. On a Bivariate XGamma Distribution Derived from Copula. Statistica 2022, 82, 15–40. [Google Scholar]
- Hassan, M.; Chesneau, C. Bivariate Generalized Half-Logistic Distribution: Properties and Its Application in Household Financial Affordability in KSA. Math. Comput. Appl. 2022, 27, 72. [Google Scholar] [CrossRef]
- Usman, U.; Aliyu, Y. Bivariate Nadarajah-Haghighi distribution derived from copula functions: Bayesian estimation and applications. Benin J. Stat. 2022, 5, 45. [Google Scholar]
- Abulebda, M.; Pandey, A.; Tyagi, S. On Bivariate Inverse Lindley Distribution Derived From Copula. Thail Stat. 2023, 21, 291–304. [Google Scholar]
- Qura, M.E.; Fayomi, A.; Kilai, M.; Almetwally, E.M. Bivariate power Lomax distribution with medical applications. PLoS ONE 2023, 18, e0282581. [Google Scholar] [CrossRef]
- Fayomi, A.; Almetwally, E.M.; Qura, M.E. A novel bivariate Lomax-G family of distributions: Properties, inference, and applications to environmental, medical, and computer science data. Aims Math. 2023, 8, 17539–17584. [Google Scholar] [CrossRef]
- Sklar, A. Random variables, joint distribution functions, and copulas. Kybernetika 1973, 9, 449–460. [Google Scholar]
- Gumbel, E.J. Bivariate exponential distributions. J. Am. Stat. Assoc. 1960, 55, 698–707. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; ISBN 978-0387286594. [Google Scholar]
- Joe, H. Dependence Modeling with Copulas; CRC Press: New York, NY, USA, 2014. [Google Scholar]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Chesneau, C. Extensions of Two Bivariate Strict Archimedean Copulas. Comput. J. Math. Stat. Sci. 2023, 2, 159–180. [Google Scholar] [CrossRef]
- Chesneau, C. On new three-and two-dimensional ratio-power copulas. Comput. J. Math. Stat. Sci. 2023, 2, 106–122. [Google Scholar] [CrossRef]
- Haj Ahmad, H.; Almetwally, E.M.; Ramadan, D.A. Investigating the Relationship between Processor and Memory Reliability in Data Science: A Bivariate Model Approach. Mathematics 2023, 11, 2142. [Google Scholar] [CrossRef]
- Kavya, P.; Manoharan, M. Some parsimonious models for lifetimes and applications. J. Stat. Comput. Simul. 2021, 91, 3693–3708. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new methods for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Awodutire, P. Statistical Properties and Applications of the Exponentiated Chen-G Family of Distributions: Exponential Distribution as a Baseline Distribution. Aust. J. Stat. 2022, 51, 57–90. [Google Scholar] [CrossRef]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar]
- Bonferroni, C.E. Elementi di Statistica Generale; Seeber: Firenze, Italy, 1930. [Google Scholar]
- Osmetti, S.A. Maximum likelihood estimate of Marshall-Olkin copula parameter: Complete and censored sample. Ital. J. Appl. Stat. 2012, 22, 211–240. [Google Scholar]
- Basu, A.P. Bivariate failure rate. J. Am. Stat. Assoc. 1971, 66, 103–104. [Google Scholar] [CrossRef]
- Popović, B.V.; Ristić, M.M.; Genç, A.İ. Dependence properties of multivariate distributions with proportional hazard rate marginals. Appl. Math. Model. 2020, 77, 182–198. [Google Scholar] [CrossRef]
- Blomqvist, N. On a measure of dependence between two random variables. Ann. Math. Stat. 1950, 21, 593–600. [Google Scholar] [CrossRef]
- Bekrizadeh, H. Generalized family of copulas: Definition and properties. Thai Stat. 2021, 19, 162–177. [Google Scholar]
- Bukovšek, D.K.; Košir, T.; Mojškerc, B.; Omladič, M. Spearman’s footrule and Gini’s gamma: Local bounds for bivariate copulas and the exact region with respect to Blomqvist’s beta. J. Comput. Appl. Math. 2021, 390, 113385. [Google Scholar] [CrossRef]
- Kundu, D.; Howlader, H. Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data. Comput. Stat. Data Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
- Dey, S.; Dey, T. On progressively censored generalized inverted exponential distribution. J. Appl. Stat. 2014, 41, 2557–2576. [Google Scholar] [CrossRef]
- Dey, S.; Ali, S.; Park, C. Weighted exponential distribution: Properties and different methods of estimation. J. Stat. Comput. Simul. 2015, 85, 3641–3661. [Google Scholar] [CrossRef]
- Dey, S.; Singh, S.; Tripathi, Y.M.; Asgharzadeh, A. Estimation and prediction for a progressively censored generalized inverted exponential distribution. Stat. Methodol. 2016, 32, 185–202. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife; Springer: New York, NY, USA, 1992; pp. 569–593. [Google Scholar]
- McGilchrist, C.A.; Aisbett, C.W. Regression with frailty in survival analysis. Biometrics 1991, 47, 461–466. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Muhammed, H.Z.; Almetwally, E.M. Bivariate Chen Distribution Based on Copula Function: Properties and Application of Diabetic Nephropathy. J. Stat. Theory Pract. 2022, 16, 54. [Google Scholar] [CrossRef]
- Barakat, H.M.; Nigm, E.M.; Alawady, M.A.; Husseiny, I.A. Concomitants of order statistics and record values from generalization of FGM bivariate-generalized exponential distribution. J. Stat. Theory Appl. 2019, 18, 309–322. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Alhussain, Z.A.; Atta, D.; Almetwally, E.M.; Eliwa, M.S. Bivariate Burr X generator of distributions: Properties and estimation methods with applications to complete and type-II censored samples. Mathematics 2020, 8, 264. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.; Bobée, B. A review of bivariate gamma distributions for hydrological application. J. Hydrol. 2021, 246, 1–18. [Google Scholar] [CrossRef]
| Model | Type of Copula | Modeling | Authors |
|---|---|---|---|
| The new suggested model (FGMBKM-T family) | FGM copula | Medical data | New |
| The new suggested model (CBKM-T family) | Clayton copula | Medical data and Sport data | New |
| Bivariate generalized exponential model | FGM copula | Medical data and simulated data | [1] |
| Bivariate generalized exponential model | Clayton copula | Sport data | [6] |
| Bivariate Birnbaum–Saunders model | Gaussian copula | Psychology or Social data | [7] |
| Bivariate generalized exponential model | Plackett copula | Medical data | [8] |
| Bivariate modified Weibull model | FGM copula | Medical data | [9] |
| Bivariate Frechet model | FGM and AMH copula | Economic and Medical data | [10] |
| Bivariate Weibull model | FGM copula | Medical data | [11] |
| Bivariate defective Gompertz model | Clayton copula | Medical data | [12] |
| Bivariate copulas based on the Kumaraswamy distortion | Gumbel, Frank, Clayton, Frank, Galambos copula | Insurance data | [13] |
| Bivariate generalized Rayleigh model | Clayton copula | Economic data | [14] |
| Bivariate inverted Topp–Leone model | FGM, Ali–Mikhail–Haq (AMH), | Medical data | [15] |
| Bivariate XGamma model | FGM copula | Sport data | [16] |
| Bivariate generalized half-logistic model | FGM copula Plackett, and Clayton copula | Economic data | [17] |
| Bivariate Nadarajah–Haghighi | FGM copula | Medical data | [18] |
| Bivariate inverse Lindley model | FGM copula | Climatological or Meteorological data | [19] |
| Bivariate Power lomax model | FGM copula | Medical data | [20] |
| Bivariate lomax-G family | FGM copula | Environmental, Medical and Computer science data | [21] |
| Model | cdf: | Pdf: |
|---|---|---|
| Exponential | ; z > 0 | |
| Weibull | ; z > 0 | |
| Pareto | ; z > 0 |
| Data | Correlation | Clayton | FGM | AMH | |
|---|---|---|---|---|---|
| I | 0.0511 | statistic | 0.1442 | 0.2903 | 0.2114 |
| parameter | 0.3033 | 0.4670 | 0.4975 | ||
| p-value | 0.7628 | 0.3944 | 0.5487 | ||
| II | 0.3690 | statistic | 0.2846 | Not Applying | 0.4849 |
| parameter | 0.6078 | 0.7888 | |||
| p-value | 0.2384 | 0.1982 |
| LL | AIC | CAIC | BIC | HQIC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| FGMBKM-Ex | estimates | 0.0068 | 0.0078 | 0.3605 | 339.4979 | 684.9959 | 685.9189 | 689.1994 | 686.3406 | ||
| SE | 0.0013 | 0.0016 | 0.4434 | ||||||||
| FGMBKM-W | estimates | 0.0070 | 0.8100 | 0.0075 | 1.5765 | 0.3611 | 334.9842 | 679.9685 | 682.4685 | 686.9745 | 682.2098 |
| SE | 0.0017 | 0.1108 | 0.0005 | 0.1304 | 0.2781 | ||||||
| FGMBF | estimates | 22.7765 | 0.7286 | 27.9028 | 0.8661 | 0.6119 | 340.7127 | 691.4254 | 693.9254 | 698.4313 | 693.6666 |
| SE | 6.1354 | 0.0979 | 6.2964 | 0.1175 | 0.5613 | ||||||
| AMHBF | estimates | 23.0689 | 0.7266 | 28.1589 | 0.8638 | 0.5393 | 340.6412 | 691.2824 | 693.7824 | 698.2884 | 693.5237 |
| SE | 6.1198 | 0.0978 | 6.2906 | 0.1171 | 0.3541 | ||||||
| FGMBW | estimates | 0.7513 | 99.9740 | 0.9291 | 95.4974 | 0.3992 | 338.9349 | 687.8698 | 690.3698 | 694.8758 | 690.1111 |
| SE | 0.1053 | 25.6610 | 0.1322 | 19.8581 | 0.4987 | ||||||
| FGMBGe | estimates | 0.6660 | 0.0063 | 0.9258 | 0.0096 | 0.3775 | 339.5445 | 689.0890 | 691.5890 | 696.0950 | 691.3302 |
| SE | 0.1485 | 0.0016 | 0.2174 | 0.0023 | 0.4848 | ||||||
| FGMBG | estimates | 0.6697 | 179.8593 | 0.9230 | 107.8414 | 0.3806 | 339.4889 | 688.9778 | 691.4778 | 695.9838 | 691.2191 |
| SE | 0.1463 | 56.1853 | 0.2076 | 31.9672 | 0.4869 | ||||||
| CBITL | estimates | 0.3605 | 0.3409 | 3.0826 | 362.7520 | 731.5039 | 732.4270 | 735.7075 | 732.8487 | ||
| SE | 0.0635 | 0.0601 | 0.9243 | ||||||||
| FGMBITL | estimates | 0.3628 | 0.3523 | 0.4670 | 370.2663 | 746.5325 | 747.4556 | 750.7361 | 747.8773 | ||
| SE | 0.0739 | 0.0397 | 1.0192 | ||||||||
| FGMBCH | estimates | 0.0504 | 0.2336 | 0.0326 | 0.2651 | 0.3921 | 343.4072 | 696.8145 | 699.3145 | 703.8204 | 699.0557 |
| SE | 0.0190 | 0.0168 | 0.0136 | 0.0181 | 0.5718 | ||||||
| BBuXexp | estimates | 0.0016 | 0.0548 | 0.0473 | 0.1021 | 373.7172 | 755.4343 | 757.0343 | 761.0391 | 757.2273 | |
| SE | 0.0002 | 0.0142 | 0.0116 | 0.0302 | |||||||
| CBKM-Ex | estimates | 0.0068 | 0.0076 | 0.2967 | 339.1936 | 684.3871 | 685.3102 | 688.5907 | 685.7319 | ||
| SE | 0.0013 | 0.0015 | 0.2826 | ||||||||
| CBKM-W | estimates | 0.0070 | 0.8179 | 0.0079 | 1.0046 | 0.4128 | 337.9455 | 685.8909 | 688.3909 | 692.8969 | 688.1322 |
| SE | 0.0017 | 0.1121 | 0.0016 | 0.1410 | 0.3586 |
| LL | AIC | CAIC | BIC | HQIC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CBKM-Ex | estimates | 0.0184 | 0.0271 | 0.4641 | 337.5242 | 681.0485 | 681.7757 | 685.8812 | 682.7522 | ||
| SE | 0.0032 | 0.0047 | 0.5251 | ||||||||
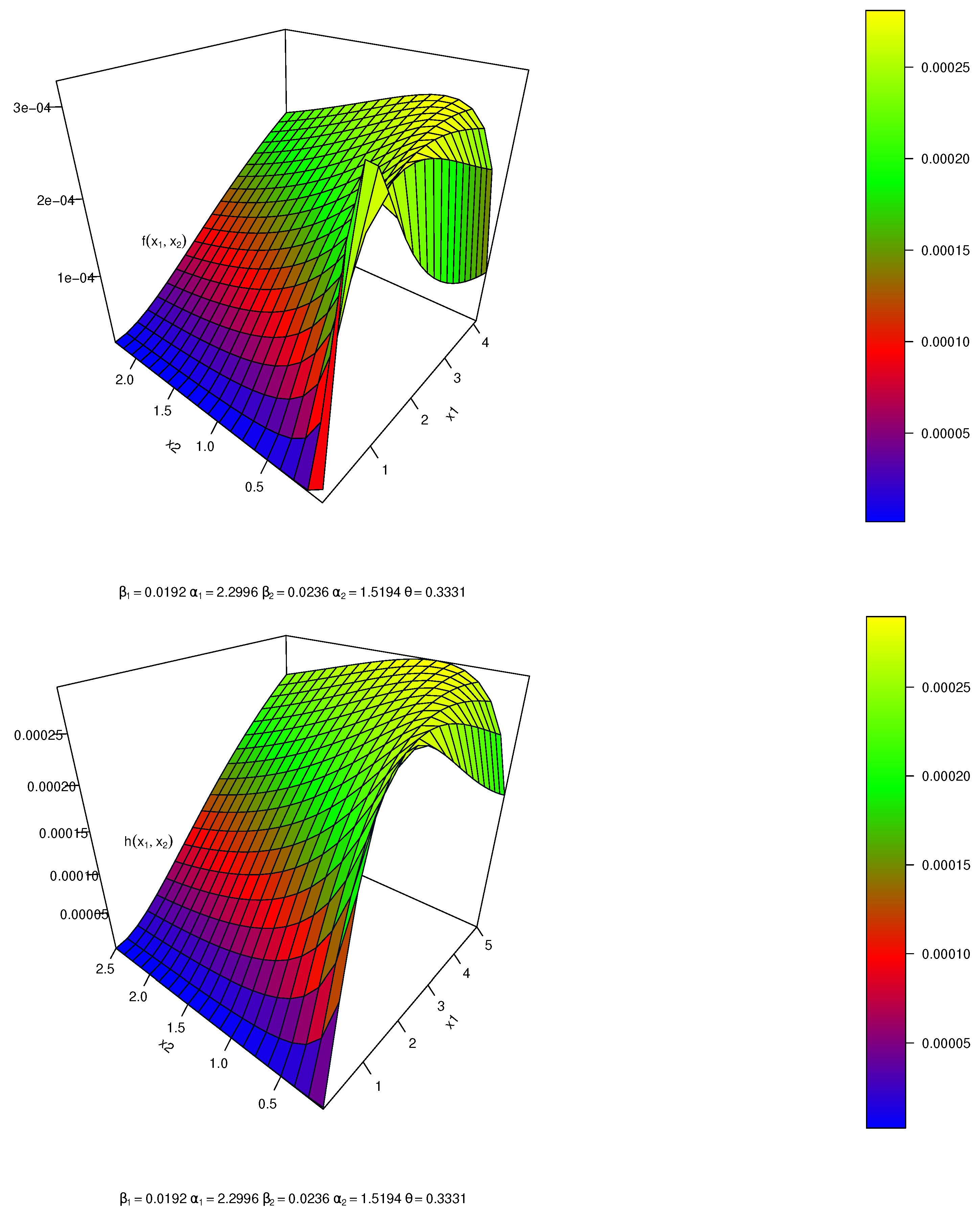
| CBKM-W | estimates | 0.0192 | 2.2996 | 0.0236 | 1.5194 | 0.3331 | 322.6669 | 655.3338 | 657.2693 | 663.3884 | 658.1734 |
| SE | 0.0016 | 0.3058 | 0.0029 | 0.1930 | 0.2061 | ||||||
| AMHBF | estimates | 20.6832 | 0.9876 | 11.7831 | 0.9202 | 0.9914 | 351.0523 | 712.1046 | 714.0400 | 720.1591 | 714.9442 |
| SE | 3.5265 | 0.1023 | 2.1454 | 0.1091 | 0.0170 | ||||||
| CBITL | estimates | 0.3437 | 0.4007 | 6.6079 | 378.3274 | 762.6548 | 763.3821 | 767.4876 | 764.3586 | ||
| SE | 0.0609 | 0.0734 | 1.3010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayomi, A.; Almetwally, E.M.; Qura, M.E. Exploring New Horizons: Advancing Data Analysis in Kidney Patient Infection Rates and UEFA Champions League Scores Using Bivariate Kavya–Manoharan Transformation Family of Distributions. Mathematics 2023, 11, 2986. https://doi.org/10.3390/math11132986
Fayomi A, Almetwally EM, Qura ME. Exploring New Horizons: Advancing Data Analysis in Kidney Patient Infection Rates and UEFA Champions League Scores Using Bivariate Kavya–Manoharan Transformation Family of Distributions. Mathematics. 2023; 11(13):2986. https://doi.org/10.3390/math11132986
Chicago/Turabian StyleFayomi, Aisha, Ehab M. Almetwally, and Maha E. Qura. 2023. "Exploring New Horizons: Advancing Data Analysis in Kidney Patient Infection Rates and UEFA Champions League Scores Using Bivariate Kavya–Manoharan Transformation Family of Distributions" Mathematics 11, no. 13: 2986. https://doi.org/10.3390/math11132986
APA StyleFayomi, A., Almetwally, E. M., & Qura, M. E. (2023). Exploring New Horizons: Advancing Data Analysis in Kidney Patient Infection Rates and UEFA Champions League Scores Using Bivariate Kavya–Manoharan Transformation Family of Distributions. Mathematics, 11(13), 2986. https://doi.org/10.3390/math11132986






