Abstract
The set-based particle swarm optimisation algorithm is a swarm-based meta-heuristic that has gained popularity in recent years. In contrast to the original particle swarm optimisation algorithm, the set-based particle swarm optimisation algorithm is used to solve discrete and combinatorial optimisation problems. The main objective of this paper is to review the set-based particle swarm optimisation algorithm and to provide an overview of the problems to which the algorithm has been applied. This paper starts with an examination of previous attempts to create a set-based particle swarm optimisation algorithm and discusses the shortcomings of the existing attempts. The set-based particle swarm optimisation algorithm is established as the only suitable particle swarm variant that is both based on true set theory and does not require problem-specific modifications. In-depth explanations are given regarding the general position and velocity update equations, the mechanisms used to control the exploration–exploitation trade-off, and the quantifiers of swarm diversity. After the various existing applications of set-based particle swarm optimisation are presented, this paper concludes with a discussion on potential future research.
Keywords:
set-based particle swarm optimisation; particle swarm optimisation; discrete optimisation; combinatorial optimisation MSC:
03E05; 03E75; 90C27; 68R01; 68R05
1. Introduction
Optimisation algorithms are methods that search for solutions to optimisation problems such that a best solution is found with respect to a given quantity [1]. The purpose of the optimisation process is to find suitable solutions which best solve the given problem while adhering to any relevant constraints. Optimisation algorithms are well studied in the literature, and a substantial number of approaches exist. For an extensive review of approaches, refer to [2].
Optimisation theory is an ancient branch of mathematics which has a rich and influential history [3]. To further illustrate the fundamental nature of optimisation theory, optimisation theory laid the foundations for the development of the fields of geometry and differential calculus [4]. Problems studied by pioneer mathematicians, such as Heron’s problem and Dido’s problem, show that optimisation theory has been relevant for thousands of years [3,5]. However, optimisation is not an archaic field in isolation, but also has relevance to active research fields such as machine learning (ML) [6]. Optimisation is a crucial part of ML, as in ML the error between predictions and ground truths is minimised [7]. Therefore, the performance of an ML model greatly depends on the implemented optimisation process.
Optimisation problems have varied levels of complexity, with optimisation problem complexity classified according to the “hardness” of the corresponding decision problem [8]. The concept of the hardness of optimisation and decision problems is covered extensively in the literature [9,10,11]. Multiple optimisation algorithms popular in the existing literature make use of gradient information from the search space in order to find optimal solutions [12]. Deterministic optimisation can be viewed as part of a classical branch of mathematics [13]. Deterministic optimisation algorithms are described as mathematically rigorous and are also referred to as mathematical programming approaches. In contrast to deterministic approaches, stochastic optimisation algorithms use elements of randomness to aid the search process [13].
A second way to classify optimisation algorithms is by the use of gradient information. Various optimisation algorithms that utilise gradient information of the search space have been developed, i.e., stochastic gradient descent [14], conjugate gradient descent [15], subgradient descent [16], and the Broyden–Fletcher–Goldfarb–Shanno algorithm [17,18,19,20]. However, gradient information is not always available; hence, gradient-free deterministic optimisations have been proposed, such as the Nelder–Mead algorithm [21].
The high level of complexity of certain optimisation problems has led to the rise in popularity of the meta-heuristic algorithms used to solve optimisation problems [22,23,24]. Meta-heuristics iteratively guide heuristic processes to search for optimal solutions without the need for problem-specific implementations [25]. Meta-heuristics tend to be both stochastic and gradient-free approaches. Distinctive meta-heuristics have fundamental differences in order to solve different types of optimisation problems, e.g., different adaptations of meta-heuristics are required to solve real-valued optimisation problems versus discrete optimisation problems.
The study of set theory is well-established and is believed to have been pioneered by Dedekind and Cantor in the 1800s [26,27,28]. From the start of the foundation of the rigorously defined set theory used to compare the sizes of infinite sets, to the widely accepted contemporary Zermelo–Fraenkel axioms, it is evident that set theory remains a fundamentally important branch of mathematics [29]. In contrast to real-valued optimisation problems, where solutions are in -dimensional real-valued space, set-based (also referred to as set-valued) optimisation problems are a form of optimisation problem where solutions are represented as sets of unordered elements. Set-valued optimisation unifies and generalises scalar optimisation with vector optimisation, which provides a more general framework for optimisation theory [30]. The importance of set-valued optimisation is further cemented due to the wide range of applications available [31,32].
This paper aims to provide a review of the current state of research on particle swarm optimisation (PSO) algorithms which utilise set-based concepts. The main aim is to consolidate and review the literature on existing set-based PSO algorithms, and to provide a comprehensive overview of the set-based particle swarm optimisation (SBPSO) algorithm, which is deemed to be the most suited set-based PSO. This paper contributes a corpus of knowledge on the background and workings of eight algorithms (i.e., discrete particle swarm optimisation (DPSO), set particle swarm optimisation (SetPSO), set swarm optimisation (SSO), set-based particle swarm optimisation (S-PSO), fuzzy particle swarm optimisation (FPSO), fuzzy evolutionary particle swarm optimisation (FEPSO), integer and categorical particle swarm optimisation (ICPSO), and rough set-based particle swarm optimisation (RoughPSO)) and also outlines the shortcomings of the reviewed algorithms. Additionally, this paper reviews the SBPSO algorithm, which proves to be the set-based algorithm which is most firmly grounded in set theory and has a wide range of existing applications. There are seven reviewed applications of SBPSO, i.e., the multi-dimensional knapsack problem (MKP), feature selection problem (FSP), portfolio optimisation, polynomial approximation, support vector machine (SVM) training, clustering, and rule induction.
Section 2 of this paper provides an introduction to discrete and combinatorial optimisation, after which Section 3 introduces the PSO algorithm. In Section 4, multiple attempts at the creation of a set-based particle swarm optimisation algorithm are review and critiqued. Section 5 presents the set-based particle swarm optimisation algorithm reviewed in this paper, followed by a description of the multi-objective optimisation and of multi-guide set-based particle swarm optimisation (MGSBPSO) in Section 6. A summary of the existing applications of the selected set-based PSO is given in Section 7. The conclusion of this paper is presented in Section 8 and proposals for future work to be conducted on the reviewed algorithm are given in Section 9.
2. Discrete and Combinatorial Optimisation Problems
Optimisation problems are solved through the search for a “best” or “most suitable” solution in the search space which minimises (or maximises) a given quantity. For example, given a search space , the feasible region in the search space is denoted as , and is an -dimensional candidate solution. A candidate solution is a global minimum of f if
where . Additionally, an optimisation problem with objective function f is defined as
where (the feasible search space), is one of the inequality constraints, is one of the equality constraints, and are the boundary constraints for . Note that this paper assumes minimisation, without the loss of generality.
Discrete optimisation is a subsection of optimisation which deals with problems that have a finite or countable number of candidate solutions in the search space. Discrete-valued and combinatorial optimisation problems differ from continuous-valued optimisation problems in that the variables of solutions do not fall within a range on , but are chosen from a finite number of possibilities. For example, an -dimensional optimisation problem that is restricted to integer solutions () is classified as a discrete optimisation problem. More formally, Strasser et al. [33] define discrete-valued optimisation problems as in Definition 1.
Definition 1
(Discrete-valued Optimisation Problem). A class of problems where an objective function is to be optimised that has decision variables whose values are limited to finite sets, numerical or categorical, ordered or unordered.
In the existing literature, the terms discrete optimisation problems and combinatorial optimisation problems are often used interchangeably. This paper restricts nomenclature to the use of “discrete optimisation problems” in reference to any optimisation problem in which there exists a non-continuous-valued input variable. More in-depth background information on combinatorial optimisation can be found in [34].
3. Particle Swarm Optimisation
The PSO algorithm is a population-based meta-heuristic that was first proposed by Kennedy and Eberhart in 1995 [35]. PSO optimises a given objective function through the use of a population of candidate solutions, referred to as particles. Each particle represents a candidate solution to the optimisation problem and is associated with a position and velocity in the search space. The particles “move” through the search space in search of an optimal solution to the given problem. The movement of a particle is dictated by the velocity of the particle, which is updated at each iteration, after which the velocity modifies the position of the particle.
The particles are organised into neighbourhoods, neighbourhoods which facilitate communication between particles as the particles search for optima. The neighbourhood topology of the swarm is an important factor in PSO performance and has been the subject of study in the literature almost since the advent of PSOs [36]. Multiple swarm topologies, or sociometries, exist (e.g., star, ring, pyramid, Von Neumann) and have been shown to influence PSO performance [37].
The velocity update equation consists of three components: the momentum term, the cognitive term, and the social term. The momentum term biases the movement of the particle to continue in the direction of the previous movement to facilitate smoother trajectories [38]. The cognitive term biases the movement of the particle towards areas of the search space that the particle has previously found to hold promise of an optimum. Finally, the social component biases the movement of the particle towards areas of the search space found by any particle in the relevant neighbourhood that have shown promise of an optimum. The social component is selected as the best position in each neighbourhood of the swarm, hence each neighbourhood best is defined as the personal best position of the most optimal particle in the neighbourhood.
The velocity update equation per dimension is
where i is the particle index, j is the dimension index, t is the iteration index, is the momentum coefficient, and and are the cognitive and social acceleration coefficients, respectively. Further, is the current particle position, is the personal best position, the neighbourhood best position, and each and are random variables sampled independently from .
The position of a particle is updated per dimension as
where is the current position and is the updated velocity as calculated by Equation (3).
The best position of a PSO swarm at the final iteration needs to be in the feasible space of the given problem in order to be accepted as a viable solution (i.e., the final global best position cannot violate any constraints). However, the manner in which constrains are handled has an impact on the performance of PSO. The existing literature outlines the use of penalty methods [39,40], conversion to unconstrained Lagrangians [41,42], and repair methods [43,44,45,46]. A full review of constrain handling strategies for PSO is given in [47].
The pseudocode for PSO is given in Algorithm 1.
| Algorithm 1 Particle Swarm Optimisation. |
|
4. Particle Swarm Optimisation Algorithms for Discrete Optimisation Problems
The original PSO [35] was developed to solve continuous-valued optimisation problems exclusively. Although the original PSO has been applied to a wide range of optimisation problems [48,49,50], PSO is not able to solve discrete optimisation problems directly.
Almost immediately after the introduction of the original PSO algorithm used to solve problems in , Kennedy and Eberhart introduced a discrete version known as binary particle swarm optimisation (BPSO) to solve problems in [51]. PSOs for discrete problems were then further studied by Schoofs and Bart in 2002 [52] as well as by Clerc in 2004 [53]. However, it was only after a further nine years that researchers started exploring the possibility of applying mathematical set concepts to create new PSO variants for discrete optimisation problems.
Set-based representations of candidate solutions are well suited for use in optimisation problems because sets are a natural representation for combinatorial solutions. Further, set theory is the canonical language of mathematics, and all mathematical objects can be constructed as sets [54]. In order to solve discrete-valued optimisation problems using sets, new set-based representations for positions and velocities need to be developed, as well as new operators that can be used with the new set-based positions and velocities.
The remainder of this section outlines some of the existing PSO variants grounded in set theory, as well as the shortcomings of the presented PSO variants. This paper does not review all discrete PSO variants, because only the set theory variants are relevant to the set-based algorithm which is reviewed.
4.1. Discrete Particle Swarm Optimisation
One of the first publications to incorporate set theory into PSOs was from Correa et al., in which the DPSO algorithm is used to perform feature selection on bioinformatics data [55].
In the original paper by Correa et al., DPSO is applied to reduce the dimensionality of a training dataset through the removal of superfluous input attributes. DPSO represents candidate solutions as combinations of selected elements, instead of points in -dimensional Euclidean space. The size of a position in the swarm is determined by a random number, k, which is sampled from a uniform distribution, . A velocity of a position consists of a matrix, where the first row contains the “proportional likelihoods” of each attribute and the second row contains the indexes of the elements. The proportional likelihood tracks how often elements form part of either a position of a particle, the personal best position of a particle, or the neighbourhood best position of a particle. The velocity update equation then selects the elements which have been frequently present in previous positions to be the next position.
A problem with the proportional likelihood approach is that the summation of likelihoods may discourage exploration and lead to premature convergence. The selection of elements with the highest likelihoods tends to reinforce the idea that previously selected elements should remain as part of particle positions.
The DPSO algorithm is claimed to be a generic set-based algorithm, but has two main limitations, namely:
- Particle position sizes are fixed (though not to the same size), which means that positions are not truly set-based;
- The proportional likelihoods do not encourage exploration of all possible combinations of elements.
4.2. Set Particle Swarm Optimisation
Independent of Correa et al., Neethling and Engelbrecht proposed the SetPSO algorithm [56], which is used to predict ribonucleic acid (RNA) secondary structures. The prediction of RNA secondary structures is achieved by representing all possible enumerations of stacks of Watson–Crick nucleotide pairs and then minimising the free energy of the structure to make the structure more stable. The SetPSO version of the PSO algorithm is more generic than the DPSO, because particle positions are actual sets, with cardinalities that can be both increased or decreased.
Although the SetPSO represents both positions and velocities of particles as sets, the analogy of velocity in the particle update equation is not as effective as it could be. The velocity set is modified by adding a close set and removing an open set. The close set is a random combination of elements from the personal best position, neighbourhood best position, and the rest of the universal set, while the open set is a random subset of the current particle position. The velocity set is used to modify the position set, but because the velocity set is not constructed with information of the search space, the velocity set is not guaranteed to aid in finding the optimum. The construction of the close set and open set can theoretically be improved, although no additional research has done so.
4.3. Set Swarm Optimisation
Veenhuis attempted to create a generic set-based PSO algorithm, the SSO algorithm [57]. The SSO approach was inspired by the need to solve problems such as data clustering, where the required number of clusters is not known beforehand. Not knowing the number of clusters beforehand makes using PSOs with particles of a fixed dimension () unsuitable. Veenhuis explicitly states that Neethling and Engelbrecht developed a set-based PSO that is not a strong enough analogy of the original PSO, and that SSO aims to be more in the spirit of the original PSO.
Veenhuis first described the abstract form that PSO update equations must have in order to be considered analogies of the original PSO. The abstract form of the velocity update equation is
where and are random variables ( and , respectively, in the original PSO), is the personal best position, and is the neighbourhood best position. The abstract operators (⊙, ⊕ and ⊖) need algorithm-specific definitions. As an example, the original PSO follows the abstract form in Equation (5) and implements the following algorithm-specific operators: ⊙ is the scalar multiplication operator, ⊕ is element-wise vector addition, and ⊖ is the element-wise vector subtraction. The abstract form of the position update equation is
where x is the position representation, v is the velocity analogy, and ⊞ is used to change the position using the velocity.
Veenhuis defined set-compatible operators for each of the abstract operators in Equations (5) and (6), and the result is a relatively generic set-based PSO. The velocity update equation of SSO implements an element-wise ⊙ operator that is defined for each domain to which the algorithm is applied. Additionally, the velocity update equation implements generic union and set difference operators. The position update equation uses the union operator to add a velocity to a position.
There are two main issues that limit the general application of SSO, namely:
- The domain-specific element-wise scalar multiplication operator, ⊙, does not act on the velocity set as a whole, and therefore does not influence the cardinality of the set;
- The cognitive and social terms in the velocity update equation strictly add terms (⊕) to particle positions, hence no terms are removed.
The fact that none of the operators in the velocity update equation are able to reduce the cardinality of a position set leads to the “set bloating” of positions. Set bloating refers to the phenomenon whereby the cardinality of a set increases monotonically, resulting in oversized (or “bloated”) sets. The issue of set bloating lead to the creation of the reduction operator, , which requires a problem-specific distance-based mechanism to function. The requirement that both the scalar multiplication and reduction operators need problem-specific implementations severely limits the generic applicability of the SSO algorithm.
4.4. Set-Based Particle Swarm Optimisation
Chen et al. presented a novel approach to combinatorial optimisation problems by using a new S-PSO algorithm [58]. The use of a set-based representation was justified, because sets can be used to characterise the discrete search space of combinatorial optimisation problems very well. The new algorithm was evaluated on two popular combinatorial problems, namely the travelling salesman problem and the MKP.
The positions of S-PSO are referred to as sets, but have a fixed dimensionality. Each “dimension” of a position set is a subset of the universal set. To update a position at a new iteration, S-PSO reinitialises the position to the empty set and uses a heuristic to reconstruct the position. The velocities of particles are defined as “sets with possibilities”, which means that velocities are sets where each element is a two-element tuple. The first element of a tuple in a velocity set contains the component of the candidate solution, while the second element of the tuple contains the probability of including the tuple in a future position. Chen et al. distinguished between the sets with possibilities for velocities and the true sets for positions through the use of the nomenclature “crisp” sets for positions.
It is important to note the drawbacks of the S-PSO implementation, namely:
- S-PSO uses both crisp sets as well as “sets with possibilities”;
- Particle positions are reconstructed for each iteration.
The inclusion of the sets with possibilities changes the nature of the positions and velocities to be set-like instead of true sets, while the position reconstruction complicates the particle update procedure. It is the opinion of the authors that S-PSO is overly complicated for use as a generic set-based PSO.
4.5. Fuzzy Particle Swarm Optimisation
The FPSO algorithm is a PSO variant by Khan and Engelbrecht originally used to solve the multi-objective optimisation of topologies for distributed local area networks [59]. The FPSO algorithm is named after one of the key components of the algorithm, i.e., the unified And-Or (UAO) fuzzy operator [60], which aggregates objectives. In FPSO, the particle positions are sets of network links, while the velocities are sets of link exchanges that are performed on the links in the position sets.
The FPSO algorithm cannot entirely be considered a set-based PSO. The positions of FPSO are fixed dimension “sets” which contain elements of the candidate solution. The velocity sets of FPSO contain instructions to substitute position set elements with different compatible elements. Although the positions and velocities are represented by sets, there are no true set-based operations performed on those sets. Furthermore, the position sizes of the FPSO are fixed, and thus do not take advantage of the inherent size variability of set-based representations.
4.6. Fuzzy Evolutionary Particle Swarm Optimisation
From the success of the FPSO, Mohiuddin et al. developed the FEPSO algorithm to solve the shortest path first weight setting problem [61]. The FEPSO algorithm incorporates the simulated evolution (SimE) heuristic [62] from evolutionary computing into the FPSO algorithm. SimE is a search strategy with three main steps, namely evaluation, selection, and allocation. These three steps are incorporated into the velocity calculation of FPSO to improve the “blind” removal of weights in the position set. The addition of the SimE technique is used to prevent the unnecessary removal of elements in the positions of particles that are possibly optimal.
Unfortunately, because FEPSO is so closely based on FPSO, FEPSO suffers from the same main shortcoming, namely that the position sets are of a fixed size and do not remain true to the analogy of the original PSO.
4.7. Integer and Categorical Particle Swarm Optimisation
The ICPSO algorithm may not claim to be a true set-based PSO, but does warrant investigation because of the approach of ICPSO to discrete optimisation. Strasser et al. [33] proposed ICPSO as an approach which combines aspects of estimation of distribution algorithms (EDA) [63] and PSOs.
From the original work of Strasser et al. [33], a position, , is a set of probability distributions (). Each component of a position is composed of probability distributions, . Each denotes the probability that variable takes on the value j for particle p. A velocity is a vector of vectors , where . The vector component is the velocity of particle p for variable i in state j. The continuous valued velocity components are used to modify the position components, i.e., the probability distributions. Similar to FPSO, the positions of ICPSO are represented by sets, but the sets are of fixed size; the velocities also simply modify the elements within the sets instead of the sets themselves.
4.8. Rough Set-Based Particle Swarm Optimisation
The RoughPSO algorithm is a competitive approach to both discrete and continuous optimisation problems from Fen et al. [64]. In the original paper, RoughPSO is evaluated on both function approximation and data classification problems, and performs well in comparison to the chosen benchmark algorithms.
The positions and velocities of the particles in RoughPSO are rough sets [65], which means that the elements of the set have a degree of membership. Rough sets are similar to fuzzy sets, but rough sets can represent both fuzzy and clear concepts in sets [64]. Rough sets also utilise the concept of “roughness”, which is a measurement based on the upper and lower approximations of the set. The membership degree is calculated based on the roughness of an element in the set, which is a value used to incorporate the uncertainty that rough sets can capture. The velocity of a RoughPSO particle is a vector similar to the velocity of the original PSO, but uses the membership degree of a velocity element instead of an inertia weight coefficient.
A characteristic of the RoughPSO algorithm, contrary to other PSO variants, is that the dimensionality of the positions remains fixed, but the number of particles in the swarm decreases. Although the RoughPSO is a generic, versatile, and well-performing algorithm, the fact that RoughPSO uses fixed dimensional positions and non-set velocities makes it unsuitable to be referred to as a true set-based PSO.
4.9. The Search for Rigorously Defined Set-Based Particle Swarm Optimisation
The PSO variants described in the preceding sections all present fundamental drawbacks which make each algorithm unsuited as a truly generic set-based PSO. The one PSO variant which is grounded in set theory and implements true sets is the SBPSO algorithm, developed by Langeveld and Engelbrecht [66]. A comprehensive background of SBPSO warrants a dedicated review, and hence is not presented in summary form as with the previous algorithms. Section 5 is dedicated to the SBPSO algorithm.
5. Set-Based Particle Swarm Optimisation
Langeveld and Engelbrecht proposed the SBPSO with the intention that SBPSO is a “generic, set-based PSO that can be applied to discrete optimisation problems” [67]. The existing “set-based” PSO approaches are rejected by Langeveld and Engelbrecht because the algorithms fall short in three main categories. The problems raised are that existing algorithms are
- not truly set-based based;
- not truly functioning in that sufficiently good results are not yielded on discrete optimisation problems;
- not generically applicable to all discrete optimisation problems, but instead require domain-specific implementations.
The remainder of this section provides a comprehensive overview of the SBPSO algorithm as presented by Langeveld and Engelbrecht.
5.1. Set-Based Concepts
The SBPSO algorithm proposed by Langeveld and Engelbrecht [66] is an attempt to develop a generic set-based PSO using true sets. The SBPSO version of PSO uses a strict mathematical definition of sets for particle positions and velocities.
One of the advantages of SBPSO is that the position sets are variable in size. Variable-sized position sets help to reduce the negative effects of the curse of dimensionality, in which high dimensional problems tend to suffer in performance. Variable-sized position sets are also able to create simpler solutions through the modification of the size of the set.
Importantly, the velocity set acts on the position set as a whole and not the elements within the position set. The fact that velocity sets act on position sets makes SBPSO more analogous to the original PSO and fulfils the requirement of an all-purpose, rigorously defined algorithm. Further, by not altering the elements in the position sets, SBPSO does not require domain-specific information to modify a position set.
5.1.1. Positions and Velocities
In the original PSO, particles “move” through an -dimensional real-valued space. The movement of particles is dictated by the attraction to different areas in the landscape, which determines the momentum and direction of the particles. However, the idea of direction and momentum is undefined in a set-based environment and the absence necessitates the development of set-based analogies of, and alternatives to, momentum and direction.
For SBPSO, the symbol i indicates the particle index, t denotes the current iteration, and f represents the objective function. The search space is defined by the universal set (the universe of discourse), U. The universal set is of size and contains elements ; the universal set is expressed as . Position sets are subsets of the universal set, alternatively stated; position sets are elements of the power set of the universal set. The position of particle i at iteration t is expressed as . The velocity of particle i at iteration t is the set . The personal best and neighbourhood best positions of particle i are and , respectively.
Continuous-valued PSOs modify position vectors by modifying the real values in each dimension of the position with the real values in the corresponding dimension of the velocity vector. The change of the real-valued components brings the position vector closer to the positions defined by the attractors. However, “moving” a set-based position closer to the attractor positions with real-valued velocity components is not definable. Instead, the velocity set adds and removes position set elements to make the position more similar to the attractors. The concept of “alikeness”/similarity is well-defined for sets and has been studied in the context of set-based meta-heuristics [68].
In order to change a position set, the elements of a velocity set are applied to the position set. Each element of a velocity set is an operation pair: a tuple consisting of an element from the universal set and the instruction indicating whether the universal set element should be added to, or removed from, a position set. Velocity set elements take the form , where adds the element e to a position set while removes e from a position set. Consider the following example as a demonstration of the application of a velocity set to a position set. If is a position set and is a velocity set, the resulting position after applying V to X is .
5.1.2. Set-Based Operators
In order to define the necessary SBPSO operators, let denote the power set of the universal set (meaning the set of all possible subsets) and let denote the Cartesian product of two sets, A and B. The following definitions are set-based operators used in the SBPSO algorithm.
Definition 2
(The addition of two velocities). The addition of two velocities, , is a mapping, , that takes two velocities and yields one velocity. Implemented as set operations, a velocity added to a velocity is interpreted as the union operator:
Definition 3
(The difference between two positions). The difference between two positions, , is a mapping, , that takes two positions and yields a velocity. The result is effectively the set operation steps which are required to convert into :
Definition 4
(The scalar multiplication of a velocity). The scalar multiplication of a velocity, , is a mapping, , which takes a scalar and a velocity, and yields a velocity. The mapping results in a randomly selected subset of size from V and is expressed as
Note that and .
Definition 5
(The addition of a velocity and a position). The addition of a velocity and a position, , is a mapping, , that takes a position and velocity and yields the resultant position. The operation is expressed as
which involves the application of the operation associated with each from to X by adding or removing each , as dictated by the elements in the velocity.
Definition 6
(The removal of elements). The removal of elements, , from a position , where S is shorthand for , is the mapping, , that takes a scalar and a set of elements and yields a velocity. The operator is implemented by randomly selecting a subset of elements from S, with a size determined by β, to be removed from :
The number of elements selected, , is defined as
for a random number ; is 1 if bool is true and 0 if bool is false.
Definition 7
(The addition of elements). The addition of elements, , to a position where A is shorthand for , is a mapping that takes a scalar and a set of elements and yields a velocity. The operator is implemented by randomly selecting a subset of elements from A, with a size determined by β, to be added to :
where is the number of elements to be added to as defined in Equation (12) and k is a user-defined parameter. To perform tournament selection, the process in Algorithm 2 is followed.
| Algorithm 2 k-Tournament . |
|
5.2. Set-Based Update Equations
After the velocity set has been calculated with the operators and equations defined above, the position update equation is defined using the velocity set as
where ⊞ has the function defined in Definition 5.
The velocity update equation is defined as
where and are calculated independently for each particle as outlined in Definitions 6 and 7, respectively. The functions of ⊕, ⊖, and ⊗ are given in Definitions 2–4. Each remains constant for all particles with and , and each , , , is independently drawn from the distribution .
5.3. Exploration and Exploitation Mechanisms
Swarm intelligence algorithms such as the PSO, as well as meta-heuristics in general, solve optimisation problems through the control of the level of exploration versus the level of exploitation performed by the agents. Exploration is the process whereby agents of the population search areas of the fitness landscape which have not previously been evaluated. Exploitation is the process whereby areas of the search space which hold promise to contain potential optima are searched in order to refine existing solutions.
One of the most important aspects needed to control the exploration–exploitation trade-off of the original PSO is the inertia weight in combination with the acceleration coefficients of the velocity update equation [38]. However, the concept of momentum does not exist in a set-based environment; hence, alternative exploration–exploitation trade-off mechanisms are required.
The SBPSO algorithm uses two attractors in the velocity update equation to encourage exploitation: the cognitive component, i.e., , and the social component, i.e., . The cognitive and social components encourage particles to return to areas of the search space which have previously been shown to contain good solutions.
In lieu of a momentum component, SBPSO implements two additional velocity components to encourage exploration: the addition operator, i.e., , and the removal operator, i.e., . The addition and removal operators are essential for exploration. A version of SBPSO which utilise only the cognitive and social attractors is not able to incorporate elements which are not in the initial population into new positions (i.e., elements will not be added to any new position set). The addition operator encourages exploration through the addition of elements to the position set which have (potentially) not previously been evaluated; the added element are not restricted to those contained in the original position sets. The removal operator balances the addition operator because the removal of elements from position sets prevents set bloating; the removal operator is also limited to , which aids in the avoidance of premature convergence and further encourages exploration.
5.4. Set-Based Diversity Measures
For a swarm-based optimisation algorithm to find a global optimum, it is important to control the trade-off between exploration and exploration [69]. In the literature, a popular method of determining whether a swarm is in an exploration phase or exploitation phase is to determine the diversity of the swarm [70]. In a real-valued environment, swarm diversity is measured by calculating how widely distributed the particles in the swarm are. For example, one popular method to determine the diversity of a swarm in a real-valued PSO is to calculate the average distance around the swarm centre [70]. The average distance to the centre of the swarm, , is calculated as
where is the number of particles in the swarm, is the dimensionality of the problem, is the j-th dimension of the i-th particle, and is the j-th dimension of the swarm centre .
Contrary to a real-valued environment, the concept of distance does not exist in a set-based environment. Because no distance can be calculated between particle positions, a different measure is needed to determine swarm diversity. Similarity measures between sets can be used to quantify swarm diversity in set-based meta-heuristics, as shown by Erwin and Engelbrecht [68]. Erwin and Engelbrecht investigated the use of the Jaccard-based distance and Hamming-based metrics as diversity measures in [68], and proposed an improved Hamming-based measure for swarm diversity [71]. Erwin and Engelbrecht stated that the behaviour of the average Jaccard distance of the swarm better represents the intuitive idea of swarm diversity [68]. The average Jaccard distance of the swarm is calculated as
where is the Jaccard distance, calculated as
where A and B are sets.
Alternatively, the average Hamming distance measure can be used to calculate swarm diversity. The average Hamming distance, or more simply the Hamming diversity, is
where is a bit vector mapping function that converts a set, S, into a bit vector in which an entry of 1 indicates the presence of the element in question and a 0 indicates the absence of the element. Further, H is the Hamming distance between two bit vectors, , calculated as
where is the Kronecker delta.
Erwin and Engelbrecht proposed an alternative formulation of the Hamming distance as an improvement over the original Hamming distance similarity measure [71]. The improved formulation modifies the bit vector mapping function to be . The improved Hamming measure utilises Equation (19) to calculate the swarm diversity, but the modified function, , causes the new measure to behave more similarly to the Jaccard similarity measure.
5.5. Control Parameter Sensitivity
Langeveld and Engelbrecht performed sensitivity analysis on the control parameters of SBPSO for the MKP [72]. The sensitivity analysis process followed by Langeveld and Engelbrecht averages 128 parameter combinations over 30 independent runs for each topology-dataset pair (12 in total). The average results are then allocated to a quartile based on the quality of the solution obtained. Based on the allocated quartiles, the control parameters are placed into predefined bins which span the permissible ranges. The MKP is the only problem for which control parameter sensitivity analysis exists for SBPSO.
Table 1 summaries the averaged best ranges for the control parameters of SBPSO for the MKP. The bins given in Table 1 represent the ranges that result in the largest number of solutions in the highest quartile, as obtained in [72].

Table 1.
Summary of average best control parameter ranges.
5.6. Algorithm
The pseudocode for SBPSO is given in Algorithm 3.
| Algorithm 3 Set-Based Particle Swarm Optimisation. |
|
6. Multi-Guide Set-Based Particle Swarm Optimisation
A further advantage of SBPSO is that an extension has been developed to solve multi-objective optimisation problems (MOOPs). The multi-objective extension of SBPSO, i.e., MGSBPSO, was developed by Erwin and Engelbrecht [73] to solve the problem of portfolio optimisation. MGSBPSO is inspired by multi-guide particle swarm optimisation (MGPSO), a multi-objective variant of PSO developed by Scheepers et al. [74].
This section aims to provide an overview of MGSBPSO, specifically how the concepts of MGPSO are added to SBPSO. Section 6.1 defines MOOPs, after which Section 6.2 provides a description of MGPSO as well as MGSBPSO.
6.1. Multi-Objective Optimisation
MOOPs are defined as problems with two or three objectives that need to be optimised simultaneously; problems with more than three objectives are referred to as many-objective optimisation problems. MOOPs tend to be more complex than single-objective optimisation problems because of the (possibly) conflicting “goals” that need to be optimised at the same time. The conflicts mean that optimisation of one objective often causes degradation in the quality of the solution in another objective. This subsection presents a brief overview of the foundational concepts regarding MOOPs; more in-depth information can be found in [75,76].
A MOOP is defined as
where is the number of objectives; (the feasible search space), , and are the inequality and equality constraints, respectively; and are the boundary constraints for .
Additionally, the following definitions regarding Pareto dominance and Pareto optimality are required for MOOP solutions.
Definition 8
(Pareto Domination). A decision vector, , dominates, ≺, a decision vector, , if
- 1.
- , ( is at least as good as in all objectives);
- 2.
- , ( is strictly better than in at least one objective).
Definition 9
(Weak Pareto Domination). A decision vector, , weakly dominates, ⪯, the decision vector, , if
- 1.
- , ( is at least as good as in all objectives).
Weak domination is similar to domination, but without the requirement that the dominating solution should be strictly better in at least one objective.
Definition 10
(Pareto Optimal). A decision vector, , is said to be Pareto optimal if there is no other vector which dominates it, i.e.,
Further, the objective vector is Pareto optimal if is Pareto optimal.
Definition 11
(Pareto Optimal Set). The Pareto optimal set (POS), , is the set that contains all Pareto optimal decision vectors, i.e.,
Definition 12
(Pareto Optimal Front). The Pareto optimal front (POF), , is the set containing all objective vectors, , that correspond to a decision vector in the POS. Expressed mathematically, the POF is
6.2. Multi-Guide Set-Based Particle Swarm Optimisation
Scheepers et al. proposed the MGPSO variant [74] in 2019 to solve MOOPs, as an improvement over existing PSO approaches for MOOPs [77,78,79,80]. MGPSO uses a sub-swarm per objective, and individual sub-swarm searches optimise with respect to a single objective. Updates to the personal best and neighbourhood best positions of each particle is done without consideration of other objectives. In order to facilitate information sharing regarding other objectives, MGPSO implements an archive, , of non-dominated solutions. Information from the archive is used to bias the search process of particles towards the POF.
The velocity update equation for MGPSO is similar to that of the original PSO, except for the addition of the archive component. The velocity update of PSO is as follows:
where is the current velocity in dimension j for particle i in sub-swarm k at iteration t. The variables , , and are the current position, personal best position, and neighbourhood best position of dimension j in particle i from sub-swarm k. Random variables , , and , while the variable is the component of the archived solution selected for particle i in sub-swarm k. The acceleration coefficients , , and control the influence of the personal best, neighbourhood best, and archive components, respectively. Finally, the coefficient is a constant sampled independently for each particle which controls the trade-off of the influence between the social and archive components in the update equation. The archive is updated based on the crowding distance [81] between the new solution and existing solutions in the archive, as shown in Algorithm 4.
| Algorithm 4 Crowding Distance-Based Bounded Archive Update. |
|
The MGSBPSO algorithm combines the SBPSO algorithm with the MGPSO algorithm to solve MOOPs. MGSBPSO uses multiple sub-swarms, where each sub-swarm independently optimises one of the objectives. The personal best position and neighbourhood best position updates for a sub-swarm, k, are updated from positions in only sub-swarm k. The same set-based operators given in Definitions 2–7 are used by MGSBPSO to implement the velocity and position update equations.
Further, MGSBPSO employs the Pareto dominance relation to estimate solutions on the POF, similar to the approach used by MGPSO. In order to share information about the POF between sub-swarms, an archive guide is used. Selection of an archive guide from the archive is done using tournament selection, with the tournament winner selected based on the lowest crowding distance. When new non-dominated solutions are found, the archive management strategy shown in Algorithm 4 is used to update the archive.
The velocity update equation for particle i in sub-swarm k is
where , , , and ; is the exploration balance coefficient (set equal to ); and , , , and all remain in the current position, personal best position, neighbourhood best position, and archive position, respectively. Additionally, is the archive coefficient for particle i and controls the influence of .
The pseudocode for MGSBPSO is given in Algorithm 5.
| Algorithm 5 Multi-Guide Set-Based Particle Swarm Optimisation. |
|
7. Existing Applications
The SBPSO algorithm has been applied successfully to a number of optimisation problems. The existing applications have proved the utility and potential of the SBPSO algorithm. Further, the range of existing applications shows that the SBPSO is a generic approach that can be applied to a wide range of optimisation problems.
Each of the subsections in this section provides an overview of an optimisation problem that has been solved with SBPSO. The overview of each problem gives a brief background on each problem, as well as SBPSO-implementation details of the approach used to solve the problem. The implementation details are centred around the formulations of the objective functions, as well as the possible universal set generation functions.
7.1. Multi-Dimensional Knapsack Problem
The MKP is a combinatorial optimisation problem. Informally, the problem can be defined as placing items into a proverbial knapsack, for which the total value of items needs to be maximised subject to predefined constraints. The MKP is often referred to as the multi-dimensional zero-one knapsack or the rucksack problem, and is NP-complete [82].
The MKP is the first problem to which Langeveld and Engelbrecht applied SBPSO [72]. MKP is a relatively old problem, as one of the first mentions in the literature of an MKP-like problem is from 1955 [83].
7.1.1. Background
This section provides the mathematical definition of the MKP. Given an MKP, the combined value of the items placed into the knapsack is calculated as
subject to the zero-one constraints
where indicates if item i is in the knapsack. MKP is also subject to weight constraints
The number of available items to add to the knapsack is . The total number of weight constraints in the problem is . The weight of each constraint, j, on each item, i, is given by . The total weight of the items placed in the knapsack for constraint j must also not exceed the capacity of the constraint, . MKP is also subject to value constraints
The total weights of the MKP have the constraints
where is defined as
and is the “tightness ratio”, which determines how restrictive the weight constraints are.
7.1.2. Multi-Dimensional Knapsack Problem Using Set-Based Particle Swarm Optimisation
Because the MKP requires an unknown number of items to be placed into a knapsack, a set-based representation of the candidate solutions is well suited. The suitability of a set-based representation is in contrast to other meta-heuristics, such as the PSO, which requires a fixed-length representation of candidate solutions, i.e., prior knowledge regarding the maximum dimension of the solution.
The universal set is generated to contain all possible items which can be added to the knapsack. The elements of U are represented as tuples which contain the details of an item. Each item has an index, i, a value, , and weights. Each weight, , corresponds to the cost of item i on constraint j. An element in U therefore takes the form . An example of a hypothetical universal set for an MKP with five items and three constraints is
The objective function of the SBPSO used on the MKP optimises MKP as a maximisation problem. It is important to note that not all particle positions necessarily represent feasible solutions, hence the objective function is piecewise defined. The objective function value for positions which satisfy all constraints is equal to the sum of all the values of the items in the position, while positions which violate at least one constraint are assigned a value of negative infinity. The objective function, f, is
The SBPSO performs well on the MKP, but Langeveld and Engelbrecht note that state-of-the-art MKP algorithms perform better. However, the MKP was merely used as a proof-of-concept for SBPSO. Considering that the work of Langeveld and Engelbrecht was used to introduce SBPSO, the approach from the paper is quite successful given that SBPSO does not require any domain-specific knowledge to solve the MKP.
7.2. Feature Selection Problem
Feature (input attribute) selection is an important step of the data preprocessing, or data wrangling, process [84,85]. If there are a larger number of features in comparison to the number of available instances, classifiers and regressors tend to overfit and are slower.
Datasets with unnecessary features have higher dimensionality than needed, which has been shown to reduce the performance of meta-heuristics such as PSOs [86]. The FSP is solved by selecting a subset of the original features of a dataset. The selected subset should ideally be free from features which are redundant, irrelevant, or too noisy.
7.2.1. Background
The FSP is defined in this section as a precursor to the application of SBPSO to FSP. Given a dataset with the set of input features I of size , define be the power set of I, i.e., the set containing all possible subsets of I. For a generic subset of I, denoted as , let the fitness of X be defined as . The fitness function, f, is a predefined minimisation or maximisation function which quantifies how well a subset of features solves an optimisation problem. Given an assumed a minimisation fitness function, the optimal solution set, X, is defined as
In order to determine how effectively the subset of features, S, captures the relationships of the underlying classification problem, the performance of a classifier (with relevance to a classification problem) is used. The performance of the classifier is measured using an evaluation metric, such as accuracy. To illustrate how the suitability of a selected subset of features can be evaluated, consider that a decision tree classifier is used to determine the fitness of a subset of features. Given two different subsets of features, and , the decision tree classifier achieves a performance on the two subsets. Let the accuracies be and . These scores show that is a better subset of features.
7.2.2. Feature Selection Using Set-Based Particle Swarm Optimisation
The feature selection problem can be solved with SBPSO, as shown by Engelbrecht et al. [87]. SBPSO is an apt approach to FSP because the feature subsets, , are easily represented as set-based particles.
The universal set contains all possible combinations of input attributes, i.e., all possibilities of . For a hypothetical dataset with four input attributes (, , and ), the generated universal set is
Further, the power set of the generated universal set is
The fitness function is
where is a performance evaluation metric which, for classification problems, quantifies the confusion matrix into a single real value. The input parameters of are the measures from the confusion matrix: is the number of true positives, is the number of false positives, is the number of false negatives, and is the number of true negatives.
The approach used to apply SBPSO to the FSP involves creating an SBPSO wrapper method to evaluate the suitability of features. The method for SBPSO for FSP is very similar to the method outlined in Algorithm 3. The main difference is that the fitness function is the evaluation function of a classifier, , instead of the standard objective function, f.
Engelbrecht et al. compare the SBPSO for feature selection against three state-of-the-art discrete PSO algorithms (binary PSO, catfish binary PSO, and probability binary PSO). SBPSO in conjunction with a k-nearest neighbours classifier outperforms all three state-of-the-art algorithms with statistical significance and is considered the most effective tool for the FSP.
7.3. Portfolio Optimisation
Portfolio optimisation is the process by which a “basket” of financial products (e.g., assets) are selected in which to be invested, as well as the ratios of capital to be allocated to each product. The goal of portfolio optimisation is to maximise the return on the invested capital, while also to minimise the risk of losing the invested money.
7.3.1. Background
Portfolio optimisation requires a mathematical description of the behaviour of the assets in the compiled portfolio in order to define the problem. A popularly used portfolio model, the mean-variance model [88], is defined as
where is used to balance the risk, , and return, R, of the portfolio. The risk of a portfolio is calculated as the weighted covariance between all assets, the formula used is
where and are the weights assigned to assets i and j, respectively, and is the covariance between assets i and j. Further, the return of a portfolio is calculated as
where is the return associated with asset i. All weights assigned to assets must be non-negative and must sum to one, i.e.,
and
The definition of the portfolio optimisation model optimised by SBPSO can be varied. These variations include the addition of constraints, the extension of portfolio optimisation as a MOOP, and the use of alternative definitions for risk and return. Constraints are added to the portfolio optimisation formulation such as, for example, the limitation of the total number of assets, the addition of a floor and ceiling to the asset weights, the incorporation of transaction costs, or the inclusion of capitalisation into the model. A multi-objective formulation of portfolio optimisation is obtained through the incorporation of more than one sub-objective in the objective function or by the use of constraints as stand-alone objectives. A multi-objective formulation can, for example, consist of the maximisation of return, the maximisation of the diversity of included assets, or the maximisation of liquidity. Alternative models of portfolio optimisation can include objectives such as semi-variance, value-at-risk, prospect theory, Sharpe ratio, or mean absolute deviation [89,90,91,92,93,94].
7.3.2. Portfolio Optimisation Using Set-Based Particle Swarm Optimisation
Erwin and Engelbrecht [95] used SBPSO as part of a portfolio optimisation approach to maximise return and minimise risk. The resultant algorithm solved portfolio optimisation by interleaving SBPSO, to select assets, and PSO, to optimise the weights of selected assets. To select an optimal combination of financial products, the PSO algorithm is interleaved with SBPSO into a bi-level optimisation process to find optimal ratios of assets [95]. The two stages of the bi-level optimisation process are solved by SBPSO and PSO. SBPSO selects the assets to be included in the portfolio, after which PSO assigns the optimal weighting to each chosen asset.
The universal set contains all possible assets that can be included in a portfolio. If, for example, a portfolio is to be constructed from the top 10 companies in a hypothetical market (companies A to J), the universal set will be
Combinations of these assets are selected and then used as input to the PSO.
7.3.3. Multi-Objective Portfolio Optimisation Using Set-Based Particle Swarm Optimisation
Erwin and Engelbrecht improved on the original SBPSO-based portfolio optimisation approach by using the MGSBPSO to solve portfolio optimisation as a MOOP [73]. The improved approach uses MGSBPSO to select assets for investment, after which MGPSO is used to find the optimal weight allocations for each selected asset. Both the upper and lower levels of the approach define portfolio optimisation as a MOOP with respect to the maximisation of return and the minimisation of risk.
The new approach uses the same mean-variance model as in Equation (39), but instead of balancing the objectives with , the objective function is redefined as
Because there are two objectives, i.e., maximise return and minimise risk, the populations of both MGSBPSO and MGPSO implement two sub-swarms, one that optimises each objective. For positions in the first sub-swarm of MGSBPSO (which minimises risk) two separate MGPSO sub-swarms are created, one which minimises risk and another which maximises return. Similarly, for the second sub-swarm of MGSBPSO (which maximises return), two separate MGPSO sub-swarms are created, one which minimises risk and another which maximises return. Visually, the structure of the multi-sub-swarm approach is shown in Figure 1.
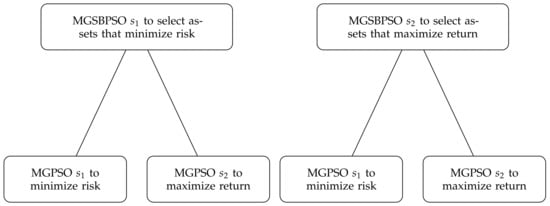
Figure 1.
Multi-guide set-based particle swarm optimisation for portfolio optimisation structure.
Erwin and Engelbrecht compared the performance of both SBPSO and MGSBPSO for portfolio optimisation against the non-dominated sorting genetic algorithm II [81] and strength Pareto evolutionary algorithm 2 [96]. In contrast to the comparison algorithms, the SBPSO-based approaches are able to approximate the whole true POF instead of only parts of the true POF. Further, MGSBPSO is able to obtain a diverse set of optimal solutions, which is beneficial to investors who have different risk preferences.
7.4. Polynomial Approximation
Supervised ML problems can be broadly classed into two main categories: classification problems and regression problems. Regression problems are a class of ML problems which calculate a real-valued label for an input vector. Problems which require a real-valued label are contrary to problems which require one of the classes as an output.
A popular approach to solving regression problems is to train a neural network (NN) which maps the input instances to output values [97,98]. However, NNs are a form of black box models and cannot be interpreted easily. An alternative approach to solve regression problems is to find a polynomial which describes the functional mapping from the input data to the output value.
7.4.1. Background
Polynomial approximation is the process by which the structure of a functional mapping from dimensional input data to a real-valued output is found, i.e., . One of the biggest advantages of learning the structure of the polynomial which maps input to output is that the model is transparent. A transparent model has an advantage over an opaque approach in that the results are more interpretable and explainable.
A polynomial is learned from an input dataset, D. The dataset D is -dimensional, with instances, where p is a specific instance, is a vector of input variables, and is the corresponding true output value. A polynomial is constructed from multiple monomials, the building blocks of a polynomial. Monomials take the form
where is the power of variable . Univariate polynomials have only a single input dimension, and are defined as
where is the order of the polynomial. Multivariate polynomials have and take the form of
where is the number of monomials and is the coefficient of the monomial. Further, is the number of input variables in the monomial and is the order of the corresponding variable.
7.4.2. Polynomial Approximation Using Set-Based Particle Swarm Optimisation
Van Zyl and Engelbrecht applied SBPSO as part of a hybrid algorithm which approximates functional mappings [99]. According to [99], polynomial approximation is defined as a MOOP with two objectives. The two objectives are to find (1) the smallest number of terms and lowest polynomial order, and (2) optimal coefficient values for the terms in order to minimise the approximation error. Although polynomial approximation is defined as a MOOP, Van Zyl and Engelbrecht implement a weighted aggregation approach in order to apply the single-objective SBPSO algorithm to polynomial approximation.
The universal set of the SBPSO used to approximate polynomials contains the monomials which can be added to the polynomial. The monomials in the universal set contain combinations of input variables. The combinations of input variables are repeated with different exponents, up to a user-specified polynomial order. The tuples in the universal set contain two components: (1) the input attribute(s) of the monomial and (2) the power of the monomial. A hypothetical dataset, with three input attributes and a specified order of two, will generate the universal set:
Equation (48) allows for monomials with different powers for each input variable; however, Van Zyl and Engelbrecht limit the monomials to have the same power for all input variables in order to reduce the universal set size.
The objective function is used to quantify how well a candidate polynomial describes the mapping from input data to output values, as well as how optimal the polynomial structure is. Polynomial approximation is defined as a MOOP, and the objective function is formulated with a weighted aggregation approach. The objective function is
where the approximation qualifier is the mean squared error, defined as
and the penalty term is defined as the ridge regression function, i.e.,
The SBPSO solves the upper part of the bi-level optimisation process needed to approximate polynomials. Bi-level optimisation processes are separated into an upper-level and lower-level optimisation process [100]. The upper part, where the structure of the polynomial is determined, is solved by SBPSO. The lower part, where the coefficients of the monomials are estimated, is solved by adaptive coordinate descent (ACD) [101]. The interleaved algorithm is presented in Algorithm 6.
| Algorithm 6 Set-Based Particle Swarm Optimisation for Polynomial Approximation. |
|
SBPSO for polynomial approximation is a promising approach to induce accurate and low complexity functions. Van Zyl and Engelbrecht conclude that SBPSO scales better than BPSO for more complex polynomials and maintains the advantage of interpretability over universal approximators such as NN.
7.5. Support Vector Machine Training
An SVM is a model which uses a hyperplane to separate instances into one of two classes [102]. An SVM has the desirable property of being both complex enough to solve real-world problems, yet simple enough to be analysed mathematically [103]. The key to training an SVM model successfully is to select the proper support vectors from the training dataset.
7.5.1. Background
In order to train an SVM, instances from a training dataset are used as support vectors to construct the optimal hyperplane. SVMs have been extended to separate non-linear data through the use of techniques such as soft margins [104] and mapping to a higher-dimensional feature space with a kernel “trick” [102,105,106]. Consider a dataset with instances; let each instance consist of an input, , and a class label, . Provided that the training data is linearly separable, all instances of each class lie on either side of a separating hyperplane. The separating hyperplane has the form , where is the normal vector to the hyperplane. The decision function used to classify an instance is
where f classifies instance as either positive () or as negative (). Under the assumption of linear separability
where ∧ represents the logical and operator and equality holds for at least one . The input instances for which the equality condition holds are referred to as support vectors and are used to construct the separating hyperplane. The margin of an SVM, which is the combined distance from the hyperplane to the support vectors on either side, is calculated by
The maximisation of the margin of a SVM results in an optimal separating hyperplane for that SVM. The maximisation of the margin is equivalent to the optimisation of
subject to the constraints outlined in Equation (54).
The introduction of a vector of Lagrange multipliers () results in the primal Lagrangian, defined as
The partial derivative of Equation (57) with respect to is
when the partial derivative is set to zero, the result is
Further, the partial derivative of Equation (57) with respect to b is
when the partial derivative is set to zero, the result is
The partial derivative results in Equations (59) and (61) are substituted into Equation (57) and results in the dual optimisation problem
subject to
where ∧ represents the logical and operator. Through Equations (53) and (59), is shown to be a linear combination of all training patterns as
Furthermore, it has been shown that only support vectors have non-zero Lagrangian multipliers, i.e., , which further simplifies the linear combination of .
In datasets with a noise where classes are not linearly separable, the soft margin approach is used to allow for misclassification of some training patterns [104]. The soft margin approach introduces slack variables, , which allow for the misclassification of training patterns. The inequality from Equation (54) is modified to and, as a result, the maximisation of the margin becomes equivalent to the optimisation of
where determines how severely constraint violations are penalised.
Furthermore, for datasets with underlying non-linear mappings, non-linear separations are achieved through the application of the kernel trick. Let be a non-linear mapping from the input space to a higher dimensional feature space () in which the data is linearly separable. By Mercer’s theorem from [107], a suitable kernel is defined, such that
The kernel function, K, can then be used to map input data to a higher dimensional space and the decision function becomes
7.5.2. Support Vector Machine Training Using Set-Based Particle Swarm Optimisation
Nel and Engelbrecht proposed the use of the SBPSO algorithm to train SVMs [108]. The SVM training problem needs to be formulated with set theory for the SBPSO to be used to find the optimal hyperplane. The procedure is referred to as SBPSO-SVM.
Tomek links refer to two neighbouring instances which have different classes [109]. The presence of a Tomek link indicates that either the two points are close to the decision boundary, or that one of the instances represents noise. Given that boundary instances of a binary classification problem are Tomek links, Tomek links are more suited for use as support vectors compared to random points from the dataset. The elements of the universal set initially consists of all input training patterns, , from the training dataset, i.e., . However, the complexity of the search space is reduced through the restriction of the universal set to consist of only Tomek links. Therefore, the universal set is defined as where is one of the Tomek links identified from the training patterns. Let there be an optimal set of support vectors (selected from U) contained in the set . From , construct the support vector matrix, , which contains the elements of as
The equation separating hyperplane can be rewritten in terms of the support vector matrix as
From Equation (69), and b must be found, such that and . Through the use of Lagrangian multipliers, as shown in Equation (64), and application of the kernel trick, the decision function of the SVM can be written as
The objective function of SBPSO-SVM aims to optimise two goals: (1) to provide the best separation between classes, and (2) to minimise the number of support vectors used for classification. The two goals lead to the weight aggregated objective function
where minimises the number of support vectors, constitutes the degree of constraint violations, and regulates the contribution of each sub-objective. The function, , is defined as
where is the mean squared error of the equality constraint violations, is the normalised number of inequality constraint violations for non-support vectors, and regulates the contribution of each component. The definition of is
The definition of is
where
The optimal values of the Lagrangian multipliers, as well as the bias term, are found by the ACD algorithm [101].
The pseudocode for the SBPSO-SVM procedure is given in Algorithm 7.
| Algorithm 7 Set-Based Particle Swarm Optimisation for Support Vector Machine Training. |
|
Nel and Engelbrecht conclude that SBPSO exhibits good performance on highly separable data, but performs suboptimally on more complex problems. The definition of the universal set as the Tomek links in the dataset, instead of the whole dataset, is an integral part of the feasibility of SBPSO for SVM training. Without the use of Tomek links, SBPSO suffers considerably in performance. SBPSO is more effective at minimising the number of support vectors, which is a desirable property for the generalisation of SVMs.
7.6. Clustering
Broadly, ML tasks are often described as either supervised or unsupervised. Supervised ML problems require instances with both input attributes and a target variable, while unsupervised problems do not utilise a target variable. A popular unsupervised problem is the problem of clustering instances into distinct groups, or clusters. Clustering has broad applications in data science and can be used for classification, prediction, or data reduction [110,111].
7.6.1. Background
The main principle behind clustering is that instances from the dataset which have similar characteristics belong to the same cluster. There are three main objectives to be taken into account when clustering data instances [112]. The first is to produce compact clusters, meaning that the spread of instances in the same cluster should be minimised. Secondly, clusters should be well-separated, i.e., the distances between cluster centroids should be maximised. Finally, the number of clusters used to perform clustering should be optimal.
Examples of popular approaches to clustering are k-means clustering [113], k-medoids clustering [114], Gaussian mixture models [115,116], and density-based spatial clustering [117].
7.6.2. Clustering Using Set-Based Particle Swarm Optimisation
Brown and Engelbrecht proposed the use of SBPSO to perform data clustering [118], after which De Wet performed an in-depth analysis of the performance of the proposed algorithm [119,120]. In order to perform clustering with SBPSO, candidate solutions are represented as sets of centroids. The centroids in the sets are used to define the clusters to which instances in the dataset can belong. The instances in the training dataset act as the points which can be selected as centroids. Hence, the universal set contains the instances in the training dataset. Because SBPSO for data clustering uses the input data points as centroids, it is categorised as k-medoids clustering instead of k-means clustering. The universal set, U, for an unlabelled dataset with instances, D, is populated as
The particle positions of SBPSO are constructed as
where is the number of clusters in the position, and represents the medoid of cluster j in the position of particle i.
To evaluate the suitability of the clusters created by particle i, a combination of two clustering performance evaluation metrics is used. The objective function is defined as
where represents the silhouette index value and represents the Dunn index value. The silhouette index [121] is the average of the silhouette values of the instances in the dataset; the silhouette value quantifies the difference in similarity of an instance to other instances in the same cluster against the similarity to instances in different clusters. The Dunn index [122] quantifies both the inter-cluster distance and the intra-cluster spread. It should be noted that the objective function used in [119] consists of only the silhouette index.
Brown and Engelbrecht conclude that none of the evaluated clustering algorithms are able to dominate over all the implemented datasets. SBPSO is not able to achieve the best performance on any of the datasets, but is successful in inducing the optimal number of clusters.
7.7. Rule Induction
Rule induction is the process by which explainable mappings are created from a set of input instances and the target variables associated with the given input instances. Rule-based models can be seen as an extension of traditional classification models because rule-based models are able to classify instances into one of distinct classes and are able to outline the conditions which justify the classification. The human-interpretable nature of the rule-based models are in contrast to black box approaches, such as NNs, which require additional post-processing to be understood [123].
Rule induction is especially relevant due to the resurgence in popularity of explainable artificial intelligence approaches, in which scientists aim to create models which can explain and justify why prediction are made.
7.7.1. Background
Generally, the output of a rule induction algorithm is a list of human-readable IF-THEN rules. The first component of a rule is known as the antecedent and follows the keyword IF. The antecedent of a rule dictates which instances in the dataset are classified by that rule. An instance is classified by a rule if it is covered by a rule; coverage by a rule is established when all the conditions, represented by selectors, in the antecedent are satisfied by the variables of the input instance. The second component of a rule is the consequent, which determines the class assigned to an input instance. The consequent follows the THEN part of the rule.
A popular approach to induce a list, or set, of rules in a rule-by-rule fashion is to use the set-covering approach. The set-covering, also referred to as separate-and-conquer, approach is a two-step process. First, set-covering induces a rule which best describes the dataset according to a predefined metric, after which the set-covering process removes all instances covered by the new rule and then repeats the process. A basic set-covering approach is presented in Algorithm 8.
| Algorithm 8 Basic Set-Covering Approach. |
|
Popular approaches in existing literature tend to be greedy algorithms which make use of gain-based approaches [124,125,126,127]. Gain-based approaches attempt to maximise the information gained at each step of the set-covering process, with the detriment that rules tend to overfit the training data.
7.7.2. Rule Induction Using Set-Based Particle Optimisation
Van Zyl and Engelbrecht proposed a new approach to rule induction by applying SBPSO to induce rule lists [128], titled rule induction using set-based particle swarm optimisation (RiSBPSO). The RiSBPSO approach follows a set-covering approach, with SBPSO used to induce individual rules. The use of SBPSO is justified, because the objective function of the algorithm can be used to avoid overfitting, more explorative freedom is afforded on the selectors, and the functionality of RiSBPSO can be expanded more easily.
To understand how the universal set is generated, consider the following example: provided with the hypothetical dataset D in Table 2, the universal set U is shown in Equation (79).

Table 2.
Summary of legitimate attribute values in a hypothetical dataset.
The prototype of RiSBPSO uses a very complex and convoluted objective function. The prototype objective function is defined as
where is the accuracy of the rule, is the purity of the rule, is the Laplace estimator, is the size of the rule, and is the entropy of the covered instances. Each and . Although the prototype objective is very convoluted, it should be noted that the effect of the composition of the objective function on performance is thoroughly studied by Van Zyl in [129].
The pseudocode for the RiSBPSO algorithm is provided in Algorithm 9.
| Algorithm 9 Rule Induction using Set-based Particle Swarm Optimisation. |
|
7.7.3. Multi-Objective Rule Induction Using Set-Based Particle Optimisation
Van Zyl and Engelbrecht reformulated rule induction as a MOOP and applied the MGSBPSO algorithm to induce rule lists, which resulted in rule induction using multi-guide set-based particle swarm optimisation (RiMGSBPSO) [129]. The MOOP version of rule induction aims to maximise the aptness (suitability, measured with a metric e.g.) of a rule given a dataset, and also to minimise the complexity of the rule. The complexity of a rule is quantified by the number of selectors in the antecedent of the rule. The number of selectors in the antecedent is minimised in order to avoid overfitting and to improve the generalisation capabilities of the rule.
The multi-objective formulation of rule induction is formulated as
where r is the induced rule, D is the training dataset, is the aptness of the rule on the dataset (e.g., accuracy), and is the complexity of the rule. The feasible region of the search space, , is all the selectors that can be used in the antecedent of a rule, i.e., the permissible attribute-value pairs.
Van Zyl and Engelbrecht found that SBPSO is a suitable algorithm for the induction of rule lists and is able to outperform the comparison algorithm based on average accuracy over all datasets. It is noted that the comparison algorithms are advantaged due to the implementation of pruning in the rule induction process of the comparison algorithms. The RiMGSBPSO version of rule induction performs worse than expected because a simple complexity penalisation approach outperforms the multi-objective formulation.
8. Conclusions
This paper provided a comprehensive overview of the set-based particle swarm optimisation (SBPSO) algorithm. The concepts of both single-objective and multi-objective problems were introduced as precursors to the outline of a generic set-based particle swarm optimisation (PSO). The differences between real-valued optimisation and set-valued optimisation problems was explained and the requirements for a well-defined set-based PSO were given. Eight existing attempts at the creation of a set-based PSO algorithm were described and critiqued, with reasons provided why the shortcomings of each approach prevent the algorithm from being a true set-based and generically applicable PSO algorithm.
An in-depth description of SBPSO was provided, with details on the necessary set-based operators, the velocity and position update equations, the exploration–exploitation control mechanisms, and the concept of set-based swarm diversity all explained. Explanations of seven existing applications of SBPSO were provided, specifically with details on the implementations of the universe generation and objective function definition.
Further, a description of how the multi-guide particle swarm optimisation (MGPSO) was used to inspire the development of the multi-guide set-based particle swarm optimisation (MGSBPSO), the variation of SBPSO used to solve multi-objective optimisation problems (MOOPs). Two existing MOOPs to which MGSBPSO has been applied were outlined, with explanations on the advantages and shortcomings of the approaches.
Overall, this paper presented a review of a generic set-based PSO algorithm, i.e., SBPSO, and the existing applications of SBPSO. The SBPSO algorithm showed clear advantages in terms of set-based definition and range of application over other algorithms which claim to be set-based PSO algorithms. There is also potential for the improvement of SBPSO, as outlined in the next section.
9. Future Work
This section outlines potential future investigations which can be performed on, or expansions that can be made to, the SBPSO algorithm. The applications of SBPSO can be expanded through the adaptation of the objective function for use on the more combinatorial optimisation problems. However, the remainder of this section is dedicated specifically to non-application expansions.
9.1. Universe Exploration Study
An important aspect of the success of a meta-heuristic is sufficient exploration of the search space in which the meta-heuristic operates. It is beneficial to understand how well a swarm is able to cover the areas of the search space in order to determine if a sufficient percentage of candidate solutions are considered. While literature on the measure of the level of exploration versus exploitation of the SBPSO swarm is available, no work has been conducted to determine if the swarm considers all elements in the universal set for use in candidate solutions. Future work should consider how well the swarm explores the search space.
9.2. Swarm Convergence Study
In contrast to the convergence studies on the original PSO [130], no work has been conducted to understand the convergence behaviour of the SBPSO swarm. Further insight into the convergence behaviour of the swarm will lead to a better understanding of how well the exploration–exploitation trade-off is managed by SBPSO.
9.3. Hyperparameter Sensitivity Analysis
The SBPSO algorithm has five hyperparameters, i.e., , , , , and k. However, the majority of existing studies do not sufficiently tune the hyperparameters of SBPSO to extract maximum performance. Only Langeveld and Engelbrecht [72] rigorously studied the effect of the hyperparameters on the performance of SBPSO when applied to MKP. Not only are the problem-specific hyperparameters not tuned, but the effect of the individual hyperparameters on SBPSO in a more general context is not understood. Therefore, a thorough study on the sensitivity of SBPSO to the hyperparameters needs to be conducted to improve future tuning approaches for new applications. Hyperparameter sensitivity analysis can be performed with functional analysis of variance (fANOVA), as seen in [131,132,133].
9.4. Hyperparameter Self-Adaptation
A further possible improvement after a hyperparameter sensitivity analysis is the implementation of self-adaptive hyperparameters. Self-adaptive variations of PSO have been developed [134]; however, there is no comprehensive study on the effect of self-adaptation on SBPSO.
9.5. Improved Diversity Injection Mechanisms
The two exploration mechanisms of SBPSO, the and operators, are rather rudimentary and unsophisticated methods of encouraging exploration during the search process. Research which proposes improvements to these two operators has the potential to increase the performance of SBPSO by ensuring that the correct areas of the search space are explored and then exploited.
9.6. High Dimensional Performance Evaluation
One of the big advantages of SBPSO is the fact that the dimensionality of particles is variable. The ability to represent candidate solutions in a simpler format in comparison to traditional fixed-dimensional algorithms holds potential for improved performance in higher dimensions. However, the current literature lacks analysis of SBPSO performance on high dimensional problems. Future research should include a thorough study on the performance of SBPSO on high dimension problems.
9.7. Dynamic Problem Adaptation
Dynamic problems are a class of optimisation problem in which the objective function varies over time. Dynamic problems are often more complex than static problems because the location of the optima and the values of the objective function at the optima tend to change. Population-based meta-heuristics are often not well-suited to solving dynamic problems because a converged swarm is unable to discover new optima due to a lack of diversity, which results in a decreased ability to explore. There are existing adaptations of PSO [135], but no adaptations of SBPSO to solve dynamic problems. Therefore, future work can include SBPSO variations to solve dynamic problems.
9.8. Constrained Problem Adaptation
Many real-world optimisation problems have additional constraints, other than the standard boundary conditions, which need to be satisfied. Candidate solutions which violate given constraints are deemed infeasible, regardless of the quality of the objective function value. Multiple methods for constraint handling in PSO have been proposed [47], and some of these methods can be adapted for use in SBPSO.
Author Contributions
Conceptualization, A.P.E.; methodology, J.-P.v.Z. and A.P.E.; investigation, J.-P.v.Z.; writing—original draft preparation, J.-P.v.Z.; writing—review and editing, A.P.E.; supervision, A.P.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the National Research Foundation of South Africa.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Engelbrecht, A.P. Computational Intelligence: An Introduction, 2nd ed.; Wiley Publishing: New York, NY, USA, 2007. [Google Scholar]
- Arora, R.K. Optimization: Algorithms and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Grötschel, M. Optimization Stories; Deutschen Mathematiker-Vereinigung: Deutschland, Germany, 2012. [Google Scholar]
- Tikhomirov, V.M. Stories about Maxima and Minima; Universities Press: Madison, CT, USA, 1990; Volume 1. [Google Scholar]
- Lange, K. Optimization; Springer Science & Business Media: New York, NY, USA, 2013; Volume 95. [Google Scholar]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2019, 50, 3668–3681. [Google Scholar] [CrossRef] [PubMed]
- Bennett, K.P.; Parrado-Hernández, E. The interplay of optimization and machine learning research. J. Mach. Learn. Res. 2006, 7, 1265–1281. [Google Scholar]
- Slaney, J.; Thiébaux, S. On the hardness of decision and optimisation problems. In Proceedings of the European Conference on Artificial Intelligence, Brighton, UK, 23–28 August 1998; John Wiley: Hoboken, NJ, USA, 1998; pp. 244–248. [Google Scholar]
- Lenstra, J.K.; Kan, A.H.G.R. Computational complexity of discrete optimization problems. In Annals of Discrete Mathematics; Elsevier: Amsterdam, The Netherlands, 1979; Volume 4, pp. 121–140. [Google Scholar]
- Ausiello, G.; Marchetti-Spaccamela, A.; Protasi, M. Toward a unified approach for the classification of NP-complete optimization problems. Theor. Comput. Sci. 1980, 12, 83–96. [Google Scholar] [CrossRef]
- Bruschi, D.; Joseph, D.; Young, P. A structural overview of NP optimization problems. In Proceedings of the Optimal Algorithms, Varna, Bulgaria, 29 May–2 June 1989. [Google Scholar]
- Saad, D. On-Line Learning in Neural Networks; Cambridge University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Cavazzuti, M. Optimization Methods: From Theory to Design Scientific and Technological Aspects in Mechanics; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Shor, N.Z. Minimization Methods for Non-Differentiable Functions; Springer Science & Business Media: New York, NY, USA, 1985; Volume 3. [Google Scholar]
- Broyden, C.G. The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Hertz, A.; Widmer, M. Guidelines for the use of meta-heuristics in combinatorial optimization. Eur. J. Oper. Res. 2003, 151, 247–252. [Google Scholar] [CrossRef]
- Voß, S. Meta-heuristics: The state of the art. In Proceedings of the Local Search for Planning and Scheduling: ECAI 2000 Workshop, Berlin, Germany, 21 August 2000; Revised Papers. Springer: Berlin/Heidelberg, Germany, 2001; pp. 1–23. [Google Scholar]
- Osman, I.H.; Kelly, J.P. Meta-heuristics: An overview. In Meta-Heuristics: Theory and Applications; Springer: New York, NY, USA, 1996; pp. 1–21. [Google Scholar]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Lejeune Dirichlet, G.; Dedekind, R. Untersuchungen über ein Problem der Hydrodynamik (Aus dessen Nachlass hergestellt von R. Dedekind). J. Math. 1861. [Google Scholar] [CrossRef]
- Cantor, G. On a property of the class of all real algebraic numbers. Crelle’s J. Math. 1874, 77, 258–262. [Google Scholar]
- Cantor, G. Contributions to the Founding of the Theory of Transfinite Numbers; Open Court Publishing Company: Chicago, IL, USA, 1915. [Google Scholar]
- Jech, T.J. Set Theory; Springer: Berlin/Heidelberg, Germany, 2003; Volume 14. [Google Scholar]
- Khan, A.A.; Tammer, C.; Zălinescu, C. Set-Valued Optimization; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Aubin, J.; Ekeland, I. Applied Nonlinear Analysis; Courier Corporation: North Chelmsford, MA, USA, 2006. [Google Scholar]
- Lalitha, C.S.; Dutta, J.; Govil, M.G. Optimality criteria in set-valued optimization. J. Aust. Math. Soc. 2003, 75, 221–232. [Google Scholar] [CrossRef]
- Strasser, S.; Goodman, R.; Sheppard, J.; Butcher, S. A new discrete particle swarm optimization algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 53–60. [Google Scholar]
- Korte, B.; Vygen, K. Combinatorial Optimization, 3rd ed.; Algorithms and Combinatorics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kennedy, J. Small worlds and mega-minds: Effects of neighborhood topology on particle swarm performance. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1931–1938. [Google Scholar]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1671–1676. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A Modified Particle Swarm Optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimization method for constrained optimization problems. Intell. Technol.-Theory Appl. New Trends Intell. Technol. 2002, 76, 214–220. [Google Scholar]
- Tandon, V.; El-Mounayri, H.; Kishawy, H. NC end milling optimization using evolutionary computation. Int. J. Mach. Tools Manuf. 2002, 42, 595–605. [Google Scholar] [CrossRef]
- Shi, Y.; Krohling, R.A. Co-evolutionary particle swarm optimization to solve min-max problems. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1682–1687. [Google Scholar]
- Laskari, E.C.; Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimization for integer programming. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1582–1587. [Google Scholar]
- Hu, X.; Eberhart, R. Solving constrained nonlinear optimization problems with particle swarm optimization. In Proceedings of the World Multiconference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 14–18 July 2002; Citeseer: Forest Grove, OR, USA, 2002; Volume 5, pp. 203–206. [Google Scholar]
- El-Gallad, A.; El-Hawary, M.; Sallam, A.; Kalas, A. Enhancing the particle swarm optimizer via proper parameters selection. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Winnipeg, MB, Canada, 12–15 May 2002; Volume 2, pp. 792–797. [Google Scholar]
- Venter, G.; Sobieszczanski-Sobieski, J. Multidisciplinary optimization of a transport aircraft wing using particle swarm optimization. Struct. Multidiscip. Optim. 2004, 26, 121–131. [Google Scholar] [CrossRef]
- Venter, G.; Sobieszczanski-Sobieski, J. Particle swarm optimization. AIAA J. 2003, 41, 1583–1589. [Google Scholar] [CrossRef]
- Jordehi, A.R. A review on constraint handling strategies in particle swarm optimisation. Neural Comput. Appl. 2015, 26, 1265–1275. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Yuhui, S. Particle swarm optimization: Developments, applications and resources. In Proceedings of the Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar]
- Song, M.; Gu, G. Research on particle swarm optimization: A review. In Proceedings of the International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; Volume 4, pp. 2236–2241. [Google Scholar]
- Jain, N.K.; Nangia, U.; Jain, J. A review of particle swarm optimization. J. Inst. Eng. 2018, 99, 407–411. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Schoofs, L.; Naudts, B. Swarm intelligence on the binary constraint satisfaction problem. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1444–1449. [Google Scholar]
- Clerc, M. Discrete particle swarm optimization, illustrated by the traveling salesman problem. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; pp. 219–239. [Google Scholar]
- Parsons, C. The structuralist view of mathematical objects. Synthese 1990, 84, 303–346. [Google Scholar] [CrossRef]
- Correa, E.S.; Freitas, A.A.; Johnson, C.G. A new discrete particle swarm algorithm applied to attribute selection in a bioinformatics data set. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 35–42. [Google Scholar]
- Neethling, M.; Engelbrecht, A.P. Determining RNA secondary structure using set-based particle swarm optimization. In Proceedings of the IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1670–1677. [Google Scholar]
- Veenhuis, C.B. A set-based particle swarm optimization method. In Proceedings of the International Conference on Parallel Problem Solving from Nature—PPSN X: 10th International Conference, Dortmund, Germany, 13–17 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 971–980. [Google Scholar]
- Chen, E.; Zhang, J.; Chung, H.S.H.; Zhong, W.; Wu, W.; Shi, Y. A novel set-based particle swarm optimization method for discrete optimization problems. IEEE Trans. Evol. Comput. 2009, 14, 278–300. [Google Scholar] [CrossRef]
- Khan, S.A.; Engelbrecht, A.P. A fuzzy particle swarm optimization algorithm for computer communication network topology design. Appl. Intell. 2012, 36, 161–177. [Google Scholar] [CrossRef]
- Khan, S.A.; Engelbrecht, A.P. A new fuzzy operator and its application to topology design of distributed local area networks. Inf. Sci. 2007, 177, 2692–2711. [Google Scholar] [CrossRef]
- Mohiuddin, M.A.; Khan, S.A.; Engelbrecht, A.P. Fuzzy particle swarm optimization algorithms for the open shortest path first weight setting problem. Appl. Intell. 2016, 45, 598–621. [Google Scholar] [CrossRef]
- Kling, R.; Banerjee, P. Optimization by simulated evolution with applications to standard cell placement. In Proceedings of the 27th ACM/IEEE Design Automation Conference, Orlando, FL, USA, 24–27 June 1991; pp. 20–25. [Google Scholar]
- Larrañaga, P.; Lozano, J.A. Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation; Springer Science & Business Media: New York, NY, USA, 2001; Volume 2. [Google Scholar]
- Fan, J.; Li, Y.; Tang, L.; Wu, G. RoughPSO: Rough set-based particle swarm optimisation. Int. J. Bio-Inspired Comput. 2018, 12, 245–253. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Langeveld, J.; Engelbrecht, A.P. A generic set-based particle swarm optimization algorithm. In Proceedings of the International Conference on Swarm Intelligence, Chongqing, China, 12–15 June 2011; pp. 1–10. [Google Scholar]
- Langeveld, J. Set-Based Particle Swarm Optimization. Master’s Thesis, University of Pretoria, Pretoria, South Africa, 2016. [Google Scholar]
- Erwin, K.H.; Engelbrecht, A.P. Diversity measures for set-based meta-heuristics. In Proceedings of the International Conference on Soft Computing & Machine Intelligence, Stockholm, Sweden, 26–27 November 2020; pp. 45–50. [Google Scholar]
- Engelbrecht, A.P. Heterogeneous particle swarm optimization. In Proceedings of the Swarm Intelligence: 7th International Conference, ANTS 2010, Brussels, Belgium, 8–10 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 191–202. [Google Scholar]
- Olorunda, O.; Engelbrecht, A.P. Measuring exploration/exploitation in particle swarms using swarm diversity. In Proceedings of the Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 1128–1134. [Google Scholar]
- Erwin, K.H.; Engelbrecht, A.P. Improved Hamming Diversity Measure for Set-Based Optimization Algorithms. In Proceedings of the Advances in Swarm Intelligence, Xi’an, China, 15–19 July 2022; Tan, Y., Shi, Y., Niu, B., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 39–47. [Google Scholar]
- Langeveld, J.; Engelbrecht, A.P. Set-based particle swarm optimization applied to the multidimensional knapsack problem. Swarm Intell. 2012, 6, 297–342. [Google Scholar] [CrossRef]
- Erwin, K.H.; Engelbrecht, A.P. Multi-Guide Set-Based Particle Swarm Optimization for Multi-Objective Portfolio Optimization. Algorithms 2023, 16, 62. [Google Scholar] [CrossRef]
- Scheepers, C.; Engelbrecht, A.P.; Cleghorn, C.W. Multi-guide particle swarm optimization for multi-objective optimization: Empirical and stability analysis. Swarm Intell. 2019, 13, 245–276. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization; Springer Science & Business Media: New York, NY, USA, 2005; Volume 491. [Google Scholar]
- Coello Coello, C.A.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5. [Google Scholar]
- Hu, X.; Eberhart, R.C. Multiobjective optimization using dynamic neighborhood particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1677–1681. [Google Scholar]
- Coello Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Fieldsend, J.E.; Singh, S. A multi-objective algorithm based upon particle swarm optimisation, an efficient data structure and turbulence. In Proceedings of the UK Workshop on Computational Intelligence, Birmingham, UK, 2–4 September 2002; pp. 34–44. [Google Scholar]
- Mostaghim, S.; Teich, J. Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO). In Proceedings of the IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 24–26 April 2003; pp. 26–33. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature PPSN VI: 6th International Conference, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Gens, G.; Levner, E. Complexity of approximation algorithms for combinatorial problems: A survey. ACM SIGACT News 1980, 12, 52–65. [Google Scholar] [CrossRef]
- Lorie, J.H.; Savage, L.J. Three problems in rationing capital. J. Bus. 1955, 28, 229–239. [Google Scholar] [CrossRef]
- Furche, T.; Gottlob, G.; Libkin, L.; Orsi, G.; Paton, N.W. Data Wrangling for Big Data: Challenges and Opportunities. In Proceedings of the EDBT, Bordeaux, France, 15–16 March 2016; Volume 16, pp. 473–478. [Google Scholar]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Oldewage, E.T.; Engelbrecht, A.P.; Cleghorn, C.W. Movement patterns of a particle swarm in high dimensional spaces. Inf. Sci. 2020, 512, 1043–1062. [Google Scholar] [CrossRef]
- Engelbrecht, A.P.; Grobler, J.; Langeveld, J. Set-Based Particle Swarm Optimization for the Feature Selection Problem. Eng. Appl. Artif. Intell. 2019, 85, 324–336. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Chang, T.; Yang, S.; Chang, K. Portfolio optimization problems in different risk measures using genetic algorithm. Expert Syst. Appl. 2009, 36, 10529–10537. [Google Scholar] [CrossRef]
- Liagkouras, K. A new three-dimensional encoding multiobjective evolutionary algorithm with application to the portfolio optimization problem. Knowl.-Based Syst. 2019, 163, 186–203. [Google Scholar] [CrossRef]
- Liu, J.; Jin, X.; Wang, T.; Yuan, Y. Robust multi-period portfolio model based on prospect theory and ALMV-PSO algorithm. Expert Syst. Appl. 2015, 42, 7252–7262. [Google Scholar] [CrossRef]
- Meghwani, S.S.; Thakur, M. Multi-objective heuristic algorithms for practical portfolio optimization and rebalancing with transaction cost. Appl. Soft Comput. 2018, 67, 865–894. [Google Scholar] [CrossRef]
- Stuart, A. Portfolio selection: Efficient diversification of investments. Q. J. Oper. Res. 1959, 10, 253. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Erwin, K.H.; Engelbrecht, A.P. Set-Based Particle Swarm Optimization for Portfolio Optimization. In Proceedings of the Twelfth International Conference on Swarm Intelligence, Barcelona, Spain, 26–28 October 2020; pp. 333–339. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK-Report; ETH Zurich: Zurich, Swizerland, 2001; Volume 103. [Google Scholar]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Van Zyl, J.; Engelbrecht, A.P. Polynomial Approximation Using Set-Based Particle Swarm Optimization. In Proceedings of the International Conference on Swarm Intelligence, Qingdao, China, 17–21 July 2021; Tan, Y., Shi, Y., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2021; Volume 12689, pp. 210–222. [Google Scholar]
- Colson, B.; Marcotte, P.; Savard, G. Bilevel programming: A survey. Q. J. Oper. Res. 2005, 3, 87–107. [Google Scholar] [CrossRef]
- Loshchilov, I.; Schoenauer, M.; Sebag, M. Adaptive Coordinate Descent. In Proceedings of the Genetic and Evolutionary Computation Conference, Dublin, Ireland, 12–16 July 2011; pp. 885–892. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.N. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Aizerman, A. Theoretical foundations of the potential function method in pattern recognition learning. Autom. Remote Control 1964, 25, 821–837. [Google Scholar]
- Schölkopf, B.; Smola, A.; Müller, K. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Mercer, J. Functions of positive and negative type, and their connection the theory of integral equations. Philos. Trans. R. Soc. Lond. 1909, 209, 415–446. [Google Scholar]
- Nel, A.; Engelbrecht, A.P. Set-Based Particle Swarm Optimisation Approach to Training a Support Vector Machine. under review.
- Tomek, I. Two Modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 769–772. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Clustering: Basic concepts. Pattern Recognit. 2006, 3, 483–516. [Google Scholar]
- Omran, M.G.H.; Engelbrecht, A.P.; Salman, A. An overview of clustering methods. Intell. Data Anal. 2007, 11, 583–605. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Berkeley Symposium on Mathematics, Statistics, and Probability, Berkeley, CA, USA, 21 June–18 July 1965; p. 281. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Partitioning around medoids (Program PAM). Find. Groups Data Introd. Clust. Anal. 1990, 344, 68–125. [Google Scholar]
- MacLahlan, G.; Peel, D. Finite Mixture Models; John & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Reynolds, D.A. Gaussian mixture models. Encycl. Biom. 2009, 741, 659–663. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Brown, L.; Engelbrecht, A.P. Set-based Particle Swarm Optimization for Data Clustering. In Proceedings of the 6th International Conference on Intelligent Systems, Metaheuristics & Swarm Intelligence, Seoul, Republic of Korea, 9–10 April 2022; pp. 43–49. [Google Scholar]
- De Wet, R.M. Set-Based Particle Swarm Optimization for Medoids-Based Clustering of Stationary Data. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2023. [Google Scholar]
- De Wet, R.M.; Engelbrecht, A.P. Set-based Particle Swarm Optimization for Data Clustering: Comparison and Analysis of Control Parameters. In Proceedings of the International Conference on Intelligent Systems, Metaheuristics and Swarm Intelligence, Kuala Lumpur, Malaysia, 23 April 2023; Association for Computer Machinery: New York, NY, USA, 2023. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Setiono, R.; Liu, H. Understanding neural networks via rule extraction. In Proceedings of the Fourteenth International. Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20–25 August 1995; Citeseer: Forest Grove, OR, USA, 1995; Volume 1, pp. 480–485. [Google Scholar]
- Cendrowska, J. PRISM: An algorithm for inducing modular rules. Int. J. Man-Mach. Stud. 1987, 27, 349–370. [Google Scholar] [CrossRef]
- Quinlan, R. C4.5: Programs for Machine Learning. Mach. Learn. 1993, 16, 235–240. [Google Scholar]
- Cohen, W.W. Fast Effective Rule Induction. In Machine Learning Proceedings; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 115–123. [Google Scholar]
- Frank, E.; Witten, I. Generating Accurate Rule Sets Without Global Optimization. In Proceedings of the Fifteenth International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998; pp. 144–151. [Google Scholar]
- Van Zyl, J.; Engelbrecht, A.P. Rule Induction Using Set-Based Particle Swarm Optimisation. In Proceedings of the Congress on Evolutionary Computation, Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Van Zyl, J. Rule Induction with Swarm Intelligence. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2023. [Google Scholar]
- van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Harrison, K.R.; Ombuki-Berman, B.M.; Engelbrecht, A.P. The parameter configuration landscape: A case study on particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Wellington, New Zealand, 10–13 June 2019; pp. 808–814. [Google Scholar]
- Harrison, K.R.; Ombuki-Berman, B.M.; Engelbrecht, A.P. An analysis of control parameter importance in the particle swarm optimization algorithm. In Proceedings of the Advances in Swarm Intelligence: 10th International Conference (ICSI 2019), Chiang Mai, Thailand, 26–30 July 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 93–105. [Google Scholar]
- Erwin, K.H.; Engelbrecht, A. Control parameter sensitivity analysis of the multi-guide particle swarm optimization algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 22–29. [Google Scholar]
- Harrison, K.R.; Engelbrecht, A.P.; Ombuki-Berman, B.M. Self-adaptive particle swarm optimization: A review and analysis of convergence. Swarm Intell. 2018, 12, 187–226. [Google Scholar] [CrossRef]
- Blackwell, T. Particle swarm optimization in dynamic environments. In Evolutionary Computation in Dynamic and Uncertain Environments; Springer: Berlin/Heidelberg, Germany, 2007; pp. 29–49. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).