Abstract
Complex systems provide an opportunity to analyze the essence of phenomena by studying their intricate connections. The networks formed by these connections, known as complex networks, embody the underlying principles governing the system’s behavior. While complex networks have been previously applied in the field of evolutionary computation, prior studies have been limited in their ability to reach conclusive conclusions. Based on our investigations, we are against the notion that there is a direct link between the complex network structure of an algorithm and its performance, and we demonstrate this experimentally. In this paper, we address these limitations by analyzing the dynamic complex network structures of five algorithms across three different problems. By incorporating mathematical distributions utilized in prior research, we not only generate novel insights but also refine and challenge previous conclusions. Specifically, we introduce the biased Poisson distribution to describe the algorithm’s exploration capability and the biased power-law distribution to represent its exploitation potential during the convergence process. Our aim is to redirect research on the interplay between complex networks and evolutionary computation towards dynamic network structures, elucidating the essence of exploitation and exploration in the black-box optimization process of evolutionary algorithms via dynamic complex networks.
Keywords:
complex system; dynamic complex network; evolutionary algorithms; differential evolution algorithms; population interaction network MSC:
90B10; 68T27; 68W50
1. Introduction
A complex system refers to a system composed of interconnected real entities. These systems are characterized by various properties, including nonlinearity, spontaneity, emergence, and others [1]. The complexity of systems arises from the inherent challenge of accurately analyzing their internal connections, making them difficult to model [2,3]. In a complex system, every component plays a crucial role in the overall functioning, yet each individual component can be understood independently of others [4]. In the field of network research, networks that exhibit a large number of interconnected nodes and intricate relationships between them are referred to as complex networks [5,6]. Today, complex networks are a highly researched topic closely tied to information science, neuroscience, and social science [7,8,9]. When studying complex networks, an essential task is to model the network of a complete system as it allows us to extract valuable information about the system through mathematical analysis [10,11]. The analysis of various phenomena using complex networks often relies on studying their topology, including concepts like small-world networks and scale-free networks [12,13]. Complex networks have been employed as a tool to comprehend diverse subjects such as brain science research [14], studies on human social relationships [15], optimization research in control engineering [16], and other related fields [17,18,19,20]. Furthermore, complex networks offer an intriguing and effective direction in the realm of optimization algorithm research [21,22].
Evolutionary algorithms (EAs) and swarm intelligence algorithms draw inspiration from real-world phenomena and formulate them as computational algorithms [23]. Complex networks are often used to study the collective behaviors exhibited by various groups. Swarm intelligence algorithms, derived from these behaviors, such as animal behavior heuristics and sociological heuristics, often exhibit a similar structure [24]. However, there are notable differences in EAs. Over time, EAs have evolved from direct inspiration from real-world entities to incorporate more mathematical methodologies [25,26,27,28]. Among these algorithms, differential evolution algorithms (DEs) stand out due to their effectiveness and the wide range of available variants [29,30,31]. For this class of algorithms, inferring their topology from the formula becomes particularly challenging, especially when they incorporate adaptive mechanisms [32,33,34]. The study of complex networks in the context of EAs has posed significant challenges. Previous studies on DEs and complex networks have primarily adopted a result-oriented approach, where experimental analysis is performed at the end of the iteration process [35,36,37,38]. However, the network structure of EAs is not static, and in the case of DEs, the connection structure of individuals continuously changes throughout the iterations. Consequently, relying solely on a result-oriented analysis approach is insufficient for comprehensively analyzing EAs in the context of complex networks. Building upon previous research, we conducted a experimental analysis of the network structure changes during the iteration of DEs to enhance the analysis of DEs from a complex network perspective.
In the domain of algorithmic research, a fundamental theory known as the “balance between exploitation and exploration” serves as a theoretical cornerstone [39,40,41]. This theory revolves around the notion that an algorithm should strike a delicate equilibrium between its exploration and exploitation capabilities. Exploration refers to the algorithm’s capacity to discover the global optimum, whereby a stronger exploration capability enables the algorithm to continuously uncover improved solutions over successive iterations. On the other hand, exploitation pertains to the algorithm’s convergence capability, indicating its ability to swiftly progress towards a solution. Consequently, algorithm developers strive to create algorithms that are both efficient and effective in problem-solving, giving rise to the emergence of the balance between exploitation and exploration theory.
However, for a significant period, researchers have relied on abstract rather than concrete descriptions when defining the exploitation and exploration of algorithms. For instance, researchers have incorporated local search to enhance exploitation ability or introduced operators to facilitate escaping from local optima to strengthen exploration ability. However, when viewed from a different perspective, the operator used for local search may also enhance exploration ability due to the larger differences among the selected individuals, while the operator used for enhanced exploration may also involve additional local searches due to the smaller differences among the selected individuals. This ambiguity in the interpretation of the operators used for exploitation and exploration often leads to subjective author-dependent perspectives, which is clearly detrimental to the theoretical study of algorithms. Therefore, the field of evolutionary algorithms urgently requires a method to precisely calibrate the exploitation and exploration of algorithms.
We propose that the complex network structure of algorithms can serve as a manifestation of their exploitation and exploration abilities, an aspect that has yet to be extensively explored in existing research. Thus, advancing the application of complex networks in algorithm research carries significant implications for the progress of evolutionary computing. By unraveling the relationship between an algorithm’s complex network structure and its exploitation/exploration characteristics, researchers can deepen their understanding of algorithmic behavior and potentially devise more robust and efficient evolutionary algorithms.
Previous studies analyzing the complex network of DEs utilized the population interaction network (PIN) method to conduct experimental analysis [42]. The PIN method involves tracking the interactions among individuals during the algorithm’s execution, specifically recording how many old individuals are directly connected to each new generation. By quantifying and categorizing these connections, the algorithm’s PIN structure can be fitted to a specific mathematical distribution that best represents its connectivity pattern. Typically, the fitted target distribution is often characterized by either a Poisson or power-law distribution dominating the results [43,44,45]. Poisson distributions are associated with more discrete or average networks, characterized by a random network [46,47]. Power-law distributions indicate tightly connected networks that belong to the scale-free network category [48,49]. Notably, these two types of distributions exhibit mutually exclusive properties, and the closer an algorithm’s structure generally is to one of these distributions, the further it is from the other. Therefore, the proximity of an algorithm’s structure to either Poisson or power-law distributions, combined with its performance on the test set, provides insights into which type of network structure yields better algorithm performance. Unfortunately, more specific explanations and the significance of the degree distribution are not given in these studies. This is due to the difficulty of obtaining a general pattern in the structure of the network performed by iteration of the algorithm.
To resolve the relevance of complex networks to algorithms, we introduce dynamically changing complex network structures and combine them with the theory of algorithm exploitation and exploration. In this paper, we focus on the network structure changes of five algorithms: DE [50], JADE [51], SHADE [52], LSHADE [53], and EBLSHADE [54], on problems 9, 19, and 29 of the IEEE CEC2017 test set. As a continuation study, we chose to only count and compare the fitting results of Poisson distribution with power-law distribution based on previous studies. In this study, we observed a little correlation between the Poisson distribution and the algorithm’s performance. Conversely, the power-law distribution demonstrated a strong correlation with the convergence speed and global optimization capability of the algorithm, as confirmed by our experimental results.
This work aims to make the following contributions:
- This paper presents the first experiment and study of the dynamic changes of complex networks of DEs.
- This paper, for the first time, experimentally obtained and validated the correlation and correspondence between the complex network structure of the Poisson distribution, power-law distribution, and the exploration and exploitation of DEs.
- This study is a complement to past research by refuting some one-sided conclusions of the study of complex networks of algorithms and presenting a more comprehensive explanation in the relationship between algorithmic network structure and performance.
In Section 2, we analyzed DEs in terms of theory and equations. In Section 3, based on the experimental results of PIN data, all experiments are analyzed and possibilities are explored from the data and images, and the concluding hypotheses of this paper are also given. Finally, in Section 4, we provide a comprehensive summary of the conclusions drawn from this research paper.
2. Methodology
2.1. Differential Evolutionary Algorithms
DE, which is widely recognized as one of the most extensively studied algorithms in EAs, encompasses a diverse range of variants. While numerous studies have proposed their own mutation formulas for DEs, the variations primarily arise from differences in individual selection methods. Thus, to simplify the categorization of DE formulas, we define the differences in formulas of DEs in the simplest way.
where X indicates the individual and F means the multiplicity of mutation. We consider that the difference in the formulations of DEs lies in the difference in their individual selection strategies from to . Since the choice of individuals in complex networks is crucial, we must explain the relevant theory. First, the following is the list of the original mutation formulas of the five DE algorithms:
- (1)
- DE
- (2)
- JADE
- (3)
- SHADE and LSHADE
- (4)
- EBLSHADE
We can easily find the correspondence of these algorithms with Equation (1). Taking DE as an example, we can use to denote , to denote , to denote , and take and to 0. Similarly, the other four algorithms can be represented by Equation (1). Therefore, it can be concluded that these five algorithms differ in the mutation only in the selection of individuals and in the multiplicity of difference amplification. We can rely on this to first analyze the possible network distribution of the algorithm from the perspective of the formula. Since the experimental approach of PIN does not need to consider the difference between + and −, we list the individuals used in each algorithmic mutation and crossover:
- (1)
- DE: , , , .
- (2)
- JADE: , , , , , .
- (3)
- SHADE and LSHADE: , , , , , .
- (4)
- EBLSHADE: , , , , , .
In DE, the individual selection strategy of DE biases it toward a uniformly distributed random network structure in the mutation process because all three individuals are selected non-repetitively and randomly from the population. Utilizing the current individual does not modify its probability distribution (since each individual of each generation is thus used once extra), resulting in the DE exhibiting a PIN structure that follows a Poisson distribution, with analysis focused on the formula. In the case of JADE, SHADE, and LSHADE, it is observed that they demonstrate a more pronounced power-law distribution during the mutation process compared to DE. Similar to DE, reusing the current individual does not alter the probability distribution of its individual selection. The inclusion of individuals from the external archive in the selection process decreases the likelihood of selecting individuals from the previous generation. This reduction can be attributed to the fact that the external archive comprises individuals that have been deemed inferior based on their historical information (continuously eliminated by the size constraint of the external archive). Moreover, the selection of from the top individuals, based on a certain proportion, significantly enhances the probability of selecting superior individuals. Consequently, this leads to an increase in the utilization of minority individuals and a decrease in the utilization of majority individuals, which aligns with the characteristics of a power-law distribution. In the EBLSHADE strategy, the increased number of elite individuals reduces their likelihood of being selected compared to the elite individuals in LSHADE. As a consequence, the number of utilized individuals in EBLSHADE is smaller than that in LSHADE. Therefore, EBLSHADE exhibits a more pronounced Poisson distribution in theory compared to LSHADE. This assertion has been supported by previous research findings.
The aforementioned conclusions are derived from theoretical analysis based on formulas. Given that all DE variants employ greedy strategies, there is a possibility of individuals not undergoing renewal in each generation due to insufficient progress. The reuse of these individuals contributes to the algorithm converging towards a biased power-law distribution. Hence, a more accurate assessment of the complex network structure of DEs would involve experimental analysis rather than relying solely on formulaic derivation. In comparison with previous studies on the complex network analysis of algorithms, our theoretical analysis of the algorithm yields similar results. The purpose of re-analyzing the algorithm’s structure in this section is to further validate the fitting conclusions regarding the algorithm itself that have been unquestionably correct in past research.
2.2. Population Interaction Network
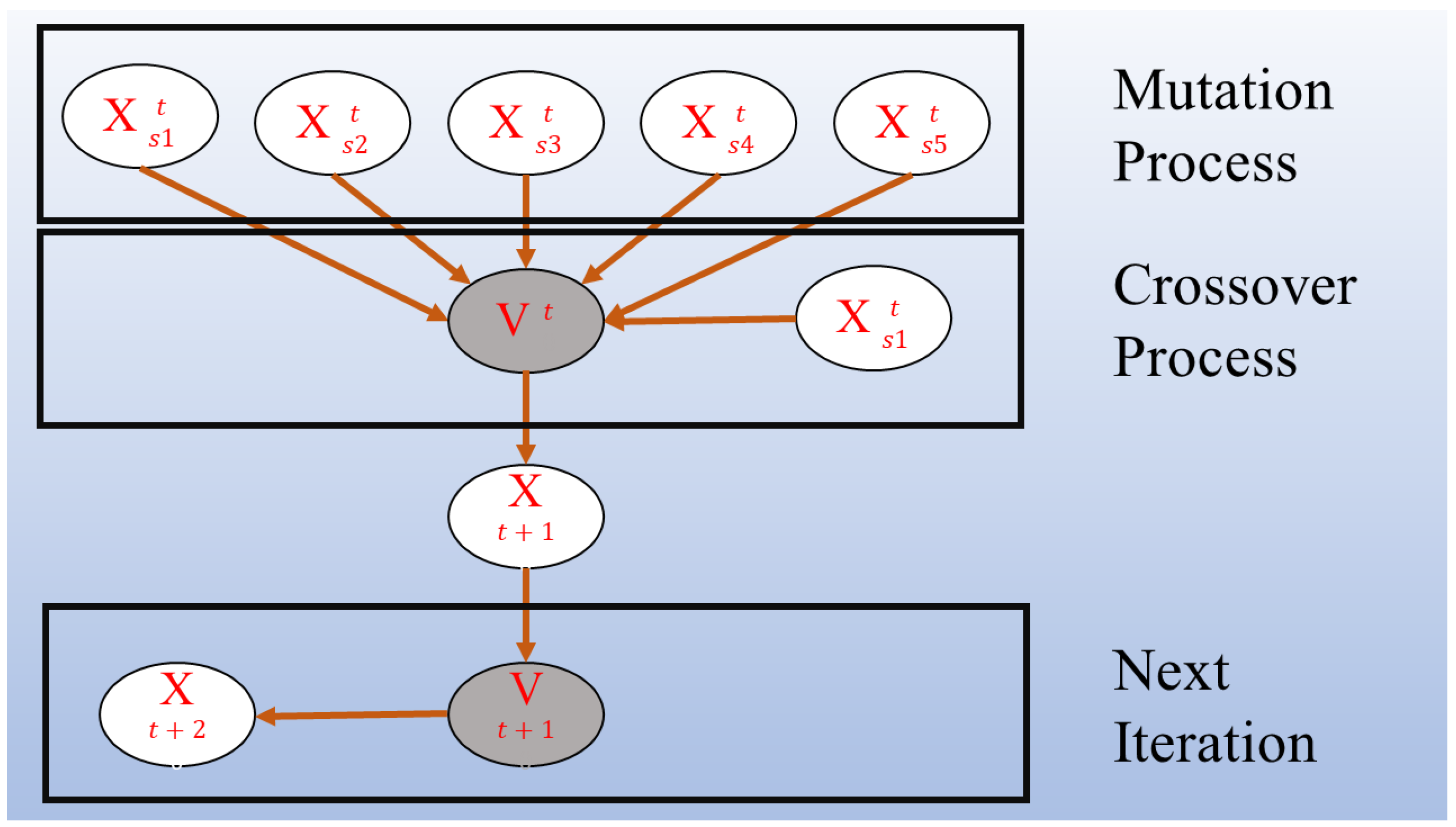
The PIN method is employed to label individuals in each generation and is recorded through the markers invoked during the generation of new individuals, ultimately yielding a count. The experimental results provide the frequency at which each marker is referenced, representing the number of times an individual is invoked. Subsequently, these invocation counts are sorted in ascending order, allowing for the determination of the distribution of individuals across different invocation levels. By analyzing this distribution, various probability distributions can be fitted, thereby revealing the underlying complex network structure. Figure 1 illustrates the schematic diagram of the PIN method in DEs. The dots represent individuals obtained from Equation (1). The individual V is obtained after the mutation process of DE and before the crossover process. The five individuals, ranging from to , along with the original individual , generate a new individual , which then acts as the source for generating the subsequent individual . When a large number of individuals are interconnected as depicted in Figure 1, the resulting network structure exhibits complexity, nonlinearity, and spontaneity (as the selection of individuals is spontaneous), thereby meeting the definition of a complex network.
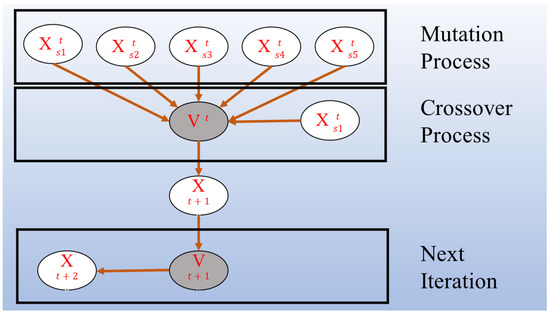
Figure 1.
Schematic diagram of the population interaction network.
2.3. Some Doubts about Past Researches
As an illustration, the Poisson distribution is characterized by the condition that the majority of individuals cluster nearby a specific number of utilizations, while only a small number of individuals exhibit more or fewer utilizations. Concerning DEs, adhering to the Poisson distribution necessitates not only the formulation itself being consistent with the average utilization probability but also the renewal of individuals being in line with the predominant trend of individuals progressing in each generation. Assuming the existence of a generation where individuals largely remain stagnant without retiring, their reuse in subsequent iterations leads to an increase in their utilization, thereby deviating from the Poisson distribution. In essence, when the algorithm adheres to the Poisson distribution, it should converge smoothly, uniformly, and exhibit continuous progress.
Likewise, in the context of the power-law distribution, a small number of individuals exhibit a significant number of utilizations, while the majority of individuals possess an equal number of utilizations. In the algorithm, when it conforms to a power-law distribution, it should converge rapidly, attaining a locally optimal solution, and subsequently enter a state of stagnation. Stagnation here does not imply that all individuals cease to be updated but rather denotes that the optimal individual ceases to change, as it becomes the most utilized one. Other individuals continue to approach the optimal individual, thereby making progress. This progression is manifested in the probability density utilized by the individual, which exhibits a high concentration at the front and a low concentration at the tail, characteristic of a long tail distribution. Therefore, an algorithm that aligns with the characteristics of the power-law distribution should converge swiftly and readily transition into a state of stagnation.
The aforementioned theory does not aim to establish superiority of any particular distribution class in terms of algorithm performance. Rather, we seek to demonstrate that the PIN distribution of an algorithm is not directly linked to its performance. Notably, Li’s study also revealed that the PIN structure of EBLSHADE exhibited deviated further from a power-law distribution compared to LSHADE, specifically when the initial population size was set to [55]. Furthermore, EBLSHADE outperformed LSHADE in the CEC2017 competition, thus providing supporting evidence for our inference. As additional compelling evidence, Wang conducted a study on the fusion of complex networks and EAs, wherein an algorithm named was specifically designed to align well with the power-law distribution [56]. Notably, although , which originally signifies a power-law distribution, outperformed DE (which conforms to the Poisson distribution) in the CEC2005 competition, it did not employ the more widely accepted population size of 100 in the DE parameter setting. To address this, we replicated the experiment using the DE parameters commonly adopted, namely , , and , as indicated by the number of evaluations specified in their original text. Table 1 presents the results and a comparison between DE and . Through the application of the Wilcoxon test, it becomes evident that while outperforms DE significantly in the case of dimension 2, it is clear that DE surpasses in dimensions 10 and 30. Does this imply that algorithms belonging to the Poisson distribution are inherently stronger than those adhering to the power-law distribution?

Table 1.
Comparison of DE and in CEC2005.
A similar issue arises in another article that focuses on enhancing DE through the utilization of scale-free networks [57]. The study by Yu constructs a structure for DE (judged by the formula with parameter pairs probably based on SHADE) that is consistent with a scale-free network, i.e., its compliance with a power-law distribution. Furthermore, when evaluated using the standard test set of CEC2017, SNDE significantly outperforms LSHADE-cnEpSin, which is an advanced improvement algorithm of LSHADE [58]. This demonstrates the crucial role of scale-free networks in enhancing the algorithm, as highlighted in the original article. If this inference holds true, it can be argued that SNDE should demonstrate a greater bias towards the power-law distribution compared to LSHADE. According to theory, EBLSHADE, which deviates further from the power-law distribution than LSHADE, should theoretically exhibit inferior performance to SNDE since a structure that aligns more closely with the scale-free network would yield better results. However, this is not the case when comparing the two algorithms using the test set. Table 2 presents a comprehensive comparison between SNDE and EBLSHADE, clearly indicating a significant performance gap between them. Although we did not experimentally analyze the PIN results for SNDE, it might be questionable to assert that SNDE exhibits a more pronounced power-law distribution. Nevertheless, the contradictions are still evident. Considering that the Yu paper elucidates the algorithm’s improvement based on the theoretical foundation established by Li, which posits that the better the algorithm fits the power-law distribution, the better its performance will be, our comparison results demonstrate that this assertion does not withstand scrutiny.

Table 2.
Comparison of SNDE and EBLSHADE in CEC2017.
Our aforementioned verification and inference should not be perceived as a dismissal of the prior work conducted by researchers. Rather, it aims to elucidate that these studies might have inadvertently fallen into a local optimum. This is evident when considering a broader comparison of the performance disparities among the algorithms, which reveals that the conclusions drawn from these studies lack rigor. Subsequent comparisons demonstrate that the PIN structure of an algorithm is not directly associated with the quality of the final solution, and the algorithm that best aligns with the power-law distribution does not necessarily exhibit superior performance. Nonetheless, this does not imply that analyzing the complex network structure of the algorithm is inconsequential, as other characteristics of the algorithm may indeed exhibit a robust correlation with its distribution structure. This brings us back to a pivotal point, namely the dynamic complex network structure of the algorithm [59,60,61].
3. Dynamic Complex Network Structure of DEs
In the experimental section, we selected problem 9, problem 19, and problem 29 from the CEC2017 benchmark set, each in a 30-dimensional setting. Due to the outstanding performance of all five algorithms on unimodal functions, it is difficult to analyze their differences. Therefore, we selected a problem from simple multimodal functions, mixed functions, and composite functions for experimentation. The error values and PIN results were obtained as the averages from 30 independent runs, with the maximum number of function evaluations () set to the standard value of 10,000. The parameter setting of the algorithms adopts the parameters recommended by the original papers. The average performance of the five algorithms in CEC2017 is presented in Table 3. In order to align with the mean fitness results obtained from PIN, an error-based mean ranking approach was employed for the algorithm ranking.

Table 3.
Average result of five algorithms in three problems of CEC2017.
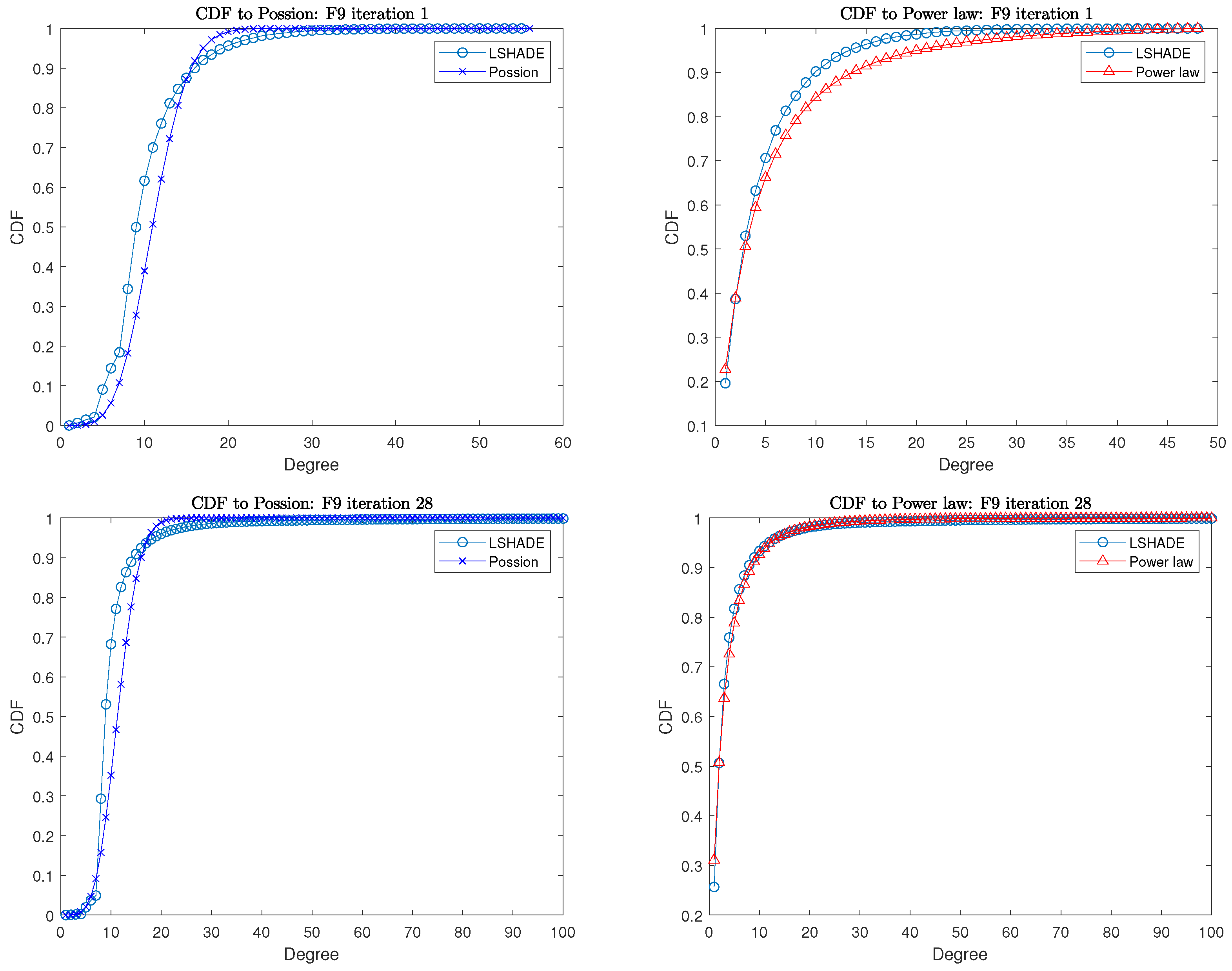
Figure 2 presents the cumulative distribution plot of LSHADE while fitting to two probability distributions at the beginning and end of the iteration. It is evident that the network structure of the algorithm undergoes significant changes during the PIN statistics iteration, as depicted from top to bottom in the figure. The results before and after fitting the Poisson distribution do not change significantly, but there is a large gap before and after fitting the power-law distribution in the figure. To gain a more comprehensive understanding of the algorithm’s dynamic changes, we further analyze its transformations using continuous experimental data. In our analysis of the experimental results, we will examine the correlation between the algorithm’s behavior, which tends to favor exploration or exploitation, and the two distributions. If a consistent pattern emerges, it can serve as a plausible explanation for the relationship between the algorithm’s perceived exploitation and exploration strategies. This interpretation should be based on a dynamic network change and not only on the results of the last recording (e.g., iteration 28 in the figure).
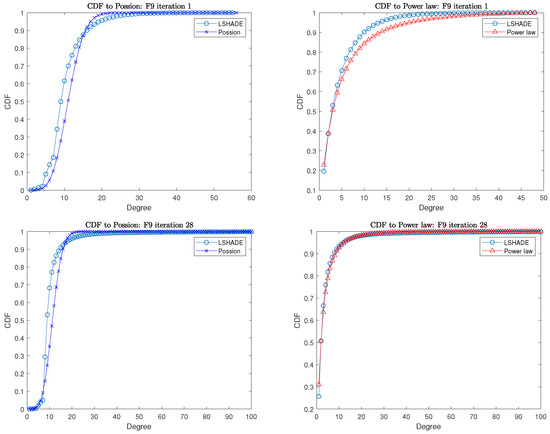
Figure 2.
CDF at the beginning and end of the iteration.
3.1. Using PIN Records for Dynamic Complex Network
The dynamic complex network analysis of DEs still relies on the utilization of the PIN method. However, it differs from previous experimental methods as we introduce multiple experimental and computational points during the iterative convergence of the algorithm. Specifically, the previous experimental approach was to insert PIN into the iterations of the algorithm and perform the calculation of the degree distribution based on the obtained data at the end of the iteration. In contrast, we take the algorithm with P as the iteration interval and perform the calculation once every P generations and continue until the end of the iteration of the algorithm. In this way, we can obtain a line graph similar to the convergence graph of the algorithm, and this process is the dynamic change of the network structure during the iteration of the algorithm. The population sizes of DE, JADE, and SHADE remain constant, ensuring uniform convergence processes and experimentally spaced data points at P generation intervals. In contrast, algorithms like LSHADE and EBLSHADE incorporate linearly decreasing population sizes, resulting in non-uniform consumption of evaluations throughout their iterations. As a result, the convergence results for the same P generation interval do not precisely correspond to the results obtained through PIN statistics. Considering the total number of iterations of approximately three thousand generations, our experimental approach maintains sufficient accuracy. During our experimental process, we set the value of P to , where represents the maximum number of function evaluations and D denotes the dimensionality of the problem. The evolution of EAs stops at the termination condition of the iteration, so we employ the distribution that exhibits the closest similarity to the power-law distribution based on the complete set of last results. This approach enables us to capture the overall trend of the algorithm and obtain a more accurate estimation of the distribution’s similarity.
3.2. Fitting Results of PIN
In fitting the Poisson distribution to the statistics of PIN, we obtained its SSE (sum of squares of errors) with (coefficient of determination). Specifically, the smaller the SSE, the larger the , implying that it is closer to this distribution. The fit results are derived from the average performance of thirty times, so if there is an extreme value in one case, it will greatly affect the magnitude of the results. Similarly, the convergence data used for comparison are from the same set of averages, so the control relationship does not change.
3.2.1. Fitting Results in Problem 9
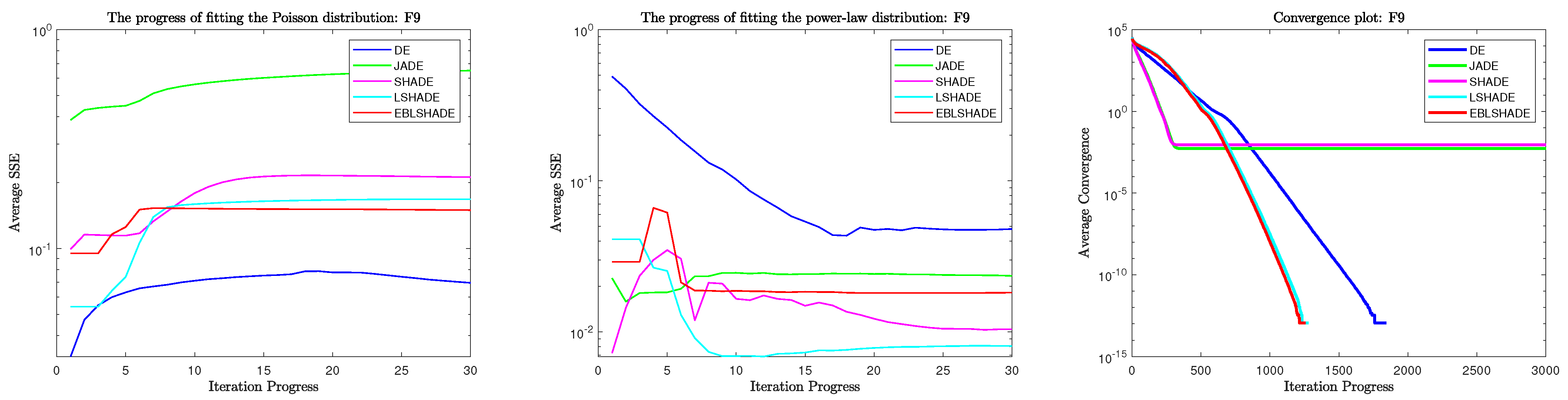
Table 4 shows all the fitting results of two distributions. In Figure 3, from left to right, the fit plots for the Poisson distribution, the fit plots for the power-law distribution, and the convergence plots are represented. Analyzing the fitting results from a single distribution, all algorithms on this problem show a tendency to move away from the Poisson distribution, and most of the convergence processes show a tendency to approach the power-law distribution. By comparing the initial result (or positive second result) with the final result in the table, we can obtain that the result of SSE becomes larger and the result of becomes smaller in the Poisson distribution, which means that these algorithms are deviating from the Poisson distribution. The results of the fit to the power-law distribution show the opposite trend.

Table 4.
Fitting results in problem 9.

Figure 3.
Fitting and convergence results during iteration in problem 9.
Combining the two probability distributions to analyze the convergence process of the algorithm is difficult, but we can still find some connections. Based on our proposed hypothesis, the Poisson distribution reflects the exploration ability of the algorithm and the power-law distribution reflects the exploitation ability of the algorithm. Then JADE, which is overall furthest from the Poisson distribution, should be the least explored of the five algorithms. The convergence results of JADE and SHADE are also indeed the worst in terms of optimal solution performance, and the rapid convergence and stagnation indicate that they fall into a local optimum, which implies their lack of exploration ability. For the fitting results with the power-law distribution, we believe that the faster the algorithm approaches the power-law distribution, the better the algorithm is exploited and the faster it converges at this time. Due to the simplicity of problem 9, all algorithms perform the development task in a short process, except DE. The trend of DE is the slowest in the process of approaching the power-law distribution, and its convergence is the slowest. JADE, on the other hand, ends the development process at the beginning of the iteration, and SHADE and EBLSHADE have a fast descent in the early part of the iteration, and LSHADE is slightly flatter. This is also reflected in the convergence plot. Therefore, the experiment in problem 9 is consistent with our hypothesis.
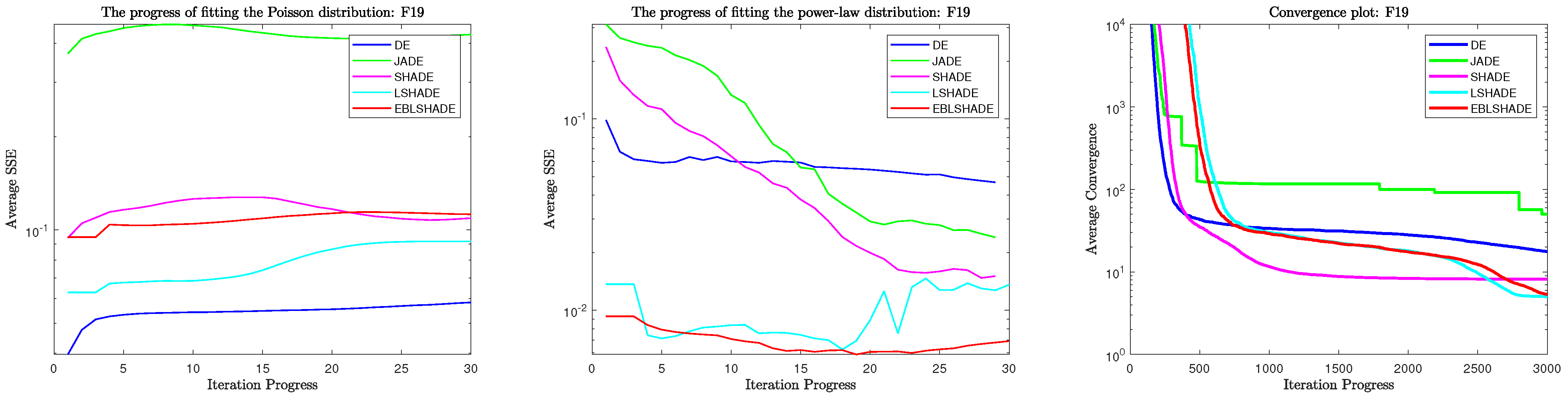
3.2.2. Fitting Results in Problem 19
In Table 5, the results in problem 19 are quite different from those in problem 9; firstly, in the degree of fitting of the Poisson distribution, it is obvious that all the algorithms have approximate fitting results of the Poisson distribution except DE, which is the closest, and JADE, which is the furthest away. What is special is that SHADE has a crossover with EBLSHADE’s Poisson distribution fitting results in the late convergence period. Again, compared with the algorithm’s exploration ability, the JADE solution has the worst quality and has a clear step-down convergence process, which is more typical of the weaker exploration ability than other algorithms. The three algorithms with close exploration ability, SHADE, LSHADE, and EBLSHADE, are very close in terms of solution quality, and they all show a trend of continuous convergence in the convergence plots, which indicates that their exploration ability is also very close. In Figure 4, to comparing the fitting trend of the power-law distribution with the convergence graph, it is clear that SHADE has the most rapid approach to the power-law distribution regarding 20 statistics, and it is indeed the fastest converging algorithm before 2500 generations. Another favorable piece of evidence that the speed of approach to the power-law distribution is positively correlated with the speed of convergence is that there is a sudden and rapid approach to the power-law distribution in the late iteration of LSHADE, which is reflected in the convergence graph as the late and rapid convergence of LSHADE and which surpasses the convergence speed and the solution quality of EBLSHADE and SHADE at one go. Then, it stalls because it is no longer close to the power-law distribution. There is no doubt that the conclusion of question 19 can still support our hypothesis.

Table 5.
Fitting results in problem 19.

Figure 4.
Fitting and convergence results during iteration in problem 19.
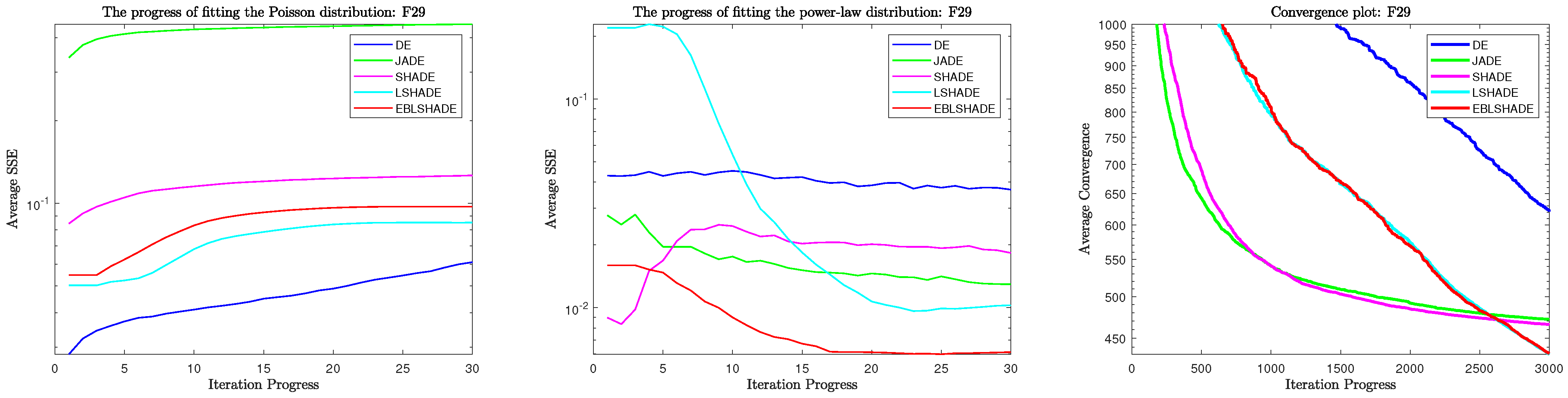
3.2.3. Fitting Results in Problem 29
In Table 6, the results of problem 29 are again very different from the two previous problems, but this does not prevent us from being able to explain them with the same hypothesis. But this time we need to analyze the convergence plots before combining the fitting results and Figure 5. First of all, it can be seen from the fact that each algorithm does not stall on this problem, which does not require high exploration ability of the algorithm. Since the algorithm does not even fall into a local optimum, there is no need to jump out of it. Therefore, even if JADE still exhibits the weakest exploration ability, it can still obtain a good solution to this problem. Second, for the fitting results of the power-law distribution, the DE is hardly close to the power-law distribution, which is shown in the convergence plots as the slowest convergence rate and the worst quality of the solution. However, it should be noted that before the fifth statistic, the fast approach to the power-law distribution is only a small part of JADE and SHADE initially, with the arms JADE clearly approaching faster. LSHADE and EBLSHADE are slower, showing in the convergence plot that JADE has the fastest initial convergence rate and, together with SHADE, slows down quickly. At the middle of the iteration, roughly the 5th to 20th statistics, JADE and SHADE at this time are very slow in approaching the power-law distribution, while LSHADE and EBLSHADE are extremely fast in approaching the power-law distribution. The convergence plots at this stage show a continuous high rate of convergence of these two algorithms and surpass JADE and SHADE at the end.

Table 6.
Fitting results in problem 29.

Figure 5.
Fitting and convergence results during iteration in problem 29.
4. Conclusions
Through experimental analysis, we obtained a conclusion that fits all experimental cases. The exploration ability of an algorithm depends on how closely its complex network structure approximates the Poisson distribution (random network), and the exploitation ability of an algorithm depends on how quickly its complex network structure approximates the power-law distribution (scale-free network). Without considering the mutual influence between exploitation and exploration, the closer the algorithm is to the Poisson distribution, the better it is at finding the global optimum. The faster the algorithm approaches the power-law distribution at some point in the iterative process, then the faster the algorithm converges, i.e., the better the exploitation capability.
Moreover, we challenge certain limitations of previous research. The quality of an algorithm cannot be determined solely by its probability distribution or by forcing a specific probability distribution to fit a predefined PIN structure. The complex network structure of an algorithm arises from a combination of operator design and strategy adaptation, and it is through this interplay that the algorithm manifests its characteristic network properties. This phenomenon reflects the emergence inherent in complex systems, and imposing rigid constraints on algorithmic processes undermines the emergence of algorithmic functionalities. The methods we propose are effective in assessing the design quality of algorithms rather than providing specific guidance for improvement. It is worth noting that certain poorly designed algorithms may yield favorable results on specific problems (such as DE in problem 9), but their complex network structures exhibit similar performance across different problem domains. Hence, algorithms that deviate significantly from or closely approximate the Poisson distribution, as well as algorithms that exhibit slow convergence towards the power-law distribution, are indicative of suboptimal design. Such algorithms are generally ill-suited for a wide range of problems. By employing the testing methods we propose, one can avoid the utilization of inadequate algorithms and instead apply more reasonable approaches that are better suited for diverse problem scenarios.
In summary, the analytical approach of dynamic complex networks provides one of the most objective and reasonable explanations for the exploitation and exploration behavior of the test algorithms so far. In subsequent studies, this approach will also be applied to more problems and more algorithms to verify and improve the theoretical structure. Eventually, we can thoroughly resolve the black-box optimization process of the algorithm.
Author Contributions
Conceptualization, Y.Y. and H.Y.; methodology, Y.Y.; software, Y.Y. and H.Y.; validation, Y.Y. and Z.Y.; formal analysis, Y.Y. and S.T.; investigation, Y.Y. and S.T.; resources, Z.T.; data curation, Y.Y.; writing—original draft preparation, Y.Y.; writing—review and editing, Y.Y. and Z.T.; visualization, Y.Y.; supervision, Z.T.; project administration, Z.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available upon request by contacting the corresponding author’s email address. The source code will be made public through the URL: https://velvety-frangollo-5d54c2.netlify.app/, accessed on 15 June 2023.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EAs | evolutionary algorithms |
| DEs | differential evolution algorithms |
| PIN | population interaction network |
| DE | differential evolution |
| JADE | adaptive differential evolution with optional external archive |
| SHADE | success-history-based parameter adaptation for DE |
| LSHADE | SHADE using linear population size reduction |
| EBLSHADE | novel mutation strategy for enhancing LSHADE |
References
- Ottino, J.M. Engineering complex systems. Nature 2004, 427, 399. [Google Scholar] [CrossRef]
- An, L.; Grimm, V.; Sullivan, A.; Turner Ii, B.; Malleson, N.; Heppenstall, A.; Vincenot, C.; Robinson, D.; Ye, X.; Liu, J.; et al. Challenges, tasks, and opportunities in modeling agent-based complex systems. Ecol. Model. 2021, 457, 109685. [Google Scholar] [CrossRef]
- Belani, H.; Vukovic, M.; Car, Z. Requirements Engineering Challenges in Building AI-Based Complex Systems. In Proceedings of the 2019 IEEE 27th International Requirements Engineering Conference Workshops (REW), Jeju Island, Republic of Korea, 23–27 September 2019; pp. 252–255. [Google Scholar] [CrossRef]
- Carmichael, T.; Hadžikadić, M. The fundamentals of complex adaptive systems. In Complex Adaptive Systems: Views from the Physical, Natural, and Social Sciences; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–16. [Google Scholar]
- Orús, R. Tensor networks for complex quantum systems. Nat. Rev. Phys. 2019, 1, 538–550. [Google Scholar] [CrossRef]
- Sporns, O. Structure and function of complex brain networks. Dialogues Clin. Neurosci. 2022. [Google Scholar] [CrossRef]
- Appeltant, L.; Soriano, M.C.; Van der Sande, G.; Danckaert, J.; Massar, S.; Dambre, J.; Schrauwen, B.; Mirasso, C.R.; Fischer, I. Information processing using a single dynamical node as complex system. Nat. Commun. 2011, 2, 468. [Google Scholar] [CrossRef]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef]
- Stylios, C.; Groumpos, P. Modeling complex systems using fuzzy cognitive maps. IEEE Trans. Syst. Man Cybern.- Part A Syst. Hum. 2004, 34, 155–162. [Google Scholar] [CrossRef]
- Haddadi, H.; Uhlig, S.; Moore, A.; Mortier, R.; Rio, M. Modeling internet topology dynamics. ACM SIGCOMM Comput. Commun. Rev. 2008, 38, 65–68. [Google Scholar] [CrossRef]
- Calvert, K.L.; Doar, M.B.; Zegura, E.W. Modeling internet topology. IEEE Commun. Mag. 1997, 35, 160–163. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Bodin, Ö.; Alexander, S.M.; Baggio, J.; Barnes, M.L.; Berardo, R.; Cumming, G.S.; Dee, L.E.; Fischer, A.P.; Fischer, M.; Mancilla Garcia, M.; et al. Improving network approaches to the study of complex social–ecological interdependencies. Nat. Sustain. 2019, 2, 551–559. [Google Scholar] [CrossRef]
- Tan, X.; Cao, J.; Rutkowski, L. Distributed dynamic self-triggered control for uncertain complex networks with Markov switching topologies and random time-varying delay. IEEE Trans. Netw. Sci. Eng. 2019, 7, 1111–1120. [Google Scholar] [CrossRef]
- Zou, Y.; Donner, R.V.; Marwan, N.; Donges, J.F.; Kurths, J. Complex network approaches to nonlinear time series analysis. Phys. Rep. 2019, 787, 1–97. [Google Scholar] [CrossRef]
- Boers, N.; Goswami, B.; Rheinwalt, A.; Bookhagen, B.; Hoskins, B.; Kurths, J. Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature 2019, 566, 373–377. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z. Multivariate time series clustering based on complex network. Pattern Recognit. 2021, 115, 107919. [Google Scholar] [CrossRef]
- Qureshi, K.A.; Malick, R.A.S.; Sabih, M.; Cherifi, H. Complex network and source inspired COVID-19 fake news classification on Twitter. IEEE Access 2021, 9, 139636–139656. [Google Scholar] [CrossRef]
- Dorronsoro, B.; Bouvry, P. Improving Classical and Decentralized Differential Evolution with New Mutation Operator and Population Topologies. IEEE Trans. Evol. Comput. 2011, 15, 67–98. [Google Scholar] [CrossRef]
- Dorronsoro, B.; Bouvry, P. Study of different small-world topology generation mechanisms for Genetic Algorithms. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Bansal, J.C.; Singh, P.K.; Pal, N.R. Evolutionary and Swarm Intelligence Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; Volume 779. [Google Scholar]
- Liu, C.; Du, W.B.; Wang, W.X. Particle swarm optimization with scale-free interactions. PLoS ONE 2014, 9, e97822. [Google Scholar] [CrossRef]
- Maier, H.R.; Razavi, S.; Kapelan, Z.; Matott, L.S.; Kasprzyk, J.; Tolson, B.A. Introductory overview: Optimization using evolutionary algorithms and other metaheuristics. Environ. Model. Softw. 2019, 114, 195–213. [Google Scholar] [CrossRef]
- Sobania, D.; Schweim, D.; Rothlauf, F. A comprehensive survey on program synthesis with evolutionary algorithms. IEEE Trans. Evol. Comput. 2022, 27, 82–97. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, Q.; Hao, K.; Jin, Y. A survey of evolutionary algorithms for multi-objective optimization problems with irregular pareto fronts. IEEE/CAA J. Autom. Sin. 2021, 8, 303–318. [Google Scholar] [CrossRef]
- Mirjalili, S. Evolutionary algorithms and neural networks. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; Volume 780. [Google Scholar]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Tanabe, R.; Fukunaga, A. Reviewing and benchmarking parameter control methods in differential evolution. IEEE Trans. Cybern. 2019, 50, 1170–1184. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Li, S.; Gu, Q.; Gong, W.; Ning, B. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 205, 112443. [Google Scholar] [CrossRef]
- Sun, G.; Yang, B.; Yang, Z.; Xu, G. An adaptive differential evolution with combined strategy for global numerical optimization. Soft Comput. 2020, 24, 6277–6296. [Google Scholar] [CrossRef]
- Zhou, S.; Xing, L.; Zheng, X.; Du, N.; Wang, L.; Zhang, Q. A self-adaptive differential evolution algorithm for scheduling a single batch-processing machine with arbitrary job sizes and release times. IEEE Trans. Cybern. 2019, 51, 1430–1442. [Google Scholar] [CrossRef]
- Skanderova, L.; Fabian, T. Differential evolution dynamics analysis by complex networks. Soft Comput. 2017, 21, 1817–1831. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Y.J.; Xu, X.K. Convergence improvement of differential evolution for community detection in complex networks. Phys. A Stat. Mech. Its Appl. 2018, 503, 762–779. [Google Scholar] [CrossRef]
- Davendra, D.; Zelinka, I.; Metlicka, M.; Senkerik, R.; Pluhacek, M. Complex network analysis of differential evolution algorithm applied to flowshop with no-wait problem. In Proceedings of the 2014 IEEE Symposium on Differential Evolution (SDE), Orlando, FL, USA, 9–12 December 2014; pp. 1–8. [Google Scholar]
- Senkerik, R.; Viktorin, A.; Pluhacek, M.; Janostik, J.; Davendra, D. On the influence of different randomization and complex network analysis for differential evolution. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3346–3353. [Google Scholar]
- Yang, H.; Yu, Y.; Cheng, J.; Lei, Z.; Cai, Z.; Zhang, Z.; Gao, S. An intelligent metaphor-free spatial information sampling algorithm for balancing exploitation and exploration. Knowl.-Based Syst. 2022, 250, 109081. [Google Scholar] [CrossRef]
- Osugi, T.; Kim, D.; Scott, S. Balancing exploration and exploitation: A new algorithm for active machine learning. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005; p. 8. [Google Scholar] [CrossRef]
- Cuevas, E.; Echavarría, A.; Ramírez-Ortegón, M.A. An optimization algorithm inspired by the States of Matter that improves the balance between exploration and exploitation. Appl. Intell. 2014, 40, 256–272. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y.; Wang, J.; Cheng, J. Understanding differential evolution: A Poisson law derived from population interaction network. J. Comput. Sci. 2017, 21, 140–149. [Google Scholar] [CrossRef]
- Consul, P.C.; Jain, G.C. A generalization of the Poisson distribution. Technometrics 1973, 15, 791–799. [Google Scholar] [CrossRef]
- Adamic, L.A.; Huberman, B.A. Power-law distribution of the world wide web. Science 2000, 287, 2115. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical thermodynamics of random networks. Proc. R. Soc. Lond. A Math. Phys. Sci. 1976, 351, 351–380. [Google Scholar]
- Mossa, S.; Barthelemy, M.; Stanley, H.E.; Amaral, L.A.N. Truncation of power law behavior in “scale-free” network models due to information filtering. Phys. Rev. Lett. 2002, 88, 138701. [Google Scholar] [CrossRef]
- Goh, K.I.; Oh, E.; Jeong, H.; Kahng, B.; Kim, D. Classification of scale-free networks. Proc. Natl. Acad. Sci. USA 2002, 99, 12583–12588. [Google Scholar] [CrossRef] [PubMed]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for Differential Evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Jambi, K.M. Novel mutation strategy for enhancing SHADE and LSHADE algorithms for global numerical optimization. Swarm Evol. Comput. 2019, 50, 100455. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Yang, H.; Wang, Y.; Gao, S. Population interaction network in representative differential evolution algorithms: Power-law outperforms Poisson distribution. Phys. A Stat. Mech. Its Appl. 2022, 603, 127764. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Yu, Y.; Xu, Z. The discovery of population interaction with a power law distribution in brain storm optimization. Memetic Comput. 2019, 11, 65–87. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, S.; Zhou, M.; Wang, Y.; Lei, Z.; Zhang, T.; Wang, J. Scale-free network-based differential evolution to solve function optimization and parameter estimation of photovoltaic models. Swarm Evol. Comput. 2022, 74, 101142. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 372–379. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Estrada, E. Introduction to complex networks: Structure and dynamics. In Evolutionary Equations with Applications in Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 93–131. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).