Abstract
Herein, we propose a novel model-based simultaneous multi-slice (SMS) reconstruction method by exploiting data-driven parameter modeling for highly accelerated T1 parameter quantification. We assume that the predefined slice-specific null space operator remains invariant along the parameter dimension. We incorporate the parameter dimension into SMS-HSL to exploit Hankel-structured and Casorati matrices. Given this consideration, the SMS signal is reformulated in k-p space as a constrained optimization problem that exploits rank deficiency for the Hankel-structured matrix and a finite-dimensional basis for a subspace containing slowly evolving signals in the parameter direction. The proposed model-based SMS reconstruction method is validated on in vivo data and compared with state-of-the-art methods with slice acceleration factors of 3 and 5, including an in-plane acceleration factor of 2. The experimental results demonstrate that the proposed method performs effective slice unfolding and signal recovery in reconstructed images and T1 maps with high precision as compared to the state-of-the-art methods.
Keywords:
magnetic resonance imaging (MRI); simultaneous multi-slice (SMS); parallel imaging; parameter mapping; null space; low rank MSC:
94A08
1. Introduction
Magnetic resonance (MR) parameter mapping has been widely used for tissue characterization because different tissues have distinct parameters, such as T1 longitudinal relaxation time and T2 transverse relaxation times, and it provides insight into the mechanics of disease processes for clinical applications [1,2]. In particular, T1 parameter mapping typically involves an inversion recovery pulse coupled with echo-planar imaging (EPI) encodings, each of which is acquired with different inversion times (TI) [3]. Many T1-weighted images must be acquired during the inversion time to accurately measure the T1 values. This makes it challenging to achieve high-resolution MR parameter mapping because of the limited imaging time.
Some studies have suggested the use of parallel imaging techniques, such as SENSE and GRAPPA, to accelerate MR parameter mapping and exploit the encoding power offered by multiple coils [4,5]. In cases in which coil-sensitivity-induced spatial modulation in the phase-encoding direction may not be well localized, parallel MRI [4,5] often fails to resolve aliasing voxels, resulting in a substantial level of residual artifacts and amplified noise, even at a slightly high acceleration factor (∼3). Compressed sensing (CS), which exploits image sparsity in certain transform domains, has also demonstrated effectiveness in achieving fast acquisition and accurate reconstruction through sparse sampling [6,7]. Model-based approaches have been successfully applied to MR parameter mapping by modeling tissue signal evolution as a temporal constraint [8,9,10]. The abovementioned undersampling strategies are highly effective in increasing the speed of the EPI encoding for multi-shot imaging because of the reduction in the number of shots; however, they are relatively less time-efficient for single-shot imaging, although they mitigate the k-space signal modulation caused by T2* decay. Additionally, all the undersampling approaches result in a direct tradeoff between encoding efficiency and signal-to-noise ratio (SNR) efficiency.
Simultaneous multi-slice (SMS) MRI [11,12,13], which employs multi-band (MB) radio-frequency (RF) pulses to excite multiple slices at the same time while exploiting spatial and interchannel correlation to resolve aliased voxels in the slice direction, can potentially alleviate the problems in the undersampling strategies that are related to the low encoding efficiency in the single-shot imaging, as well as the inherent loss of signals resulting from insufficient sampling. In order to improve the SNR efficiency, some studies have combined controlled aliasing with SMS imaging to evenly distribute the aliasing between the two axes of the phase-encoding and slice directions, followed by unaliasing of the overlap voxels using parallel imaging [14]. Split slice-GRAPPA (SP-SG) is a reconstruction technique that imposes a slice leakage block constraint to effectively remove neighboring slice signals, thus allowing for improved slice separation in SMS imaging [15,16,17,18]. Recently, a SPIRiT [19]-type reconstruction method was introduced, which uses readout concatenation in the image domain to accelerate SMS encoding and enhance coil self-consistency as in SPIRiT reconstruction in an extended k-space, allowing for noise reduction (ROCK-SPIRiT) [20]. Several low-rank-promoting constraint approaches have been proposed for aliasing separation in SMS imaging [20,21,22,23,24,25,26,27,28]. The concept of virtual slices has been incorporated into SP-SG as a single-step method. In this approach, in-plane aliasing artifacts are considered additional slices that are eliminated during the reconstruction process [23]. Hankel-structured low-rank SMS reconstruction, referred to as SMS-MUSSELS [24,25], was introduced by combining the annihilating filter concept with SENSE reconstruction. Low-rank matrix modeling of local k-space neighborhoods (LORAKS) has also been applied to SMS acquisition with low-rank completion [27,28]. The hybrid-space SENSE method represents a 3D reconstruction with low-rank constraints of the SMS acquisition [29]. Furthermore, there has been a recent expansion of the SMS reconstruction method to incorporate a deep learning network [30,31].
In our previous work [32], using an SMS reconstruction method that exploits Hankel subspace learning for aliasing separation in the slice direction (SMS-HSL), we modeled an SMS signal with a Hankel matrix as a linear combination of all slices and decomposed the Hankel-structured SMS signal into slices of interest and combined complementary slices. Employing the complementary null space, the signal model is projected onto the subspace, where slices of no interest are nulled, and only a slice of interest is left.
In the present study, we extend our preliminary work to a model-based SMS-HSL framework by exploiting a data-driven parameter model for T1 mapping. First, we incorporate the parameter dimension into the SMS-HSL formulation to exploit the plural properties of both Hankel- and Casorati-structured [33] matrices. We introduce a data-driven parameter model as prior knowledge to use the similarity among different TIs and reduce the degrees of freedom of reconstruction for accurate spatial map coefficients. Thus, the proposed method estimates both spatial map coefficients and parameter image series within a single SMS optimization framework. The efficacy of this technique is validated first on the human brain. The reconstruction results of existing state-of-the art SMS algorithms such as SP-SG, SMS-HSL, SMS-MUSSELS, and ROCK-SPIRiT are also compared to demonstrate the superiority of the proposed method.
2. Methods
2.1. Related Studies
- (1)
- Simultaneous Multi-slice (SMS) Acquisition: An SMS signal is modeled by combining multiple slices:where is the measured aliased SMS signal in k space for the coil, is the desired voxel signal at the slice, is the coil sensitivity map at the coil, is the desired k-space signal at the slice, and is the additive noise. The coil sensitivity map () refers to the sensitivity a particular channel to a specific location in space. To cover the desired field of view (FOV), individual receiver coils are arranged in an array, and their sensitivity maps are designed accordingly. When conducting an MR scan using multiple coils, the resulting images from each channel need to be combined to create a single image. This combination can be achieved by summing the squares of the images (sum of squares) [34,35,36]. For slice unfolding, is estimated using slice-specific coil sensitivity maps in either the image or k-space domain as the solution of an inverse problem in Equation (1).
- (2)
- SMS-GRAPPA: To synthesize a slice of interest on the collapsed k-space data, we calculate a slice-specific SMS kernel using the collapsed and aliasing-free k-space data:where is a vector of k-space data at the m slice acquired from the calibration, is a vector of SMS k-space data emulated from the calibration, and is a matrix that generates the m slice by convolving the k-space data with a series of SMS kernels. To explicitly control the cross-talk artifacts between neighboring slices, the SP-SG is introduced by enforcing signals in other slices to zero while keeping the target slice signals preserved in the k-space domain [15,16,17,18]:Once the SMS kernel is calculated using the inverse problem, each slice is estimated by projecting the SMS k-space data onto the subspace spanned by the SMS kernel.
- (3)
- SMS-HSL: Hankel Subspace Learning for Slice Nulling: To take advantage of low-rank properties for both slice separation and data correlation in k-space, we reorganize the SMS signals as a Hankel-structured matrix, then decompose them into a slice of interest and its complementary slices:where is the complementary slice that combines all slices other than the slice, and is the Hankel-structured noise matrix. is the Hankel operator that produces a Hankel-structured matrix by sliding × patches with frequency encoders, phase encoders, and coils.
Conceptually, a slice of interest is estimated by projecting the aliased SMS signal onto the complementary null space:
The complementary null space passes a slice of interest while nulling those in the other slices. SMS-HSL further exploits the k-space correlation across all coils by imposing a low-rank prior for a slice of interest:
where is the regularization parameter for the Hankel low-rank prior; is the Frobenius norm; and is the nuclear norm, which is defined as the sum of the singular values of the matrix.
2.2. Proposed Method
- (1)
- SMS Signal Model in the k-Parameter Dimension: The signal model for the SMS with parameter dimensions can be represented by:where is the measured aliased SMS signal in k space for the coil, p is the parameter index, is the desired voxel signal at the slice, is the coil sensitivity at the coil, is the desired k-space signal at the slice, and is the additive noise that is modeled to have a complex white Gaussian distribution. To separate the aliased SMS signal, the complementary null space can be learned from the low-resolution reference data. It was observed in a previous study [32] that the idea of estimating a set of vectors in the noise subspace can be extended to separate overlapping slices using a mathematical model in which the null space project enforces the acquired SMS data to lie in the noise subspace only for the neighboring slice; consequently, slices of no interest are filtered out. The null space concept can be applied extensively to MR parameter mapping under the assumption that the predefined null space remains invariant along the parameter dimension. In Figure 1, the slice-specific null space shows a strong dependence on slice encoding rather than on image contrast. To avoid time-consuming calibration along the parameter dimension, the complementary null space is learned from the complementary Hankel-structured SMS signal through singular value decomposition (SVD) by taking right singular vectors corresponding to low singular values from the first TI low-resolution reference datum and projecting all parameter dimensions to separate aliasing SMS signals. Then, the null space projection effectively filters out a slice of no interest while passing through a slice of interest, regardless of the parameter dimension. An illustration is also provided in Figure S1.
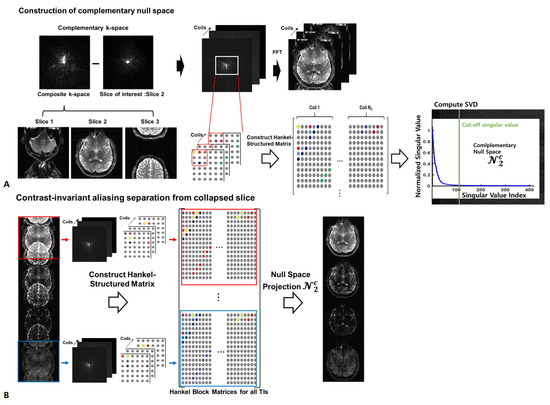 Figure 1. Conceptual illustration of contrast-invariant slice separation based on the complementary null space. (A) Construction of a Hankel-structured matrix from the complementary k space using reference data. Extraction of complementary null space () computed through singular value decomposition on the Hankel-structured matrix, followed by selection of the appropriate singular vectors corresponding to small singular values. (B) Contrast-invariant null space projection to obtain a slice of interest (second slice) by nulling signals derived from the neighboring slices (first and third slices).Given the multi-channel SMS signals in k-p space for parameter mapping, strong correlations among neighboring signals can be selected in the Hankel matrix by using sliding patches ( × ) in k-p space over coils using a Hankel operator:Then, the SMS signal model can be represented in matrix form as:where is the aliased Hankel matrix including all parameter dimensions, is the Hankel matrix, and N is the Hankel-structured noise matrix.
Figure 1. Conceptual illustration of contrast-invariant slice separation based on the complementary null space. (A) Construction of a Hankel-structured matrix from the complementary k space using reference data. Extraction of complementary null space () computed through singular value decomposition on the Hankel-structured matrix, followed by selection of the appropriate singular vectors corresponding to small singular values. (B) Contrast-invariant null space projection to obtain a slice of interest (second slice) by nulling signals derived from the neighboring slices (first and third slices).Given the multi-channel SMS signals in k-p space for parameter mapping, strong correlations among neighboring signals can be selected in the Hankel matrix by using sliding patches ( × ) in k-p space over coils using a Hankel operator:Then, the SMS signal model can be represented in matrix form as:where is the aliased Hankel matrix including all parameter dimensions, is the Hankel matrix, and N is the Hankel-structured noise matrix.
We observe that contrast dynamics slowly vary according to different TIs on the time-invariant background signals, while tissues of interest exist even in the different slices, although their spatial locations differ from one another. The former means that the contrast dynamics of a single-slice image can be represented on the low-dimensional subspace across different TIs while sharing the same spatial basis functions. The latter implies that all slices share similar temporal basis functions, as evidenced by similar contrast dynamics across slices. Figure 2A shows the T1 weighted multi-contrast images that describe a mono-exponential relaxation process. Using principal component analysis, we can express the desired T1-weighted multi-contrast images as the product of spatial coefficient maps and parameter basis functions. For example, the first three principal components are selected as the parameter basis functions computed from each slice and SMS, as shown in Figure 2B, in which the singular values drop quite rapidly by decomposing the information into a significant signal and noise-like subspaces. Interestingly, the parameter basis functions of SMS acquisition are considerably similar to those of slice-by-slice acquisition. Because such a parameter subspace is complementary to the redundancy between slices, its use might provide additional gain by reducing the degrees of freedom in the spatial coefficient maps with predefined parameter basis functions. Accordingly, the Casorati matrix can be represented as a product of the two subspaces:
where is the spatial coefficient, is the temporal basis, and is the number of principal components. Given the SMS signal model that considers signal evolution in the parameter dimension, we can rewrite Equation (11) as:
where is the operator for , and N is the Hankel-structured noise matrix. It is assumed that acquired SMS data along the parameter dimension are followed by an exponential increase in T1 relation times. We hypothesize that this increase can be delineated by linear combination of the temporal basis found by performing singular value decomposition (SVD) of the measured SMS data (Figure S2).
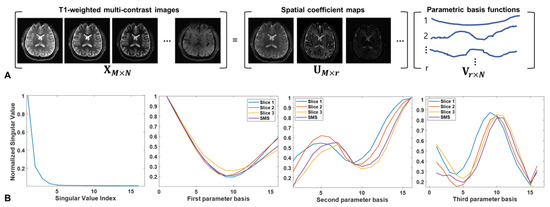
Figure 2.
(A) Casorati matrix representation of T1-weighted multi-contrast images: spatial coefficient maps and corresponding parameter basis functions using principal component analysis. (B) Singular value distribution and the first three parameter basis functions for slice-by-slice and SMS acquisitions. Note that the parameter basis functions of each slice acquisition are similar to those of the SMS acquisition.
- (2)
- Aliasing Separation: Given the considerations mentioned above, we incorporate null space projection () and a low-rank prior () into the single optimization problem with data fidelity. The proposed method is summarized in (Algorithm 1):where the first term is data fidelity, the second term is the reconstruction fidelity, the third term () is the low-rank prior, and is the regularization parameter. The null-space projection errors in the second term are independent of slices, and the low rankness of is independent of slices. Therefore, we can use projection onto convex sets (POCS) to ensure the data fidelity of every iteration.The above equation is reformulated by introducing new auxiliary variables for a low-rank prior under the variable-splitting algorithm [37,38,39]:where is the desired signal (), and is the auxiliary matrix for the slice-specific Hankel-matrix. The unknown variables can be recovered by solving the following minimization problem using the alternating direction method (ADM) [37,38,39]. The first step is to minimize with respect to , which is estimated using a singular-value soft thresholding method:where is the singular value shrinkage function that is defined by:
The second step is to minimize with respect to , which is reduced to a least squares approximation problem by:
Q and U estimations are performed for all simultaneously excited slices. Then data fidelity is enforced, convergence is checked as follows.
where is the predetermined tolerance, and is the maximum number of iterations.
| Algorithm 1: Model-based SMS Reconstruction of MR T1 Mapping |
|
3. Experiments
Experimental studies were performed to evaluate the performance of the proposed reconstruction method using retrospective SMS data was acquired via conventional inversion recovery EPI. To compare image reconstruction algorithms, undersampled data were reconstructed with SP-SG, SMS-MUSSELS, and the proposed method. All reconstruction algorithms were implemented offline using Matlab software (R2017b; MathWorks Inc., Natick, MA, USA). All processes of the proposed algorithm were implemented in the k-space domain.
- (1)
- IR-GE-EPI: Fully sampled brain k-space data were collected by a 3T GE Discovery scanner equipped with a 32-channel receiver head coil using a 2D IR-GE-EPI sequence. The following parameters were used for IR-GE-EPI: FOV = , matrix size = , slice thickness = 2 mm, number of slices = 25, TR/TE = 30,000 ms/40 ms, and 15 IR scans (TI = 50, 250, 450, 650, 850, 1050, 1250, 1450, 1650, 1850, 2050, 2250, 2450, 2650, and 2850 ms). For algorithm validation, our experiments used four slices (3rd, 10th, 17th, and 24th slices) from this dataset with an SMS factor of 4.
- (2)
- IR-SE-EPI: Fully sampled brain k-space data were collected by a 3T Prisma equipped with a 20-channel receiver head coil using a 2D IR-SE-EPI sequence. The following parameters were used for IR-SE-EPI: FOV = , matrix size = , slice thickness = 3 mm, number of slices = 30, TR/TE = 20,000 ms/27 ms, 16 IR scans (TI = 34, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1200, 1400, 1600, 1800, and 2000 ms), and partial Fourier (PF) = 62.5%. To compare the slice unaliasing performance of the current state-of-the-art techniques listed in the Introduction, our experiments used five slices (1st, 7th, 13th, 19th, and 25th slices) from this dataset with ab SMS factor of 5.
- (3)
- Slice-Shuffled SMS IR-SE-EPI: Prospective brain k-space data were collected by a 3T GE Discovery scanner equipped with a 32-channel receiver head coil using a slice-shuffled SMS IR-SE-EPI sequence [40]. The following parameters were used for slice-shuffled SMS IR-EPI: FOV = , matrix size = , slice thickness = 2 mm, number of slices = 75, TR/TE = 3000 ms/25 ms, 13 IR scans (TI = 50 + × TR/N ms, with n = 0, 1, …, 24), specific CAIPI phase shift = FOV/3, in-plane acceleration = 2, and SMS factor = 5.
All datasets were processed offline on a personal computer with 3.3 GHz CPU and 64 GB RAM using MATLAB (The Math Works, Natick, MA, USA). For retrospective SMS experiments, we applied a CAIPI-induced phase shift to the fully sampled k-space data of each slice, then linearly combined all the excited slices. To unalias the collapsed slices, we compared model-based SMS-SHL with SP-SG and SMS-HSL using codes available at https://doi.org/10.5281/zenodo.5149780 and https://misl-skku.github.io/software.html, respectively. The reconstructed images were visualized after combining the multichannel images using the root sum of squares, yielding a single image at each TI. To estimate the T1 values, a nonlinear least-squares fitting method was performed on a pixel-by-pixel basis. Experimental datasets and reconstruction parameters are shown in table in the Supplementary Materials.
For quantitative evaluation, the normalized root mean square error (nRMSE) was used as , where and are the reference and estimated images, respectively, and is the total number of pixels. To clearly visualize the differences between the reconstruction methods, we calculated the relative image error maps using and the T1 error maps using [6,41].
SMS-MUSSELS reconstruction was performed with a kernel size, and Fista iterations (number of iterations = 100, predefined tolerance = 0.3) with a regularization factor of = 1.25. Regularized ROCK-SPIRiT was implemented with a kernel size and the Tikhonov regularization parameter set to for calibration. The regularization parameters for reconstruction were set to default values, and conjugate-gradient (CG) and outer-loop iterations were 5 and 20, respectively. In SP-SG reconstruction, the two-step approach, which involved slice unaliasing followed by in-plane reconstruction, was implemented (SP-SG + GRAPPA). For a fair comparison, a reconstruction kernel of SP-SG, which produces the smallest nRMSE, was manually determined by changing the kernel size from to and set to . Each kernel was estimated using 32 phase-encoding lines in the central region of k space by sweeping Tikhonov regularization parameters from to and set to .
For the model-based SMS-HSL, we used a window size in the Hankel-structured matrix while employing five principal components of the parameter basis functions in the Casorati matrix. The cutoff singular value for null-space selection was set to a maximum of 0.05. The effect of the regularization parameters in Equation (16) on the image reconstruction was investigated by calculating nRMSE between the reference and the estimated proposed model-based SMS-HSL with varying and values. Reconstruction errors were lowest with and and gradually increased as and deviated from the optimal values. and were set to and , respectively. Figure S3 shows the sensitivity of the proposed method to the regularization parameters ( and ) and convergence behaviors with patch size. For SMS-HSL without a magnitude prior, all reconstruction parameters were identical to those of the model-based SMS-HSL.
The calibration region consisted of 32 fully sampled phase-encoding lines in the central k space of the first TI data for retrospective studies. In a prospective study, we acquired fully sampled single-band EPI data for calibration. Representative results from the above datasets validate the effectiveness of the proposed method.
4. Results
4.1. Image Reconstruction: Stepwise Validation
To validate the model-based SMS-HSL, we tested the stepwise performance by generating the following four sets of images with an SMS factor of 4: (1) reference, (2) null space only, (3) null space + low rank, and (4) null space + low rank + parameter subspace model. Figure 3 shows the reconstructed images (TI = 2050 ms) and their corresponding T1 maps. The null-space-only reconstruction creates signal shading by reducing tissue conspicuity, particularly in the aliased location between neighboring slices. Accordingly, the T1 maps obtained using the null-space-only method are corrupted by noise-like artifacts resulting from ill-conditioned problems. Imposing a low-rank prior on the Hankel-structured matrix effectively increases the signal intensity in the collapsed area, leading to improved T1 maps.
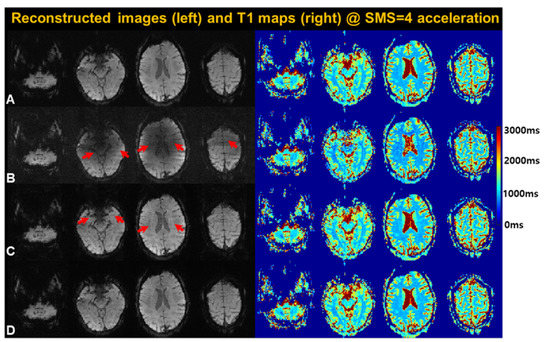
Figure 3.
Stepwise validation: the reconstructed images and the corresponding T1 maps generated using (B) null space only, (C) null space + low rank, and (D) null space + low rank + parameter model compared to the reference (A). Compared to the reference, the null-space-only models with/without priors suffer from signal distortions and noise amplification (red arrows). The proposed method with low-rank and parameter priors ensures that signal estimates lie in a low-dimensional subspace, substantially reducing loss of signal.
However, it exhibits aliasing artifacts in the low-SNR area, as indicated by the red arrows, although not clearly observed in the corresponding T1 maps. In contrast, by imposing a parameter subspace on the Casorati matrix with the Hankel low rank, the proposed method achieves the best reconstruction results by removing the aliasing artifacts, as indicated by the white arrows, yielding more accurate T1 values comparable to those of the reference.
4.2. Retrospective Studies: SMS Simulation
We compared our model-based SMS-HSL with SP-SG and SMS-HSL without magnitude priors with an SMS factor of 5.
Figure 4A,B illustrate the reconstructed images and their corresponding error maps at TI = 34 ms. SP-SG is severely contaminated with noise, particularly in the central region of the brain, owing to the restriction of the interslice leakage constraint. Despite substantially mitigating noise amplification, SMS-HSL without a magnitude prior suffers from blurring and a lack of sharpness. By imposing parameter basis functions, our proposed method suppresses noise while introducing slight image blurring. Note that the complementary properties derived from the Casorati and Hankel matrices are less vulnerable to the aliasing and noise observed in SP-SG and SMS-HSL without magnitude priors. Consistent with the results shown in the error maps, our proposed method presents the lowest nRMSE for all slices.
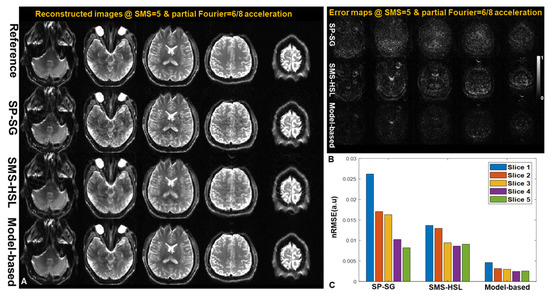
Figure 4.
(A) Images reconstructed using SP-SG, SMS-HSL without a magnitude prior, and the model-based method with an SMS factor of 5. (B) Corresponding error maps. (C) nRMSEs of each slice for the above three methods. SP-SG exhibits noise amplification, especially in the middle of the FOV. SMS-HSL without a magnitude prior yields a minor improvement in the cost of image blurring. The model-based method provides the lowest error with better artifact suppression, both qualitatively and quantitatively.
Figure 5 shows a single exemplary slice at four TIs, which provide different T1 contrasts for subsequent T1 mapping. As indicated by the red arrows, both SP-SG and SMS-HSL without magnitude priors exhibit severe noise and aliasing artifacts in the late TIs because of the SNR penalty around a signal null point for gray- and white-matter tissues, whereas the results from the model-based SMS-HSL are consistent with those of the reference.
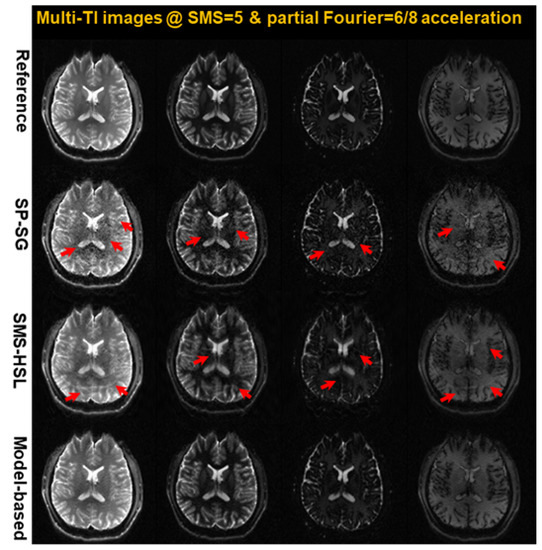
Figure 5.
Images reconstructed at 4 TIs selected among 16 (100 ms, 500 ms, 800 ms, and 1200 ms) using SP-SG, SMS-HSL without a magnitude prior, and model-based methods with an SMS factor of 5 (displaying the third of five slices). As indicated by the red arrows, both SP-SG and SMS-HSL exhibit severe noise and aliasing artifacts. Note that the reconstruction quality of the model-based method is the most robust to the contrast changes, even around a signal-nulling point.
Figure 6A,B show the corresponding T1 values and voxel-wise error maps estimated using different TIs. Because of the high-noise g factor, the T1 map obtained by SP-SG is corrupted around the cerebrospinal fluid (CSF), whereas the edge structures of the T1 maps obtained by SMS-HSL without a magnitude prior tend to be oversmoothed around the boundaries of the brain. In contrast, the T1 values estimated by the proposed method agree well with those estimated by the reference, yielding more accurate T1 values. This trend is pronounced in the magnified images of the fourth slice, as shown in Figure 6C. Table S4 confirms the excellent T1 accuracy and precision for all reconstructed slices compared to other methods.
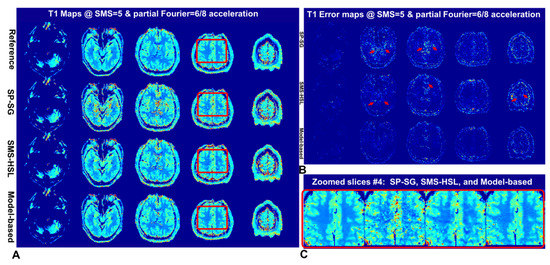
Figure 6.
T1 maps, corresponding T1 error maps, and zoomed-in T1 maps (red box) were generated using SP-SG, SMS-HSL without a magnitude prior, and model-based methods with an SMS factor of 5 (A–C). Note that the results obtained using the model-based method are the most consistent with the reference, although minor T1 errors remain in the region of brain boundaries, whereas the T1 maps of SP-SG and SMS-HSL without magnitude priors are severely amplified by aliasing artifacts and noise. The red arrows shown in the T1 error maps indicate amplified noise and aliasing artifacts, particularly in the second and third slices.
Such an improvement can also be observed in the T1 signal evolution across multiple TIs of representative voxels in the image. Figure 7A,B show the signal intensity curves along the parameter dimension in the white- and gray-matter tissues. The specific regions of interest (ROIs) were manually selected from each tissue within the yellow circle (A: white matter; B: gray matter) by averaging pixel values within a 3 × 3 window. For white matter, SP-SG and SMS-HSL without magnitude priors showed some bias from the actual T1 curve at the late TIs in the opposite direction. For gray matter, SP-SG deviates the most from the reference, while SMS-HSL without a magnitude prior is relatively close to the reference, although there are signal drops in the middle of the T1 curve. In contrast, the proposed method recovers a more accurate signal curve with reduced noise and errors for both white- and gray-matter tissues, especially at the late TIs. Figure 7C shows the corresponding histograms of the T1 values for the central slice presented in Figure 6. We observe that the T1 histogram of SP-SG is significantly lower than those of SMS-HSL without a magnitude prior and model-based approaches around 1000 ms because of the presence of white matter, in addition to exhibiting the highest peak around 3000 ms, demonstrating increased noise amplification in the center of the FOV. However, SMS-HSL without a magnitude prior and model-based approaches agree well with the reference results, indicating that null-space-based slice separation is performed in a stable manner, despite the different reconstruction qualities of SMS-HSL without a magnitude prior and model-based approaches.
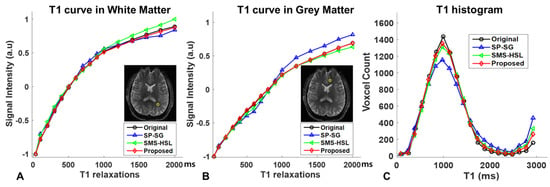
Figure 7.
(A,B) Signal intensity curves of T1 for white− and gray−matter regions were manually selected from each tissue within the yellow circle. The signal curves were calculated as the average of the voxels from the reconstructed images with the reference, SP-SG, SMS-HSL without a magnitude prior, and model-based methods in each ROI. (C) Histograms of the T1 values over the entire brain. Note that the signal intensity curves fitted by the model-based method strictly follow the signal curve from the reference while showing the most similar T1 distribution in the histogram.
Figure 8 shows a comparison between SMS-MUSSELS and model-based SMS-HSL reconstructions with an SMS factor of 3SMS-MUSSEL exhibits structure-aliasing artifacts with noise amplification, whereas model-based SMS-HSL can address these issues in the reconstructed images and T1 maps. There are two reasons for this result. For slice separation, the model-based SMS-HSL further generalizes multiple null-space vectors by flexibly controlling the signal and null-space vectors, unlike SMS-MUSSELS, which uses a main eigenvector for sensitivity estimation [42]. Additionally, the higher performance of the model-based SMS-HSL suggests that the estimation of the spatial coefficient maps in the Casorati matrix can complement the low rankness in the Hankel-structured matrix by reducing the number of degrees of freedom during signal recovery.
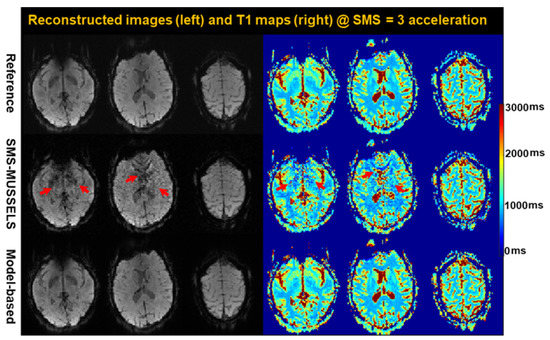
Figure 8.
Reconstructed images and the corresponding T1 maps using the reference, SMS-MUSSELS, and model-based method with an SMS factor of 3. Note that SMS-MUSSELS produces structured aliasing and amplified noises, particularly in the second slice (red arrows), owing to the inaccurate estimation of coil sensitivity maps that rely on a main eigenvector, whereas the model-based method mitigates these issues, improving the performance of slice unfolding resulting from the use of multiple generalized eigenvectors.
4.3. Prospective Studies: Experimental Validation
Figure 9 shows the resulting images obtained using SP-SG, ROCK-SPIRiT, SMS-HSL without a magnitude prior, and the proposed model-based SMS-HSL method on undersampled SMS data at 10-fold acceleration. The SP-SG-reconstructed images show significant noise amplification in the third slices and severe aliasing artifacts in the fourth slices. The regularized ROCK-SPIRiT method reduced the noises compared to SP-SG while maintaining the aliasing artifacts. SMS-HSL without a magnitude prior substantially reduced the noise but did not eliminate aliasing artifacts. Note that compared with other methods, the proposed model-based method exhibits better image quality, reducing aliasing artifacts, as indicated by the red arrows.
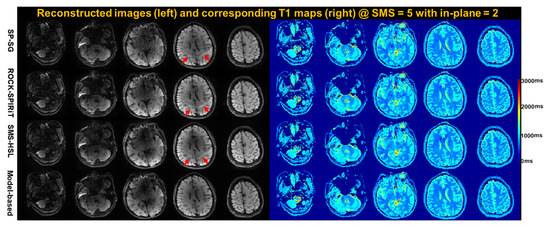
Figure 9.
Images and corresponding T1 maps reconstructed using SP-SG, regularized ROCK-SPIRiT, SMS-HSL without a magnitude prior, and the proposed model-based method with an SMS factor of 5 and an in-plane GRAPPA factor of 2. SP-SG images suffer from noise in the third slice. Additionally, the red arrows indicate the presence of aliasing artifacts in the fourth slice. Regularized ROCK-SPIRiT reduced the noise compared to SP-SG but maintained aliasing artifacts (red arrows). On the other hand, SMS-HSL substantially mitigated aliasing artifacts (red arrows) and noise. Note that the proposed method shows better performance in suppressing aliasing artifacts and noise while producing more robust T1 estimates compared to the other methods.
5. Discussion and Conclusions
In this work, we describe a novel SMS T1-mapping technique that combines Hankel subspace learning with a parameter model for slice separation. In contrast to previously proposed SMS reconstruction methods that only take advantage of slice-specific encoding information, the proposed method incorporates a parameter basis directly from the aliased slices into the SMS-HSL reconstruction framework to enable improved slice separation and more accurate parameter fitting under the assumption that the parameter variations for all inversion times are invariant across slices. The shared parameter subspace provides prior information in addition to the existing slice-specific null-space constraint, outperforming the state-of-the-art methods and increasing accelerations with good accuracy and precision in image reconstruction and T1 mapping.
The proposed model-based SMS-HSL uses parameter redundancy across slices to estimate the parameter subspace of the Casorati matrix, which results in a simplified problem that can be solved efficiently by reducing the number of degrees of freedom. The parameter subspace is estimated from the observed aliased slice under the assumption that all slices share the same parameter subspace. As shown in [32], conventional SMS-HSL suffers from severe contrast loss without a magnitude prior during slice separation because of the sharing of null-space information between slices. In contrast, the parameter subspace is complementary to the slice-specific null space and can improve the SMS-HSL in reconstruction and T1 mapping. Additionally, the proposed framework can be extended to jointly estimate the spatial and parameter bases for each slice using a power factorization algorithm [43,44], in which and are estimated in an alternating manner.
In the case of acceleration along both the slice- and phase-encoding directions, the proposed method sequentially reconstructs unaliased slices, followed by in-plane GRAPPA reconstruction. The proposed algorithm, which exploits rank deficiency using a Hankel-structured matrix and temporal basis priors, can be applied to data obtained with an SMS acceleration only and in combination with in-plane undersampling. This is evidenced by Figure 9, where among the methods examined for image reconstruction from prospectively undersampled data with both SMS and in-plane accelerations, the proposed model-based technique presents relatively higher performance in aliasing separation and noise suppression.
The proposed reconstruction method was implemented using an ADM algorithm that typically requires 30 iterations to converge, although its computation time depends on the data dimension. For each iteration, the algorithm involves two matrix inversions and SVD calculations for each variable update. The computational complexity depends on several factors, including the number of parameter dimensions, the patch size, the number of coils, the number of stacked patches, the effective rank, and the number of simultaneously excited slices:
where is the total number of iterations, is the number of slices, is the number of parameters, × is the patche size, r is the rank, and is the number of coils. To address the computational challenges associated with an increasing number of coils and larger patch size in the Hankel operation, it becomes impractical to perform singular-value decomposition at each iteration while minimizing the nuclear norm in Equation (16). In order to overcome this computational problem, we employed a matrix factorization method [38,39], implementing a conjugate gradient algorithm for matrix inversion in Equation (17) and the precomputed inversion of in Equation (17) [43,44]. The computational complexity of our method per iteration is slightly higher than that of SMS-HSL in the presence of the parameter basis model. In our reconstruction, the computation times of SMS-HSL and our method were 15 min and 28 min, respectively, for all T1-weighted images. However, our codes were implemented in MATLAB and were not optimized for speed. Accordingly, we believe that there are several approaches to mitigate the computational burden, such as channel compression in the preprocessing step and element-wise multiplication in the image space rather than convolution in k space for the null space projection in Equation (17), making our reconstruction framework more practical.
The proposed model-based SMS-HSL estimates the slice-specific null space from a separate calibration scan. It potentially yields signal inconsistencies between the calibrated and “true” null spaces in the presence of either subject motions or magnetic field drifts, leading to quantitative errors with cross-talk artifacts between the neighboring slices. To mitigate potential mismatches, we believe that the calibration process can be incorporated into our proposed framework by controlling the EPI blips without loss of generality. Similar to regular undersampling of the dynamic parallel MRI with shifts in the k-space grids across time [45], the sampling pattern is temporally interleaved with different slice encodings across TIs to simultaneously provide complementary slice encoding and k-space whole coverage, and inverse Fourier transform is performed along the slice direction for null-space estimation. Accordingly, integrated calibration in echo-planar trajectories can further help address this limitation.
In conclusion, this work introduces a model-based SMS-HSL by exploiting a data-driven parameter model for T1 quantification, utilizing the combined properties of Hankel- and Casorati-structured matrices. To resolve the SMS reconstruction, we employ a complementary null space based on a time-invariant slice-specific null-space operator. This null-space operator preserves the slice of interest while nulling the signal from the other slices. Furthermore, the proposed framework can be extended to jointly estimate the spatial and parameter bases for each slice in Equation (11), resulting in a reduction in the degrees of freedom during the reconstruction process. Thus, we incorporate null-space projection and low-rank priors into a single SMS framework in Equation (13). The experimental results show that even when subjected to high SMS acceleration, the proposed method consistently outperforms SP-SG, SMS-MUSSELS, and ROCK-SPIRiT. We successfully demonstrated the effectiveness of accelerated SMS T1 quantification for aliasing separation.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math11132963/s1, Figure S1: Conceptual illustration of contrast invariant slice separation based on the complementary null space, including; Figure S2: Parameter basis functions V can be estimated by performing SVD on the acquired SMS data, followed by taking the right singular vectors; Figure S3: Sensitivity of the regularization parameters in the proposed model-based SMS-HSL; Table S1: Experimental datasets; Table S2: Retrospective studies using reconstruction parameters (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8); Table S3: Prospective studies using reconstruction parameters (Figure 9); Table S4: T1 relaxation times (ms, ± mean SD) of the brain white matter (ROI) in the result of Figure 6; Table S5: Model-based algorithm performance table.
Author Contributions
Conceptualization, S.K. and J.-H.H.; methodology, S.K.; software, S.K. and H.W.; validation, S.K. and H.W.; writing—original draft preparation, S.K. and J.-H.H.; supervision, J.-H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2023-RS-2022-00156225) and under the ICT Creative Consilience program (IITP-2023-2020-0-01819) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).
Institutional Review Board Statement
This study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Institutional Review Board of Sungkyunkwan University (SKKU 2018-05-005).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Additional data are available from the first/corresponding author upon reasonable request.
Acknowledgments
The authors acknowledge Prof. Suhyung Park and Prof. Jaeseok Park for helpful discussions and guidance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Warntjes, J.; Leinhard, O.D.; West, J.; Lundberg, P. Rapid magnetic resonance quantification on the brain: Optimization for clinical usage. Magn. Reson. Med. 2008, 60, 320–329. [Google Scholar] [CrossRef] [PubMed]
- Alexander, A.L.; Hurley, S.A.; Samsonov, A.A.; Adluru, N.; Hosseinbor, A.P.; Mossahebi, P.; Tropm, D.P.; Zakszewski, E.; Field, A.S. Characterization of cerebral white matter properties using quantitative magnetic resonance imaging stains. Brain Connect. 2011, 1, 423–446. [Google Scholar] [CrossRef] [PubMed]
- Barra, J.K.; Gudmundson, E.; Stikov, N.; Etezadi-Amoli, M.; Stoica, P.; Nishimura, D.G. A robust methodology for in vivo T1 mapping. Magn. Reson. Med. 2011, 64, 1057–1067. [Google Scholar] [CrossRef] [PubMed]
- Griswold, M.A.; Jakob, P.M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef]
- Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger, P. SENSE: Sensitivity encoding for fast mri. Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar] [CrossRef]
- Lee, D.; Jin, K.H.; Kim, Y.E.; Park, S.-H.; Ye, J.C. Acceleration of mr parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn. Reson. Med. 2016, 76, 1848–1864. [Google Scholar] [CrossRef]
- Doneva, M.; Bornert, P.; Eggers, H.; Stehning, C.; Senegas, J.; Mertins, A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med. 2010, 64, 1114–1120. [Google Scholar] [CrossRef]
- Block, K.T.; Uecker, M.; Frahm, J. Model-based iterative reconstruction for radial fast spin-echo mri. IEEE Trans. Med. Imaging 2009, 28, 1759–1769. [Google Scholar] [CrossRef]
- Sumpf, T.; Uecker, M.; Boretius, S.; Frahm, J. Model-based nonlinear inverse reconstruction for T2 mapping using higly undersampled spin-echo mri. J. Magn. Reson. Imaging 2011, 34, 420–428. [Google Scholar] [CrossRef]
- Peng, X.; Ying, L.; Liu, Y.; Yuan, J.; Liu, X.; Liang, D. Accelerated exponential parameterization of T2 relaxation woth model-driven low rank and sparsity priors (MORASA). Magn. Reson. Med. 2016, 76, 1865–1878. [Google Scholar] [CrossRef]
- Larkman, D.J.; Hajnal, J.V.; Herlihy, A.H.; Coutts, G.A.; Young, I.R.; Ehnholm, G. Use of multicoil arrays for separation of signal from multiple slices imultaneously excited. J. Magn. Reson. Imaging 2001, 13, 313–317. [Google Scholar] [CrossRef] [PubMed]
- Moeller, S.; Yacoub, E.; Olman, C.A.; Auerbach, E.; Strupp, J.; Harel, N.; Uğurbil, K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fmri. Magn. Reson. Med. 2010, 63, 1144–1153. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, D.A.; Moeller, S.; Smith, S.M.; Auerbach, E.; Ramanna, S.; Gunther, M.; Glasser, M.F.; Miller, K.L.; Uğurbil, K.; Yacoub, E. Multiplexed echo planar imaging for sub-second whole brain fmri and fast diffusion imaging. PLoS ONE 2010, 5, e15710. [Google Scholar] [CrossRef] [PubMed]
- Setsompop, K.; Gagoski, B.A.; Polimeni, J.R.; Witzel, T.; Wedeen, V.J.; Wald, L.L. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med. 2012, 67, 1210–1224. [Google Scholar] [CrossRef]
- Cauley, S.F.; Polimeni, J.R.; Bhat, H.; Wald, L.L.; Setsompop, K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn. Reson. Med. 2014, 72, 93–102. [Google Scholar] [CrossRef]
- HashemizadehKolowri, S.K.; Chen, R.-R.; Adluru, G.; Yian, L.; Dibella, E.V. Coil-combined split slice-GRAPPA for simultaneous multi-slice diffusion MRI. Magn. Reson. Imaging 2020, 66, 9–32. [Google Scholar] [CrossRef]
- HashemizadehKolowri, S.K.; Chen, R.-R.; Adluru, G.; Dean, D.C.; Wilde, E.A.; Alexander, A.L.; Dibella, E.V. Simultaneous multi-slice image reconstruction using regularized image domain split slice-GRAPPA for diffusion MRI. Med. Image Anal. 2021, 70, 102000. [Google Scholar] [CrossRef]
- Moeller, S.; Pisharady, K.P.; Andersson, J.; Akcakaya, M.; Harel, N.M.; Wu, X.; Yacoub, E.; Lenglet, C.; Ugurbil, K. Diffusion imaging in the post HCP Era. J. Magn. Reson. Imaging 2021, 54, 36–57. [Google Scholar] [CrossRef]
- Lustig, M.; Pauly, J.M. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 2010, 64, 457–471. [Google Scholar] [CrossRef]
- Demirel, O.B.; Weingartner, S.; Moeller, S.; Akcakaya, M. Improved simultaneous multislice cardiac mri using readout concatenated k-space spirit (ROCK-SPIRiT). Magn. Reson. Med. 2021, 85, 3035–3048. [Google Scholar] [CrossRef]
- Dai, E.; Mani, M.; McNab, J.A. Multi-band multi-shot diffusion MRI reconstruction with joint usage of structured low-rank constraints and explicit phase mapping. Magn. Reson. Med. 2023, 89, 95–111. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Park, S. Simultaneous Multislice Brain MRI T1 Mapping with Improved Low-Rank Modeling. Tomography 2021, 7, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Chen, L.; Beckett, A.; Feinberg, D.A. Virtual slice concept for improved simultaneous multi-slice MRI employing an extended leakage constraint. Magn. Reson. Med. 2019, 82, 377–386. [Google Scholar] [CrossRef] [PubMed]
- Bilgic, B.; Chatnuntawech, I.; Manhard, M.K.; Tian, Q.; Liao, C.; Iyer, S.S.; Cauley, S.F.; Huang, S.Y.; Polimeni, J.R.; Wald, L.L.; et al. Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction. Magn. Reson. Med. 2019, 82, 1343–1358. [Google Scholar] [CrossRef] [PubMed]
- Mani, M.; Jacob, M.; McKinnon, G.; Yang, B.; Rutt, B.; Kerr, A.; Magnotta, V. SMS MUSSELS: A navigator-free reconstruction for simultaneous multi-slice-accelerated multishot diffusion weighted imaging. Magn. Reson. Med. 2020, 83, 154–169. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, C.; Cao, X.; Poser, B.A.; Xu, Z.; Lo, W.-C.; Wen, M.; Cho, J.; Tian, Q.; Wang, Y.; et al. 3D-EPI blip-up/down acquisition (BUDA) with CAIPI and joint Hankel structured low-rank reconstruction for rapid distortion-free high-resolution T2* mapping. Magn. Reson. Med. 2023, 89, 1961–1974. [Google Scholar] [CrossRef]
- Kim, T.H.; Haldar, J.P. SMS-LORAKS: Calibrationless simultaneous multislice mri using low-rank matrix modeling. In Proceedings of the 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), Brooklyn, NY, USA, 16–19 April 2015; pp. 323–326. [Google Scholar]
- Haldar, J.P. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans. Med. Imaging 2014, 33, 668–681. [Google Scholar] [CrossRef]
- Zhu, K.; Dougherty, R.F.; Wu, H.; Middione, M.J.; Takahashi, A.M.; Zhang, T.; Pauly, J.M.; Kerr, A.B. Hybrid-space SENSE reconstruction for simultaneous multi-sliceMRI. IEEE Trans. Med. Imaging 2016, 35, 1824–1836. [Google Scholar] [CrossRef]
- Nencka, A.S.; Arpinar, V.E.; Bhave, S.; Yang, B.; Banerjee, S.; McCrea, M.; Mickevicius, N.J.; Muftuler, L.T.; Koch, K.M. Split-slice training and hyperparameter tuning of RAKI networks for simultaneous multi-slice reconstruction. Magn. Reson. Med. 2021, 85, 3272–3280. [Google Scholar] [CrossRef]
- Li, S.; Wu, J.; Ma, L.; Cai, S.; Cai, C. A simultaneous multi-slice T2 mapping framework based on overlapping-echo detachment planar imaging and deep learning reconstruction. Magn. Reson. Med. 2022, 87, 2239–2253. [Google Scholar] [CrossRef]
- Park, S.; Park, J. SMS-HSL: Simultaneous multislice aliasing separation exploiting hankel subspace learning. Magn. Reson. Med. 2017, 78, 1392–1404. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Haldar, J.P.; Christodoulou, A.G.; Liang, Z.P. Image reconstruction from highly undersampled (k,t)-space data with joint partial separability and sparsity constraints. IEEE. Trans. Med. Imag. 2012, 31, 1809–1820. [Google Scholar] [CrossRef] [PubMed]
- Roemer, P.B.; Edelstein, W.A.; Hayes, C.E.; Souza, S.P.; Mueller, O.M. The NMR phased array. Magn. Reson. Med. 1990, 16, 192–225. [Google Scholar] [CrossRef]
- Deshmane, A.; Gulani, V.; Griswold, M.A.; Seiberlich, N. Parallel MR imaging. J. Magn. Reson. Imaging 2012, 36, 55–72. [Google Scholar] [CrossRef]
- Hamilton, J.; Franson, D.; Seiberlich, N. Recent advances in parallel imaging for, MR. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 101, 75–95. [Google Scholar] [CrossRef] [PubMed]
- Ramani, S.; Fessler, J. Parallel MR image reconstruction using augmented Lagrangian methods. IEEE Trans. Med. Imaging 2011, 30, 694–706. [Google Scholar] [CrossRef]
- Wen, Z.; Yin, W.; Zhang, Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math. Prog. Comp. 2012, 4, 333–361. [Google Scholar] [CrossRef]
- Shen, Y.; Wen, Z.; Zhang, Y. Augmented lagrangian alternating direction method for matrix separation based on low-rank factorization. Optim. Methods Softw. 2014, 29, 239–263. [Google Scholar] [CrossRef]
- Wu, H.; Dougherty, R.; Kerr, A.B.; Zhu, K.; Middione, M.J.; Mezer, A. Fast t1 mapping using slice-shuffled simultaneous multi-slice inversion recovery EPI. In Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, ON, Canada, 30 May–5 June 2015; Volume 0440. [Google Scholar]
- Elahi, S.; Kaleem, M.; Omer, H. Compressively sampled MR image reconstruction using generalized thresholding iterative algorithm. J. Magn. Reson. 2018, 286, 91–98. [Google Scholar] [CrossRef]
- Uecker, M.; Lai, P.; Murphy, M.J.; Virtue, P.; Elad, M.; Pauly, J.M.; Vasanawala, S.S.; Lustig, M. ESPIRiT—An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014, 71, 990–1001. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Process 2010, 19, 2345–2356. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, J.; Yin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imag. Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Zhu, K.; Kerr, A.; Pauly, J.M. Autocalibrating CAIPIRINHA: Reformulating CAIPIRINHA as a 3D problem. In Proceedings of the 20rd Annual Meeting of ISMRM, Melbourne, Australia, 5–11 May 2012; Volume 0518. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).