Calculation of the Electrostatic Field of a Circular Cylinder with a Slot by the Wiener–Hopf Method

Abstract

The paper presents an exact solution to the internal boundary value problem of the field distribution in an electrostatic lens formed by two identical semi-infinite coaxially located round cylinders separated by a slit of finite width and located inside an infinite outer cylinder. The problem is reduced to a system of singular Wiener–Hopf integral equations, which is further solved by the Wiener–Hopf method using factorized Bessel functions. Solutions to the problem for each region inside the infinite outer cylinder are presented as exponentially converging series in terms of eigenfunctions and eigenvalues. Using the obtained formulas, a numerical calculation of the axial distribution of the potential of a two-electrode lens was made for various values of the radii of the outer and inner cylinders.

1. Introduction

Electrostatic mirrors have become indispensable structural elements of modern scientific and technological instrumentation, which determine the quality of focusing of such instruments as time-of-flight mass spectrometers and electron microscopes. In this regard, electrostatic mirrors of rotational symmetry are of particular interest, since they perform stigmatic focusing of electron beams, i.e., create the correct electron optical image of the object. However, the most studied and highly demanded in practical implementation are the designs of mirrors constructed as sets of coaxial circular cylinders. The advantage of cylindrical electrodes is the possibility of shielding the beam from scattered electric fields. For this reason, it is expedient to solve the internal boundary value problem for such structures rather than the external one. In works [1,2], devoted to the study of the focusing properties of electrostatic mirrors with cylindrical electrodes, the calculation of the field was performed under the assumption that the width of the gap between the electrodes is infinitely small. However, practical application of such mirrors in high-voltage electron microscopy [3,4] imposes high requirements on the width of the gap between the electrodes in terms of ensuring electrostatic strength at high field intensity. However, with an increase in the width of the inter-electrode gap, the effect of scattered electric fields on the quality of electron beam focusing increases. The aim of the work is to use the Wiener–Hopf (WH) method to solve the problem of field distribution in an electrostatic lens formed by two identical semi-infinite coaxially located circular cylinders, separated by gaps (slits) of finite width and located inside an infinite outer cylinder. Such an electrode design makes it possible to simultaneously provide electrostatic strength at high field intensities and the screening of the electron beam from external electric fields at large gap widths between the internal electrodes. It should be noted that it was N.N. Lebedev [5] who first used the WH method to solve the boundary value problem of the electrostatic field of an electron lens consisting of a semi-infinite circular cylinder coaxially located inside an infinite cylinder, which is a key for solving a number of other problems. However, a well-known powerful WH method has not been used since then even to calculate the field of the simplest system of electrodes with two semi-infinite cylinders, not to mention the case when the finite width between the electrodes is taken into account. The studied boundary value problem, as a rule, is reduced to solving pairwise integral equations with kernels of Bessel functions, which were studied by L.A. Weinstein [6], Titchmarsh [7], Noble [8], Erdelyi and Sneddon [9], and others.

A comprehensive review of the historical development of pairwise integral equations is given by Eswaran [10] and Sneddon [11], where they are reduced to a system of algebraic equations or to a Fredholm-type equation. The methodology for solving paired integral equations is considered in detail in the works of N.N. Lebedev [5], V.A. Fock, P.L. Kapitsa, and L.A. Weinstein [12].

In these works, pairwise integral equations describing the problem of a conducting hollow cylinder of finite length were reduced to the Fredholm integral equation of the second kind [13] or solved by the variational method when the length of the cylinder is large enough compared to its diameter [14,15]. However, the proposed methods are very cumbersome and require a large amount of computational time.

It is known that the WH method [6,8,10,16,17,18,19], like the Riemann method, is a rigorous method for solving pairwise singular integral equations (SIEs) for semi-infinite structures whose solutions automatically satisfy the additional Meixner condition or the so-called condition on a sharp edge, which determines the uniqueness of the solution to the problem as well as the behavior of the field at small distances from the sharp edge. Note that, as a rule, this condition is not mentioned in approximate methods. It should be recalled that the classical WH method was previously used mainly for solving dynamic problems, for example, in the theory of electromagnetic wave diffraction.

2. Statement of the Problem

Let us consider a lens consisting of two thin semi-infinite cylinders of radius a with a common axis z and given potentials $V_1$ and $V_2$, coaxially located towards each other inside a shielding infinite cylinder of radius b, which is at zero potential (Figure 1).

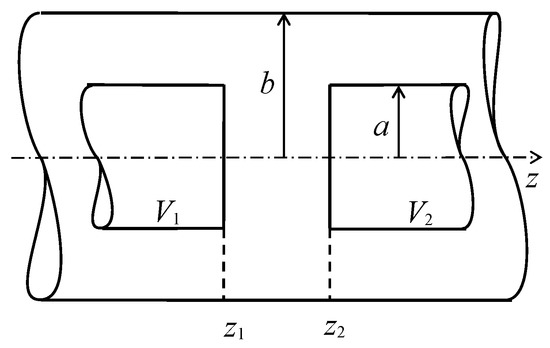
Figure 1. Electrostatic lens with a slit ($z_2-z_1$) of finite width.

The desired potential $\phi (r,z)$ satisfies the Laplace equation

$$△\phi (r,z)=0$$

and boundary conditions

$$\begin{array}{cc}& \phi (b,z)=0,\phi (a,z<a)=V_1,\phi (a,z>a)=V_2,\end{array}$$

(1)

$$\begin{array}{cc}& \phi (a-0,z)-\phi (a+0,z)=0,\end{array}$$

(2)

$$\begin{array}{cc}& \left({\displaystyle \frac{\partial }{\partial r}}\phi (r-0,z)-{\displaystyle \frac{\partial }{\partial r}}\phi (r+0,z)\right){|}_{r=a}=0\mathrm{at}{z}_1<z<z_2,\\ & \phi (a\pm 0)=\underset{0<ϵ\to 0}{lim}\phi (a\pm ϵ).\end{array}$$

(3)

Let us introduce the notations

$$\begin{array}{c}L(r,w)=\frac{\pi }{2ln\frac{a}{b}{\mathrm{J}}_0\left(vb\right)}\left\{\begin{array}{c}{\mathrm{J}}_0\left(vr\right)(a,b),\mathrm{at}0\le r\le a;\hfill \\ {\mathrm{J}}_0\left(va\right)(r,b),\mathrm{at}a\le r\le b,\hfill \end{array}\right.\\ (r,b)={\mathrm{N}}_0\left(vr\right){\mathrm{J}}_0\left(vb\right)-{\mathrm{N}}_0\left(vb\right){\mathrm{J}}_0\left(vr\right),\hfill \\ v=\sqrt{k^2-w^2},\mathrm{Im}v>0,\end{array}$$

(4)

where ${\mathrm{J}}_0\left(vr\right)$, ${\mathrm{N}}_0\left(vr\right)$ are zero-order Bessel and Neumann functions, and $(r,b)$ is a combination of Bessel functions, and search for a solution in the form

$$\phi (r,z)=\frac{1}{2\pi i}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{e}^{iwz}L(r,w)\frac{F\left(w\right)}{L(a,w)}dw$$

(5)

with respect to the desired function $F\left(w\right)$.

For electrostatic problems, k should be assumed to have a vanishingly small positive imaginary part, and we transfer to the limit $\left|k\right|\to 0$ only in finite expressions.

The cuts of the function $L(r,w)$ in (4) are located in the plane of the complex variable w on the curves $\mathrm{Im}v=0$.

Due to the properties of the Bessel functions and boundary conditions (1) and (3), we obtain a system of singular integral equations (SIE)

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2\pi i}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{e}^{iwz}F\left(w\right)dw=V_1,z\le z_1,\end{array}$$

(6)

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2\pi i}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{e}^{iwz}F\left(w\right)dw=V_2,z\ge z_2,\end{array}$$

(7)

$$\begin{array}{c}\hfill {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{e}^{iwz}{L}^{-1}(a,w)F\left(w\right)dw=0,z_1<z<z_2.\end{array}$$

(8)

The last, Equation (8), can be obtained from the boundary condition (3) due to the property of the Bessel functions

$$\frac{\partial }{\partial r}\left(\frac{{\mathrm{J}}_0\left(vr\right)(a,b)}{{\mathrm{J}}_0\left(vb\right)}-\frac{{\mathrm{J}}_0\left(va\right)(r,b)}{{\mathrm{J}}_0\left(vb\right)}\right){|}_{r=a}\equiv -\frac{2}{\pi a}.$$

3. Solution of a System of Integral Equations

The solution of SIE (6)–(8) is constructed by the Wiener–Hopf method in the form [20]

$$\begin{array}{c}\hfill F\left(w\right)=L_{-}(a,w)\left(A_{+}^1\left(w\right)+B_{+}^1\left(w\right)\right)e^{-iw{z}_1}+\\ \hfill +L_{+}(a,w)\left(A_{-}^2\left(w\right)+B_{-}^2\left(w\right)\right)e^{-iw{z}_2}.\end{array}$$

(9)

Here, the subscripts ‘+’ and ‘−’ denote holomorphic functions in the upper half-plane (UHP) $\mathrm{Im}w\ge 0$, and lower half-plane (LHP) $\mathrm{Im}w\le 0$, respectively, which do not have zeros and poles there, and the functions $L_{+}$ and $L_{-}$ are factorized functions, $L=L_{-}·L_{+}$ [6,8].

It should be noted that for the SIE solution to be unique, the desired function $F\left(w\right)$ must satisfy the Meixner condition [21,22] on the edge or the so-called sharp edge condition ($E_z,E_r\sim {\rho }^{-1/2},E_{\varphi }\sim \sqrt{\rho }$), which is equivalent to the behavior of the function $F\left(\right|w\left|\right)\sim {\left|w\right|}^{-3/2}$ at infinity $\left|w\right|\to \infty$.

For convenience, we introduce the notations for the eigenvalues for each region inside the infinite tube of radius b: $\left(a\right)$, $\left(b\right)$, $\left(c\right)$. The regions $\left(a\right)$ and $\left(b\right)$ correspond to the regions inside and outside the semi-infinite circular cylinder of radius a, respectively. The region $0<r<b$ and $z_1<z<z_2$ is denoted as $\left(c\right)$. Further, the superscripts of the eigenvalues will denote the corresponding region. Note that $L_{+}$ has zeros at the points $-w_n^a,$ $-w_n^c$ and poles in $-w_n^b$ ($n=1,2,\dots$) in the LHP of the complex variable w. The function $L_{-}$ has the same zeros and poles only in the UHP, due to the property of factorized functions:

$$L_{+}(a,-w)=L_{-}(a,w).$$

(10)

The roots of the functions ${\mathrm{J}}_0\left(va\right)$, ${\mathrm{J}}_0\left(vb\right),$ and $(a,b)$ with respect to the variable v in (4) are $v_n^a={\gamma }_n/a;$ $v_n^b={\gamma }_n/b$ and $v_n^c={\delta }_n/(b-a)$ ($n=1,2,\dots$), where ${\gamma }_n$ and ${\delta }_n$ denote the roots of the equations with respect to arguments $\gamma$ and $\delta$ [23]:

$$\begin{array}{cc}& {\mathrm{J}}_0\left(\gamma \right)=0,\\ & {\mathrm{N}}_0\left(\frac{a\delta }{b-a}\right){\mathrm{J}}_0\left(\frac{b\delta }{b-a}\right)-{\mathrm{N}}_0\left(\frac{b\delta }{b-a}\right){\mathrm{J}}_0\left(\frac{a\delta }{b-a}\right)=0.\end{array}$$

Equation (6), due to the function $A_{+}^1$, will satisfy the solution if the function $F\left(w\right)$ is holomorphic everywhere in LHP ($\mathrm{Im}w\le 0)$ except for a single simple pole at the point $w=-k$ and uniformly tends to zero as $\left|w\right|\to \infty$. Therefore, the remaining poles contained in the LHP at the points $w=-w_n^b(n=1,2,\dots )$ of the function $L_{+}$ must be compensated using the function $B_{+}^1\left(w\right)$.

To find a solution to Equation (7), we require the same conditions for the functions $A_{-}^2\left(w\right)$ and $B_{-}^2\left(w\right)$ in the UHP ($\mathrm{Im}w\ge 0)$.

Using the theory of residues to calculate the integrals (6) and (7), as well as compensating all singular points inside the integration contour (IC), except for the poles $\pm k$, we obtain the desired functions in (9):

$$\left\{\begin{array}{c}{A}_{+}^1\left(w\right)=-{\displaystyle \frac{V_1}{w+k}},\hfill \\ \\ A_{-}^2\left(w\right)={\displaystyle \frac{V_2}{w-k}}\left(0<\mathrm{Im}\left(k\right),\left|k\right|\to 0\right),\hfill \end{array}\right.$$

(11)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle B_{+}^1\left(w\right)=-{\displaystyle \sum _{n=1}^{\infty }}\frac{e^{i{w}_n^b(z_2-z_1)}}{(w+w_n^b)}\frac{L_{+}^{*}(a,-w_n^b)}{L_{-}(a,-w_n^b)}\left(A_{-}^2(-w_n^b)+B_{-}^2(-w_n^b)\right),}\hfill \\ \\ {\displaystyle B_{-}^2\left(w\right)=-{\displaystyle \sum _{n=1}^{\infty }}\frac{e^{i{w}_n^b(z_2-z_1)}}{(w-w_n^b)}\frac{L_{-}^{*}(a,w_n^b)}{L_{+}(a,w_n^b)}\left(A_{+}^1\left(w_n^b\right)+B_{+}^1\left(w_n^b\right)\right),}\hfill \end{array}\right.\end{array}$$

(12)

where

$$\begin{array}{c}\hfill L_{+}^{*}(a,-w_n^b)=\underset{w\to -w_n^b}{lim}(w+w_n^b)L_{+}(a,w)=\\ \hfill -\underset{w\to w_n^b}{lim}(w-w_n^b)L_{-}(a,w)=-L_{-}^{*}(a,w_n^b).\end{array}$$

The validity of the obtained solution of SIE (6)–(8) can be checked directly by substituting it into the Equations (6)–(8) and closing the IC in the LHP or UHP w, according to the Jordan lemma, then calculating the residues at all poles of the integrand inside this IC.

It should be noted that the resulting solution (9) automatically satisfies (8), since the integrand turns out to be holomorphic inside the corresponding IC.

Solution of a System of Functional Equations

The exact solution of the system of functional Equation (12) can be represented in the form of rapidly convergent infinite series

$$\begin{array}{c}{B}_{+}^1\left(w\right)=-V_2({\displaystyle \sum _{n_1}^{\infty }}\frac{g_{n_1}}{(w+w_{n_1}^b)l^{\left(1\right)}}+{\displaystyle \sum _{n_1,n_2,n_3}^{\infty }}\frac{g_{n_1}{g}_{n_2}{g}_{n_3}}{(w+w_{n_3}^b)l^{\left(3\right)}}+\dots \\ +{\displaystyle \sum _{n_1,\dots ,n_{2i-1}}^{\infty }}\frac{{\prod }_{k=1}^{2i-1}{g}_k}{(w+w_{2i-1}^b)l^{(2i-1)}})-V_1({\displaystyle \sum _{n_1,n_2}^{\infty }}\frac{g_{n_1}{g}_{n_2}}{(w+w_{n_2}^b)l^{\left(2\right)}}+\\ {\displaystyle \sum _{n_1,n_2,n_3,n_4}^{\infty }}\frac{g_{n_1}{g}_{n_2}{g}_{n_3}{g}_{n_4}}{(w+w_{n_4}^b)l^{\left(4\right)}}+\dots {\displaystyle \sum _{n_1,\dots ,n_{2i}}^{\infty }}\frac{{\prod }_{k=1}^{2i}{g}_k}{(w+w_{2i}^b)l^{\left(2i\right)}}),\end{array}$$

(13)

$$\begin{array}{c}{B}_{-}^2\left(w\right)=V_1({\displaystyle \sum _{n_1}^{\infty }}\frac{g_{n_1}}{(w-w_{n_1}^b)l^{\left(1\right)}}+{\displaystyle \sum _{n_1,n_2,n_3}^{\infty }}\frac{g_{n_1}{g}_{n_2}{g}_{n_3}}{(w-w_{n_3}^b)l^{\left(3\right)}}+\dots \\ +{\displaystyle \sum _{n_1,\dots ,n_{2i-1}}^{\infty }}\frac{{\prod }_{k=1}^{2i-1}{g}_k}{(w+w_{2i-1}^b)l^{(2i-1)}})+V_2({\displaystyle \sum _{n_1,n_2}^{\infty }}\frac{g_{n_1}{g}_{n_2}}{(w-w_{n_2}^b)l^{\left(2\right)}}+\\ +{\displaystyle \sum _{n_1,n_2,n_3,n_4}^{\infty }}\frac{g_{n_1}{g}_{n_2}{g}_{n_3}{g}_{n_4}}{(w-w_{n_4}^b)l^{\left(4\right)}}+\dots {\displaystyle \sum _{n_1,\dots ,n_{2i}}^{\infty }}\frac{{\prod }_{k=1}^{2i}{g}_k}{(w-w_{2i}^b)l^{\left(2i\right)}}),\end{array}$$

(14)

where the following notations are used:

$$\begin{array}{c}{g}_n=\frac{L_{-}^{*}(a,w_n^b)}{L_{+}(a,w_n^b)}{e}^{i{w}_n^b(z_2-z_1)},\\ l^{\left(k\right)}=\underset{k}{\underbrace{w_{n_1}^b(w_{n_1}^b+w_{n_2}^b)\cdots (w_{n_{k-1}}^b+w_{n_k}^b)}},\\ n_k=1,2,\dots ,k=1,2,\dots .\end{array}$$

(15)

Factorized function $L_{-}^{*}(a,w_n^b)$ is calculated by Formula (22). Indeed, system (12) can be easily divided into separate recursive equations

$$\begin{array}{c}{B}_{+}^1\left(w\right)=-V_2{\displaystyle \sum _{n_1=1}^{\infty }}\frac{g_{n_1}}{(w+w_{n_1}^b)w_{n_1}^b}-V_1{\displaystyle \sum _{n_1,n_2=1}^{\infty }}\frac{g_{n_1}{g}_{n_2}}{(w+w_{n_1}^b)(w_{n_1}^b+w_{n_2}^b)w_{n_2}^b}+\\ +{\displaystyle \sum _{n_1,n_2=1}^{\infty }}\frac{g_{n_1}{g}_{n_2}}{(w+w_{n_1}^b)(w_{n_1}^b+w_{n_2}^b)}{B}_{+}^1\left(w_{n_2}^b\right),\\ B_{-}^2\left(w\right)=V_1{\displaystyle \sum _{n_1=1}^{\infty }}\frac{g_{n_1}}{(w-w_{n_1}^b)w_{n_1}^b}+V_2{\displaystyle \sum _{n_1,n_2=1}^{\infty }}\frac{g_{n_1}{g}_{n_2}}{(w-w_{n_1}^b)(w_{n_1}^b+w_{n_2}^b)w_{n_2}^b}+\\ +{\displaystyle \sum _{n_1,n_2=1}^{\infty }}\frac{g_{n_1}{g}_{n_2}}{(w-w_{n_1}^b)(w_{n_1}^b+w_{n_2}^b)}{B}_{-}^2(-w_{n_2}^b),\end{array}$$

(16)

from which we directly obtain solutions in (16), cyclically using the equation itself in its right side.

4. Potential Distribution in the Lens

Substituting the resulting solution $F\left(w\right)$ (9) into (5) and calculating the integral along the real axis w using the residue theory, we determine the potential $\phi$.

Let us consider each case for different cylinder regions separately.

1. 

$z\le z_1,$ $0\le r\le a.$

In the region $\left(a\right)$ to the left from $z_1$, the IC should be closed in the LHP w. After making calculations and passing to the limit $k\to 0$, we obtain the potential distribution inside the semi-infinite cylinder

$$\begin{array}{c}\hfill \phi (r,z)=V_1-{\displaystyle \sum _{n=1}^N}\frac{{\mathrm{J}}_0\left(v_n^{a}r\right)}{{\mathrm{J}}_0^{*}(-w_n^{a}a)}{\left\{L_{-}(a,w)\left(A_{+}^1\left(w\right)+B_{+}^1\left(w\right)\right)e^{iw(z-z_1)}\right\}}_{w=-w_n^a}=\\ \hfill {\displaystyle V_1-{\displaystyle \sum _{n=1}^N}{e}^{\frac{{\gamma }_n}{a}(z-z_1)}\frac{{\mathrm{J}}_0\left({\gamma }_n\frac{r}{a}\right)}{{\gamma }_n{\mathrm{J}}_1\left({\gamma }_n\right)}{L}_{+}(a,i\frac{{\gamma }_n}{a})\left(V_1+i\frac{{\gamma }_n}{a}{B}_{+}^1(-i\frac{{\gamma }_n}{a})\right).}\end{array}$$

(17)

Here we took into account that

$${\mathrm{J}}_0^{*}(-w_n^{a}a)=\underset{w\to -w_n^a}{lim}{(w+w_n^a)}^{-1}{\mathrm{J}}_0\left(va\right)=-ia{\mathrm{J}}_1\left(v_n^{a}a\right)=-ia{\mathrm{J}}_1\left({\gamma }_n\right)$$

(18)

and the property of factorized functions $L_{\pm }$ in (10).

2. 

$z\le z_1,$ $a\le r\le b.$

In this case for the region $\left(c\right)$ to the left from $z_1$, integration along the real axis w in this case must also be closed, according to the Jordan lemma, in the LHP, then the integral can be easily transformed into a series of residues

$$\begin{array}{c}\phi (r,z)=V_1\frac{ln\frac{b}{r}}{ln\frac{b}{a}}-{\displaystyle \sum _{n=1}^N}{\left\{\frac{(r,b)}{{(a,b)}^{*}}{L}_{-}(a,w)\left(A_{+}^1\left(w\right)+B_{+}^1\left(w\right)\right)e^{iw(z-z_1)}\right\}}_{-w_n^c}=\\ {\displaystyle V_1\frac{ln\frac{b}{r}}{ln\frac{b}{a}}-\frac{\pi }{2}{\displaystyle \sum _{n=1}^N}\frac{{\mathrm{J}}_0\left(\frac{{\delta }_{n}a}{b-a}\right){\mathrm{J}}_0\left(\frac{{\delta }_{n}b}{b-a}\right)}{{\mathrm{J}}_0^2\left(\frac{{\delta }_{n}b}{b-a}\right)-{\mathrm{J}}_0^2\left(\frac{{\delta }_{n}a}{b-a}\right)}\left({\mathrm{N}}_0\left(\frac{{\delta }_{n}r}{b-a}\right){\mathrm{J}}_0\left(\frac{{\delta }_{n}b}{b-a}\right)-{\mathrm{N}}_0\left(\frac{{\delta }_n}{b-a}b\right){\mathrm{J}}_0\left(\frac{{\delta }_{n}r}{b-a}\right)\right)}\\ L_{+}(a,i\frac{{\delta }_n}{b-a})\left(V_1+\frac{i{\delta }_n}{b-a}{B}_{+}^1(-i\frac{{\delta }_n}{b-a})\right)e^{\frac{{\delta }_n}{b-a}(z-z_1)}.\end{array}$$

(19)

Note that there is a transformation

$$\begin{array}{c}\hfill {(a,b)}_{-w_n^c}^{*}=\underset{w\to -w_n^c}{lim}{(w+w_n^c)}^{-1}(a,b)=-i\frac{2}{\pi v_n^c}{\left(\frac{(a^{\prime },b)}{(a^{\prime },a)}-\frac{(a,b^{\prime })}{(b,b^{\prime })}\right)}_{v_n^c}=\\ \hfill -i\frac{2(b-a)}{\pi {\delta }_n}\left(\frac{{\mathrm{J}}_0\left(\frac{{\delta }_{n}b}{b-a}\right)}{{\mathrm{J}}_0\left(\frac{{\delta }_{n}a}{b-a}\right)}-\frac{{\mathrm{J}}_0\left(\frac{{\delta }_{n}a}{b-a}\right)}{{\mathrm{J}}_0\left(\frac{{\delta }_{n}b}{b-a}\right)}\right),\end{array}$$

(20)

where in the derivation the Wronskian $(z^{\prime },z)={\mathrm{N}}_0\left(z\right){\mathrm{J}}_1\left(z\right)-{\mathrm{N}}_1\left(z\right){\mathrm{J}}_0\left(z\right)=2/\left(\pi z\right)$ is used [23]. Here the primes in the combination of Bessel functions (a,b) denote their derivatives.

3. 

$z_1\le z\le z_2,$ $0\le r\le b.$

For area $\left(a\right)$ between semi-infinite round cylinders, according to the Jordan lemma, closing the IC in (5) for terms with an exponential factor $e^{iw(z-z_1)}$ in the UHP, and with a factor $e^{iw(z-z_2)}$ in the LHP w, taking into account all the contributions of the poles inside the IC, we similarly find the potential distribution in the slit region

$$\begin{array}{c}\hfill {\displaystyle \phi (r,z)={\displaystyle \sum _{n=1}^N}\frac{{\mathrm{J}}_0\left({\gamma }_n\frac{r}{b}\right)}{{\mathrm{J}}_0\left({\gamma }_n\frac{a}{b}\right)}{L}_{-}^{*}(a,w_n^b)(\left(-V_1/w_n^b+B_{+}^1\left(w_n^b\right)\right)e^{i{w}_n^b(z-z_1)}+}\\ \hfill \left(V_2/w_n^b+B_{-}^2(-w_n^b)\right)e^{-i{w}^b(z-z_2)}),\end{array}$$

or it can be written as

$$\begin{array}{c}\hfill {\displaystyle \phi (r,z)=\frac{1}{ln\frac{b}{a}}{\displaystyle \sum _{n=1}^N}\frac{{\mathrm{J}}_0\left({\gamma }_n\frac{r}{b}\right){\mathrm{J}}_0\left({\gamma }_n\frac{a}{b}\right)}{{\gamma }_n^2{\mathrm{J}}_1^2\left({\gamma }_n\right)}{L}_{+}^{-1}(a,i\frac{{\gamma }_n}{b})\left(e^{-\frac{{\gamma }_n}{b}(z-z_1)}\right(V_1-}\\ \hfill \frac{i{\gamma }_n}{b}{B}_{+}^1\left(i\frac{{\gamma }_n}{b}\right))+e^{\frac{{\gamma }_n}{b}(z-z_2)}\left(V_2-\frac{i{\gamma }_n}{b}{B}_{-}^2(-i\frac{{\gamma }_n}{b})\right)),\end{array}$$

(21)

using the properties of the Bessel functions

$$\frac{{(a,b)}_{v_n^b}}{{\mathrm{J}}_0\left({\gamma }_n\frac{a}{b}\right)}=\frac{{(b^{\prime },b)}_{v_n^b}}{{\mathrm{J}}_1\left({\gamma }_n\right)}=-\frac{2}{\pi {\gamma }_n{\mathrm{J}}_1\left({\gamma }_n\right)},$$

in the expression for

$$L_{-}^{*}(a,w_n^b)=\underset{w\to w_n^b}{lim}(w-w_n^b)L_{-}(a,w)=\frac{i}{bln\frac{a}{b}}\frac{{\mathrm{J}}_0^2\left({\gamma }_n\frac{a}{b}\right)}{{\gamma }_n{\mathrm{J}}_1^2\left({\gamma }_n\right)L_{+}(a,w_n^b)}.$$

(22)

4. 

$z_2\le z,$ $0\le r\le a.$

Similarly, in the region $\left(a\right)$ to the right from the semi-infinite tube, closing the IC in the UHP of the complex variable w, we obtain

$$\begin{array}{c}\hfill {\displaystyle \phi (r,z)=V_2-{\displaystyle \sum _{n=1}^N}{e}^{-\frac{{\gamma }_n}{a}(z-z_2)}\frac{{\mathrm{J}}_0\left({\gamma }_n\frac{r}{a}\right)}{{\gamma }_n{\mathrm{J}}_1\left({\gamma }_n\right)}{L}_{+}(a,i\frac{{\gamma }_n}{a})}\\ \hfill \left(V_2+i\frac{{\gamma }_n}{a}{B}_{-}^2\left(i\frac{{\gamma }_n}{a}\right)\right).\end{array}$$

(23)

5. 

$z_2\le z,$ $a\le r\le b.$

In region $\left(c\right)$ to the right outside the semi-infinite circular cylinder, deforming the IC upwards, we also obtain

$$\begin{array}{c}\hfill {\displaystyle \phi (r,z)=V_2\frac{ln\frac{b}{r}}{ln\frac{b}{a}}-\frac{\pi }{2}{\displaystyle \sum _{n=1}^N}\frac{{\mathrm{J}}_0\left(\frac{{\delta }_{n}a}{b-a}\right){\mathrm{J}}_0\left(\frac{{\delta }_{n}b}{b-a}\right)}{{\mathrm{J}}_0^2\left(\frac{{\delta }_{n}b}{b-a}\right)-{\mathrm{J}}_0^2\left(\frac{{\delta }_{n}a}{b-a}\right)}{L}_{+}(a,i\frac{{\delta }_n}{b-a})(r,b){|}_{v_n^c}}\\ \hfill \left(V_2+\frac{i{\delta }_n}{b-a}{B}_{-}^2\left(i\frac{{\delta }_n}{b-a}\right)\right)e^{-\frac{{\delta }_n}{b-a}(z-z_2)}.\end{array}$$

(24)

5. Numerical Calculation of the Potential in a Lens

The numerical implementation of the factorized Bessel functions can be performed optimally using Formula (A5) with a given accuracy, which is expressed through the functions P and Q [5] (Appendix A). It should be noted that the potential distribution is ultimately expressed by a real function in the form of exponentially convergent series in (17)–(24). In particular, let us consider the distribution of the potential along the lens axis calculated by Formulas (17), (21) and (23).

Figure 2 and Figure 3 show the results of calculating the potential in a two-electrode electrostatic lens depending on the radii of its inner and outer electrodes. The linear dimensions are given in units of the radius of the inner cylinders: $a=1$, $b\to b/a$, $z\to z/a$. The width of the slit $z_2-z_1=2$ ($z_1=-1$, $z_2=1$).

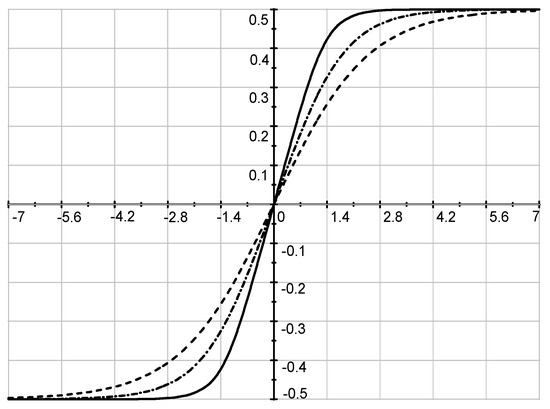
Figure 2. Potential distribution along the lens axis. $b=6$: $a=1$ is a solid line, $a=2$ is a dash−dotted line, $a=3$ is a dashed line.

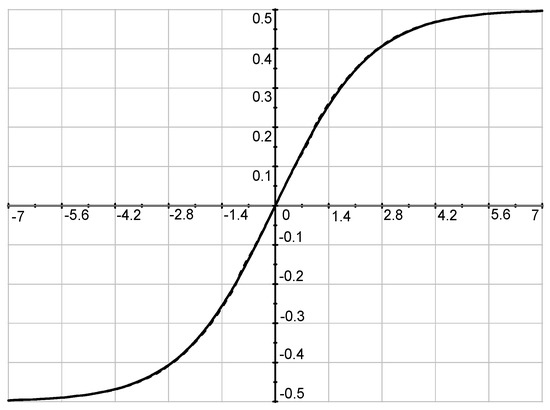
Figure 3. Influence of the outer cylinder radius on the potential distribution. $a=1$: $b=2$ is a solid line, $b=4$ is a dashed line.

As can be seen from Figure 2, as the radius of the semi-infinite cylinder increases, the steepness of the curve decreases.

It should be noted, as calculations show (see Figure 3), that the radius of an infinite cylinder b has an insignificant effect on the potential distribution along the z axis.

6. Discussion

Thus, the exact solution (9) of the boundary value problem for the potential $\phi$ in (5) is found, where the auxiliary functions $B_{+}^1$ and $B_{-}^2$ are represented as rapidly convergent infinite series, as well as the factorized Bessel functions (see Appendix A).

As expected, when passing to the limit $z_1\to -\infty$, when the end of the first semi-infinite cylinder is shifted by a considerable distance to the left, the expressions for the potential (21)–(24) coincide with the final results of N.N. Lebedev [5].

For each area $\left(a\right)$, $\left(b\right)$, and $\left(c\right)$ inside an infinite round tube, the graphs of the distribution of potentials are calculated through their eigenfunctions and plotted for demonstration, for example, on the z axis (see Figure 2 and Figure 3). As can be seen in the above figures, the curves turned out to be quite smooth, especially at the junctions of these regions, which shows that the calculation of factorized functions is sufficiently accurate.

Note that the problem for a nonzero wavenumber k transforms into the corresponding problem of wave diffraction in electrodynamics [20].

It should be expected that it will not be difficult to apply the WH method to similar problems with three or more electrodes, since only the rank of the system of algebraic equations will increase.

So, the internal boundary value problem of the distribution of the electrostatic field in a lens formed by two identical semi-infinite circular cylinders coaxially located inside an infinite outer cylinder is reduced to solving a system of singular integral equations WH and further solved by the WH method using factorized Bessel functions, which is reduced to a system of linear algebraic equations, splitting into separate recursive equations. Solutions to the problem for each region inside the infinite outer cylinder are presented as exponentially converging series in terms of eigenfunctions and eigenvalues.

The final results of this problem can be useful for testing approximate methods as the WH method is one of the mathematically rigorous methods.

7. Conclusions

The WH method was used to solve the internal boundary value problem of the elliptic type on the distribution of the electrostatic potential inside the structure formed by a round cylinder with a slot of finite width coaxially located inside an infinite round cylinder. The potentials of the cylinders are assumed to be constant and are set arbitrarily. The studied problem is first, with the help of boundary conditions, reduced to a system of singular integral Wiener–Hopf equations, the exact solution of which is constructed by the WH method in the class of meromorphic functions with respect to two desired auxiliary functions interconnected by a system of linear algebraic functions. This system breaks down into recursive equations, as a result of which the solution of the problem is obtained in the form of an infinite exponentially convergent series. It should be noted that the rigorous solution automatically satisfies the so-called edge condition or the Meixner condition, which, in fact, is responsible for the uniqueness of the solution to the boundary value problem, since the electric field must tend to infinity according to a given power law as it approaches the edge. Thus, the solution of the boundary value problem $\phi$ for each region is represented by eigenfunctions in the form of Bessel functions and eigenvalues, which are their roots at the corresponding radius of the cylinder inside the infinite outer cylinder. On the basis of analytical formulas, a quantitative analysis of the axial distribution of the potential of a two-electrode lens was carried out for various values of the radii of the outer and inner cylinders. The WH method can be applied without significant changes to similar boundary value problems with three or more internal electrodes. Undoubtedly, similar external boundary value problems are also of theoretical interest for the WH method. In modern electron microscopes, high resolution is provided by the use of aberration correctors, which eliminate the main reason that limits the resolution of an electron microscope—spherical and axial chromatic aberration of the electron lens that acts as its objective [1,24]. However, the use of a two-electrode mirror enables us to eliminate only one of these aberrations, either spherical or chromatic [1]. The development of aberration correctors with the simultaneous elimination of both spherical and axial chromatic aberrations using electron mirrors with three or more internal electrodes opens up great opportunities for increasing the resolving power of a new generation of transmission electron microscopes. At the same time, such an electrode design simultaneously provides electrostatic strength at high field strengths and screening of the electron beam from scattered electric fields at large gap widths between the internal electrodes.