Application of Leak 2D to Describe Preferential Water Flow in a Soil Containing Artificial Macropores
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Description
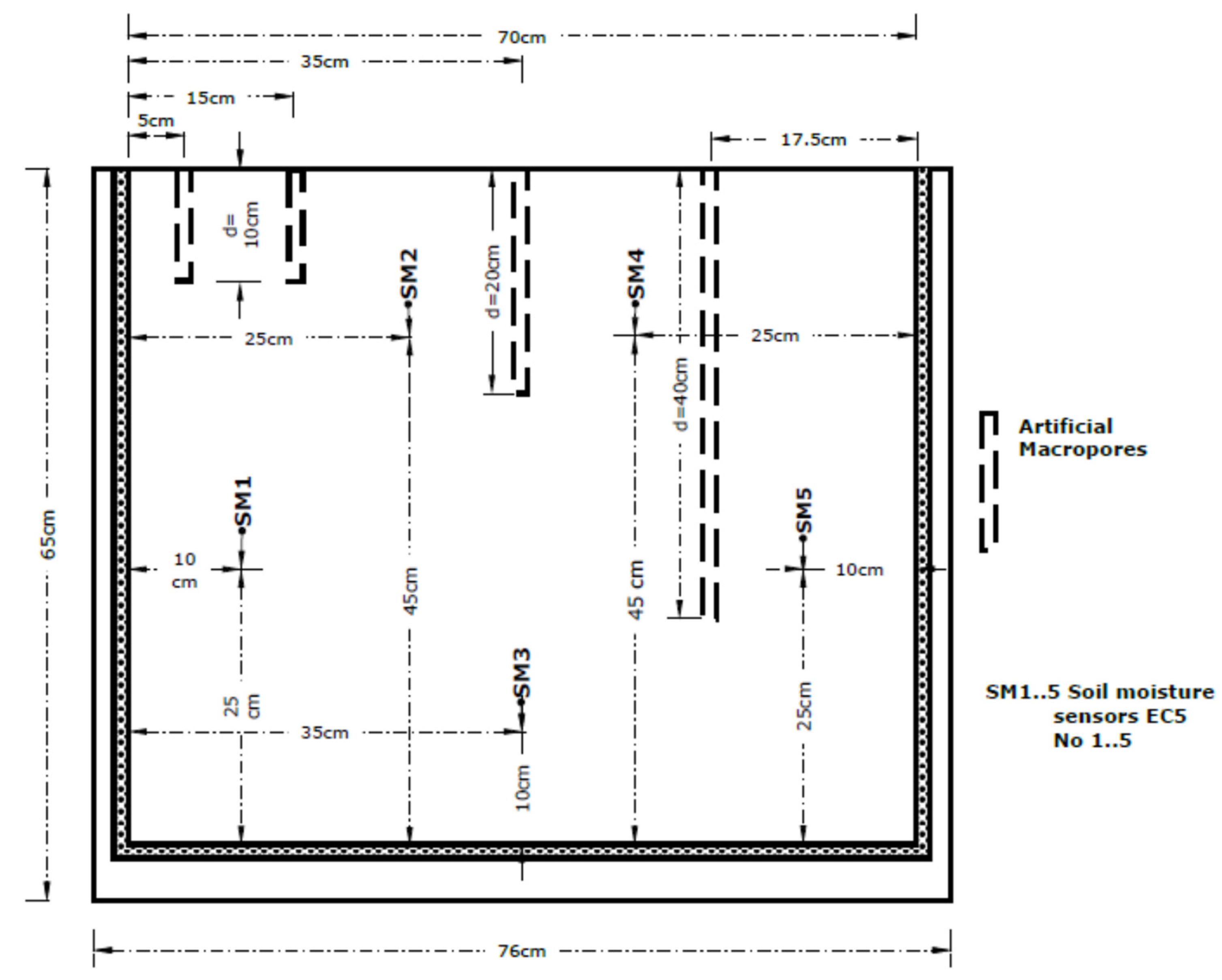
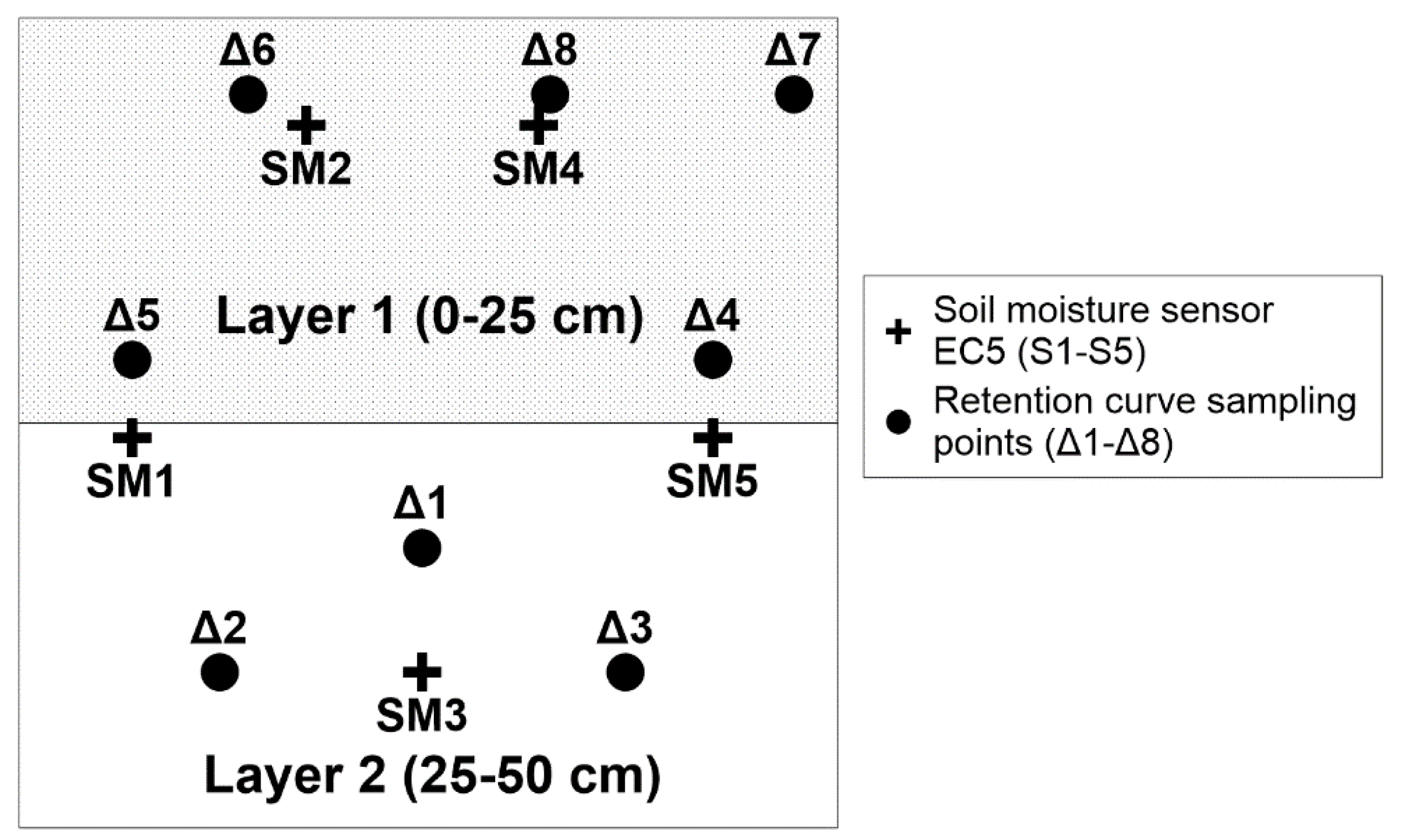
2.2. Hele-Shaw Cell
2.3. Hydraulic Properties
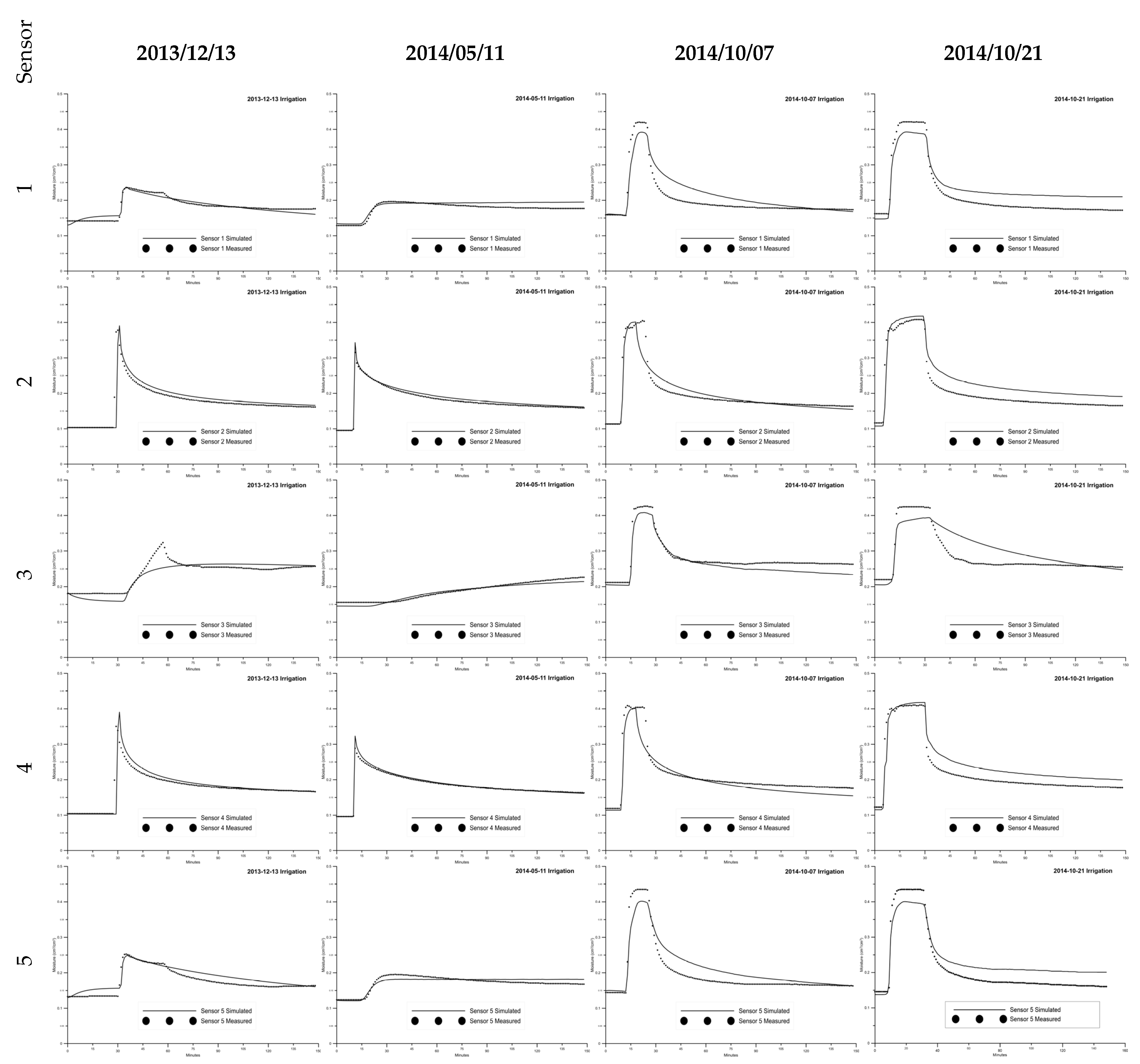
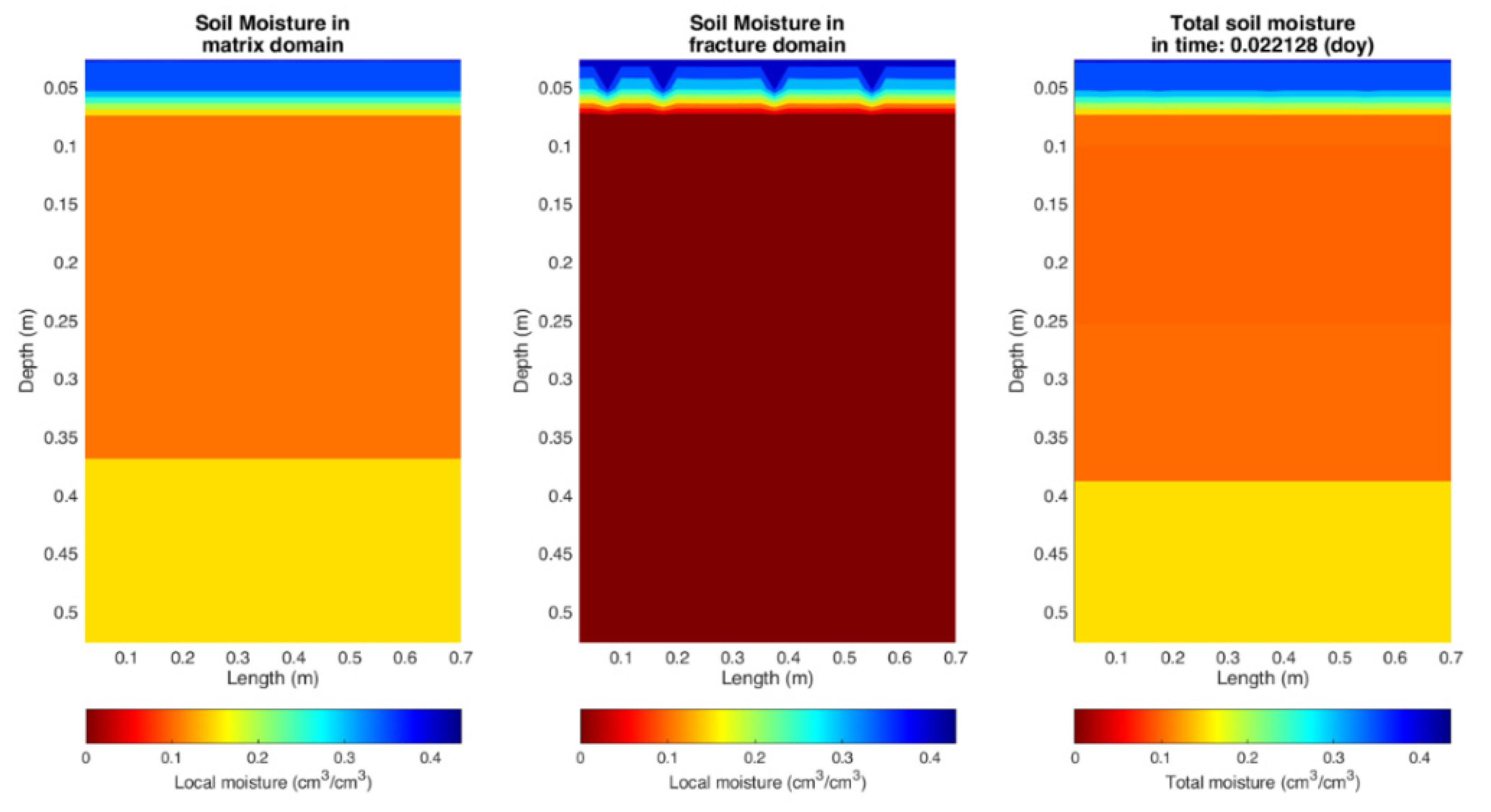
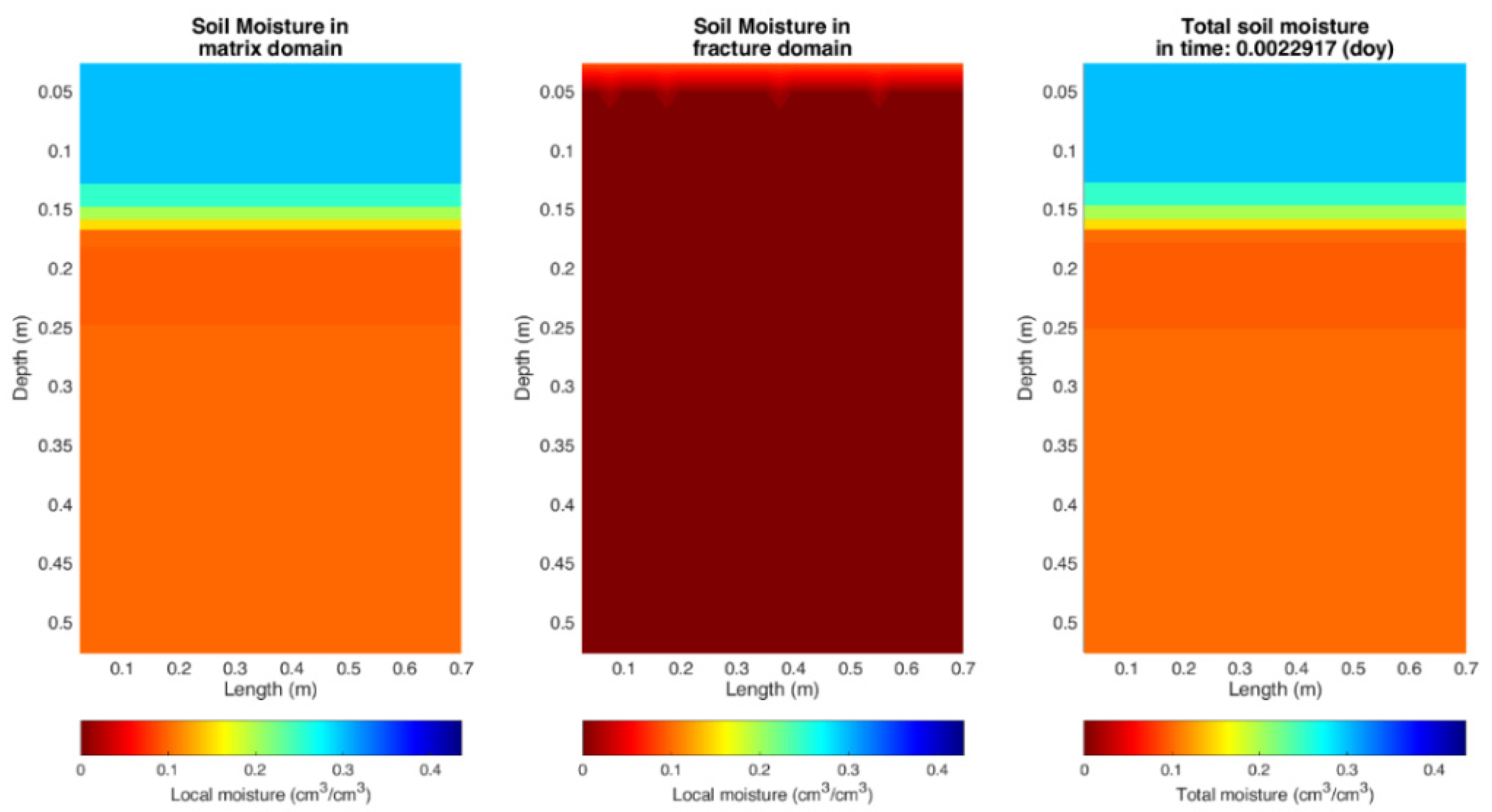
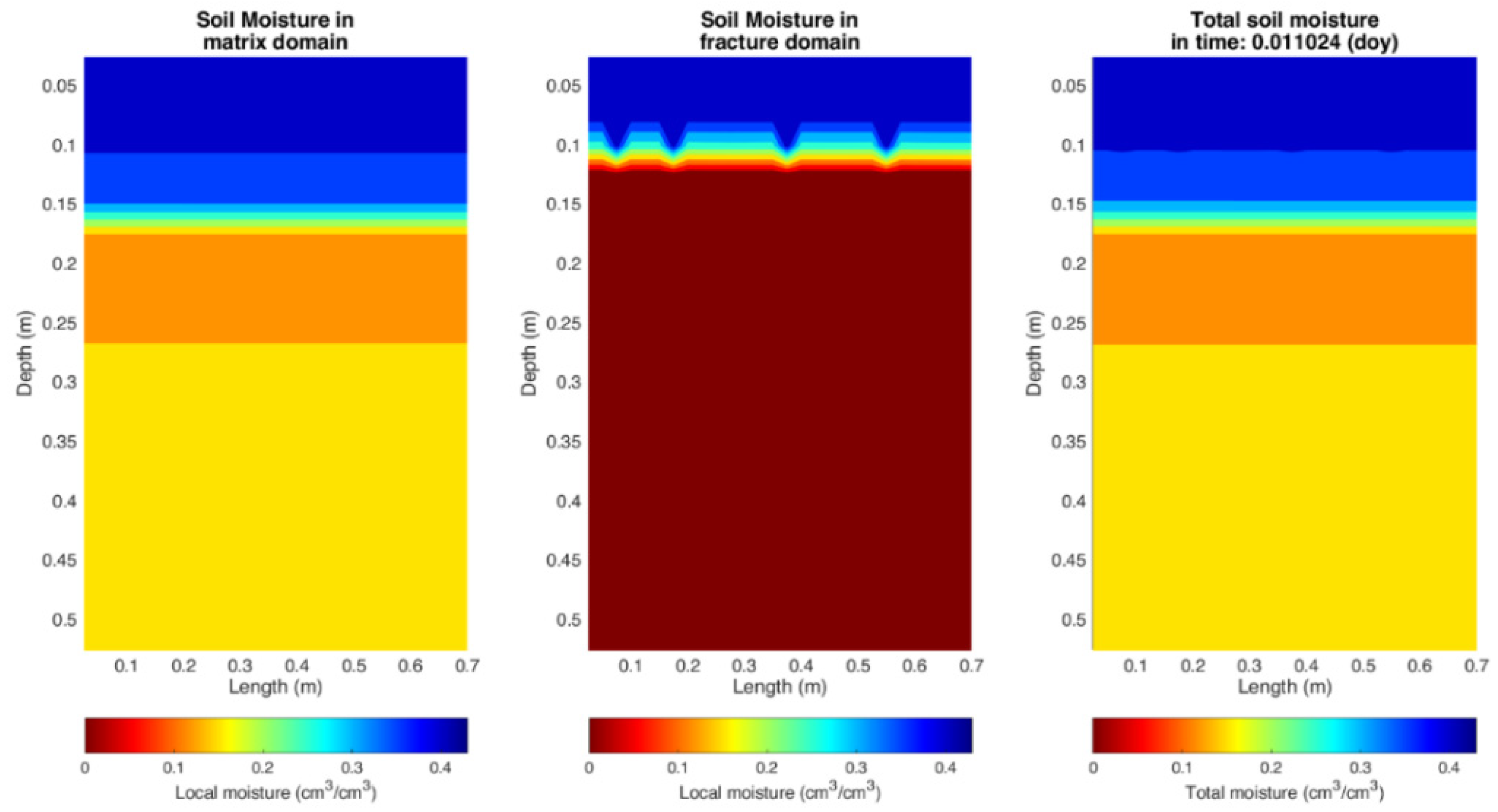
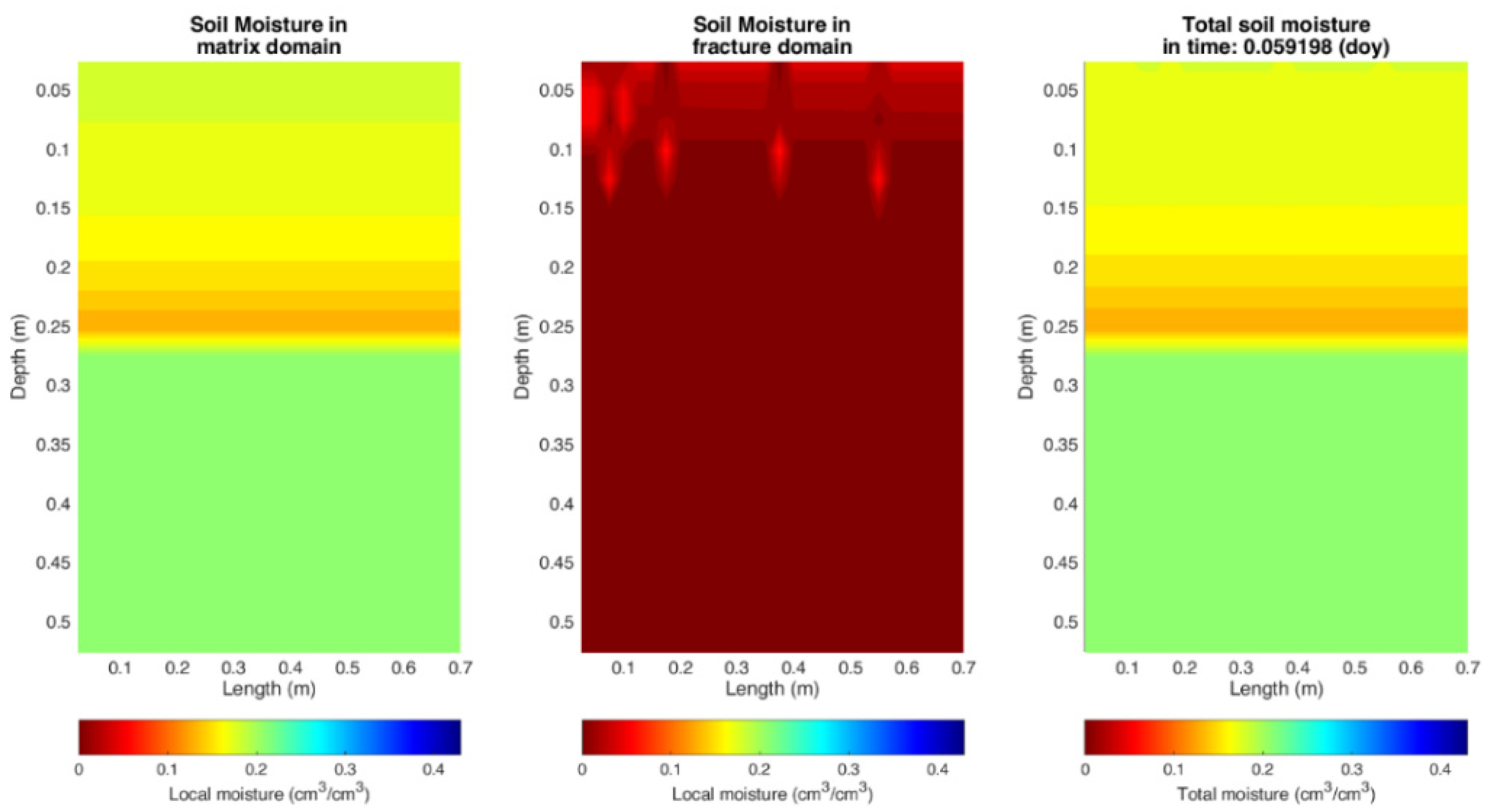
3. Results
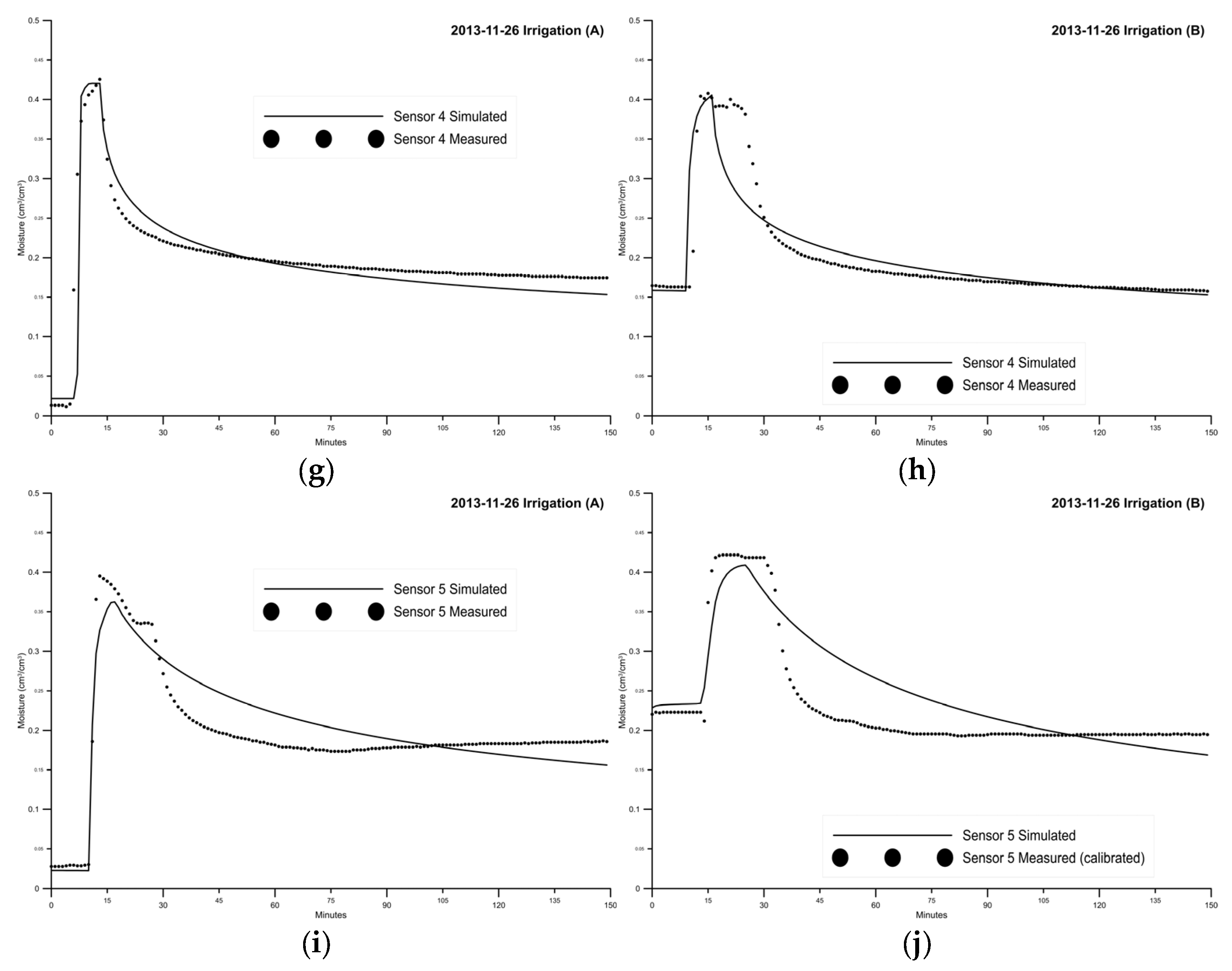
3.1. Calibration of the Mathematical Model
3.2. Validation of the Mathematical Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Yao, J.; Yan, R.; Cheng, J. Effects of infiltration amounts on preferential flow characteristics and solute transport in the protection forest soil of southwestern china. Water 2021, 13, 1301. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, R.; Sheng, F. Characterizing heterogeneous processes of water flow and solute transport in soils using multiple tracer experiments. Vadose Zone J. 2013, 12, vzj2012.0125. [Google Scholar] [CrossRef]
- Nimmo, J.R. The processes of preferential flow in the unsaturated zone. Soil Sci. Soc. Am. J. 2021, 85, 1–27. [Google Scholar] [CrossRef]
- Ahuja, L.R.; Johnsen, K.E.; Heathman, G.C. Macropore Transport of a Surface-Applied Bromide Tracer: Model Evaluation and Refinement. Soil Sci. Soc. Am. J. 1995, 59, 1234–1241. [Google Scholar] [CrossRef]
- Köhne, J.M.; Mohanty, B.P. Water flow processes in a soil column with a cylindrical macropore: Experiment and hierarchical modeling. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Version 4.17; Department of Environmental Sciences, University of California: Riverside, CA, USA, 2013; p. 343. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.; Šejna, M. The HYDRUS Software Package for Simulating Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Technical Manual, Version 2.0; Department of Environmental Sciences, University of California: Riverside, CA, USA, 2012; p. 260. [Google Scholar]
- Ross, P.J.; Smettem, K.R.J. A simple treatment of physical nonequilibrium water flow in soils. Soil Sci. Soc. Am. J. 2000, 64, 1926–1930. [Google Scholar] [CrossRef]
- Moradzadeh, M.; Boroomandnasab, S.; Moazed, H.; Alavi, J.; Jamalian, A.; Khaledian, M.; Ruy, S. A new kinematic–dispersive wave van Genuchten (KDW-VG) model for numerical simulation of preferential water flow in soil. J. Hydrol. 2020, 582, 124480. [Google Scholar] [CrossRef]
- Jabro, J.; Toth, J.; Fox, R. Evaluation and Comparison of Five Simulation Models for Estimating Water Drainage Fluxes under Corn. J. Environ. Qual. 1998, 27, 1376–1381. [Google Scholar] [CrossRef]
- Jarvis, N. Modeling the impact of preferential flow on nonpoint source pollution. In Physical nonequilibrium in soils: Modeling and application; Magdi Selim, H., Liwang, M., Eds.; Ann Arbor Press: Chelsea, Michigan, 1998; pp. 195–221. [Google Scholar]
- Larsbo, M.; Jarvis, N. MACRO 5.0. A Model of Water Flow and Solute Transport in Macroporous Soil. Technical Description; Department of Soil Sciences, Swedish University of Agricultural Sciences: Uppsala, Sweden, 2003; p. 52. [Google Scholar]
- Addiscott, T.M.; Bailey, N.J.; Bland, G.J.; Whitmore, A.P. Simulation of nitrogen in soil and winter wheat crops: A management model that makes the best use of limited information. Fertil. Res. 1991, 27, 305–312. [Google Scholar] [CrossRef]
- Jansson, P. Soil model user’s manual. In Avdelningsmeddelande-Sveriges Lantbruksuniversitet, Institutionen foer Markvetenskap, Avdelningen foer Lantbrukets Hydroteknik (Sweden); Department of Soil Sciences, Division of Agricultural Hydrotechnics, Swedish University of Agricultural Sciences: Uppsala, Sweden, 1991. [Google Scholar]
- Hutson, J.; Wagenet, R. Simulating nitrogen dynamics in soils using a deterministic model. Soil Use Manag. 1991, 7, 74–78. [Google Scholar] [CrossRef]
- Lengnick, L.L.; Fox, R.H. Simulation by NCSWAP of seasonal nitrogen dynamics in corn: I. soil nitrate. Agron. J. 1994, 86, 167–175. [Google Scholar] [CrossRef]
- Jiang, S.; Pang, L.; Buchan, G.D.; Simůnek, J.; Noonan, M.J.; Close, M.E. Modeling water flow and bacterial transport in undisturbed lysimeters under irrigations of dairy shed effluent and water using HYDRUS-1D. Water Res. 2010, 44, 1050–1061. [Google Scholar] [CrossRef] [PubMed]
- Shajari, F.; Einsiedl, F.; Rein, A. Characterizing Water Flow in Vegetated Lysimeters with Stable Water Isotopes and Modeling. Groundwater 2020, 58, 759–770. [Google Scholar] [CrossRef]
- Gerke, H.; Dusek, J.; Vogel, T. Solute Mass Transfer Effects in Two-Dimensional Dual-Permeability Modeling of Bromide Leaching from a Tile-Drained Field. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z.; Georgiou, P.E.; Kolotouros, C.A. Soil water dynamics in cropped and uncropped fields in northern Greece using a dual-permeability model. Hydrol. Sci. J. 2013, 58, 1748–1759. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; van Genuchten, M.T.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Germann, P.; Beven, K. Kinematic wave approximation to infiltration into soils with sorbing macropores. Water Resour. Res. 1985, 21, 990–996. [Google Scholar] [CrossRef]
- An, H.; Ichikawa, Y.; Tachikawa, Y.; Shiiba, M. A new Iterative Alternating Direction Implicit (IADI) algorithm for multi-dimensional saturated–unsaturated flow. J. Hydrol. 2011, 408, 127–139. [Google Scholar] [CrossRef]
- Babajimopoulos, C. Revisiting the Douglas–Jones method for modelling unsaturated flow in a cultivated soil. Environ. Model. Softw. 2000, 15, 303–312. [Google Scholar] [CrossRef]
- Douglas, J.; Rachford, H.H. On the numerical solution of heat conduction problems in two and three space variables. Trans. Am. Math. Soc. 1956, 82, 421–439. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Paraskevas, C.; Babajimopoulos, C. A New Two-dimensional Dual-permeability Model of Preferential Water Flow in the Vadose Zone. J. Water Manag. Model. 2023, 31, C502. [Google Scholar]
- Larsbo, M.; Roulier, S.; Stenemo, F.; Kasteel, R.; Jarvis, N. An Improved Dual-Permeability Model of Water Flow and Solute Transport in the Vadose Zone. Vadose Zone J. 2005, 4, 398–406. [Google Scholar] [CrossRef]
- Gerke, H.; van Genuchten, M. Macroscopic representation of structural geometry for simulating water and solute movement in dual-porosity media. Adv. Water Resour. 1996, 19, 343–357. [Google Scholar] [CrossRef]
- Gerke, H.; van Genuchten, M. Evaluation of a first-order water transfer term for variably saturated dual-porosity flow models. Water Resour. Res. 1993, 29, 1225–1238. [Google Scholar] [CrossRef]
- Dusek, J.; Gerke, H.; Vogel, T. Surface boundary conditions in two-dimensional dual-permeability modeling of tile drain bromide leaching. Vadose Zone J. 2008, 7, 1287–1301. [Google Scholar] [CrossRef]
- Paraskevas, C.; Karpouzos, D.; Babajimopoulos, C. Estimation of soil waterfront velocity and saturated hydraulic conductivity in a Hele-Shaw apparatus with an optical flow method. Comput. Electron. Agric. 2021, 184, 106086. [Google Scholar] [CrossRef]
- Buttle, J.; Leigh, D. The influence of artificial macropores on water and solute transport in laboratory soil columns. J. Hydrol. 1997, 191, 290–313. [Google Scholar] [CrossRef]
- Castiglione, P.; Mohanty, B.P.; Shouse, P.J.; Simunek, J.; van Genuchten, M.T.; Santini, A. Lateral water diffusion in an artificial macroporous system. Vadose Zone J. 2003, 2, 212. [Google Scholar] [CrossRef]
- Czapar, G.; Horton, R.; Fawcett, R. Herbicide and Tracer Movement in Soil Columns Containing an Artificial Macropore. J. Environ. Qual. 1992, 21, 110–115. [Google Scholar] [CrossRef]
- Lamy, E.; Lassabatere, L.; Bechet, B.; Andrieu, H. Modeling the influence of an artificial macropore in sandy columns on flow and solute transfer. J. Hydrol. 2009, 376, 392–402. [Google Scholar] [CrossRef]
- Zhou, B.B.; Li, Y.; Wang, Q.J.; Jiang, Y.L.; Li, S. Preferential water and solute transport through sandy soil containing artificial macropores. Environ. Earth Sci. 2013, 70, 2371–2379. [Google Scholar] [CrossRef]
- Decagon Devices. EC-5 Soil Moisture Sensor User’s Manual (Version 2); Decagon Devices: Pullman, WA, USA, 2012; p. 24. [Google Scholar]
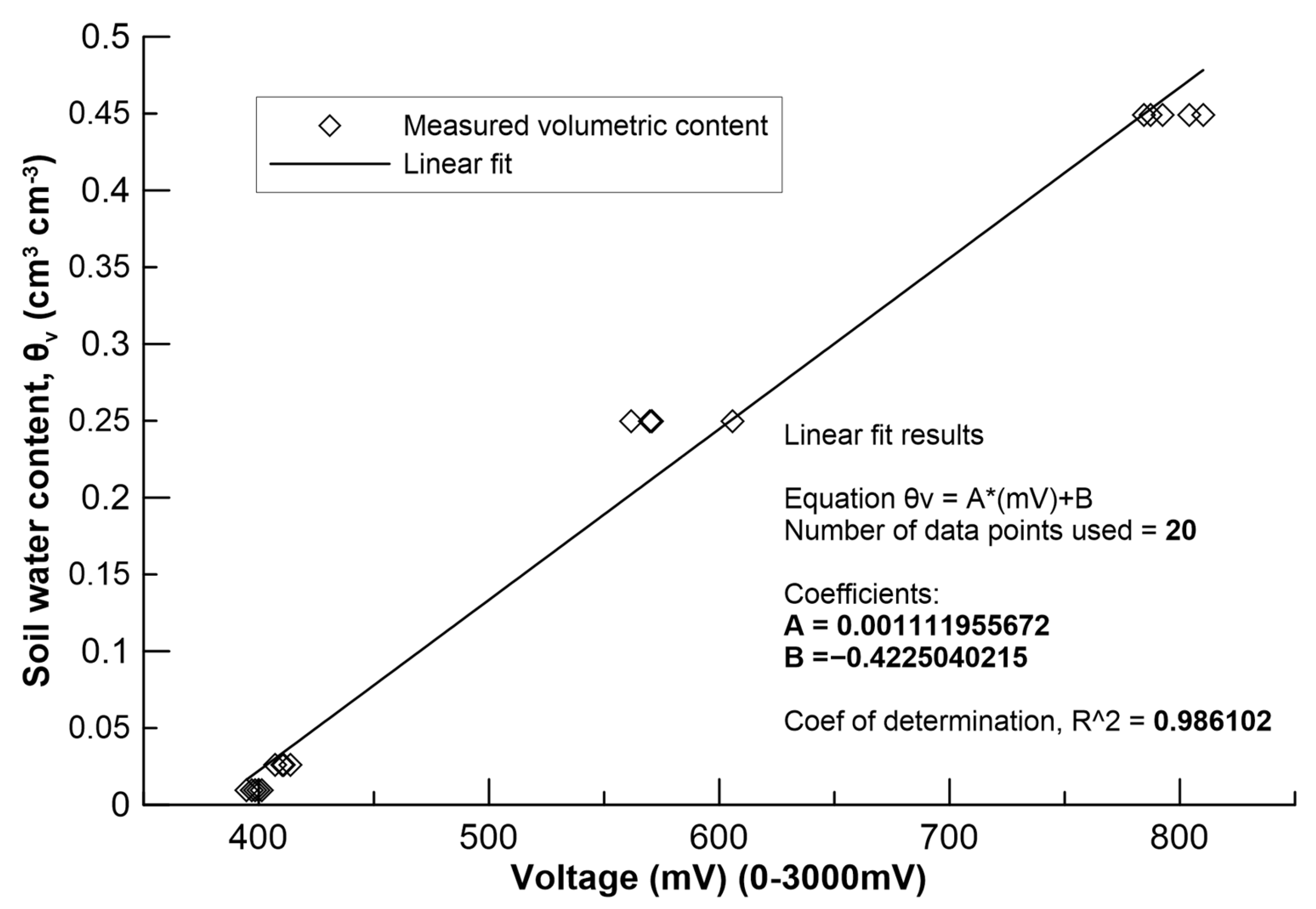
- Paraskevas, C.; Georgiou, P.; Ilias, A.; Panoras, A.; Babajimopoulos, C. Calibration equations for two capacitance water content probes. Int. Agrophysics 2012, 26, 285–293. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, H.V.; Sorooshian, S.; Rousseau, A.N.; Turcotte, R. (Eds.) Calibration of Watershed Models; Water science and application; American Geophysical Union: Washington, DC, USA, 2003; Volume 6, ISBN 0-87590-355-X. [Google Scholar]
- Radcliffe, D.E.; Simunek, J. Soil Physics with HYDRUS: Modeling and Applications; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781315275666. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Loague, K.; Green, R.E. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]
- Gärdenäs, A.; Šimůnek, J.; Jarvis, N.; van Genuchten, M. Two-dimensional modelling of preferential water flow and pesticide transport from a tile-drained field. J. Hydrol. 2006, 329, 647–660. [Google Scholar] [CrossRef]
- Kalkwarf, D.; Henkens, R. Protolysis and hydrolysis reactions of erioglaucine in aqueous solutions. HW-SA US At. Energy Comm. 1960, HW-63824, 50–54. [Google Scholar]
- Flury, M.; Flühler, H. Brilliant Blue FCF as a Dye Tracer for Solute Transport Studies-A Toxicological Overview. J. Environ. Qual. 1994, 23, 1108–1112. [Google Scholar] [CrossRef]
- Ketelsen, H.; Meyer-Windel, S. Adsorption of brilliant blue FCF by soils. Geoderma 1999, 90, 131–145. [Google Scholar] [CrossRef]
- Vryzas, Z.; Papadakis, E.N.; Papadopoulou-Mourkidou, E. Leaching of Br-, metolachlor, alachlor, atrazine, deethylatrazine and deisopropylatrazine in clayey vadoze zone: A field scale experiment in north-east Greece. Water Res. 2012, 46, 1979–1989. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, M.; Argiriou, A.A.; Wang, S.; Qu, D.; Zhang, Y.; Su, P. Recharge and Infiltration Mechanisms of Soil Water in the Floodplain Revealed by Water-Stable Isotopes in the Upper Yellow River. Sustainability 2021, 13, 9369. [Google Scholar] [CrossRef]








| Layer Number | θs | θr * | αvg * | nvg * | mvg | R2 | ρb |
|---|---|---|---|---|---|---|---|
| (cm3/cm3) | (cm3/cm3) | (m) | (−) | (=1−1/nvg) | (−) | (gr/cm3) | |
| 1st (0–25 cm) | 0.433 | 0.0 | 0.2487 | 1.5535 | 0.3563 | 0.9907 | 1.16 |
| 2nd (25–50 cm) | 0.424 | 0.0 | 0.1995 | 1.5625 | 0.3600 | 0.9909 | 1.14 |
| Date | h (mm)/ t (mins) | θ (°C)/RH (%) | Sensor # | RMS | MAE | MEF | CRM | n |
|---|---|---|---|---|---|---|---|---|
| (cm3/cm3) | (-) | |||||||
| 2013/11/26 (A) | h = 125 mm/ t = 5 min | θ = 19.4–19.7 °C/ RH = 62–64% | SM1 | 0.024 | 0.018 | 0.862 | −0.051 | 150 |
| SM2 | 0.027 | 0.012 | 0.831 | −0.003 | 150 | |||
| SM3 | 0.023 | 0.016 | 0.910 | −0.049 | 150 | |||
| SM4 | 0.028 | 0.015 | 0.803 | 0.032 | 150 | |||
| SM5 | 0.029 | 0.024 | 0.843 | −0.034 | 150 | |||
| Total | 0.026 | 0.017 | 0.854 | −0.022 | 750 | |||
| 2013/11/26 (B) | h = 80 mm/ t = 3.25 min | θ = 19.4–19.7 °C/ RH = 62–64% | SM1 | 0.038 | 0.029 | 0.777 | −0.044 | 150 |
| SM2 | 0.039 | 0.020 | 0.634 | −0.003 | 150 | |||
| SM3 | 0.033 | 0.024 | 0.892 | −0.061 | 150 | |||
| SM4 | 0.031 | 0.015 | 0.751 | 0.003 | 150 | |||
| SM5 | 0.041 | 0.032 | 0.788 | −0.072 | 150 | |||
| Total | 0.037 | 0.024 | 0.793 | −0.039 | 750 | |||
| Date | h (mm)/ t (mins) | θ (°C)/RH (%) | Sensor # | RMS | MAE | MEF | CRM | n |
|---|---|---|---|---|---|---|---|---|
| (cm3/cm3) | (-) | |||||||
| 2013/12/13 | h = 60 mm/ t = 2 min | θ = 21–23 °C/ RH = 45–47% | SM1 | 0.008 | 0.007 | 0.913 | 0.005 | 150 |
| SM2 | 0.025 | 0.010 | 0.733 | −0.026 | 150 | |||
| SM3 | 0.018 | 0.013 | 0.760 | 0.018 | 150 | |||
| SM4 | 0.024 | 0.008 | 0.717 | −0.014 | 150 | |||
| SM5 | 0.014 | 0.012 | 0.818 | −0.057 | 150 | |||
| Total | 0.019 | 0.010 | 0.763 | −0.013 | 750 | |||
| 2014/05/11 | h = 35 mm/ t~1 min | θ = 22–23 °C/ RH = 63–65% | SM1 | 0.011 | 0.009 | 0.681 | −0.045 | 150 |
| SM2 | 0.006 | 0.005 | 0.978 | −0.026 | 150 | |||
| SM3 | 0.007 | 0.006 | 0.925 | 0.017 | 150 | |||
| SM4 | 0.004 | 0.002 | 0.984 | −0.009 | 150 | |||
| SM5 | 0.009 | 0.007 | 0.820 | −0.006 | 150 | |||
| Total | 0.008 | 0.006 | 0.928 | −0.014 | 750 | |||
| 2014/10/07 | h = 110 mm/ t = 4 min | θ = 23–24 °C/ RH = 75–76% | SM1 | 0.028 | 0.021 | 0.808 | −0.062 | 150 |
| SM2 | 0.023 | 0.013 | 0.887 | −0.001 | 150 | |||
| SM3 | 0.018 | 0.015 | 0.865 | 0.053 | 150 | |||
| SM4 | 0.025 | 0.016 | 0.860 | 0.061 | 150 | |||
| SM5 | 0.029 | 0.022 | 0.858 | −0.066 | 150 | |||
| Total | 0.025 | 0.017 | 0.856 | 0.002 | 750 | |||
| 2014/10/21 | h = 150 mm/ t = 6 min | θ = 22–23 °C/ RH = 64–66% | SM1 | 0.032 | 0.031 | 0.846 | −0.092 | 150 |
| SM2 | 0.032 | 0.029 | 0.845 | −0.121 | 150 | |||
| SM3 | 0.035 | 0.028 | 0.661 | −0.050 | 150 | |||
| SM4 | 0.029 | 0.025 | 0.874 | −0.096 | 150 | |||
| SM5 | 0.035 | 0.033 | 0.863 | −0.095 | 150 | |||
| Total | 0.033 | 0.029 | 0.835 | −0.088 | 750 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paraskevas, C.; Karpouzos, D.; Babajimopoulos, C. Application of Leak 2D to Describe Preferential Water Flow in a Soil Containing Artificial Macropores. Mathematics 2023, 11, 2889. https://doi.org/10.3390/math11132889
Paraskevas C, Karpouzos D, Babajimopoulos C. Application of Leak 2D to Describe Preferential Water Flow in a Soil Containing Artificial Macropores. Mathematics. 2023; 11(13):2889. https://doi.org/10.3390/math11132889
Chicago/Turabian StyleParaskevas, Charalampos, Dimitrios Karpouzos, and Christos Babajimopoulos. 2023. "Application of Leak 2D to Describe Preferential Water Flow in a Soil Containing Artificial Macropores" Mathematics 11, no. 13: 2889. https://doi.org/10.3390/math11132889
APA StyleParaskevas, C., Karpouzos, D., & Babajimopoulos, C. (2023). Application of Leak 2D to Describe Preferential Water Flow in a Soil Containing Artificial Macropores. Mathematics, 11(13), 2889. https://doi.org/10.3390/math11132889







