Optimal Fault-Tolerant Resolving Set of Power Paths

Abstract

In a simple connected undirected graph G, an ordered set R of vertices is called a resolving set if for every pair of distinct vertices u and v, there is a vertex $w\in R$ such that $d(u,w)\ne d(v,w)$. A resolving set F for the graph G is a fault-tolerant resolving set if for each $v\in F$, $F\setminus \left\{v\right\}$ is also a resolving set for G. In this article, we determine an optimal fault-resolving set of r-th power of any path $P_n$ when $n\ge r(r-1)+2$. For the other values of n, we give bounds for the size of an optimal fault-resolving set. We have also presented an algorithm to construct a fault-tolerant resolving set of $P_m^r$ from a fault-tolerant resolving set of $P_n^r$ where $m<n$.

1. Introduction

An undirected simple connected graph G has a vertex set $V\left(G\right)$ and an edge set $E\left(G\right)$, and the distance between the vertices u and v is called $d_G(u,v)$. This distance is equal to the length of the shortest $u-v$ path within G. With an understanding of G, we use $d(u,v)$ instead of $d_G(u,v)$. A vertex w resolves two vertices u and v if $d(u,w)\ne d(v,w)$. The code of a vertex u with respect to an ordered set $R=\{r_1,r_2,\dots ,r_k\}\subset V\left(G\right)$ is the $k-$tuple $c\left(u\right|R)=(d(u,r_1),d(u,r_2),\dots ,d(u,r_k))$. The set R is called a resolving set (RS) if for every two distinct vertices u, v in G, $c\left(u\right|R)\ne c(v\left|R\right)$. Equivalently, R is said to be a resolving set for G if for every two distinct vertices u and v in $V\left(G\right)$, there is a vertex w in R that resolves u and v. The minimum cardinality of a resolving set of G is called the metric  dimension of G and it is denoted by $\beta \left(G\right)$.

Harry and Melter [1] and Slater [2] presented metric dimension concepts independently. The metric basis for a graph G is the resolving set of G containing the minimum number of vertices. Elements of metric bases were called censors in an application given in [3]. For a general graph, finding the metric dimension is an NP-hard problem. In [4], Khuller et al. provided a construction that proves that the graph’s metric dimension is NP-hard. It is important to note that metric bases can be utilized in a wide variety of applications, including robot navigation, network optimization, and sensor networks, all of which are heavily used by different government organizations. However, they still have some reservations because if some detectors (elements of the metric basis) are faulty, it will not be possible to identify the nodes (or vertices) uniquely. A malfunctioning censor will not give us enough information to deal with an intruder (fire, thief, etc). Hernando et al. introduced a fault-tolerant metric dimension in order to address these kind of problems and in order to improve the accuracy of detection or robustness of the system [5]. A resolving set F of a graph G is a fault-tolerant  resolving  set (FTRS) if for each $v\in F$, $F\setminus \left\{v\right\}$ is also a resolving set for G. The fault-tolerant  metric  dimension of G, denoted by ${\beta }^{\prime }\left(G\right)$, is the minimum cardinality of a fault-tolerant resolving set. A fault-tolerant resolving set of order ${\beta }^{\prime }\left(G\right)$ is called a fault-tolerant  metric  basis. Fault-tolerant metric dimensions are NP-hard problems. Determining the fault-tolerant metric dimension of a graph is an interesting yet difficult combinatorial problem with potential applications to censor networks. So far, it has been explored for a few basic families of graphs. In their introductory paper [5], Hernendo et al. have characterized the fault-tolerant resolving sets in a tree T. They have also shown that the fault-tolerant metric dimension is bounded by a function of the metric dimension (independent of any graph) as ${\beta }^{\prime }\left(G\right)⩽\beta \left(G\right)(1+2·5^{\beta \left(G\right)-1})$ for every graph’s G. In [6], Javaid et al. determined the fault-tolerant metric dimension for a cycle $C_n$. Basak et al. [7] determine the fault-tolerant metric dimension of $C_n^3$.

Due to their interesting properties and wide range of applications, the power graph has been widely studied in the past. Power graphs can be applied in different fields such as routing in networks, quantum random walk in physics, etc. The problem of the metric dimension or fault-tolerant metric dimension of the power of graphs has also been considered in the past. For the power of paths, Alholi et al. [8] have determined some exact value and upper bound for the metric dimension of the power of paths as follows: $\beta \left(P_n^k\right)\le k$, $\beta \left(P_n^3\right)=3$, $\beta \left(P_n^4\right)=4$. Basak et al. [7] studied and envisioned the fault-tolerant metric dimension for the circulant graphs $C_n(1,2,3)$, which are basically the 3rd power of cycles. Saha et al. in [9] calculated the metric dimension of the power of finite paths and also characterized all metric bases for the same. There are several interesting recent results on this topic; see [10,11,12]. Due to the widespread applications of power graphs and motivated by the above results, in this article, we study an optimal fault-tolerant resolving set of $P_n^r$.

The rest of the paper is organized as follows: Firstly, Section 2 presents a detailed explanation of the various terms and expressions we will use later on to establish the corresponding basic results for the fault-tolerant metric dimension of $P_n^r$. In Section 3, we have given some basic properties and results of the resolving set and fault-tolerant resolving set of $P_n^r.$ We have proven certain essential lemmas that facilitate the determination of the resolving set and fault-tolerant set of $P_n^r$. Moreover, in this section, we have presented an algorithm to construct a fault-tolerant resolving set of $P_m^r$ from a fault-tolerant resolving set of $P_n^r$ when $m<n$. In Section 4, we determine fault-tolerant resolving sets of $P_n^r$ and have given different examples in support of our results. In Section 5, we presented the lower bounds of ${\beta }^{{}^{\prime }}\left(P_n^r\right)$ for all n and r and then show the optimality of the FTRS presented in Theorems 1 and 2. In Section 6, we applied lower and upper bounds presented in Section 4 and Section 6 to $P_n^r$, where $r\in \{2,3,4,5,6,8\}$. Our bounds have been verified with some examples. We have used an algorithm (Algorithm 1) to construct an optimal fault-tolerant resolving set of $P_n^r$, when $r(r-1)+2\le n\le 2r(r-1)+1$, from an optimal fault-tolerant resolving set of $P_{2r(r-1)+2}^r$. In the concluding remarks, we have announced an open problem.

2. Preliminaries and Notations

In this section, we give some definitions, notations, and lemmas that will be beneficial for a better understanding of the paper and its contents. We denote the vertices of $P_n^r$ by $v_0,v_1,\dots ,v_{n-1}$. The distance between two vertices $v_i$ and $v_j$ in $P_n^r$ is given by $d(v_i,v_j)=⌈\frac{\left|i-j\right|}{r}⌉$ and hence the diameter of $P_n^r$ is $⌈\frac{n-1}{r}⌉$. A vertex $v_i$ is the left-side or right-side vertex of a vertex $v_{\ell }$ according to $i<\ell$ and $i>\ell$.

The following lemma gives the basic property of a fault-tolerant resolving set for an arbitrary graph.

Lemma 1

([6]). A set $F\subset V\left(G\right)$ is a fault-tolerant resolving set of G if and only if every pair of vertices in G is resolved by at least two vertices of F.

Notation 1.

We denote $W_{a,a+1}$ as the set of all vertices that resolve the consecutive vertices $v_a$ and $v_{a+1}$.

Remark 1.

If F is any fault-tolerant resolving set for $P_n^r$, then every pair of vertices must be resolved by at least two elements of F due to Lemma 1, that is, $|F\cap W_{a,a+1}|\ge 2$ for every fault-tolerant resolving set F of $P_n^r$ and for every pair of vertices $v_a$ and $v_{a+1}$.

Definition 1.

For $m\in \{2,3,\dots ,r+1\}$, define $K_m^j$ to be the complete subgraph of $P_n^r$ induced by $\{v_j,v_{j+1},\dots ,$$v_{j+m-1}\}$. For the clique $K_m^j$, we call the vertices $v_j$, $v_{j+m-1}$ as the end  vertices and the others are intermediate  vertices of $K_m^j$. For a clique $K_m^i$, we denote $I\left(K_m^i\right)$ as the set of all intermediate vertices of $K_m^i$.

Definition 2

(Distance-hereditary graph). A graph G is called a distance-hereditary graph if distances in any connected induced subgraph are the same as they are in the original graph G.

Definition 3.

In $P_n^r$, a vertex $v_j$ is calleds-class  element, if $j\equiv s(modr)$, where $0\le s\le r-1$. We shall denote $V^s\left(P_n^r\right)$ as the set of all s-th class elements in $P_n^r$. Note that $V\left(P_n^r\right)={\cup }_{s=0}^{r-1}{V}^s\left(P_n^r\right)$. The largest s-th class element is the s-th class vertex $v_{\ell }$ with a maximum index ℓ. For example, in $P_{16}^3$,

$$\begin{array}{ccc}\hfill V^0\left(P_{16}^3\right)& =& \{v_0,v_3,v_6,v_9,v_{12},v_{15}\},\hfill \\ \hfill V^1\left(P_{16}^3\right)& =& \{v_1,v_4,v_7,v_{10},v_{13}\},\hfill \\ \hfill V^2\left(P_{16}^3\right)& =& \{v_2,v_5,v_8,v_{11},v_{14}\}.\hfill \end{array}$$

The largest 0-class element is $v_{15}$ in $P_{16}^3$, whereas the largest 1-class element is $v_{13}$ in $P_{16}^3$. Note that $V\left(P_{16}^3\right)=V^0\left(P_{16}^3\right)\cup V^1\left(P_{16}^3\right)\cup V^2\left(P_{16}^3\right)$.

Proposition 1.

Let $a,b$ and r be three positive integers, where both a and b are greater that r. Then, $⌈\frac{a}{r}⌉\ne ⌈\frac{b}{r}⌉$ if and only if $min\{a,b\}$ is a multiple of r.

The workflow of the article may be stated as follows. To prove a set W is an RS, we need to verify the globalized conditions in which each pair of vertices is resolved by some vertex of $W.$ First, we transform these globalized conditions into localized conditions in Lemma 3. After that, we show that ${\beta }^{\prime }\left(P_n^r\right)$ is a non-decreasing function with n (see Lemma 5 and Algorithm 1). Finally, we search for a revolving set F which resolves each consecutive pair vertices of $P_n^r$ by at least two elements of F (see Theorem 1, Theorem 2). To test the optimality of the FTRS presented in Theorems 1 and 2, we give lower bounds in Section 5.

3. Some Basic Properties of RS and FTRS of ${\mathit{P}}_{\mathit{n}}^{\mathit{r}}$

In this section, we give some basic properties and results of the resolving set and fault-tolerant resolving set of $P_n^r.$ We have proved certain essential lemmas that are beneficial for determining the resolving set and fault-tolerant set of $P_n^r$. We have also provided an algorithm to construct a fault-tolerant resolving system of $P_m^r$ from a fault-tolerant resolving system of $P_n^r$ when $m<n$.

Definition 4.

For a fault-tolerant resolving set F, the location of an element $u\in F$, we mean the position of u in F. For every fault-tolerant resolving set F of $P_n^r$, there is an arrangement of vertices $v_{i_1},v_{i_2},\dots ,v_{i_m}$ in F such that $i_1<i_2<\dots <i_m$ and location of $v_{i_{\ell }}$ is ℓ.

In the lemma below, we determine the vertices which resolve two consecutive vertices of $P_n^r$.

Lemma 2.

For any two vertices $v_a$ and $v_{a+1}$,

$$W_{a,a+1}=\{v_j:j\equiv a(modr),0\le j\le a\}\cup \{v_j:j\equiv a+1(modr),a+1\le j\le n-1\}.$$

Proof. 

Let $v_{\ell }$ be a vertex that resolved $v_a$ and $v_{a+1}$. The distances of $v_a$ and $v_{a+1}$ from $v_{\ell }$ are given by

$$\begin{array}{c}\hfill d(v_a,v_{\ell })=⌈\frac{|a-\ell |}{r}⌉,d(v_{a+1},v_{\ell })=⌈\frac{|a+1-\ell |}{r}⌉.\end{array}$$

Using Proposition 1, we obtain the following result:    □

Corollary 1.

For two non-negative integers a and b with $a<b$,

$$W_{a,a+1}\cap W_{b,b+1}=\left\{\begin{array}{cc}\left\{v_{a+1}\right\}\hfill & \mathit{if}b=a+1,\hfill \\ Ø\hfill & \mathit{if}a+2\le b\le a+r-1.\hfill \end{array}\right.$$

Lemma 3.

A set $W\subset V\left(P_n^r\right)$ is a resolving set of $P_n^r$ if and only if it resolves every pair of consecutive vertices of $P_n^r$.

Proof. 

If W is a resolving set, then it must resolve every pair of consecutive vertices of $P_n^r$. So, we assume W resolves every consecutive vertex of $P_n^r$. We show that W is a resolving set for $P_n^r$. Let $v_i$ and $v_j$ be two arbitrary non-consecutive vertices in $P_n^r$. With no loss of generality, we assume $i<j$. We consider the following two cases.

Case 1. $j-i\le r$. Then, the vertices $v_i$ and $v_j$ are in the same clique, say K. Let $v_{\ell }$ resolve the pair $(v_i,v_{i+1})$. Then, using Lemma 2, either $\ell <i$ with $\ell \equiv i(modr)$ or $\ell \ge i+1$ with $\ell \equiv i+1(modr)$. Thus, we consider two sub-cases.

Case 1.1. $\ell <i$ with $\ell \equiv i(modr)$. Here, we assume $\ell \equiv s(modr)$. Then, $\ell =rm+s$ and $i=rq+s$ and so, we have

$$\begin{array}{c}\hfill d(v_{\ell },v_i)=q-m,d(v_{\ell },v_j)=⌈\frac{j-\ell }{r}⌉\ge ⌈\frac{i+2-\ell }{r}⌉=⌈\frac{r(q-m)+2}{r}⌉=q-m+1.\end{array}$$

Thus, $v_{\ell }$ resolves the pair $(v_i,v_j)$.

Case 1.2. $\ell \ge i+1$ with $\ell \equiv i+1(modr)$. First, we take $\ell \ne i+1$. Then, $\ell >j$ as $j-i\le r$. Let $\ell \equiv s(modr)$. Then, $\ell =rm+s$ and $i+1=rq+s$ for some non-negative integers m and q. Now, the distances of $v_i$ and $v_j$ from $v_{\ell }$ are given by

$$\begin{array}{c}\hfill d(v_{\ell },v_i)=m-q+1,d(v_{\ell },v_j)=⌈\frac{\ell -j}{r}⌉\le ⌈\frac{\ell -i-1}{r}⌉=⌈\frac{r(m-q)}{r}⌉=m-q.\end{array}$$

Thus, $v_{\ell }$ resolves the pair $(v_i,v_j)$ when $\ell \ne i+1$. If $\ell =i+1$, then $v_{\ell }$ cannot resolve the pair $(v_i,v_j)$ as $d(v_{\ell },v_i)=1=d(v_{\ell },v_j)$. Then, by similar argument, it can be shown that the vertex $v_{{\ell }^{\prime }}$ resolves the pairs $(v_i,v_j)$, where $v_{{\ell }^{\prime }}$ is the vertex that resolves the pair of consecutive vertices $(v_{i-1},v_i)$.

$\mathbf{Case}\mathbf{2}.$ $j-i>r$. If W consists of a vertex $v_{\ell }$ such that either $\ell \ge j$ or $\ell \le i$, then $d(v_{\ell },v_i)\ne d(v_{\ell },v_j)$ because

$$\begin{array}{c}\hfill d(v_{\ell },v_j)=⌈\frac{j-\ell }{r}⌉\ge ⌈\frac{i+r-\ell }{r}⌉=d(v_{\ell },v_i)+1\mathrm{when}\ell \le i,\end{array}$$

and

$$\begin{array}{c}\hfill d(v_{\ell },v_i)=⌈\frac{\ell -i}{r}⌉\ge ⌈\frac{\ell -j+r}{r}⌉=d(v_{\ell },v_j)+1\mathrm{when}\ell \ge j.\end{array}$$

When all the vertices are between $v_i$ and $v_j$, then we can prove the result by using a similar argument as shown in $\mathbf{Case}\mathbf{1}$.    □

Lemma 4.

A set $F\subset V\left(P_n^r\right)$ is an FTRS of $P_n^r$ if and only if for each of the consecutive vertices u and v of $P_n^r$, there are at least two elements of F that resolve u and v.

Proof. 

Using Lemmas 1 and 3, we obtain the result.    □

Lemma 5.

If $P_{n+1}^r$ has an FTRS having the cardinality p, then $P_n^r$ has also an FTRS with the cardinality p. In particular, ${\beta }^{\prime }\left(P_n^r\right)\le {\beta }^{\prime }\left(P_{n+1}^r\right)$.

Proof. 

Let F be an FTRS of $P_{n+1}^r$. Note that $P_n^r$ is a distance-hereditary graph. If $v_n\notin F$, then F will also be an FTRS of $P_n^r$. Hence the result is true in this case. So we assume $v_n\in F$. Let ℓ be the largest index such that $\ell \equiv n(modr)$. Let us define a set $F_1$ by

$$F_1=\left\{\begin{array}{cc}F\cup \left\{v_{\ell }\right\}\setminus \left\{v_n\right\}\hfill & \mathrm{if}{v}_{\ell }\notin F,\hfill \\ F\cup \left\{v_{n(modr)-1}\right\}\setminus \left\{v_n\right\}\hfill & \mathrm{if}{v}_{\ell }\in F\mathrm{and}n\not\equiv 0(modr),\hfill \\ F\cup \left\{v_{r-1}\right\}\setminus \left\{v_n\right\}\hfill & \mathrm{if}{v}_{\ell }\in F\mathrm{and}n\equiv 0(modr).\hfill \end{array}\right.$$

Our claim $F_1$ is an FTRS of $P_n^r$. Due to Lemma 4, it is sufficient to prove that every pair of consecutive vertices are resolved by at least two elements of $F_1$. Let $(v_{i-1},v_i)$ be a pair consecutive vertices. If $i\not\equiv n(modr)$, then $v_n$ can not resolve this pair due to Lemma 2. Therefore, there exists at least two vertices $v_x$ and $v_y$ in $F\setminus \left\{v_n\right\}$ that resolve the pair $(v_{i-1},v_i)$. Hence, this pair is resolved by two elements of $F_1$ when $i\not\equiv n(modr)$. So, we assume $i\equiv n(modr)$. Since F is a fault-tolerant resolving set of $P_n^r$, so there exists a vertex $v_x$ ($x\ne n$) that resolve $(v_{i-1},v_i)$. Then due to Lemma 2, either $v_x$ is a left side vertex of $v_{i-1}$ with $x\equiv i-1(modr)$ or $v_x$ is a right side vertex of $v_i$ with $x\equiv i(modr)$. In any case the pair $(v_{i-1},v_i)$ are resolved by at least two elements of F when $i\equiv n(modr)$. This completes the proof.    □

Algorithm to Construct an FTRS of $P_m^r$ from an FTRS of $P_n^r$, Where $m<n$

In this section, we have presented an algorithm to construct an FTRS of $P_m^r$ from an FTRS of $P_n^r$, where $m<n$. In this algorithm, the cost of Step III is $O\left(r\right)$ and the cost of Step V is $O\left(\right|F\left|\right)$. These are the most expensive cases. So our proposed algorithm has linear time complexity.

Remark 2.

Using Lemma 5 we can prove the correctness of the proposed algorithm (Algorithm 1).

Algorithm 1: Construction of an FTRS of $P_m^r$ from an FTRS of $P_n^r$, where $m<n$

Input: A k-size FTRS $F=\left\{v_{i_1},v_{i_2},\dots ,v_{i_k}\right\}$ for $P_n^r$, where $i_1<i_2<\dots <i_k$. Initialization: The set $V\left(P_n^r\right)=\{v_0,v_1,\dots ,v_{n-1}\}$ and $V\left(P_m^r\right)=\{v_0,v_1,\dots ,v_{m-1}\}$, where $m<n$. Step I: If $F\setminus V\left(P_m^r\right)=Ø$, then go to Step-VII. Step II: For a vertex $u\in F\setminus V\left(P_m^r\right)$, calculate the class of u, say it is a-class element. Step III: Find the largest a-class element in $P_m^r$, say it is $v_{\ell }$. Step IV: Update F by $$F=\left\{\begin{array}{cc}F\cup \left\{v_{\ell }\right\}\setminus \left\{u\right\}\hfill & \mathrm{if}{v}_{\ell }\notin F,\hfill \\ F\cup \left\{v_{a-1}\right\}\setminus \left\{u\right\}\hfill & \mathrm{if}{v}_{\ell }\in F\mathrm{and}a\ne 0,\hfill \\ F\cup \left\{v_{r-1}\right\}\setminus \left\{u\right\}\hfill & \mathrm{if}{v}_{\ell }\in F\mathrm{and}a=0.\hfill \end{array}\right.$$ Step V: Remove duplicate elements from F. Step VI: Repeat Step I to Step IV with the new F. Step VII: F is an FTRS.

Example 1.

In this example, we explain the intermediate stages of our presented algorithm by taking the graphs $P_{21}^5$ and $P_{41}^5$. We start with the FTRS of $P_{41}^5$ as $F=\{v_4,v_8,v_{12},v_{16},v_{20},$ $v_{24},v_{28},v_{32},v_{36}\},V(P_{41}^5)=\{v_0,v_1,\dots ,v_{40}\}$ and $V\left(P_{21}^5\right)=\{v_0,v_1,\dots ,v_{20}\}$.

Step I:

Here, $v_{24}\in F\setminus V\left(P_{21}^5\right)$ and it is a 4-class element of $V\left(P_{41}^5\right)$.

Step II:

 The vertex $v_{19}$ is the largest 4-class element of $V\left(P_{21}^5\right)$ and $v_{19}\notin F$.

Step III:

So, we update F by replacing $v_{24}$ by $v_{19}$ (according to Step IV of Algorithm 1).

Step IV:

Repeat Step I to Step III for the vertices $v_{28}$ and $v_{32}$ and update F by replacing $v_{28}$ by $v_{18}$ and replacing $v_{32}$ by $v_{17}$. However, for the vertex $v_{36}$ we obtain $v_{16}$ as the largest class element of $V\left(P_{21}^5\right)$ and $v_{16}\in F$. So, here, we update F by replacing $v_{36}$ by $v_0$ (according to STEP-IV of Algorithm 1).

OUTPUT:

$F=\{v_4,v_8,v_{12},v_{16},v_{20},v_{19},v_{18},v_{17},v_0\}$ is an FTRS for $P_{21}^5$.

Example 2.

In this example, we explain the intermediate stages of our presented algorithm by taking the graphs $P_{26}^5$ and $P_{41}^5$. We start with the FTRS $F=\{v_4,v_8,v_{12},v_{16},v_{20},v_{24},v_{28},v_{32},v_{36}\}$ of $P_{41}^5$, $V\left(P_{41}^5\right)=\{v_0,v_1,\dots ,v_{40}\}$ and $V\left(P_{26}^5\right)=\{v_0,v_1,\dots ,v_{25}\}$.

Step I:

Here, $v_{28}\in F\setminus V\left(P_{26}^5\right)$ and it is a 3-class element of $V\left(P_{41}^5\right)$.

Step II:

The vertex $v_{23}$ is the largest 3-class element of $V\left(P_{26}^5\right)$ and $v_{23}\notin F$.

Step III:

So, we update F by replacing $v_{28}$ by $v_{23}$ (according to Step IV of Algorithm 1).

Step IV:

Repeat Step I to Step III for the other two elements $v_{32}$ and $v_{36}$ and update F by replacing $v_{32}$ by $v_{22}$ and by replacing $v_{36}$ by $v_{21}$.

OUTPUT:

$F=\{v_4,v_8,v_{12},v_{16},v_{20},v_{24},v_{23},v_{22},v_{21}\}$ is an FTRS for $P_{26}^5$.

4. FTRS of ${\mathit{P}}_{\mathit{n}}^{\mathit{r}}$

In this section, we determine fault-tolerant resolving sets of $P_n^r$ and jotted down different examples to justify our result. In the next section, we show that these are optimal FTRS values.

Theorem 1.

The set $F=\{v_0,v_1,\dots ,v_{2r-1}\}$ is a fault-tolerant resolving set of $P_n^r$.

Proof. 

To prove the result, we have to show that for every pair of distinct vertices u and v of $P_n^r$, there exist at least two elements in F that resolved u and v. Let $v_i$ and $v_j$ be two vertices of $P_n^r$. Without loss of generality, we assume $i<j$. If $v_i$ and $v_j$ both are in F, then we have nothing to prove because in that case, one resolves the another. We consider the following two cases according to $v_i$ and $v_j$ are in F or not.

$\mathbf{Case}\mathbf{1}.$ Both $v_i$ and $v_j$ are outside of F. Let $i\equiv s(modr)$, where $s\in \{0,1,\dots ,r-1\}$, i.e., $i=mr+s$ for some positive integer m. Define $U=\{v_s,v_{r+s}\}\subset F$. The distances of $v_i$ and $v_j$ from every vertex $v_{\ell }\in U$ are given below.

$$\begin{array}{ccc}\hfill d(v_i,v_{\ell })& =& ⌈\frac{i-\ell }{r}⌉=\left\{\begin{array}{cc}m\hfill & \mathrm{if}\ell =s,\hfill \\ m-1\hfill & \mathrm{if}\ell =r+s.\hfill \end{array}\right.\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill d(v_i,v_{\ell })& =& ⌈\frac{j-\ell }{r}⌉\ge \left\{\begin{array}{cc}m+1\hfill & \mathrm{if}\ell =s,\hfill \\ m\hfill & \mathrm{if}\ell =r+s.\hfill \end{array}\right.\left[\mathrm{as}j>i\mathrm{and}i-\ell \mathrm{is}\mathrm{multiple}\mathrm{of}r\right]\hfill \end{array}$$

Therefore, $d(v_i,v_{\ell })\ne d(v_j,v_{\ell })$ for all $v_{\ell }\in U$, i.e., $v_i$ and $v_j$ are resolved by both $v_s$ and $v_{r+s}$ whenever $i\equiv s(modr)$.

$\mathbf{Case}\mathbf{2}.$ Exactly one of $v_i$ and $v_j$ is in F. As $i<j$ and F consists of consecutive vertices starting from the lower index vertex, in this case, $v_i\in F$, and $v_j\notin F$; otherwise, $v_j\in F$ gives $v_i\in F$. Here, we show there exists an element $v_{\ell }\in F$ $(\ell \ne i)$ that resolved $v_i$ and $v_j$. Since $v_i\in F$ and $v_j\notin F$, so $0\le i\le 2r-1$ and $j\ge 2r$. We consider the following sub-cases.

Case 2.1. $0\le i\le r-1$. In this case, for each $\ell \ne i$ with $0\le \ell \le r-1$, we obtain

$$\begin{array}{ccc}\hfill d(v_i,v_{\ell })& =& 1,\hfill \\ \hfill d(v_j,v_{\ell })& =& ⌈\frac{j-\ell }{r}⌉\ge ⌈\frac{2r-(r-1)}{r}⌉\ge 2.\hfill \end{array}$$

Thus, if $0\le i\le r-1$, then $v_i$ and $v_j$ are resolved by $v_{\ell }$, where $0\le \ell \le r-1$. For better understanding, the reader may follow Example 3. In this example, we see that $d(v_{\ell },v_j)=2$ or 1, and $d(v_{\ell },v_j)\ge 2$ for all $j\ge 10$ and $0\le i,\ell \le 5.$

Case 2.2. $r\le i\le 2r-1$. In this case, $v_{i-r}\in F$ and

$$\begin{array}{ccc}\hfill d(v_i,v_{i-r})& =& 1,\hfill \\ \hfill d(v_j,v_{i-r})& =& ⌈\frac{j+r-i}{r}⌉\ge ⌈\frac{3r-(2r-1)}{r}⌉\ge 2.\hfill \end{array}$$

Thus, in this case, $v_i$ and $v_j$ are resolved by $v_{i-r}$. □

Example 3.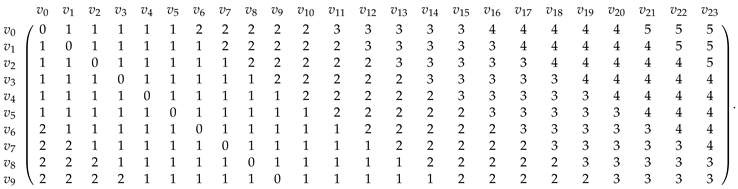

In the following, we construct the code matrix $C\left(P_{24}^5\right)$ of $P_{24}^5$ with respect to $F=\{v_0,v_1,\dots ,v_9\}$. In this matrix, the i-th column, $0\le i\le 23$, represents the code of the vertex $v_i$ with respect to the set F.

From this code matrix, we see that every pair of vertices is resolved by at least two elements of F. For example, the vertices $v_{10}$ and $v_{11}$ are resolved by $v_0$ and $v_5$. More generally, any pair $(v_i,v_{i+1})$ of two consecutive vertices which are not in F is resolved by exactly two elements of F, namely, $v_{i(mod5)}$ and $v_{5+i(mod5)}$. The pair $(v_8,v_{19})$ is resolved by every vertex of F. More generally, the pair $(v_i,v_j)$ with $|i-j|\ge 11$ is resolved by every vertex of F.

Theorem 2.

There exists a fault-tolerant resolving set of $P_n^r$ with a cardinality of $2r-1$ if $r(r-1)+2\le n\le 2r(r-1)+1$.

Proof. 

Since ${\beta }^{\prime }\left(P_m^r\right)\le {\beta }^{\prime }\left(P_n^r\right)$ for $m\le n$ due to Lemma 5, it is sufficient to show that there is an FTRS of $P_{2r(r-1)+1}^r$ with the cardinality $2r-1$. Our claim is to show that the set $F=\{v_{\ell (r-1)}:1\le \ell \le 2r-1\}$ is an FTRS of $P_{2r(r-1)+1}^r$. To determine the classes of the elements of F, we may write $\ell (r-1)$, where $1\le \ell \le 2r-1$, as in below

$$\begin{array}{c}\hfill \ell (r-1)=\left\{\begin{array}{cc}(\ell -1)r+r-\ell \hfill & \mathrm{for}1\le \ell \le r,\hfill \\ (\ell -2)r+2r-\ell \hfill & \mathrm{if}r+1\le \ell \le 2r-1.\hfill \end{array}\right.\end{array}$$

Thus, $\left|F\cap V^s\left(P_n^r\right)\right|=2$ for each $s\in \{1,2,\dots ,r-1\}$ and $\left|F\cap V^0\left(P_n^r\right)\right|=1$. In addition, the first and the last elements in F are $r-1$ class and 1 class, respectively. First, we show that any two consecutive vertices of $P_{2r(r-1)+1}^r$ are resolved by at least two elements of F. Let $v_i$ and $v_{i+1}$ be two consecutive vertices of $P_{2r(r-1)+1}^r$. Then, $0\le i\le 2r(r-1)-1$. We consider the following cases.

$\mathbf{Case}\mathbf{1}.$ $0\le i\le r-1$. The pair $(v_{r-1},v_r)$ is resolved by the vertices $v_{r-1}$ and $v_{r(r-1)}$. Thus, we assume $0\le i\le r-2$. Then, both the vertices $v_{(r-(i+1\left)\right)(r-1)}$ and $v_{(2r-(i+1\left)\right)(r-1)}$ are in $F\cap V^{i+1}\left(P_{2r(r-1)+1}^r\right)$. In addition, note that these two vertices are on the right side of the pair $(v_i,v_{i+1})$. Thus, by using Lemma 2, the pair $(v_i,v_{i+1})$ are resolved by both the vertices $v_{(r-(i+1\left)\right)(r-1)}$ and $v_{(2r-(i+1\left)\right)(r-1)}$.

$\mathbf{Case}\mathbf{2}.$ $(2r-1)(r-1)\le i\le 2r(r-1)-1$. The pair $\left(v_{(2r-1)(r-1)},v_{(2r-1)(r-1)+1}\right)$, if taken, is resolved by both the vertices $v_{(r-1)(r-1)}$ and $v_{(2r-1)(r-1)}$ of F. So, we assume $(2r-1)(r-1)+1\le i\le 2r(r-1)-1$. Then, $v_i\in V^s\left(P_{2r(r-1)+1}^r\right)$ for some integer s with $1\le s\le r-1$. Thus, we may assume $i\equiv s(modr)$, where $1\le s\le r-1$. Then, the vertices $v_{(r-s)(r-1)}$ and $v_{(2r-s)(r-1)}$ are in $F\cap V^s\left(P_{2r(r-1)+1}^r\right)$. In addition, both the elements are on the left side of the pair $(v_i,v_{i+1})$. By using Lemma 2, in this case, the pair $(v_i,v_{i+1})$ is resolved by both the vertices $v_{(r-s)(r-1)}$ and $v_{(2r-s)(r-1)}$ of F.

$\mathbf{Case}\mathbf{3}.$ $r\le i\le (2r-1)(r-1)-1$. Let $i\equiv s(modr)$, where $0\le s\le r-1$. We consider the following sub-cases.

Case 3.1. $s\in \{1,2,\dots ,r-2\}$. Recall that $\left|F\cap V^s\left(P_n^r\right)\right|=2$. If the two elements of $F\cap V^s\left(P_n^r\right)$ are in the left side of the pair $(v_i,v_{i+1})$ or the two elements of $F\cap V^{s+1}\left(P_n^r\right)$ are in the right side of $(v_i,v_{i+1})$, then Lemma 2 gives that the pair $(v_i,v_{i+1})$ is resolved by two elements of F. Again, if at least one element of $F\cap V^s\left(P_n^r\right)$ is in the left side of the pair $(v_i,v_{i+1})$ and at least one element of $F\cap V^{s+1}\left(P_n^r\right)$ is in the right side of $(v_i,v_{i+1})$, then by the same lemma, this pair is resolved by two elements of F. The largest $s+1$-class element of F is $v_{(2r-(s+1\left)\right)(r-1)}$ and the smallest s-class element of F is $v_{(r-s)(r-1)}$. Now, we show that the following statement does not hold for F: “All elements of $F\cap V^{s+1}\left(P_n^r\right)$ are in the left side of the pair $(v_i,v_{i+1})$ and all the elements of $F\cap V^s\left(P_n^r\right)$ are in the right of $(v_i,v_{i+1})$”. If all the elements of $F\cap V^{s+1}\left(P_n^r\right)$ are in the left side of the pair $(v_i,v_{i+1})$ and all the elements of $F\cap V^s\left(P_n^r\right)$ are in the right of $(v_i,v_{i+1})$, then $(2r-(s+1\left)\right)(r-1)\le i\le (r-s)(r-1)$, which is not possible because $r\ge 2$. Thus, in this case, the pair $(v_i,v_{i+1})$ is resolved by at least two vertices of F.

Case 3.2. $s\in \{0,r-1\}$. First, we assume $s=0$. If $i\le (r-1)(r-1)-1$, then $v_{(r-1)(r-1)}$ and $v_{(2r-1)(r-1)}$ resolved the pair $(v_i,v_{i+1})$ due to Lemma 2. Since $(r-1)(r-1)-1\equiv 0(modr)\equiv i(modr)$, so we take $i\ge r(r-1)$. By using same lemma, this pair is resolved by $v_{r(r-1)}$ and $v_{(2r-1)(r-1)}$, provided $r(r-1)\le i\le (2r-1)(r-1).$ By similar argument, we can prove the result when $s=r-1$. □

Example 4.

In this example, we construct an optimal FTRS of $P_{13}^3$ as presented in Theorem 2. Here, $r=3$ and $n=13$, so $n=6·2+1=2r(r-1)+1$. According to Theorem 2, the set F is given by

$$\begin{array}{c}\hfill F=\{v_{2i}:1\le i\le 5\}=\{v_2,v_4,v_6,v_8,v_{10}\}.\end{array}$$

Note that $F\cap V^0\left(P_{13}^3\right)=\left\{v_6\right\}$, $F\cap V^1\left(P_{13}^3\right)=\{v_4,v_{10}\}$ and $F\cap V^2\left(P_{13}^3\right)=\{v_2,v_8\}$. According to $\mathbf{Case}\mathbf{1}$ of Theorem 2, each element of $\{v_2,v_6\}$ resolves the vertices $v_2$ and $v_3$, and each vertex of $\{v_4,v_{10}\}$ resolves vertices $v_0$ and $v_1$ (see the code matrix $C\left(P_{13}^3\right)$). As for $\mathbf{Case}\mathbf{2}$ of Theorem 2, the pair $(v_{10},v_{11})$ is resolved by the vertices $v_4$ and $v_{10}$. From the code matrix $C\left(P_{13}^3\right)$ with respect to $F=\{v_2,v_4,v_6,v_8,v_{10}\}$, we see that every pair of vertices is resolved by at least two elements of F, where

5. Lower Bounds of ${\mathit{\beta }}^{\mathit{\prime }}\mathbf{\left(}{\mathit{P}}_{\mathit{n}}^{\mathit{r}}\mathbf{\right)}$

Theorems 1 and 2 give two fault-tolerant resolving sets for $P_n^r$. However, the question that can be posed is: are these optimal? In this section, first, we determine lower bounds of ${\beta }^{\prime }\left(P_n^r\right)$ for all n and r, and then, we show that the FTRS presented in Theorems 1 and 2 are optimal for all most all values of n. To present lower bounds, we need the following notations, lemmas and definitions.

Lemma 6.

Let F be fault-tolerant resolving set for $P_n^r$ and $K_{r+1}$ be a clique in $P_n^r$. If $F\cap I\left(K_{r+1}\right)=Ø$, then $\left|F\right|\ge 2r$, where $I\left(K_{r+1}\right)$ denotes the set of all intermediate vertices of $K_{r+1}$.

Proof. 

Let $V\left(K_{r+1}\right)=\{v_i,v_{i+1},\dots ,v_{i+r-1},v_{i+r}\}$. So, $I\left(K_{r+1}\right)=\{v_{i+1},\dots ,v_{i+r-1}\}$. Since $F\cap I\left(K_{r+1}\right)=Ø$, applying Corollary 1, we have $(F\cap W_{a,a+1})\cap (F\cap W_{a+1,a+2})=Ø$ for each $a\in \{i,i+1,\dots ,i+r-2\}$. Again, from Remark 1, we have $|F\cap W_{a,a+1}|\ge 2$ for every $a\in \{i,i+1,\dots i+r-1\}$. Hence, we obtain the result as $(F\cap W_{a,a+1})\cap (F\cap W_{a+1,a+2})=Ø$ for each $a\in \{i,i+1,\dots ,i+r-2\}$. □

Lemma 7.

For any fault-tolerant resolving set F and a clique $K_{r+1}$, $\left|F\right|\ge 2r-|F\cap I(K_{r+1}\left)\right|$, where $I\left(K_{r+1}\right)$ denotes the set of all intermediate vertices of $K_{r+1}$.

Proof. 

Let $V\left(K_{r+1}\right)=\{v_i,v_{i+1},\dots ,v_{i+r-1},v_{i+r}\}$. For a fault-tolerant resolving set F with $F\cap V\left(K_{r+1}\right)=Ø$, $\left|F\right|\ge 2r$ due to Lemma 6. Now, our claim is that if $v_{\ell }\in I\left(K_{r+1}\right)\cap F$, then the cardinality of F is reduced by at most one. Let $F\cap I\left(K_{r+1}\right)=\left\{v_{\ell }\right\}$. Let $F_1=F\setminus \left\{v_{\ell }\right\}$. Then, $|W_{a,a+1}\cap F_1|\ge 2$ or $|W_{a,a+1}\cap F_1|\ge 1$ according to $a\in \{i,i+1,\dots ,i+r-1\}\setminus \{\ell -1,\ell \}$ or $a\in \{\ell -1,\ell \}$. Thus, $|F_1|\ge 2(r-2)+2$ and consequently, $\left|F\right|\ge 2r-1$. Hence, the result is true for $|F\cap I(K_{r+1}\left)\right|=1$. □

Corollary 2.

Let F be the FTRS of $P_n^r$ having $2r-a$ elements. Then, for every clique $K_{m+1}$, $\left|F\cap I\left(K_{m+1}\right)\right|\ge 2m-2r+a$.

From here onward, we denote $K_{p+1}^{\ell }$ as the clique with the vertex set ${\displaystyle \{}{v}_{\ell },v_{\ell +1},\dots ,v_{\ell +p}{\displaystyle \}}$.

Lemma 8.

Let F be a fault-tolerant resolving set for $P_n^r$ consisting of a gap r or more; then, $\left|F\right|\ge 2r$.

Proof. 

Since F has a gap r or more, there exists vertices $v_{i+1},\dots ,v_{i+r-1}$ which are not in F. Now, consider the clique $K_{r+1}$ with $V\left(K_{r+1}\right)=\{v_i,v_{i+1},\dots ,v_{i+r}\}$. Then, $F\cap I\left(K_{r+1}\right)=Ø$ and so applying Lemma 6, we have $\left|F\right|\ge 2r$. □

Lemma 9.

Let $n\ge 2r(r-1)+2$. Then, every fault-tolerant resolving set for $P_n^r$ has a cardinality of at least $2r$.

Proof. 

Let F be a fault-tolerant resolving set of $P_n^r$ with cardinality m. Without loss of generality, we may assume $F=\{v_{i_1},v_{i_2},\dots ,v_{i_m}\}$, where $i_1<i_2<\dots <i_m$. We consider the following two cases.

$\mathbf{Case}\mathbf{1}.$ F consists of an internal gap with a size r or more. In this case, $i_{\ell +1}-i_{\ell }\ge r$ for some $\ell \in \{1,2,\dots ,m-1\}$; then, $F\cap I\left(K_{r+1}\right)=Ø$, where $V\left(K_{r+1}\right)=\{v_{i_{\ell }},v_{i_{\ell }+1},\dots ,v_{i_{\ell }+r-1},v_{i_{\ell }+r}\}$. Then, applying Lemma 6 to the clique $K_{r+1}$, we obtain $\left|F\right|\ge 2r$.

$\mathbf{Case}\mathbf{2}.$ F does not have any internal gap with size r or more. In this case, $i_{\ell +1}-i_{\ell }\le r-1$ for every $\ell \in \{1,2,\dots ,m-1\}$. Our claim is that an external gap exists with size r or more. Since $i_{\ell +1}-i_{\ell }\le r-1$ for each $\ell \in \{1,2,\dots ,m-1\}$, we obtain

$$\begin{array}{c}\hfill i_m-i_1\le (m-1)(r-1).\end{array}$$

(1)

We take the following two sub-cases.

Case 2.1. $i_1\ge r$. In this case, F does not contains any vertex from the segment $v_0{v}_1\dots v_{r-1}$. Let $K_{r+1}^{\prime }$ be the clique on $(r+1)$ vertices $v_0,v_1,\dots ,v_r$. Then, $F\cap I\left(K_{r+1}^{\prime }\right)=Ø$ and so applying Lemma 6 to this clique, we obtain $\left|F\right|\ge 2r$.

Case 2.2. $i_1\le r-1$. In this case, we prove the result by the contrary. Suppose that $\left|F\right|<2r$. Since $i_1\le r-1$, by using (1), we have $i_m\le m(r-1)$. Since $\left|F\right|\le 2r-1$, $m\le 2r-1$ and so $i_m\le (2r-1)(r-1)$. Since $i_m\le (2r-1)(r-1)$ and $n\ge 2r(r-1)+2$, $i_m+r-1\le n-2$. Then, $v_{i_m},v_{i_m+1},v_{i_m+2},\dots ,v_{i_m+r-1},v_{i_m+r}$ forms a clique in $P_n^r$ on $(r+1)$ vertices, and we name this clique as $K_{r+1}$. Then, applying Lemma 7 to the clique $K_{r+1}$, we have $|F\cap I(K_{r+1}\left)\right|\ge 1$, i.e., $F\cap \left\{v_{i_m+1},v_{i_m+2},\dots ,v_{i_m+r-1}\right\}\ne Ø$, which contradicts that $i_m$ is the last index such that $v_{i_m}\in F$. Thus, $\left|F\right|\ge 2r$. In view of the above cases, we obtain the result. □

Theorem 3.

The fault-tolerant metric dimension of $P_n^r$ is $2r$ provided $n\ge 2r(r-1)+2$.

Proof. 

The result follows immediately from Lemma 9 and Theorem 1. □

Definition 5.

The two vertices $v_i$ and $v_j$ in $P_n^r$ are said to be the same class elements if $i\equiv j(modr)$. For example, $v_{33}$ and $v_{41}$ are the same class elements in $P_{47}^4$.

Theorem 3 determines the fault-tolerant metric dimension of $P_n^r$ when $n\ge 2r(r-1)+2$. Now, we find the FTRS and fault-tolerant metric dimension of $P_n^r$ for smaller values of n.

Lemma 10.

Let $r(r-1)+2\le n\le 2r(r-1)+1$ and F be a fault-tolerant resolving set of $P_n^r$. Then, $\left|F\right|\ge 2r-1$.

Proof. 

We prove the lemma by the contrary. Suppose that there is a fault-tolerant resolving set F with a cardinality of at most $2r-2$. Then, $|F\cap I(K_{r+1}^i\left)\right|\ge 2$ for every $i\in \{0,r-1,2(r-1),\dots ,(r-2\left)\right(r-1\left)\right\}$ and $|F\cap I(K_r^i\left)\right|\ge 1$ for $i=(r-1)(r-1)$, which implies that $\left|F\right|\ge 2r-1$. Thus, we obtain a contradiction. □

Theorem 4.

The fault-tolerant metric dimension of $P_n^r$ is $2r-1$, provided $r(r-1)+2\le n\le 2r(r-1)+1$.

Proof. 

The result follows immediately from Lemma 10 and Theorem 2. □

On account of Theorems 3 and 4, we say that the exact value of the fault-tolerant metric dimension has been obtained when $n\ge r(r-1)+2.$ Again, in virtue of Lemma 5 and Algorithm 1, ${\beta }^{\prime }\left(P_n^r\right)\le 2r-1$ for all $n\le r(r-1)+1.$ The lemmas and theorems given below give the range of ${\beta }^{\prime }\left(P_n^r\right)$ for the values of $n\le r(r-1)+1.$

Lemma 11.

Let a be an integer such that $1\le a\le ⌊\frac{2r}{3}⌋$. If $n\ge ⌈\frac{2r-a}{a+1}⌉(r-1)+2$; then, ${\beta }^{\prime }\left(P_n^r\right)\ge 2r-a$.

Proof. 

Let F be an arbitrary fault-tolerant resolving set of $P_n^r$. If there exists a clique $K_{r+1}$ such that $\left|F\cap I\left(K_{r+1}\right)\right|\le a$, then using Lemma 7, F consists of at least $2r-a$ elements. Thus, we assume that $\left|F\cap I\left(K_{r+1}\right)\right|\ge a+1$ for every clique $K_{r+1}$ on $r+1$ vertices. The given condition $n\ge ⌈\frac{2r-a}{a+1}⌉(r-1)+2$ gives $\left(⌈\frac{2r-a}{a+1}⌉-1\right)(r-1)+r\le n-1$. Let $p=⌈\frac{2r-a}{a+1}⌉$ and $S=\{0,r-1,2(r-1),\dots ,(p-1\left)\right(r-1\left)\right\}$. Then, for each $i\in S$, we obtain

$$\begin{array}{c}\hfill |F\cap I(K_{r+1}^i\left)\right|\ge a+1.\end{array}$$

(2)

Note that $\left(F\cap I\left(K_{r+1}^i\right)\right)\cap \left(F\cap I\left(K_{r+1}^j\right)\right)=Ø$ for distinct $i,j\in S$, so using (2), we have

$$\begin{array}{ccc}\hfill \left|F\right|\ge \sum _{\ell \in S}\left|F\cap I\left(K_{r+1}^{\ell }\right)\right|& \ge & (a+1)\left|S\right|\hfill \\ & =& (a+1)p\hfill \\ & =& (a+1)⌈\frac{2r-a}{a+1}⌉\hfill \\ & \ge & 2r-a.\hfill \end{array}$$

So finally, $\left|F\right|\ge 2r-a$ for every fault-tolerant resolving set F provided $n\ge ⌈\frac{2r-a}{a+1}⌉(r-1)+2$. This completes the proof. □

Theorem 5.

For $P_n^r$, ${\beta }^{\prime }\left(P_n^r\right)\ge 2r$, provided $n\ge 2r(r-1)+2$. Moreover, ${\beta }^{\prime }\left(P_n^r\right)\ge 2r-a$ provided $⌈\frac{2r-a}{a+1}⌉(r-1)+2\le n\le ⌈\frac{2r-a+1}{a}⌉(r-1)+1$.

Proof. 

If $n\ge 2r(r-1)+2$, then applying Lemma 7, we obtain that $\left|F\right|\ge 2r$ for every fault-tolerant resolving set F of $P_n^r$. Thus, ${\beta }^{\prime }\left(P_n^r\right)\ge 2r$, provided $n\ge 2r(r-1)+2$. Applying Lemma 11, we obtain that

$$\begin{array}{c}\hfill {\beta }^{\prime }\left(P_n^r\right)\ge \left\{\begin{array}{cc}2r-a\hfill & \mathrm{if}n\ge ⌈\frac{2r-a}{a+1}⌉(r-1)+2,\hfill \\ 2r-a+1\hfill & \mathrm{if}n\ge ⌈\frac{2r-a+1}{a}⌉(r-1)+2.\hfill \end{array}\right.\end{array}$$

(3)

Inequality (3) gives the result. □

Theorem 6.

Let $n\equiv s(mod(r-1\left)\right)$ and a be a positive integer with $1\le a\le ⌊\frac{2r}{3}⌋$. If ${\beta }^{\prime }\left(P_n^r\right)=2r-a$, then the upper bound on n is as follows:

(a)

For $s\notin \{0,1\}$,

$$\begin{array}{c}\hfill n\le \left\{\begin{array}{cc}{\displaystyle ⌊\frac{4r-2s-2a+2}{a}⌋(r-1)+s}\hfill & \mathit{if}a>2(r-s+1),\hfill \\ {\displaystyle ⌊\frac{2r-a}{a}⌋(r-1)+s}\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

(b)

For $s=0$,

$$\begin{array}{c}\hfill n\le \left\{\begin{array}{cc}{\displaystyle ⌊\frac{2r-a+4}{a}⌋(r-1)}\hfill & \mathit{if}a>4,\hfill \\ {\displaystyle \left(⌊\frac{2r-a}{a}⌋+1\right)(r-1)}\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

(c)

For $s=1$,

$$\begin{array}{c}\hfill n\le \left\{\begin{array}{cc}{\displaystyle ⌊\frac{2r-a+2}{a}⌋(r-1)+1}\hfill & \mathit{if}a>2,\hfill \\ {\displaystyle \left(⌊\frac{2r-a}{a}⌋+1\right)(r-1)+1}\hfill & \mathit{otherwise}.\hfill \end{array}\right.\end{array}$$

Proof. 

By division algorithm, we may write $n=m(r-1)+s$ for some integers m and s with $0\le s\le r-2$. Let F be an FTRS such that $\left|F\right|=2r-a$. Using Lemma 7, we obtain $\left|F\cap I\left(K_{r+1}\right)\right|\ge a$ for every clique $K_{r+1}$. We consider the following two cases.

$\mathbf{Case}\mathbf{1}.$ $s\notin \{0,1\}$, i.e., $2\le s\le r-2$. Let $U=\{0,r-1,2(r-1),\dots ,(m-1\left)\right(r-1\left)\right\}$. Since $s\ge 2$, $(m-1)(r-1)+(r-1)=m(r-1)<n-1$ and so for each $i\in U$, we have the following inequality

$$\begin{array}{c}\hfill \left|F\cap \{v_{i+1},v_{i+2},\dots ,v_{i+r-1}\}\right|\ge a.\end{array}$$

(4)

Note that $F\cap \{v_i,v_{i+1},\dots ,v_{i+r-1}\}$ and $F\cap \{v_j,v_{j+1},\dots ,v_{j+r-1}\}$ are disjoint for two distinct elements i and j of U. Thus, on account of the above inequalities for all $i\in U$, we obtain $\left|F\cap \{v_1,\dots ,v_{m(r-1)}\}\right|\ge ma$. Again, if $a>2(r-s+1)$, then applying Corollary 2 to the clique on the vertices $\{v_{m(r-1)},\dots ,v_{m(r-1)+s-1}\}$, we obtain

$${\displaystyle |}F\cap \{v_{m(r-1)+1},\dots ,v_{m(r-1)+s-2}\}{\displaystyle |}\ge 2(s-1)-2r+a=a-2(r-s+1).$$

Since $\left|F\right|=2r-a$, $ma\le 2r-a$ or $ma+a-2(r-s+1)\le 2r-a$ according to $a\le 2(r-s+1)$ or $a>2(r-s+1)$. Thus, $m\le ⌊\frac{2r-a}{a}⌋$ or $m\le ⌊\frac{4r+2s-2a+2}{a}⌋$ according to $a\le 2(r-s+1)$ or $a>2(r-s+1)$. Using the maximum possible value of m in $n=m(r-1)+s$, we obtained the result.

$\mathbf{Case}\mathbf{2}.$ $s\in \{0,1\}$. We consider the following two sub-cases.

Case 2.1. $s=0$. In this case, $n=m(r-1)$. Let $U_1=\{0,r-1,\dots ,(m-2)(r-1)\}.$ Then, by similar argument as described in $\mathbf{Case}\mathbf{1}$, we obtain that the inequality

$$\begin{array}{c}\hfill \left|F\cap \{v_i,v_{i+1},\dots ,v_{i+r-1}\}\right|\ge a\end{array}$$

is true for each $i\in U_1$. Again, if $a>4$, then using Corollary 2 to the clique with vertices $\{v_{(m-1)(r-1)},\dots ,v_{m(r-1)-1}\}$, we obtain

$${\displaystyle |}F\cap \{v_{(m-1)(r-1)+1},\dots ,v_{m(r-1)-2}\}{\displaystyle |}\ge 2(r-2)-(2r-a)=a-4.$$

Thus, F consists of at least $(m-1)a+a-4$ elements or at least $(m-1)a$ according to $a>4$ or $a\le 4$. Since $\left|F\right|=2r-a$, so $(m-1)a+a-4\le 2r-a$ or $(m-1)a\le 2r-a$ according to $a>4$ or $a\le 4$. Thus, $m\le ⌊\frac{2r-a+4}{a}⌋$ or $m\le ⌊\frac{2r-a}{a}⌋+1$ according to $a>4$ or $a\le 4$. By putting the maximum possible values of m in $n=m(r-1)$ for different values of a, we obtain the result.

Case 2.2. $s=1$. In this case, $n=m(r-1)+1$. Let $U_1=\{0,r-1,\dots ,(m-2)(r-1)\}$. By a similar argument as in $\mathbf{Case}\mathbf{1}$, we have that the inequality

$$\begin{array}{c}\hfill \left|F\cap \{v_i,v_{i+1},\dots ,v_{i+r-1}\}\right|\ge a\end{array}$$

is true for each $i\in U_1$. Again, if $a>2$, then using Corollary 2 to the clique with vertices $\{v_{(m-1)(r-1)},\dots ,v_{m(r-1)}\}$, we obtain

$${\displaystyle |}F\cap \{v_{(m-1)(r-1)+1},\dots ,v_{m(r-1)-1}\}{\displaystyle |}\ge 2(r-1)-(2r-a)=a-2.$$

Then, by a similar argument as of $\mathbf{Case}\mathbf{2}.\mathbf{1}$, we obtain the result. □

6. Applications of Bounds

In this section, we apply the results of lower and upper bounds that we have obtained in previous sections for $P_n^r$, where $r\in \{2,3,4,5,6,8\}$. We have presented some examples to verify the sharpness of our bounds. Algorithm 1 is also used to construct an optimal fault-tolerant resolving set of $P_n^r$, when $r(r-1)+2\le n\le 2r(r-1)+1$, from an optimal fault-tolerant resolving set of $P_{2r(r-1)+2}^r$, which can be found from the proof of Theorem 2.

Example 5.

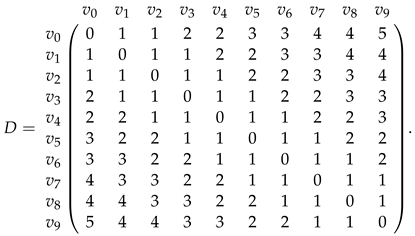
Theorem 5 gives that ${\beta }^{\prime }\left(P_n^2\right)\ge 4$ for $n\ge 6$, whereas Theorem 1 shows that ${\beta }^{\prime }\left(P_n^2\right)\le 4$. Thus, we obtain the result that the fault-tolerant metric dimension of the square of path $P_n^2$ is 4 when $n\ge 6$. In the below, we calculate the codes of each vertex for $P_{10}^2$ with respect to the fault-tolerant resolving set $F=\{v_0,v_1,v_2,v_3\}$ (Figure 1). The distance matrix D for $P_{10}^2$ has been given below.

In the matrix, D, the $(i,j)$-th entry represents the distance between $v_i$ and $v_j$. Now, if we choose a $4\times 10$ sub-matrix $D_F$ consisting of the first four rows, we have the following matrix whose $(j+1)$-th column represents the code of $v_j$ with respect to the set $F=\{v_0,v_1,v_2,v_3\}$.

In the above matrix $D_F$, every pair of columns is different in two places, and hence, F is a fault-tolerant resolving set. For example, if we take the 6-th and 7-th columns, then these two columns differ in the 2nd and 4th places. Again, if we choose a $3\times 10$ sub-matrix consisting of the first three rows, we have the following matrix whose $(j+1)$-th column represents the code of $v_j$ with respect to the set $F^{\prime }=\{v_0,v_1,v_2\}$.

Here, the 6-th and 7-th columns differ in only one place. So, $F^{\prime }$ cannot be a fault-tolerant resolving set for $P_n^2$.

Example 6.

Applying the result of Theorem 5, we have

$$\begin{array}{c}\hfill {\beta }^{\prime }\left(P_n^3\right)\ge \left\{\begin{array}{cc}6\hfill & \mathit{if}n\ge 14,\hfill \\ 5\hfill & \mathit{if}8\le n\le 13.\hfill \end{array}\right.\end{array}$$

(5)

Again, applying Theorem 1, the set $\left\{v_0,v_1,\dots ,v_5\right\}$, say F, is a fault-tolerant resolving set of $P_n^3$. Inequality (5) gives that the set F is optimal fault-tolerant when $n\ge 14$.

Table 1. Fault-tolerant metric basis of $P_n^3$ for $8\le n\le 13$.

Values of n	Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^3\right)$	Elements of Fault-Tolerant Metric Basis
8	5	$\{v_0,v_1,v_2,v_3,v_5\}$
9	5	$\{v_0,v_1,v_2,v_4,v_6\}$
$10,11$	5	$\{v_0,v_2,v_4,v_6,v_8\}$
$12,13$	5	$\{v_1,v_3,v_5,v_7,v_9\}$

gives an optimal fault-tolerant resolving set of $P_n^3$ for $8\le n\le 13$.

Example 7.

Applying Theorem 5, we obtain a lower bound for the fault-tolerant metric dimension of $P_n^4$ as

$$\begin{array}{c}\hfill {\beta }^{\prime }\left(P_n^4\right)\ge \left\{\begin{array}{cc}8\hfill & \mathit{if}n\ge 26,\hfill \\ 7\hfill & \mathit{if}14\le n\le 25,\hfill \\ 6\hfill & \mathit{if}8\le n<13.\hfill \end{array}\right.\end{array}$$

(6)

Using inequality (6) and Theorem 1, the set $\left\{v_0,v_1,\dots ,v_7\right\}$ is an optimal FTRS of $P_n^4$ provided $n\ge 26$. Again, using inequality (6) and Lemma 10, we obtain an optimal FTRS of $P_n^4$, provided $14\le n\le 25$. Using Sage-Math, we determine an optimal fault-tolerant resolving set for $P_n^4$ when $8\le n\le 12$. In

Table 2. Fault-tolerant metric basis of $P_n^4$ for $8\le n\le 25$.

Values of n	Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^4\right)$	Elements of Fault-Tolerant Metric Basis
8	6	$\{v_0,v_1,v_2,v_3,v_4,v_6\}$
$9,10$	6	$\{v_0,v_1,v_3,v_4,v_6,v_7\}$
11	6	$\{v_1,v_2,v_4,v_5,v_7,v_8\}$
12	6	$\{v_2,v_3,v_5,v_6,v_8,v_9\}$
$13,14$	7	$\{v_0,v_1,v_2,v_3,v_4,v_7,v_{10}\}$
15	7	$\{v_0,v_1,v_2,v_3,v_5,v_8,v_{11}\}$
16	7	$\{v_0,v_1,v_2,v_3,v_6,v_9,v_{12}\}$
$17,18,19$	7	$\{v_0,v_1,v_3,v_6,v_9,v_{12},v_{15}\}$
$20,21,22$	7	$\{v_0,v_3,v_6,v_9,v_{12},v_{15},v_{18}\}$
23	7	$\{v_1,v_4,v_7,v_{10},v_{13},v_{16},v_{19}\}$
24	7	$\{v_2,v_5,v_8,v_{11},v_{14},v_{17},v_{20}\}$
25	7	$\{v_3,v_6,v_9,v_{12},v_{15},v_{18},v_{21}\}$

, we show an optimal fault-tolerant resolving set of $P_n^4$ for $8\le n\le 25$.

Example 8.

Theorem 5 generates a lower bound for the fault-tolerant metric dimension of $P_n^5$ as

$$\begin{array}{c}\hfill {\beta }^{\prime }\left(P_n^5\right)\ge \left\{\begin{array}{cc}10\hfill & \mathit{if}n\ge 42,\hfill \\ 9\hfill & \mathit{if}22\le n\le 41,\hfill \\ 8\hfill & \mathit{if}14\le n\le 21,\hfill \\ 7\hfill & \mathit{if}10\le n\le 13.\hfill \end{array}\right.\end{array}$$

(7)

By similar argument as in the above example, $\left\{v_0,v_1,\dots ,v_9\right\}$ is an optimal FTRS when $n\ge 42$. From the proof of Theorem 2 and inequality (7), we can say that $\{v_4,v_8,v_{12},v_{16},v_{20},v_{24},v_{28},v_{32},v_{36}\}$ forms an optimal FTRS of $P_{41}^5$. In addition, using Algorithm 1, we can construct an FTRS of $P_n^5$ with a cardinality of 9. Thus, using (7), we obtain ${\beta }^{\prime }\left(P_n^5\right)=9$ for $22\le n\le 41$. In

Table 3. Fault-tolerant metric basis of $P_n^5$ for $12\le n\le 20$.

Values of n	Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^5\right)$	Elements of Fault-Tolerant Metric Basis
12	8	$\{v_0,v_1,v_2,v_3,v_4,v_5,v_7,v_9\}$
13	8	$\{v_0,v_1,v_2,v_3,v_4,v_6,v_8,v_{10}\}$
14	8	$\{v_0,v_1,v_2,v_4,v_5,v_8,v_9,v_{12}\}$
$15,16,17$	8	$\{v_0,v_1,v_4,v_5,v_8,v_9,v_{12},v_{13}\}$
18	8	$\{v_1,v_2,v_5,v_6,v_9,v_{10},v_{13},v_{14}\}$
19	8	$\{v_2,v_3,v_6,v_7,v_{10},v_{11},v_{14},v_{15}\}$
20	8	$\{v_3,v_4,v_7,v_8,v_{11},v_{12},v_{15},v_{16}\}$

, we have provided an optimal FTRS of $P_n^5$ when $12\le n\le 20$. For $n=10$ and $n=11$, the sets $F_1=\{v_0,v_1,v_3,v_4,v_5,v_7,v_8\}$ and $F_2=\{v_1,v_2,v_3,v_4,v_5,v_6,v_8,v_9\}$ are the optimal FTRS of $P_n^5$, respectively.

Example 9.

In

Table 4. Lower bound on ${\beta }^{\prime }\left(P_n^6\right)$ for different values of n.

Values of n	Values of a	Lower Bound on ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^6\right)$ from Theorem 5
$n\ge 62$	0	12
$32\le n\le 61$	1	11
$22\le n\le 31$	2	10
$17\le n\le 21$	3	9
$12\le n\le 16$	4	8

, we consider the graph $P_n^6$ and find the ranges of n for different values of ${\beta }^{\prime }\left(P_n^6\right)$ and a from Theorem 5. In

Table 5. Upper bound on n from Theorem 6.

Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^6\right)$	Values of a	Upper Bound on n from Theorem 6
11	1	61
10	2	31
9	3	20
8	4	15
7	5	10

, we calculate the upper bounds on n for all possible values of a for the graph $P_n^6$. In

Table 6. Exact value of ${\beta }^{\prime }\left(P_n^6\right)$ using Sage-Math.

Values of n	Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^6\right)$	Elements of Fault-Tolerant Metric Basis
7	7	$\{v_0,v_1,v_2,v_3,v_4,v_5,v_6\}$
$8,9$	8	$\{v_0,v_1,v_2,v_3,v_4,v_5,v_6,v_7\}$
10	8	$\{v_0,v_1,v_2,v_3,v_4,v_5,v_6,v_8\}$
$11,12$	8	$\{v_1,v_2,v_4,v_5,v_6,v_7,v_9,v_{10}\}$
$13,14$	9	$\{v_0,v_1,v_2,v_3,v_5,v_6,v_8,v_{10},v_{11}\}$
$15,16$	9	$\{v_0,v_2,v_4,v_5,v_7,v_9,v_{10},v_{12},v_{14}\}$
17	9	$\{v_1,v_3,v_5,v_6,v_8,v_{10},v_{11},v_{13},v_{15}\}$
18	10	$\{v_0,v_1,v_2,v_3,v_4,v_5,v_7,v_{10},v_{12}\}$
30	10	$\{v_4,v_5,v_9,v_{10},v_{14},v_{15},v_{19},v_{20},v_{24},v_{25}\}$

, we calculate the exact value of ${\beta }^{\prime }\left(P_n^6\right)$ for different values of n using Sage-Math, where $V\left(P_n^6\right)=\{v_0,v_1,\dots ,v_{n-1}\}$. Finally, we summarize the fault-tolerant metric basis for $P_n^6$ for different values of n.

$$\begin{array}{c}\hfill {\beta }^{\prime }\left(P_n^6\right)=\left\{\begin{array}{cc}7\hfill & n\in [1,7],\hfill \\ 8\hfill & n\in [8,12],\hfill \\ 9\hfill & n\in [13,17],\hfill \\ 10\hfill & n\in [18,30],\hfill \\ 11\hfill & n\in [31,61],\hfill \\ 12\hfill & n\ge 62.\hfill \end{array}\right.\end{array}$$

(8)

Example 10.

In this example, we take the graph $P_n^8$. In

Table 7. Lower bound on ${\beta }^{\prime }\left(P_n^8\right)$ for different values of n.

Values of n	Values of a	Lower Bound on ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^8\right)$ from Theorem 5
$n\ge 114$	0	16
$58\le n\le 113$	1	15
$37\le n\le 57$	2	14
$30\le n\le 36$	3	13
$23\le n\le 29$	4	12
$16\le n\le 22$	5	11

, we find the lower bound on ${\beta }^{\prime }\left(P_n^8\right)$ for different ranges of n and a.

In

Table 8. Exact value of ${\beta }^{\prime }\left(P_n^8\right)$ using Sage-Math.

Values of n	Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^8\right)$	Elements of Fault-Tolerant Metric Basis
16	11	$\{v_0,v_1,v_3,v_4,v_6,v_7,v_8,v_{10},v_{11},v_{13},v_{14}\}$
17	11	$\{v_1,v_2,v_4,v_5,v_7,v_8,v_9,v_{11},v_{12},v_{14},v_{15}\}$
24	12	$\{v_2,v_3,v_6,v_7,v_9,v_{10},v_{13},v_{14},v_{16},v_{17},v_{20},v_{21}\}$
$25,26,27$	13	$\{v_0,v_1,v_3,v_5,v_7,v_{10},v_{12},v_{14},v_{17},v_{19},v_{21},v_{23},v_{24}\}$
$28,29,30$	13	$\{v_3,v_5,v_7,v_{10},v_{12},v_{14},v_{17},v_{19},v_{21},v_{23},v_{24},v_{25},v_{26}\}$
$31,32$	14	$\{v_0,v_1,v_2,v_6,v_7,v_{13},v_{14},v_{20},v_{21},v_{24},v_{25},v_{26},v_{27},v_{28}\}$
33	14	$\{v_0,v_1,v_2,v_6,v_7,v_{13},v_{14},v_{20},v_{21},v_{25},v_{26},v_{27},v_{28},v_{32}\}$
34	14	$\{v_0,v_1,v_2,v_6,v_7,v_{13},v_{14},v_{20},v_{21},v_{26},v_{27},v_{28},v_{32},v_{33}\}$
35	14	$\{v_0,v_1,v_2,v_6,v_7,v_{13},v_{14},v_{20},v_{21},v_{27},v_{28},v_{32},v_{33},v_{34}\}$

, we calculate the exact value of ${\beta }^{\prime }\left(P_n^8\right)$ for different values of n using Sage-Math, where $V\left(P_n^8\right)=\{v_0,v_1,\dots ,v_{n-1}\}$. In

Table 9. Upper Bound on n from Theorem 6.

Values of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^8\right)$	Values of a	Upper bound on n from Theorem 6
15	1	113
14	2	57
13	3	36
12	4	28
11	5	21
10	6	15

, we calculate the upper bounds on n for possible values of a for the graph $P_n^8$. In

Table 10. An optimal FTRS of $P_n^8$ and the values of ${\beta }^{\prime }\left(P_n^8\right)$.

Values of n	Lower Bound of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^8\right)$	Exact Value of ${\mathit{\beta }}^{\prime }\left({\mathit{P}}_{\mathit{n}}^8\right)$	An Optimal FTRS
$n\ge 114$	16 (using Theorem 5)	16	$\left\{v_0,v_1,\dots ,v_{15}\right\}$ by using Theorem 1
$58\le n\le 113$	15 (using Lemma 10)	15	For $n=113$, $\{v_7,v_{14},\dots ,v_{105}\}$ the set is an optimal FTRS
			(from the proof of Theorem 2). Algorithm 1 generates
			an optimal FTRS for each $n\in \{58,59,\dots ,112\}$.

, given below, we state the fault-tolerant metric dimension and an optimal FTRS of $P_n^8$ for different values of n.

7. Concluding Remark

In this article, we study the fault-tolerant metric dimension of $P_n^r$ for all n and r. We have presented an algorithm to construct a fault-tolerant resolving system of $P_m^r$ from a fault-tolerant resolving system of $P_n^r$ when $m<n$. We have found the exact value of ${\beta }^{\prime }\left(P_n^r\right)$ and presented an optimal FTRS for $n\ge r(r-1)+2$. For the other values of n, we presented several bounds. These results have been applied to $P_n^r$ for $r\in \{3,4,5,6,8\}$ and we obtained exact values or bounds for ${\beta }^{\prime }\left(P_n^r\right)$. Although we have presented several bounds for ${\beta }^{\prime }\left(P_n^r\right)$ when $n\le r(r-1)+1$, the problem below is still open.

Problem: Determine the fault-tolerant metric dimension of $P_n^r$ when $n\le r(r-1)+1$.