The Evolution of Probability Density Function for Power System Excited by Fractional Gaussian Noise

Abstract

This article is devoted to investigating the evolution of the probability density function for power system excited by fractional stochastic noise. First, the single-machine-infinite-bus (SMIB) power system model excited by fractional Gaussian noise (FGN) is established. Second, we derive the Fokker–Planck–Kolmogorov (FPK) equation for the proposed model and solve the FPK equation using the finite difference method. Finally, the numerical results verify that the addition of FGN would influence dynamical stability of the SMIB power system under certain conditions.

1. Introduction

In the past half century, Gaussian white noise has been widely used as an ideal mathematic model for many noises and random processes in nature sciences and engineering [1,2,3]. However, some real noises or excitations have long-range (long-memory), strong spatial and temporal correlations which are not described by Gaussian white noise. Fractional Brownian motion (FBM) provides an important theoretical basis for the investigation of long-correlation noise which is a more extensive stochastic process than Brownian motion (BM).

In 1968, Mandelbrot and Van Ness [4] defined the FBM for the first time and provided the construction of FBM. Since then, studies on stochastic dynamical systems driven by FBM have attracted an increasing amount of attention. The fact that FBM is neither semi-martingale nor Markov process renders the complete Itô stochastic analysis theory not applicable to FBM. Therefore, the development of a new stochastic calculus is needed. Duncan and Hu [5] provided the stochastic calculus of FBM with the Hurst parameter in $(1/2,1)$. In Ref. [6], the Fokker–Planck–Kolmogorov (FPK) equation for the expectations and distribution densities of the solutions for one-dimensional stochastic differential equations (SDEs) controlled by FBM with Hurst exponent $H\in (0,1)$ are obtained. These results generalized similar findings for one-dimensional SDEs driven by FBM with Hurst exponents $H>1/3$ [7,8]. Kleptsyna et al. [9] employed models with multivariate FBM to describe signal processes in filtering systems. Pei and Xu [10,11,12] investigated the stochastic averaging principle for FBM and proved that the FBM-driven dynamical system would be converged to the averaged stochastic dynamical system in the mean square sense. Deng and Zhu [13] constructed a stochastic averaging method of quasi-non-integrable Hamiltonian systems excited by fractional Gaussian noise (FGN). FBM has recently found extensive applications in finance [14,15], geophysics [16], biology [17,18], signal analysis of functional brain [19] and so on.

With the development of renewable energy, the uncertainties have created great challenges to the new energy industry, especially in wind power generation, photovoltaic generation and so on. Thus, the research on power systems with the uncertainty was paid more significant attention [20,21,22,23] in which the uncertainty is considered as a stochastic process into the power system. Therefore, the power system under stochastic disturbances can be modeled by a set of SDEs [24,25,26]. Wang et al. [27] improved the FPK equation to analyze the evolution of the states probability density function (PDF) and determined the impact of stochastic load perturbations on the single-machine-infinite-bus (SMIB) power system stability. In Ref. [28], SDEs were adopted to describe continuous wind speed models. Ju et al. [29] discussed the effect of additive Gaussian white noise on power system dynamics based on the stochastic averaging method. Lin et al. [30] established a novel optimal control strategy for power systems under Gaussian white noise excitation using the dynamic programming method.

The studies above all focus on power systems excited by Gaussian white noise. There are few studies on power systems under FGN excitation. In fact, in the modeling of randomness of new energy power, the long-range dependence and probabilistic distribution properties of different variables require consideration. Therefore, establishing a more reasonable model to accurately describe the randomness of new energy power is necessary. Thus, the proposed SMIB power system excited by FGN is established to explore the dynamical stability in this paper.

This article is structured as follows. In Section 2, the stochastic model of SMIB power system excited by FGN is proposed. In Section 3, the FPK equation for the proposed model is derived. Section 4 provides a numerical solution of an SMIB power system excited by FGN. In Section 5, according to the finite difference method (FDM), the solution of the FPK equation is obtained. Finally, the conclusions are presented in Section 6.

2. Modeling Description

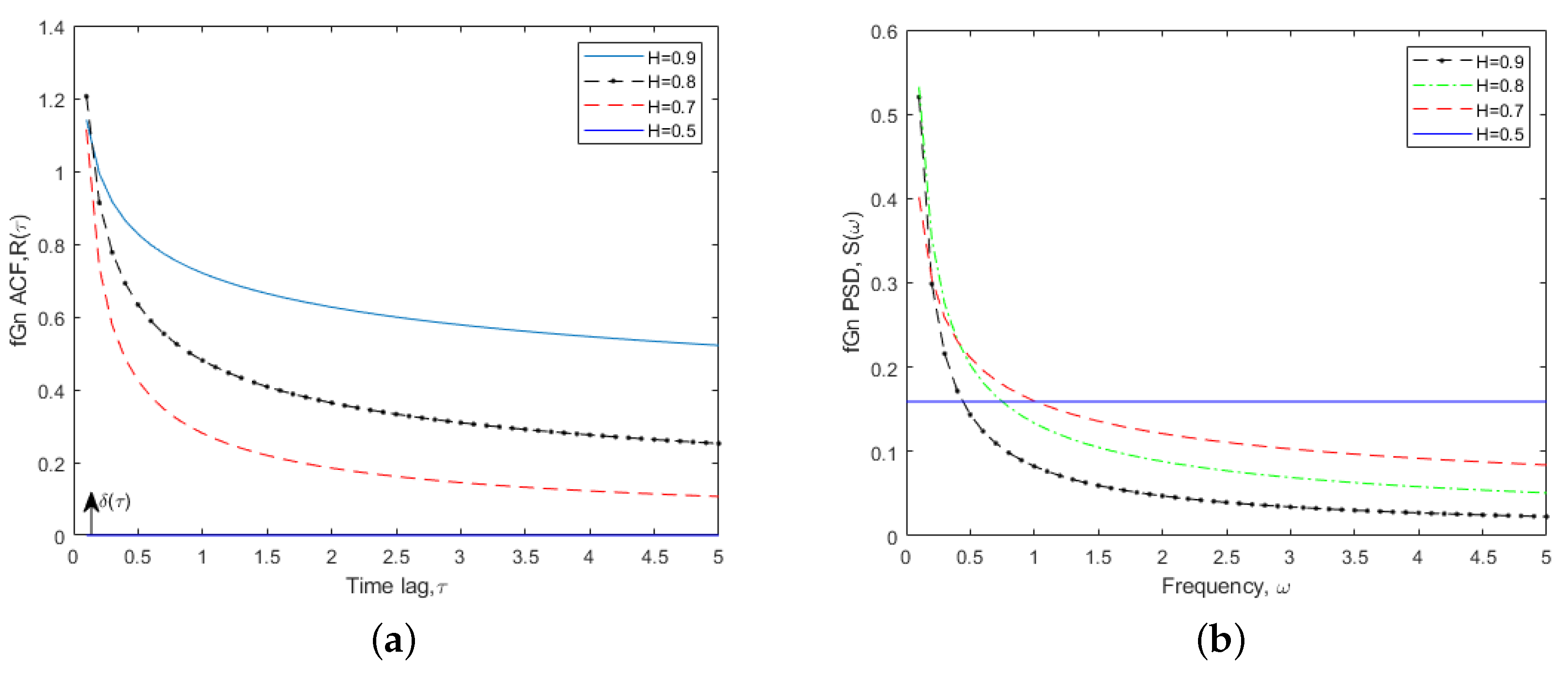
2.1. The FBM and FGN

FBM was named by Mandelbrot and Van Ness who provided in [4] a stochastic integral representation of this process in terms of a standard BM, i.e.,

$$\begin{array}{cc}\hfill B^H\left(t\right)=& C_H\{{\int }_{-\infty }^0[{(t-s)}^{H-\frac{1}{2}}-{(-s)}^{H-\frac{1}{2}}]\mathrm{d}B\left(s\right)\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{H-\frac{1}{2}}\mathrm{d}B\left(s\right)\},\hfill \end{array}$$

(1)

where $B\left(t\right)$ is a standard BM and $C_H$ is a normalized constant.

Definition 1.

Let the Hurst index $H\in (0,1)$, a FBM ${\left(B^H\left(t\right)\right)}_{t\ge 0}$ of Hurst H is a continuous and centered Gaussian process with covariance function

$$\mathbb{E}\left[B^H\left(t\right)B^H\left(s\right)\right]=\frac{1}{2}(t^{2H}+s^{2H}-{|t-s|}^{2H}),t,s\ge 0$$

(2)

where $t,s\in {\mathbb{R}}_{+}$.

For $H=1/2$, then the FBM is a standard BM. By Definition 1 we obtain that if $H>1/2$, the process $(B^H\left(t\right),t\ge 0)$ exhibits a long-range dependence, that is, if $r\left(n\right)=\mathbb{E}\left[B^H\left(1\right)(B^H(n+1)-B^H\left(n\right))\right]$, then we have ${\sum }_{n=1}^{\infty }r\left(n\right)=\infty$. An FBM is also self-similar, that is, $(B^H\left(\alpha t\right),t\ge 0)$ has the same probability law as $({\alpha }^H{B}^H\left(t\right),t\ge 0)$. Similar to the standard BM, the FBM is not differentiable a.s. (almost surely). As the “derivative” of a BM is usually referred to as Gaussian white noise, that of the FBM is referred to as FGN, i.e.,

$$W^H\left(t\right)=\frac{\mathrm{d}{B}^H\left(t\right)}{\mathrm{d}t}=\frac{B^H(t+▵t)-B^H\left(t\right)}{▵t}.$$

(3)

Then, according to (2) and (3), the auto-correlation function (ACF) $R\left(\tau \right)$ of FGN $W^H$ can be derived as

$$R\left(\tau \right)=\mathbb{E}\left[W^H(t+\tau )W^H\left(t\right)\right]=H(H+1){\left|\tau \right|}^{2H-2}+2H{\left|\tau \right|}^{2H-1}\tilde{\delta }\left(\tau \right),$$

(4)

where $\tilde{\delta }(·)$ is the Dirac function.

It is easy to know (4) indicates that $R\left(\tau \right)$ is the Dirac function $\delta \left(\tau \right)$ when $H=1/2$, which is the ACF of Gaussian white noise. Using Fourier transformation, the power spectral density (PSD) $S\left(\omega \right)$ of FGN with $1/2\le H<1$ can be obtained as follow

$$S\left(\omega \right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }R\left(\tau \right)e^{-j\omega \tau }\mathrm{d}\tau =\frac{H\Gamma \left(2H\right)sin\left(H\pi \right)}{\pi }{\left|\omega \right|}^{1-2H}.$$

(5)

Figure 1 displays a few simulation results with ACF and PSD of the FGN when $1/2\le H<1$. According to Figure 1, the PSD is close to a constant while the ACF approaches Dirac function $\delta \left(\tau \right)$ as H approaches $1/2$. When H is close to 1, the PSD is close to Dirac function $\delta \left(\tau \right)$ while ACF is close to a constant. When H between $1/2$ and 1, the ACF is limited value in a long time interval, which indicates long-range correlation. Thus, when H with $1/2$ and 1 the FGN is a steady Gaussian process. Figure 2 provides an intuitive observation for the FGN with different Hurst index H.

It is known that the FBM is not semimartingale. Therefore, the Itô stochastic analysis theory is not applicable to FBM for $H\ne 1/2$. The Stratonovich type stochastic integral ${\int }_0^t{f}_s\delta B^H\left(s\right)$, with respect to the FBM introduced by Lin [31], Dai and Heyde [32], does not satisfy in general the following property: $\mathbb{E}\left[{\int }_0^t{f}_s\delta B^H\left(s\right)\right]=0$. An Itô type stochastic integral, $\left[{\int }_0^t{f}_s\mathrm{d}{B}^H\left(s\right)\right]$, is introduced by Duncan et al. [5], satisfying $\mathbb{E}\left[{\int }_0^t{f}_s\mathrm{d}{B}^H\left(s\right)\right]=0$. This property seems to be important in the modeling problem by SDEs with FGN as the driving random process.

2.2. Malliavin Derivative and Stochastic Integration for FBM

For a fixed $H\in (\frac{1}{2},1)$, denote a function $\varphi :{\mathbb{R}}_{+}\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ by

$$\varphi (s,t):={H(2H-1)|s-t|}^{2H-2}.$$

(6)

Let $f:{\mathbb{R}}_{+}\to \mathbb{R}$ be a Borel measurable (deterministic) function. The function f belongs to the Hilbert space $L_{\varphi }^2\left({\mathbb{R}}_{+}\right)$ if

$${\left|f\right|}_{\varphi }^2:={\int }_0^{\infty }{\int }_0^{\infty }\varphi (s,t)f_s{f}_t\mathrm{d}s\mathrm{d}t<\infty .$$

(7)

The inner product on $L_{\varphi }^2\left({\mathbb{R}}_{+}\right)$ is denoted by ${\langle ·,·\rangle }_{\varphi }$.

Lemma 1.

If $f,g\in L_{\varphi }^2\left({\mathbb{R}}_{+}\right)$, then ${\int }_0^{\infty }{f}_{s}d{B}^H\left(s\right)$ and ${\int }_0^{\infty }{g}_{s}d{B}^H\left(s\right)$ are well defined zero mean, Gaussian random variables with variances ${\left|f\right|}_{\varphi }^2$ and ${\left|g\right|}_{\varphi }^2$, respectively, and

$$\mathbb{E}\left[{\int }_0^{\infty }{f}_{s}d{B}^H\left(s\right){\int }_0^{\infty }{g}_{s}d{B}^H\left(s\right)\right]={\int }_0^{\infty }{\int }_0^{\infty }f\left(s\right)g\left(t\right)\varphi (s,t)dsdt={\langle f,g\rangle }_{\varphi }.$$

(8)

Define a mapping $\Phi$ on $L_{\varphi }^2\left({\mathbb{R}}_{+}\right)$:

$${(\Phi g)}_t:={\int }_0^T\varphi (t,s)g_s\mathrm{d}s,\forall g\in L_{\varphi }^2\left([0,T]\right).$$

(9)

Definition 2

(Malliavin Derivative). Let $g\in L_{\varphi }^2\left([0,T]\right)$. The ϕ-derivative of a random variable $F\in L^p$ in the direction of ${\Phi }_g$ is defined by

$$D_{{\Phi }_g}F\left(\omega \right)=\underset{\delta \to 0}{lim}\frac{1}{\delta }\left\{F\left(\omega +\delta {\int }_0^{·}\left({\Phi }_g\right)\left(u\right)\mathrm{d}u\right)-F\left(\omega \right)\right\},$$

(10)

if the limit exists in $L^p(\Omega ,\mathcal{F},\mathbb{P})$. Moreover, if there exists a process $(D_s^{\varphi }{F}_s,s\ge 0)$ such that $D_{{\Phi }_g}F={\int }_0^{\infty }{D}_s^{\varphi }{F}_s{g}_s\mathrm{d}s,\mathrm{a}.\mathrm{s}.,$ for all $g\in L_{\varphi }^2\left({\mathbb{R}}_{+}\right)$, then F is said to be ϕ-differentiable.

Next, we define a stochastic integral with respect to FBM considered in [33]. Let ${\left\{F_t\right\}}_{t\ge 0}$ be a stochastic process such that $F\in \mathcal{L}(0,T)$, and define ${\int }_0^T{F}_s\mathrm{d}{B}^H\left(s\right)$ by

$${\int }_0^T{F}_s\mathrm{d}{B}^H\left(s\right)=\underset{\left|\pi \right|\to 0}{lim}\sum _{i=0}^{n-1}{F}_{t_i}^{\pi }\diamond \left(B^H\left(t_{i+1}\right)-B^H\left(t_i\right)\right),$$

(11)

where $\left|\pi \right|=max\left\{t_{i+1}-t_i,i=0,1,\dots ,n-1\right\}$ and ⋄ is the Wick product. The Wick product is a commutative, associative and distributive (over addition) binary operation.

Definition 3

(The Wick product). Let $F\left(\omega \right)={\sum }_{\alpha }{c}_{\alpha }{H}_{\alpha }\left(\omega \right)$ and $G\left(\omega \right)={\sum }_{\beta }{b}_{\beta }{H}_{\beta }\left(\omega \right)$ are two elements. Then the Wick product

$$\begin{array}{c}\hfill F\diamond G\left(\omega \right):=\sum _{\alpha ,\beta }{a}_{\alpha }{b}_{\beta }{H}_{\alpha +\beta }\left(\omega \right)=\sum _{\gamma }\left(\sum _{\alpha +\beta =\gamma }{a}_{\alpha }{b}_{\beta }\right)H_{\gamma }\left(\omega \right),\end{array}$$

(12)

where ⋄ presents the Wick product for F and G.

2.3. An Itô Formula

Lemma 2.

Let $(F_u,0\le u\le T)$ be a stochastic process and let $\mathbb{E}\left[{sup}_{0\le s\le T}\left|G_s\right|\right]<\infty$. Denote

$${\eta }_t=\xi +{\int }_0^t{G}_u\mathrm{d}u+{\int }_0^t{F}_u\mathrm{d}{B}^H\left(u\right),\xi \in \mathbb{R}$$

(13)

for $t\in [0,T]$. Let $\left(\frac{\partial f}{\partial x}(s,{\eta }_s)F_s,s\in [0,T]\right)\in \mathcal{L}(0,T)$. Then, for $t\in [0,T]$, the fractional Itô formula is obtained

$$\begin{array}{cc}\hfill f\left(t,{\eta }_t\right)=& f(0,\xi )+{\int }_0^t\frac{\partial f}{\partial s}\left(s,{\eta }_s\right)\mathrm{d}s+{\int }_0^t\frac{\partial f}{\partial x}\left(s,{\eta }_s\right)G_s\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t\frac{\partial f}{\partial x}\left(s,{\eta }_s\right)F_s\mathrm{d}{B}^H\left(s\right)+{\int }_0^t\frac{{\partial }^{2}f}{\partial x^2}\left(s,{\eta }_s\right)F_s{D}_s^{\varphi }{\eta }_s\mathrm{d}s.\hfill \end{array}$$

(14)

Now the Itô formula for ${\mathbb{R}}^n$-valued processes is given.

Lemma 3.

Let $(F_s^i,i=1,\dots ,n,s\in [0,T])$ satisfy the conditions of Lemma 2 for F. Let

$${\xi }_t^k={\int }_0^t{F}_s^k\mathrm{d}{B}^H\left(s\right),k=1,2,\dots ,n$$

(15)

for $t\in [0,T]$. For $k=1,2,\dots ,n$, let $\left(f_{x_k}(s,{\xi }_s^1,\dots ,{\xi }_s^n)F_s^k,s\in [0,T]\right)$ be in $\mathcal{L}(0,T)$. Let $f:{\mathbb{R}}_{+}\times {\mathbb{R}}^n\to \mathbb{R}$ be twice continuously differentiable with bounded derivatives to second order, then default

$$\begin{array}{cc}\hfill f(t,{\xi }_t^1,\dots ,{\xi }_t^n)=& f(0,0,\dots ,0)+{\int }_0^t\frac{\partial f}{\partial s}(s,{\xi }_s^1,\dots ,{\xi }_s^n)\mathrm{d}s\hfill \\ \hfill & +\sum _{k=1}^n{\int }_0^t\frac{\partial f}{\partial x_k}(s,{\xi }_s^1,\dots ,{\xi }_s^n)F_s^k\mathrm{d}{B}^H\left(s\right)\hfill \\ \hfill & +\sum _{k,l=1}^n{\int }_0^t\frac{{\partial }^{2}f}{\partial x_k\partial x_l}(s,{\xi }_s^1,\dots ,{\xi }_s^n)F_s^k{D}_s^{\varphi }{\xi }_s^l\mathrm{d}s.a.s.\hfill \end{array}$$

(16)

In particular, if $({\sigma }_s^i,i=1,\dots ,n,s\in [0,T])$ be in $L_{\varphi }^2$ then we have

$$\begin{array}{cc}\hfill f(t,{\xi }_t^1,\dots ,{\xi }_t^n)=& f(0,0,\dots ,0)+{\int }_0^t\frac{\partial f}{\partial s}(s,{\xi }_s^1,\dots ,{\xi }_s^n)\mathrm{d}s\hfill \\ \hfill & +\sum _{k=1}^n{\int }_0^t\frac{\partial f}{\partial x_k}(s,{\xi }_s^1,\dots ,{\xi }_s^n){\sigma }_s^k\mathrm{d}{B}^H\left(s\right)\hfill \\ \hfill & +\sum _{k,l=1}^n{\int }_0^t\frac{{\partial }^{2}f}{\partial x_k\partial x_l}(s,{\xi }_s^1,\dots ,{\xi }_s^n){\sigma }_s^k\left({\int }_0^s{\sigma }_v^l\varphi (s,u)\mathrm{d}u\right)\mathrm{d}s,a.s.\hfill \end{array}$$

(17)

where $\varphi (s,u)={H(2H-1)|s-u|}^{2H-2}$.

2.4. Model of Power System Excited by FGN

To provide a framework for exploring the PDF, an SMIB power system excited by FGN is initially considered. The SMIB power system is shown in Figure 3. This FGN can be described as the stochastic disturbance of the bus load power with long-range dependence. The normalized SMIB model with additive FGN is modeled as default

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill \mathrm{d}\delta =& \omega \mathrm{d}t\hfill \\ \hfill \mathrm{d}\omega =& ({\overline{P}}_m-sin\delta -\overline{D}\omega )\mathrm{d}t+\sigma \mathrm{d}{B}^H\left(t\right),\hfill \end{array}\hfill \end{array}\right.$$

(18)

where $\delta$ is the relative rotating corner to the infinite bus, $\omega$ is the rotating rate with respect to synchronous speed. The status vector is $\mathit{x}={[x_1,x_2]}^T={[\delta ,\omega ]}^T$. The constants ${\overline{P}}_m$ and $\overline{D}$ are, respectively, the normalized machine-based power and damping coefficients. The $\mathrm{d}{B}^H\left(t\right)$ denotes the FGN excitation and H is the Hurst index in a range of $1/2<H<1$. The parameter $\sigma$ indicates the intensity of the additive FGN.

Writing Equation (18) in vector form

$$\mathrm{d}\mathit{x}=f\left(\mathit{x}\right)\mathrm{d}t+g\mathrm{d}{B}^H\left(t\right),$$

(19)

where

$$f\left(\mathit{x}\right)=\left[\begin{array}{c}{f}_1\left(x\right)\hfill \\ f_2\left(x\right)\hfill \end{array}\right]=\left[\begin{array}{c}{x}_2\\ {\overline{P}}_m-sin{x}_1-\overline{D}{x}_2\end{array}\right]$$

and

$$g=\left[\begin{array}{c}0\hfill \\ \sigma \hfill \end{array}\right].$$

3. The FPK Equation for SMIB Power System Excited by FGN

Applying fractional Itô formula Lemma 3 to the scalar function $h\left(x\right)$, it will be given as

$$\begin{array}{cc}\hfill \mathrm{d}h\left(x\right)=& \left(\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}f\left(x\right)+\frac{{\mathrm{d}}^{2}h\left(x\right)}{\mathrm{d}{x}^2}g{\int }_0^{t}g\varphi (s,t)\mathrm{d}s\right)\mathrm{d}t+\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}g\mathrm{d}{B}^H\left(t\right),\hfill \end{array}$$

(20)

where the function $\varphi (s,t)$ is defined by

$$\varphi (s,t)={H(2H-1)|s-t|}^{2H-2}.$$

(21)

Taking the expectation of Equation (20), we have

$$\begin{array}{cc}\hfill \mathbb{E}\left[\mathrm{d}h\right(x\left)\right]=& \mathbb{E}\left[\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}f\left(x\right)+\frac{{\mathrm{d}}^{2}h\left(x\right)}{\mathrm{d}{x}^2}g{\int }_0^{t}g\varphi (s,t)\mathrm{d}s\right]\mathrm{d}t+\mathbb{E}\left[\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}g\mathrm{d}{B}^H\left(t\right)\right].\hfill \end{array}$$

(22)

Therefore, we obtain

$$\mathbb{E}\left[\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}t}\right]=\mathbb{E}\left[\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}f\left(x\right)+\frac{{\mathrm{d}}^{2}h\left(x\right)}{\mathrm{d}{x}^2}g{\int }_0^{t}g\varphi (s,t)\mathrm{d}s\right].$$

(23)

Denote $p(x,t)$ as the PDF for the system state x at time t, we now recall

$$\mathbb{E}\left[h\left(x\right)\right]={\int }_{-\infty }^{\infty }h\left(x\right)p(x,t)\mathrm{d}x,$$

(24)

which implies that

$$\mathbb{E}\left[\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}t}\right]={\int }_{-\infty }^{\infty }h\left(x\right)\frac{\partial p(x,t)}{\partial t}\mathrm{d}x.$$

(25)

This leads to default

$$\begin{array}{cc}\hfill {\int }_{-\infty }^{\infty }h\left(x\right)\frac{\partial p(x,t)}{\partial t}\mathrm{d}x=& {\int }_{-\infty }^{\infty }\left(\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}f\left(x\right)+\frac{{\mathrm{d}}^{2}h\left(x\right)}{\mathrm{d}{x}^2}g{\int }_0^{t}g\varphi (s,t)\mathrm{d}s\right)p(x,t)\mathrm{d}x\hfill \end{array}$$

(26)

After the integration by part, we yield

$${\int }_{-\infty }^{\infty }\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}{f\left(x\right)p(x,t)\mathrm{d}x=p(x,t)f\left(x\right)h\left(x\right)|}_{-\infty }^{\infty }-{\int }_{-\infty }^{\infty }h\left(x\right)\frac{\partial \left(f\right(x\left)p\right(t,x\left)\right)}{\partial x}\mathrm{d}x.$$

(27)

The first term on the right side of Equation (26) must vanish since $p(x,t)=0$ at $x=\pm \infty$. Then

$${\int }_{-\infty }^{\infty }\frac{\mathrm{d}h\left(x\right)}{\mathrm{d}x}f\left(x\right)p(x,t)\mathrm{d}x=-{\int }_{-\infty }^{\infty }h\left(x\right)\frac{\partial \left(f\right(x\left)p\right(t,x\left)\right)}{\partial x}\mathrm{d}x.$$

(28)

In a similar way, we treat the second integral in Equation (26) to obtain

$$\begin{array}{c}{\int }_{-\infty }^{\infty }\frac{{\mathrm{d}}^{2}h\left(x\right)}{\mathrm{d}{x}^2}g{\int }_0^{t}g\varphi (s,t)\mathrm{d}sp(x,t)\mathrm{d}x={\int }_{-\infty }^{\infty }h\left(x\right)\frac{{\partial }^2\left(g{\int }_0^{t}g\varphi (s,t)\mathrm{d}sp(x,t)\right)}{\partial x^2}\mathrm{d}x.\hfill \end{array}$$

(29)

Rendering back Equations (28) and (29) into Equation (26), the following equation can be yielded

$$\begin{array}{cc}\hfill {\int }_{-\infty }^{\infty }h\left(x\right)& \left(\frac{\partial p(x,t)}{\partial t}+\frac{\partial \left(f\right(x\left)p\right(x,t\left)\right)}{\partial x}-\frac{{\partial }^2\left(g{\int }_0^{t}g\varphi (s,t)\mathrm{d}sp(x,t)\right)}{\partial x^2}\right)\mathrm{d}x=0.\hfill \end{array}$$

(30)

Hence, we deduce that

$$\begin{array}{cc}\hfill \frac{\partial p(t,x)}{\partial t}& +\frac{\partial \left(f\left(x\right)p(x,t)\right)}{\partial x}-\frac{{\partial }^2\left(g{\int }_0^{t}g\varphi (s,t)\mathrm{d}sp(x,t)\right)}{\partial x^2}=0.\hfill \end{array}$$

(31)

It is claimed the FBM-driven FPK equation for fractional SDE (19) because the diffusion term in Equation (19) is the FBM.

From Equation (31), the corresponding FPK equation of SMIB power system excited by FGN is given by

$$\frac{\partial p(x,t)}{\partial t}=-\frac{\partial f_1\left(x\right)p(x,t)}{\partial x_1}-\frac{\partial f_2\left(x\right)p(x,t)}{\partial x_2}+H{t}^{2H-1}\frac{{\sigma }^2{\partial }^{2}p(x,t)}{\partial x_2^2},$$

(32)

where H is the Hurst index in a range $1/2<H<1$ and $p(x,t)$ is the time-dependent PDF. The FPK Equation (32) is a parabolic two-dimensional partial differential equation having given initial and boundary conditions. The initial condition for Equation (31) is

$$p\left(x_0\mid x,t\right)=\prod _{i=1}^n\tilde{\delta }\left(x_i-x_0\right)\mathrm{as}t\to 0,$$

(33)

where $x_0$ is the initial running status and $\tilde{\delta }(·)$ is the Dirac function.

The solution of the FPK Equation (32) relies heavily on the boundary condition. Thus, the two sets of boundary conditions are applied to the SMIB power system. On the one hand, natural boundary conditions are presented

$$\begin{array}{c}p\left(x_1,+\infty ,t\right)=0\hfill \\ p\left(x_1,-\infty ,t\right)=0.\hfill \end{array}$$

(34)

The PDF should vanish at $x_2\to \pm \infty$ according to these boundary conditions. Among the numerical solution of the appropriate FPK Equation (32), the two limited values are adopted to approach the boundary of $x_2$, as shown in Figure 4. Therefore, the natural boundary conditions would be taken over the absorbing boundary conditions

$$\begin{array}{c}p\left(x_1,x_{2\hspace{0.17em}min},t\right)=0\hfill \\ p\left(x_1,x_{2\hspace{0.17em}max},t\right)=0,\hfill \end{array}$$

(35)

where the $x_{2\hspace{0.17em}max}$, $x_{2\hspace{0.17em}min}$ are limited and defined the boundary of the calculation region in the direction of $x_2$. On the other hand, the periodic boundary conditions are given by

$$p\left(x_1,x_2,t\right)=p\left(x_1+2\pi ,x_2,t\right).$$

(36)

Since $f\left(x\right)$ is periodical in $2\pi$ with $x_1\left(\delta \right)$, the statud space $(x_1,x_2)$ will be observed in planar ${\mathbb{R}}^2$ or cylindrical $\mathbb{S}\times \mathbb{R}$. For the sake of brevity, the cylindrical state-space $\mathbb{S}\times \mathbb{R}$ will be supposed to the solution of the FPK Equation (32) for capturing the approximately periodic behavior of limit cycle. The normalized condition of PDF must also be satisfied

$$\int p(x,t)\mathrm{d}x=1.$$

To some extent, the steady-state solution of the FPK equation is the most interesting, i.e., the dynamical behavior of the system approaches steady status. It is worth noting that the FPK equation may not have a stationary solution. Provided that the stationary solution holds with $t⟶\infty$, thus $p_{\infty }(x\mid x_0)$ is the steady-state PDF. That is to say, $p_{\infty }\left(x\mid x_0\right)={lim}_{t⟶\infty }p\left(x,t\mid x_0\right)$. Under this stationary condition, Equation (32) becomes the stationary FPK equation

$$\frac{\partial f_1\left(x\right)p(x,t)}{\partial x_1}+\frac{\partial f_2\left(x\right)p(x,t)}{\partial x_2}-H{t}^{2H-1}\frac{{\sigma }^2{\partial }^{2}p(x,t)}{\partial x_2^2}=0.$$

(37)

4. Numerical Solution of SMIB Power System Excited by FGN

The numerical solution of fractional SDEs requires the time-domain numerical integration of Equation (18). The primary difference between the numerical solution of the system for ordinary differential equations and fractional SDEs is the additional of the FBM over the simulation interval $[0,T]$.

To illustrate the numerical solution of the fractional SDE, Monte Carlo simulation (MCS) is applied to solve Equation (18). The initial conditions can be chosen to locate in the attractive zone for the stable equilibrium point (SEP) of the non-perturbed power system, but near the stability boundary. In the non-perturbed power system, the trajectory is supposed to be converged to the SEP. Figure 5a,b show the trajectories of random rotating corner and frequency based on 20 Monte Carlo tests. Most trajectories intimately mimic the deterministic dynamical trajectories. Nevertheless, an unpredicted behavior was exhibited and rendered unstable in two of the 20 trajectories. The two unexpected trajectories suggest that these two trajectories create a rotating orbit actually. Provided that the corners were graphed on the rotating reference system, the two erratic phase diagrams seen in Figure 6 will match a limit cycle.

Though each single operation offers a separate trajectory, multiple trials of the MCS are required to produce statistical information for the SMIB power system excited by FGN. It is worth noting that the two vertical lines marking $p(x,t_1)$ at 5 s and $p(x,t_2)$ at 15 s in Figure 5a,b. The crossing section of the trajectory represented by the vertical lines approaches status PDF $x={[\delta ,\omega ]}^T$ for time t. With an increasing number of experiments, the MCS will provide a more precise approximation of the actual PDF. However, the number of trials is limited, therefore an approximate PDF can only be acquired.

The histograms offers a straightforward way to estimate and visualize the joint PDF. Figure 7 and Figure 8 display the approximate PDF for time t = 5 s and t = 25 s for 1500 runs, respectively. Figure 7 indicates that the system states are intricate which can not stabilize near the SEP at t = 5 s. When t = 25 s, Figure 8 indicates that a significant amount of system status cluster surrounding the SEP $(\delta ,\omega )=(0,0.5)$ and the arc encircles the SEP. This arc and ridge respond to a set of status that locate on the limit cycle surrounding the SEP.

Though the histogram method offers a reliable approximate view of the PDF, the MCS has the shortcoming of high computational load. In addition, because of the discretized nature of this method, slight dynamical characteristics may be discarded or ignored. Hence, there is a requirement to develop a method that can accurately predict the evolution of PDFs and identify significant dynamical characteristics. The FPK equation offers such a reliable method.

5. Solution of the FPK Equation

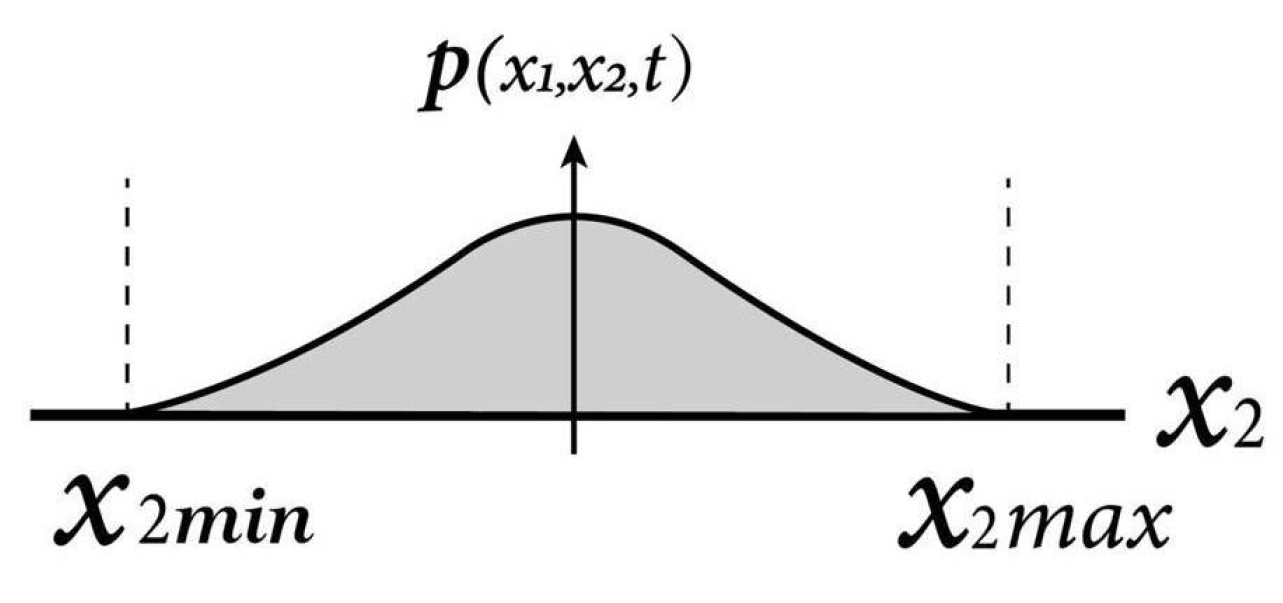
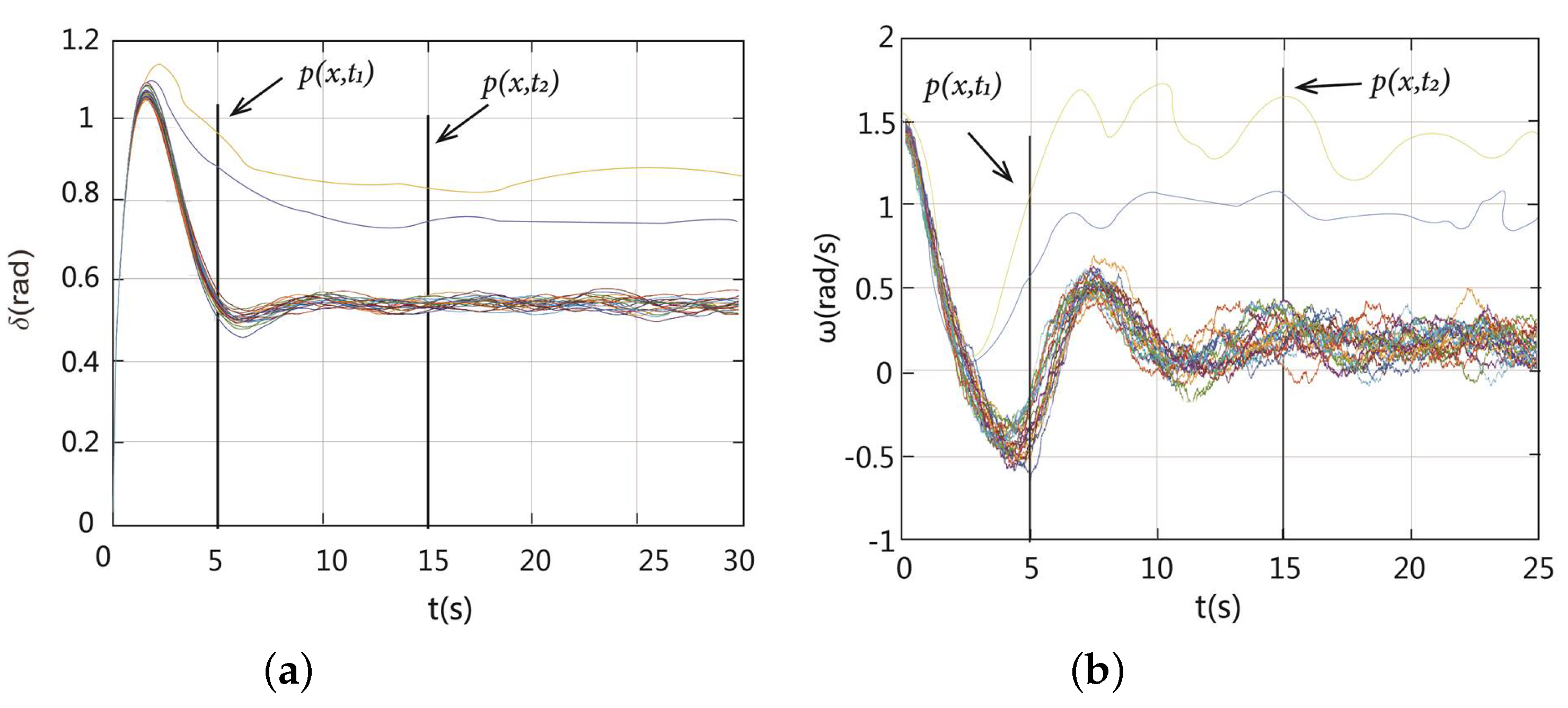
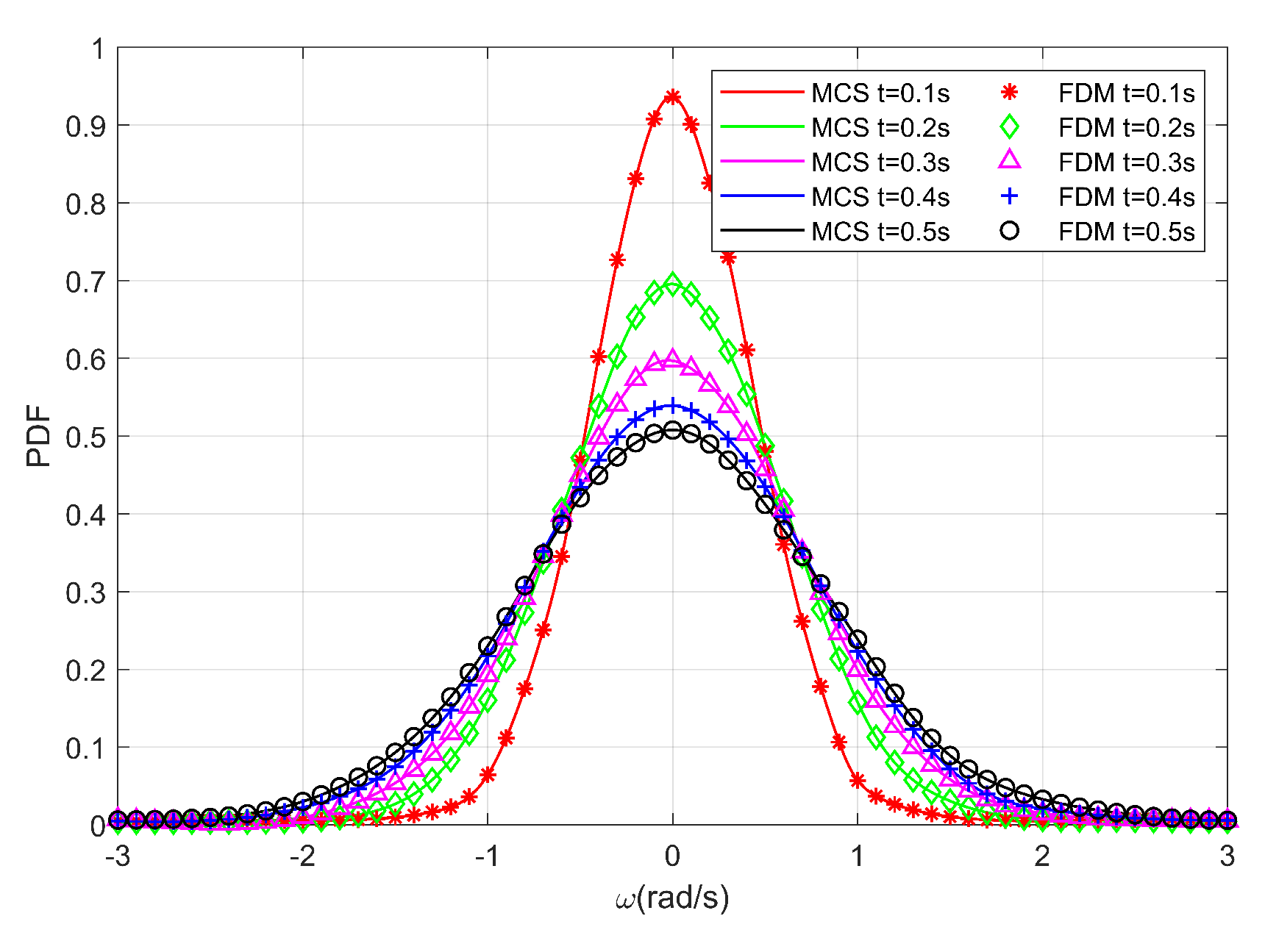
5.1. Time-Dependent PDF

The FPK Equation (32) describes the evolution of the PDF for SMIB power system excited by FGN. It is difficult to obtain the analytical solution by solving the FPK Equation (32). Therefore, the FDM is used for numerical calculation [34,35]. Using the FDM, the derivatives in FPK Equation (32) are approximated as the form of finite differences. In this method, the system state is preprocessed by discretization of space. Specifically, the state space can be discretized as the $[h_{min},\dots ,h,h+\mathrm{d}t,\dots ,h_{max}]$ where $\mathrm{d}t$ represented the step size and h belongs to the $[h_{min},h_{max}]$. Meanwhile, the time interval $[0,T]$ is discretized as $[0,\dots ,t,t+\mathrm{d}t,\dots ,T]$. The differential in the FPK Equation (32) can then be formulated as follows

$$\frac{\partial p_t^h}{\partial t}=\frac{p_{t+1}^h-p_t^h}{\mathrm{d}t},$$

(38)

$$\frac{\partial p_t^h}{\partial x_1}=\frac{p_{t+1}^h-p_t^{h-1}}{\mathrm{d}{x}_1},$$

(39)

$$\frac{\partial p_t^h}{\partial x_2}=\frac{p_{t+1}^h-p_t^{h-1}}{\mathrm{d}{x}_2},$$

(40)

$$\frac{{\partial }^2{p}_t^h}{{\partial }^2{x}_2}=\frac{p_t^{h+1}-2p_t^h+p_t^{h-1}}{{\left(\mathrm{d}{x}_2\right)}^2}.$$

(41)

Thus, the FPK Equation (32) is described as

$$\begin{array}{cc}\hfill p_{t+1}^h=& p_t^h+\frac{\mathrm{d}t}{\mathrm{d}{x}_1}\left[f_1^{h-1}{p}_t^{h-1}-f_1^h{p}_t^h\right]+\frac{\mathrm{d}t}{\mathrm{d}{x}_2}\left[f_2^{h-1}{p}_t^{h-1}-f_2^h{p}_t^h\right]\hfill \\ \hfill & -\frac{H{t}^{2H-1}{\sigma }^2\mathrm{d}t}{{\left(\mathrm{d}{x}_2\right)}^2}\left[2p_t^h-p_t^{h+1}-p_t^{h-1}\right].\hfill \end{array}$$

(42)

Here, the absorbing boundary conditions (35) are considered during the iterations. The convergent solution can be acquired by solving Equation (42). For the FDM, the space size $s=X\times Y$, where X, Y are, respectively, the space size of time interval and altitude interval. In each iteration, we go through all the space two times and there are finite computing times in each traversal. So the computation complexity of every iteration is small enough, which means the iteration is also finite. Therefore, the computational complexity is acceptable in practical application. The iteration ends when the iterative times exceed the threshold.

With the Hurst index fixed $H=0.65$, Figure 9 exhibits the numerical results of the time-dependent PDF in three-dimensional contours as well as the projection of the contours in the plane at three different times t = 0.1 s, t = 5 s and t = 25 s, respectively.

At t = 0.1 s, the initial values approximately satisfy Equation (33). The evolution of PDF is far from unstable equilibrium point (UEP) and SEP. In Figure 9, the initial state $x=(\delta ,\omega )=(2,2)$ is chosen. When t = 5 s, the time-dependent PDF experiences transient changes. Most of the probability flows are closing the SEP, yet a few of them have gone out of the main flow and are nearing the limit cycle ridge. Meanwhile, a small number of probability flows are approaching UEP. Following a period of time, such as t = 25 s, the probability flows around the UEP gradually decrease. The PDF is convergent to its stationary solution. Two prominent features are found in the stationary solution. One is a peak around the SEP and the other is a ridge that defines the limit cycle.

Based on the FDM, the PDFs for several different times are plotted in Figure 10 and Figure 11 using discrete points. For the purpose of comparison, the MCS are also included in Figure 10 and Figure 11 using solid lines. A very good agreement between the FDM and MCS for different times is observed. Therefore, the correctness of results obtained by the FDM is verified.

Because the stability of the SMIB power system is forecasted from the stationary PDF, the rest of this paper will concentrate on the stationary PDF.

5.2. Stationary PDF

The stationary PDF is the solution of the FPK equation after it has attained steady-state. In the case of high-damping or high-dissipation power system, the steady-state PDF would be focused on the SEP. Yet in lightly damped power systems, the stationary PDF will largely flow along the limit cycle ridge. Figure 12 and Figure 13 display two extreme examples. The PDF is closely aggregated in the peak surrounding the SEP in Figure 12. It is indicated that almost all trajectories will be close to the SEP at high probability. Figure 13 illustrates the other extreme of a very light-damping power system where almost all trajectories are caught by the limit cycle.

Generally, the steady-state PDF will have both peak and ridge features, depending on the systematic parameters. For instance, let ${\overline{P}}_m$ be fixed and $\overline{D}$ be increased, then the height of the peak will decrease, while the height of the ridge will increase. The peak corresponds to the stability for the SMIB power system excited by FGN. The ridge is typically regarded as unstable dynamical behavior, because the limit cycle is only present when the generator angle is increasing.

A quantified criterion $S_{sindex}$ is presented to express the steady-state PDF and the damping factor

$$S_{index}=\frac{p_{max}^p}{p_{max}^r},$$

(43)

where $p_{max}^p$ and $p_{max}^r$ are, respectively, the neighborhood maximum values of stationary PDF near the peak and the ridge. The $p_{max}^p$ is corresponding to the SEP with the deterministic system. Although the precise position of $p_{max}^r$ on the ridge is not easy to identify since it is near the limit cycle, one will be guessed from the numerical solution. Figure 14 displays how the different stable regions vary with the damping parameter when parameters $H=0.65$, ${\overline{P}}_m=0.5$ and $\sigma =0.1$ are fixed. A range of data points were obtained under various damping factors shown in Figure 14. Note that the relationship between $ln\left(S_{index}\right)$ and the damping coefficient can be linearly approximated. The critical damping level is calculated to be ${\overline{D}}_c=0.419$. In the SMIB power system excited by FGN, if the damping factor is greater than ${\overline{D}}_c$, the system will just present SEP and without limit cycle. Nevertheless, if the damping parameter is reduced to ${\overline{D}}_c$, the limit cycle will occur and exist with the SEP at the same time. When the damping parameter is reduced further still, the SEP will not appear, only leaving the limit cycle.

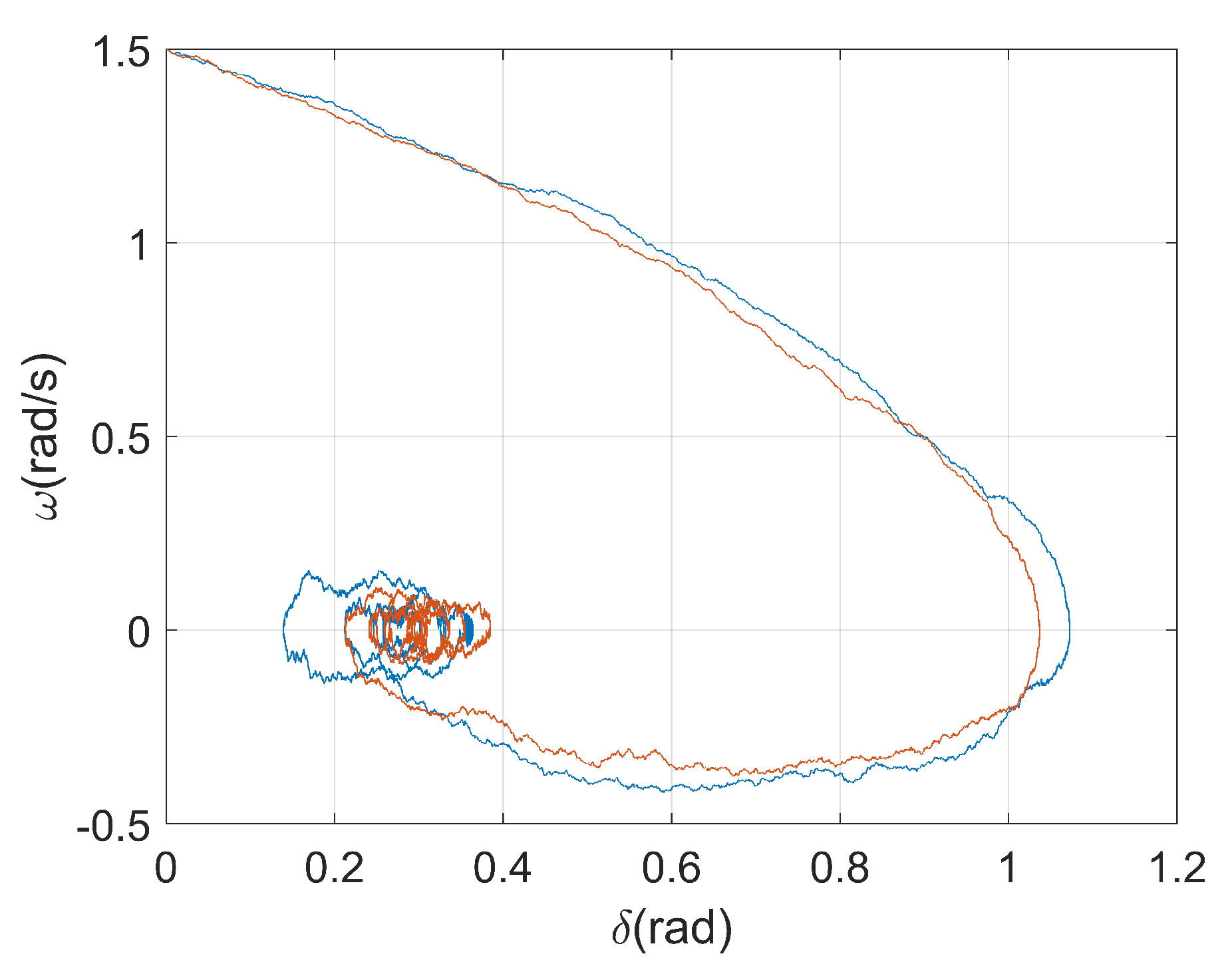
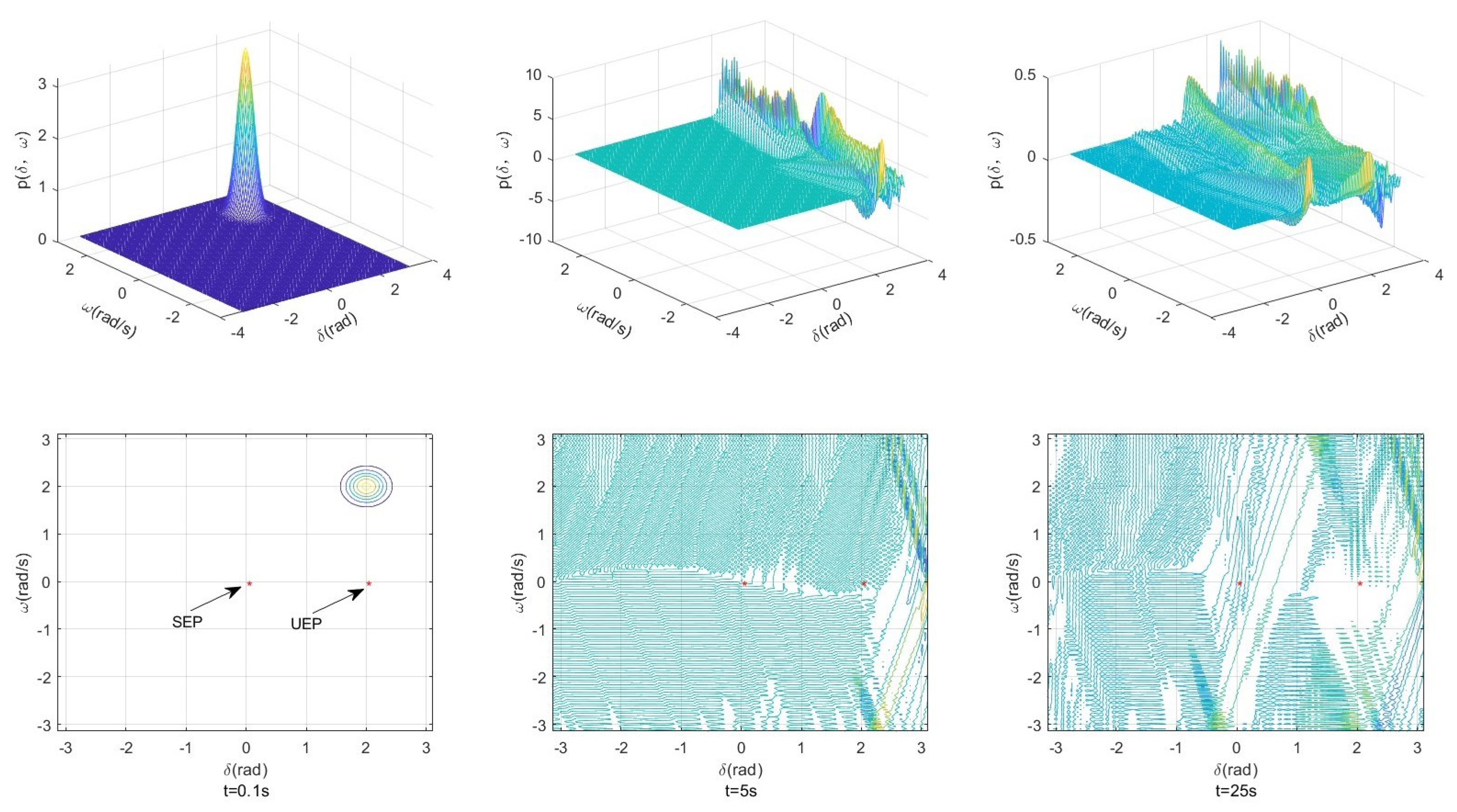
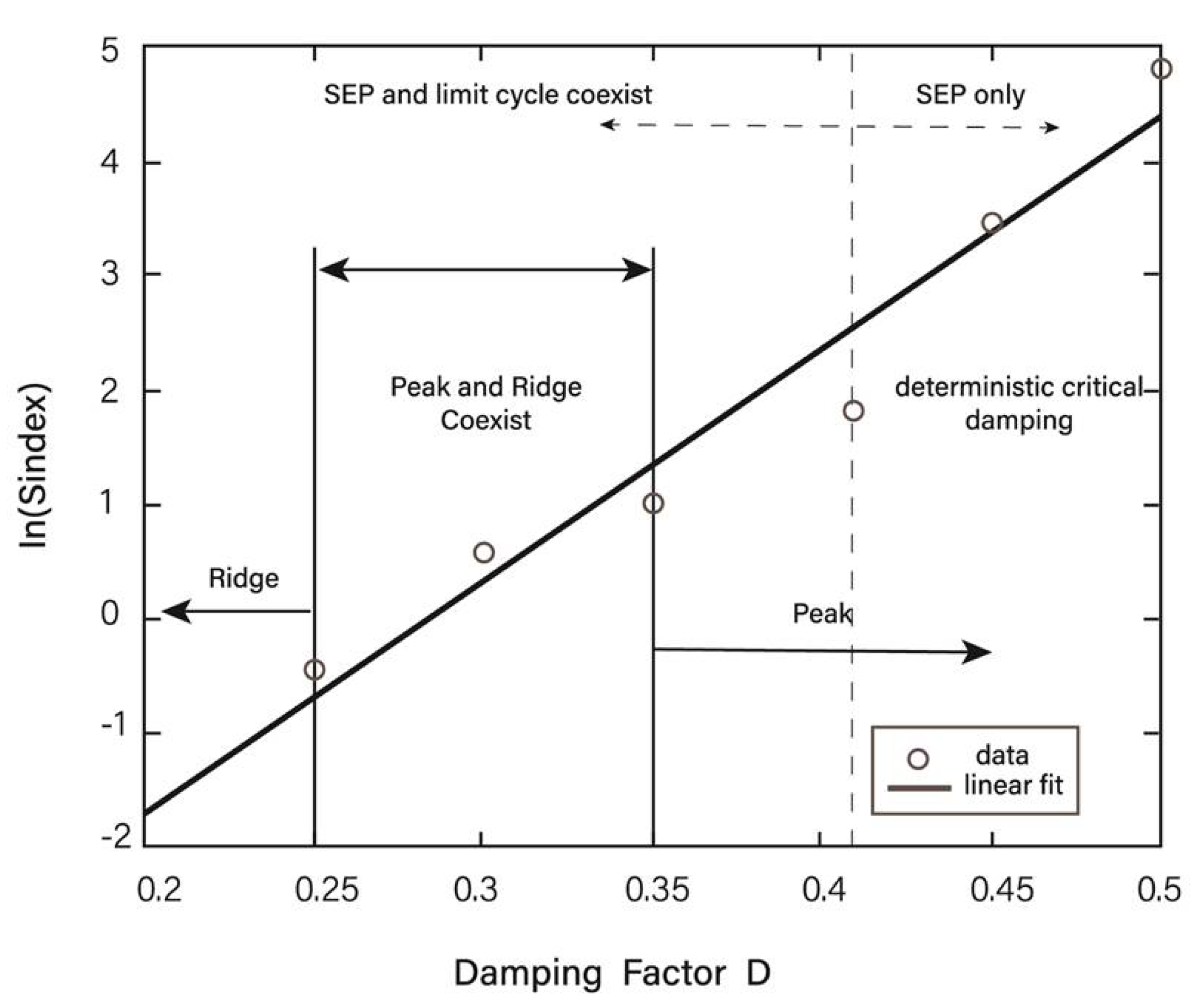
5.3. Impact of FGN on Stability

When FGN is introduced into the SMIB power system, the trajectories near boundaries will pass over the boundaries inadvertently and exhibit unpredictable behavior in a deterministic system. When damping parameter approaches the critical damping value ${\overline{D}}_c$, from Figure 12 and Figure 13, the PDF shows both ridge and peak features. It can be seen from Figure 14, while the peak and ridge features appear at the same time, the peak is dominant in the probability stream. Thus, although the damping parameter is likely to be below the critical value, the vast number of trajectories will remain drawn to the SEP rather than the limit cycle. Simply put, the FGN in the SMIB power system indeed will improve system stability under certain conditions.

6. Conclusions

With the rising popularity of solar power generation, wind power generation and other new energy sources, noise influence on new power systems is attracting significant attention. Our intention is to solve the FPK equation to explore the evolution of the PDF in the SMIB power system excited by FGN.

First, we introduced FGN into an SMIB power system to describe the random perturbation of the bus loading power with long-range dependence. Second, based on the fractional Itô formula, the FPK equation for the SMIB power system excited by FGN was derived. The MCS of the proposed power system showed that the evolution of the state PDF over time would make the stability regions as the function of damping coefficient. Finally, the FPK equation was solved numerically using the FDM. The qualitative analysis indicated that the PDF exhibited several main characteristics that peaks and ridges are associated with different stability responses. The numerical results verified that the FGN would improve dynamical stability for certain conditions.

Though this article has concentrated only on the simplified SMIB power system, it still expressed basic dynamical characteristics for large-scale power systems.