Abstract
Reliability-based robust design methods have been widely used in the field of product design; however, they are difficult to apply to the fatigue reliability design process of rolling bearings due to the problems of determining fatigue accumulated damage caused by the internal cyclic time-varying load distribution of rolling bearings and the computational cost of time-varying reliability. Therefore, a reliability-based robust design method for rolling bearing fatigue failure is proposed, which derives the formula for fatigue accumulated damage of a rolling bearing under cyclic load spectrum and significantly reduces the computational cost of rolling bearing time-varying reliability compared with existing methods. First, the state response of a rolling bearing under random design parameters is obtained by finite element simulation. Then, the adaptive kriging method is used to characterize the correlation between the random parameters and the state response. The Miner fatigue cumulative damage theory is improved and the rolling bearing fatigue time-varying equation of state under cyclic load spectrum is derived. Subsequently, a fatigue time-varying reliability model based on an improved fourth-order moment method is developed, and a reliability robust optimization design method is proposed. Finally, a rolling bearing example is presented to demonstrate that the method achieves time-varying fatigue reliability design under cyclic load spectrum and effectively improves the reliability and robustness of the product design.
Keywords:
reliability-based robust design; fatigue damage accumulation; kriging surrogate model; time-varying reliability; reliability sensitivity MSC:
62N05; 93B51
1. Introduction
Rolling bearings are one of the key components in mechanical transmission systems and in order to ensure high quality rolling bearing products, reliability analysis and design have become the core content of rolling bearing production engineering. Usually, during the in-service period, rolling bearings operate under cyclic load spectrum conditions, and cyclic alternating stresses during the in-service period lead to fatigue cracks on the roller and raceway contact surfaces that sprout and expand over time, eventually leading to fatigue failure [1,2,3]. During the in-service period, the fatigue reliability of rolling bearings varies with time, and the design of rolling bearings on this basis is a typical time-varying reliability design problem.
The current design of rolling bearings still relies heavily on widely studied theories of fatigue life theories, such as the Weibull distribution method [4,5] obtained through a large number of fatigue tests, the Lundberg–Palmgren method [6,7] by constructing the equivalent load of the inner and outer raceway, and the ISO standard method [8] developed on the basis of the Lundberg–Palmgren method; however, there are few methods which combine time-varying reliability design. Time-varying reliability design can reflect the load variation and time-varying response during the service process of specific products [9]. It can determine the reliability-life curve of products without conducting a large number of life tests and provides highly reliable design results that can significantly save time and resources when combined with the product design process of rolling bearings [10].
The fatigue life of rolling bearings is mainly affected by the material and load factor, and the S-N curve [11], which is usually obtained by fitting the test results, is used to indicate the relationship between the current load factor and fatigue life under the current material. Figure 1 shows the S-N curve of typical high-carbon chromium-bearing steel, where S indicates the stress amplitude to which the rolling bearing is subjected, and N indicates the fatigue life corresponding to the current constant amplitude stress, and the corresponding fatigue life can be determined in the figure according to the current stress amplitude. In practice, it is usually assumed that fatigue damage of the material is accumulated smoothly under a constant amplitude load [12].
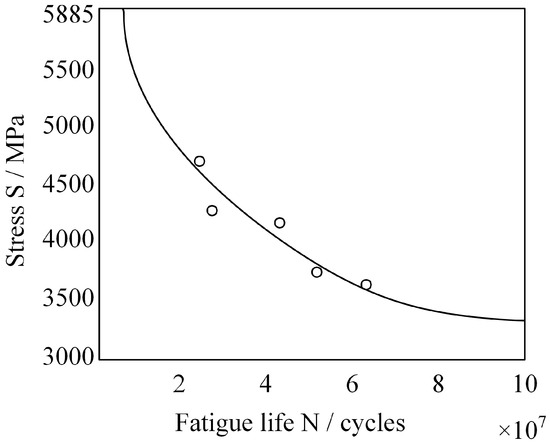
Figure 1.
The S-N curve of a typical high-carbon chromium-bearing steel.
However, due to the fact that external service conditions change with time, the stress amplitude on rolling bearing material will change with time accordingly, and the determination of the accumulated fatigue damage of rolling bearings under time-varying conditions becomes a difficult problem. However, rolling bearings actually operate under a cyclic variable amplitude load spectrum and, in this regard, the Miner theory [13] has been widely used to calculate the accumulated fatigue damage of engineering structures under cyclic stresses because of its simplicity and ease of implementation [14]. Later, Kwofie and Rahbar [15] improved the Miner method by considering the effects of loading sequence on fatigue life and interpreting the traditional Miner theory as one of the special cases.
In terms of time-varying reliability analysis, Wang et al. [16] used the dimension reduction method to convert time-varying probability constraints into time-invariant constraints, resulting in a time-varying reliability analysis with a more mature time-invariant reliability theory. Zhang et al. [17] derived the relationship between the first fourth-order statistical moments of the random input parameters and the moments of the explicit state function, which could be used in a time-varying reliability analysis under uncertainty in the type of distribution of the random parameters [18,19]. Lannacone et al. [20] proposed a time-varying reliability model that considered the role of post-failure resilience forces, which was successfully used to simulate the drinking water infrastructure in Seaside, Oregon, USA. All of the above studies have contributed to the application of time-varying reliability design to rolling bearings.
However, while rolling bearings are subjected to time-varying external loads in the operating load spectrum, their internal roller-race structure generates an internal time-varying cyclic load distribution, resulting in the fatigue accumulation failure process of rolling bearings as a two-layer iterative problem that cannot be directly calculated using existing methods. In addition, the calculation of a mechanical response at a single point in time is more complicated for rolling bearings than for single mechanical components, and the overall time-varying reliability curve can be computed at a significant time cost. The surrogate model method [21,22] has gained much attention for its ability to improve the computational efficiency of a reliability analysis by approximating the correspondence between the stochastic parameters and the response. The current surrogate modeling methods are mainly divided into the following: kriging model [23,24], response surface method (RSM) [25,26], and neural network (NN) [27,28]. Among them, the kriging model is preferred by researchers because of its characteristics of minimum variance estimation and local estimation [29].
In order to overcome the above problems, an efficient reliability-based robust design optimization method of rolling bearings is proposed by combining the improved Miner theory and a kriging model. First, the method uses a finite element simulation to obtain the state response of a rolling bearing under stochastic design parameters. Then, the adaptive kriging method is used to characterize the association between the stochastic parameters and the state response, the Miner fatigue cumulative damage theory is improved for the roller-race contact structure of the rolling bearings, and the rolling bearing fatigue time-varying equation of state under cyclic load spectrum is derived. Subsequently, a fatigue time-varying reliability model is established based on the improved fourth-order moment method, and a robust design method for fatigue reliability of rolling bearings is formed by considering the robustness factors. Finally, the optimized design results of rolling bearings with good robustness and reliability are obtained by using a multi-objective optimization algorithm.
The remainder of the paper is organized as follows: Section 2 starts with a brief introduction of the rolling bearing dynamic response kriging model combined with the finite element method, then a rolling bearing fatigue reliability model based on the improved Miner theory and the fourth-moment method is presented, followed by the details of the time-varying reliability sensitivity analysis; an example based on rolling bearing fatigue reliability is described in Section 3 to illustrate the validity and accuracy of the proposed method; Section 4 contains the discussion and conclusions.
2. Materials and Methods
2.1. Kriging Model of Rolling Bearings Based on the Finite Element Method
The finite element method (FEM) has high computational accuracy [30] and can be used to analyze accurate mechanical and kinematic responses of rolling bearings under different loads. However, due to its high computational cost, it is difficult to use for the analysis of a large number of random parameter samples (Figure 2).

Figure 2.
FEM model of a rolling bearing.
The kriging model uses a collection of training samples to construct a functional relationship between the input variables and the response, and predicts the response value at the estimated point accordingly, so that it can be combined with FEM to obtain accurate mechanical responses efficiently.
Assume that the vector of sample input parameters of the rolling bearing is , and the corresponding mechanical response vector obtained by FEM is , then the corresponding relation between the two can be expressed by the kriging model as follows:
where is the regression model of , is the regression coefficient, and is the random factor whose mean, variance, and covariance can be expressed as:
where is the spatial correlation function between the sample points and , which is usually expressed as a Gaussian-type spatial correlation function as follows:
where is the correlation coefficient and is the variable dimension.
The variance can be expressed as:
where is the total number of sample points, is the regression matrix of sample points, and is the matrix composed of .
in Equation (1) can be estimated by the least square method as:
Therefore, the output estimate at the unknown point can be expressed as:
where is the correlation function vector between the unknown point and the training sample parameters.
The correlation coefficient can be obtained by the maximum likelihood estimation method, and the maximum likelihood function is:
By substituting the obtained into Equation (6), a surrogate model with optimal fitting accuracy can be obtained under the training set.
On this basis, the adaptive kriging model is continuously updated by introducing a learning function to obtain the optimal kriging model for the current sample set, and in this paper, a learning function defined by B. Echard et al. [31] is chosen, denoted as:
This learning function also considers the distance between the model predicted value and the failure surface as well as the standard deviation, and usually chooses as the convergence condition for the updating process [32].
Based on the learning function, the adaptive updating strategy of the kriging model is formed. The specific steps are shown in Figure 3.
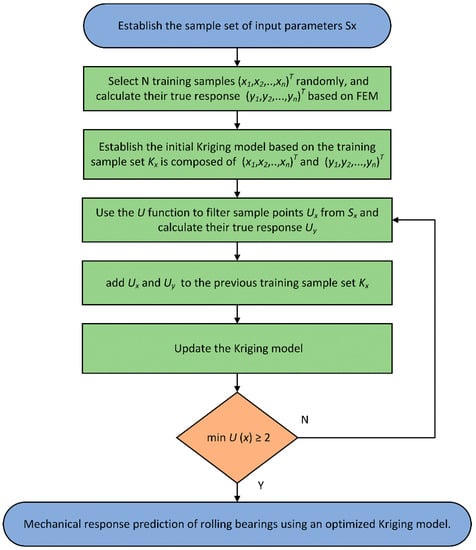
Figure 3.
Process of the adaptive kriging model based on function.
2.2. Time-Varying Fatigue Reliability Model of a Rolling Bearing
Fatigue failure is the most common form of rolling bearing failure, the essence of which is the change in material properties caused by cyclic stress [33]. The fatigue performance of the material is often expressed in the curve, which is a curve describing the correspondence between the applied stress level and the fatigue life.
According to the widely used Miner theory [34], the total damage of a structural member subjected to random loading is a linear accumulation of damage superimposed at all levels of stress, and failure occurs when accumulates to , which can be expressed as follows:
Miner’s theory is a linear fatigue cumulative damage theory, which is simple and easy to implement but does not consider the effect of load order. Kwofie et al. [15] proposed a modified Miner theory based on the cumulative fatigue damage equation by considering the sequence of load changes as follows:
where is the number of cycles under loading , is the fatigue life under loading , and is the fatigue life under initial loading .
Thus, Equation (10) can be expressed as:
However, rolling bearings are often subjected to a variety of operating conditions during actual use, and these conditions can be divided into multiple load levels in the load spectrum by the rain flow counting method [35]. Suppose there are load levels in the load spectrum, under any load level, there is internal load distribution in the rolling bearing leading to stress levels at any point on the inner and outer ring raceway during a rotation cycle . Then, in a load spectrum cycle, , the accumulated fatigue damage at a point on the rolling bearing raceway is:
where is the number of cycles under loading , is the fatigue life under loading , and is the fatigue life under initial loading . can be calculated as follows:
where is the operating time corresponding to the load level in the load spectrum, is the number of contact cycles corresponding to the contact level on the inner/outer ring per unit time, which can be approximated according to the current speed operating conditions and bearing structure parameters.
Therefore, the average rolling bearing fatigue accumulated damage per unit time can be expressed as follows:
When the rolling bearing service time increases, fatigue accumulation damage gradually increases, when the fatigue accumulation damage reaches 1, this is defined as rolling bearing fatigue failure.
Therefore, the time-varying fatigue reliability state function of rolling bearings can be expressed as:
where is the vector composed of input random parameter of the rolling bearing.
In engineering applications, the distribution law of the random input parameters is usually difficult to determine due to limited data. In this case, the relationship between the first fourth-order moments of the random input parameters and the first fourth-order moments of the state function is derived from the analysis of the reliability of mechanical products by using an improved fourth-moment method proposed by Zhang et al. [17].
By applying the stochastic perturbation theory to the equation of state derived above, the mean value , variance , third-order moment , and fourth-order moment of the equation of state of time-varying fatigue of a rolling bearing can be obtained as follows:
where , , and represent the mean vector, second-order moment matrix, third-order moment matrix, and fourth-order moment matrix of random input vector , respectively.
When the first four moments of the random input vector are known, the time-varying fatigue reliability index of rolling bearings can be obtained according to the improved fourth-moment method without determining the probability distribution law of as follows:
Therefore, the approximate estimated fatigue reliability of the rolling bearing at time can be expressed as:
where represents the standard normal distribution function.
2.3. Sensitivity Analysis and Time-Varying Reliability Robust Design
A reliability sensitivity analysis is a method to quantitatively assess the influence of random variables on the reliability of mechanical structures on the basis of reliability. In engineering design, on the one hand, if a certain input random variable of a rolling bearing has a serious influence on fatigue failure, it should be controlled in the manufacturing process based on economy and design requirements; on the other hand, if the random variable has a weak influence on wear reliability, it can be treated as a constant to reduce the number of variables. Therefore, it is of great engineering value to study the fatigue reliability sensitivity of rolling bearings. It is generally only necessary, in engineering, to obtain the sensitivity of reliability to the first two orders of moments of random input parameters for guidance of mechanical product design and machining.
Based on the matrix description of differential relations of moment functions [36], the sensitivity of the fatigue reliability of rolling bearings to the mean vector and the variance vector of the random parameter vector can be deduced as follows:
where can be calculated as follows:
where is the probability density function of the standard normal distribution.
To integrate the sensitivity of reliability to the mean and variance of the underlying random variables, the reliability sensitivity gradient is constructed as follows:
The goal of the reliability-based robust design optimization is to satisfy the reliability requirements while keeping the value of the reliability sensitivity gradient as low as possible. The reliability in Equation (20) and the reliability sensitivity gradient in Equation (24) above are brought into the optimization model to obtain the optimized design results, and the proposed reliability-based robust design optimization model is expressed as
where is the given reliability requirement; and represent inequality constraint and equality constraint, respectively. Then, the above optimization problem can be solved by using various optimization methods and mathematical software, such as a genetic algorithm or MATLAB 9.2.0.538062 (R2017a) optimization toolbox.
3. Results
In order to perform the RBRDO for the fatigue reliability of a rolling bearing, each step, as shown in Figure 4, needs to be completed in turn. Firstly, the mechanical response of the rolling bearing under the action of random input parameters is obtained by using the FEM; then, the surrogate model between the random input parameters and mechanical response is established based on the adaptive kriging method. Then, the equation of the fatigue state of the raceway-roller contact under an external cyclic load spectrum is proposed in combination with the improved Miner theory; then, the rolling bearing wear reliability is established by using the improved fourth-moment method. Finally a sensitivity analysis is performed combined with the optimization algorithm to solve the rolling bearing fatigue reliability for the robustness optimization design problem and to obtain the optimized design parameters.
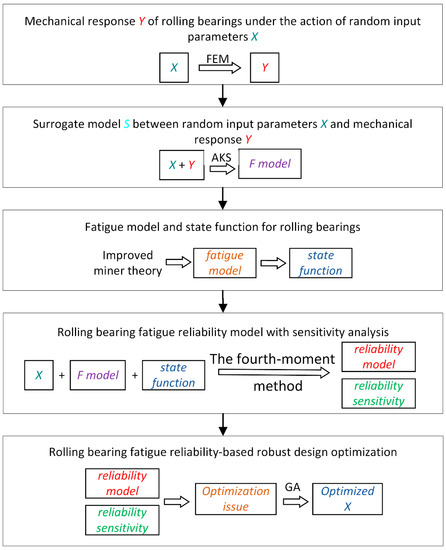
Figure 4.
Time-varying wear RBRDO process for rolling bearings.
A deep groove 6016-type rolling bearing was selected as the object of the time-varying fatigue RBRDO with the following conditions: Bearing outside diameter , bearing bore diameter , the number of rolling bodies , material GCr15. The bearing is assumed to be in service under the cyclic load spectrum conditions shown in Table 1 below.

Table 1.
The 6016-type rolling bearing service cycle load spectrum settings.
The random parameters associated with fatigue failure were selected as input variables to construct the vector . The average value of each dimensional parameter in X was obtained by measuring a set of 6016-type rolling bearings with a coordinate measuring machine (CMM), and the remaining parameters were obtained by making assumptions based on empirical error ranges, as shown in Table 2.

Table 2.
The 6016-type rolling bearing input random parameters with the first fourth-order moments.
According to Table 2, the random input parameters are generated, and the mechanical response of the 6016-type rolling bearing is obtained by using the FEM method, as shown in Figure 5. The random input parameters and the mechanical response are formed into a training dataset and the kriging model between the mechanical response and the input parameters is obtained by training with this dataset. Afterwards, the kriging model is combined with the wear reliability model of the rolling bearing and the first four moments of the wear reliability state function of the rolling bearing can be obtained using Equations (16)–(19). Finally, these moments are substituted into Equations (20) and (21) for different time intervals to obtain the time-varying reliability curve for rolling bearing wear, as shown in Figure 6.
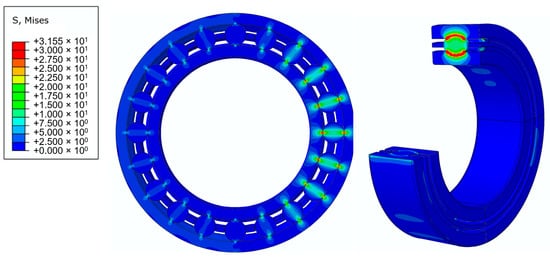
Figure 5.
Mechanical response of rolling bearings obtained from FEM.
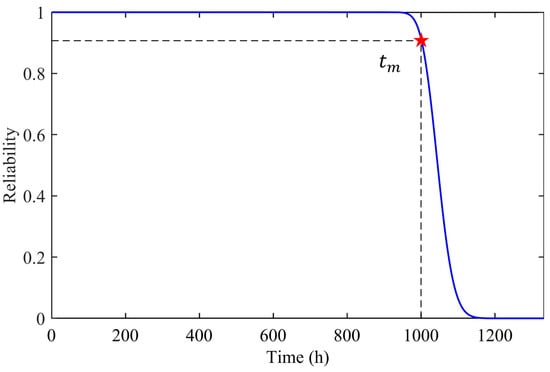
Figure 6.
Time-varying wear reliability curve of the 6016-type rolling bearing.
The moment in the reliability reduction process is selected, and the reliability calculation results at are shown in Table 3.

Table 3.
Comparison of reliability calculation results at the selected moment.
The time-varying fatigue reliability curves obtained by the proposed method were compared using the MCS method, and the intercepted time period of 800–1200 h is shown in Figure 7. It can be seen that the calculation results of the two methods are very close to each other, and the relative error between the two methods at this point is calculated to be 0.1751%, which proves the accuracy of the proposed method. The sample size of the MCS method used in this case is , which can be considered to be the exact solution.
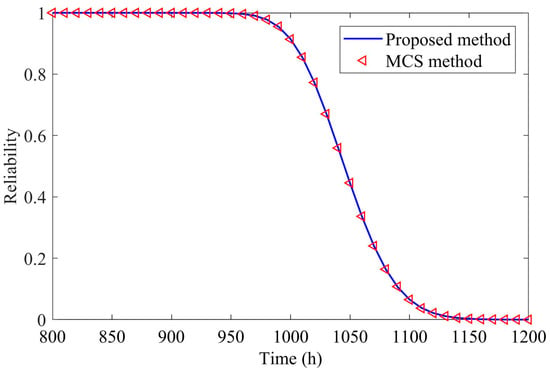
Figure 7.
Comparison between the proposed method and the MCS method.
By bringing the above reliability calculation results into Equations (22) and (23), the sensitivity of rolling bearing fatigue reliability to the mean and variance of input parameters can be obtained, as shown in Table 4, the total gradient of reliability sensitivity and the gradient of reliability sensitivity of each parameter are calculated by Equation (24), and the weights are calculated as shown in Figure 7.

Table 4.
The sensitivity of rolling bearing wear reliability to input parameters.
Table 4 demonstrates the following:
- The sensitivity of reliability to the mean values of and is positive, and the sensitivity to the mean values of and is negative. This means that when the mean values of and increase within the allowed initial value interval, the reliability increases, and when the mean values of and increase, the reliability decreases. The sensitivity of reliability to the variance of all parameters is negative. This means that when the variance of any one of the input parameters increases, the reliability decreases with it.
- In the calculation result of the sensitivity gradient of reliability to input parameters, the sensitivity gradient of reliability to is the largest, that is, the first two order statistical moments of have the greatest comprehensive influence on the fatigue reliability of rolling bearings under this moment, and it is necessary to appropriately invest production resources for design and processing accuracy control.
- In the calculation result of the sensitivity gradient of reliability to input parameters, the sensitivity gradient of reliability to is the smallest, that is, the first two order statistical moments of have the smallest comprehensive influence on the fatigue reliability of rolling bearing under this moment, and the design and processing accuracy control can be relaxed appropriately to save production cost.
According to the above reliability and sensitivity calculation results at the moment , we can establish the robustness optimization design model of rolling bearing fatigue reliability in the shape of Equation (25), after which we need to determine the constraints of the optimization problem according to the structural characteristics of rolling bearings.
The fatigue reliability target of the rolling bearing is set to ; therefore, the reliability constraint is:
In order to keep the inner/outer raceways of the rolling bearing in point contact with the rollers before, establish the dimensional constraint as follows:
According to the structural parameters of the rolling bearing design requirements, establish the boundary constraints as follows:
Based on the above constraints, the optimization model in Equation (25) is solved by using a genetic algorithm and the optimization results are obtained as shown in Table 5.

Table 5.
The optimized design parameters of rolling bearings.
According to the optimized design parameters, the corresponding time-varying fatigue reliability curves of a rolling bearing were obtained and compared with the reliability curves before optimization in Figure 8. In addition, the total reliability sensitivity gradient after optimization was also calculated, as shown in Table 6.
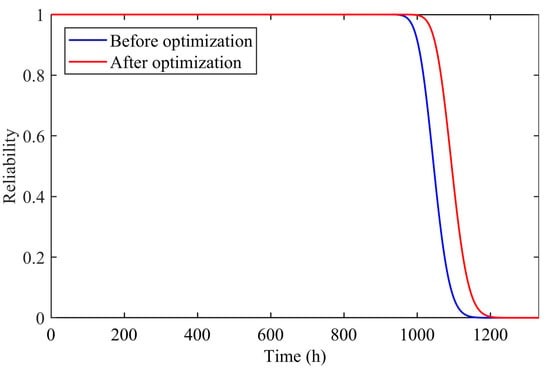
Figure 8.
6016-type rolling bearing fatigue reliability-time curve after optimization.

Table 6.
Reliability and sensitivity gradient comparison before and after optimization.
As can be seen from Figure 8, the fatigue reliability curve of the optimized rolling bearing lags significantly behind that before optimization, which indicates that the reliable life of the rolling bearing has been extended, implying a more reasonable structural design. On the one hand, the reliability at the moment of in Table 6 reaches the constraint target , which also supports the above point. On the other hand, the reliability sensitivity gradient after optimization in Table 6 is greatly reduced, which indicates that the reliability is more robust under the optimized design parameters and verifies the effectiveness of the method proposed in this paper.
4. Discussion
In this study, by combining the adaptive kriging method with the FEM of rolling bearings, a surrogate model between the mechanical response of rolling bearings and the stochastic parameters is constructed, and the computational efficiency of the mechanical response of a rolling bearing is improved; the time-varying equation of the state of a rolling bearing under cyclic load spectrum is derived by improving the Miner fatigue cumulative damage theory; the time-varying reliability model of fatigue and proposed reliability robust design index is established based on the improved fourth-order moment method, and finally a time-varying fatigue RBRDO method of a rolling bearing under cyclic load spectrum is formed. The numerical example results of the 6016-type rolling bearing under cyclic load spectrum show that the method can improve the fatigue reliability of the rolling bearing and can significantly reduce the sensitivity gradient of the rolling bearing fatigue reliability, which means that maximum robustness can be effectively achieved while meeting the reliability requirements.
This study has the following advantages: On the one hand, compared with the traditional time-varying reliability calculation method based on the FEM, this study achieves rapid calculation of the mechanical response of rolling bearings based on the kriging method, which significantly improves the overall calculation efficiency of time-varying reliability and overcomes the problem of large calculation costs of time-varying reliability of complex structures at different time points. On the other hand, for the roller-race structure inside the rolling bearing, the fatigue accumulation damage model based on Miner’s theory is improved and established for the internal cyclic alternating load distribution of rolling bearings under external cyclic load.
Despite the good progress made in this study, there are still some limitations to overcome. First, it is clear from the whole design process that the results of this design method depend on the accuracy of establishing the FEM of the study object, so an accurate understanding of the structure and failure mechanism of the study object is indispensable. The second challenge is that for rolling bearing materials, the randomness brought by the properties of the bearing steel itself can be further discussed in depth, for example, the steel inclusions in the bearing steel material can have a large impact on the initial generation of fatigue cracks [37]. Finally, under the premise of using a suitable and accurate FEM model, the method proposed in this paper can also be applied to the fatigue reliability design process of other mechanical products, and comprehensive application exploration can be carried out in the design of other mechanical products in the future.
Author Contributions
Methodology, S.E.; software, S.E.; validation, S.E.; formal analysis, S.E.; investigation, S.E.; resources, S.E.; data curation, S.E.; writing—original draft preparation, S.E.; writing—review and editing, S.E.; visualization, S.E.; supervision, B.X.; project administration, Y.W.; funding acquisition, F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2019YFB2004400 and the National Key Laboratory of Science and Technology on Helicopter Transmission, grant number HTL-O-21K02.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cerrada, M.; Sánchez, R.E.V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.E.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Proc. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
- Mcfadden, P.D.; Smith, J.D. Vibration monitoring of rolling element bearings by the high-frequency resonance technique—A review. Tribol. Int. 1984, 17, 3–10. [Google Scholar] [CrossRef]
- Kam, O.M.; Noël, S.E.P.; Ramenah, H.; Kasser, P.; Tanougast, C. Comparative Weibull distribution methods for reliable global solar irradiance assessment in France areas. Renew. Energy 2021, 165, 194–210. [Google Scholar] [CrossRef]
- Shuto, S.; Amemiya, T. Sequential Bayesian inference for Weibull distribution parameters with initial hyperparameter optimization for system reliability estimation. Reliab. Eng. Syst. Saf. 2022, 224, 108516. [Google Scholar] [CrossRef]
- Lundberg, G.; Palmgren, A. Dynamic capacity of rolling bearings. J. Appl. Mech. 1949, 16, 165–172. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, H.; Wei, P.; Guagliano, M.; Hou, S. A modified model of Lundberg—Palmgren rolling contact fatigue formula considering the effects of surface treatments. Friction 2023. [Google Scholar] [CrossRef]
- ISO 281:2007; Rolling Bearings: Dynamic Load Ratings and Rating Life. ISO: Geneva, Switzerland, 2007.
- Tian, X.; Shi, X.; Peng, C.; Yi, X. A Reliability Growth Process Model with Time-Varying Covariates and Its Application. Mathematics 2021, 9, 905. [Google Scholar] [CrossRef]
- Meng, D.; Lv, Z.; Yang, S.; Wang, H.; Xie, T.; Wang, Z. A time-varying mechanical structure reliability analysis method based on performance degradation. Structures 2021, 34, 3247–3256. [Google Scholar] [CrossRef]
- Aeran, A.; Siriwardane, S.C.; Mikkelsen, O.; Langen, I. A new nonlinear fatigue damage model based only on SN curve parameters. Int. J. Fatigue 2017, 103, 327–341. [Google Scholar] [CrossRef]
- Harris, T.A. A New Fatigue Life Model for Rolling Bearings. J. Tribol. 1985, 107, 367–377. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A cumulative damage theory of fatigue failure. Mater. Sci. Eng. 1978, 34, 147–160. [Google Scholar] [CrossRef]
- Bjørheim, F.; Pavlou, D.G.; Siriwardane, S.C. Nonlinear fatigue life prediction model based on the theory of the S-N fatigue damage envelope. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 1480–1493. [Google Scholar] [CrossRef]
- Kwofie, S.; Rahbar, N. A fatigue driving stress approach to damage and life prediction under variable amplitude loading. Int. J. Damage Mech. 2013, 22, 393–404. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Z.; Almaktoom, A.T. Dynamic reliability-based robust design optimization with time-variant probabilistic constraints. Eng. Optimiz. 2014, 46, 784–809. [Google Scholar] [CrossRef]
- Zhang, T. An improved high-moment method for reliability analysis. Struct. Multidiscip. Optim. 2017, 56, 1225–1232. [Google Scholar] [CrossRef]
- Zhang, T. Robust reliability-based optimization with a moment method for hydraulic pump sealing design. Struct. Multidiscip. Optim. 2018, 58, 1737–1750. [Google Scholar] [CrossRef]
- Zhang, T.; He, D. A Reliability-Based Robust Design Method for the Sealing of Slipper-Swash Plate Friction Pair in Hydraulic Piston Pump. IEEE Trans. Reliab. 2018, 67, 459–469. [Google Scholar] [CrossRef]
- Iannacone, L.; Sharma, N.; Tabandeh, A.; Gardoni, P. Modeling time-varying reliability and resilience of deteriorating infrastructure. Reliab. Eng. Syst. Saf. 2022, 217, 108074. [Google Scholar] [CrossRef]
- Zafar, T.; Zhang, Y.; Wang, Z. An efficient Kriging based method for time-dependent reliability based robust design optimization via evolutionary algorithm. Comput. Meth. Appl. Mech. Eng. 2020, 372, 113386. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, J.; Huang, F.; Lv, Y.; Wan, L. A novel adaptive Kriging method: Time-dependent reliability-based robust design optimization and case study. Comput. Ind. Eng. 2021, 162, 107692. [Google Scholar] [CrossRef]
- Jeong, S.; Murayama, M.; Yamamoto, K. Efficient optimization design method using kriging model. J. Aircr. 2005, 42, 413–420. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.; Fei, C.; Bu, S. Improved decomposed-coordinated kriging modeling strategy for dynamic probabilistic analysis of multicomponent structures. IEEE Trans. Reliab. 2019, 69, 440–457. [Google Scholar] [CrossRef]
- Allaix, D.L.; Carbone, V.I. An improvement of the response surface method. Struct. Saf. 2011, 33, 165–172. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Jiang, C.; Liu, J.; Li, Q. Time-dependent reliability analysis through response surface method. J. Mech. Des. 2017, 139, 41404. [Google Scholar] [CrossRef]
- Tripathy, R.K.; Bilionis, I. Deep UQ: Learning deep neural network surrogate models for high dimensional uncertainty quantification. J. Comput. Phys. 2018, 375, 565–588. [Google Scholar] [CrossRef]
- White, D.A.; Arrighi, W.J.; Kudo, J.; Watts, S.E. Multiscale topology optimization using neural network surrogate models. Comput. Meth. Appl. Mech. Eng. 2019, 346, 1118–1135. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging method vs RSM, MARS and M5 model tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Chai, Y.; Huang, K.; Wang, S.; Xiang, Z.; Zhang, G. The Extrinsic Enriched Finite Element Method with Appropriate Enrichment Functions for the Helmholtz Equation. Mathematics 2023, 11, 1664. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Mai, H.T.; Lee, J.; Kang, J.; Nguyen-Xuan, H.; Lee, J. An Improved Blind Kriging Surrogate Model for Design Optimization Problems. Mathematics 2022, 10, 2906. [Google Scholar] [CrossRef]
- Cui, L.; Su, Y. Contact fatigue life prediction of rolling bearing considering machined surface integrity. Ind. Lubr. Tribol. 2022, 74, 73–80. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.; Correia, J.A.F.O.; De Jesus, A.M.P.; Veljkovic, M.; Berto, F. Fatigue reliability of wind turbines: Historical perspectives, recent developments and future prospects. Renew. Energy 2022, 200, 724–742. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, D.D.; Siwakoti, Y.P. Circuit-Based Rainflow Counting Algorithm in Application of Power Device Lifetime Estimation. Energies 2022, 15, 5159. [Google Scholar] [CrossRef]
- Zhang, T. Matrix description of differential relations of moment functions in structural reliability sensitivity analysis. Appl. Math. Mech. 2017, 38, 57–72. [Google Scholar] [CrossRef]
- El Laithy, M.; Wang, L.; Harvey, T.J.; Vierneusel, B.; Correns, M.; Blass, T. Further understanding of rolling contact fatigue in rolling element bearings—A review. Tribol. Int. 2019, 140, 105849. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).