1. Basic Concepts and Introduction
Before clarifying the objectives of this paper, we first introduce the necessary basic concepts. We identify several definitions and properties and present the goals of this paper based on them.
Let
with
. The quantum number,
q-number, discovered by Jackson is
and we note that
. In particular, for
,
is called
q-integer; see [
1,
2,
3,
4].
Many mathematicians in various fields have worked on the introduction of
q-numbers, such as
q-discrete distribution,
q-differential equations,
q-series,
q-calculus, and so on; see [
5,
6,
7,
8].
The following equation,
is the
q-Gaussian binomial coefficient where
m and
r are non-negative integers; see [
4,
5]. For
, the value of
q-Gaussian binomial coefficients is 1 since the numerator and the denominator are both empty products. One notes that
and
.
In [
9], a two-parameter time scale
was introduced as follows:
Definition 1 ([
9,
10]).
Let be any function. Then, the delta -derivative of f is defined by From the above definition, we can see several properties as follows:
- (i)
For , if and only if is a constant;
- (ii)
for all if and only if with some constant c;
- (iii)
For , if and only if , where and are constant.
In Definition 1, we can see that , the delta -derivative of f reduces to , the q-derivative of f for and reduces to , the h-derivative of f for .
In addition, we can find the product rule and quotient rule for the delta -derivative.
Theorem 1 ([
9,
10]).
Let be arbitrary functions. Definition 2 ([
10,
11]).
The generalized quantum binomial is defined bywhere . The generalized quantum binomial reduces to q-binomial as and to h-binomial when . Also, we note .
Definition 3 ([
10]).
The generalized quantum exponential function is defined aswhere α is an arbitrary nonzero constant. Clearly, we note
. As
and
, the generalized quantum exponential function
becomes the so-called
q-exponential function
; see [
4,
5]. Also, as
and
, the generalized quantum exponential function
reduces to the so-called
h-exponential function
; see [
4].
Based on the above concepts, many mathematicians have studied
q-special functions,
q-differential equations,
q-calculus, and so on; see [
12,
13,
14,
15,
16]. For example, Duran, Acikgoz and Araci [
16] considered different trigonometric functions and hyperbolic functions related to quantum numbers and looked for properties related to them. Mathematicians also discovered various theorems about basic concepts related to
h-numbers. Benaoum [
11] obtained Newton’s binomial formula in terms of
, and Cermak and Nechvatal [
9] created a
version of fractional calculus. In 2011, Rahmat [
17] studied the
-Laplace transform. Silindir and Yantir [
10] studied the quantum generalization of Taylor’s formula and the
q-binomial coefficient in 2019; their work motivated the research reported in this paper. Mathematicians who study polynomials have already defined and characterized degenerate Euler polynomials. They also studied the definition and properties of Euler polynomials when combined with quantum numbers.
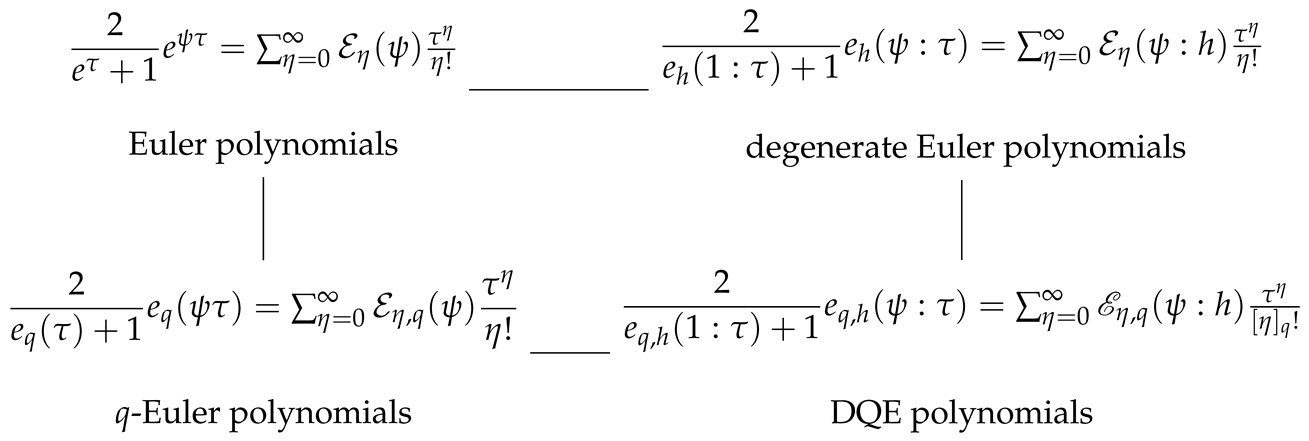
The main purpose of this paper is to construct degenerate quantum Euler polynomials (DQE polynomials) using properties of
q-numbers and the
-derivative. The topic of this paper is a field of mathematics that can be expanded into subareas such as series methods or generalizations of existing series. Its results can also be applied in interdisciplinary areas such as nonlinear physics, as well as for solutions to nonlinear differential equations providing instrumental defects such as kinks, vortices, etc. The diagram below shows the relationship of Euler,
q-Euler, and degenerate Euler polynomials to the degenerate quantum Euler polynomials (DQE polynomials) that we define here.
Definition 4 ([
14,
18]).
q-Euler numbers and polynomials are defined as: Definition 5 ([
19,
20]).
Degenerate Euler numbers and polynomials are defined as: The structure of this paper is as follows. In
Section 2, we define DQE numbers and polynomials. We find several properties of these polynomials by using
q-numbers and
-derivatives. In addition, we construct several higher-order differential equations whose solutions are DQE polynomials.
Section 3 shows the structure of approximate roots of DQE polynomials, which are solutions of the higher-order differential equations obtained in
Section 2. By observing various structures of these approximate roots, we can make several conjectures.
3. Properties for Approximate Roots of DQE Polynomials
In this section, we use Mathematica to show the structures and shapes of approximate roots of DQE polynomials. These DQE polynomials share several properties with both degenerate Euler polynomials and q-Euler polynomials. Here, the purpose of changing the q-number is to explore the properties of q-Euler polynomials, while the reason for changing the value of h is to explore the properties of degenerate Euler polynomials.
Let
. From the generating function of DQE numbers, we have
Using the Cauchy product in the above equation, we obtain
From the above equation, we show several DQE numbers
as follows:
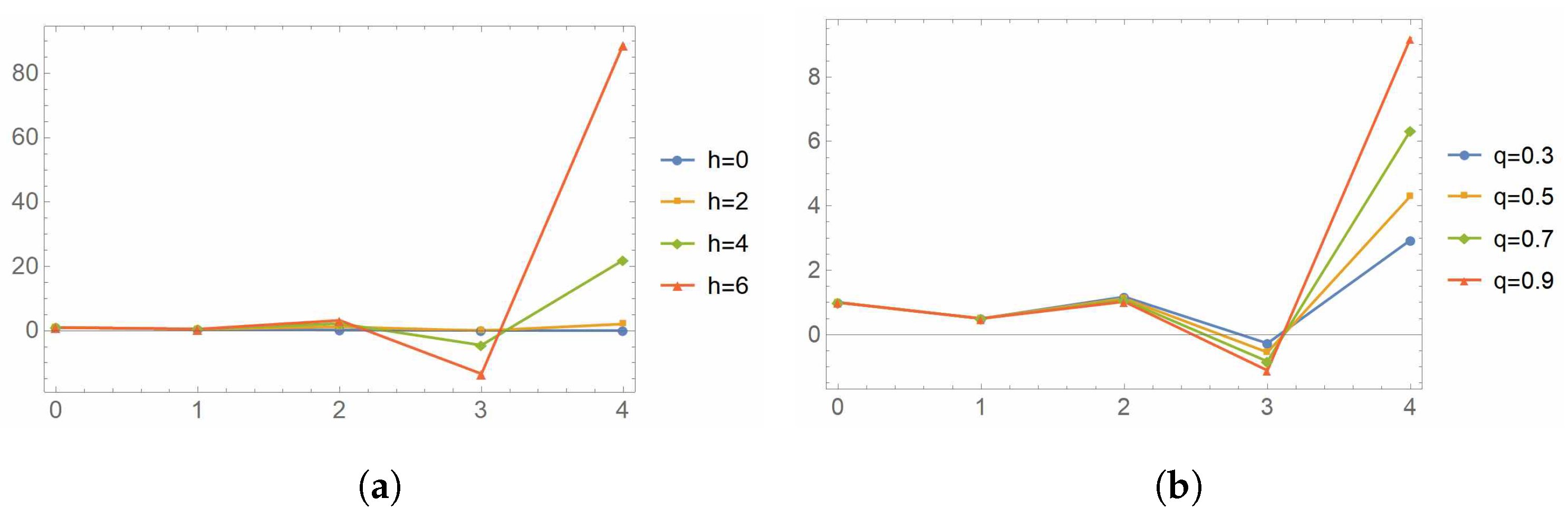
Figure 1 shows the values of
obtained by varying the values of
q,
, and
h. Non-negative integers on the
x-axis in
Figure 1 represent the value of
, with the 0 mark on the
x-axis corresponding to
, the 1 mark indicating
, and so on. The lines represent variations of the approximate values for DQE numbers. The approximate values of
-Euler numbers in
Figure 1a are the blue dots, yellow squares, green rhombuses, and red triangles, respectively, for
. Here, we can think of the blue dots as approximate values of
q-Euler numbers. In
Figure 1b, the blue dots, yellow squares, green rhombuses, and red triangles are the approximate values of
-Euler numbers in the respective cases
. The red triangles can be thought of as approximate values of
h-Euler numbers.
We next consider the approximate roots of DQE polynomials. In order to identify some of these approximate roots and their properties, we need the exact shapes of the polynomials. Several DQE polynomials
are shown in the following:
Based on the DQE polynomials obtained above, we hope to find out about the various behaviors of their approximate roots according to the changes in the values of q and h. We will restrict the value of q to less than 1, since DQE polynomials become degenerate Euler polynomials when q approaches 1 Also, DQE polynomials become q-Euler polynomials when h goes to 0, so the value of h has to exclude 0. According to the above condition, we can check the structures of approximate roots of DQE polynomials. Consider the case when the value of h is changed and but the value of q is fixed.
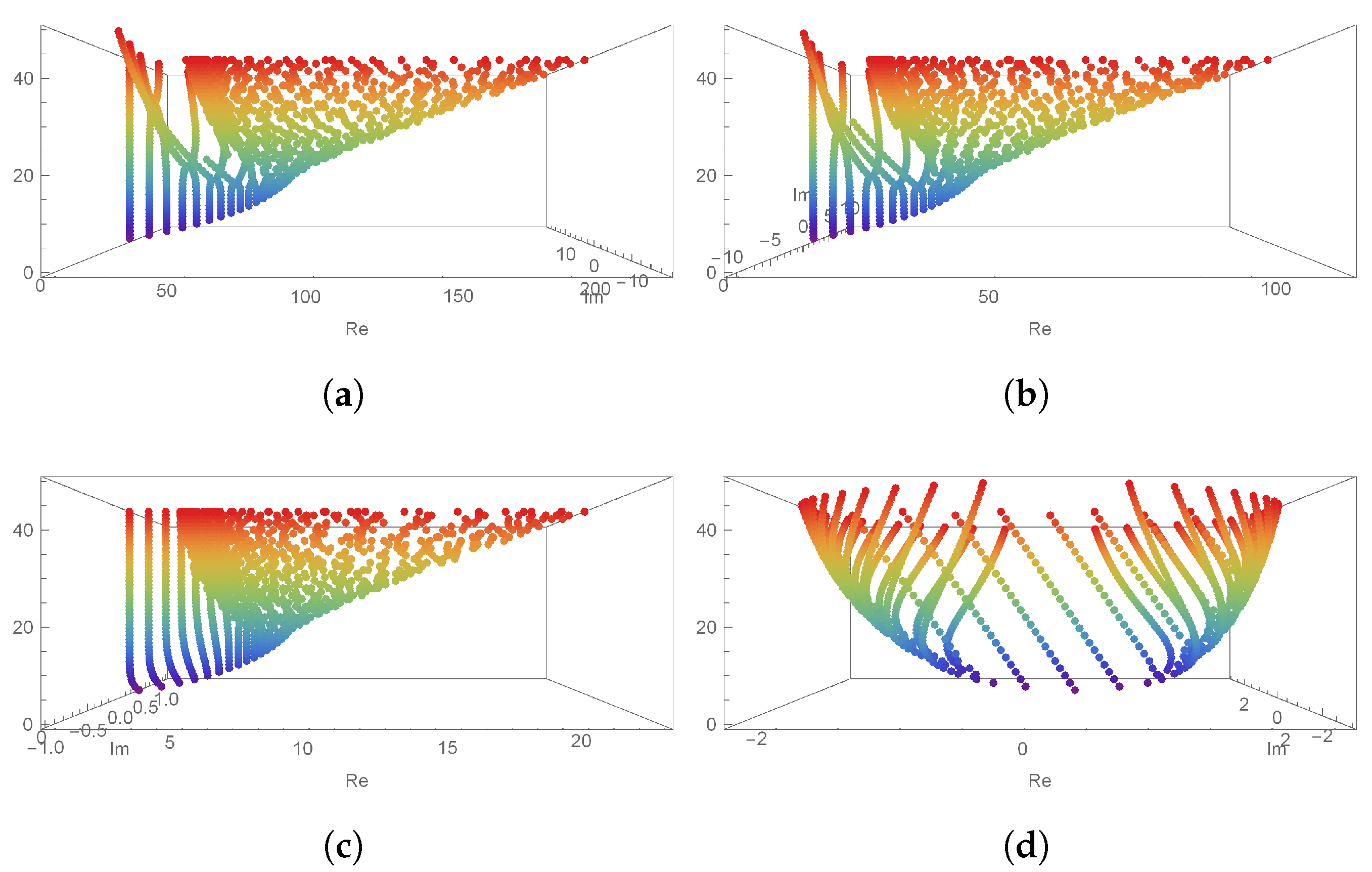
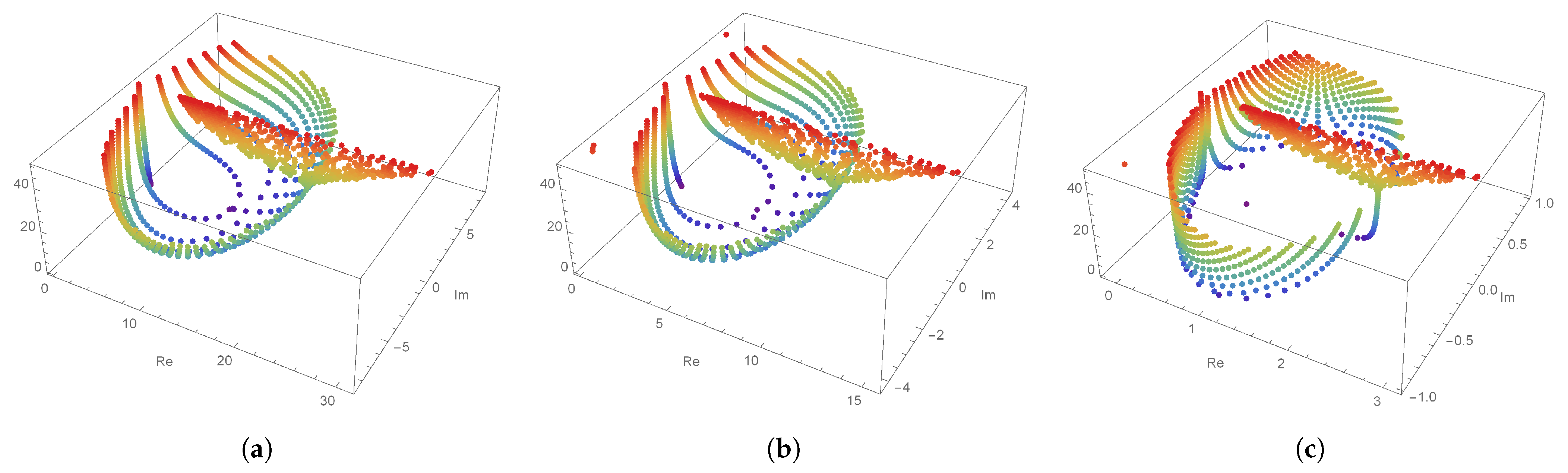
Let us fix
and
. Then,
Figure 2 illustrates the structures of the approximate roots of DQE polynomials obtained by varying
h. The condition of the top-left panel
Figure 2a shows the case where
; the condition of the top-right
Figure 2b is shown when
; the condition of the bottom-left
Figure 2c is shown when
; and the condition of the bottom-right
Figure 2d is shown when
. From
Figure 2d, it can be seen that, when the value of
h becomes 0, the shape of the approximate roots reduces to the approximate roots of
q-Euler polynomials. The blue dots are the positions of the approximate roots that appear when the value of
n is small, and the red dots are the positions of the approximate roots that appear when
in
Figure 2,
Figure 3,
Figure 4 and
Figure 5.
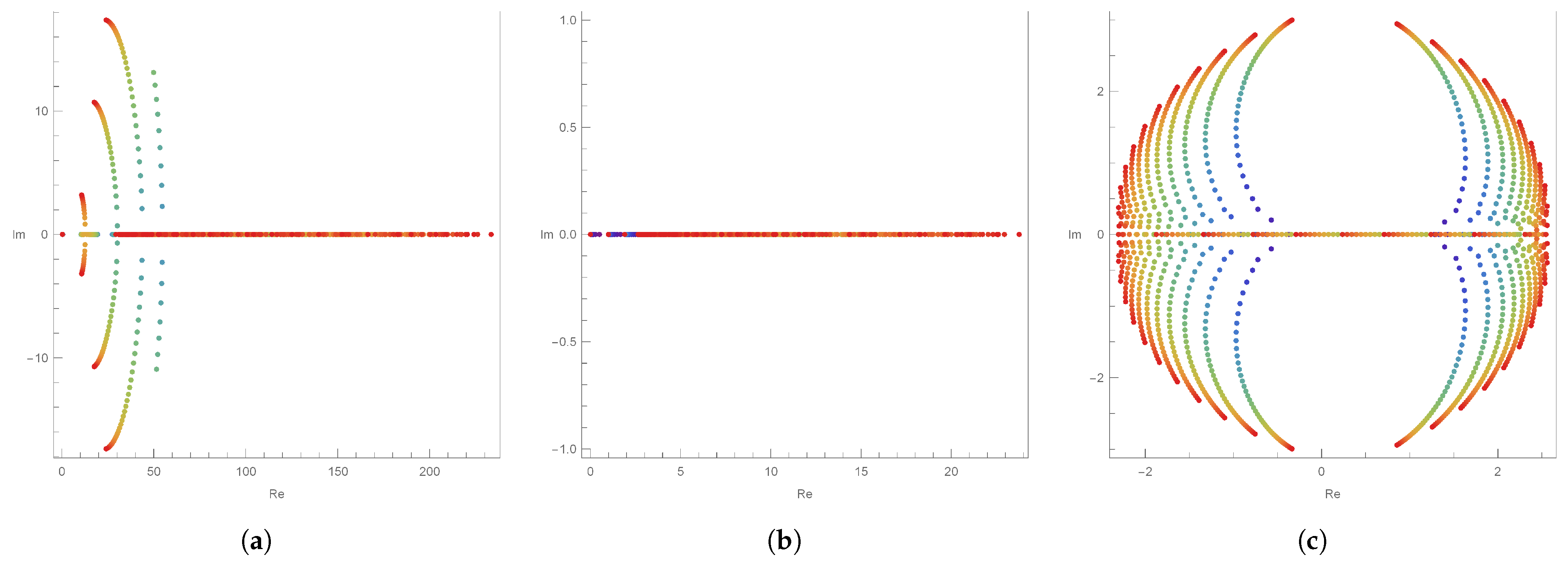
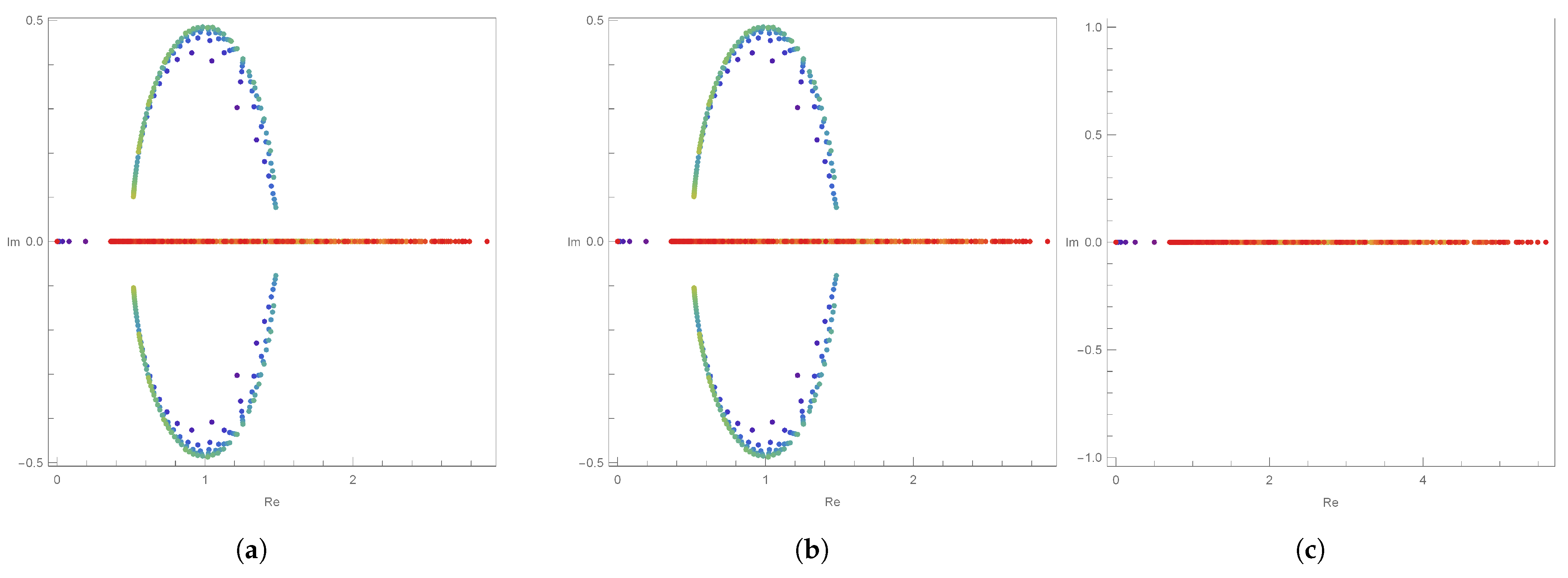
Looking at
Figure 2 from above gives the features shown in
Figure 3. There, we can see an interesting phenomenon:
Figure 3 shows the change in
h with
fixed for
. For
, it seems that all values of real numbers are approximate roots in
Figure 3a. In
Figure 3b with
, it can be seen that the approximate roots all have values of real numbers. In
Figure 3c, where
, we see that the shapes of the approximate roots have symmetric properties.
Based on
Figure 3, we can see real values shown in
Table 1, which shows approximate values of real numbers that appear when
h is changed.
Table 1 shows that the numbers of approximate real roots match the value of
when
h is 1. When
h is 1, the numbers of approximated real roots are also equal to the value of
n. However, when
h is 0, we can see that the approximated roots come out with both real and imaginary values. Considering
Figure 2 and
Figure 3, and
Table 1, we can make the following conjecture:
Conjecture 1. Let us fix . If , , then all values of approximate roots for DQE polynomials will be found on the real axis.
Figure 4 shows the shapes that appear when
q is fixed at
. The conditions of panels (a), (b), and (c) in
Figure 4 are as follows:
- (a)
for ,
- (b)
for ,
- (c)
for .
In
Figure 4, the blue dots correspond to
, and the red dots indicate
. In (a), (b), and (c) of
Figure 4, it can be seen that the approximate roots continue to accumulate even if
increases and the value of
h changes at one position.
Table 2 shows the approximate roots of one pillar location in
Figure 4; we can see that the positions of approximate roots stacked are close to 0. Based on
Figure 4 and
Table 2, we can make the following conjecture:
Conjecture 2. One of the approximate roots of the DQE polynomial has a value close to zero under the conditions , , and .
Next, we explore further properties of DQE polynomials by varying the
q-number, given the conditions
and
.
Figure 5 shows a view from above of the 3D shape that appears when the
q-number is changed under these constraints. The blue dots represent the low values of
n; the red dots indicate where
. In
Figure 5, the
q value of the shape on the left is
, the
q value in the middle is
, and the
q value on the right is
.
Figure 5 shows that the position of the red dots changes according to the value of
q and, based on this, we can make the following conjecture:
Conjecture 3. Let us fix . Then, all values of approximate roots for higher-order DQE polynomials will appear on the real axis as the q-number approaches 0.