Neuroadaptive Dynamic Surface Asymptotic Tracking Control of a VTOL Aircraft with Unknown Dynamics and External Disturbances
Abstract
1. Introduction
2. Problem Statement and Preliminaries
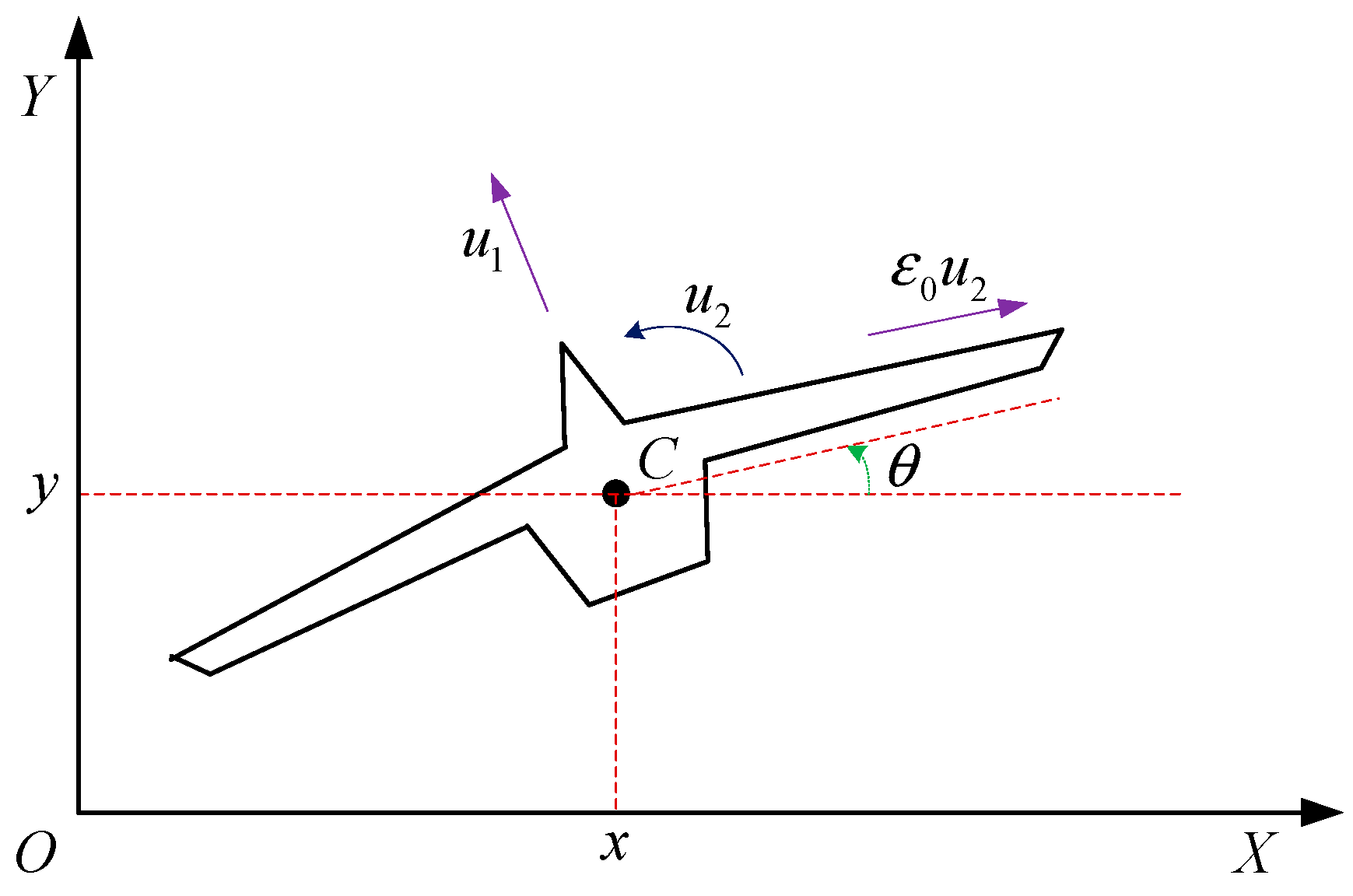
2.1. VTOL Aircraft System Model
2.2. Radial Basis Function Neural Network
3. Main Results
3.1. Control Law Design
3.2. Stability Analysis
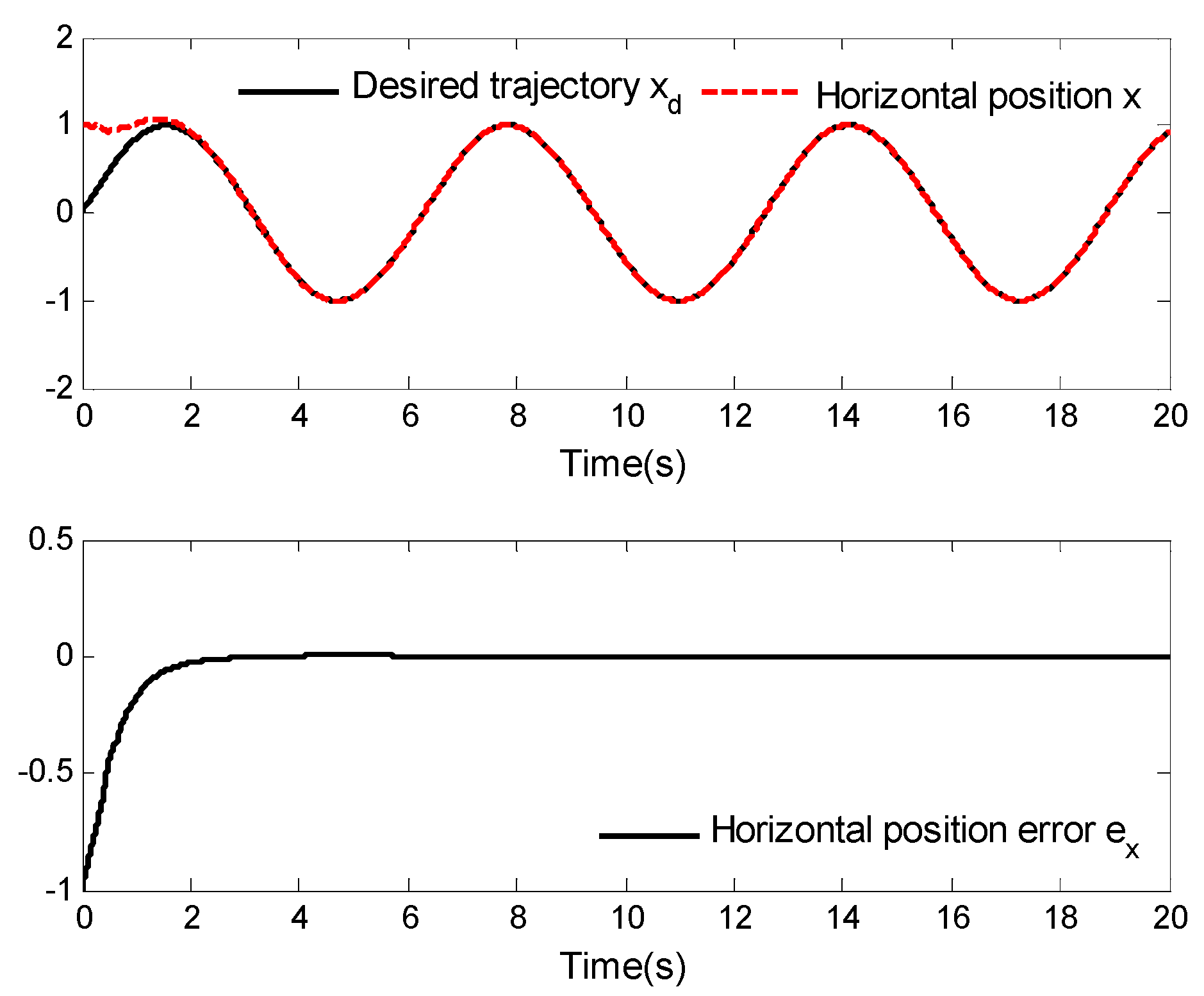
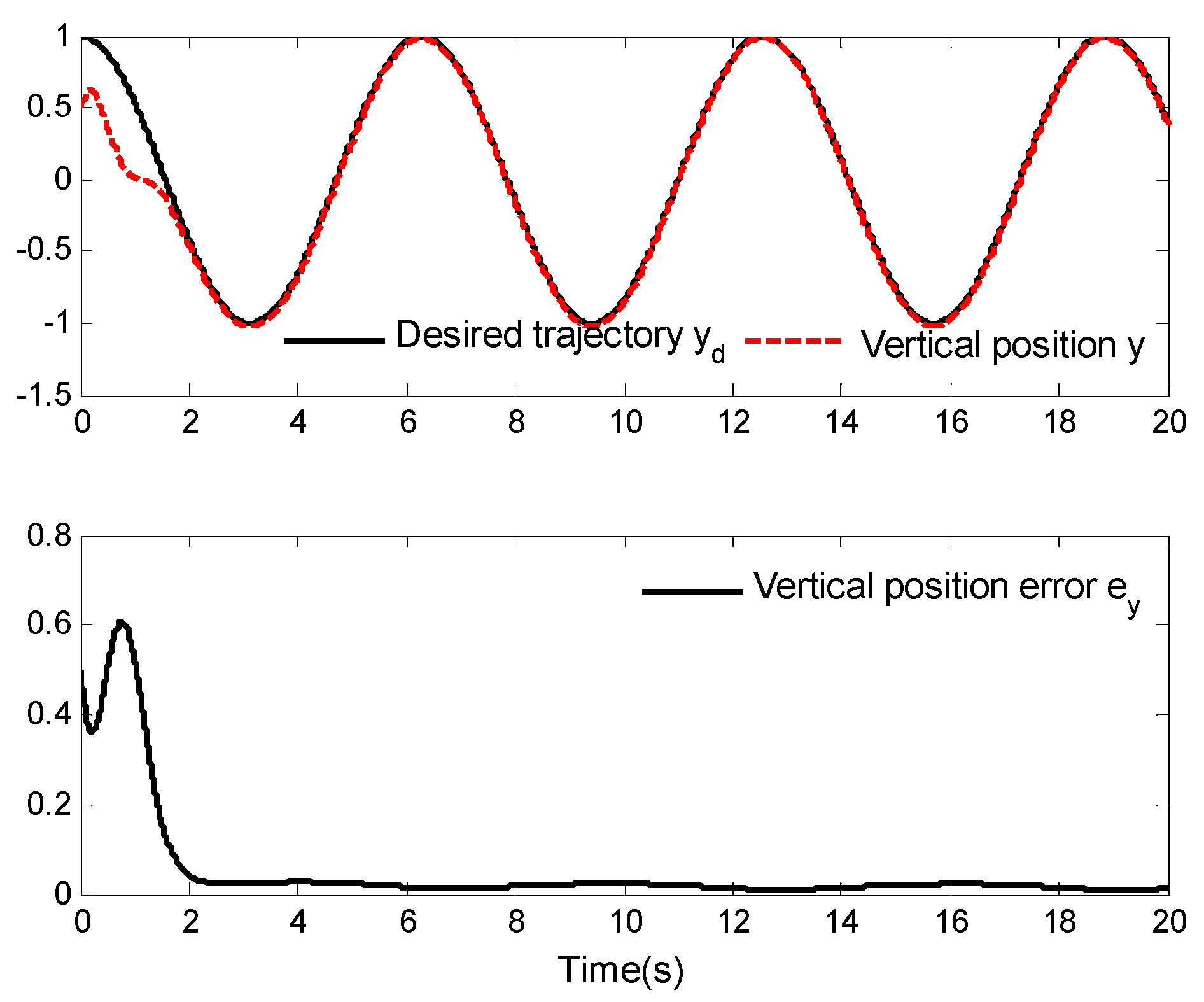
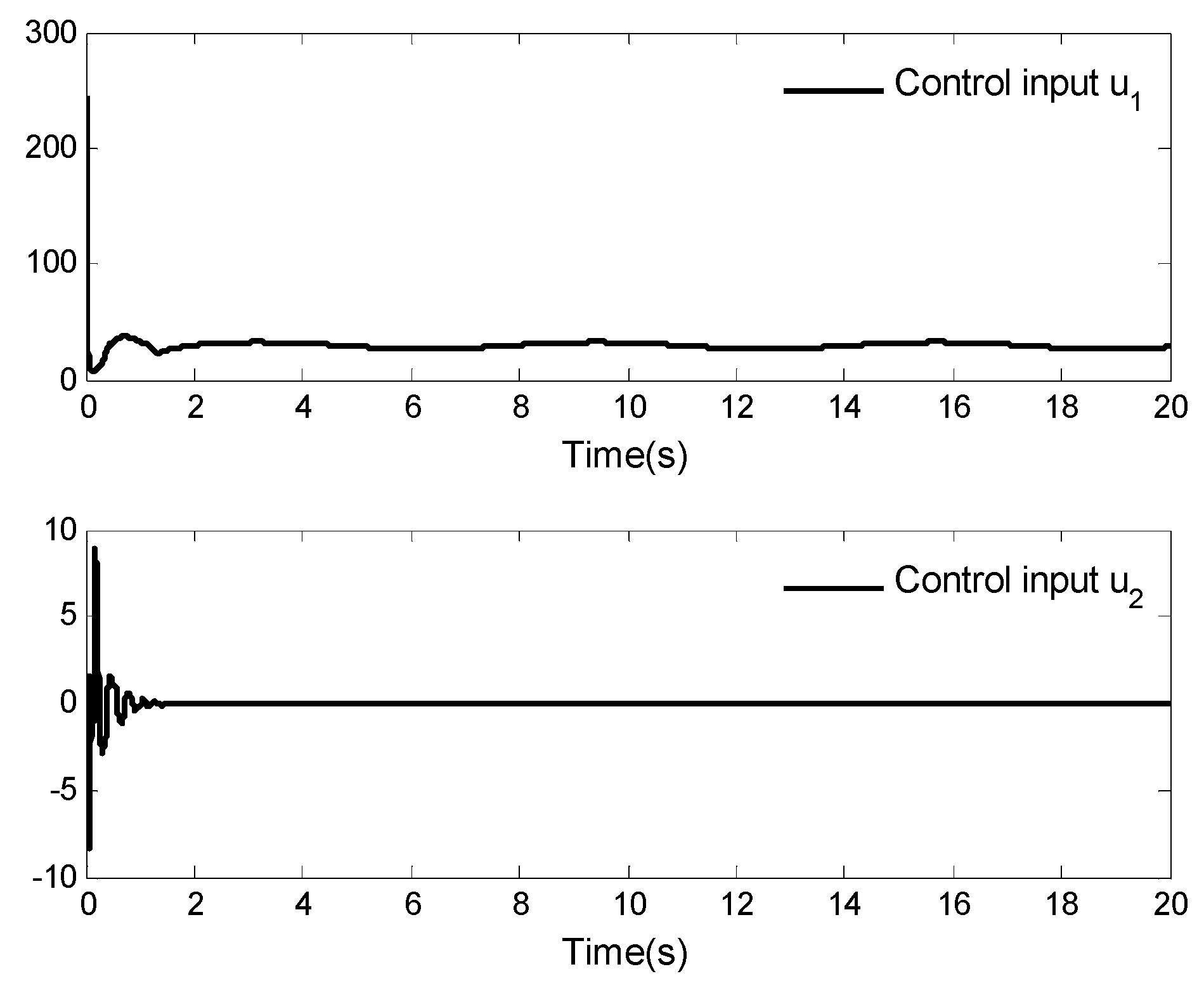
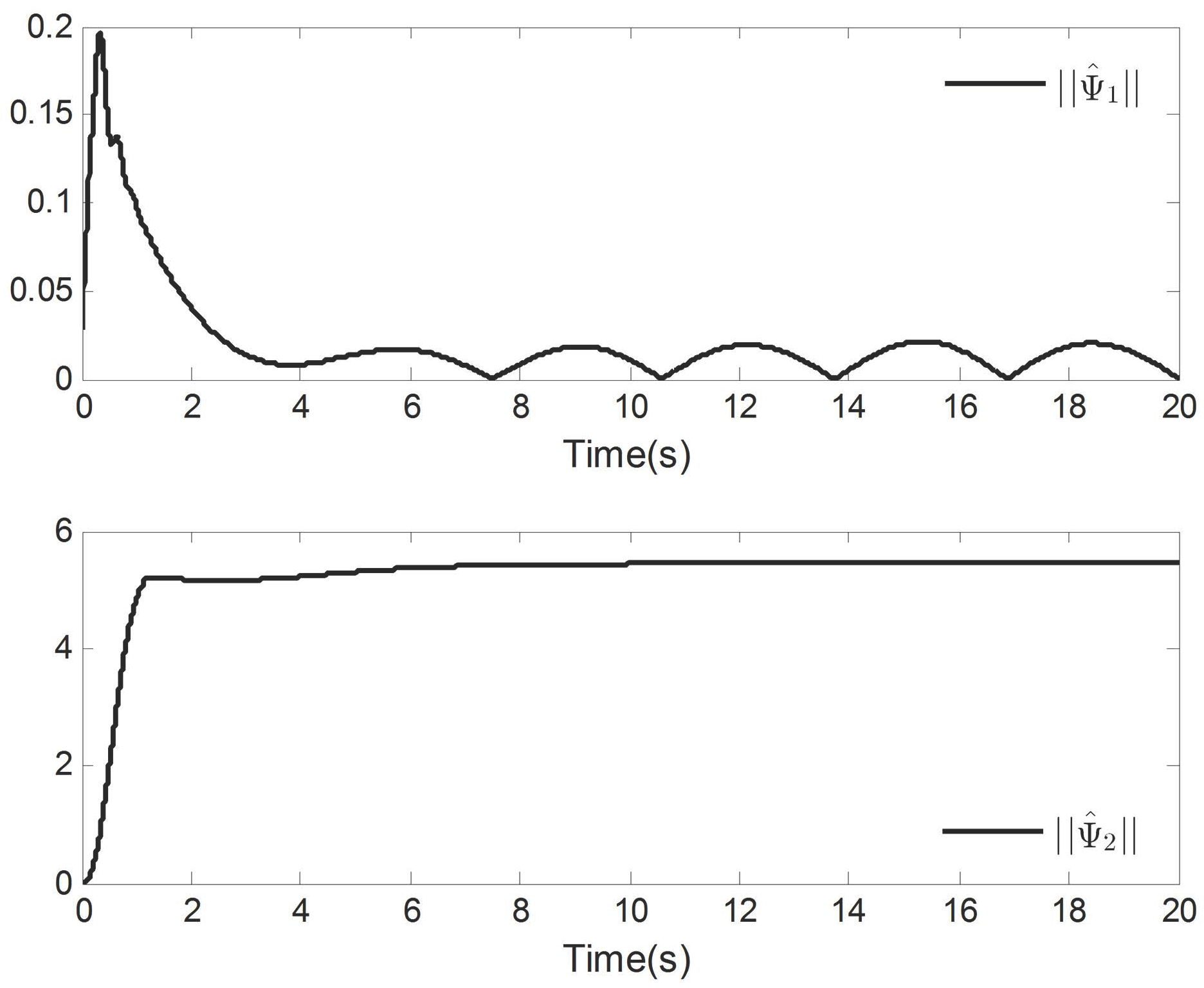
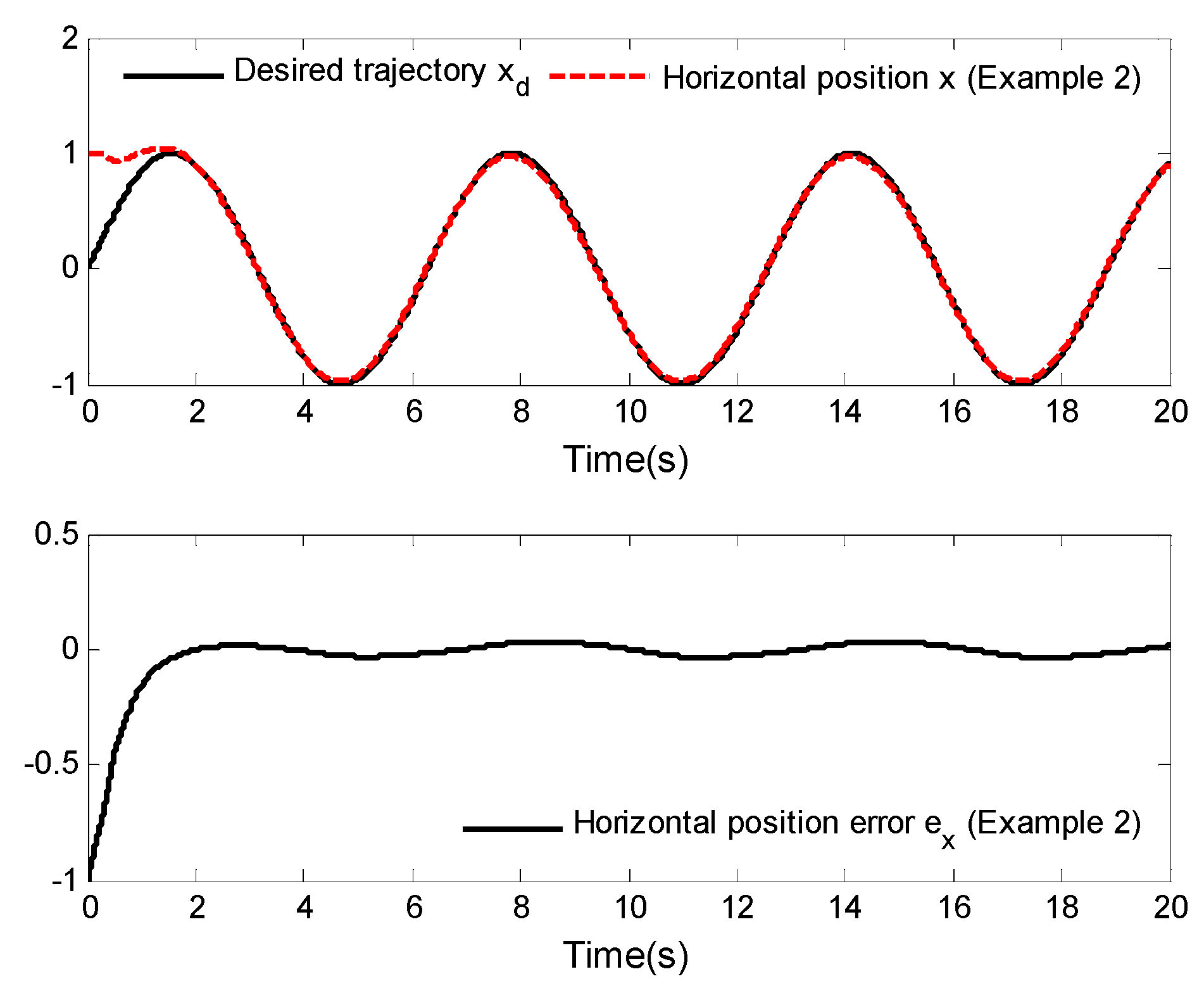
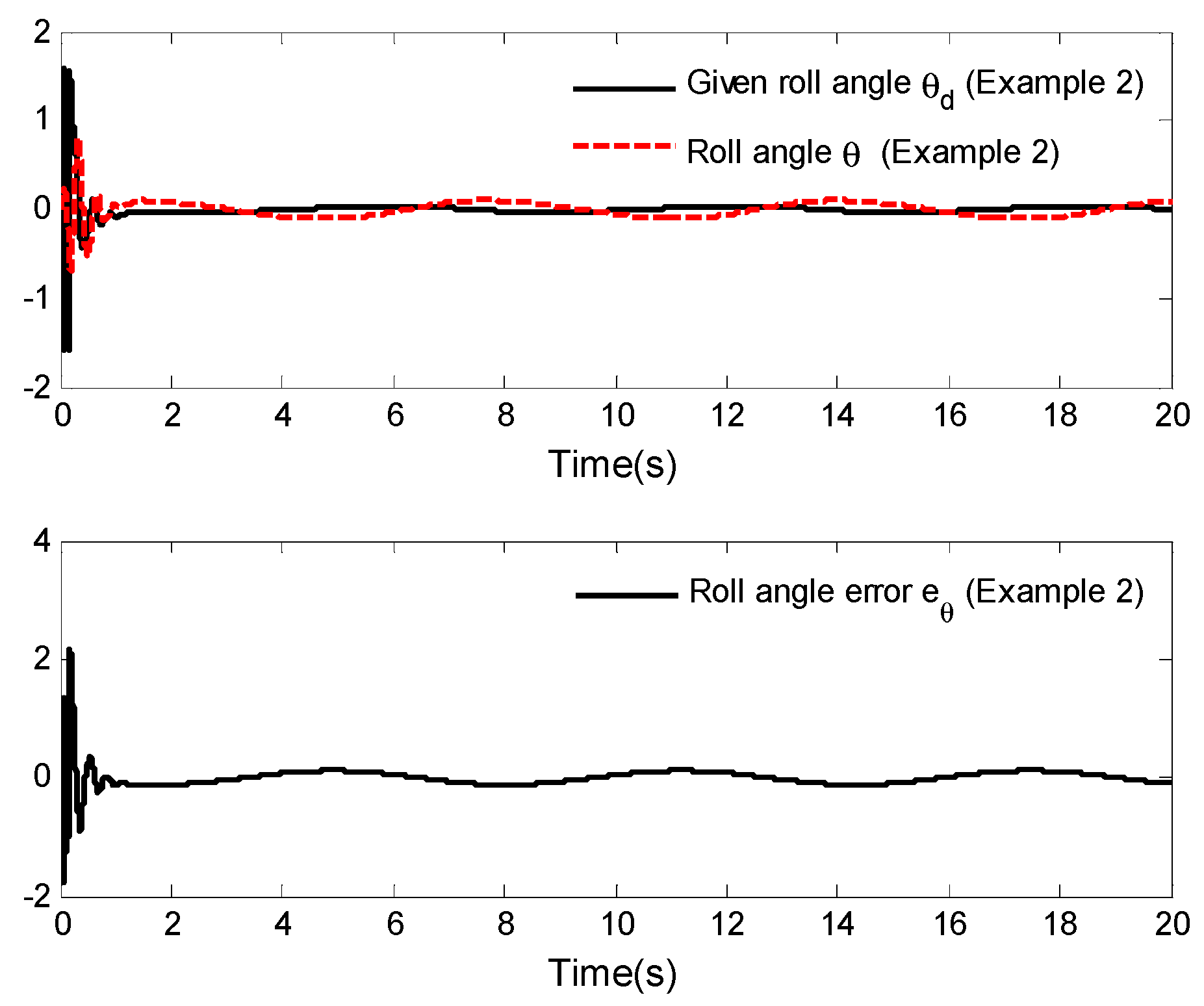
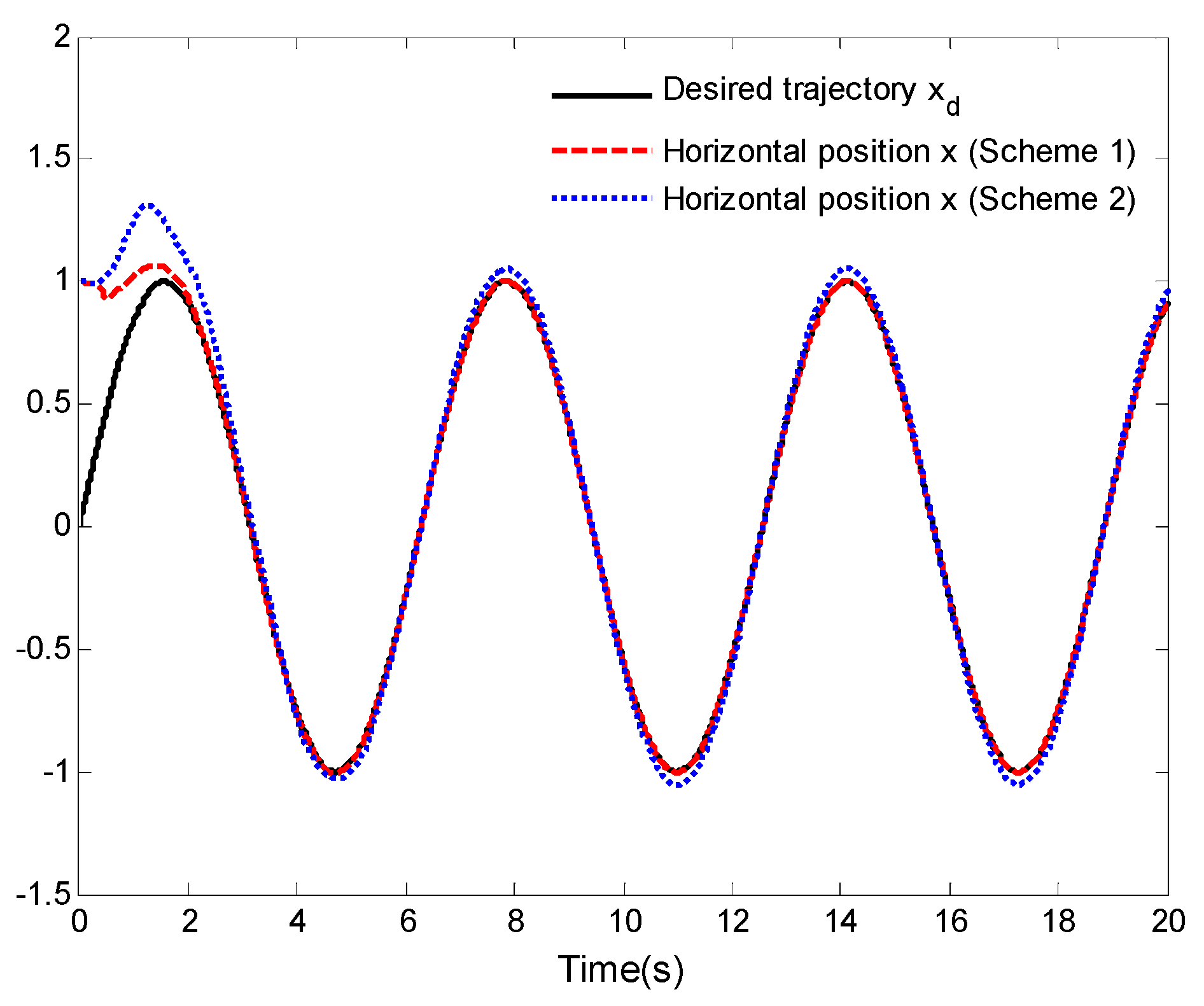
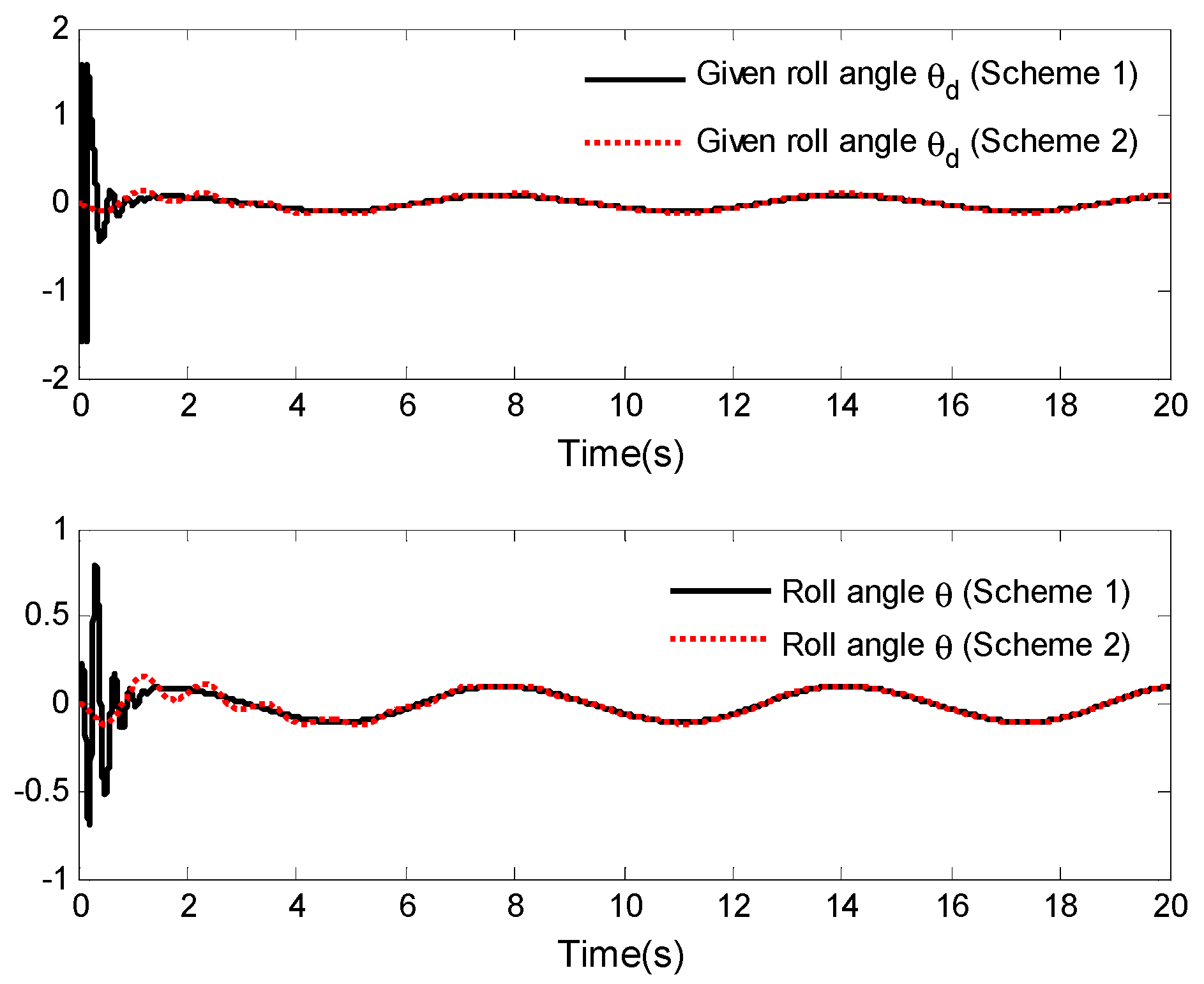
4. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chadli, M.; Aouaouda, S.; Karimi, H.; Shi, P. Robust fault tolerant tracking controller design for a VTOL aircraft. J. Frankl. Inst. 2012, 350, 2627–2645. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H. Immersion and invariance based command-filtered adaptive backstepping control of VTOL vehicles. Automatica 2013, 49, 2160–2167. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, J. Control of VTOL aircraft with position state constraints using the Barrier Lyapunov Function. Asian J. Control. 2020, 22, 1221–1229. [Google Scholar] [CrossRef]
- Ailon, A. Simple Tracking Controllers for Autonomous VTOL Aircraft with Bounded Inputs. IEEE Trans. Autom. Control 2010, 55, 737–743. [Google Scholar] [CrossRef]
- Chwa, D. Fuzzy Adaptive Output Feedback Tracking Control of VTOL Aircraft with Uncertain Input Coupling and Input-Dependent Disturbances. IEEE Trans. Fuzzy Syst. 2015, 23, 1505–1518. [Google Scholar] [CrossRef]
- Aguilar-Ibanez, C.; Suarez-Castanon, M.S.; Sossa-Azuela, J.H. A backstepping-based procedure with saturation functions to control the PVTOL system. Nonlinear Dyn. 2016, 83, 1247–1257. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, X. Improved adaptive NN backstepping control design for a perturbed PVTOL aircraft. Neurocomputing 2020, 410, 51–60. [Google Scholar] [CrossRef]
- Wood, R.; Cazzolato, B. An Alternative Nonlinear Control Law for the Global Stabilization of the PVTOL Vehicle. IEEE Trans. Autom. Control 2007, 52, 1282–1287. [Google Scholar] [CrossRef]
- Chen, P.; Wu, S.; Hsu, C.; Chang, K. Gain-scheduled control of PVTOL aircraft dynamics with parameter dependent disturbance. J. Frankl. Inst. 2008, 345, 906–925. [Google Scholar]
- Guo, B.-Z.; Wu, Z.-H.; Zhou, H.-C. Active Disturbance Rejection Control Approach to Output-Feedback Stabilization of a Class of Uncertain Nonlinear Systems Subject to Stochastic Disturbance. IEEE Trans. Autom. Control. 2016, 61, 1613–1618. [Google Scholar] [CrossRef]
- Han, H.; Zhang, J.; Yang, H.; Hou, Y.; Qiao, J. Data-driven robust optimal control for nonlinear system with uncertain disturbances. Inf. Sci. 2023, 621, 248–264. [Google Scholar] [CrossRef]
- Song, R.; Lewis, F.L. Robust optimal control for a class of nonlinear systems with unknown disturbances based on disturbance observer and policy iteration. Neurocomputing 2020, 390, 185–195. [Google Scholar] [CrossRef]
- Gil, J.; You, S.; Lee, Y.; Kim, W. Nonlinear sliding mode controller using disturbance observer for permanent magnet synchronous motors under disturbance. Expert Syst. Appl. 2023, 214. [Google Scholar] [CrossRef]
- Zhao, J.; Tong, S.; Li, Y. Fuzzy adaptive output feedback control for uncertain nonlinear systems with unknown control gain functions and unmodeled dynamics. Inf. Sci. 2021, 558, 140–156. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, Z.-Y.; Chen, C.-C.; Meng, Q. Global stabilization via output feedback for a class of uncertainty nonlinear systems with time-varying delay and zero dynamics. ISA Trans. 2023, 132, 235–245. [Google Scholar] [CrossRef]
- Cui, R.; Yang, C.; Li, Y.; Sharma, S. Adaptive neural network control of AUVs with control input non-linearities using reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1019–1029. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, C.; Gao, W.; Zhou, L. Reinforcement Learning and Optimal Setpoint Tracking Control of Linear Systems with External Disturbances. IEEE Trans. Ind. Inform. 2022, 18, 7770–7779. [Google Scholar] [CrossRef]
- Yin, Q.; Zhang, H.; Mu, Q.; Yang, J.; Ma, Q. Multilayer-neural-network observer with compensator and command-filter-based adaptive backstepping tracking control of switched nonlinear systems. J. Frankl. Inst. 2023, 360, 2976–3000. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.; Yu, J. Event-triggered adaptive neural network tracking control for uncertain systems with unknown input saturation based on command filters. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Guettal, L.; Chelihi, A.; Ajgou, R.; Touba, M.M. Robust tracking control for quadrotor with un-known nonlinear dynamics using adaptive neural network based fractional-order backstepping control. J. Frankl. Inst. 2022, 359, 7337–7364. [Google Scholar] [CrossRef]
- Vijay, M.; Jena, D. Backstepping terminal sliding mode control of robot manipulator using radial basis functional neural networks. Comput. Electr. Eng. 2018, 67, 690–707. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Zhao, Q.; Li, J.; Wu, Z.-G. Adaptive Neural Dynamic Surface Control with Prespecified Tracking Accuracy of Uncertain Stochastic Nonstrict-Feedback Systems. IEEE Trans. Cybern. 2022, 52, 3408–3421. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, Q.; Yue, D.; Han, Q.-L. Predictor-Based Neural Dynamic Surface Control for Bipartite Tracking of a Class of Nonlinear Multiagent Systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1791–1802. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S. Neural-Network-Based Adaptive resilient dynamic surface control against unknown deception attacks of un-certain nonlinear time-delay cyberphysical systems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4341–4353. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, Q.; Yu, J. Convex optimization-based adaptive fuzzy control for uncertain nonlinear systems with input saturation using command filtered backstepping. IEEE Trans. Fuzzy Syst. 2022, 31, 2086–2091. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Q.; Hu, C. Adaptive fuzzy command filtered backstepping control for uncertain pure-feedback systems. ISA Trans. 2022, 129, 204–213. [Google Scholar] [CrossRef]
- Hauser, J.; Sastry, S.; Meyer, G. Nonlinear control design for slightly non-minimum phase systems: Application to V/STOL aircraft. Automatica 1992, 28, 665–679. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, C.; Ge, Y. Adaptive neural network dynamic surface control of uncertain strict-feedback non-linear systems with unknown control direction and unknown actuator fault. J. Frankl. Inst. 2022, 359, 4054–4073. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive Neural Control for Output Feedback Nonlinear Systems Using a Barrier Lyapunov Function. IEEE Trans. Neural. Netw. 2010, 21, 1339–1345. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Deng, X.; Tao, L.; Xu, B. Neuroadaptive Dynamic Surface Asymptotic Tracking Control of a VTOL Aircraft with Unknown Dynamics and External Disturbances. Mathematics 2023, 11, 2725. https://doi.org/10.3390/math11122725
Yang X, Deng X, Tao L, Xu B. Neuroadaptive Dynamic Surface Asymptotic Tracking Control of a VTOL Aircraft with Unknown Dynamics and External Disturbances. Mathematics. 2023; 11(12):2725. https://doi.org/10.3390/math11122725
Chicago/Turabian StyleYang, Xianhao, Xiongfeng Deng, Liang Tao, and Binzi Xu. 2023. "Neuroadaptive Dynamic Surface Asymptotic Tracking Control of a VTOL Aircraft with Unknown Dynamics and External Disturbances" Mathematics 11, no. 12: 2725. https://doi.org/10.3390/math11122725
APA StyleYang, X., Deng, X., Tao, L., & Xu, B. (2023). Neuroadaptive Dynamic Surface Asymptotic Tracking Control of a VTOL Aircraft with Unknown Dynamics and External Disturbances. Mathematics, 11(12), 2725. https://doi.org/10.3390/math11122725



