On Recovering Sturm–Liouville-Type Operators with Global Delay on Graphs from Two Spectra
Abstract
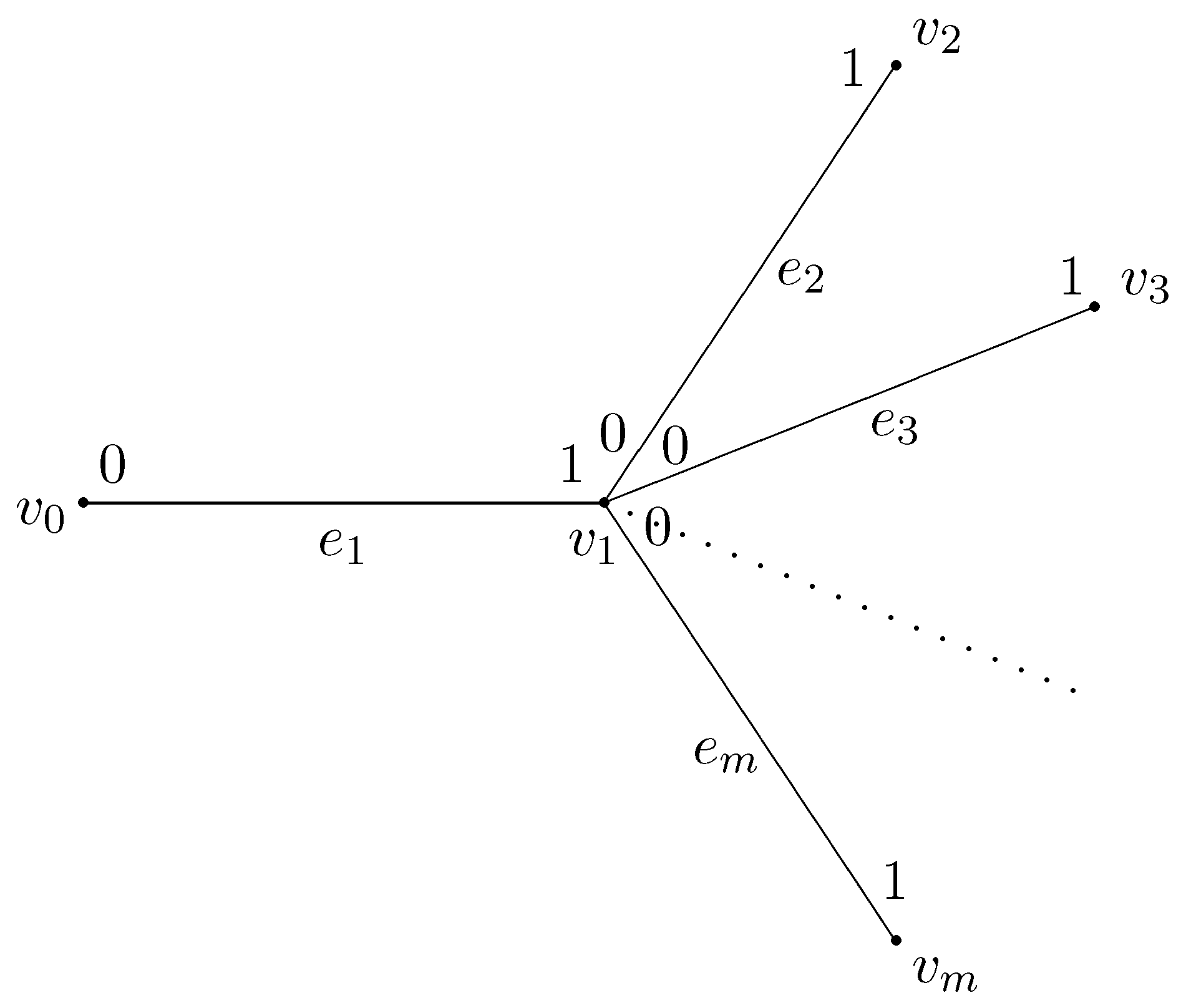
1. Introduction and Main Result
2. Characteristic Determinants
3. Solution of the Inverse Problem
| Algorithm 1 Let the spectra and be given. Then: |
| (i) Calculate the characteristic functions and by the formulae in (17); (ii) Construct the sequences and for and by the formulae in (21) and using (7)–(9); (iii) Find the sequences for and via relations (20); (iv) Calculate the numbers using (31); (v) In accordance with (30) and Lemma 4, construct the functions by the formula (vi) Finally, find the functions by (32) and calculate by (33). |
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buterin, S. Functional-differential operators on geometrical graphs with global delay and inverse spectral problems. Results Math. 2023, 78, 79. [Google Scholar] [CrossRef]
- Montrol, E. Quantum theory on a network. J. Math. Phys. 1970, 11, 635–648. [Google Scholar]
- Nicaise, S. Some results on spectral theory over networks, applied to nerve impulse transmission. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1985; Volume 1771, pp. 532–541. [Google Scholar]
- von Below, J. Sturm–Liouville eigenvalue problem on networks. Math. Methods Appl. Sci. 1988, 10, 383–395. [Google Scholar] [CrossRef]
- Langese, J.; Leugering, G.; Schmidt, J. Modelling, Analysis and Control of Dynamic Elastic Multi-Link Structures; Birkhäuser: Boston, MA, USA, 1994. [Google Scholar]
- Kuchment, P. Graphs models for waves in thin structures. Waves Rand. Media 2002, 12, R1–R24. [Google Scholar] [CrossRef]
- Berkolaiko, G.; Carlson, R.; Fulling, S.; Kuchment, P. Quantum Graphs and Their Applications; Cont. Math. 415; AMS: Providence, RI, USA, 2006. [Google Scholar]
- Berkolaiko, G.; Kuchment, P. Introduction to Quantum Graphs; AMS: Providence, RI, USA, 2013. [Google Scholar]
- Pokornyi, Y.V.; Penkin, O.M.; Pryadiev, V.L.; Borovskikh, A.V.; Lazarev, K.P.; Shabrov, S.A. Differential Equations on Geometrical Graphs; Fizmatlit: Moscow, Russia, 2005. [Google Scholar]
- Kuznetsova, M.A. Asymptotic formulae for weight numbers of the Sturm–Liouville boundary problem of a star-shaped graph. Izv. Saratov Univ. (N.S.) Ser. Math. Mech. Inform. 2018, 18, 40–48. [Google Scholar] [CrossRef]
- Borisov, B. Resolvents of elliptic operators on quantum graphs with small edges: Holomorphy and Taylor series. Adv. Math. 2022, 397, 108125. [Google Scholar] [CrossRef]
- Gerasimenko, N.I. Inverse scattering problem on a noncompact graph. Teoret. Mat. Fiz. 1988, 74, 187–200, English Transl. in Theor. Math. Phys. 1988, 75, 460–470. [Google Scholar] [CrossRef]
- Belishev, M.I. Boundary spectral inverse problem on a class of graphs (trees, by the BC method. Inverse Probl. 2004, 20, 647–672. [Google Scholar] [CrossRef]
- Brown, B.M.; Weikard, R. A Borg–Levinson theorem for trees. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2005, 461, 3231–3243. [Google Scholar] [CrossRef]
- Yurko, V.A. Inverse spectral problems for Sturm–Liouville operators on graphs. Inverse Probl. 2005, 21, 1075–1086. [Google Scholar] [CrossRef]
- Pivovarchik, V. Inverse problem for the Sturm–Liouville equation on a star-shaped graph. Math. Nachr. 2007, 280, 1595–1619. [Google Scholar] [CrossRef]
- Ignatyev, M. Inverse scattering problem for Sturm–Liouville operator on non-compact A-graph. Uniqueness result. Tamkang J. Math. 2015, 46, 401–422. [Google Scholar] [CrossRef]
- Yurko, V.A. Inverse spectral problems for differential operators on spatial networks. Uspekhi Mat. Nauk 2016, 71, 149–196, English Transl. in Russ. Math. Surv. 2016, 71, 539–584. [Google Scholar] [CrossRef]
- Bondarenko, N.P. Spectral data characterization for the Sturm–Liouville operator on the star-shaped graph. Anal. Math. Phys. 2020, 10, 83. [Google Scholar] [CrossRef]
- Avdonin, S.A.; Kravchenko, V.V. Method for solving inverse spectral problems on quantum star graphs. J. Inv. Ill-Posed Probl. 2023, 31, 31–42. [Google Scholar] [CrossRef]
- Borg, G. Eine Umkehrung der Sturm–Liouvilleschen Eigenwertaufgabe. Acta Math. 1946, 78, 1–96. [Google Scholar] [CrossRef]
- Freiling, G.; Yurko, V.A. Inverse Sturm–Liouville Problems and Their Applications; NOVA Science Publishers: New York, NY, USA, 2001. [Google Scholar]
- Buterin, S.A.; Kuznetsova, M.A. On Borg’s method for non-selfadjoint Sturm–Liouville operators. Anal. Math. Phys. 2019, 9, 2133–2150. [Google Scholar] [CrossRef]
- Nizhnik, L.P. Inverse eigenvalue problems for nonlocal Sturm–Liouville operators on a star graph. Methods Funct. Anal. Topol. 2012, 18, 68–78. [Google Scholar]
- Bondarenko, N.P. An inverse problem for an integro-differential operator on a star-shaped graph. Math. Meth. Appl. Sci. 2018, 41, 1697–1702. [Google Scholar] [CrossRef]
- Hu, Y.-T.; Bondarenko, N.P.; Shieh, C.-T.; Yang, C.-F. Traces and inverse nodal problems for Dirac-type integro-differential operators on a graph. Appl. Math. Comput. 2019, 363, 124606. [Google Scholar] [CrossRef]
- Hu, Y.-T.; Huang, Z.-Y.; Yang, C.-F. Traces for Sturm–Liouville operators with frozen argument on star graphs. Results Math. 2020, 75, 37. [Google Scholar] [CrossRef]
- Wang, F.; Yang, C.-F. Traces for Sturm–Liouville operators with constant delays on a star graph. Results Math. 2021, 76, 220. [Google Scholar] [CrossRef]
- Wang, F.; Yang, C.-F. A partial inverse problem for the Sturm–Liouville operator with constant delays on a star graph. Results Math. 2022, 77, 192. [Google Scholar] [CrossRef]
- Bondarenko, N.P. Inverse problem for a differential operator on a star-shaped graph with nonlocal matching condition. Bol. Soc. Mat. Mex. 2023, 29, 2. [Google Scholar] [CrossRef]
- Pikula, M. Determination of a Sturm–Liouville-type differential operator with delay argument from two spectra. Mat. Vestn. 1991, 43, 159–171. [Google Scholar]
- Freiling, G.; Yurko, V.A. Inverse problems for Sturm–Liouville differential operators with a constant delay. Appl. Math. Lett. 2012, 25, 1999–2004. [Google Scholar] [CrossRef]
- Yang, C.-F. Inverse nodal problems for the Sturm–Liouville operator with a constant delay. J. Diff. Eqns. 2014, 257, 1288–1306. [Google Scholar] [CrossRef]
- Ignatiev, M.Y. On an inverse Regge problem for the Sturm–Liouville operator with deviating argument. J. Samara State Tech. Univ. Ser. Phys. Math. Sci. 2018, 22, 203–211. [Google Scholar] [CrossRef]
- Bondarenko, N.; Yurko, V. An inverse problem for Sturm–Liouville differential operators with deviating argument. Appl. Math. Lett. 2018, 83, 140–144. [Google Scholar] [CrossRef]
- Buterin, S.A.; Yurko, V.A. An inverse spectral problem for Sturm–Liouville operators with a large delay. Anal. Math. Phys. 2019, 9, 17–27. [Google Scholar] [CrossRef]
- Pikula, M.; Vladičic, V.; Vojvodić, B. Inverse spectral problems for Sturm–Liouville operators with a constant delay less than half the length of the interval and Robin boundary conditions. Results Math. 2019, 74, 45. [Google Scholar] [CrossRef]
- Djurić, N.; Vladičić, V. Incomplete inverse problem for Sturm–Liouville type differential equation with constant delay. Results Math. 2019, 74, 161. [Google Scholar] [CrossRef]
- Sat, M.; Shieh, C.-T. Inverse nodal problems for integro-differential operators with a constant delay. J. Inverse Ill-Posed Probl. 2019, 27, 501–509. [Google Scholar] [CrossRef]
- Wang, Y.P.; Shieh, C.T.; Miao, H.Y. Reconstruction for Sturm–Liouville equations with a constant delay with twin-dense nodal subsets. Inv. Probl. Sci. Eng. 2019, 27, 608–617. [Google Scholar] [CrossRef]
- Djurić, N. Inverse problems for Sturm–Liouville-type operators with delay: Symmetric case. Appl. Math. Sci. 2020, 14, 505–510. [Google Scholar] [CrossRef]
- Djurić, N.; Buterin, S. On an open question in recovering Sturm–Liouville-type operators with delay. Appl. Math. Lett. 2021, 113, 106862. [Google Scholar] [CrossRef]
- Djurić, N.; Buterin, S. On non-uniqueness of recovering Sturm–Liouville operators with delay. Commun. Nonlinear Sci. Numer. Simulat. 2021, 102, 105900. [Google Scholar] [CrossRef]
- Djurić, N.; Buterin, S. Iso-bispectral potentials for Sturm–Liouville-type operators with small delay. Nonlin. Anal. Real World Appl. 2020, 63, 103390. [Google Scholar] [CrossRef]
- Buterin, S.A.; Malyugina, M.A.; Shieh, C.-T. An inverse spectral problem for second-order functional-differential pencils with two delays. Appl. Math. Comput. 2021, 411, 126475. [Google Scholar] [CrossRef]
- Buterin, S.; Djurić, N. Inverse problems for Dirac operators with constant delay: Uniqueness, characterization, uniform stability. Lobachevskii J. Math. 2022, 43, 1492–1501. [Google Scholar] [CrossRef]
- Wang, Y.P.; Keskin, B.; Shieh, C.-T. A partial inverse problem for non-self-adjoint Sturm–Liouville operators with a constant delay. J. Inverse Ill-Posed Probl. 2023. [Google Scholar] [CrossRef]
- Buterin, S.; Vasilev, S. An inverse Sturm–Liouville-type problem with constant delay and non-zero initial function. arXiv 2023, arXiv:2304.05487. [Google Scholar]
- Djurić, N.; Vojvodić, B. Inverse problem for Dirac operators with a constant delay less than half the length of the interval. Appl. Anal. Discrete Math. 2023. [Google Scholar] [CrossRef]
- Buterin, S.A. On the uniform stability of recovering sine-type functions with asymptotically separated zeros. Matem. Zametki 2022, 111, 339–353, English Transl. in Math. Notes 2022, 111, 343–355. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buterin, S. On Recovering Sturm–Liouville-Type Operators with Global Delay on Graphs from Two Spectra. Mathematics 2023, 11, 2688. https://doi.org/10.3390/math11122688
Buterin S. On Recovering Sturm–Liouville-Type Operators with Global Delay on Graphs from Two Spectra. Mathematics. 2023; 11(12):2688. https://doi.org/10.3390/math11122688
Chicago/Turabian StyleButerin, Sergey. 2023. "On Recovering Sturm–Liouville-Type Operators with Global Delay on Graphs from Two Spectra" Mathematics 11, no. 12: 2688. https://doi.org/10.3390/math11122688
APA StyleButerin, S. (2023). On Recovering Sturm–Liouville-Type Operators with Global Delay on Graphs from Two Spectra. Mathematics, 11(12), 2688. https://doi.org/10.3390/math11122688




