Bifurcation Analysis, Synchronization and FPGA Implementation of a New 3-D Jerk System with a Stable Equilibrium

Abstract

This research paper addresses the modelling of a new 3-D chaotic jerk system with a stable equilibrium. Such chaotic systems are known to exhibit hidden attractors. After the modelling of the new jerk system, a detailed bifurcation analysis has been performed for the new chaotic jerk system with a stable equilibrium. It is shown that the new jerk system has multistability with coexisting attractors. Next, we apply backstepping control for the synchronization design of a pair of new jerk systems with a stable equilibrium taken as the master-slave chaotic systems. Lyapunov stability theory is used to establish the synchronization results for the new jerk system with a stable equilibrium. Finally, we show that the FPGA design of the new jerk system with a stable equilibrium can be implemented using the FPGA Zybo Z7-20 development board. The design of the new jerk system consists of multipliers, adders and subtractors. It is observed that the experimental attractors are in good agreement with simulation results.

1. Introduction

Nonlinear dynamical systems with chaotic attractors have numerous applications in engineering such as cryptosystem [1,2], secure communication [3,4], encryption [5,6], memristors [7,8,9,10], circuits [11,12], chemical systems [13,14], etc.

Autonomous jerk differential equations have the general structure given as follows:

$$\frac{d^{3}x}{d{t}^3}=F\left(x,\frac{dx}{dt},\frac{d^{2}x}{d{t}^2}\right)$$

(1)

In mechanical engineering, the term jerk stands for the third order derivative. Hence, (1) is called a jerk differential equation. It is easy to express the ODE (1) as a system of differential equations by introducing the phase variables as follows:

$$\left\{\begin{array}{ccc}\dot{x}& =& y\hfill \\ \dot{y}& =& z\hfill \\ \dot{z}& =& F(x,y,z)\hfill \end{array}\right.$$

(2)

Jerk systems have several applications in science [15,16,17,18,19]. Li and Zheng [15] proposed a 3-D jerk system with a sinusoidal term and noted that the system has an infinite number of equilibrium points. Dongmo et al. [16] discussed the field programmable gate array (FPGA) implementation of an autonomous jerk oscillator arising in a Josephson junction. Qin and Lai [17] proposed a new memristive chaotic system by modification of a jerk system with a typical memristor. Ramadoss et al. [18] proposed a new chaotic jerk system with a septic nonlinearity and discussed its PSpice simulation.

Many of the jerk systems reported in the chaos literature involve jerk systems without any equilibrium point [20] or with unstable equilibrium points [17,18,21,22,23,24], etc. In 2021, Vijayakumar et al. [25] proposed a new chaotic jerk system with a stable equilibrium. The motivation of this research work is to report a new chaotic jerk system with a stable equilibrium. By modifying the dynamics of the Vijayakumar jerk system [25], we obtain a new chaotic jerk system with a stable equilibrium.

Lyapunov exponents provide a direct measure of sensitive dependence on initial conditions of a trajectory of a chaotic system by quantifying the exponential rates at which neighboring orbits on an attractor diverge (or converge) as the system evolves in time.

To define the Lyapunov exponents of a dynamical system, we consider an n-dimensional dynamical system described by

$$\dot{x}=f\left(x\right),(x\in R^n)$$

(3)

Suppose that $f_i$ denotes the ith component of the vector field f for $i=1,2,\dots ,n$.

The Lyapunov exponents of the system (3) describe the behavior of vectors in the tangent space of the phase space and are defined from the Jacobian matrix $J=\left[J_{ij}\right]$, where

$$J_{ij}\left(t\right)={\left.\frac{\partial f_i\left(x\right)}{\partial x_j}\right|}_{x\left(t\right)}$$

(4)

Next, we consider the matrix differential equation

$$\dot{Y}=JY$$

(5)

with the initial condition $Y_{ij}\left(0\right)={\delta }_{ij}$.

The matrix Y describes how a small change at the initial state $x\left(0\right)$ propagates to the final state $x\left(t\right)$ for the dynamical system (3). Next, we consider the matrix $\mathrm{\Lambda }$ defined by

$$\mathrm{\Lambda }=\underset{t\to \infty }{lim}\frac{1}{2t}log\left[Y\left(t\right)Y^T\left(t\right)\right]$$

(6)

The Lyapunov exponents of the dynamical system (3) are defined as the eigenvalues of the matrix $\mathrm{\Lambda }$ [26]. The maximal Lyapunov exponent (MLE) of the dynamical system (3) is the largest eigenvalue of the matrix $\mathrm{\Lambda }$. If the MLE of the system (3) is positive and the phase space is compact, then the system (3) is chaotic [26]. If the sum of Lyapunov exponents of the system (3) is negative, then the system is called dissipative and the phase space of the system is compact [26]. Thus, a dissipative system (3) is chaotic when the MLE of the system is positive [26]. We also note that the MLE of the system (3) signifies the exponential rate of growth of small perturbations along each of the principal axes in the phase space [27].

In this work, we show that the MLE of the new chaotic jerk system exhibits a higher value than the MLE of the Vijayakumar jerk system [25] for the same initial conditions.

Kaplan-Yorke dimension of a chaotic system gives the fractal dimension of a chaotic system in terms of the Lyapunov exponents of the system [28]. For a 3-D dissipative chaotic system with the Lyapunov exponents ${\tau }_1>0$, ${\tau }_2=0$ and ${\tau }_3<0$, the Kaplan-Yorke dimension of the system is defined as

$$D_K=2+\frac{{\tau }_1+{\tau }_2}{|{\tau }_3|}$$

(7)

In this work, we show that the Kaplan-Yorke dimension of the new chaotic jerk system is greater than that of the Vijayakumar jerk system [25].

Modelling of the new chaotic jerk system with a stable equilibrium is detailed in Section 2. Bifurcation analysis of dynamical systems aids in elucidating the qualitative properties of the systems [29,30]. We describe the bifurcation analysis of the new chaotic jerk system in Section 3. Multistability and coexisting attractors of the new chaotic jerk system are some special properties which are detailed in Section 4.

Synchronization of chaotic and hyperchaotic systems have several applications in the literature [31,32,33,34]. Using backstepping control, we achieve complete synchronization of a pair of new chaotic jerk systems considered as master and slave systems for communication. The synchronization results for the new chaotic jerk system with a stable equilibrium are detailed in Section 5.

Hardware implementations allow us to observe the behavior of chaotic systems in a physical environment, as well as to evaluate the system in aspects such as the use of hardware resources required for its implementation, and the maximum frequency of the system, among others. In this manner, one can infer that the design of chaotic systems is quite good when they are implemented on hardware that is ready for an engineering application. This is the case when using an FPGA which helps to perform a fast prototyping of a dynamical system to observe experimental attractors. Recently, one can find several FPGA implementations of chaotic systems, as shown in [16,35,36,37,38,39]. In Section 6, we show the FPGA implementation of the new jerk system with a stable equilibrium using the FPGA Zybo Z7-20 development board.

2. Modelling of the New Jerk System with a Stable Equilibrium

In 2021, Vijayakumar et al. [25] proposed a new chaotic jerk system with the dynamics

$$\left\{\begin{array}{ccc}\dot{x}& =& y\hfill \\ \dot{y}& =& z\hfill \\ \dot{z}& =& -x-y-z-\alpha z^2+xy-\beta \hfill \end{array}\right.$$

(8)

The equilibrium points or rest points of an autonomous system $\dot{X}=f\left(X\right)$ are defined as the roots of the equation $f\left(X\right)=0$. The equilibrium points refer to the constant solutions of the system $\dot{X}=f\left(X\right)$.

For the Vijayakumar jerk system (8), the equilibrium points are got by solving the following system of equations:

$$\begin{array}{ccc}\hfill y& =\hfill & \hfill 0\end{array}$$

(9a)

$$\begin{array}{ccc}\hfill z& =\hfill & \hfill 0\end{array}$$

(9b)

$$\begin{array}{c}\hfill -x-y-z-\alpha z^2+xy-\beta =0\end{array}$$

(9c)

From the Equations (9a) and (9b), we get $y=0$ and $z=0$, respectively.

Thus, we can simplify the Equation (9c) as

$$-x-\beta =0,$$

(10)

which has the unique solution $x=-\beta$.

This simple calculation establishes that $E_0(-\beta ,0,0)$ is the unique equilibrium point of the Vijayakumar jerk system (8).

As shown in [25], the Vijayakumar jerk system (8) has a chaotic attractor and a locally asymptotically stable equilibrium point for the parameter values taken in the following two cases:

Case (A): $\alpha =2.3$, $\beta =0.02$

We take the initial state as $x\left(0\right)=0, y\left(0\right)=-1, z\left(0\right)=0$.

For this case, the Lyapunov exponents of the Vijayakumar jerk system (8) can be numerically calculated in MATLAB using Wolf’s algorithm [40] as follows:

$${\tau }_1=0.0391,{\tau }_2=0,{\tau }_3=-1.0395$$

(11)

Since the sum of the Lyapunov exponents of the Vijayakumar jerk system (8) is negative, we conclude that the system (8) is dissipative. A dissipative system is chaotic if its MLE is positive [26]. Thus, the Vijayakumar jerk system (8) has a chaotic attractor.

Also, the Kaplan-Yorke dimension of the Vijayakumar jerk system (8) is found in Case A as follows:

$$D_K=2+\frac{{\tau }_1+{\tau }_2}{|{\tau }_3|}=2.0376$$

(12)

Linearization of the Vijayakumar jerk system (8) at $E_0(-0.02,0,0)$ has the eigenvalues given as follows:

$${\mu }_1=-0.99,{\mu }_{2,3}=-0.005\pm 1.005i$$

(13)

This shows that $E_0(-0.02,0,0)$ is a locally asymptotically stable equilibrium of the Vijayakumar jerk system (8).

Case (B): $\alpha =2.3$, $\beta =0.005$

We take the initial state as $x\left(0\right)=0, y\left(0\right)=-1, z\left(0\right)=0$.

For this case, the Lyapunov exponents of the Vijayakumar jerk system (8) can be numerically calculated in MATLAB using Wolf’s algorithm [40] as follows:

$${\tau }_1=0.0878,{\tau }_2=0,{\tau }_3=-1.0883$$

(14)

Since the sum of the Lyapunov exponents of the Vijayakumar jerk system (8) is negative, we conclude that the system (8) is dissipative. A dissipative system is chaotic if its MLE is positive [26]. Thus, the Vijayakumar jerk system (8) has a chaotic attractor.

Also, the Kaplan-Yorke dimension of the Vijayakumar jerk system (8) is found in Case B as follows:

$$D_K=2+\frac{{\tau }_1+{\tau }_2}{|{\tau }_3|}=2.0807$$

(15)

Linearization of the Vijayakumar jerk system (8) at $E_0(-0.005,0,0)$ has the eigenvalues given as follows:

$${\mu }_1=-0.9975,{\mu }_{2,3}=-0.0012\pm 1.0013i$$

(16)

This shows that $E_0(-0.005,0,0)$ is a locally asymptotically stable equilibrium of the Vijayakumar jerk system (8).

In this research work, we propose a new jerk system by introducing a cubic nonlinearity into Vijayakumar jerk system (8). Our new jerk system is described as follows:

$$\left\{\begin{array}{ccc}\dot{x}& =& y\hfill \\ \dot{y}& =& z\hfill \\ \dot{z}& =& -x-y-z-\alpha z^2+xy-\beta +\gamma z^3\hfill \end{array}\right.$$

(17)

We use the notation $X=(x,y,z)$ to depict the state of the new jerk system (17).

For the new jerk system (17), the equilibrium points are obtained by solving the following system of equations:

$$\begin{array}{ccc}\hfill y& =\hfill & \hfill 0\end{array}$$

(18a)

$$\begin{array}{ccc}\hfill z& =\hfill & \hfill 0\end{array}$$

(18b)

$$\begin{array}{c}\hfill -x-y-z-\alpha z^2+xy-\beta +\gamma z^3=0\end{array}$$

(18c)

From the Equations (18a) and (18b), we get $y=0$ and $z=0$, respectively.

Thus, we can simplify the Equation (18c) as

$$-x-\beta =0,$$

(19)

which has the unique solution $x=-\beta$.

This simple calculation establishes that $E_0(-\beta ,0,0)$ is the unique equilibrium point of the new jerk system (17).

We will establish that the new jerk system (17) has a chaotic attractor and a locally asymptotically stable equilibrium point for the parameter values taken in the following two cases:

Case (A): $\alpha =2.3$, $\beta =0.02$, $\gamma =0.05$

We take the initial state as $x\left(0\right)=0, y\left(0\right)=-1, z\left(0\right)=0$.

For this case, the Lyapunov exponents of the new jerk system (17) can be numerically evaluated in MATLAB using Wolf’s algorithm [40] as follows:

$${\tau }_1=0.0915,{\tau }_2=0,{\tau }_3=-1.0615$$

(20)

Since the sum of the Lyapunov exponents of the new jerk system (17) is negative, we conclude that the system (17) is dissipative. A dissipative system is chaotic if its MLE is positive [26]. Thus, the new jerk system (17) has a chaotic attractor.

Also, the Kaplan-Yorke dimension of the new jerk system (17) is found in Case A as follows:

$$D_K=2+\frac{{\tau }_1+{\tau }_2}{|{\tau }_3|}=2.0862$$

(21)

Linearization of the new jerk system (17) at $E_0(-0.02,0,0)$ has the eigenvalues given as follows:

$${\mu }_1=-0.99,{\mu }_{2,3}=-0.005\pm 1.005i$$

(22)

This shows that $E_0(-0.02,0,0)$ is a locally asymptotically stable equilibrium of the new jerk system (17).

Case (B): $\alpha =2.3$, $\beta =0.005$, $\gamma =0.01$

We take the initial state as $x\left(0\right)=0, y\left(0\right)=-1, z\left(0\right)=0$.

For this case, the Lyapunov exponents of the new jerk system (17) can be numerically evaluated in MATLAB using Wolf’s algorithm [40] as follows:

$${\tau }_1=0.0901,{\tau }_2=0,{\tau }_3=-1.0835$$

(23)

Since the sum of the Lyapunov exponents of the new jerk system (17) is negative, we conclude that the system (17) is dissipative. A dissipative system is chaotic if its MLE is positive [26]. Thus, the new jerk system (17) has a chaotic attractor.

Linearization of the new jerk system (17) at $E_0(-0.005,0,0)$ has the eigenvalues given as follows:

$${\mu }_1=-0.9975,{\mu }_{2,3}=-0.0012\pm 1.0013i$$

(24)

Also, the Kaplan-Yorke dimension of the new jerk system (17) is found in Case B as follows:

$$D_K=2+\frac{{\tau }_1+{\tau }_2}{|{\tau }_3|}=2.0832$$

(25)

This shows that $E_0(-0.005,0,0)$ is a locally asymptotically stable equilibrium of the new jerk system (17).

In summary, the new jerk system (17) has a chaotic attractor with a unique, locally asymptotically stable equilibrium for the Cases (A) and (B). For the cases (A) and (B), the maximum Lyapunov exponent (MLE) of new chaotic jerk system (17) is greater than that of the Vijayakumar jerk system (8). Moreover, for the cases (A) and (B), the Kaplan-Yorke dimension of the new chaotic jerk system (17) is greater than that of the Vijayakumar jerk system (8). These results are tabulated in Table 1.

Table 1. Comparison of the Vijayakumar Jerk System [25] and the New Jerk system (17).

Jerk System	Case	MLE	Kaplan-Yorke Dimension
Vijayakumar Jerk system (8)	Case A	$0.0391$	$2.0376$
New Jerk system (17)	Case A	$0.0915$	$2.0862$
Vijayakumar Jerk system (8)	Case B	$0.0878$	$2.0807$
New Jerk system (17)	Case B	$0.0901$	$2.0832$

Figure 1, Figure 2 and Figure 3 display the MATLAB simulation plots for Case (A) of the new jerk system (17), where $(\alpha ,\beta ,\gamma )=(2.3,0.02,0.05)$ and the initial state is taken as $X\left(0\right)=(0,-1,0)$.

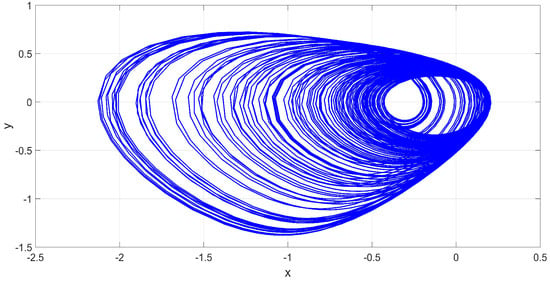
Figure 1. MATLAB phase plot in $(x-y)$ plane of the 3-D chaotic jerk system (17) for Case (A), where $(\alpha ,\beta ,\gamma )=(2.3,0.02,0.05)$ and $X\left(0\right)=(0,-1,0)$.

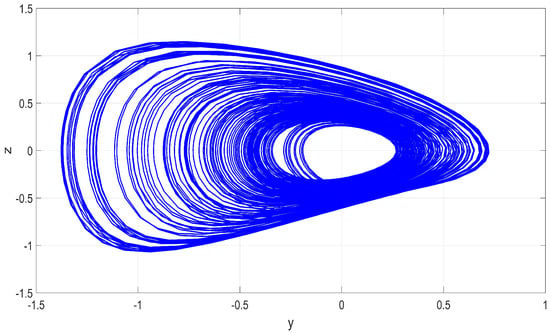
Figure 2. MATLAB phase plot in $(y-z)$ plane of the 3-D chaotic jerk system (17) for Case (A), where $(\alpha ,\beta ,\gamma )=(2.3,0.02,0.05)$ and $X\left(0\right)=(0,-1,0)$.

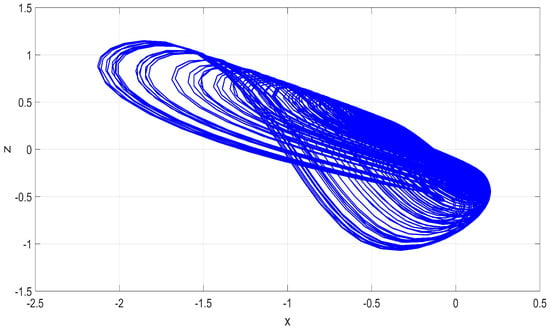
Figure 3. MATLAB phase plot in $(x-z)$ plane of the 3-D chaotic jerk system (17) for Case (A), where $(\alpha ,\beta ,\gamma )=(2.3,0.02,0.05)$ and $X\left(0\right)=(0,-1,0)$.

Figure 4, Figure 5 and Figure 6 display the MATLAB simulation plots for Case (B) of the new jerk system (17), where $(\alpha ,\beta ,\gamma )=(2.3,0.005,0.01)$ and the initial state is taken as $X\left(0\right)=(0,-1,0)$.

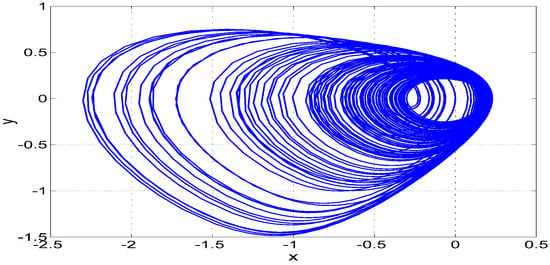
Figure 4. MATLAB phase plot in $(x-y)$ plane of the 3-D chaotic jerk system (17) for Case (B), where $(\alpha ,\beta ,\gamma )=(2.3,0.005,0.01)$ and $X\left(0\right)=(0,-1,0)$.

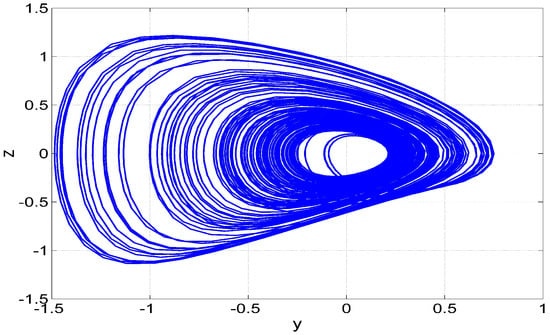
Figure 5. MATLAB phase plot in $(y-z)$ plane of the 3-D chaotic jerk system (17) for Case (B), where $(\alpha ,\beta ,\gamma )=(2.3,0.005,0.01)$ and $X\left(0\right)=(0,-1,0)$.

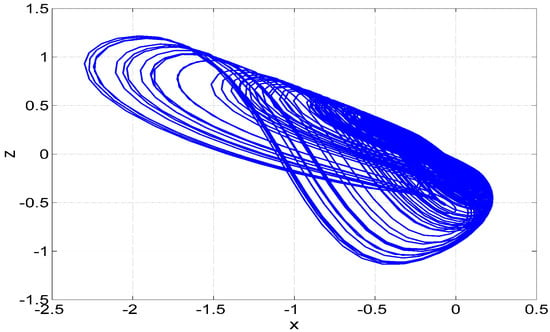
Figure 6. MATLAB phase plot in $(x-z)$ plane of the 3-D chaotic jerk system (17) for Case (B), where $(\alpha ,\beta ,\gamma )=(2.3,0.005,0.01)$ and $X\left(0\right)=(0,-1,0)$.

3. Bifurcation Analysis of the New Jerk System with a Stable Equilibrium

The dynamic behaviors of nonlinear systems vary significantly based on the values of their parameters. The system can transition from one type of behavior to another, called a bifurcation, when certain parameter ranges are reached. This section will explore the dynamic behaviors of the new jerk system (17) through numerical calculations, when the parameters $\alpha$, $\beta$ and $\gamma$ are varied.

3.1. Variation with Respect to the Parameter $\alpha$

By holding the values of $\beta$ and $\gamma$ at $0.02$ and $0.05$, respectively, we can observe the effect of varying $\alpha$ between 2 and $2.3$ on the new jerk system (17). The Lyapunov exponents spectrum and the corresponding bifurcation diagram of the jerk system (17) are presented in Figure 7 indicating that the system can display periodic and chaotic behavior as Tincreases within the range $[2,2.3]$.

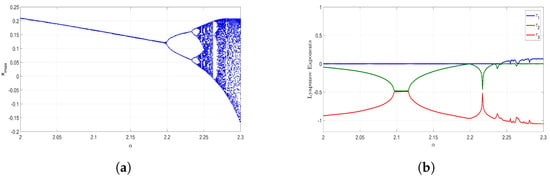
Figure 7. (a) Bifurcation Diagram and (b) Lyapunov Exponents (LE) Spectrum of the new jerk system (17) when $\alpha \in [2,2.3]$, $\beta =0.02$, $\gamma =0.05$.

Define $L=[2,2.2424]\cup [2.2470,2.2476]\cup [2.2630,2.2672]$.

When $\alpha \in L$, the behavior of the jerk system (17) is periodic, which is supported by the presence of one zero Lyapunov exponent and two negative Lyapunov exponents. For example, when $\alpha =2.1$, the corresponding Lyapunov exponents have the following values:

$${\tau }_1=0,{\tau }_2=-0.478,{\tau }_3=-0.493$$

(26)

Define $M=[2.2425,2.2469]\cup [2.2477,2.2629]\cup [2.2673,2.3]$.

When $\alpha \in M$, the jerk system (17) displays chaotic behavior, with one positive Lyapunov exponent. In particular, when $\alpha =2.26$, the corresponding Lyapunov exponents are:

$${\tau }_1=0.064,{\tau }_2=0,{\tau }_3=-1.030$$

(27)

In this case, the Kaplan-Yorke dimension of the jerk system (17) is a non-integer value of $D_K=2.0621$.

Moreover, the bifurcation diagram depicted in Figure 7 reveals that the jerk system (17) experiences the well-known period-doubling route to chaos.

The bifurcation diagram presented in Figure 7 illustrates that the system experiences a series of period-doubling as the parameter $\alpha$ increases, resulting in the well-known period-doubling route to chaos within specific ranges of parameter $\alpha$.

When the value of $\alpha$ is within the interval $[2,2.1978]$, the system (17) exhibits a period-1 attractor. When $\alpha \in [2.1978,2.2336]$, the system (17) has a period-2 attractor. When $\alpha \in [2.2338,2.2404]$, the system (17) displays a period-4 attractor. When $\alpha \in [2.2406,2.2418]$, the system (17) exhibits a period-8 attractor. When $\alpha \in [2.2420,2.2424]$, the system (17) demonstrates a period-16 attractor. Finally, when $\alpha \in [2.2425,2.2469]$, the system (17) displays a chaotic attractor, which signifies the end of the period-doubling cascade.

Table 2 summarizes the various attractors observed through numerical simulations, illustrating the period-doubling route to chaos discussed earlier. Additionally, Figure 8 provides a graphical representation of these attractors.

Table 2. Period-doubling route to chaos with parameter $\alpha$ varying.

$\mathit{\alpha }$ Range	$\mathit{\alpha }$ Value	Dynamics	Attractor
$[2,2.1978]$	2.1	Period-1	Figure 8a
$[2.1980,2.2336]$	2.22	Period-2	Figure 8b
$[2.2338,2.2404]$	2.236	Period-4	Figure 8c
$[2.2406,2.2418]$	2.2412	Period-8	Figure 8d
$[2.2420,2.2424]$	2.2424	Period-16	Figure 8e
$[2.2425,2.2469]$	2.2465	Chaos	Figure 8f

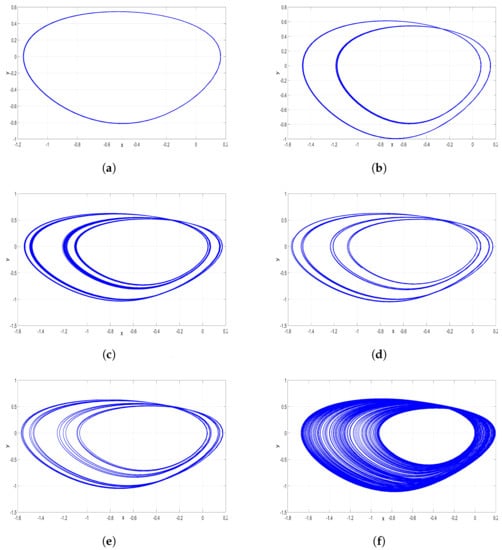
Figure 8. 2-D MATLAB plots of the new jerk system (17) in $(x,y)$ plane for $\beta =0.02$, $\gamma =0.05$ and $X\left(0\right)=(0,-1,0)$. (a) Period-1 for $\alpha =2.1$; (b) Period-2 for $\alpha =2.22$; (c) Period-4 for $\alpha =2.236$; (d) Period-8 for $\alpha =2.2412$; (e) Period-16 for $\alpha =2.2424$; (f) Chaos for $\alpha =2.2465$.

3.2. Variation with Respect to the Parameter $\beta$

To analyze how changes in the values of $\beta$ affect the qualitative behavior of the jerk system (17), we fix the values of $\alpha$ and $\gamma$ as $\alpha =2.3$ and $\gamma =0.05$, and vary the values of $\beta$ in the interval $[0.02,0.06]$. The Lyapunov exponents spectrum and the bifurcation diagram of the jerk system (17) are illustrated in Figure 9, indicating that as $\beta$ increases within this range, the 3-D jerk system (17) can exhibit both periodic and chaotic behavior.

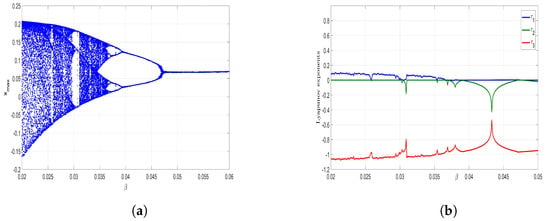
Figure 9. (a) Bifurcation Diagram and (b) Lyapunov Exponents (LE) Spectrum of the new jerk system (17) when $\beta \in [0.02,0.06]$, $\alpha =2.3$, $\gamma =0.05$.

Define $N=[0.02,0.0256]\cup [0.0259,0.0297]\cup [0.0311,0.036]$. When $\beta \in N$, the jerk system (17) generates chaotic behavior with a single positive Lyapunov exponent. When $\beta =0.034$, the Lyapunov exponents for the jerk system (17) are found as follows:

$${\tau }_1=0.049,{\tau }_2=0,{\tau }_3=-1.107$$

(28)

Define $P=[0.0257,0.0258]\cup [0.0298,0.0310]\cup [0.037,0.06]$.

When $\beta \in P$, the behavior of the jerk system (17) is periodic, which is supported by the presence of one zero Lyapunov exponent and two negative Lyapunov exponents. For example, when $\beta =0.06$, the corresponding Lyapunov exponents have the following values:

$${\tau }_1=0,{\tau }_2=-0.172,{\tau }_3=-0.769$$

(29)

Moreover, the bifurcation diagram depicted in Figure 9 reveals that the jerk system (17) experiences the well-known reverse period-doubling route from chaos to a period-1 orbit.

The bifurcation diagram presented in Figure 9 illustrates that the jerk system (17) experiences a series of period-doubling as the parameter $\beta$ increases. As a result, within certain intervals of $\beta$, the well-known phenomenon of reverse period-doubling occurs, where the jerk system (17) makes transitions from chaos to period-16, period-8, period-4, period-2 attractors and ultimately to a period-1 attractor.

The values of the parameter $\beta$ have a significant impact on the behavior of the jerk system (17). For instance, when $\beta$ takes values in the interval $[0.0311,0.0365]$, the jerk system (17) exhibits a chaotic attractor. When $\beta$ takes values in the interval $[0.0366,0.0367]$, a period-16 attractor for the jerk system (17) is observed. Similarly, a period-8 attractor occurs for the jerk system (17) when $\beta$ takes values in the interval $[0.0368,0.0375]$. Also, a period-4 attractor is observed for the jerk system (17) when $\beta$ takes values in the interval $[0.0376,0.0391]$. Furthermore, a period-2 attractor is observed for the jerk system (17) when $\beta$ takes values in the interval $[0.0392,0.0475]$. Finally, a period-1 attractor is observed for the jerk system (17) when $\beta$ takes values in the interval $[0.0476,0.06]$.

Table 3 enumerates the different attractors obtained from numerical simulations that illustrate the reverse period-doubling route mentioned earlier. Additionally, Figure 10 provides a graphical representation of these attractors.

Table 3. Reverse period-doubling route from chaos to a period-1 attractor with parameter $\beta$ varying.

$\mathit{\beta }$ Range	$\mathit{\beta }$ Value	Dynamics	Attractor
$[0.0311,0.0365]$	$0.034$	Chaos	Figure 10a
$[0.0366,0.0367]$	$0.0366$	Period-16	Figure 10b
$[0.0368,0.0375]$	$0.0369$	Period-8	Figure 10c
$[0.0376,0.0391]$	$0.039$	Period-4	Figure 10d
$[0.0392,0.0475]$	$0.042$	Period-2	Figure 10e
$[0.0476,0.06]$	$0.06$	Period-1	Figure 10f

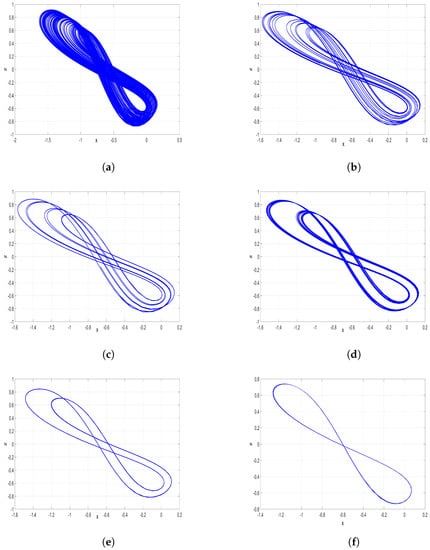
Figure 10. 2-D MATLAB plots of the new jerk system (17) in $(x,z)$ plane for $\alpha =2.3$, $\gamma =0.05$ and $X\left(0\right)=(0,-1,0)$; (a) Chaos for $\beta =0.034$; (b) Period-16 for $\beta =0.0366$; (c) Period-8 for $\beta =0.0369$; (d) Period-4 for $\beta =0.039$; (e) Period-2 for $\beta =0.042$; (f) Period-1 for $\beta =0.06$.

3.3. Variation with Respect to the Parameter $\gamma$

To investigate the effect of $\gamma$ on the jerk system (17), $\alpha$ and $\beta$ are kept constant at the values $\alpha =2.3$ and $\beta =0.02$, while $\gamma$ varies in the interval $[-0.1,0.05]$. The corresponding results are shown in Figure 11, which displays the Lyapunov exponent values and the corresponding bifurcation diagram as $\gamma$ increases. The analysis reveals that the 3-D jerk system (17) can exhibit both chaotic behavior and periodic behavior as $\gamma$ increases.

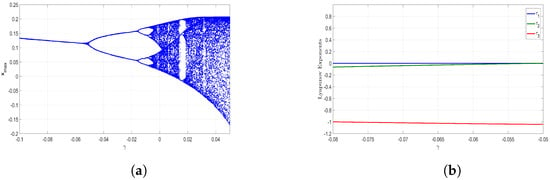
Figure 11. (a) Bifurcation Diagram and (b) Lyapunov Exponents (LE) Spectrum of the new jerk system (17) when $\gamma \in [-0.1,0.05]$, $\alpha =2.3$, $\beta =0.02$.

We define $Q=[-0.1,-0.006]\cup [0.015,0.0182]$. When $\gamma \in Q$, the jerk system (17) exhibits periodic behavior and does not have any positive Lyapunov exponent. For example, when $\gamma =0.075$, the corresponding Lyapunov exponents of the jerk system (17) are found as

$${\tau }_1=0,{\tau }_2=-0.053,{\tau }_3=-1.008$$

(30)

We define $R=[-0.005,0.014]\cup [0.0183,0.05]$. When $\gamma \in R$, the jerk system (17) exhibits chaotic behavior and has a positive Lyapunov exponent. For example, when $\gamma =0.004$, the corresponding Lyapunov exponents are found as

$${\tau }_1=0.057,{\tau }_2=0,{\tau }_3=-1.008$$

(31)

Moreover, the bifurcation diagram depicted in Figure 11 reveals that the jerk system (17) experiences the well-known period-doubling route to chaos.

The bifurcation diagram presented in Figure 11 illustrates that the system experiences a series of period-doubling as the parameter $\gamma$ increases, resulting in the well-known period-doubling route to chaos within specific ranges of parameter $\gamma$, which progresses from period-1 to period-2, period-4, period-8, period-16 and, ultimately, to chaos.

The behavior of the jerk system (17) varies depending on the values of $\gamma$. Specifically, when $\gamma$ falls within the interval $[-0.1,-0.055]$, the jerk system (17) exhibits a period-1 attractor. When $\gamma$ falls within the interval $[-0.054,-0.017]$, the jerk system (17) displays a period-2 attractor. When $\gamma$ takes values in the interval $[-0.016,-0.0095]$, the jerk system (17) displays a period-4 attractor. When $\gamma$ takes values in the interval $[-0.0096,-0.008]$, the jerk system (17) displays a period-8 attractor. When $\gamma$ takes values in the interval $[-0.0096,-0.006]$, the jerk system (17) displays a period-16 attractor. Finally, when $\gamma$ falls within the interval $[-0.0079,-0.006]$, the jerk system (17) displays a chaotic attractor, which marks the end of the period-doubling cascade.

Table 4 summarizes the various attractors observed through numerical simulations, illustrating the period-doubling route to chaos discussed earlier. Additionally, Figure 12 provides a graphical representation of these attractors.

Table 4. Period-doubling route to chaos with parameter $\gamma$ varying.

$\mathit{\gamma }$  Range	$\mathit{\gamma }$ Value	Dynamics	Attractor
$[2,2.1978]$	2.1	Period-1	Figure 12a
$[2.1980,2.2336]$	2.22	Period-2	Figure 12b
$[2.2338,2.2404]$	2.236	Period-4	Figure 12c
$[2.2406,2.2418]$	2.2412	Period-8	Figure 12d
$[2.2420,2.2424]$	2.2424	Period-16	Figure 12e
$[2.2425,2.2469]$	2.2465	Chaos	Figure 12f

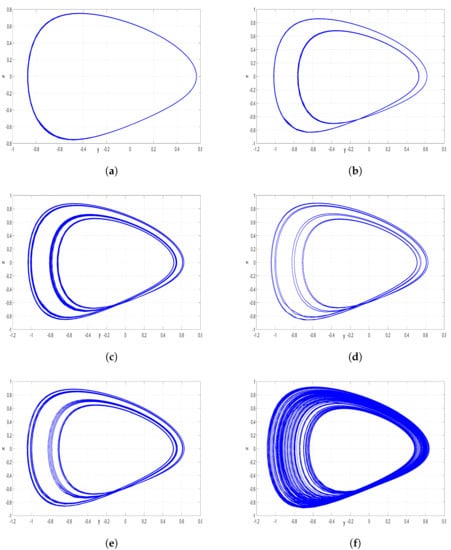
Figure 12. 2-D MATLAB plots of the new jerk system (17) in $(x,z)$ plane for $\alpha =2.3$, $\beta =0.02$ and $X\left(0\right)=(0,-1,0)$. (a) Period-1 for $\gamma =-0.075$; (b) Period-2 for $\gamma =-0.018$; (c) Period-4 for $\gamma =-0.012$; (d) Period-8 for $\gamma =-0.0088$; (e) Period-16 for $\gamma =-0.0076$; (f) Chaos for $\gamma =0.004$.

4. Multistability and Coexisting Attractors of the New Jerk System with a Stable Equilibrium

Multistability is a special property of a nonlinear dynamical system that refers to the coexistence of periodic orbits or chaotic attractors for the same set of parameter values but different sets of initial states [41,42]. Multistability makes a chaotic system more complex and more useful in many applications that require complexity and provide a great degree of freedom for the engineering chaos-based applications such as secure communication.

The 3-D jerk system (17) is a mathematical model that shows the existence of multiple coexisting attractors. The system (17) can exhibit various coexisting attractors depending on the initial points. In this work, we have used sensitivity analysis, which involves systematically varying the initial values or parameters of the system to assess their impact on the system’s behavior. By performing sensitivity analysis, we can identify the ranges of initial values and parameters that lead to the appearance of coexisting attractors.

To investigate the multistability properties of the jerk system (17), we consider three distinct starting points:

$$X_{01}=(0.07,0.07,0.07),X_{02}=(0.15,0.15,0.15),X_{03}=(0,-1,0)$$

(32)

4.1. CASE(A): $\alpha =2.2625$, $\beta =0.02$ and $\gamma =0.05$

In this case, the 3-D jerk system (17) demonstrates two distinct behaviors based on its initial conditions $X_{01}$ and $X_{02}$ as demonstrated in Figure 13. If the system starts from $X_{01}$, it will converge to the equilibrium. However, if it starts from $X_{02}$, then it will exhibit chaotic behavior.

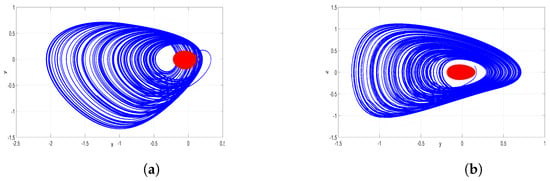
Figure 13. MATLAB plots of the coexisting stable orbit and chaotic attractor generated by the 3-D system (17) for the parameter values at $\alpha =2.2625$, $\beta =0.02$ and $\gamma =0.05$, where the attractor generated from $X_{01}$ is in red, while the attractor generated from $X_{02}$ is in blue. (a) $(x-y)$ plot; (b) $(y-z)$ plot.

The Lyapunov exponents of the jerk system (17) at $X_{01}$ are numerically found in MATLAB using Wolf algorithm [40] as

$${\tau }_1=-0.0047,{\tau }_2=-0.0049,{\tau }_3=-0.9902,$$

(33)

which shows the existence of a stable orbit starting from $X_{01}$.

The Lyapunov exponents of the jerk system (17) at $X_{02}$ are numerically found in MATLAB using Wolf algorithm [40] as

$${\tau }_1=0.0572,{\tau }_2=0,{\tau }_3=-1.0186,$$

(34)

which shows the existence of a chaotic attractor starting from $X_{02}$.

Figure 13 depicts the MATLAB plots of the coexisting stable orbit and chaotic attractor generated by the 3-D jerk system (17) for Case (A), where the attractor generated from $X_{01}$ is in red, while the attractor generated from $X_{02}$ is in blue.

4.2. CASE(B): $\alpha =2.3$, $\beta =0.019$ and $\gamma =0.05$

In this case, the 3-D jerk system (17) demonstrates two distinct behaviors based on its initial conditions $X_{02}$ and $X_{03}$ as demonstrated in Figure 14. The jerk system (17) exhibits coexisting chaotic attractors for the solutions starting from $X_{02}$ and $X_{03}$.

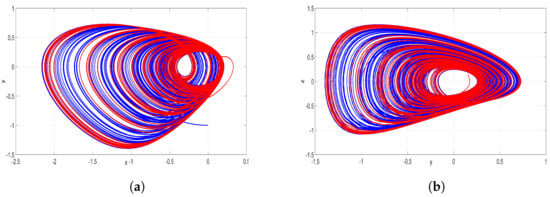
Figure 14. MATLAB plots of the coexisting chaotic attractors generated by the 3-D system (17) for the parameter values at $\alpha =2.3$, $\beta =0.019$ and $\gamma =0.05$, where the attractor generated from $X_{02}$ is in red, while the attractor generated from $X_{03}$ is in blue. (a) $(x-y)$ plot; (b) $(y-z)$ plot.

The Lyapunov exponents of the jerk system (17) at $X_{02}$ are numerically found in MATLAB using Wolf algorithm [40] as

$${\tau }_1=0.0837,{\tau }_2=0,{\tau }_3=-1.0552,$$

(35)

which shows the existence of a chaotic attractor starting from $X_{02}$.

The Lyapunov exponents of the jerk system (17) at $X_{03}$ are numerically found in MATLAB using Wolf algorithm [40] as

$${\tau }_1=0.0867,{\tau }_2=0,{\tau }_3=-1.0591,$$

(36)

which shows the existence of a chaotic attractor starting from $X_{03}$.

5. Complete Synchronization of the New Jerk Systems Using Backstepping Control

Taking advantage of the special structure of the jerk systems, we use the backstepping control method to achieve complete synchronization between the master and slave chaotic jerk systems [43]. Backstepping control method has also been applied for the synchronization of other types of chaotic systems [44,45]. Synchronization of chaotic systems has several applications in secure communication systems [3,4,46].

The master and slave jerk systems considered for the synchronization design are described as follows:

$$\left\{\begin{array}{ccc}{\dot{x}}_m& =& y_m\hfill \\ {\dot{y}}_m& =& z_m\hfill \\ {\dot{z}}_m& =& -x_m-y_m-z_m-\alpha z_m^2+x_m{y}_m-\beta +\gamma z_m^3\hfill \end{array}\right.$$

(37)

$$\left\{\begin{array}{ccc}{\dot{x}}_s& =& y_s\hfill \\ {\dot{y}}_s& =& z_s\hfill \\ {\dot{z}}_s& =& -x_s-y_s-z_s-\alpha z_s^2+x_s{y}_s-\beta +\gamma z_s^3+v\hfill \end{array}\right.$$

(38)

In Equation (38), v is an active backstepping control which is to be designed in this section.

We define the complete synchronization error by means of the following equations:

$$\left\{\begin{array}{ccc}{ϵ}_x& =& x_s-x_m\hfill \\ {ϵ}_y& =& y_s-y_m\hfill \\ {ϵ}_z& =& z_s-z_m\hfill \end{array}\right.$$

(39)

The error dynamics is derived by means of the following equations:

$$\left\{\begin{array}{ccc}{\dot{ϵ}}_x& =& {ϵ}_y\hfill \\ {\dot{ϵ}}_y& =& {ϵ}_z\hfill \\ {\dot{ϵ}}_z& =& -{ϵ}_x-{ϵ}_y-{ϵ}_z-\alpha (z_s^2-z_m^2)+x_s{y}_s-x_m{y}_m+\gamma (z_s^3-z_m^3)+v\hfill \end{array}\right.$$

(40)

In this section, we shall establish the following main result.

Theorem 1.

The backstepping control law defined by the equation

$$v=-2{ϵ}_x-4{ϵ}_y-2{ϵ}_z-x_s{y}_s+x_m{y}_m+\alpha (z_s^2-z_m^2)-\gamma (z_s^3-z_m^3)-\kappa {\varphi }_z$$

(41)

with gain $\kappa >0$ and ${\varphi }_z=2{ϵ}_x+2{ϵ}_y+{ϵ}_z$ globally and exponentially stabilizes the chaotic jerk systems (37) and (38) for all initial states in ${\mathbf{R}}^3$.

Proof. 

We begin with the Lyapunov function

$$P_1\left({\varphi }_x\right)=\frac{1}{2}{\varphi }_x^2,$$

(42)

where

$${\varphi }_x={ϵ}_x$$

(43)

A simple calculation shows that

$$\dot{P_1}={\varphi }_x{\dot{\varphi }}_x=-{\varphi }_x^2+{\varphi }_x({ϵ}_x+{ϵ}_y)$$

(44)

To simplify the calculations, we define

$${\varphi }_y={ϵ}_x+{ϵ}_y$$

(45)

Then we can express Equation (44) as follows:

$$\dot{P_1}=-{\varphi }_x^2+{\varphi }_x{\varphi }_y$$

(46)

Next, we define the Lyapunov function

$$P_2({\varphi }_x,{\varphi }_y)=P_1\left({\varphi }_x\right)+\frac{1}{2}{\varphi }_y^2=\frac{1}{2}{\varphi }_x^2+\frac{1}{2}{\varphi }_y^2$$

(47)

A simple calculation shows that

$${\dot{P}}_2=-{\varphi }_x^2-{\varphi }_y^2+{\varphi }_y(2{ϵ}_x+2{ϵ}_y+{ϵ}_z)$$

(48)

To simplify the calculations, we define

$${\varphi }_z=2{ϵ}_x+2{ϵ}_y+{ϵ}_z$$

(49)

Then we can express Equation (48) as follows:

$$\dot{P_2}=-{\varphi }_x^2-{\varphi }_y^2+{\varphi }_y{\varphi }_z$$

(50)

As a final step of the backstepping control design, we consider the quadratic Lyapunov function defined as follows:

$$P({\varphi }_x,{\varphi }_y,{\varphi }_z)=P_2({\varphi }_x,{\varphi }_y)+\frac{1}{2}{\varphi }_z^2=\frac{1}{2}{\varphi }_x^2+\frac{1}{2}{\varphi }_y^2+\frac{1}{2}{\varphi }_z^2$$

(51)

Differentiating P with respect to t, we get the following:

$$\dot{P}=-{\varphi }_x^2-{\varphi }_y^2-{\varphi }_z^2+{\varphi }_{z}Q$$

(52)

where

$$Q=2{ϵ}_x+4{ϵ}_y+2{ϵ}_z+x_s{y}_s-x_m{y}_m-\alpha (z_s^2-z_m^2)+\gamma (z_s^3-z_m^3)+v$$

(53)

Substituting the formula given in Equation (41) for v into Equation (53), we get

$$Q=-\kappa {\varphi }_z$$

(54)

Combining (52) and (54), we get

$$\dot{P}=-{\varphi }_x^2-{\varphi }_y^2-{\varphi }_z^2(1+\kappa )$$

(55)

Since $\kappa >0$, we see that $\dot{P}$ is a quadratic and negative definite function defined on ${\mathbf{R}}^3$.

By Lyapunov Stability Theory, we deduce that the error dynamics (40) is locally exponentially stable at $({ϵ}_x,{ϵ}_y,{ϵ}_z)=(0,0,0)$.

This completes the proof. □

For MATLAB simulations, we pick the parameter values as in the chaotic situation, viz. $\alpha =2.3$, $\beta =0.02$ and $\gamma =0.05$. We choose $\kappa =10$.

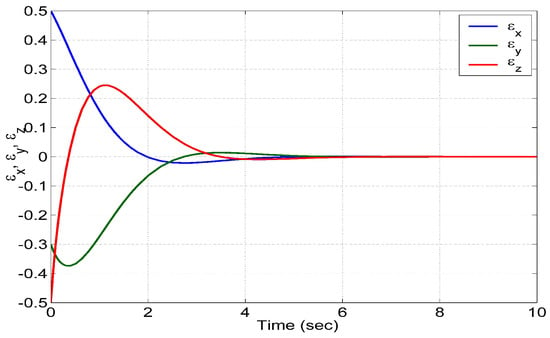
The initial states of the master and slave jerk systems represented by (37) and (38) are taken as follows:

$$x_m\left(0\right)=-0.1,y_m\left(0\right)=0.2,z_m\left(0\right)=0.3,x_s\left(0\right)=0.4,y_s\left(0\right)=-0.1,z_s\left(0\right)=-0.2$$

(56)

Figure 15 shows the convergence of the synchronization error $({ϵ}_x\left(t\right),{ϵ}_y\left(t\right),{ϵ}_z\left(t\right))$ between the jerk systems (37) and (38).

Figure 15. MATLAB plot showing the synchronization error $({ϵ}_x,{ϵ}_y,{ϵ}_z)$ between the jerk systems (37) and (38).

6. FPGA-Based Implementation of the New Jerk System with a Stable Equilibrium

Due to the advantages of the FPGA for fast prototyping, it is very useful to observe experimental attractors of different chaotic systems. As mentioned in [35], the FPGA implementation depends on the numerical method that is used to solve the dynamical system, as in the one given in (17), which can be solved by applying the Forward Euler method. The hardware resources of an FPGA implementation depend on the numerical method, and the throughput depends on the choice of the time-step, which is another challenge to maximize the operating frequency of an FPGA, as shown in [37].

The application of the Forward Euler method to (17) leads us to the discretized equations given in (57), where one can infer the need of using multipliers, adders and subtractors to perform all the operations.

$$\left\{\begin{array}{c}{x}_{n+1}=x_n+h{y}_n\hfill \\ y_{n+1}=y_n+h{z}_n\hfill \\ z_{n+1}=z_n+h(-x_n-y_n-z_n-\alpha z_n^2+x-n{y}_n-\beta -\gamma z_n^3)\hfill \end{array}\right.$$

(57)

It is worth mentioning that Forward Euler method is quite useful for an implementation with the lowest count of hardware resources, although it has less precision than other numerical methods, such as the fourth-order Runge-Kutta method or multi-steps methods [37]. To observe an attractor, it is necessary to estimate the step-size h. In this work, it is set to $h=0.001$, and the computer arithmetic is performed using 32-bit, with a fixed-point notation in the format 8.24, which means that one bit is associated with the sign, seven bits with the integer part, and 25 bits with the fractional part. The equations given in (57), can be described in a block diagram, as the one shown in Figure 16, where it can be appreciated that the circuit is composed of eight multipliers, five adders, and four subtractors.

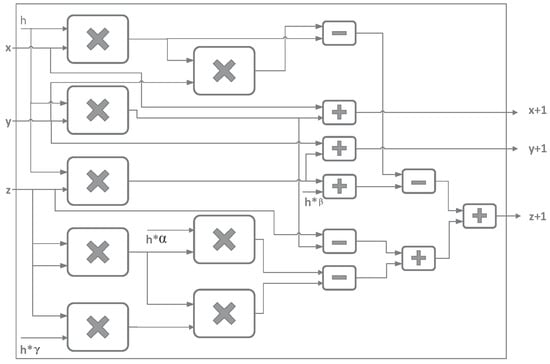
Figure 16. Circuit diagram of the new jerk system (57).

The block description of the design shown in Figure 16, can be described under the language named Very-High-Speed Integrated Circuit Hardware Description Language (VHDL in short). The synthesis of the VHDL description is performed using Xilinx Vivado tool. As a result, the discretized new jerk system with a stable equilibrium given in (57), is implemented herein on the Zybo Z7-20 development board with xc7z020clg400-1. The experimental setup is shown in Figure 17, where one can see the oscilloscope, the FPGA Zybo Z7-20, and two digital-to-analog (DAC) converters to observe the signals. The latency of the FPGA design is two clock cycles. In this manner, the hardware resources are summarized in Table 5.

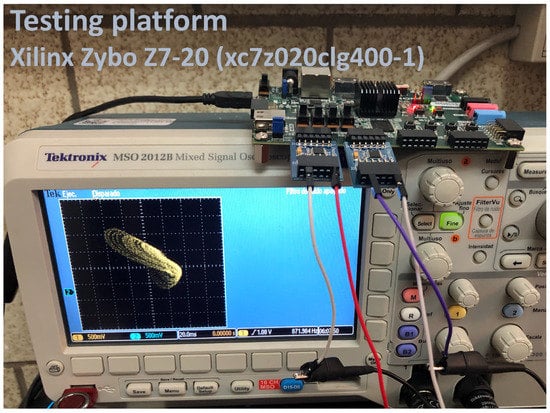
Figure 17. Experimental setup.

Table 5. Hardware resources of the FPGA implementation of (57) using Xilinx Zybo Z7-20 (xc7z020clg400-1).

Resources	Used	Util
Slice	134	1.01%
LUTs	302	0.57%
FFs	192	0.17%
DSPs	16	5.18%
Frequency Max	123 MHz	-

The experimental attractors can be observed as depicted in the Figure 18 and Figure 19. Two Cases (A and B) have been tested, both with initial conditions equal to $x\left(0\right)=0$, $y\left(0\right)=-1$, $z\left(0\right)=0$, and with a time-step set to $h=0.001$. Case A works with the coefficient values $\alpha =2.3$, $\beta =0.02$, $\gamma =0.05$, and the experimental attractors are shown in Figure 18. Case B works with the coefficient values $\alpha =2.29$, $\beta =0.005$, $\gamma =0.01$, and the experimental attractors are shown in Figure 19.

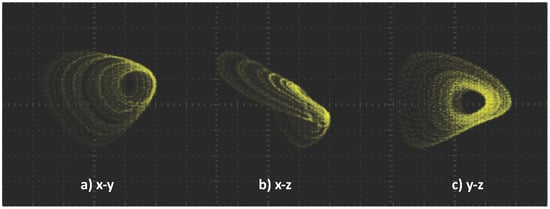
Figure 18. Experimental views for Case A of the attractors $x-y$, $x-z$, and $y-z$. With coefficient values $\alpha =2.3$, $\beta =0.02$, $\gamma =0.05$, initial conditions $x\left(0\right)=0$, $y\left(0\right)=-1$, $z\left(0\right)=0$, and the value of time-step is set to $h=0.001$.

Figure 19. Experimental views for Case B of the attractors $x-y$, $x-z$, and $y-z$. With coefficient values $\alpha =2.29$, $\beta =0.005$, $\gamma =0.01$, initial conditions $x\left(0\right)=0$, $y\left(0\right)=-1$, $z\left(0\right)=0$, and the value of time-step is set to $h=0.001$.

7. Conclusions

In this research paper, we discussed the modelling of a new 3-D chaotic jerk system with a stable equilibrium. Such chaotic systems are known to exhibit hidden attractors. A detailed bifurcation analysis was performed for the new chaotic jerk system with a stable equilibrium. We showed that the new jerk system has multistability with coexisting attractors. Using backstepping control theory, we derived new results for the synchronization design of a pair of new jerk systems with a stable equilibrium taken as the master-slave chaotic systems. The experimental attractors have been generated from the discretization of the jerk system with a stable equilibrium and its implementation using the FPGA Zybo Z7-20 development board. Two cases were implemented in the FPGA board, and one can see that the experimental attractors are quite similar to those simulated from the mathematical model of the new chaotic jerk system with a stable equilibrium reported in this work.