Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Generation of a Virtual Digital Phantom of a Glycinergic Synapse
2.2. A Grid of Gephyrins and Its Schematic Presentation for GlyR Distribution
2.3. Estimation of GlyR Clustering in a Synaptic Membrane
2.4. The Description of Chloride Ions Electro-Diffusion near a Post-Synaptic Membrane after GlyRs Channel Openings
2.5. Numerical Evaluation of the Model
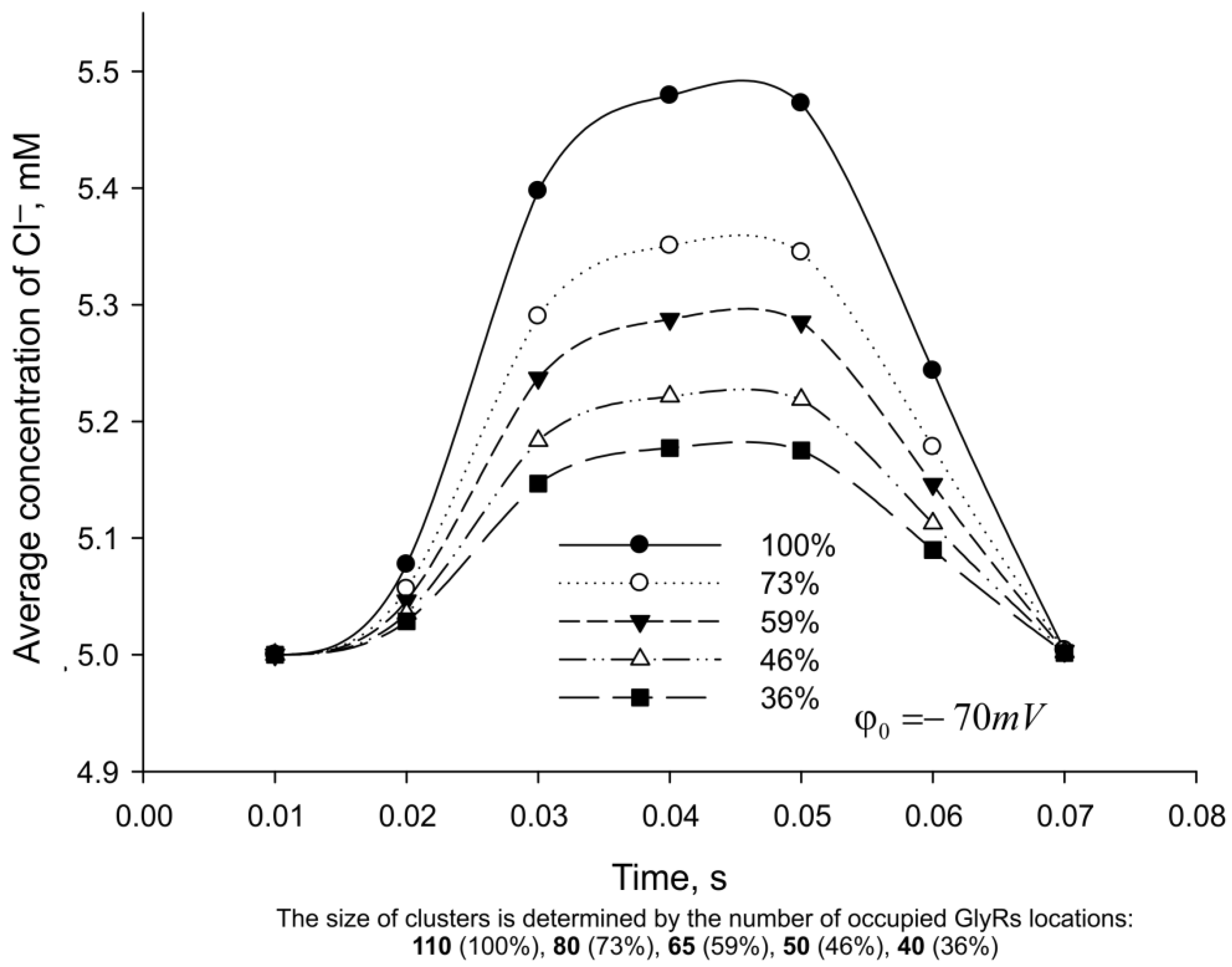
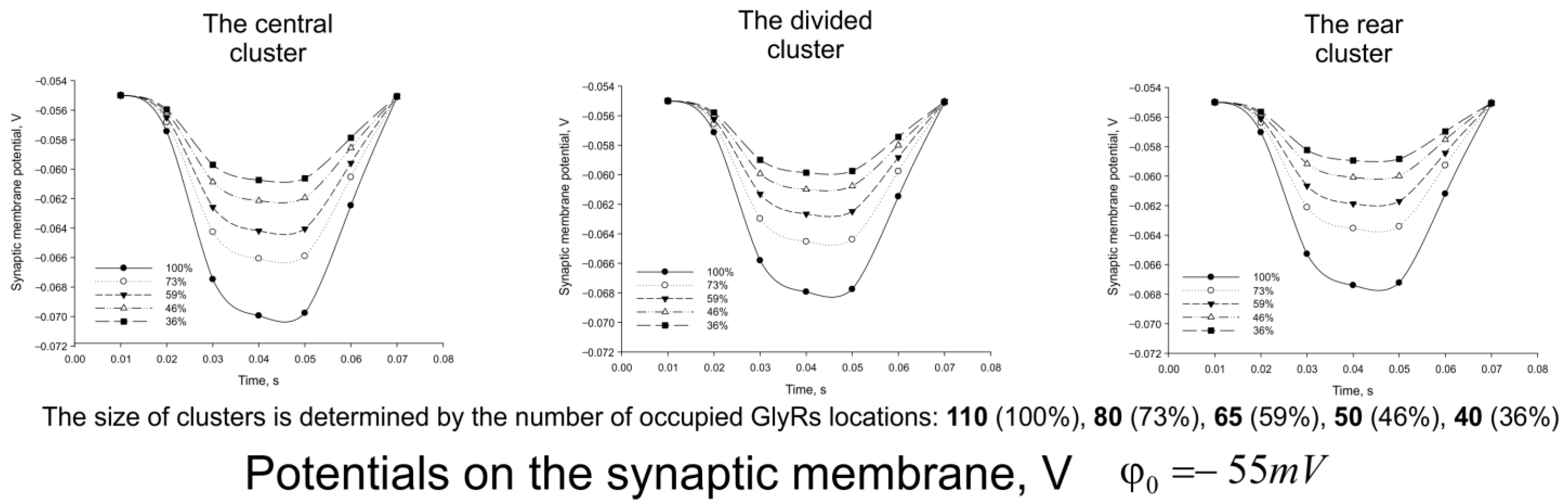
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNS | central nervous system |
| GlyR | glycine receptor |
| IPSP | inhibitory post-synaptic potential |
| GABA | gamma aminobutyric acid |
| CCC | cation-chloride co-transporter |
| KCC2 | K+–Cl− co-transporter type 2 |
| PSD | postsynaptic density |
| ISF | interstitial fluid |
| ECS | extracellular space |
| FEM | finite element method |
| CC | cluster capacity |
References
- Burgos, C.F.; Yevenes, G.E.; Aguayo, L.G. Structure and pharmacologic modulation of inhibitory glycine receptors. Mol. Pharmacol. 2016, 90, 318–325. [Google Scholar] [CrossRef]
- Dufour, A.; Tell, F.; Kessler, J.; Baude, A. Mixed GABA-glycine synapses delineate a specific topography in the nucleus tractus solitarii of adult rat. J. Physiol. 2010, 588, 1097–1115. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, H.; Yamaguchi, J.; Nakahata, Y.; Nabekura, J. Dynamic regulation of glycine-GABA co-transmission at spinal inhibitory synapses by neuronal glutamate transporter. J. Physiol. 2013, 591, 3821–3832. [Google Scholar] [CrossRef]
- Moore, L.A.; Trussell, L.O. Corelease of inhibitory neurotransmitters in the mouse auditory midbrain. J. Neurosci. 2017, 37, 9453–9464. [Google Scholar] [CrossRef] [PubMed]
- Delpire, E.; Staley, K.J. Novel determinants of the neuronal Cl- concentration. J. Physiol. 2014, 592, 4099–4114. [Google Scholar] [CrossRef] [PubMed]
- Ben-Ari, Y.; Khalilov, I.; Kahle, K.T.; Cherubini, E. The GABA excitatory/inhibitory shift in brain maturation and neurological disorders. Neuroscientist 2012, 18, 467–486. [Google Scholar] [CrossRef] [PubMed]
- Kaila, K.; Price, T.J.; Payne, J.A.; Puskarjov, M.; Voipio, J. Cation-chloride cotransporters in neuronal development, plasticity and disease. Nat. Rev. Neurosci. 2014, 15, 637–654. [Google Scholar] [CrossRef] [PubMed]
- Berndt, N.; Hoffmann, S.; Benda, J.; Holzhutter, H.-G. The influence of the chloride currents on action potential firing and volume regulation of excitable cells studied by a kinetic model. J. Theor. Biol. 2011, 276, 42–49. [Google Scholar] [CrossRef]
- Moore, Y.E.; Kelley, M.R.; Brandon, N.J.; Deeb, T.Z.; Moss, S.J. Seizing Control of KCC2: A New Therapeutic Target for Epilepsy. Trends Neurosci. 2017, 40, 555–571. [Google Scholar] [CrossRef]
- Price, T.J.; Cervero, F.; Gold, M.S.; Hammond, D.L.; Prescott, S.A. Chloride regulation in the pain pathway. Brain Res. Rev. 2009, 60, 149–170. [Google Scholar] [CrossRef]
- Gagnon, M.; Bergeron, M.J.; Lavertu, G.; Castonguay, A.; Tripathy, S.; Bonin, R.P.; Perez-Sanchez, J.; Boudreau, D.; Wang, B.; Dumas, L.; et al. Chloride extrusion enhancers as novel therapeutics for neurological diseases. Nat. Med. 2013, 19, 1524–1528. [Google Scholar] [CrossRef]
- Martin-Aragon Baudel, M.A.S.; Poole, A.V.; Darlison, M.G. Chloride co-transporters as possible therapeutic targets for stroke. J. Neurochem. 2017, 140, 195–209. [Google Scholar] [CrossRef] [PubMed]
- Ellender, T.J.; Raimondo, J.V.; Irkle, A.; Lamsa, K.P.; Akerman, C.J. Excitatory effects of parvalbumin-expressing interneurons maintain hippocampal epileptiform activity via synchronous afterdischarges. J. Neurosci. 2014, 34, 15208–15222. [Google Scholar] [CrossRef]
- Doyon, N.; Prescott, S.A.; Castonguay, A.; Godin, A.G.; Kroger, H.; de Koninck, Y. Efficacy of synaptic inhibition depends on multiple, dynamically interacting mechanisms implicated in chloride homeostasis. PLoS Comput. Biol. 2011, 7, e1002149. [Google Scholar] [CrossRef]
- Alvarez, F.J. Gephyrin and the regulation of synaptic strength and dynamics at glycinergic inhibitory synapses. Brain Res. Bull. 2017, 129, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Nartsissov, Y.R. The Effect of Flux Dysconnectivity Functions on Concentration Gradients Changes in a Multicomponent Model of Convectional Reaction-Diffusion by the Example of a Neurovascular Unit. Defect Diffus. Forum 2021, 413, 19–28. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. Application of a multicomponent model of convectional reaction-diffusion to description of glucose gradients in a neurovascular unit. Front. Physiol. 2022, 13, 1624. [Google Scholar] [CrossRef]
- Nicholson, C.; Phillips, J.M. Ion diffusion modified by tortuosity and volume fraction in the extracellular microenvironment of the rat cerebellum. J. Physiol. 1981, 321, 225–257. [Google Scholar] [CrossRef]
- Nicholson, C. Diffusion and related transport mechanisms in brain tissue. Rep. Prog. Phys. 2001, 64, 815–884. [Google Scholar] [CrossRef]
- Syková, E.; Nicholson, C. Diffusion in brain extracellular space. Physiol. Rev. 2008, 88, 1277–1340. [Google Scholar] [CrossRef]
- Thorne, R.G.; Nicholson, C. In vivo diffusion analysis with quantum dots and dextrans predicts the width of brain extracellular space. Proc. Natl. Acad. Sci. USA 2006, 103, 5567–5572. [Google Scholar] [CrossRef]
- Nicholson, C. Anomalous diffusion inspires anatomical insights. Biophys. J. 2015, 108, 2091–2093. [Google Scholar] [CrossRef]
- Nicholson, C.; Hrabětová, S. Brain Extracellular Space: The Final Frontier of Neuroscience. Biophys. J. 2017, 113, 2133–2142. [Google Scholar] [CrossRef] [PubMed]
- Faraji, A.H.; Rajendran, S.; Jaquins-Gerstl, A.S.; Hayes, H.J.; Richardson, R.M. Convection-Enhanced Delivery and Principles of Extracellular Transport in the Brain. World Neurosurg. 2021, 151, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Verisokin, A.; Verveyko, D.; Kirsanov, A.; Brazhe, A.; Postnov, D. Computational Model of Noradrenaline Modulation of Astrocyte Responses to Synaptic Activity. Mathematics 2023, 11, 628. [Google Scholar] [CrossRef]
- Kashaju, N.; Kimathi, M.; Masanja, V.G. Modeling the Effect of Binding Kinetics in Spatial Drug Distribution in the Brain. Comput. Math. Methods Med. 2021, 2021, 5533886. [Google Scholar] [CrossRef] [PubMed]
- Calvetti, D.; Cheng, Y.; Somersalo, E. A spatially distributed computational model of brain cellular metabolism. J. Theor. Biol. 2015, 376, 48–65. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. A novel algorithm of the digital nervous tissue phantom creation based on 3D Voronoi diagram application. J. Phys. Conf. Ser. 2021, 2090, 012009. [Google Scholar] [CrossRef]
- Rusakov, D.A.; Harrison, E.; Stewart, M.G. Synapses in hippocampus occupy only 1–2% of cell membranes and are spaced less than half-micron apart: A quantitative ultrastructural analysis with discussion of physiological implications. Neuropharmacology 1998, 37, 513–521. [Google Scholar] [CrossRef]
- Calamai, M.; Specht, C.G.; Heller, J.; Alcor, D.; Machado, P.; Vannier, C.; Triller, A. Gephyrin oligomerization controls GlyR mobility and synaptic clustering. J. Neurosci. 2009, 29, 7639–7648. [Google Scholar] [CrossRef]
- Luscher, B.; Fuchs, T.; Kilpatrick, C. GABAA Receptor Trafficking-Mediated Plasticity of Inhibitory Synapses. Neuron 2011, 70, 385–409. [Google Scholar] [CrossRef] [PubMed]
- Eun, Y.K.; Schrader, N.; Smolinsky, B.; Bedet, C.; Vannier, C.; Schwarz, G.; Schindelin, H. Deciphering the structural framework of glycine receptor anchoring by gephyrin. EMBO J. 2006, 25, 1385–1395. [Google Scholar] [CrossRef]
- Tretter, V.; Mukherjee, J.; Maric, H.-M.; Schindelin, H.; Sieghart, W.; Moss, S.J. Gephyrin, the enigmatic organizer at GABAergic synapses. Front. Cell. Neurosci. 2012, 6, 23. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Sola, M.; Kneussel, M.; Heck, I.S.; Betz, H.; Weissenhorn, W. X-ray Crystal Structure of the Trimeric N-terminal Domain of Gephyrin. J. Biol. Chem. 2001, 276, 25294–25301. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Basak, S.; Rao, S.; Gicheru, Y.; Mayer, M.L.; Sansom, M.S.P.; Chakrapani, S. Mechanisms of activation and desensitization of full-length glycine receptor in lipid nanodiscs. Nat. Commun. 2020, 11, 3752. [Google Scholar] [CrossRef]
- Maynard, S.A.; Rostaing, P.; Schaefer, N.; Gemin, O.; Candat, A.; Dumoulin, A.; Villmann, C.; Triller, A.; Specht, C.G. Identification of a stereotypic molecular arrangement of endogenous glycine receptors at spinal cord synapses. eLife 2021, 10, e74441. [Google Scholar] [CrossRef]
- Turchenkov, D.A.; Boronovsky, S.E.; Nartsissov, Y.R. Model of ion diffusion in synaptic cleft based on stochastical integration of langevin equation at dielectric friction approximation. Biophysics (Russ. Fed.) 2013, 58, 796–803. [Google Scholar] [CrossRef]
- Boronovsky, S.E.; Nartsissov, Y.R. Computer Simulator of Glycine Receptor Activity: A New Window into a Virtual World. Bull. Math. Biol. 2016, 78, 1380–1393. [Google Scholar] [CrossRef]
- Moroni, M.; Biro, I.; Giugliano, M.; Vijayan, R.; Biggin, P.C.; Beato, M.; Sivilotti, L.G. Chloride ions in the pore of glycine and GABA channels shape the time course and voltage dependence of agonist currents. J. Neurosci. 2011, 31, 14095–14106. [Google Scholar] [CrossRef]
- Williams, J.R.; Payne, J.A. Cation transport by the neuronal K+-Cl- cotransporter KCC2: Thermodynamics and kinetics of alternate transport modes. Am. J. Physiol.-Cell Physiol. 2004, 287, C919–C931. [Google Scholar] [CrossRef] [PubMed]
- Currin, C.B.; Trevelyan, A.J.; Akerman, C.J.; Raimondo, J.V. Chloride dynamics alter the input-output properties of neurons. PLoS Comput. Biol. 2020, 16, e1007932. [Google Scholar] [CrossRef]
- Mercado, A.; Gamba, G.; Mount, D.B. Molecular physiology of mammalian K+-CL- cotransporters. Adv. Exp. Med. Biol. 2005, 559, 29–41. [Google Scholar] [CrossRef]
- Hall, J.E.; Hall, M.E. Guyton and Hall Textbook of Medical Physiology, 11th ed.; Elsevier: Amsterdam, The Netherlands, 2012; p. 1112. [Google Scholar]
- Kress, G.J.; Mennerick, S. Action potential initiation and propagation: Upstream influences on neurotransmission. Neuroscience 2009, 158, 211–222. [Google Scholar] [CrossRef]
- Johnson, A.S.; Winlow, W. The soliton and the action potential—Primary elements underlying sentience. Front. Physiol. 2018, 9, 779. [Google Scholar] [CrossRef]
- Avoli, M.; Krnjević, K. The Long and Winding Road to Gamma-Amino-Butyric Acid as Neurotransmitter. Can. J. Neurol. Sci. 2015, 43, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Isomura, Y.; Sugimoto, M.; Fujiwara-Tsukamoto, Y.; Yamamoto-Muraki, S.; Yamada, J.; Fukuda, A. Synaptically activated Cl- accumulation responsible for depolarizing GABAergic responses in mature hippocampal neurons. J. Neurophysiol. 2003, 90, 2752–2756. [Google Scholar] [CrossRef]
- Berglund, K.; Schleich, W.; Wang, H.; Feng, G.; Hall, W.C.; Kuner, T.; Augustine, G.J. Imaging synaptic inhibition throughout the brain via genetically targeted Clomeleon. Brain Cell Biol. 2008, 36, 101–118. [Google Scholar] [CrossRef]
- Jedlicka, P.; Deller, T.; Gutkin, B.S.; Backus, K.H. Activity-dependent intracellular chloride accumulation and diffusion controls GABA A receptor-mediated synaptic transmission. Hippocampus 2011, 21, 885–898. [Google Scholar] [CrossRef]
- Williams, S.R.; Stuart, G.J. Role of dendritic synapse location in the control of action potential output. Trends Neurosci. 2003, 26, 147–154. [Google Scholar] [CrossRef]
- Deisz, R.A.; Lehmann, T.N.; Horn, P.; Dehnicke, C.; Nitsch, R. Components of neuronal chloride transport in rat and human neocortex. J. Physiol. 2011, 589, 1317–1347. [Google Scholar] [CrossRef] [PubMed]
- Chamma, I.; Chevy, Q.; Poncer, J.C.; Levi, S. Role of the neuronal K-Cl co-transporter KCC2 in inhibitory and excitatory neurotransmission. Front. Cell. Neurosci. 2012, 6, 5. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, A.M.; Nothwang, H.G. NKCC1 and KCC2: Structural insights into phospho-regulation. Front. Mol. Neurosci. 2022, 15, 964488. [Google Scholar] [CrossRef]
- Doyon, N.; Vinay, L.; Prescott, S.A.; De Koninck, Y. Chloride Regulation: A Dynamic Equilibrium Crucial for Synaptic Inhibition. Neuron 2016, 89, 1157–1172. [Google Scholar] [CrossRef]
- Raimondo, J.V.; Richards, B.A.; Woodin, M.A. Neuronal chloride and excitability—The big impact of small changes. Curr. Opin. Neurobiol. 2017, 43, 35–42. [Google Scholar] [CrossRef]
- Otsu, Y.; Donneger, F.; Schwartz, E.J.; Poncer, J.C. Cation–chloride cotransporters and the polarity of GABA signalling in mouse hippocampal parvalbumin interneurons. J. Physiol. 2020, 598, 1865–1880. [Google Scholar] [CrossRef] [PubMed]
- Glykys, J.; Dzhala, V.; Egawa, K.; Balena, T.; Saponjian, Y.; Kuchibhotla, K.V.; Bacskai, B.J.; Kahle, K.T.; Zeuthen, T.; Staley, K.J. Local impermeant anions establish the neuronal chloride concentration. Science 2014, 343, 670–675. [Google Scholar] [CrossRef]
- Staley, K.J.; Proctor, W.R. Modulation of mammalian dendritic GABA(A) receptor function by the kinetics of Cl- and HCO3- transport. J. Physiol. 1999, 519, 693–712. [Google Scholar] [CrossRef]
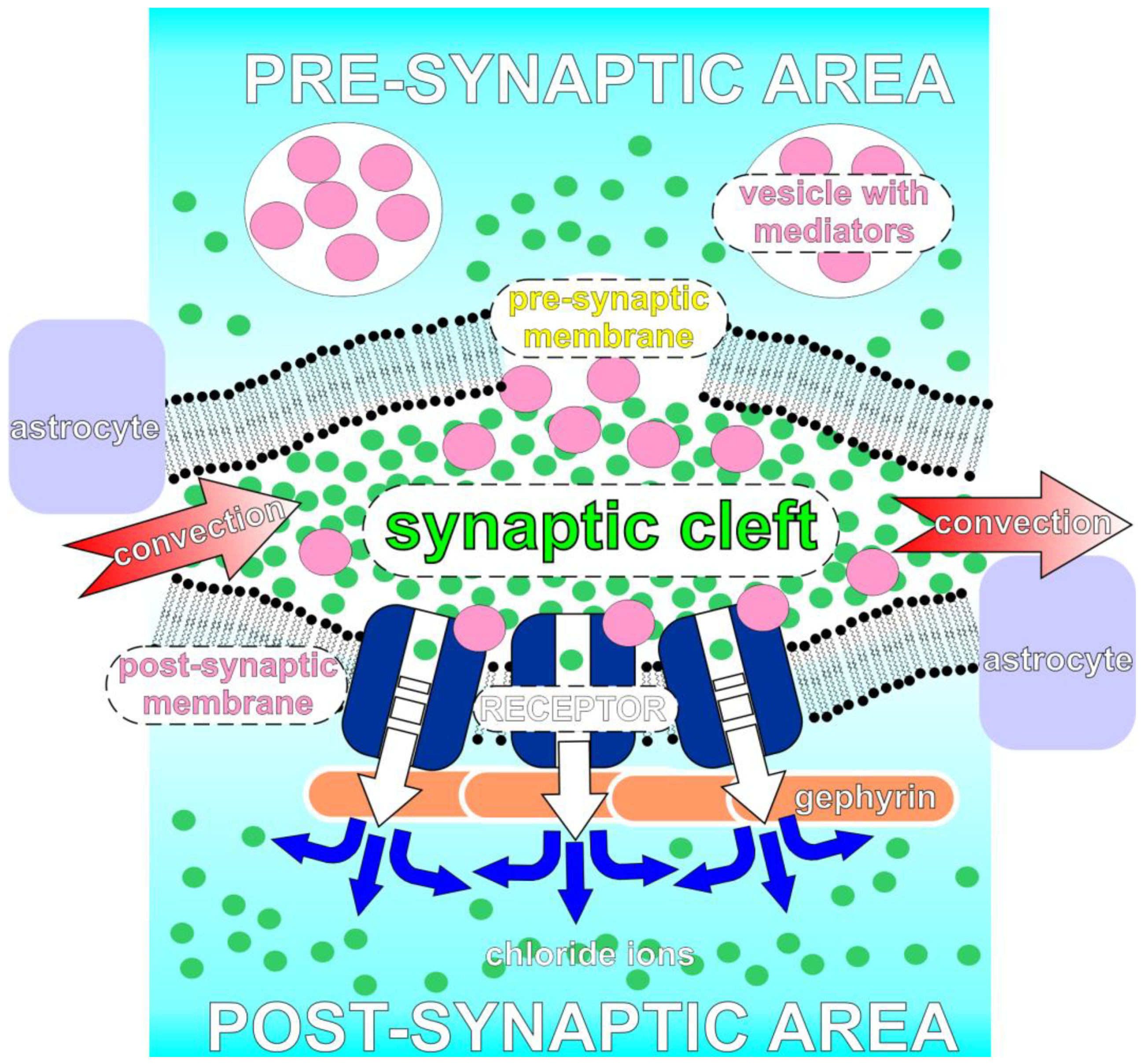






| The Object | Description | Comments |
|---|---|---|
| The first 3D body chosen from the Voronoi diagram. | This object can be chosen fluently. | |
| The second 3D body chosen from the Voronoi diagram. | This object is selected as a close neighbor of . | |
| The first ellipsoid included in the synapse phantom. | The shape of the object is determined by the experimental data 1. | |
| The second ellipsoid included in the synapse phantom. | (see above). | |
| The central part of the synaptic phantom. | (see above). | |
| The final form of pre- and post-synaptic boutons with embedded track of the synaptic phantom. | The object consists of two bodies which can be used separately in the modelling. | |
| The phantom of an astrocyte part lies near to the synaptic area. | The object includes the part of an astrocyte and a small geometrical shape (“claws”) surrounding the synaptic area. | |
| An ellipsoid used for indication of the considering borders of ISF. | The object has a free type of the geometrical parameters with a common restriction 2. | |
| The final complex shape of the area contains the space between and . | The object includes the properties of the interstitial fluid, and it determines the ranges of membrane surfaces. | |
| A part of corresponds to a post-synaptic neuronal bouton. | This object is obtained by omitting all surrounding and connecting bodies. | |
| The surface corresponds to the plasmatic membrane of a neuron. | This complex surface has the properties of the outer neuron membrane. In the considered model it is defined for a post-synaptic bouton. | |
| The surface separates the parts of a neuron. | In the model there is a border which confines the inner space of consideration. One surface is related with the outer neuronal membrane (see above) and another one divides the neuron localizing the post-synaptic bouton. | |
| The area on the post-synaptic membrane where GlyRs are supposed to be placed. | The place for possible GlyR localizations is indicated in Figure 3. Somewhere in the set of total locations the receptors can really exist. These locations are united by the indicated term. | |
| The area on the post-synaptic membrane, which is suitable for GlyRs placing, but this location contains no receptors. | As it was described above, there is an area where GlyRs may be localized but this location is not occupied by the receptors. |
| The Parameter | Description | Value | Source |
|---|---|---|---|
| Diffusion coefficient of Cl− | 2.03 × 10−9 m2/s | [38] | |
| Current of a single GlyR channel | 4.5 pA | [39] | |
| Conductivity of a single GlyR | 47.3 pS | [40] | |
| Elementary charge of Cl− | −1.6 × 10−19 C | Tabulated value | |
| Avogadro constant | 6.022 × 1023 mol−1 | Tabulated value | |
| Vacuum permittivity | 8.854 × 10−12 F⋅m−1 | Tabulated value | |
| Cl charge number | −1 | Tabulated value | |
| Faraday constant | 9.649 × 104 C⋅mol−1 | Tabulated value | |
| Universal gas constant | 8.31 J⋅K−1⋅mol−1 | Tabulated value | |
| Temperature | 37 °C | The temperature of a living tissue | |
| The potential generated by a GlyR single channel | −95.1 mV | Calculated value | |
| The membrane potential on the synaptic membrane | −55 mV −70 mV −89 mV | A variated parameter corresponding to the inside neuron conditions | |
| Relative permittivity of the medium at 37 °C | 72.91 | Tabulated value | |
| Maximal rate of KCC2 transport | 17.5 nmol/mg/min | [41] | |
| The level of KCC2 | 3.78 g/m2 | Calculated on the base of [42] | |
| Affinity of KCC2 to chloride | 6.8 mM | [43] | |
| Radius of the GlyR inside vestibule | 1.25 nm | Calculated on the base of pdb structures | |
| Radius of the GlyR synapse | 130 nm | [37] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nartsissov, Y.R.; Ivontsin, L.A. Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism. Mathematics 2023, 11, 2499. https://doi.org/10.3390/math11112499
Nartsissov YR, Ivontsin LA. Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism. Mathematics. 2023; 11(11):2499. https://doi.org/10.3390/math11112499
Chicago/Turabian StyleNartsissov, Yaroslav R., and Leonid A. Ivontsin. 2023. "Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism" Mathematics 11, no. 11: 2499. https://doi.org/10.3390/math11112499
APA StyleNartsissov, Y. R., & Ivontsin, L. A. (2023). Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism. Mathematics, 11(11), 2499. https://doi.org/10.3390/math11112499







