Development of CAVLAB—A Control-Oriented MATLAB Based Simulator for an Underground Coal Gasification Process
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Major Contributions and Overview
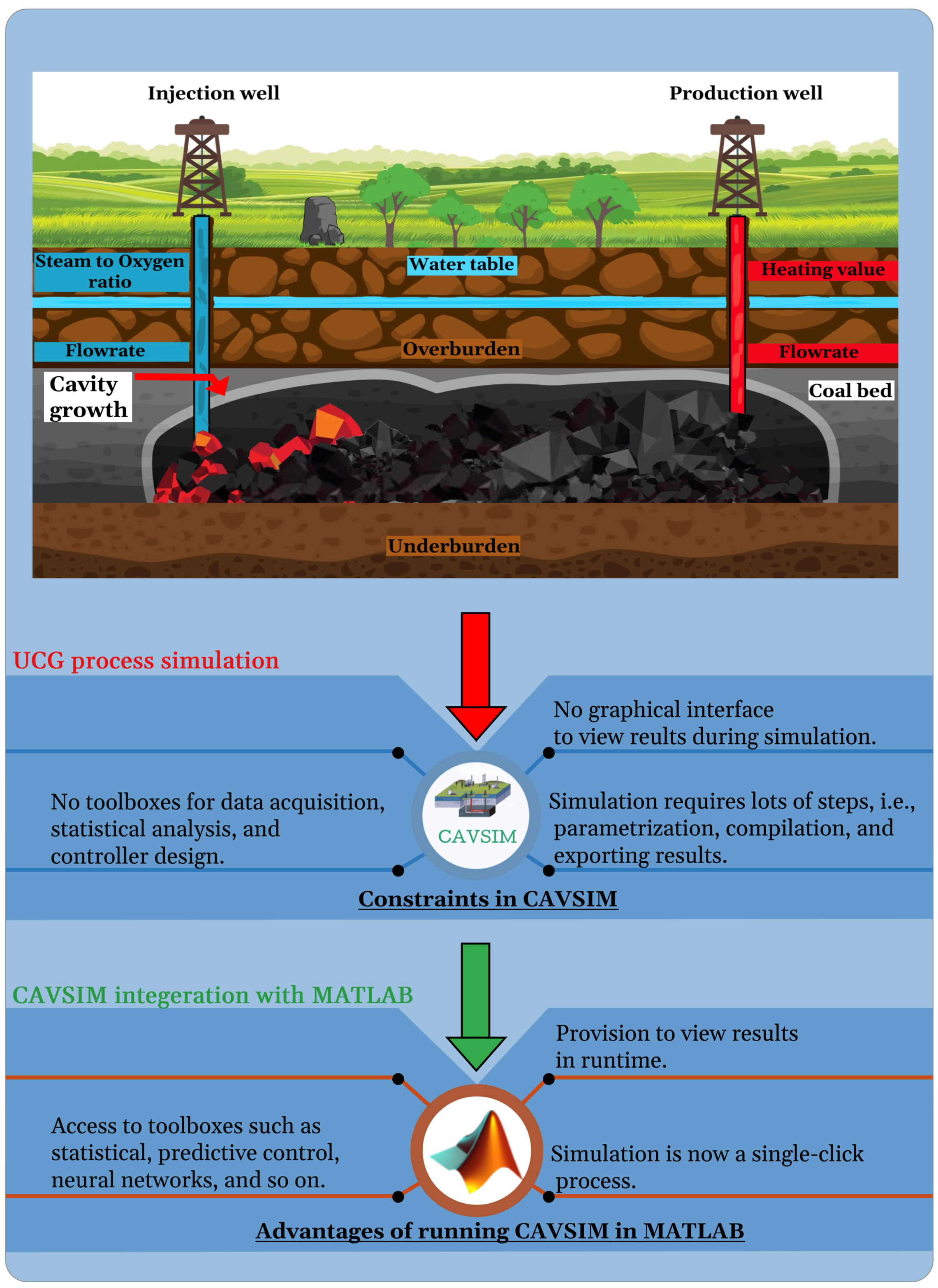
- The step-by-step development of CAVLAB—an augmented computational framework with a controllable structure for CAVSIM by integrating it with MATLAB. Beyond that, the additional structures appended to CAVSIM by virtue of integration constitute the following: ease of design and transmission of input signals; adjusting the plant’s parameters to simulate different variants of coal reactor is now just a one-click process; and provision to visualise the input and output data as the simulation is running.
- A case study of MPC design for UCG plant, demonstrating the ease of implementation and investigation of a UCG control design problem due to integration.
- CAVLAB has also been made available online, and to the best of our knowledge, this is the only software package that provides the capabilities of simulation, system identification, and optimal control of the UCG process.
2. Simulation Framework and Integration Scheme
2.1. Generalised Structure of UCG Simulation Framework
2.2. Simulation Framework Components: MATLAB and CAVSIM
2.2.1. MATLAB: Computational Platform
2.2.2. CAVSIM: UCG Simulator
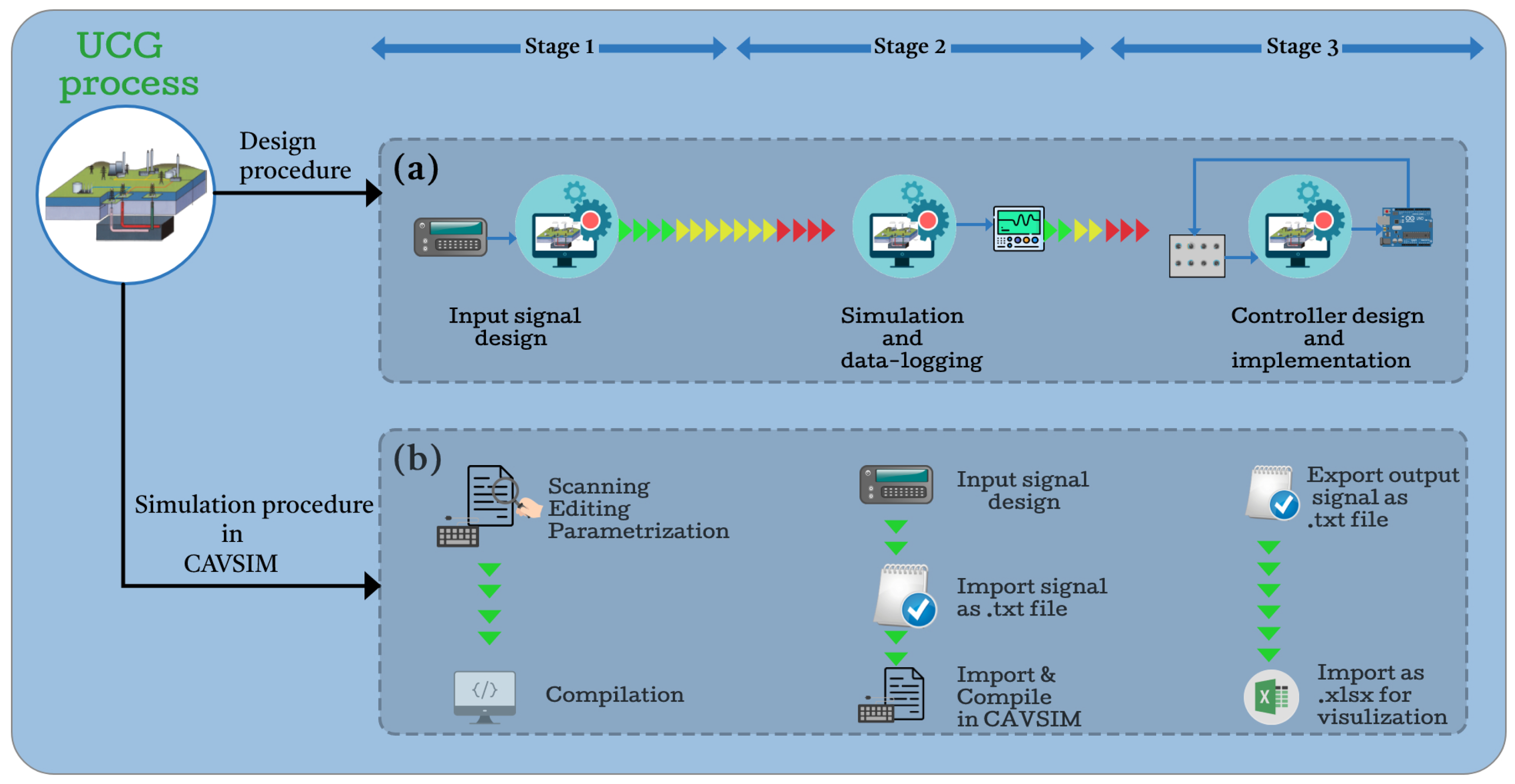
3. Working Pipeline of CAVSIM Integration with MATLAB
- 1.
- Compiler selection and Installation:
- (a)
- Two compilers need to be installed on the workstation:
- i.
- Intel parallel studio (IP) to compile FORTRAN files.
- ii.
- Microsoft visual studio (VS) to compile C/C++ files.
- (b)
- To make sure that compilers are correctly installed and detectable by MATLAB, use the following commands in the MATLAB command window:mex -setup Fortran % detects the IPmex -setup c % detects the VS
- 2.
- Code Transfer:
- (a)
- Since MATLAB can only call FORTRAN’s subroutines, any main function in FORTRAN’s files must be changed into a subroutine. Any input/output variables that MATLAB needs to send or receive from FORTRAN must be declared as the functional parameters of that subroutine.
- (b)
- Every FORTRAN file must be transferred to a separate file in MATLAB’s editor and should either be saved as a ’.f ’ or ’.for’ extension.
- (c)
- Every ’.f’ or ’.for’ file transferred in MATLAB in 2b should be compiled using the following command in the MATLAB command window:mex -c abc.f
- i.
- Where ’abc.f’ is the pseudonym of the FORTRAN file in MATLAB.
- ii.
- Additionally, ’c’ is the additional flag to force the compiler to only compile and not link with C-mex file; otherwise, MATLAB expects the name of C-mex file to be given.
- iii.
- Running the command in 2c should generate an ’abc.obj’ file that should have been saved in MATLAB’s working directory.
Once all the computational routines are successfully transferred and compiled, they need to be linked with the S-function via special gateway functions using ’.obj’ files. - 3.
- C-mex file preparation and compilation:A C-mex file is a collection of callback functions that SIMULINK invokes at each simulation timestep. Table 1 outlines the basic functionalities of the most important callback routines.
- (a)
- As gleaned from Table 1, the C-mex file should be edited according to the user’s specific needs, i.e., the total number of plant’s inputs and outputs, their sizes, and data types should be appropriately declared to avoid compatability issues.
- (b)
- Once the C-file has been prepared, it must be saved with a ’.c’ extension, i.e., ’xyz.c’, and compiled using the following command in MATLAB’s command window:mex -c xyz.c
- (c)
- The ’abc.obj’ file generated in 2(c)iii is used to link the FORTRAN’s computational routines with the C-mex file compiled in 3b using the following command:mex(abc.obj,xyz.c)
- i.
- If there is more than one FORTRAN computational routine, they can be compiled in a similar fashion using the following command:mex(abc1.obj,abc2.obj,xyz.c)
4. Challenges and Solutions
4.1. Pre-Integration Challenges
- Col. 1: Blank, or a ’c’ or ’*’ for comments.
- Col. 1–5: Statement label.
- Col. 6: Continuation of the previous line.
- Col. 7–72: Statement.
- Col. 73–80: Sequence number.
4.2. Post-integration Challenges
Missing Libraries
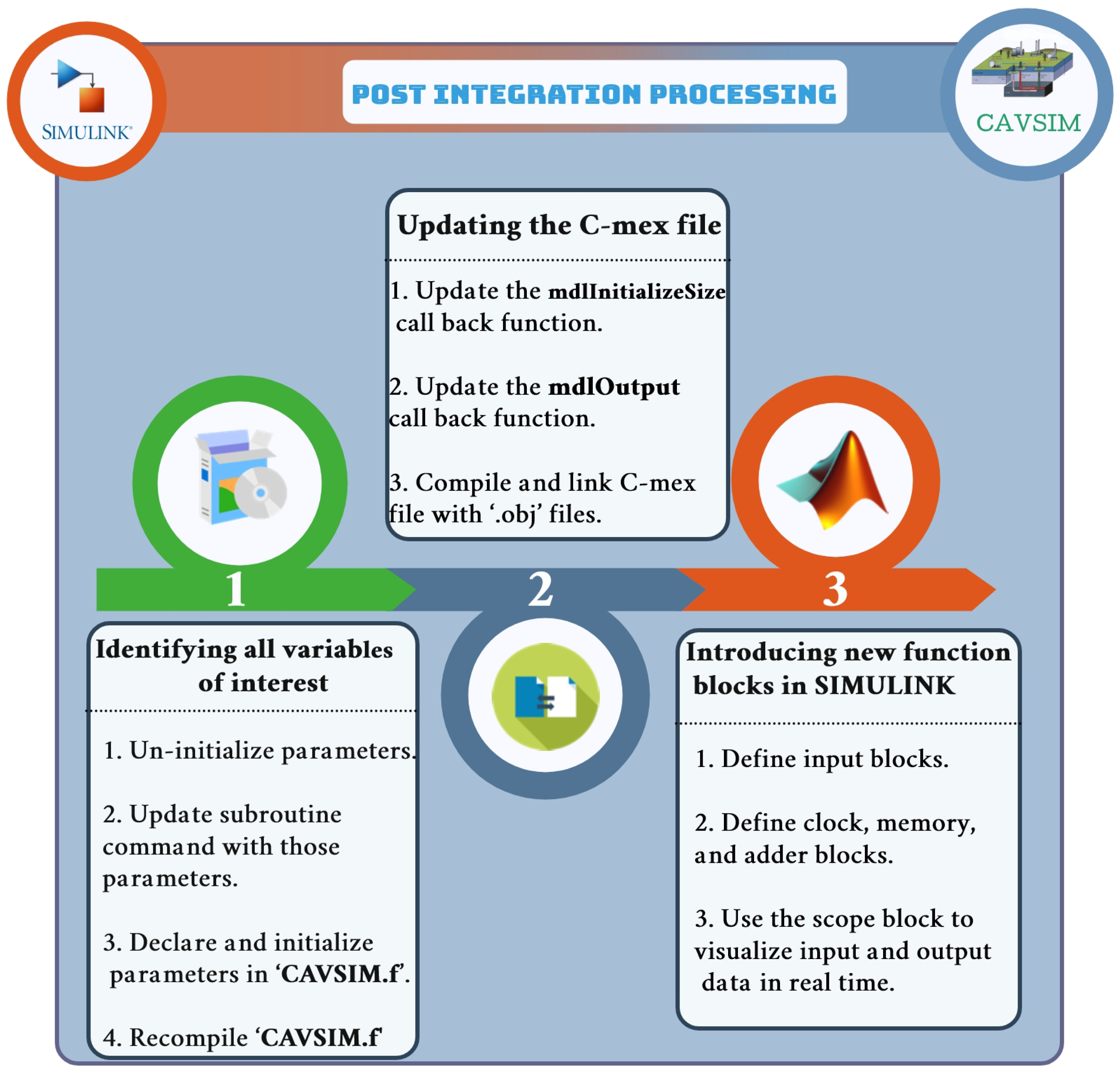
5. Post-Integration Processing
5.1. Asynchronous Clocks
5.2. Input Output In-Dependency
- 1.
- Identifying all the variables of interest:
- (a)
- This step involves (1) figuring out the parameterisable quantities that define the coal bed properties, process inputs, and outputs defined in CAVSIM; (2) locating their positions in the computational routine, and (3) initialising them. This step strips the CAVSIM of the capacity to initialise or update the variables from within.
- (b)
- Adding as many function parameters to the CAVSIM.f file’s subroutine command as the number of variables uninitialised in 1a. Doing so allows the user to give input to and retrieve output from CAVSIM using MATLAB.
- (c)
- Declaring new variables that are to be taken in from MATLAB via a subroutine command in the CAVSIM.f file
- (d)
- Re-initialising all the variables from 1a to the corresponding function parameters as newly defined in the subroutine command. This makes sure that all variables taken in now from MATLAB are mapped to their corresponding variables in CAVSIM.
- (e)
- Re-compiling the cavsim.f file as illustrated in 2c.
- 2.
- Updating the C-mex file:The following updates are necessary for the C-mex file to create a bi-directional channel for the data to be transferred between MATLAB and CAVSIM.
- (a)
- Updating the mdlInitializeSize call back function by declaring as many variables as identified in 1a. This step not only declares the new variables but also sets the data type, dimension, etc. Therefore, care must be exercised that all features defined here should be identical to 1d to avoid compatibility issues.
- (b)
- Updating the mdlOutput callback function by introducing as many variables as identified in 1a. This is a callback method that calls the main subroutine whilst transferring the input and output data.
- (c)
- Compiling and linking the newly updated C-mex file with all other ”.obj” files as illustrated in 3. This results in the upgrading of the S-function block with the associated input and output ports. The order of the input and the output channels of the S-function block is similar to the order of the variables defined in the C-mex and CAVSIM.f files, which must be the same as well.
- 3.
- Introducing new function blocks in SIMULINK:The previous steps taken have developed the desired interface between CAVSIM and MATLAB through which data from MATLAB can be mapped onto the corresponding variables in CAVSIM. However, for plant parameters to be directly updatable from SIMULINK, some additional blocks need to be introduced.
- (a)
- Define input blocks
- i
- The input can either be generated using SIMULINK’s source block or be imported from the workspace as a MATLAB timeseries object.
- (b)
- Define clock, memory, and adder blocks to give simulation time and time-step information from SIMULINK.
- (c)
- Use the scope block to visualise input and output data in real time.
- (d)
- Attach all these blocks to their respective ports of S-function as identified in 2c.
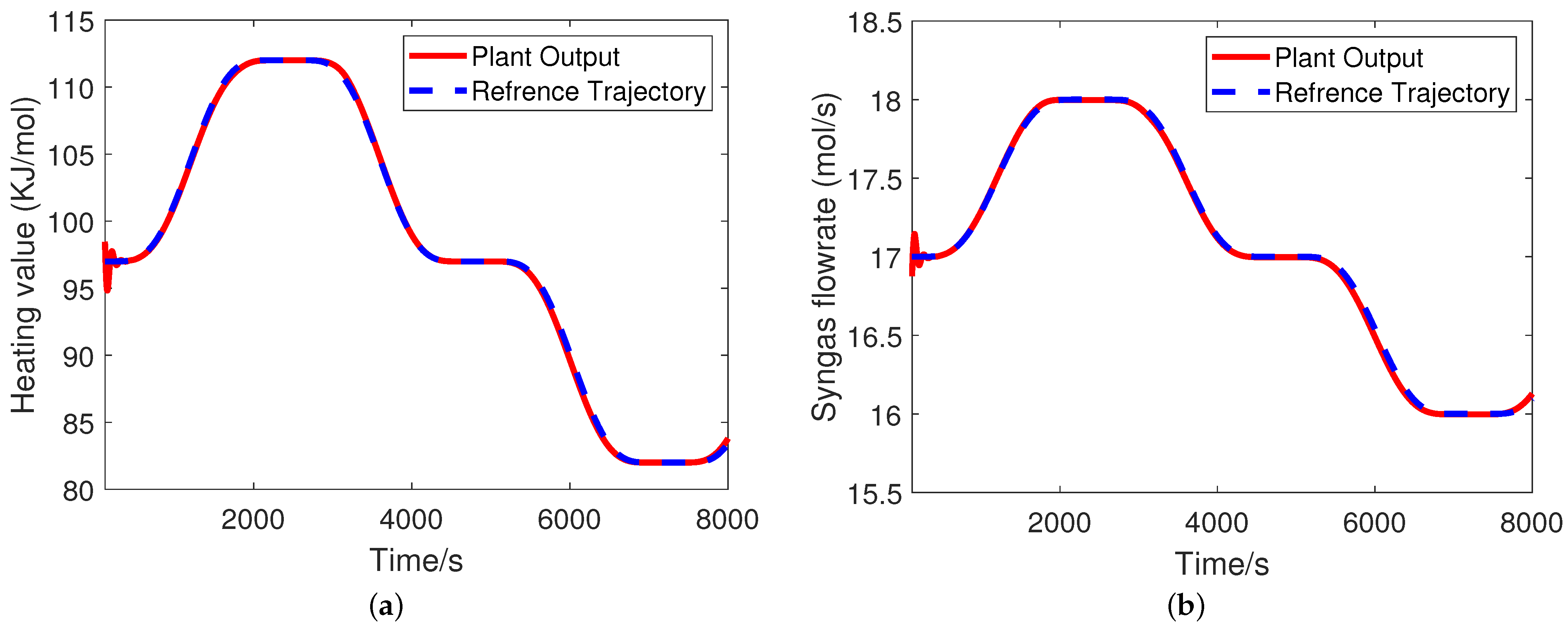
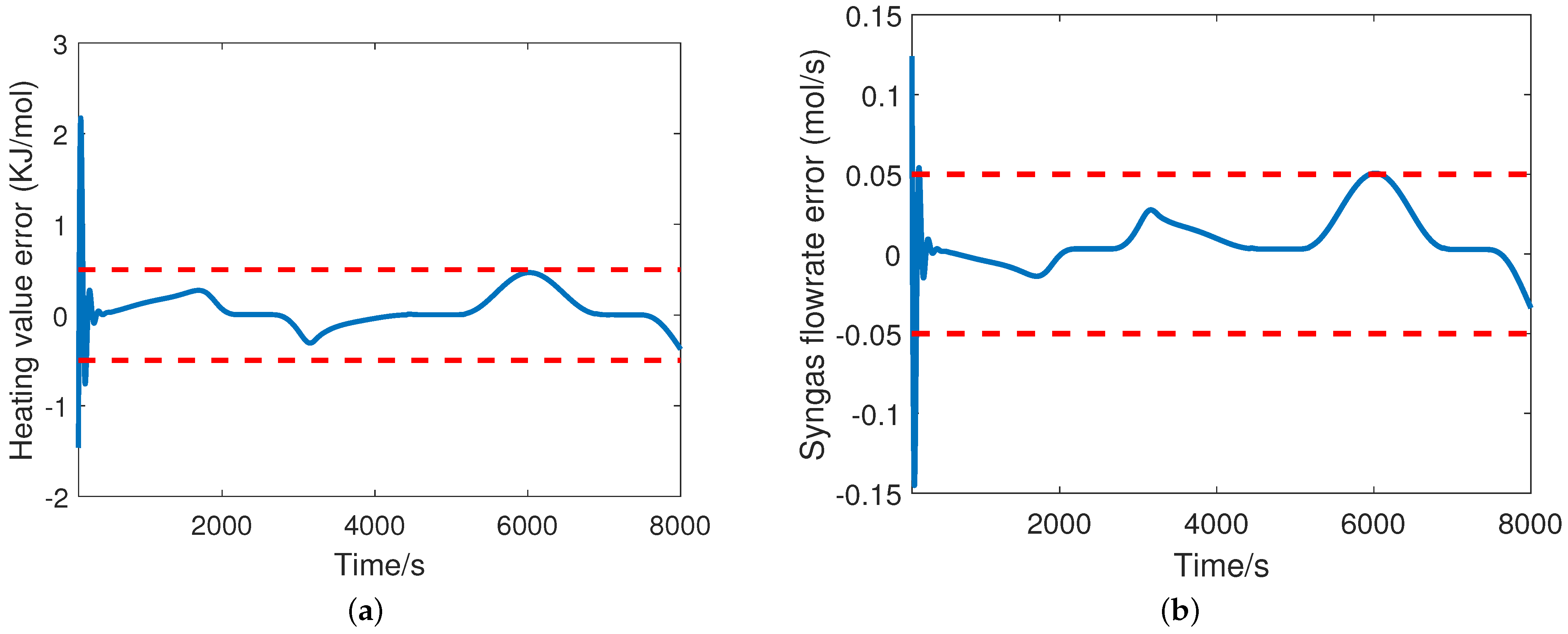
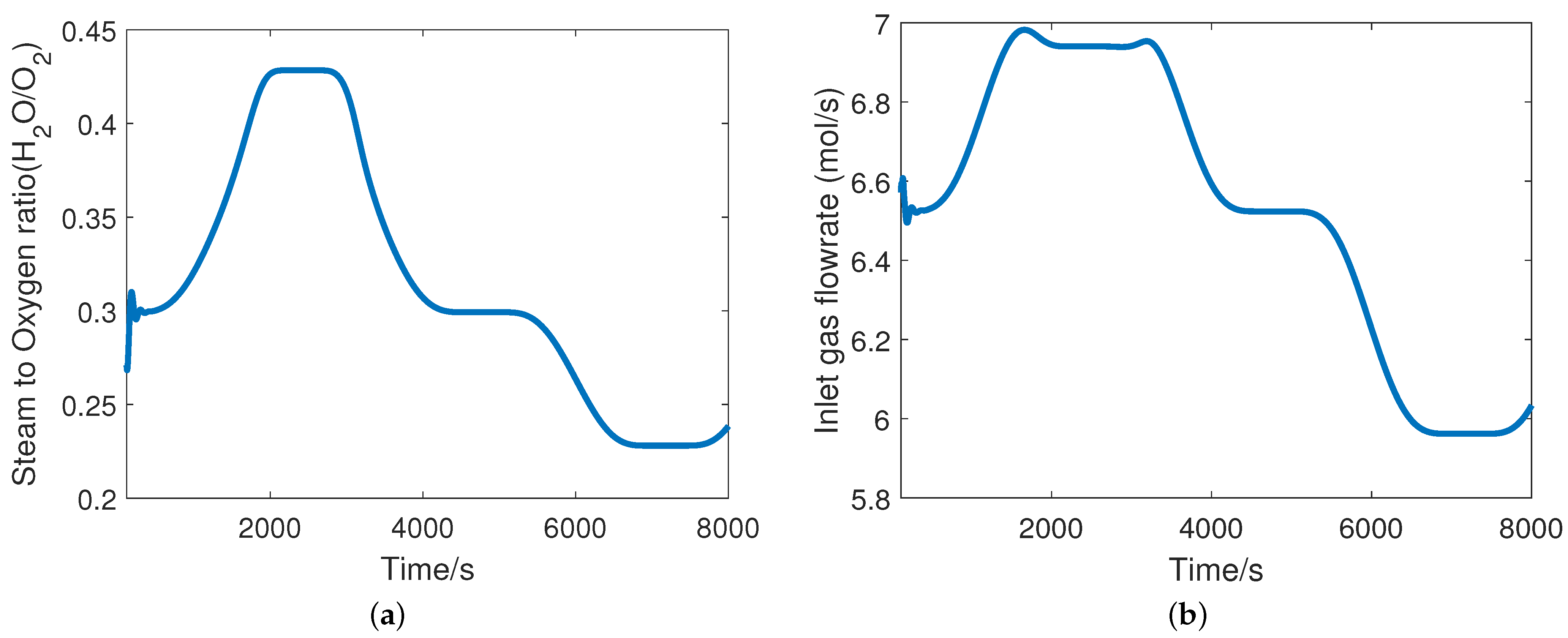
6. CAVLAB Testing
7. Case Study: MPC Design for UCG Plant Using MATLAB’s Toolbox
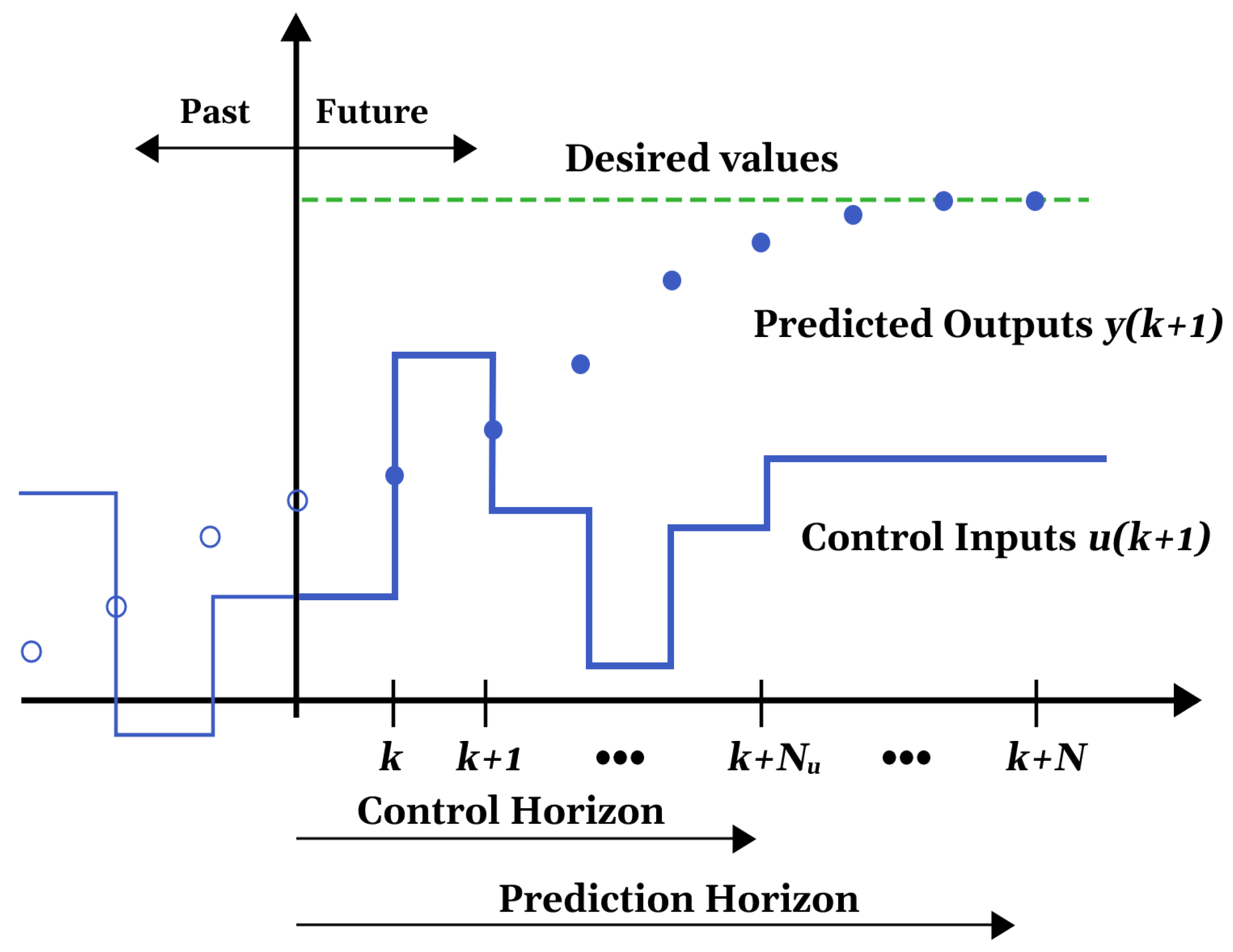
7.1. MPC Problem Formulation
7.2. MPC Implementation
- 1.
- The first step in designing an MPC controller in MATLAB is to define the plant, which is the mathematical model of the system that is to be controlled. This can be done by creating a SIMULINK model or using system identification techniques to obtain a mathematical model from input-output data. The plant model should capture the dynamic behaviour of the system to be controlled.
- 2.
- The second step is to specify the type of input signals that will be used in the MPC controller, such as setpoints, disturbances, and measured outputs.
- 3.
- This step involves defining the prediction and control horizons, constraints on the input and output signals, and the cost function.
- 4.
- Once the MPC object is created, a closed-loop simulation is performed to evaluate the performance of the MPC controller. This involves simulating the system’s response to different input signals and comparing it with the desired response.
- 5.
- This step involves adjusting the tuning parameters of the MPC controller, such as the weights in the cost function and the prediction horizon. The simulation results are used to evaluate the controller’s performance, and the tuning parameters are adjusted iteratively until the desired performance is achieved.
- 6.
- The controller takes measurements from the plant model and calculates the control inputs that optimize the system’s performance. The simulation results are used to evaluate the controller’s performance, and the tuning parameters are adjusted if necessary to maintain optimal performance.
8. Extension in Research Scope of UCG
8.1. Optimal Resource Utilisation
8.2. Data-Driven Modelling
9. Conclusions
- Name of simulator: CAVLAB.slx
- Software used: MATLAB 2019b
- Availability: The whole package, along with instructions, is available at github (accessed on 1 March 2023): https://github.com/Hilberto-inf/CAVLAB–UCG-process-simulator.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, L.; Chen, S.; Chen, Y.; Chen, Z.; Sun, F.; Dong, X.; Wu, K. Underground coal gasification modelling in deep coal seams and its implications to carbon storage in a climate-conscious world. Fuel 2023, 332, 126016. [Google Scholar] [CrossRef]
- Klebingat, S.; Kempka, T.; Schulten, M.; Azzam, R.; Fernández-Steeger, T.M. Innovative thermodynamic underground coal gasification model for coupled synthesis gas quality and tar production analyses. Fuel 2016, 183, 680–686. [Google Scholar] [CrossRef]
- Ammarullah, M.I.; Hartono, R.; Supriyono, T.; Santoso, G.; Sugiharto, S.; Permana, M.S. Polycrystalline Diamond as a Potential Material for the Hard-on-Hard Bearing of Total Hip Prosthesis: Von Mises Stress Analysis. Biomedicines 2023, 11, 951. [Google Scholar] [CrossRef] [PubMed]
- Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Wibowo, D.B.; Kurdi, O.; Tauviqirrahman, M.; Jamari, J. Minimizing Risk of Failure from Ceramic-on-Ceramic Total Hip Prosthesis by Selecting Ceramic Materials Based on Tresca Stress. Sustainability 2022, 14, 13413. [Google Scholar] [CrossRef]
- Ammarullah, M.I.; Afif, I.Y.; Maula, M.I.; Winarni, T.I.; Tauviqirrahman, M.; Akbar, I.; Basri, H.; van der Heide, E.; Jamari, J. Tresca Stress Simulation of Metal-on-Metal Total Hip Arthroplasty during Normal Walking Activity. Materials 2021, 14, 7554. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Li, Y.; Meng, D.; Wang, X. Stiffness Modeling and Dynamics Co-Modeling for Space Cable-Driven Linkage Continuous Manipulators. Mathematics 2023, 11, 1874. [Google Scholar] [CrossRef]
- Thorsness, C.B.; Britten, J.A. CAVISM User Manual. 1989. Available online: https://doi.org/10.2172/6307133 (accessed on 27 April 2023).
- Javed, S.B.; Uppal, A.A.; Bhatti, A.I.; Samar, R. Prediction and parametric analysis of cavity growth for the underground coal gasification project Thar. Energy 2019, 172, 1277–1290. [Google Scholar] [CrossRef]
- Javed, S.B. Cavity Prediction and Multi-variable Control of Underground Coal Gasification Process. Ph.D. Thesis, Capital University of Science and Technology, Islamabad. Available online: https://cust.edu.pk/static/uploads/2021/09/PhD-EE-Thesis-Syed-Bilal-Javed.pdf (accessed on 24 May 2023).
- Javed, S.B.; Uppal, A.A.; Samar, R.; Bhatti, A.I. Design and implementation of multi-variable H∞ robust control for the underground coal gasification project Thar. Energy 2021, 216, 119000. [Google Scholar] [CrossRef]
- Javed, S.B.; Utkin, V.I.; Uppal, A.A.; Samar, R.; Bhatti, A.I. Data-Driven Modeling and Design of Multivariable Dynamic Sliding Mode Control for the Underground Coal Gasification Project Thar. IEEE Trans. Control Syst. Technol. 2021, 30, 153–165. [Google Scholar] [CrossRef]
- Prakoso, A.T.; Basri, H.; Adanta, D.; Yani, I.; Ammarullah, M.I.; Akbar, I.; Ghazali, F.A.; Syahrom, A.; Kamarul, T. The Effect of Tortuosity on Permeability of Porous Scaffold. Biomedicines 2023, 11, 427. [Google Scholar] [CrossRef]
- Jamari, J.; Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Permana, M.S.; Winarni, T.I.; van der Heide, E. Adopted walking condition for computational simulation approach on bearing of hip joint prosthesis: Review over the past 30 years. Heliyon 2022, 8, e12050. [Google Scholar] [CrossRef] [PubMed]
- Thorsness, C.B.; Rozsa, R.B. In-Situ Coal Gasification: Model Calculations and Laboratory Experiments. SPE J. 1978, 18, 105–116. [Google Scholar] [CrossRef]
- Abdel-Hadi, E.A.A.; Hsu, T.R. Computer Modeling of Fixed Bed Underground Coal Gasification Using the Permeation Method. J. Energy Res. Technol. 1987, 109, 11–20. [Google Scholar] [CrossRef]
- Uppal, A.A.; Bhatti, A.I.; Aamir, E.; Samar, R.; Khan, S.A. Control oriented modeling and optimization of one dimensional packed bed model of underground coal gasification. J. Process Control 2014, 24, 269–277. [Google Scholar] [CrossRef]
- Żogała, A. Critical Analysis of Underground Coal Gasification Models. Part I: Equilibrium Models – Literary Studies. J. Sustain. Min. 2014, 13, 22–28. [Google Scholar] [CrossRef]
- Perkins, G.; Sahajwalla, V. Steady-State Model for Estimating Gas Production from Underground Coal Gasification. Energy Fuels 2008, 22, 3902–3914. [Google Scholar] [CrossRef]
- 2009. Available online: https://www.cfd.com.au/cfd_conf09/PDFs/196LUO.pdf (accessed on 2 September 2022).
- Seifi, M.; Abedi, J.; Chen, Z. The Analytical Modeling of Underground Coal Gasification through the Application of a Channel Method. Energy Sources Part A 2013, 35, 1717–1727. [Google Scholar] [CrossRef]
- Massaquoi, J.G.M.; Riggs, J.B. Mathematical modeling of combustion and gasification of a wet coal slab—I: Model development and verification. Chem. Eng. Sci. 1983, 38, 1747–1756. [Google Scholar] [CrossRef]
- Perkins, G.; Sahajwalla, V. A Mathematical Model for the Chemical Reaction of a Semi-infinite Block of Coal in Underground Coal Gasification. Energy Fuels 2005, 19, 1679–1692. [Google Scholar] [CrossRef]
- Samdani, G.; Aghalayam, P.; Ganesh, A.; Sapru, R.K.; Lohar, B.L.; Mahajani, S. A process model for underground coal gasification—Part-II growth of outflow channel. Fuel 2016, 181, 587–599. [Google Scholar] [CrossRef]
- Biezen, E.N.J.; Bruining, J.; Molenaar, J. An Integrated 3D Model for Underground Coal Gasification. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 22 October 1995. [Google Scholar] [CrossRef]
- Nitao, J.J.; Buscheck, T.A.; Ezzedine, S.M.; Friedmann, S.J.; Camp, D.W. An Integrated 3-D UCG Model for Predicting Cavity Growth, Product Gas, and Interactions with the Host Environment. 2017. Available online: https://www.osti.gov/servlets/purl/1573942 (accessed on 27 April 2023).
- Hasse, C.; Debiagi, P.; Wen, X.; Hildebrandt, K.; Vascellari, M.; Faravelli, T. Advanced modeling approaches for CFD simulations of coal combustion and gasification. Prog. Energy Combust. Sci. 2021, 86, 100938. [Google Scholar] [CrossRef]
- Tauviqirrahman, M.; Jamari, J.; Susilowati, S.; Pujiastuti, C.; Setiyana, B.; Pasaribu, A.H.; Ammarullah, M.I. Performance Comparison of Newtonian and Non-Newtonian Fluid on a Heterogeneous Slip/No-Slip Journal Bearing System Based on CFD-FSI Method. Fluids 2022, 7, 225. [Google Scholar] [CrossRef]
- Putra, R.U.; Basri, H.; Prakoso, A.T.; Chandra, H.; Ammarullah, M.I.; Akbar, I.; Syahrom, A.; Kamarul, T. Level of Activity Changes Increases the Fatigue Life of the Porous Magnesium Scaffold, as Observed in Dynamic Immersion Tests, over Time. Sustainability 2023, 15, 823. [Google Scholar] [CrossRef]
- Mahseredjian, J.; Benmouyal, G.; Lombard, X.; Zouiti, M.; Bressac, B.; Gerin-Lajoie, L. A link between EMTP and MATLAB for user-defined modeling. IEEE Trans. Power Deliv. 1998, 13, 667–674. [Google Scholar] [CrossRef]
- Ahsan, M.; Saramaki, T. Significant improvements in translating the Parks-McClellan Algorithm from its FORTRAN code to its corresponding MATLAB code. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 289–292. [Google Scholar] [CrossRef]
- Bagal, K.; Kadu, C.; Parvat, B.; Vikhe, P. PLC Based Real Time Process Control Using SCADA and MATLAB. In Proceedings of the 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 16–18 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ivan, G.; Nikolay, S.; Vladislav, L.; Andrei, P. Solving of Mathematical Problems in the C# Based on Integration with MATLAB. In Proceedings of the 2020 Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 14–15 May 2020; pp. 432–435. [Google Scholar] [CrossRef]
- Sokos, E.N.; Zahradnik, J. ISOLA a Fortran code and a Matlab GUI to perform multiple-point source inversion of seismic data. Comput. Geosci. 2008, 34, 967–977. [Google Scholar] [CrossRef]
- Andersson, C.; Führer, C.; Åkesson, J. Assimulo: A unified framework for ODE solvers. Math. Comput. Simul. 2015, 116, 26–43. [Google Scholar] [CrossRef]
- Lee, S.K.; Kim, H.J.; Song, Y.; Lee, C.K. MT2DInvMatlab—A program in MATLAB and FORTRAN for two-dimensional magnetotelluric inversion. Comput. Geosci. 2009, 35, 1722–1734. [Google Scholar] [CrossRef]
- Quaglia, D.; Muradore, R.; Bragantini, R.; Fiorini, P. A SystemC/Matlab co-simulation tool for networked control systems. Simul. Model. Pract. Theory 2012, 23, 71–86. [Google Scholar] [CrossRef]
- Hatledal, L.I.; Chu, Y.; Styve, A.; Zhang, H. Vico: An entity-component-system based co-simulation framework. Simul. Model. Pract. Theory 2021, 108, 102243. [Google Scholar] [CrossRef]
- Dehghanimohammadabadi, M.; Keyser, T.K. Intelligent simulation: Integration of SIMIO and MATLAB to deploy decision support systems to simulation environment. Simul. Model. Pract. Theory 2017, 71, 45–60. [Google Scholar] [CrossRef]
- Wallmark, O.; Bitsi, K. Iron-Loss Computation Using Matlab and Comsol Multiphysics. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; Volume 1, pp. 916–920. [Google Scholar] [CrossRef]
- Benbarrowes. f2matlab. 2022. Available online: https://github.com/benbarrowes/f2matlab (accessed on 27 April 2023).
- Tauviqirrahman, M.; Ammarullah, M.I.; Jamari, J.; Saputra, E.; Winarni, T.I.; Kurniawan, F.D.; Shiddiq, S.A.; van der Heide, E. Analysis of contact pressure in a 3D model of dual-mobility hip joint prosthesis under a gait cycle. Sci. Rep. 2023, 13, 3564. [Google Scholar] [CrossRef] [PubMed]
- Nitao, J.J.; Camp, D.W.; Buscheck, T.A.; White, J.A.; Burton, G.C.; Wagoner, J.L.; Chen, M. Progress on a New Integrated 3-D UCG Simulator and its Initial Application. In Proceedings of the International Pittsburgh Coal Conference, Pittsburgh, PA, USA, 13–15 September 2011. [Google Scholar]
- Varga, A. A Descriptor Systems Toolbox for MATLAB. In Proceedings of the CACSD, Conference Proceedings, IEEE International Symposium on Computer-Aided Control System Design (Cat. No.00TH8537), Anchorage, AK, USA, 25–27 September 2000; pp. 150–155. [Google Scholar] [CrossRef]
- Renes, W.; Vanbegin, M.; Van Dooren, P.; Beckers, J. The MATLAB Gateway Compiler. A Tool For Automatic Linking of Fortran Routines to MATLAB. IFAC Proc. Vol. 1991, 24, 95–100. [Google Scholar] [CrossRef]
- fpscomp. 2022. Available online: https://www.intel.com/content/www/us/en/develop/documentation/fortran-compiler-oneapi-dev-guide-and-reference/top/compiler-reference/compiler-options/compatibility-options/fpscomp.html (accessed on 27 April 2023).
- Nordli, A.S.; Khawaja, H. Comparison of Explicit Method of Solution for CFD Euler Problems using MATLAB® and FORTRAN 77. Int. J. Multiphys. 2019, 13, 203–214. [Google Scholar]
- Jamari, J.; Ammarullah, M.I.; Saad, A.P.M.; Syahrom, A.; Uddin, M.; van der Heide, E.; Basri, H. The Effect of Bottom Profile Dimples on the Femoral Head on Wear in Metal-on-Metal Total Hip Arthroplasty. J. Funct. Biomater. 2021, 12, 38. [Google Scholar] [CrossRef] [PubMed]
- Jamari, J.; Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Prakoso, A.T.; Basri, H.; van der Heide, E. Computational Contact Pressure Prediction of CoCrMo, SS 316L and Ti6Al4V Femoral Head against UHMWPE Acetabular Cup under Gait Cycle. J. Funct. Biomater. 2022, 13, 64. [Google Scholar] [CrossRef]
- Kumar, A.S.; Ahmad, Z. Model Predictive Control (MPC) and Its Current Issues in Chemical Engineering. Chem. Eng. Commun. 2012, 199, 472–511. [Google Scholar] [CrossRef]
- Ali, S.U.; Waqar, A.; Aamir, M.; Qaisar, S.M.; Iqbal, J. Model predictive control of consensus-based energy management system for DC microgrid. PLoS ONE 2023, 18, e0278110. [Google Scholar] [CrossRef]
- Ullo, J. Computational challenges in the search for and production of hydrocarbons. Sci. Model. Simul. 2008, 15, 313–337. [Google Scholar] [CrossRef]
- Nourozieh, H.; Kariznovi, M.; Chen, Z.; Abedi, J. Simulation Study of Underground Coal Gasification in Alberta Reservoirs: Geological Structure and Process Modeling. Energy Fuels 2010, 24, 3540–3550. [Google Scholar] [CrossRef]
- Jowkar, A.; Sereshki, F.; Najafi, M. Numerical simulation of UCG process with the aim of increasing calorific value of syngas. Int. J. Coal Sci. Technol. 2020, 7, 196–207. [Google Scholar] [CrossRef]
- Żogała, A.; Janoszek, T. CFD simulations of influence of steam in gasification agent on parameters of UCG process. J. Sustain. Min. 2015, 14, 2–11. [Google Scholar] [CrossRef]
- Haddadi, B.; Jordan, C.; Harasek, M. Cost efficient CFD simulations: Proper selection of domain partitioning strategies. Comput. Phys. Commun. 2017, 219, 121–134. [Google Scholar] [CrossRef]




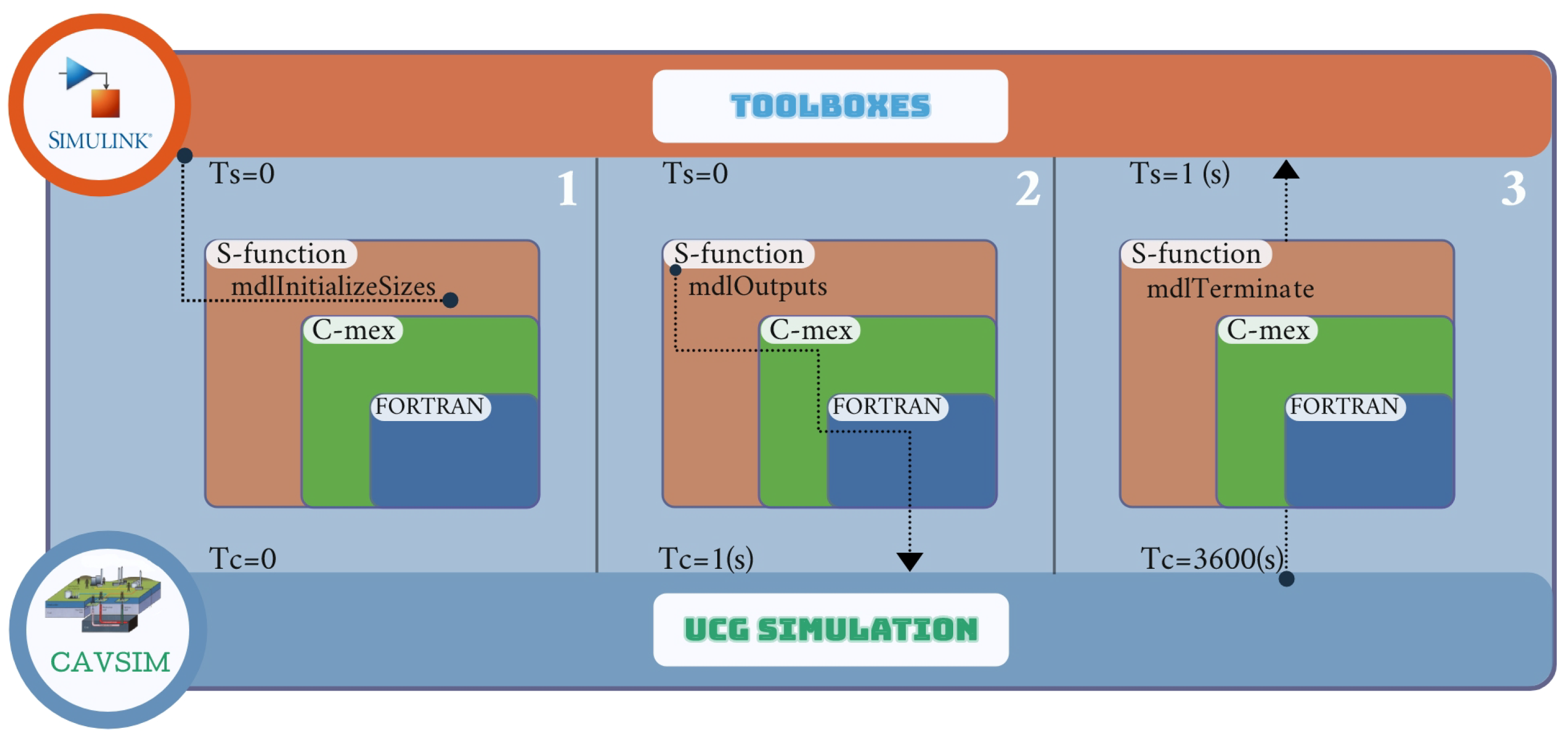





| Callback Function | Description |
|---|---|
| mdlInitializeSizes | Allocates the total number of input and output ports, their sizes, and other parameters of the S-function. |
| mdlInitializeSampleTimes | Specifies the time samples at which the S-function is invoked. |
| mdlOutputs | Calls and runs the FORTRAN computational subroutine. |
| mdlTerminate | Perform any actions required at termination of the simulation. |
| Pre-Integration Challenges | Post-Integration Challenges | Remarks |
|---|---|---|
| Choosing the right MATLAB API to interface with FORTRAN subroutines | Optimising the performance and accuracy of the integration | Different MATLAB APIs have varying pros and cons depending on the problem type and complexity. For instance, the FORTRAN MEX API enables FORTRAN subroutines to be accessed by MATLAB functions, while the FORTRAN Engine API allows running and evaluating MATLAB functions from FORTRAN programs. |
| Writing a MEX file to call FORTRAN routines from MATLAB | Debugging and testing the integrated code | Creating a MEX file involves adhering to some specific rules and conventions for compiling and linking the FORTRAN code with MATLAB. External tools or libraries, such as gdb or f2py, may be needed for debugging and testing the integrated code. |
| Converting MATLAB data types to FORTRAN data types | Updating and maintaining the code for compatibility and functionality | MATLAB and FORTRAN differ in data types and memory layouts, which may lead to errors or inefficiencies if not managed properly. For instance, MATLAB uses column-major order for matrices, while FORTRAN uses row-major order. The code may need to be updated and maintained according to changes in MATLAB or FORTRAN versions, libraries, or platforms. |
| Learning the syntax and features of FORTRAN | Comparing the advantages and disadvantages of MATLAB and FORTRAN | FORTRAN is a lower-level language than MATLAB, which may offer more control over memory management, data structures, loops, etc. However, it may also lack built-in functions, libraries, or tools for matrix computations, symbolic manipulations, or visualisation. |
| Finding reliable and compatible FORTRAN libraries or routines | Dealing with potential errors or bugs in FORTRAN libraries or routines | FORTRAN has a long history and legacy of numerical software development, which means there may be many available libraries or routines for various problems. However, some of them may be outdated, incompatible, or poorly documented. Some of them may also have errors or bugs that are hard to detect or fix. |
| Plant Inputs | Plant Outputs |
|---|---|
| Steam to oxygen ratio | Heating value (KJ/mol) |
| Inlet gas flowrate (mol/s) | Flowrate (mol/s) |
| Tool | Formulas | Values |
|---|---|---|
| RMSE | heating value = 0.23 flowrate = 0.02 | |
| MAE | heating value = 0.13 flowrate = 0.012 | |
| CE | heating value = 28.48 flowrate = 580.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Javed, S.B.; Uppal, A.A.; Iqbal, J. Development of CAVLAB—A Control-Oriented MATLAB Based Simulator for an Underground Coal Gasification Process. Mathematics 2023, 11, 2493. https://doi.org/10.3390/math11112493
Ahmed A, Javed SB, Uppal AA, Iqbal J. Development of CAVLAB—A Control-Oriented MATLAB Based Simulator for an Underground Coal Gasification Process. Mathematics. 2023; 11(11):2493. https://doi.org/10.3390/math11112493
Chicago/Turabian StyleAhmed, Afaq, Syed Bilal Javed, Ali Arshad Uppal, and Jamshed Iqbal. 2023. "Development of CAVLAB—A Control-Oriented MATLAB Based Simulator for an Underground Coal Gasification Process" Mathematics 11, no. 11: 2493. https://doi.org/10.3390/math11112493
APA StyleAhmed, A., Javed, S. B., Uppal, A. A., & Iqbal, J. (2023). Development of CAVLAB—A Control-Oriented MATLAB Based Simulator for an Underground Coal Gasification Process. Mathematics, 11(11), 2493. https://doi.org/10.3390/math11112493








