The Square of Some Generalized Hamming Graphs

Abstract

In this paper, we study the square of generalized Hamming graphs by the properties of abelian groups, and characterize some isomorphisms between the square of generalized Hamming graphs and the non-complete extended p-sum of complete graphs. As applications, we determine the eigenvalues of the square of some generalized Hamming graphs.

1. Introduction

All graphs considered in this paper are finite, undirected and simple. Let G be a graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. The adjacency matrix of G of order n, denoted by $A\left(G\right)$, is a $0-1$ matrix of order n with entries $a_{ij}$ such that $a_{ij}=1$ if the ith and jth vertices are adjacent and $a_{ij}=0$ otherwise. The eigenvalues of $A\left(G\right)$ are called the eigenvalues of G, and the collection of eigenvalues of G with multiplicities is called the spectrum of G. A graph is integral [1,2] if all its eigenvalues are integers.

Let $m_1,\dots ,m_r$ be positive integers and $D=\{d_1,\dots ,d_s\}$ be a set of integers with $1\le d_i\le r$ for each i. The generalized Hamming graph $H(m_1,\dots ,m_r;D)$ is a graph with a vertex set of the abelian group ${\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$ such that two elements of ${\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$ are adjacent if and only if the Hamming distance between them belongs to D, where the Hamming distance between the two elements $\mathbf{x}=(x_1,\dots ,x_r)$ and $\mathbf{y}=(y_1,\dots ,y_r)$ of ${\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$ is defined as $d(\mathbf{x},\mathbf{y})=|\{i:x_i\ne y_i,1\le i\le r\}|$. The Hamming weight of $\mathbf{x}$ is defined to be $w\left(\mathbf{x}\right)=d(\mathbf{x},\mathbf{0})$, where $\mathbf{0}=(0,\dots ,0)$ is the identity element of the abelian group ${\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$. The Hamming weight $w\left(\beta \right)$ of $\beta =({\beta }_1,\dots ,{\beta }_n)\in {\mathbb{Z}}_2^n$ is similarly understood and easily seen to be equal to ${\sum }_{i=1}^n{\beta }_i$.

Hamming graphs are an important class of Cayley graphs [3,4,5]. These graphs have been and still are studied intensively because of their symmetry properties and their connections to communication networks, quantum physics, coding theory, and other areas (see, e.g., [3,6,7]). However, only few results on generalized Hamming graphs have been obtained so far. In 2010, Sander studied the eigenspaces of $H(p_1,\dots ,p_r;\{1,\dots ,d\})$ for distinct primes $p_1,\dots ,p_r$ [8]. In the same year, Klotz and Sander observed that $H(m_1,\dots ,m_r;D)$ is an integral Cayley graph [9]. In 2022, Li, Liu, and Zhang provided a few sufficient conditions for the existence of perfect state transfer in generalized hamming graphs [7].

Let $G_1,\dots ,G_n$ be graphs and $\varnothing \ne B\subseteq {\mathbb{Z}}_2^n\backslash \left\{(0,0,\dots ,0)\right\}$, where as usual ${\mathbb{Z}}_2=\{0,1\}$ denotes the group of integers modulo 2. The non-complete extended p-sum (NEPS) of $G_1,\dots ,G_n$ with basis B, denoted by $\mathrm{NEPS}(G_1,\dots ,G_n;B)$, is the graph with vertex set $V\left(G_1\right)\times \cdots \times V\left(G_n\right)$ such that two vertices $(x_1,\dots ,x_n)$ and $(y_1,\dots ,y_n)$ are adjacent if and only if there exists $\beta =({\beta }_1,\dots ,{\beta }_n)\in B$ such that $x_i=y_i$ when ${\beta }_i=0$, and $x_i$ is adjacent to $y_i$ in $G_i$ when ${\beta }_i=1$. We call $G_1,\dots ,G_n$ the factors of $\mathrm{NEPS}(G_1,\dots ,G_n;B)$. This notion is a generalization of several graph operations such as tensor product, Cartesian product, and strong product. See [10,11,12,13,14,15] for more properties of this operation. In 2013, Klotz and Sander showed that $H(m_1,\dots ,m_r;D)$ is an NEPS of the complete graphs $K_{m_1},\dots ,K_{m_r}$ (a complete graph is a graph in which every pair of vertices are adjacent) [16], and in this paper, we will provide the eigenvalue of the square of generalized Hamming graphs through NEPS.

Let G be a graph and $\rho (x,y)$ denote the $distance$ between two vertices $x,y$ of G. That is, $\rho (x,y)$ is the length of the shortest path between x and y in G or ∞ if no path between them exists. For a positive integer k, the kth power $G^k$ of G, is the graph obtained from G by adding an edge between each pair of vertices with distance at most k. The second power $G^2$ is usually called the square of G. Graph powers are useful in distributed computing (see [17]) and designing algorithms for certain combinatorial optimization problems. Das and Guo produced bounds on the largest and second-largest Laplacian eigenvalues of $G^2$ and $T^2$ for any graph G and tree T [18], and they gave bounds on the spectral radii of $G^k$ and $T^k$ [19]. Klotz and Sander proved that distance powers of integral Cayley graphs over an abelian group are also integral Cayley graphs over the same group [20]. Liu and Li computed the energies of distance powers of unitary Cayley graphs, and characterized which distance powers of unitary Cayley graphs are Ramanujan graphs [21]. Naser gave the diameter of random Cayley graph [22]. For more results, we refer the reader to papers [23,24,25,26,27].

The main goal of this paper is to study the square of generalized Hamming graphs. The remainder of this paper is organized as follows. The theories about Hamming graph and Cayley graph are introduced in Section 2. Section 3 characterizes isomorphisms between $H{(m_1,\dots ,m_r;D)}^2$ and NEPS of complete graphs $K_{m_1},\dots ,K_{m_r}$. This relation is remarkable, since it allows us to define the square of some generalized Hamming graphs purely combinatorially (via NEPS). NEPS of complete graphs can reveals some new access to structural properties of the square of some generalized Hamming graphs. As applications, Section 4 determines the eigenvalues of the square of some generalized Hamming graphs.

2. Preliminaries

We consider only Cayley graphs over abelian groups. Let $\Gamma$ be a finite abelian group with the operation written additively. Let S be a subset of $\Gamma$ such that $-S:=\{-s:s\in S\}=S$ and $0\notin S$, where 0 is the identity element of $\Gamma$. The Cayley graph over $\Gamma$ with connection set S, denoted by $\mathrm{Cay}(\Gamma ,S)$, is a graph with vertex set $\Gamma$ such that the two vertices $a,b\in \Gamma$ are adjacent if and only if $a-b\in S$. As usual, for $A_1,\dots ,A_l\subseteq \Gamma$, where $l\ge 1$, denote $A_1+\cdots +A_l=\{a_1+\cdots +a_l:a_i\in A_i,1\le i\le l\}$, and set $lA=A_1+\cdots +A_l$ with each $A_i=A$ and $0A=\left\{0\right\}$. For $N\subset \mathbb{N}\cup \{\infty \}$, define:

$$S^{\left(N\right)}={\cup }_{n\in N}{S}^{\left(n\right)},$$

(1)

where:

$$S^{\left(n\right)}=nS\backslash \left({\cup }_{l=0}^{n-1}lS\right),S^{(\infty )}=\Gamma \backslash \langle S\rangle ,$$

(2)

where $\langle S\rangle$ is the subgroup of $\Gamma$ generated by S.

Theorem 1

(see [20] [Theorem 3]). Let $\mathrm{Cay}(\Gamma ,S)$ be an integral Cayley graph over a finite abelian group Γ. Let $N\subset \mathbb{N}\cup \{\infty \}$. Then:

$$\mathrm{Cay}{(\Gamma ,S)}^N\cong \mathrm{Cay}(\Gamma ,S^{\left(N\right)}).$$

In particular, $\mathrm{Cay}{(\Gamma ,S)}^N$ is an integral Cayley graph.

Notation 1.

In the sequel we assume that $m_1,\dots ,m_r\ge 2$ are integers and $D=\{d_1,\dots ,d_s\}$ is a set of integers with $1\le d_i\le r$ for each i, where r and s are positive integers.

Lemma 1

(see [9] [Proposition 14]). Let $\Gamma ={\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$ and $S=\{\mathbf{x}\in \Gamma :w(\mathbf{x})\in D\}$. Then:

$$H(m_1,\dots ,m_r;D)\cong \mathrm{Cay}(\Gamma ,S).$$

By Theorem 1 and Lemma 1, we obtain the following result.

Lemma 2.

Let Γ and S be as in Lemma 1, and let $k\ge 1$ be an integer. Then:

$$H{(m_1,\dots ,m_r;D)}^k\cong \mathrm{Cay}{(\Gamma ,S)}^k.$$

Theorem 2.

Let $\Gamma ={\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$, and let S be the set of elements of Γ with Hamming weights in D. Set $B=\left\{\beta \right(\mathbf{x}):\mathbf{x}\in S\}$, where $\beta \left(\mathbf{x}\right)=({\beta }_1,\dots ,{\beta }_r)\in {\mathbb{Z}}_2^r$ with ${\beta }_i=1$ if $x_i\ne 0$ and ${\beta }_i=0$ if $x_i=0$. Then:

$$\mathrm{Cay}(\Gamma ,S)\cong \mathrm{NEPS}(K_{m_1},\dots ,K_{m_r};B).$$

Proof. 

It was shown in [16] [Example 2.8] that $H(m_1,\dots ,m_r;D)$ is an NEPS of the complete graphs $K_{m_1},\dots ,K_{m_r}$. By Lemma 1, $H(m_1,\dots ,m_r;D)\cong \mathrm{Cay}(\Gamma ,S)$. Hence, both $\mathrm{Cay}(\Gamma ,S)$ and $\mathrm{NEPS}(K_{m_1},\dots ,K_{m_r};B)$ have vertex set $\Gamma$.

Let $\mathbf{x}$ and $\mathbf{y}$ be distinct elements of $\Gamma$. Then, $\mathbf{x}$ and $\mathbf{y}$ are adjacent in $\mathrm{Cay}(\Gamma ,S)$ if and only if $w(\mathbf{x}-\mathbf{y})\in D$, which in turn is true if and only if ${\beta }_i=1$ when $x_i\ne y_i$ and ${\beta }_i=0$ when $x_i=y_i$. From this and the definition of B the result follows immediately. □

3. Squares of Generalized Hamming Graphs and NEPS of Complete Graphs

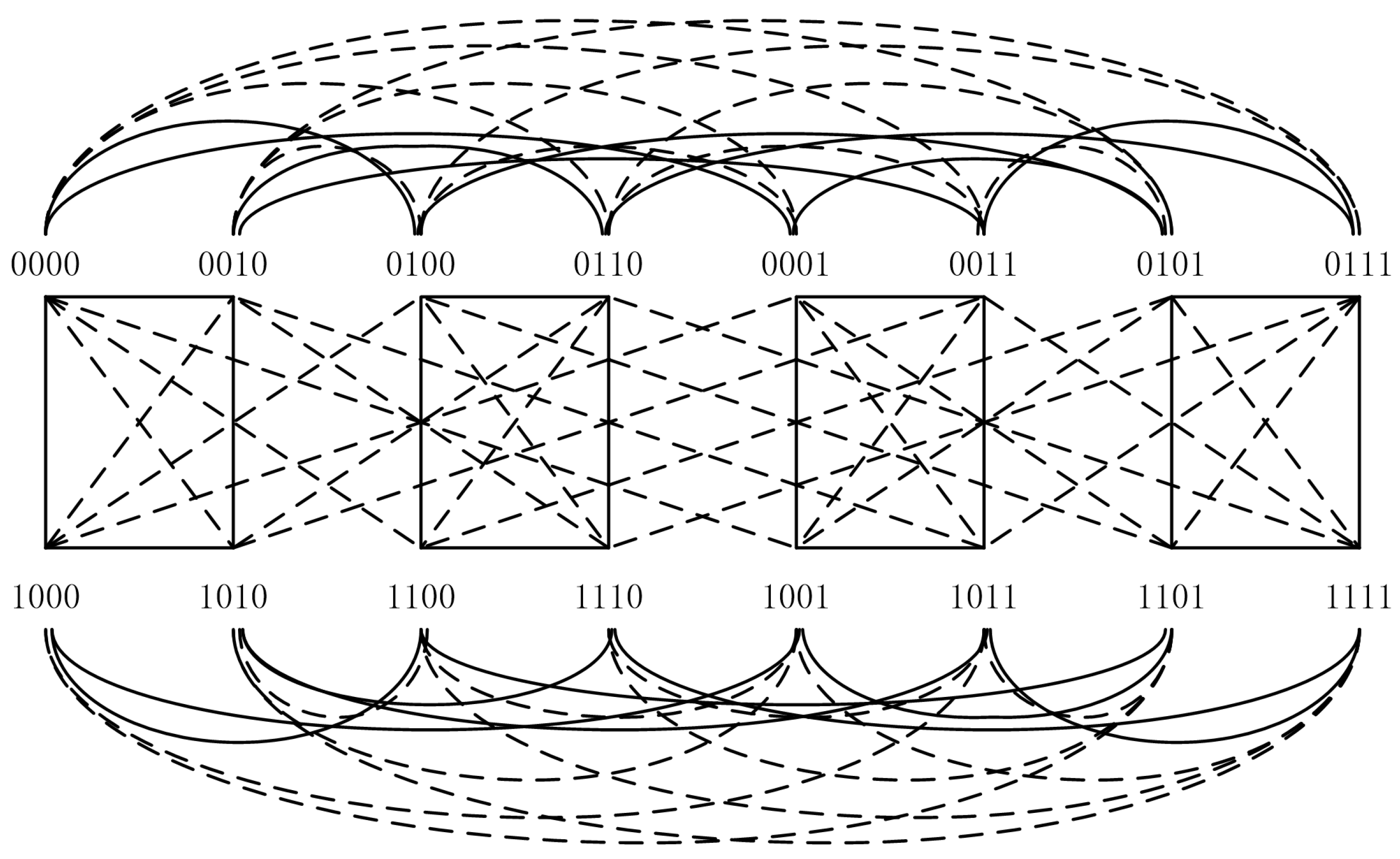
3.1. The Square of $H(m_1,\dots ,m_r;D)$ with Each $m_i\ge 3$

In this section, we determine the isomorphism between $H{(m_1,\dots ,m_r;D)}^2$ with all $m_i\ge 3$ and a certain NEPS of $K_{m_1},\dots ,K_{m_r}$.

Theorem 3.

Suppose that $m_1,\dots ,m_r\ge 3$. Let $D=\{d_1,\dots ,d_s\}$ and $1\le d_i\le r$ for each i. Denote $d={max}_{1\le i\le s}{d}_i$. Set:

$$B_1=\left\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:1\le w\left(\beta \right)\le min\{2d,r\}\right\}.$$

Then:

$$H{(m_1,\dots ,m_r;D)}^2\cong \mathrm{NEPS}(K_{m_1},\dots ,K_{m_r};B_1).$$

In particular, if $d\ge \lceil r/2\rceil$, then $H{(m_1,\dots ,m_r;D)}^2\cong K_{m_1{m}_2\cdots m_r}$.

Proof. 

Let $\Gamma ={\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_r}$ and $D=\{d_1,\dots ,d_s\}$. Let $S=\{\mathbf{x}\in \Gamma \backslash \{\mathbf{0}\}:w(\mathbf{x})\in D\}$. By Lemma 2 and Theorem 1,

$$H{(m_1,\dots ,m_r;D)}^2\cong \mathrm{Cay}{(\Gamma ;S)}^2\cong \mathrm{Cay}(\Gamma ;S^{\left(\right\{1,2\left\}\right)}),$$

where $S^{\left(\right\{1,2\left\}\right)}=S^{\left(1\right)}\cup S^{\left(2\right)}=S\cup \{2S\backslash \left\{\mathbf{0}\right\}\}$ (see (1) and (2)). Thus, by Theorem 2, it suffices to prove the following: for any $\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}$, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$ holds if and only if it satisfies:

$$1\le w\left(\mathbf{x}\right)\le min\{2d,r\}.$$

(3)

We achieve this in the next two claims.

Claim 1. Every $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$ satisfies (3).

By the definition of S, this is obviously true when $\mathbf{x}\in S$. Henceforth we assume that $\mathbf{x}\in 2S\backslash \left\{\mathbf{0}\right\}$. Then, there exist $\mathbf{y},\mathbf{z}\in S$ such that $\mathbf{x}=\mathbf{y}+\mathbf{z}$. Define:

$$l(\mathbf{y},\mathbf{z})=|\{i:y_i\ne 0,z_i\ne 0,1\le i\le r\}|.$$

Case 1. $w\left(\mathbf{y}\right)=w\left(\mathbf{z}\right)=d_i$, where $i\in \{1,2,\dots ,s\}$.

Assume that $2d_i\ge r$. Then, $2d_i-r\le l(\mathbf{y},\mathbf{z})\le d_i$. If $l(\mathbf{y},\mathbf{z})=d_i$, and then $1\le w\left(\mathbf{x}\right)\le d_i$. If $2d_i-r\le l(\mathbf{y},\mathbf{z})<d_i$, then $2(d_i-l(\mathbf{y},\mathbf{z}))\le w\left(\mathbf{x}\right)\le 2d_i-l(\mathbf{y},\mathbf{z})$, which implies that $2\le w\left(\mathbf{x}\right)\le r$.

Assume that $2d_i<r$. Then, $0\le l(\mathbf{y},\mathbf{z})\le d_i$. If $l(\mathbf{y},\mathbf{z})=d_i$, and then $1\le w\left(\mathbf{x}\right)\le d_i$. If $0\le l(\mathbf{y},\mathbf{z})<d_i$, then $2(d_i-l(\mathbf{y},\mathbf{z}))\le w\left(\mathbf{x}\right)\le 2d_i-l(\mathbf{y},\mathbf{z})$, which implies that $2\le w\left(\mathbf{x}\right)\le 2d_i$.

In either case, we have $1\le w\left(\mathbf{x}\right)\le min\{2d_i,r\}$.

Case 2. $(w\left(\mathbf{y}\right),w\left(\mathbf{z}\right))=(d_i,d_j)$ or $(d_j,d_i)$, where $i,j\in \{1,2,\dots ,s\}$ and $i\ne j$.

Without loss of generality, we may assume that $d_i\le d_j$ and $(w\left(\mathbf{y}\right),w\left(\mathbf{z}\right))=(d_i,d_j)$. Assume that $d_i+d_j\ge r$. Then, $d_i+d_j-r\le l(\mathbf{y},\mathbf{z})\le d_i$. If $l(\mathbf{y},\mathbf{z})=d_i$, then $d_j-d_i\le w\left(\mathbf{x}\right)\le d_j$. If $d_i+d_j-r\le l(\mathbf{y},\mathbf{z})<d_i$, then $d_i+d_j-2l(\mathbf{y},\mathbf{z})\le w\left(x\right)\le d_i+d_j-l(\mathbf{y},\mathbf{z})$, which implies that $d_j-d_i+2\le w\left(\mathbf{x}\right)\le r$.

Assume that $d_i+d_j\le r$. Then, $0\le l(\mathbf{y},\mathbf{z})\le d_i$. If $l(\mathbf{y},\mathbf{z})=d_i$, then $d_j-d_i\le w\left(\mathbf{x}\right)\le d_j$. If $0\le l(\mathbf{y},\mathbf{z})<d_i$, then $d_i+d_j-2l(\mathbf{y},\mathbf{z})\le w\left(\mathbf{x}\right)\le d_i+d_j-l(\mathbf{y},\mathbf{z})$, which implies that $d_j-d_i+2\le w\left(\mathbf{x}\right)\le d_i+d_j$.

In either case, we have $1<d_j-d_i+2\le w\left(\mathbf{x}\right)\le min\{d_i+d_j,r\}$.

It is readily seen that (3) holds in either of Cases 1 and 2 above. This proves Claim 1.

Claim 2. Every $\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}$ that satisfies (3) is an element of $S^{\left(\right\{1,2\left\}\right)}$.

Suppose that $\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}$ satisfies (3).

Case 1. $2d\le r$.

Set $w:=w\left(\mathbf{x}\right)\le 2d$. Suppose that $x_{i_1},x_{i_2},\dots ,x_{i_w}\ne 0$ with $1\le i_1<i_2<\cdots <i_w\le r$.

Case 1.1. $1\le w\le d$.

Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i\ge 3$ for each i, there exist $y_{i_a},z_{i_a}\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $x_{i_a}=y_{i_a}+z_{i_a}$ for $1\le a\le w$, and $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $t\in \{1,2,\dots ,r\}\backslash \{i_1,\dots ,i_w\}$. Choose $j_1,\dots ,j_{d-w}\in \{1,2,\dots ,r\}\backslash \{i_1,\dots ,i_w\}$ with $j_1<j_2<\cdots <j_{d-w}$. Then, $x_{j_a}=y_{j_a}+z_{j_a}=0$ for $a\in \{1,2,\dots ,d-w\}$. Define ${\mathbf{y}}^{\prime }$ and ${\mathbf{z}}^{\prime }$ such that $y_t^{\prime }=y_t$ and $z_t^{\prime }=z_t$ if $t\in \{i_1,\dots ,i_w\}\cup \{j_1,\dots ,j_{d-w}\}$ and $y_t^{\prime }=z_t^{\prime }=0$ otherwise. Then, $w\left({\mathbf{y}}^{\prime }\right)=w\left({\mathbf{z}}^{\prime }\right)=d$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Therefore, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Case 1.2. $d+1\le w\le 2d$.

In this case, there exist $y_{i_a},z_{i_a}\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $x_{i_a}=y_{i_a}+z_{i_a}$ for $1\le a\le w$, and $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $t\in \{1,2,\dots ,r\}\backslash \{i_1,\dots ,i_w\}$. Choose $2d-w$ terms from $\{i_1,\dots ,i_w\}$, say, $i_{w-d+1}<\cdots <i_d$. Then, $x_{i_a}=y_{i_a}+z_{i_a}$ for $a\in \{w-d+1,w-d+2,\dots ,d\}$. Define ${\mathbf{y}}^{\prime }$ such that $y_t^{\prime }=x_t$ if $t\in \{i_1,\dots ,i_{w-d}\}$, $y_t^{\prime }=y_t$ if $t\in \{i_{w-d+1},\dots ,i_d\}$, and $y_t^{\prime }=0$ for all other t. Define ${\mathbf{z}}^{\prime }$ in such a way that $z_t^{\prime }=z_t$ if $t\in \{i_{w-d+1},\dots ,i_d\}$, $z_t^{\prime }=x_t$ if $t\in \{i_{d+1},\dots ,i_w\}$, and $z_t^{\prime }=0$ for all other t. Then, $w\left({\mathbf{y}}^{\prime }\right)=w\left({\mathbf{z}}^{\prime }\right)=d$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$, and therefore $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Case 2. $2d>r$.

Similar to Case 1, one can show $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$ in this case.

So far we have proved Claims 1 and 2 and thus completed the proof. □

3.2. The Square of $H(2,\dots ,2;D)$

In this section, we determine the isomorphism between $H{(2,\dots ,2;D)}^2$ and a certain NEPS of $K_2,\dots ,K_2$. Denote:

$$\mathbf{1}=(1,\dots ,1),H(r\odot 2;D)=H(\underset{r}{\underbrace{2,\dots ,2}};D),\mathrm{NEPS}(r\odot K_2;B)=\mathrm{NEPS}(\underset{r}{\underbrace{K_2,\dots ,K_2}};B).$$

Theorem 4.

Let $r\ge 1$ be an integer and $D=\{d_1,\dots ,d_s\}$ with $1\le d_i\le r$ for each i. Let:

$$B_2=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D\cup L\cup S\},$$

where:

$$L=\left\{d_i+d_j-2h_{ij}\left|\begin{array}{c}{d}_i,d_j\in D\mathrm{and}{d}_i+d_j\le r,\hfill \\ h_{ij}\in \{0,1,2,\dots ,min\{d_i,d_j\}\}\hfill \end{array}\right.\right\}\backslash \left\{0\right\}$$

and:

$$S=\left\{d_i+d_j-2h_{ij}\left|\begin{array}{c}{d}_i,d_j\in D\mathrm{and}{d}_i+d_j>r,\hfill \\ h_{ij}\in \{d_i+d_j-r,d_i+d_j-r+1,\dots ,min\{d_i,d_j\}\}\hfill \end{array}\right.\right\}\backslash \left\{0\right\}.$$

Then:

$$H{(r\odot 2;D)}^2\cong \mathrm{NEPS}(r\odot K_2;B_2).$$

In particular,

(a)

If $2d_i\le r$ for $1\le i\le r$, then:

$$H{(r\odot 2;D)}^2\cong \mathrm{NEPS}(r\odot K_2;B_3),$$

where $B_3=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D\cup L\}$;

(b)

If $2d_i>r$ for $1\le i\le r$, then:

$$H{(r\odot 2;D)}^2\cong \mathrm{NEPS}(r\odot K_2;B_4),$$

where $B_4=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D\cup S\}$.

Proof. 

Denote $S=\{\mathbf{x}\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\mathbf{x}\right)\in D\}$. By Lemma 2 and Theorem 1, we have:

$$H{(r\odot 2;D)}^2\cong \mathrm{Cay}{({\mathbb{Z}}_2^r;S)}^2\cong \mathrm{Cay}({\mathbb{Z}}_2^r;S^{\left(\right\{1,2\left\}\right)}),$$

where $S^{\left(\right\{1,2\left\}\right)}=S\cup \{2S\backslash \left\{\mathbf{0}\right\}\}$ by (1) and (2). By Theorem 2, it suffices to prove:

$$S^{\left(\right\{1,2\left\}\right)}=\left\{\mathbf{x}\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\mathbf{x}\right)\in D\cup L\cup S\right\}.$$

(4)

The proof of this consists of the following two claims.

Claim 1. $S^{\left(\right\{1,2\left\}\right)}\subseteq \left\{\mathbf{x}\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\mathbf{x}\right)\in D\cup L\cup S\right\}$.

Let $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$. If $\mathbf{x}\in S$, then Claim 1 is true, as $w\left(\mathbf{x}\right)=d$. Assume that $\mathbf{x}\in 2S\backslash \left\{\mathbf{0}\right\}$ in the sequel. Then, there exist $\mathbf{y},\mathbf{z}\in S$ such that $\mathbf{x}=\mathbf{y}+\mathbf{z}$. Define:

$$l(\mathbf{y},\mathbf{z})=|\{i:y_i\ne 0,z_i\ne 0,1\le i\le r\}|.$$

Case 1. $d_i+d_j\le r$.

When $d_i\ne d_j$, we have $0\le l(\mathbf{y},\mathbf{z})\le min\{d_i,d_j\}$ and $w\left(\mathbf{x}\right)=w\left(\mathbf{y}\right)+w\left(\mathbf{z}\right)-2l(\mathbf{y},\mathbf{z})=d_i+d_j-2l(\mathbf{y},\mathbf{z})$.

When $d_i=d_j$, we have $0\le l(\mathbf{y},\mathbf{z})\le d_i$. If $l(\mathbf{y},\mathbf{z})=d_i$, then $w\left(\mathbf{x}\right)=0$ and so $\mathbf{x}=\mathbf{0}$, which is a contradiction. If $0\le l(\mathbf{y},\mathbf{z})<d_i$, we have $w\left(\mathbf{x}\right)=w\left(\mathbf{y}\right)+w\left(\mathbf{z}\right)-2l(\mathbf{y},\mathbf{z})=2d_i-2l(\mathbf{y},\mathbf{z})$.

In either case, we have $w\left(\mathbf{x}\right)\in L$.

Case 2. $d_i+d_j>r$.

When $d_i\ne d_j$, we have $d_i+d_j-r\le l(\mathbf{y},\mathbf{z})\le min\{d_i,d_j\}$ and $w\left(\mathbf{x}\right)=w\left(\mathbf{y}\right)+w\left(\mathbf{z}\right)-2l(\mathbf{y},\mathbf{z})=d_i+d_j-2l(\mathbf{y},\mathbf{z})$.

When $d_i=d_j$, we have $2d_i-r\le l(\mathbf{y},\mathbf{z})\le d_i$. If $l(\mathbf{y},\mathbf{z})=d_i$, then $w\left(\mathbf{x}\right)=0$ and so $\mathbf{x}=\mathbf{0}$, which is a contradiction. If $2d_i-r<l(\mathbf{y},\mathbf{z})<d_i$, then $w\left(\mathbf{x}\right)=w\left(\mathbf{y}\right)+w\left(\mathbf{z}\right)-2l(\mathbf{y},\mathbf{z})=2d_i-2l(\mathbf{y},\mathbf{z})$.

In either case, we have $w\left(\mathbf{x}\right)\in S$.

In summary, we have $w\left(\mathbf{x}\right)\in D\cup L\cup S$ and Claim 1 is proven.

Claim 2.  $\{\mathbf{x}\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\mathbf{x}\right)\in D\cup L\cup S\}\subseteq S^{\left(\right\{1,2\left\}\right)}.$

Let $\mathbf{x}\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}$ be such that $w\left(\mathbf{x}\right)\in D\cup L\cup S$. Set $w:=w\left(\mathbf{x}\right)$. Suppose that $x_{i_1},x_{i_2},\dots ,x_{i_w}\ne 0$, where $1\le i_1<i_2<\cdots <i_w\le r$. If $w\in D$, then $\mathbf{x}\in S\subseteq S^{\left(\right\{1,2\left\}\right)}$. It remains to consider the case where $\mathbf{x}\in L\cup S$.

Case 1. $w\in L$, that is, $w=d_i+d_j-2h_{ij}$ with $0\le h_{ij}\le min\{d_i,d_j\}$ for some pair $i,j$.

In this case, we have $x_a=0$ for every $a\in \{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,i_{d_i+d_j-2h_{ij}}\}$. Since $0\le h_{ij}\le min\{d_i,d_j\}$, we can choose $j_1,\dots ,j_{h_{ij}}\in \{1,\dots ,r\}\backslash \{i_1,i_2,\dots ,i_{d_i+d_j-2h_{ij}}\}$ with $j_1<\cdots <j_{h_{ij}}$. Define ${\mathbf{y}}^{\prime }$ in such a way that $y_t^{\prime }=1$ if $t\in \{i_1,\dots ,i_{d_i-h_{ij}}\}\cup \{j_1,\cdots ,j_{h_{ij}}\}$ and $y_t^{\prime }=0$ otherwise. Define ${\mathbf{z}}^{\prime }$ such that $z_t^{\prime }=1$ if $t\in \{i_{d_i-h_{ij}+1},\dots ,i_{d_i+d_j-2h_{ij}}\}\cup \{j_1,\cdots ,j_{h_{ij}}\}$ and $z_t^{\prime }=0$ otherwise. Then, $w\left({\mathbf{y}}^{\prime }\right)=d_i$, $w\left({\mathbf{z}}^{\prime }\right)=d_j$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Hence, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Case 2. $w\in S$, that is, $w=d_i+d_j-2h_{ij}$ with $d_i+d_j-r\le h_{ij}\le min\{d_i,d_j\}$ for some pair $i,j$.

Similar to Case 1, in this case one can verify that $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$. □

In the special case, where $D=\left\{d\right\}$, Theorem 4 yields the following result.

Corollary 1.

Let d and r be positive integers with $1\le d\le r$.

(a)

If $1\le d\le \frac{r}{2}$, then:

$$H{(r\odot 2;\left\{d\right\})}^2\cong \mathrm{NEPS}(r\odot K_2;B_5),$$

where $B_5=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=d\mathit{or}2h\mathit{for}1\le h\le d\}$.

(b)

If $\frac{r}{2}<d\le r$, then:

$$H{(r\odot 2;\left\{d\right\})}^2\cong \mathrm{NEPS}(r\odot K_2;B_6),$$

where $B_6=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=d\mathit{or}2h\mathit{for}1\le h\le r-d\}$.

In particular, if $d=r$, then:

$$H{(r\odot 2;\left\{d\right\})}^2\cong \mathrm{NEPS}(r\odot K_2;\left\{\mathbf{1}\right\}).$$

Example 1.

We have $H{(4\odot 2;\left\{1\right\})}^2\cong \mathrm{NEPS}(4\odot K_2;B)$ with $B=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=1,2\}$ and $H{(4\odot 2;\left\{3\right\})}^2\cong \mathrm{NEPS}(4\odot K_2;B)$ with $B=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=2,3\}$. These two graphs are shown in Figure 1 and Figure 2, respectively.

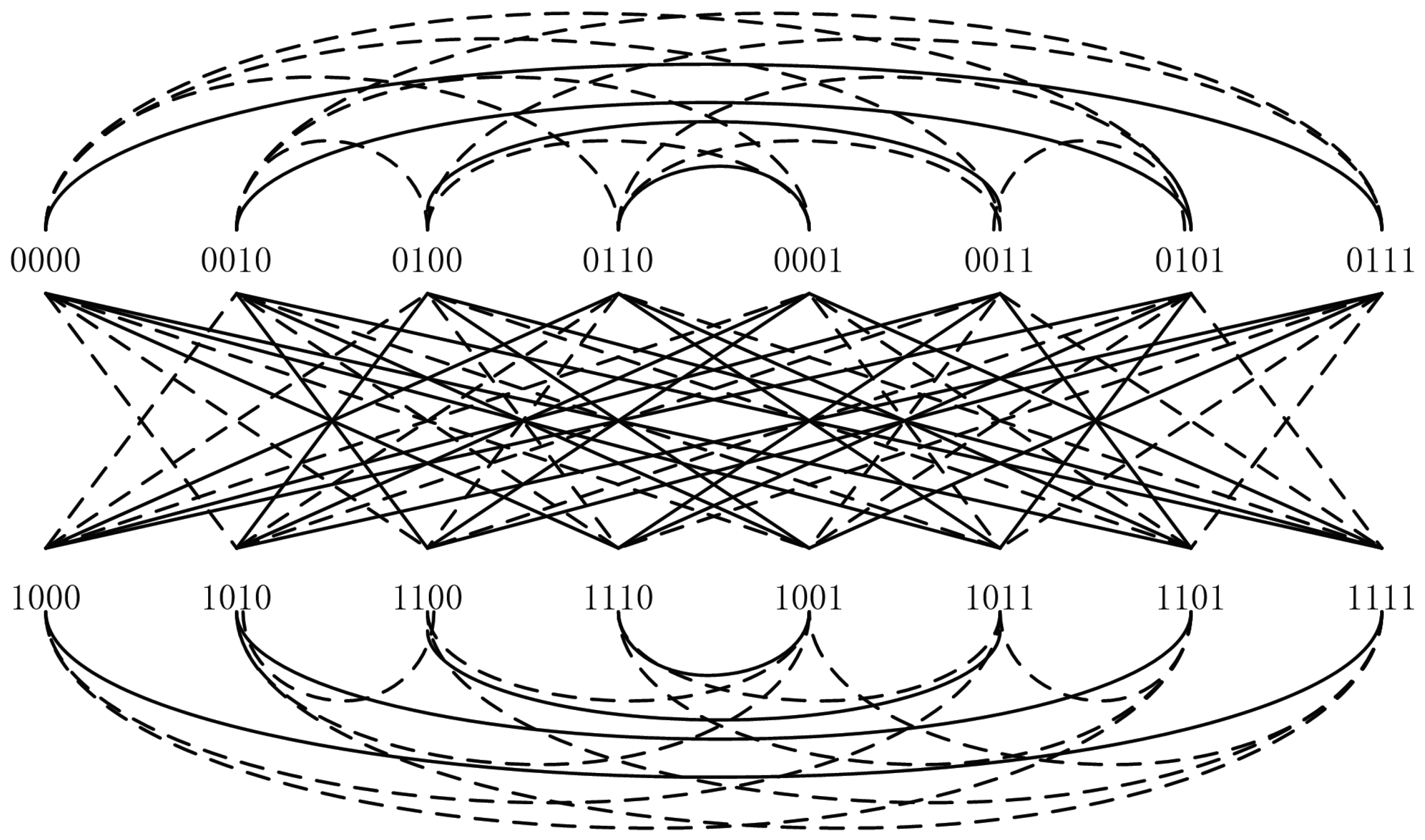
3.3. The Square of $H(2,\dots ,2,m_1,\dots ,m_v;D)$ with Each $m_i\ge 3$

In this section, we determine the isomorphism between $H{(2,\dots ,2,m_1,\dots ,m_v;D)}^2$ and a certain NEPS of complete graphs $K_2,\dots ,K_2,K_{m_1},\dots ,K_{m_v}$ with each $m_i\ge 3$. Denote:

$$H(r\odot 2,m_1,\dots ,m_v;D)=H(\underset{r}{\underbrace{2,\dots ,2}},m_1,\dots ,m_v;D)$$

and:

$$\mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B)=\mathrm{NEPS}(\underset{r}{\underbrace{K_2,\dots ,K_2}},K_{m_1},\dots ,K_{m_v};B).$$

Theorem 5.

Let $m_1,\dots ,m_v\ge 3$ and $r\ge 1$ be integers. Let $D=\{d_1,\dots ,d_s\}$ such that: $1\le d_i\le r+v$ for each i. Denote $d={max}_{1\le i\le s}{d}_i$. Set:

$$D_1=\{d_i\mid d_i\in D,d_i\le r\},$$

$$L=\left\{d_i+d_j-2h_{ij}\left|\begin{array}{c}{d}_i,d_j\in D\mathrm{and}{d}_i+d_j\le r+v,\hfill \\ h_{ij}\in \{0,1,2,\dots ,min\{d_i,d_j\}\}\hfill \end{array}\right.\right\}\backslash \left\{0\right\},$$

and:

$$T=\left\{d_i+d_j-2h_{ij}\left|\begin{array}{c}{d}_i,d_j\in D\mathrm{and}{d}_i+d_j>r+v,\hfill \\ h_{ij}\in \{d_i+d_j-r-v,d_i+d_j-r-v+1,\dots ,min\{d_i,d_j\}\}\hfill \end{array}\right.\right\}\backslash \left\{0\right\}.$$

(a)

Suppose that $2d\le r+v$ and $\{1,\dots ,2d\}\cap \{1,\dots ,r\}\subseteq L\cup D_1$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B_7),$$

where $B_7=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:1\le w\left(\beta \right)\le 2d\}$.

(b)

Suppose that $2d>r+v$, $\{1,\dots ,r\}\subseteq L\cup T\cup D_1$, and there exist a and b with $1\le a,b\le s$ (possibly with $a=b$) such that $r+v\le d_a+d_b\le r+2v$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong K_{2^r{m}_1\cdots m_v}.$$

Proof. 

Denote $\Gamma =\underset{r}{\underbrace{{\mathbb{Z}}_2\oplus \cdots \oplus {\mathbb{Z}}_2}}\oplus {\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_v}$ and $S=\{\mathbf{x}\in \Gamma \backslash \{\mathbf{0}\}:w(\mathbf{x})\in D\}$. By Lemma 2 and Theorem 1,

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{Cay}{(\Gamma ;S)}^2\cong \mathrm{Cay}(\Gamma ;S^{\left(\right\{1,2\left\}\right)}),$$

where $S^{\left(\right\{1,2\left\}\right)}=S\cup \{2S\backslash \left\{\mathbf{0}\right\}\}$ by (1) and (2).

(a) Suppose that $2d\le r+v$ and $\{1,\dots ,2d\}\cap \{1,\dots ,r\}\subseteq L\cup D_1$. By Theorem 2, it suffices to prove:

$$S^{\left(\right\{1,2\left\}\right)}=\left\{\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}:1\le w\left(\mathbf{x}\right)\le 2d\right\}.$$

(5)

We achieve this by proving the following two claims.

Claim 1. $S^{\left(\right\{1,2\left\}\right)}\subseteq \left\{\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}:1\le w\left(\mathbf{x}\right)\le 2d\right\}$.

Let $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$. If $\mathbf{x}\in S$, then Calim 1 is true, as $w\left(\mathbf{x}\right)\in D$. Henceforth we assume that $\mathbf{x}\in 2S\backslash \left\{\mathbf{0}\right\}$. Then, there exist $\mathbf{y},\mathbf{z}\in S$ such that $\mathbf{x}=\mathbf{y}+\mathbf{z}$ and $(w\left(\mathbf{y}\right),w\left(\mathbf{z}\right))=(d_i,d_j)$. Set ${\mathbf{y}}^{\left(1\right)}=(y_1,\dots ,y_r)$, ${\mathbf{z}}^{\left(1\right)}=(z_1,\dots ,z_r)$, ${\mathbf{y}}^{\left(2\right)}=(y_{r+1},\dots ,y_{r+v})$ and ${\mathbf{z}}^{\left(2\right)}=(z_{r+1},\dots ,z_{r+v})$. Denote:

$$q_1:=\mid \{i:y_i\ne 0,z_i\ne 0,i\in \{1,2,\dots ,r\}\}\mid ,$$

(6)

$$q_2=\mid \{i:y_i\ne 0,z_i\ne 0,i\in \{r+1,r+2,\dots ,r+v\}\}\mid .$$

(7)

Case 1. $d_i\ne d_j$.

Without loss of generality, we may assume $d_i<d_j$ and $(w\left(\mathbf{y}\right),w\left(\mathbf{z}\right))=(d_i,d_j)$. Then, $0\le q_1+q_2\le d_i$. If $q_1+q_2=d_i$, then $d_j-d_i\le w\left(\mathbf{x}\right)\le d_i+d_j-2q_1-q_2=d_j-q_1\le d_j-(d_i-min\{v,d_i\})=d_j-d_i+min\{v,d_i\}$. If $0\le q_1+q_2<d_i$, then $d_i+d_j-2q_1-2q_2\le w\left(\mathbf{x}\right)\le d_i+d_j-2q_1-q_2$, which implies that $d_j-d_i+2\le w\left(\mathbf{x}\right)\le d_i+d_j$.

Case 2. $d_i=d_j$.

In this case, $0\le q_1+q_2\le d_i$. If $q_1+q_2=d_i$, then $0\le w\left(\mathbf{x}\right)\le 2d_i-2q_1-q_2=d_i-q_1\le d_i-(d_i-min\{v,d_i\})=min\{v,d_i\}$. Then, $1\le w\left(\mathbf{x}\right)\le min\{v,d_i\}$ as $\mathbf{x}\ne \mathbf{0}$. If $0\le q_1+q_2<d_i$, then $2d_i-2q_1-2q_2\le w\left(\mathbf{x}\right)\le 2d_i-2q_1-q_2$, which implies that $2\le w\left(\mathbf{x}\right)\le 2d_i$.

Since $\{1,\dots ,2d\}\cap \{1,\dots ,r\}\subseteq L\cup D_1$, we obtain $1\le w\left(\mathbf{x}\right)\le 2d$ in each case above. This proves Claim 1.

Claim 2.  $\left\{\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}:1\le w\left(\mathbf{x}\right)\le 2d\right\}\subseteq S^{\left(\right\{1,2\left\}\right)}.$

Let $\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}$ such that $1\le w\left(\mathbf{x}\right)\le 2d$. Set $w:=w\left(\mathbf{x}\right)$ and assume that $x_{i_1},\dots ,x_{i_w}\ne 0$ for $1\le i_1<i_2<\cdots <i_w\le r+v$.

Case 1. $i_w\le r$.

When $w\in D_1$, $\mathbf{x}\in S\subseteq S^{\left(\right\{1,2\left\}\right)}$.

When $w\notin D_1$, $\mathbf{x}\in L$, that is, there exist $d_i,d_j\in D$ such that $w=d_i+d_j-2h_{ij}$ and $0\le h_{ij}\le min\{d_i,d_j\}$. Note that $x_{\alpha }=0$ for each $\alpha \in \{1,\dots ,r\}\backslash \{i_1,i_2,\dots ,i_w\}$. Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i$ for each i, there exist $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $1\le t\le v$. Denote $q_1=\mid \{i\mid i\in \{1,\dots ,r\}\backslash \{i_1,\dots ,i_w\}and{y}_i=z_i=1\}\mid$. Since $0\le h_{ij}\le min\{d_i,d_j\}$, we can choose $h_{ij}=(d_i+d_j-w)/2$ terms from $\{1,\dots ,r+v\}\backslash \{i_1,i_2,\cdots ,i_w\}$ in such a way that $q_1$ terms, say $j_1<\dots <j_{q_1}$, are chosen from $\{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,i_w\}$, and the remaining terms, say $j_{q_1+1}<\cdots <j_{h_{ij}}$, are chosen from $\{r+1,\dots ,r+v\}$ (note that $q_1\le r-w$). Then, $0=x_{\alpha }=y_{\alpha }+z_{\alpha }$ for $\alpha \in \{j_{q_1+1},\dots ,j_{h_{ij}}\}$. Define ${\mathbf{y}}^{\prime }$ such that $y_u^{\prime }=1$ for $u\in \{i_1,\dots ,i_{\frac{d_i-d_j+w}{2}}\}\cup \{j_1,\dots ,j_{q_1}\}$, $y_u^{\prime }=y_u$ for $u\in \{j_{q_1+1},\dots ,j_{h_{ij}}\}$, and $y_u^{\prime }=0$ for all other u. Define ${\mathbf{z}}^{\prime }$ in such a way that $z_u^{\prime }=1$ for $u\in \{i_{\frac{d_i-d_j+w}{2}+1},\dots ,i_w\}\cup \{j_1,\dots ,j_{q_1}\}$, $z_u^{\prime }=z_u$ for $u\in \{j_{q_1+1},\dots ,j_{h_{ij}}\}$ and $z_u^{\prime }=0$ for all other u. Then, $w\left({\mathbf{y}}^{\prime }\right)=d_i$, $w\left({\mathbf{z}}^{\prime }\right)=d_j$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Hence, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Case 2. $i_w>r$.

Denote $c=|\{i_1,\dots ,i_w\}\cap \{1,\dots ,r\}|$. Then, $x_{\alpha }=0$ for each $\alpha \in \{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,$$i_c\}$. Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i$ for each i, there exist $y_{i_{\alpha }},z_{i_{\alpha }}\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $x_{i_{\alpha }}=y_{i_{\alpha }}+z_{i_{\alpha }}$ for $c+1\le \alpha \le w$, and $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $t\in \{r+1,r+2,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$. Denote $q_1=\mid \{i\mid i\in \{1,\dots ,r\}\backslash \{i_1,\dots ,i_c\}and{y}_i=z_i=1\}\mid$, $q_2=\mid \{i\mid i\in \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i\}\mid$, and $q_3=\mid \{i\mid i\in \{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i=0\}\mid$. Since $2d\le r+v$, we have $0\le q_1+q_2+q_3\le min\{r+v-c,d\}$. Thus, we may choose $q_1\le r-c$ terms from $\{1,2,\dots ,r\}\backslash \{i_1,\dots ,i_c\}$, say $j_1<j_2<\cdots <j_{q_1}$, $q_2\le w-c$ terms from $\{i_{c+1},\dots ,i_w\}$, say $i_{w-q_2+1}<\cdots <i_w$ and choose $q_3\le v-(w-c)$ terms from $\{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$, say $j_{q_1+1}<\cdots <j_{q_1+q_3}$. Define ${\mathbf{y}}^{\prime }$ such that $y_u^{\prime }=1$ for $u\in \{i_1,\dots ,i_l\}\cup \{j_1,\dots ,j_{q_1}\}$, $y_u^{\prime }=x_u$ for $u\in \{j_{c+1},\dots ,j_{c+d-q_1-q_2-q_3-l}\}$, $y_u^{\prime }=y_u$ for $u\in \{i_{w-q_2+1},\dots ,i_w\}\cup \{j_{q_1+1},\dots ,j_{q_1+q_3}\}$, and $y_u^{\prime }=0$ for all other u. Define ${\mathbf{z}}^{\prime }$ such that $z_u^{\prime }=1$ for $u\in \{i_{l+1},\dots ,i_c\}\cup \{j_1,\dots ,j_{q_1}\}$, $z_u^{\prime }=x_u$ for $u\in \{j_{c+d-q_1-q_2-q_3-l+1},\dots ,j_{2d-2q_1-2q_2-2q_3}\}$, $z_u^{\prime }=y_u$ for $u\in \{i_{w-q_2+1},\dots ,i_w\}$$\cup \{j_{q_1+1},\dots ,j_{q_1+q_3}\}$, and $z_u^{\prime }=0$ for all other u. Then, $w\left({\mathbf{y}}^{\prime }\right)=w\left({\mathbf{z}}^{\prime }\right)=d$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Therefore, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

(b) Suppose that $2d>r+v$, $\{1,\dots ,r\}\subseteq L\cup T\cup D_1$, and that there exist $1\le a,b\le s$ (possibly with $a=b$) such that $r+v\le d_a+d_b\le r+2v$. By Lemma 2 and Theorems 1 and 2, it suffices to prove $S^{\left(\right\{1,2\left\}\right)}=\Gamma \backslash \left\{\mathbf{0}\right\}$, or equivalently, $\Gamma \backslash \left\{\mathbf{0}\right\}\subseteq S^{\left(\right\{1,2\left\}\right)}$.

Let $\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}$, and set $w=w\left(\mathbf{x}\right)$. Then, $1\le w\left(\mathbf{x}\right)\le r+v$. We may assume that $x_{i_1},x_{i_2},\dots ,x_{i_w}\ne 0$ for $1\le i_1<i_2<\cdots <i_w\le r+v$. When $i_w\le r$, similar to the proof of (a), we can show that $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$. In the following, we consider the following two cases.

Case 1. $i_w>r$ and $1<w\le d$.

Denote $c=|\{i_1,\dots ,i_w\}\cap \{1,\dots ,r\}|$. Then $x_{\alpha }=0$ for each $\alpha \in \{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,$$i_c\}$. Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i$ for each i, there exist $y_{i_{\alpha }},z_{i_{\alpha }}\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $x_{i_{\alpha }}=y_{i_{\alpha }}+z_{i_{\alpha }}$ for $c+1\le \alpha \le w$, and $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $t\in \{r+1,r+2,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$. Denote $q_1=\mid \{i\mid i\in \{1,\dots ,r\}\backslash \{i_1,\dots ,i_c\}and{y}_i=z_i=1\}\mid$, $q_2=\mid \{i\mid i\in \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i\}\mid$, and $q_3=\mid \{i\mid i\in \{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i=0\}\mid$. Since $i_w>r$ and $1<w\le d$, then $c\le min\{r,d-2\}$, which means that $d_a+d_b-r-v\le r+v-c$; also note that there exist a and b with $1\le a,b\le s$ (possibly with $a=b$) such that $r+v\le d_a+d_b\le r+2v$, and then $d_a+d_b-r-v\le q_1+q_2+q_3\le min\{r+v-c,d\}$. Thus, we may choose $q_1$ terms from $\{1,2,\dots ,r\}\backslash \{i_1,\dots ,i_c\}$, say $j_1<j_2<\cdots <j_{q_1}$, $q_2$ terms from $\{i_{c+1},\dots ,i_w\}$, say $i_{w-q_2+1}<\cdots <i_w$, and choose $q_3$ terms from $\{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$, say $j_{q_1+1}<\cdots <j_{q_1+q_3}$. Define ${\mathbf{y}}^{\prime }$ such that $y_u^{\prime }=1$ for $u\in \{i_1,\dots ,i_l\}\cup \{j_1,\dots ,j_{q_1}\}$, $y_u^{\prime }=x_u$ for $u\in \{j_{c+1},\dots ,j_{c+d_a-q_1-q_2-q_3-l}\}$, $y_u^{\prime }=y_u$ for $u\in \{i_{w-q_2+1},\dots ,i_w\}\cup \{j_{q_1+1},\dots ,j_{q_1+q_3}\}$, and $y_u^{\prime }=0$ for all other u. Define ${\mathbf{z}}^{\prime }$ such that $z_u^{\prime }=1$ for $u\in \{i_{l+1},\dots ,i_c\}\cup \{j_1,\dots ,j_{q_1}\}$, $z_u^{\prime }=x_u$ for $u\in \{j_{c+d_a-q_1-q_2-q_3-l+1},\dots ,j_{d_a+d_b-2q_1-2q_2-2q_3}\}$, $z_u^{\prime }=y_u$ for $u\in \{i_{w-q_2+1},\dots ,$$i_w\}\cup \{j_{q_1+1},\dots ,j_{q_1+q_3}\}$, and $z_u^{\prime }=0$ for all other u. Then, $w\left({\mathbf{y}}^{\prime }\right)=d_a,w\left({\mathbf{z}}^{\prime }\right)=d_b$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Therefore, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Case 2. $i_w>r$ and $d<w\le r+v$.

Denote $c=|\{i_1,\dots ,i_w\}\cap \{1,\dots ,r\}|$. Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i\ge 3$ for each i, there exist $y_{i_{\alpha }},z_{i_{\alpha }}\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $x_{i_{\alpha }}=y_{i_{\alpha }}+z_{i_{\alpha }}$ for $c+1\le \alpha \le w$, and $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $\alpha \in \{r+1,r+2,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$. Denote $q_1=\mid \{i\mid i\in \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i\}\mid$, and $q_2=\mid \{i\mid i\in \{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i=0\}\mid$. Since there exist a and b with $1\le a,b\le s$ (possibly with $a=b$) such that $r+v\le d_a+d_b\le r+2v$, we may choose $q_1$ terms from $\{i_{c+1},\dots ,i_w\}$, say $i_{w-q_1+1}<\cdots <i_w$, and choose $q_2$ terms from $\{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$, say $j_1<\cdots <j_{q_2}$. Define ${\mathbf{y}}^{\prime }$ such that $y_u^{\prime }=1$ for $u\in \{i_1,\dots ,i_l\}$, $y_u^{\prime }=x_u$ for $u\in \{i_{c+1},\dots ,i_{c+d_a-q_1-q_2-l}\}$, $y_u^{\prime }=y_u$ for $u\in \{i_{w-q_1+1},\dots ,i_w\}\cup \{j_1,\dots ,j_{q_2}\}$, and $y_u^{\prime }=0$ for all other u. Define ${\mathbf{z}}^{\prime }$ such that $z_u^{\prime }=1$ for $u\in \{i_{l+1},\dots ,i_c\}$, $z_u^{\prime }=x_u$ for $u\in \{j_{c+d_a-l-q_1-q_2+1},\dots ,j_{d_a+d_b-2q_1-2q_2}\}$, $z_u^{\prime }=z_u$ for $u\in \{i_{w-q_1+1},\dots ,i_w\}\cup \{j_1,\dots ,j_{q_2}\}$, and $z_u^{\prime }=0$ for all other u. Then, $w\left({\mathbf{y}}^{\prime }\right)=d_a$, $w\left({\mathbf{z}}^{\prime }\right)=d_b$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Hence, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$. □

We next determine $H{(r\odot 2,m_1,\dots ,m_v;D)}^2$ with $d_a+d_b>r+2v$ for any $d_a,d_b\in D$, that is, $2min\{d_i\mid d_i\in D\}>r+2v$.

Theorem 6.

Let $m_1,\dots ,m_v\ge 3$ and let $r\ge 1$ be an odd (even) number. Let $D=\{d_1,\dots ,d_s\}$ be such that: $1\le d_i\le r+v$ for each i. Set $d={min}_{1\le i\le s}{d}_i$ and $2d>r+2v$. Let:

$$B_8=\{\beta \mid \beta \in {\mathbb{Z}}_2^{r+v}\backslash \left\{\mathbf{0}\right\},1\le w\left(\beta \right)\le d+1\},$$

and:

$$B_9=\{\beta \mid \beta \in {\mathbb{Z}}_2^{r+v}\backslash \left\{\mathbf{0}\right\},1\le w\left(\beta \right)\le 2r+3v-2d\}.$$

(a)

If $2r=3d-3v+1$ and $v=1,2$, let $D=\{d,d+1\}$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B_8).$$

(b)

If $2r=3d-3v$ and $v=1$, let $D=\{d,d+1\}$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B_8).$$

(c)

If $2r=3d-2v+1$ and $v\ge 1$, let $D=\{d,d+1,2r+2v-2d+1,\dots ,2r+3v-2d\}$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B_9).$$

(d)

If $2r=3d-2v$ and $v\ge 2$, let $D=\{d,d+1,2r+2v-2d+2,\dots ,2r+3v-2d\}$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B_9).$$

(e)

If $2r=3d-2v-1$ and $v\ge 3$, let $D=\{d,d+1,2r+2v-2d+3,\dots ,2r+3v-2d\}$. Then:

$$H{(r\odot 2,m_1,\dots ,m_v;D)}^2\cong \mathrm{NEPS}(r\odot K_2,K_{m_1},\dots ,K_{m_v};B_9).$$

Proof. 

(a) Let $\Gamma =\underset{r}{\underbrace{{\mathbb{Z}}_2\oplus \cdots \oplus {\mathbb{Z}}_2}}\oplus {\mathbb{Z}}_{m_1}\oplus \cdots \oplus {\mathbb{Z}}_{m_v}$. Let $S=\{\mathbf{x}\in \Gamma \backslash \mathbf{0}:w(\mathbf{x})\in D\}$. By Lemma 2 and Theorem 1,

$$H{(r\odot 2,m_1,\dots ,m_t;D)}^2\cong \mathrm{Cay}{(\Gamma ;S)}^2\cong \mathrm{Cay}(\Gamma ;S^{\left(\right\{1,2\left\}\right)}).$$

where $S^{\left(\right\{1,2\left\}\right)}=S^{\left(1\right)}\cup S^{\left(2\right)}=S\cup \{2S\backslash \left\{\mathbf{0}\right\}\}$ (see (1) and (2)). By Theorem 2, it suffices to prove:

$$S^{\left(\right\{1,2\left\}\right)}=\left\{x\in \Gamma \backslash \left\{\mathbf{0}\right\}:1\le w\left(x\right)\le d+1\right\}.$$

(8)

The proof of this consists of the following two claims.

Claim 1. $S^{\left(\right\{1,2\left\}\right)}\subseteq \left\{\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}:1\le w\left(\mathbf{x}\right)\le d+1\right\}$.

Let $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$. If $\mathbf{x}\in S$, then Claim 1 is true, as $w\left(\mathbf{x}\right)=d\in D$. Assume that $\mathbf{x}\in 2S\backslash \left\{\mathbf{0}\right\}$ in the sequel. Then, there exist at least two elements $\mathbf{y},\mathbf{z}\in S\backslash \left\{\mathbf{0}\right\}$ such that $\mathbf{x}=\mathbf{y}+\mathbf{z}$ and $(w\left(\mathbf{y}\right),w\left(\mathbf{z}\right))=(d_i,d_j)$. Define ${\mathbf{y}}^{\left(1\right)}:=(y_1,\dots ,y_r),{\mathbf{z}}^{\left(1\right)}:=(z_1,\dots ,z_r),{\mathbf{y}}^{\left(2\right)}:=(y_{r+1},\dots ,y_{r+v})$ and ${\mathbf{z}}^{\left(2\right)}:=(z_{r+1},\dots ,z_{r+v})$. Define:

$$l({\mathbf{y}}^{\left(1\right)},{\mathbf{z}}^{\left(1\right)})=\mid \{i:y_i\ne 0,z_i\ne 0,i\in \{1,2,\dots ,r\}\}\mid =q_1,$$

(9)

$$l({\mathbf{y}}^{\left(2\right)},{\mathbf{z}}^{\left(2\right)})=\mid \{i:y_i\ne 0,z_i\ne 0,i\in \{r+1,r+2,\dots ,r+v\}\}\mid =q_2.$$

(10)

Case 1. $x_i\ne 0$ for some $i\in \{r+1,\dots ,r+v\}$.

Case 1.1. $d_i=d_j=d$.

In this case, $2d-r-v\le q_1+q_2\le d$. If $q_1+q_2=d$, then $1\le w\left(\mathbf{x}\right)\le 2d-2(d-v)-v=v$. If $2d-r-v<q_1+q_2<d$, then: $2=2d-2(d-1)\le w\left(\mathbf{x}\right)\le 2d-2(2d-r-2v+1)-v=2r+3v-2d-2$. If $q_1+q_2=2d-r-v$, then $2r-2d+2v=2d-2(2d-r-v)\le w\left(\mathbf{x}\right)\le 2d-2(2d-r-2v)-v=2r+3v-2d$. Since $2r+3v-2d-2=2r-2d+2v-1,2r-2d+2v$ with regard to $v=1,2$, respectively, it follows that $1\le w\left(\mathbf{x}\right)\le 2r+3v-2d$.

Case 1.2. $d_i=d_j=d+1$.

Similar to Case 1.1, one can verify that $1\le w\left(\mathbf{x}\right)\le 2r+3v-2d-2.$

Case 1.3. $d_i=d,d_j=d+1$.

Similar to Case 1.1, we obtain that $1\le w\left(\mathbf{x}\right)\le 2r+3v-2d-1.$

In either case, we have $1\le w\left(\mathbf{x}\right)\le 2r+3v-2d.$

Case 2. $x_i=0$ for any $i\in \{r+1,\dots ,r+v\}$.

Case 2.1. $d_i=d_j=d$.

In this case, $2d-r-v\le q_1+q_2\le d$. If $q_1+q_2=d$, then $w\left(\mathbf{x}\right)=0$ and so $\mathbf{x}=\mathbf{0}$, which is a contradiction. If $2d-r-v\le q_1+q_2<d$, then: $w\left(\mathbf{x}\right)=2d-2(q_1+q_2)$. Hence, $w\left(\mathbf{x}\right)=2d-2(q_1+q_2)\mathrm{for}{q}_1+q_2=2d-r-v,\dots ,d-1.$

Case 2.2. $d_i=d_j=d+1$.

Similar to Case 2.1, one can easily verify that $w\left(\mathbf{x}\right)=2d+2-2(q_1+q_2)\mathrm{for}{q}_1+q_2=2d-r-v+2,\dots ,d.$

Case 2.3. $d_i=d,d_j=d+1$.

Similar to Case 2.1, one can easily verify that $w\left(\mathbf{x}\right)=2d+1-2(q_1+q_2)\mathrm{for}{q}_1+q_2=2d-r-v+1,\dots ,d.$

In either case, we have $1\le w\left(\mathbf{x}\right)\le 2r+2v-2d.$

In the following, we compare $2r+3v-2d$, $2r+2v-2d$, d and $d+1$. Note that $2r=3d-3v+1$, and we have $d<2r+3v-2d=d+1$. If $v=1$, then $2r+2v-2d=d<2r+2v-2d+1=d+1$. If $v=2$, then $2r+2v-2d=d-1<d<2r+2v-2d+2=d+1$. Thus, we obtain that $1\le w\left(\mathbf{x}\right)\le d+1forv=1,2.$

Claim 2. $\left\{\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}:1\le w\left(\mathbf{x}\right)\le d+1\right\}\subseteq S^{\left(\right\{1,2\left\}\right)}\}$.

Let $\mathbf{x}\in \Gamma \backslash \left\{\mathbf{0}\right\}$ be such that $1\le w\left(\mathbf{x}\right)\le d$. Set $w=w\left(\mathbf{x}\right)$. Suppose that $x_{i_1},\dots ,x_{i_w}\ne 0$ with $1\le i_1<i_2<\cdots <i_w\le r+v$. If $\mathbf{x}\in D$, then $\mathbf{x}\in S\subseteq S^{\left(\right\{1,2\left\}\right)}$. It remains to consider $1\le w\left(\mathbf{x}\right)\le d-1.$ Since $2r=3d-3v+1$, we have $1\le w\left(\mathbf{x}\right)\le 2r+2v-2d-1$ or $1\le w\left(\mathbf{x}\right)\le 2r+2v-2d$ with regard to $v=1$ or $v=2$, respectively.

Case 1. $i_w\le r$.

In this case, $x_{\alpha }=0$ for any $\alpha \in \{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,i_w\}$. Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i\ge 3$ for each i, there exist $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{\mathbf{0}\right\}$ such that $0=x_t=y_t+z_t$ for $t\in \{1,2,\dots ,v\}$. Denote $q_1=\mid \{i\mid i\in \{1,\dots ,r\}\backslash \{i_1,\dots ,i_w\}and{y}_i=z_i=1\}\mid$, $q_2=\mid \{i\mid i\in \{r+1,\dots ,r+v\}and{y}_i+z_i=0\}\mid$.

Subcase 1.1. w is odd.

Since $w\left(\mathbf{x}\right)\le 2r+2v-2d-1$ or $\le 2r+2v-2d$, we have $w=2d+1-2(q_1+q_2)$ with $2d-r-v+1\le q_1+q_2\le d$. Then, we can choose $q_1$ terms from $\{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,i_w\}$, say $j_1<\dots <j_{q_1}$, and choose $q_2$ terms from $\{r+1,\dots ,r+v\}$, say $j_{q_1+1}<\cdots <j_{q_1+q_2}$. Define ${\mathbf{y}}^{\prime }$ in such a way that $y_u^{\prime }=1$ if $u\in \{i_1,\dots ,i_{d-(q_1+q_2)}\}\cup \{j_1,\dots ,j_{q_1}\}$, $y_u^{\prime }=y_u$ if $u\in \{j_{q_1+1},\dots ,j_{q_1+q_2}\}$, and $y_u^{\prime }=0$ for all other u. Define ${\mathbf{z}}^{\prime }$ in such a way that $z_u^{\prime }=1$ if $u\in \{i_{d-(q_1+q_2)+1},\dots ,i_w\}\cup \{j_1,\dots ,j_{q_1}\}$, $z_u^{\prime }=z_u$ if $u\in \{j_{q_1+1},\dots ,j_{q_1+q_2}\}$, and $z_u^{\prime }=0$ for all other u. Then, $w\left(y\right)=d,w\left(z\right)=d+1$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Therefore, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Subcase 1.2. w is even.

Similar to Subcase 1.1, one can verify $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

Case 2. $i_w>r$.

Denote $c=|\{i_1,\dots ,i_w\}\cap \{1,\dots ,r\}|$. Then, $x_{\alpha }=0$ for $\alpha \in \{1,\dots ,r\}\backslash \{i_1,i_2,\cdots ,i_c\}$. Since ${\mathbb{Z}}_{m_i}$ is a cyclic group of order $m_i$ and $m_i\ge 3$ for each i, then there exist $y_{i_{\alpha }},z_{i_{\alpha }}\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $x_{i_{\alpha }}=y_{i_{\alpha }}+z_{i_{\alpha }}$ for $c+1\le \alpha \le w$, and $y_t,z_t\in {\mathbb{Z}}_{m_i}\backslash \left\{0\right\}$ such that $0=x_t=y_t+z_t$ for $t\in \{r+1,r+2,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$. Denote $q_1=\mid \{i\mid i\in \{1,\dots ,r\}\backslash \{i_1,\dots ,i_c\}and{y}_i=z_i=1\}\mid$, $q_2=\mid \{i\mid i\in \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i\}\mid$, and $q_3=\mid \{i\mid i\in \{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}and{x}_i=y_i+z_i=0\}\mid$. Since $2r=3d-3v+1$, $c\le w-1\le d-2$ and $v=1,2$, we have $2d-r-v\le r+v-c$; also note that $2d>r+v$, and then $2d-r-v\le q_1+q_2+q_3\le min\{r+v-c,d\}$. Thus, we can choose $q_1$ terms from $\{1,2,\dots ,r\}\backslash \{i_1,\dots ,i_c\}$, say, $j_1<j_2<\cdots <j_{q_1}$, choose $q_2$ terms from $\{i_{c+1},\dots ,i_w\}$, say, $i_{w-q_2+1}<\cdots <i_w$, and choose $q_3$ terms from $\{r+1,\dots ,r+v\}\backslash \{i_{c+1},\dots ,i_w\}$, say, $j_{q_1+1}<\cdots <j_{q_1+q_3}$. Define ${\mathbf{y}}^{\prime }$ in such a way that $y_u^{\prime }=1$ if $u\in \{i_1,\dots ,i_l\}\cup \{j_1,\dots ,j_{q_1}\}$, $y_u^{\prime }=x_u$ if $u\in \{i_{c+1},\dots ,i_{c+d-q_1-q_2-q_3-l}\}$, $y_u^{\prime }=y_u$ if $u\in \{i_{w-q_2+1},\dots ,i_w\}\cup \{j_{q_1+1},\dots ,j_{q_1+q_3}\}$, and $y_u^{\prime }=0$ for all other u. Define ${\mathbf{z}}^{\prime }$ in such a way that $z_u^{\prime }=1$ if $u\in \{i_{l+1},\dots ,i_c\}\cup \{j_1,\dots ,j_{q_1}\}$, $z_u^{\prime }=x_u$ if $u\in \{i_{c+d-q_1-q_2-q_3-l+1},\dots ,i_{2d-2q_1-2q_2-2q_3}\}$, $z_u^{\prime }=y_u$ if $u\in \{i_{w-q_2+1},\dots ,i_w\}\cup \{j_{q_1+1},\dots ,j_{q_1+q_3}\}$, and $z_u^{\prime }=0$ for all other u. Then, $w\left({\mathbf{y}}^{\prime }\right)=w\left({\mathbf{z}}^{\prime }\right)=d$ and $\mathbf{x}={\mathbf{y}}^{\prime }+{\mathbf{z}}^{\prime }$. Therefore, $\mathbf{x}\in S^{\left(\right\{1,2\left\}\right)}$.

(b)–(e) Similar to the proof of (a). Please see the Appendix A for the detailed modification.

□

Example 2.

(1)

Consider the square of the generalized Hamming graph $H(2,2,2,2,2,2,2,2,3;$$\{6,7\})$. Obviously, $r=8,v=1,d=6$, and by Theorem 6 (a), we have:

$$H{(2,2,2,2,2,2,2,2,3;\{6,7\})}^2\cong \mathrm{NEPS}(8\odot K_2,K_3;B),$$

where $B=\{x\mid x\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\},1\le w\left(x\right)\le 7\}$.

(2)

Consider the square of the generalized Hamming graph $H(2,2,2,2,2,2,3;\{5,6\left\}\right)$. Obviously, $r=6,v=1,d=5$, and by Theorem 6 (b), we have:

$$H{(2,2,2,2,2,2,3;\{5,6\})}^2\cong \mathrm{NEPS}(6\odot K_2,K_3;B),$$

where $B=\{x\mid x\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\},1\le w\left(x\right)\le 6\}$.

(3)

Consider the square of the generalized Hamming graph $H(2,2,2,2,2,2,2,2,2,3,3;\{7,8,9,10\left\}\right)$. Obviously, $r=9,v=2,d=7$, and by Theorem 6 (c), we have:

$$H{(2,2,2,2,2,2,2,2,2,3,3;\{7,8,9,10\})}^2\cong \mathrm{NEPS}(9\odot K_2,K_3,K_3;B),$$

where $B=\{x\mid x\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\},1\le w\left(x\right)\le 10\}$.

(4)

Consider the square of the generalized Hamming graph $H(2,2,2,2,2,2,2,2,2,3,3,3;\{8,9,10,11\left\}\right)$. Obviously, $r=9,v=3,d=8$, and by Theorem 6 (d), we have:

$$H{(2,2,2,2,2,2,2,2,2,3,3,3;\{8,9,10,11\})}^2\cong \mathrm{NEPS}(6\odot K_2,K_3,K_3,K_3;B),$$

where $B=\{x\mid x\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\},1\le w\left(x\right)\le 11\}$.

(5)

Consider the square of the generalized Hamming graph $H(2,2,2,2,2,2,2,2,2,2,3,3,3;\{9,10,11\left\}\right)$. Obviously, $r=10,v=3,d=9$, and by Theorem 6 (e), we have:

$$H{(2,2,2,2,2,2,2,2,2,2,3,3,3;\{9,10,11\})}^2\cong \mathrm{NEPS}(7\odot K_2,K_3,K_3,K_3;B),$$

where $B=\{x\mid x\in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\},1\le w\left(x\right)\le 11\}$.

4. Eigenvalues of the Square of Generalized Hamming Graphs

In this section, we investigate eigenvalues of the square of generalized Hamming graphs. Before proceeding, we give one result from [12].

Lemma 3

([12] [Theorem 2.23]). Let $G_i$ be a graph with $m_i$ vertices. Suppose that ${\lambda }_{i,1},\dots ,{\lambda }_{i,m_i}$ are the eigenvalues of $G_i(i=1,\dots ,n)$. Then, the spectrum of $G=\mathrm{NEPS}(G_1,\dots ,G_n;B)$ with respect to basis B consists of all possible values:

$${\Lambda }_{j_1,\dots ,j_n}=\sum _{\beta \in B}{\lambda }_{1,j_1}^{{\beta }_1}\cdots {\lambda }_{n,j_n}^{{\beta }_n},j_i=1,\dots ,m_i;i=1,\dots ,n.$$

Recall that $H(m_1,\dots ,m_r;D)$ is an NEPS of complete graphs $K_{m_1},\dots ,K_{m_r}$ (see Lemma 1 and Theorem 2). Note that the spectrum of $K_{m_i}$ consists of $m_i-1$ with multiplicity 1, and $-1$ with multiplicity $m_i-1$. Then, by Lemma 3, we obtain the following result.

Theorem 7.

Let $m_1,\dots ,m_r$ be positive integers, and $D=\{d_1,\dots ,d_s\}$ with $1\le d_i\le r$ for each i. Let $B=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D\}$. Then, the spectrum of $H(m_1,\dots ,m_r;D)$ consists of all possible values:

$${\Lambda }_{j_1,\dots ,j_r}=\sum _{\beta \in B}{\lambda }_{1,j_1}^{{\beta }_1}\cdots {\lambda }_{r,j_r}^{{\beta }_r},j_i=1,\dots ,m_i;i=1,\dots ,r,$$

where ${\lambda }_{i,1}=m_i-1$, and ${\lambda }_{i,j}=-1$ for $2\le j\le m_i$.

Suppose $m_1,\dots ,m_r\ge 3$ and $D=\{d_1,\dots ,d_s\}$, where $1\le d_i\le r$ for each i. Set $d={max}_{1\le i\le s}{d}_i$. By Theorems 2 and 3, Lemma 1, we see that:

$$H{(m_1,\dots ,m_r;D)}^2\cong H(m_1,\dots ,m_r;D^{\prime }),$$

where $D^{\prime }=\left\{1,\dots ,2d\right\}$ if $2d<r$, and $D^{\prime }=\left\{1,\dots ,r\right\}$ if $2d\ge r$. Note that isomorphic graphs have the same spectrum. Then, by Theorem 7, we have the following result.

Theorem 8.

Let $m_1,\dots ,m_r$, D and $D^{\prime }$ be as above. Let $B=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D^{\prime }\}$.

(a)

For $2d\ge r$, $H{(m_1,\dots ,m_r;D)}^2$ is a complete graph.

(b)

For $2d<r$, let $L=\left\{i\right|{\lambda }_{i,j_k}=-1,i=1,\dots ,r\}$ and $l:=\left|L\right|$. Assume the elements in L are $a_1<a_2<\cdots <a_l$.

(b.1)

If $l<2d<r$, then the eigenvalues of $H{(m_1,\dots ,m_r;D)}^2$ are:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=1}^l\left[\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right)\right]\hfill \\ \hfill & +\sum _{s=l+1}^{2d}\left[\sum _{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right)\right].\hfill \end{array}$$

(b.2)

If $2d\le l$, then the eigenvalues of $H{(m_1,\dots ,m_r;D)}^2$ are:

$${\Lambda }_l=\sum _{s=1}^{2d}\left[\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right)\right],$$

where $\phi \left(b\right)=1$ if $b\in S$ and $\phi \left(b\right)=0$ if $b\notin S$.

Proof. 

(a) If $2d\ge r$, then $D^{\prime }=\{1,\dots ,r\}$. Thus, it is a complete graph.

(b) For any $s\in D^{\prime }$, define $B_s=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=s\}$.

If $s\le l$, we choose $j(0\le j\le s)$ terms of $\{a_1,a_2,\dots ,a_l\}$ and j terms of $\{1,\dots ,r\}\backslash \{a_1,a_2,\dots ,a_l\}$, and assume that the $s-j$ terms are $b_1,\dots ,b_{s-j}$. Then, by Theorem 7,

$${\Lambda }_{\left\{s\right\}}=\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right).$$

If $s>l$, we choose $j(0\le j\le l)$ terms of $\{a_1,a_2,\dots ,a_l\}$ and j terms of $\{1,\dots ,r\}\backslash \{a_1,a_2,\dots ,a_l\}$, and assume that the $s-j$ terms are $b_1,\dots ,b_{s-j}$. Then, by Theorem 7,

$${\Lambda }_{\left\{s\right\}}=\sum _{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right).$$

If $l\le 2d<r$, then:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=1}^{2d}{\Lambda }_{\left\{s\right\}}\hfill \\ \hfill =& \sum _{s=1}^l{\Lambda }_{\left\{s\right\}}+\sum _{s=l+1}^{2d}{\Lambda }_{\left\{s\right\}}\hfill \\ \hfill =& \sum _{s=1}^l\left[\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right)\right]\hfill \\ \hfill & +\sum _{s=l+1}^{2d}\left[\sum _{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right)\right],\hfill \end{array}$$

yielding (b.1).

If $2d<l$, then:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=1}^{2d}{\Lambda }_{\left\{s\right\}}\hfill \\ \hfill =& \sum _{s=1}^{2d}\left[\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j}\}}{\subseteq \{1,\dots ,r\}\backslash \{a_1,\dots ,a_l\}}}\prod _{b\in \{1,\dots ,r\}}{(m_b-1)}^{\phi \left(b\right)}\right)\right],\hfill \end{array}$$

yielding (b.2).

This completes the proof. □

Let $m_1=\dots =m_r=2$, $D=\{1,\dots ,d\}$ with $1\le d\le r$. By Theorems 2 and 4, we see that:

$$H{(r\odot 2;D)}^2=H(r\odot 2;D^{\prime }),$$

where $D^{\prime }=\left\{1,\dots ,2d\right\}$ if $2d<r$ and $D^{\prime }=\left\{1,\dots ,r\right\}$ if $2d\ge r$. Then, by Theorem 7, we have the following result.

Theorem 9.

Let r be a positive integer, and D and $D^{\prime }$ be as above. Let $B=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D^{\prime }\}$.

(a)

If $2d\ge r$, then $H{(r\odot 2;D)}^2$ is a complete graph.

(b)

If $2d<r$, let $L=\left\{i\right|{\lambda }_{i,j_k}=-1,i=1,\dots ,r\}$ and $l:=\left|L\right|$. Assume the elements in L are $a_1<a_2<\cdots <a_l$.

(b.1)

If $l\le 2d<r$, then the eigenvalues of $H{(r\odot 2;D)}^2$ consist of all possible values:

$${\Lambda }_l=\sum _{s=1}^l\left(\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}\right)+\sum _{s=l+1}^{2d}\left(\sum _{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}\right).$$

(b.2)

If $2d<l$, then the eigenvalues of $H{(r\odot 2;D)}^2$ consist of all possible values:

$${\Lambda }_l=\sum _{s=1}^{2d}\left(\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}\right).$$

Proof. 

(a) If $2d\ge r$, then $D^{\prime }=\{1,\dots ,r\}$. Thus, it is a complete graph.

(b) For any $s\in D^{\prime }$, define $B_s=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=s\}$.

If $s\le l$, there are ${\displaystyle \sum _{j=0}^s}\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right)$ ways to choose $j(0\le j\le s)$ terms of $\{a_1,a_2,\dots ,a_l\}$ and $s-j$ terms of $\{1,\dots ,r\}\backslash \{a_1,a_2,\dots ,a_l\}$. Then, by Theorem 7,

$${\Lambda }_{\left\{s\right\}}=\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}.$$

If $s>l$, there are ${\displaystyle \sum _{j=0}^l}\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right)$ ways to choose $j(0\le j\le l)$ terms of $\{a_1,a_2,\dots ,a_l\}$ and $s-j$ terms of $\{1,\dots ,r\}\backslash \{a_1,a_2,\dots ,a_l\}$. Then, by Theorem 10,

$${\Lambda }_{\left\{s\right\}}=\sum _{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}.$$

If $l\le 2d<r$, then:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=1}^{2d}{\Lambda }_{\left\{s\right\}}\hfill \\ \hfill =& \sum _{s=1}^l{\Lambda }_{\left\{s\right\}}+\sum _{s=l+1}^{2d}{\Lambda }_{\left\{s\right\}}\hfill \\ \hfill =& \sum _{s=1}^l\left(\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}\right)+\sum _{s=l+1}^{2d}\left(\sum _{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}\right),\hfill \end{array}$$

yielding (b.1).

If $2d<l$, then:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=0}^{2d}{\Lambda }_{\left\{s\right\}}\hfill \\ \hfill =& \sum _{s=1}^{2d}\left(\sum _{j=0}^s\left(\genfrac{}{}{0pt}{}{l}{j}\right)\left(\genfrac{}{}{0pt}{}{r-l}{s-j}\right){(-1)}^j{1}^{s-j}\right),\hfill \end{array}$$

yielding (b.2).

This completes the proof. □

Let $m_1,\dots ,m_t$ be positive integers with $m_i\ge 3$ for each i, and D a set of integers with $1\le d_i\le r+v$. By Theorems 2, 5 and 6, we have:

$$H{(r\odot 2,m_1,\dots ,m_t;D)}^{\{1,2\}}\cong H(r\odot 2,m_1,\dots ,m_v;D^{\prime }),$$

where $D^{\prime }=\left\{1,\dots ,d^{\prime }\right\}$ if $d^{\prime }<r+v$, and $D^{\prime }=\left\{1,\dots ,r+v\right\}$ if $d^{\prime }\ge r+v$, and in here $d^{\prime }=max\left\{w\left(x\right)\right|x\in B_i\}$ for $i=7,8,9$ having different values with respect to Theorems 5 and 6.

Theorem 10.

Let $m_1,\dots ,m_v$, D, and $D^{\prime }$ be as above. Let $B=\{\beta \in {\mathbb{Z}}_2^{r+v}\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)\in D^{\prime }\}$.

(a)

If $d^{\prime }\ge r+v$, then $H{(r\odot 2,m_1,\dots ,m_v;D)}^2$ is a complete graph.

(b)

If $d^{\prime }<r+v$, let $L=\left\{i\right|{\lambda }_{i,j_k}=-1,i=1,\dots ,r+v\}$ and $l+l^{\prime }:=\left|L\right|$. Assume that the elements in L are $a_1<\cdots <a_l<a_{l+1}<\cdots <a_{l+l^{\prime }}$. Then, the eigenvalues of $H{(r\odot 2,m_1,\dots ,m_v;D)}^2$ are:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=1}^{d^{\prime }}\left\{\sum _{j=0}^s\left[\sum _{j^{\prime }=0}^j\left(\genfrac{}{}{0pt}{}{l}{j^{\prime }}\right)\left(\genfrac{}{}{0pt}{}{r-l}{j-j^{\prime }}\right){(-1)}^{j^{\prime }}\right]\right.\hfill \\ \hfill & ·\left.\left[\sum _{j^{″}=0}^{s-j}\left(\genfrac{}{}{0pt}{}{l^{\prime }}{j^{″}}\right){(-1)}^{j^{\prime \prime }}\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j-j^{″}}\}}{\subseteq \{r+1,\dots ,r+v\}\backslash \{a_{l+1},\dots ,i_{l+l^{\prime }}\}}}\prod _{b\in \{r+1,\dots ,r+v\}}{(m_{(b-r)}-1)}^{\phi \left(b\right)}\right)\right]\right\},\hfill \end{array}$$

where $\phi \left(b\right)=1$ if $b\in S$ and $\phi \left(b\right)=0$ if $b\notin S$.

Proof. 

(a) If $2d\ge r$, then $D^{\prime }=\{1,\dots ,r\}$. Thus, it is a complete graph.

(b) For any $s\in D^{\prime }$, define $B_s=\{\beta \in {\mathbb{Z}}_2^r\backslash \left\{\mathbf{0}\right\}:w\left(\beta \right)=s\}$. We choose $j^{\prime }(0\le j^{\prime }\le l)$ terms of $\{a_1,a_2,\dots ,a_l\}$, $j-j^{\prime }$ terms of $\{1,\dots ,r\}\backslash \{a_1,a_2,\dots ,a_l\}$, $j^{″}$ terms of $\{a_{l+1},a_{l+2},\dots ,a_{l+l^{\prime }}\}$, and $s-j-j^{″}$ terms of $\{r+1,\dots ,r+v\}\backslash \{a_{l+1},\dots ,a_{l+l^{\prime }}\}$, and assume that the $s-j-j^{″}$ terms are $b_1,\dots ,b_{s-j-j^{″}}$. Then, by Theorem 7,

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{j=0}^s\left[\sum _{j^{\prime }=0}^j\left(\genfrac{}{}{0pt}{}{l}{j^{\prime }}\right)\left(\genfrac{}{}{0pt}{}{r-l}{j-j^{\prime }}\right){(-1)}^{j^{\prime }}\right]\hfill \\ \hfill & ·\left[\sum _{j^{″}=0}^{s-j}\left(\genfrac{}{}{0pt}{}{l^{\prime }}{j^{″}}\right){(-1)}^{j^{″}}\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j-j^{\prime \prime }}\}}{\subseteq \{r+1,\dots ,r+v\}\backslash \{a_{l+1},\dots ,i_{l+l^{\prime }}\}}}\prod _{b\in \{r+1,\dots ,r+v\}}{(m_{(b-r)}-1)}^{\phi \left(b\right)}\right)\right].\hfill \end{array}$$

Then:

$$\begin{array}{cc}\hfill {\Lambda }_l=& \sum _{s=1}^{d^{\prime }}\left\{\sum _{j=0}^s\left[\sum _{j^{\prime }=0}^j\left(\genfrac{}{}{0pt}{}{l}{j^{\prime }}\right)\left(\genfrac{}{}{0pt}{}{r-l}{j-j^{\prime }}\right){(-1)}^{j^{\prime }}\right]\right.\hfill \\ \hfill & ·\left.\left[\sum _{j^{″}=0}^{s-j}\left(\genfrac{}{}{0pt}{}{l^{\prime }}{j^{″}}\right){(-1)}^{j^{\prime \prime }}\left(\sum _{\genfrac{}{}{0pt}{}{S=\{b_1,\dots ,b_{s-j-j^{″}}\}}{\subseteq \{r+1,\dots ,r+v\}\backslash \{a_{l+1},\dots ,i_{l+l^{\prime }}\}}}\prod _{b\in \{r+1,\dots ,r+v\}}{(m_{(b-r)}-1)}^{\phi \left(b\right)}\right)\right]\right\}.\hfill \end{array}$$

This completes the proof. □

Example 3.

(1)

Consider the generalized Hamming graph $H{(3,3,4;\left\{1\right\})}^{\{1,2\}}$. Obviously, Theorem 3 implies that:

$$H{(3,3,4;\left\{1\right\})}^2\cong H(3,3,4;\{1,2\}).$$

By Theorem 8, its eigenvalues are $23,5,3,0,-3$, and $-4$ with respective multiplicities $1,4,3,12,$ 12 and 4.

(2)

Consider the generalized Hamming graph $H{(2,2,2,2,2;\left\{1\right\})}^{\{1,2\}}$. Obviously, Theorem 4 implies that:

$$H{(2,2,2,2,2;\left\{1\right\})}^2\cong H(2,2,2,2,2;\{1,2\}).$$

By Theorem 9, its eigenvalues are $15,5,-1,-3$ with respective multiplicities $1,6,15,10$.

(3)

Consider the generalized Hamming graph $H{(2,3,3;\left\{1\right\})}^{\{1,2\}}$. Obviously, Theorem 6 implies that:

$$H{(2,3,3;\left\{1\right\})}^2\cong H(2,3,3;\{1,2\}).$$

By Theorem 10, its eigenvalues are $13,3,1,0,-2$, and $-3$ with respective multiplicities $1,1,4,4,4$ and 4.

5. Conclusions

Characterizing the square of some generalized Hamming graphs is useful for studying the $kth$ power of the graph. This article provides some characterizations of $H{(m_1,\dots ,m_r;D)}^2$ with NEPS of complete graphs through group calculations. In addition, we can directly obtain the eigenvalues of $H{(m_1,\dots ,m_r;D)}^2$ by NEPS. We are sure that the method used in this article can also be applied to the study of other Caley graphs, and any attempts on other graphs would be welcome; maybe the diameter of $H{(m_1,\dots ,m_r;D)}^2$ can be studied too.