Dynamic Analysis of Delayed Two-Species Interaction Model with Age Structure: An Application to Larch-Betula Platyphylla Forests in the Daxing’an Mountains, Northeast China

Abstract

Since plant–plant interaction has been the fundamental issue of the ecology community and is essential for the multispecies forest community, it is necessary to analyze the interaction mechanisms and provide suggestions for collaborative management of multispecies forests with the background of double carbon goals in China. To explore the interaction mechanisms in different interaction modes and assist China’s green development, we choose the most promising area, the Daxing’an Mountains, and its dominant species, Larch and Betula platyphylla, as research objects and establish a delayed two-species interaction model with an age structure. First, we calculate the equilibria of our model and analyze the stability of equilibria. Then, we study the existence of the Hopf bifurcation near the equilibria. Furthermore, we determine reasonable parameter values based on official data through mathematical methods, such as cluster analysis and model fitting. Finally, we carry out numerical simulations from three aspects, the evolution of a stand structure without interactions, the population dynamics in different interaction modes, and the influences of the parameters on the equilibria. Combined with simulation results, we provide biological interpretations for simulations of the stand structure evolution process and the interactions between Larch and Betula platyphylla; we also give reasonable values of the growth rates and mortalities for developing forest strategies.

1. Introduction

Since the mid-19th century, global temperatures have increased significantly. Official data show that the global mean temperature for 2021 was approximately 1.11 degrees above the preindustrial level (Available online: https://public.wmo.int/en (accessed on 1 February 2023)). It is widely believed that excessive greenhouse gases are a significant cause of global warming. As one of the most important greenhouse gases, carbon dioxide continues to increase, rising from 339.64 ppm in 1980 to 416.22 ppm in 2022 and exhibiting an upward trend (Available online: https://gml.noaa.gov/ccgg/ (accessed on 1 February 2023)). The continuous increase in carbon dioxide aggravates the greenhouse effect, affects the ecosystem on the earth, and hinders the sustainable development of humankind. With the global climate changing in an increasingly obvious manner, global warming has attracted extensive attention from the international community. Many countries have taken active measures and signed the United Nations Framework Convention on Climate Change, which sets a limit on the rise of the global temperature. Moreover, the Chinese government has made pledges to reach their peak emission level before 2030 and become carbon neutral before 2060 to promote the green growth and sustainable development of China.

As important carbon depots and carbon absorption sinks of terrestrial ecosystems, forest ecosystems play an important role in the global carbon cycle and carbon balancing. Four billion hectares of forest ecosystems account for 30% of the global terrestrial area, store 45% of the terrestrial carbon, and contribute 50% of the net primary terrestrial productivity [1]. It has been shown that not only reforestation and afforestation can mitigate carbon emissions; reasonable forest management practices, such as stand-scale management and pest control are also beneficial for net carbon sequestration [2]. Therefore, it is necessary to make full use of forest resources and explore reasonable forest strategies to respond to climate change.

The Daxing’an Mountains form the largest bright coniferous forest area in the cold temperate zone in China. Their forest resource area is 8.3702 million hectares, accounting for nearly 1/3 of the national key state-owned forest area, which has important economic and ecological benefits. Larch is the main tree species for forest regeneration in the Daxing’an Mountains, with strong competitiveness and carbon sink capacity [3]. However, due to frequent forest fires and overcutting in the last century, the Daxing’an Mountains have been significantly degraded, and the original pure Larch and Betula platyphylla forests have been heavily reduced. To restore the ecological environment, Betula platyphylla first invades and propagates as a pioneer species. Subsequently, the Larch forest develops, gradually forming a mixed forest dominated by Larch and Betula platyphylla. Currently, most Larch forests are still in the juvenile and middle ages, so they have enormous ecological value and carbon sink potential. Therefore, by studying the evolution of stands and the interactions between Larch and Betula platyphylla, we can better predict the population dynamics and manage forests to expedite the achievement of the double carbon goals of China.

The study of plant–plant interactions is one of the most fundamental issues in the community ecology and essential for understanding how the ecosystem responds to environmental changes and for predicting population dynamics [4,5]. Both positive interaction (i.e., facilitation) and negative interaction (i.e., competition) are a kind of self-protection and dynamic adjustment mechanisms that widely exist in nature and drive population dynamics [6], community structures [7], ecosystem functions [8], and even biological evolution processes [9]. Although much of the previous research focused on competition, recent studies still further emphasized the important impact of positive interactions on community structures [10] and biodiversity [11,12], especially under harsh environmental conditions [13]. It has been shown that the mutualistic relationship, as one of the main interaction modes, promotes the composition of complex communities as ecological engineers [14]. Furthermore, recent studies have suggested that indirect facilitation can promote coexistence and the construction of communities, which indicates that positive interactions should be more common in nature [15]. Although plant–plant interaction studies have developed rapidly, a modeling approach for exploring interaction mutualisms has not been widely investigated or employed [15]. Moreover, one aspect worth considering in plant–plant interaction studies is that a specific characteristic can influence the effect and result of plant–plant interactions [16]. Another understudied aspect is how interaction modes influence population dynamics. Recent studies have shown that symmetric and asymmetric facilitation modes cause distinctly varied spatial patterns by influencing the aggregation of plants [17]. Therefore, it is necessary to establish models that consider the above problems and carry out more simulations to further clarify the interaction mechanism.

The research methods for determining the interactions between plants mainly include experiments and modeling approaches. Despite the wide application of experiments in studies, it is not accurate to study population dynamics and interaction mechanisms merely according to experimental results. This is because positive and negative interactions are simultaneously present in population dynamics, and they are difficult to fully distinguish with existing technologies [18]. Therefore, models are widely adopted as tools to simulate different phenomena and predict the development of populations. Numerous studies have established individual-based models, including the FRN model, the ZOI model [19], the FON model [20,21], and other extended models [22]. However, individual-based models mainly focus on plant competition in the circular areas where plants acquire resources, without considering the impact of plants on nutrient resources through their interactions [23]. Different from individual-based models, the Lotka–Volterra model reflects the changes in resources caused by population interactions. Based on the classical model, many studies have established extended models incorporating population heterogeneity, harvesting, time delays, and stage structures to solve various problems [24,25].

Based on the above background, we choose Larch and Betula platyphylla from the Daxing’an Mountains of Heilongjiang Province in China as our research objects. We consider that population characteristics at different age stages and interaction modes can affect the responses of the population to interactions. Therefore, we establish a four-dimensional differential equation with two-time delays incorporating stage structure and interaction modes to analyze population dynamics and provide suggestions for forest management.

The rest of the content is arranged as follows. In Section 2, we establish a differential equation model with two delays based on the characteristics of different age stages and the interactions between Larch and Betula platyphylla. In Section 3, we analyze the existence and stability of equilibria and the existence of Hopf bifurcation of our model. In Section 4, we determine reasonable parameter values based on official data and conduct numerical simulations involving different subjects. Finally, the conclusion is given in Section 5.

2. Mathematical Modeling

Considering the differences in mortality, competitiveness, and responses to interactions between the immature and the mature [26], we divide Larch and Betula platyphylla into separate mature and immature groups [27,28,29,30]. We define x, y, u, and v as the amounts of immature Larch, mature Larch, immature Betula platyphyll, and mature Betula platyphylla, respectively. Based on the background, we discuss the model in terms of the following aspects.

(i)

Since plant growth cannot be completed immediately, there will be a time delay during the shift of plants toward maturity. We use time delays ${\tau }_1$ to represent the mature time required for the immature Larch (x) to grow into mature Larch (y). Similarly, we define ${\tau }_2$ as the mature time required for the immature Betula platyphyll (u) to grow into mature Betula platyphyll (v). It is believed that the mature time, considered a plant trait, can affect population dynamics and the regeneration of plants after fires [31], which is consistent with the forest recovery background observed after the frequent fires of the last century in the Daxing’an Mountains. Based on the large mature time differences between Larch and Betula platyphylla, we consider the mature time as a population characteristic in our model.

(ii)

Considering the limited competitiveness of the immature population, we focus on the effect of the mature population on the immature population. We assume that the number of the immature population at t is related to the number of the mature population at $t-{\tau }_i(i=1,2)$ [28] because some immature plants grow into mature plants at $t-{\tau }_i(i=1,2)$. Due to the loss of populations while plants grow, we let $m_1$ and $m_2$ denote the transition factor of the immature population growing into the mature population, for Larch and Betula platyphylla, respectively.

(iii)

To explore the interaction mechanism between Larch and Betula platyphylla in different interaction modes, we define interaction factors to vary the interaction mode. It has been shown that Betula platyphylla litter contributes to the decomposition of Larch litter, which accelerates the shift of nutrients from litter to soil and improves soil fertility. Moreover, Betula platyphylla improves the damaged ecological environments of the Daxing’an Mountains as a pioneer species. Therefore, we define $b_1$ as the interaction factor of Betula platyphylla on Larch. Then, considering the competition of Larch against Betula platyphylla, we define $b_2$ as the interaction factor of Larch on Betula platyphylla.

(iv)

We assume that the mature population has the ability to propagate, while the immature population does not. Thus, we believe that birth into the immature population with time is proportional to its mature population with a growth rate. Then, we discuss the expression of growth rates.

Due to the restriction of environmental carrying capacity, the population size cannot continue to grow, and its growth rate will decrease with increasing population size. Therefore, we define $N_1$ and $N_2$ as the environmental carrying capacities of Larch and Betula platyphylla to constrain their growth rates, respectively. Based on the net growth rates ${\alpha }_1$ and ${\alpha }_2$ belonging to Larch and Betula platyphylla, respectively, we suggest that the growth rates are negatively proportional to their own population sizes, which are ${\alpha }_1(1-(x+y)/N_1)$ and ${\alpha }_2(1-(u+v)/N_2)$, respectively. Interactions are the main driving forces of plant community organization and dynamics [5]. Considering the actual situation, we suggest that the Larch population can reproduce more rapidly with improvements in damaged environments provided by Betula platyphylla. Thus, different from the classical Lotka–Volterra model that simply focuses on competition, we consider the effects of interactions including facilitation and competition on the growth rate. We assume that the growth rate is related to the number of neighbor species with interaction factors of $b_i(i=1,2)$. Then, the growth rates of Larch and Betula platyphylla are as follows, ${\alpha }_1(1-(x+y)/N_1+b_1(u+v)/N_1)$ and ${\alpha }_2(1-(u+v)/N_2+b_2(x+y)/N_2)$, respectively.

(v)

We assume that the immature death with time is proportional to the existing immature population with mortalities $r_1$ and $r_3$ for immature Larch and immature Betula platyphylla, respectively. In addition to the capacity of the population, mature death is also related to the intense competition among mature plants. With an increasing size of the mature population, the intraspecific competition among the mature members becomes increasingly intense, which increases the mature death. Thus, we suppose that the mature death with time is proportional to the square of the mature population with mortalities $r_2$ and $r_4$ [27,28,29,30] for mature Larch and mature Betula platyphylla, respectively. That is the reason we divide the population into immature and mature groups.

Based on the background and above analysis, a Larch-Betula platyphylla interaction model with two-time delays divided into different age stages is established

$$\left\{\begin{array}{c}\frac{dx}{dt}={\alpha }_{1}y(1-\frac{x+y}{N_1}+b_1\frac{u+v}{N_1})-r_{1}x-m_{1}y(t-{\tau }_1),\hfill \\ \frac{dy}{dt}=m_{1}y(t-{\tau }_1)-r_2{y}^2,\hfill \\ \frac{du}{dt}={\alpha }_{2}v(1-\frac{u+v}{N_2}+b_2\frac{x+y}{N_2})-r_{3}u-m_{2}v(t-{\tau }_2),\hfill \\ \frac{dv}{dt}=m_{2}v(t-{\tau }_2)-r_4{v}^2,\hfill \end{array}\right.$$

(1)

where x, y, u, and v are the amounts of immature Larch, mature Larch, immature Betula platyphyll, and mature Betula platyphylla, respectively; $r_1,r_2,r_3,r_4$, ${\alpha }_1$, ${\alpha }_2$, $N_1,N_2,m_1$, and $m_2$ are positive constants; $b_1$ and $b_2\in [-1,1]$ are constants; and ${\tau }_1,{\tau }_2$ are time delays representing the mature times required for immature plants to grow into mature Larch and Betula platyphylla, respectively. The specific descriptions are given in

Table 1. Descriptions of the variables and parameters in system (1).

Symbol	Description	Unit
x	Amount of immature Larch	${10}^4/\mathrm{ha}$
y	Amount of mature Larch	${10}^4/\mathrm{ha}$
u	Amount of immature Betula platyphylla	${10}^4/\mathrm{ha}$
v	Amount of mature Betula platyphylla	${10}^4/\mathrm{ha}$
$N_1$	Environmental carrying capacity of Larch	${10}^4/\mathrm{ha}$
$N_2$	Environmental carrying capacity of Betula platyphylla	${10}^4/\mathrm{ha}$
${\alpha }_1$	Net growth rate of Larch	-
${\alpha }_2$	Net growth rate of Betula platyphylla	-
$b_1$	Interaction factor of Betula platyphylla on Larch	-
$b_2$	Interaction factor of Larch on Betula platyphylla	-
$m_1$	Transition factor of immature Larch growing into mature Larch	-
$m_2$	Transition factor of immature Betula platyphylla growing into mature Betula platyphylla	-
$r_1$	Mortality of immature Larch	-
$r_2$	Mortality of mature Larch	-
$r_3$	Mortality of immature Betula platyphylla	-
$r_4$	Mortality of mature Betula platyphylla	-
${\tau }_1$	Time delay for immature Larch to grow into mature Larch	year
${\tau }_2$	Time delay for immature Betula platyphylla to grow into mature Betula platyphylla	year

, where ${10}^4/\mathrm{ha}$ represents ${10}^4$ trees per hectare.

3. Stability of Equilibria and the Existence of Hopf Bifurcation

In this section, we analyze the stability of equilibria and the existence of Hopf bifurcation for system (1) near equilibria. We first determine the equilibrium of system (1). Letting $dx/dt=dy/dt=du/dt=dv/dt=0$, we obtain:

$$\left\{\begin{array}{c}{\alpha }_{1}y(1-\frac{x+y}{N_1}+b_1\frac{u+v}{N_1})-r_{1}x-m_{1}y=0,\hfill \\ y(m_1-r_{2}y)=0,\hfill \\ {\alpha }_{2}v(1-\frac{u+v}{N_2}+b_2\frac{x+y}{N_2})-r_{3}u-m_{2}v=0,\hfill \\ v(m_2-r_{4}v)=0.\hfill \end{array}\right.$$

Obviously, system (1) has four equilibria:

$$E_0=(x_0,y_0,u_0,v_0),E_1=(x_1,y_1,u_1,v_1),E_2=(x_2,y_2,u_2,v_2),E_3=(x_3,y_3,u_3,v_3),$$

where

$$\begin{array}{cc}\hfill & x_0=y_0=u_0=v_0=0,\hfill \\ \hfill & x_1=\frac{{\alpha }_1{m}_1{N}_1{r}_2-{\alpha }_1{m}_1^2-m_1^2{N}_1{r}_2}{{\alpha }_1{m}_1{r}_2+r_1{r}_2^2{N}_1},y_1=\frac{m_1}{r_2},u_1=v_1=0,\hfill \\ \hfill & x_2=y_2=0,u_2=\frac{{\alpha }_2{m}_2{N}_2{r}_4-{\alpha }_2{m}_2^2-m_2^2{N}_2{r}_4}{{\alpha }_2{m}_2{r}_4+r_3{r}_4^2{N}_2},v_2=\frac{m_2}{r_4},\hfill \\ \hfill & x_3=\frac{ak+cd}{dg-kh},y_3=\frac{m_1}{r_2},u_3=\frac{ag+ch}{dg-kh},v_3=\frac{m_2}{r_4},\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill & a=m_1-{\alpha }_1+\frac{{\alpha }_1{m}_1}{r_2{N}_1}-\frac{{\alpha }_1{m}_2{b}_1}{r_4{N}_1},c=m_2-{\alpha }_2+\frac{{\alpha }_2{m}_2}{r_4{N}_2}-\frac{{\alpha }_2{m}_1{b}_2}{N_2{r}_2},\hfill \\ \hfill & d=\frac{{\alpha }_1{b}_1}{N_1},g=\frac{{\alpha }_2{b}_2}{N_2},h=\frac{{\alpha }_1}{N_1}+\frac{r_1{r}_2}{m_1},k=\frac{{\alpha }_2}{N_2}+\frac{r_3{r}_4}{m_2}.\hfill \end{array}$$

Considering the biological meanings of the equilibria $E_1,E_2$, and $E_3$, we should ensure they are non-negative.

For the equilibrium $E_1$, we let $x_1>0$ and $y_1>0$. Since that ${\alpha }_1,m_1,r_1,r_2$, and $N_1$ are positive constants, $y_1>0$ and $x_1>0$ is equal to ${\alpha }_1{m}_1{N}_1{r}_2-{\alpha }_1{m}_1^2-m_1^2{N}_1{r}_2>0$. Then, we obtain that $1/m_1>(1/r_2{N}_1+1/{\alpha }_1)$.

For the equilibrium $E_2$, considering ${\alpha }_1,m_2,r_3,r_4,N_2$ all positive, $v_2>0$, and, thus, we simply need to make ${\alpha }_2{m}_2{N}_2{r}_4-{\alpha }_2{m}_2^2-m_2^2{N}_2{r}_4>0$. Thus, we obtain $1/m_2>(1/r_4{N}_2+1/{\alpha }_2$) to make sure $E_2$ is non-negative.

For the equilibrium $E_3$, with $m_1,m_2,r_2,r_4$ positive, $y_3$ and $v_3$ are positive, and, thus, we simply need to discuss the condition of $(ak+cd)/(dg-kh)$ and $(ag+ch)/(dg-kh)$. Considering the two expressions have the same denominator, we make sure $ak+cd$, $ag+ch$, and $dg-kh$ are all positive or all negative. Thus, we obtain $dg-kh>0,ag+ch>0,ak+ch>0ordg-kh<0,ag+ch<0,ak+ch<0$. As a practical matter, we consider the following hypothesis, such that the equilibria are all non-negative.

Hypothesis 1 (H1).

$\frac{1}{m_1}>\frac{1}{r_2{N}_1}+\frac{1}{{\alpha }_1}$.

Hypothesis 2 (H2).

$\frac{1}{m_2}>\frac{1}{r_4{N}_2}+\frac{1}{{\alpha }_2}$.

Hypothesis 3 (H3).

$dg-kh>0,ag+ch>0,ak+ch>0ordg-kh<0,ag+ch<0,ak+ch<0$.

When $\left(\mathrm{H}1\right)$ holds, the equilibrium $E_1$ is non-negative. When $\left(\mathrm{H}2\right)$ holds, the equilibrium $E_2$ is non-negative. When $\left(\mathrm{H}3\right)$ holds, the equilibrium $E_3$ is positive.

Considering the biological meaning of variables, we are more concerned with the condition of semi-trivial equilibria $E_1,E_2$, and non-trivial equilibrium $E_3$. Thus, we simply discuss the stability and Hopf bifurcation of system (1) at $E_1,E_2$, and $E_3$. We let $E_k=(x_k^{*},y_k^{*},u_k^{*},v_k^{*})(k=1,2,3)$. The characteristic equation of system (1) at $E_k$ is as follows

$$(\lambda +2r_4{v}_k^{*}-m_2{\mathrm{e}}^{-\lambda {\tau }_2})(\lambda +2r_2{y}_k^{*}-m_1{\mathrm{e}}^{-\lambda {\tau }_1})[(\lambda +A)(\lambda +B)-C]=0,k=1,2,3,$$

(2)

where

$$A=\frac{{\alpha }_1{y}_k^{*}}{N_1}+r_1,B=\frac{{\alpha }_2{v}_k^{*}}{N_2}+r_3,C=\frac{{\alpha }_1{\alpha }_2{b}_1{b}_2{y}_k^{*}{v}_k^{*}}{N_1{N}_2}.$$

3.1. Analysis for Equilibrium $E_1$

For the equilibrium $E_1$, the characteristic equation of system (1) becomes the following form

$$\begin{array}{c}\hfill (\lambda -m_2{\mathrm{e}}^{-\lambda {\tau }_2})(\lambda +2m_1-m_1{\mathrm{e}}^{-\lambda {\tau }_1})(\lambda +\frac{{\alpha }_1{m}_1}{r_2{N}_1}+r_1)(\lambda +r_3)=0.\end{array}$$

(3)

when ${\tau }_1=0,{\tau }_2=0$, Equation (3) has four roots, which are ${\lambda }_1=m_2>0,{\lambda }_2=-m_1<0,{\lambda }_3=-{\alpha }_1{m}_1/r_2{N}_1-r_1<0,{\lambda }_4=-r_3<0$. Obviously, Equation (3) has at least one positive root and no zero eigenvalue when ${\tau }_1\ge 0,{\tau }_2\ge 0$. The equilibrium $E_1$ is unstable, and system (1) has no fixed point bifurcation at $E_1$ when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$.

3.2. Analysis for Equilibrium $E_2$

The characteristic equation of system (1) at $E_2$ is as follows

$$(\lambda +2m_2-m_2{\mathrm{e}}^{-\lambda {\tau }_2})(\lambda -m_1{\mathrm{e}}^{-\lambda {\tau }_1})(\lambda +\frac{{\alpha }_2{m}_2}{r_4{N}_2}+r_3)(\lambda +r_1)=0.$$

(4)

when ${\tau }_1=0,{\tau }_2=0$, Equation (4) has four roots, which are ${\lambda }_1=-m_2<0,{\lambda }_2=m_1>0,{\lambda }_3=-{\alpha }_2{m}_2/r_4{N}_2-r_3<0,{\lambda }_4=-r_1<0$. Obviously, Equation (4) has at least one positive root and no zero eigenvalue when ${\tau }_1\ge 0,{\tau }_2\ge 0$. The equilibrium $E_2$ is unstable, and system (1) has no fixed point bifurcation at $E_2$ when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$.

3.3. Analysis for Equilibrium $E_3$

3.3.1. Case 1 for ${\tau }_1=0,{\tau }_2=0$

The characteristic equation of system (1) at $E_3$ is as follows

$$(\lambda +2m_2-m_2{\mathrm{e}}^{-\lambda {\tau }_2})(\lambda +2m_1-m_1{\mathrm{e}}^{-\lambda {\tau }_1})({\lambda }^2+\mathsf{\Gamma }\lambda +\mathsf{\Pi })=0,$$

(5)

where

$$\mathsf{\Gamma }=\frac{{\alpha }_1{m}_1}{N_1{r}_2}+\frac{{\alpha }_2{m}_2}{N_2{r}_4}+r_1+r_3,\mathsf{\Pi }=(\frac{{\alpha }_1{m}_1}{N_1{r}_2}+r_1)(\frac{{\alpha }_2{m}_2}{N_2{r}_4}+r_3)-\frac{{\alpha }_1{\alpha }_2{m}_1{m}_2{b}_1{b}_2}{N_1{N}_2{r}_2{r}_4}.$$

When ${\tau }_1=0,{\tau }_2=0$, we simply need to consider the roots of the following equation:

$$\begin{array}{c}\hfill {\lambda }^2+(\frac{{\alpha }_1{m}_1}{N_1{r}_2}+\frac{{\alpha }_2{m}_2}{N_2{r}_4}+r_1+r_3)\lambda +(\frac{{\alpha }_1{m}_1}{N_1{r}_2}+r_1)(\frac{{\alpha }_2{m}_2}{N_2{r}_4}+r_3)-\frac{{\alpha }_1{\alpha }_2{m}_1{m}_2{b}_1{b}_2}{N_1{N}_2{r}_2{r}_4}=0.\end{array}$$

(6)

According to the Routh-Hurwitz criterion, we obtain that

$$\begin{array}{c}\hfill \frac{1}{N_1{N}_2}(\frac{{\alpha }_1{m}_1}{N_1{r}_2}+\frac{{\alpha }_2{m}_2}{N_2{r}_4}+r_1+r_3)[\frac{{\alpha }_1{\alpha }_2{m}_1{m}_2}{r_2{r}_4}(1-b_1{b}_2)+Q]>0,\end{array}$$

(7)

where

$$Q=\frac{{\alpha }_1{m}_1{r}_3{N}_2}{r_2}+\frac{{\alpha }_2{m}_2{r}_1{N}_1}{r_4}+r_1{r}_3{N}_1{N}_2>0.$$

If $1-b_1{b}_2\ge 0$, Equation (7) holds obviously. Therefore, we show the following hypothesis:

Hypothesis 4 (H4).

$b_1{b}_2\le 1$.

If $\left(\mathrm{H}4\right)$ is satisfied, Equation (7) holds. Thus, all eigenvalues of Equation (6) have negative real parts. Thus, the equilibrium $E_4$ is locally asymptotically stable when ${\tau }_1=0$ and ${\tau }_2=0$.

Remark 1.

We know that parameters $b_1$ and $b_2$ represent the strength of species interactions on growth rates, which is limited. Considering the actual condition, we suppose that $b_1$ and $b_2$ are between $[-1,1]$. Therefore, our assumption is reasonable.

3.3.2. Case 2 for ${\tau }_1=0,{\tau }_2>0$

For the equilibrium $E_3$, the characteristic Equation (5) becomes the following form when ${\tau }_1=0$ and ${\tau }_2>0$

$$\begin{array}{c}\hfill (\lambda +2m_2-m_2{\mathrm{e}}^{-\lambda {\tau }_2})(\lambda +m_1)({\lambda }^2+\mathsf{\Gamma }\lambda +\mathsf{\Pi })=0,\end{array}$$

(8)

where $\mathsf{\Gamma }$ and $\mathsf{\Pi }$ are the same expressions as Equation (5).

Note that $\lambda =-m_1<0$ is a root of Equation (8). Therefore, when $\left(\mathrm{H}4\right)$ holds, we simply need to analyze the roots of the following equation for ${\tau }_1=0$ and ${\tau }_2>0$:

$$\begin{array}{c}\hfill \lambda +2m_2-m_2{\mathrm{e}}^{-\lambda {\tau }_2}=0.\end{array}$$

(9)

We assume $\lambda =\mathrm{i}{\omega }_1({\omega }_1>0)$ is a pure imaginary root of Equation (9). Substituting $\lambda =\mathrm{i}{\omega }_1$ into Equation (9) and separating the real and imaginary parts, we obtain:

$$\left\{\begin{array}{c}{\omega }_1+m_{2}sin\left({\omega }_1{\tau }_2\right)=0,\hfill \\ 2m_2-m_{2}cos\left({\omega }_1{\tau }_2\right)=0.\hfill \end{array}\right.$$

(10)

Obviously, Equation (10) has no positive root for ${\omega }_1$. Thus, system (1) has no Hopf bifurcation at the equilibrium $E_3$ when ${\tau }_1=0$ and ${\tau }_2>0$. When (H4) holds, the equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1=0$ and ${\tau }_2\ge 0$.

3.3.3. Case 3 for ${\tau }_1>0,{\tau }_2>0$

We let ${\tau }_2={\tau }_2^{*}\in (0,+\infty )$. When ${\tau }_1>0,{\tau }_2={\tau }_2^{*}$, the characteristic equation of system (1) at equilibrium $E_3$ is transformed to the following form

$$\begin{array}{c}\hfill (\lambda +2m_2-m_2{\mathrm{e}}^{-\lambda {\tau }_2^{*}})(\lambda +2m_1-m_1{\mathrm{e}}^{-\lambda {\tau }_1})({\lambda }^2+\mathsf{\Gamma }\lambda +\mathsf{\Pi })=0,\end{array}$$

(11)

where $\mathsf{\Gamma }$ and $\mathsf{\Pi }$ are the same expressions as Equation (5).

Similar to the analysis for $E_2$, for the equilibrium $E_3$, we simply need to discuss the following equation:

$$\begin{array}{c}\hfill (\lambda +2m_2-m_2{\mathrm{e}}^{-\lambda {\tau }_2^{*}})(\lambda +2m_1-m_1{\mathrm{e}}^{-\lambda {\tau }_1})=0.\end{array}$$

(12)

We assume that $\lambda =\mathrm{i}{\omega }_2({\omega }_2>0)$ is a pure imaginary root of Equation (12). Substituting it into Equation (12) and separating the real part and the imaginary part, we have:

$$\left\{\begin{array}{c}-{\omega }_2^2-m_{2}sin\left({\omega }_2{\tau }_2^{*}\right){\omega }_2+2m_1{m}_2(2-cos\left({\omega }_2{\tau }_2^{*}\right))\hfill \\ =(m_1\omega +m_1{m}_{2}sin\left({\omega }_2{\tau }_2^{*}\right))sin\left({\omega }_2{\tau }_1\right)+(2m_1{m}_2-m_1{m}_{2}cos\left({\omega }_2{\tau }_2^{*}\right))cos\left({\omega }_2{\tau }_1\right),\hfill \\ 2{\omega }_2(m_1+m_2)+2m_1{m}_{2}sin\left({\omega }_2{\tau }_2^{*}\right)-m_{2}cos\left({\omega }_2{\tau }_2^{*}\right){\omega }_2\hfill \\ =(m_1\omega +m_1{m}_{2}sin\left({\omega }_2{\tau }_2^{*}\right))cos\left({\omega }_2{\tau }_1\right)-(2m_1{m}_2-m_1{m}_{2}cos\left({\omega }_2{\tau }_2^{*}\right))sin\left({\omega }_2{\tau }_1\right).\hfill \end{array}\right.$$

(13)

Adding the square of two expressions in Equation (13), we obtain:

$$\begin{array}{cc}\hfill F\left({\omega }_2\right)=& {\omega }_2^4+2m_{2}sin\left({\omega }_2{\tau }_2^{*}\right){\omega }_2^3+(3m_1^2+5m_2^2-4m_2^{2}cos\left({\omega }_2{\tau }_2^{*}\right)){\omega }_2^2\hfill \\ \hfill & +6m_1^2{m}_{2}sin\left({\omega }_2{\tau }_2^{*}\right){\omega }_2+15m_1^2{m}_2^2-12m_1^2{m}_2^{2}cos\left({\omega }_2{\tau }_2^{*}\right).\hfill \end{array}$$

(14)

If Equation (14) has no positive roots, the equilibrium $E_3$ is locally asymptotically stable, and system (1) has no Hopf bifurcation at the equilibrium $E_3$ when ${\tau }_1\ge 0,{\tau }_2\ge 0$. If Equation (14) has l positive roots, we mark the roots as ${\omega }_{2l}$. For every fixed ${\omega }_{2l}$, there is a sequence of ${\tau }_{1l}^{\left(j\right)}$ defined by

$${\tau }_{1l}^{\left(j\right)}=\left\{\begin{array}{c}\frac{1}{{\omega }_{2l}}[arccos\left(P_{1l}\right)+2j\pi ],Q_{1l}\ge 0,\hfill \\ \frac{1}{{\omega }_{2l}}[2\pi -arccos\left(P_{1l}\right)+2j\pi ],Q_{1l}<0,j=1,2,\dots ,\hfill \end{array}\right.$$

(15)

where $Q_{1l}=sin({\omega }_{2l}{\tau }_{1l}^{\left(j\right)}),P_{1l}=cos({\omega }_{2l}{\tau }_{1l}^{\left(j\right)})$.

We let ${\tau }_1^{*}=min{\tau }_{1l}^{\left(j\right)}(j=1,2,\dots )$. When ${\tau }_1={\tau }_1^{*}$, Equation (12) has a pair of purely imaginary roots $\pm \mathrm{i}{\omega }_2$ for ${\tau }_2={\tau }_2^{*}$. Assume

Hypothesis 5 (H5).

${\mathrm{Re}{(\frac{\mathrm{d}\lambda }{\mathrm{d}{\tau }_1})}^{-1}\mid }_{{\tau }_1={\tau }_1^{*}}\ne 0$.

If (H4) and (H5) hold, equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1\in [0,{\tau }_1^{*})$ and ${\tau }_2\ge 0$. System (1) undergoes Hopf bifurcation near $E_3$ when ${\tau }_1={\tau }_{1l}^{\left(j\right)}$ and ${\tau }_2\ge 0$.

Theorem 1.

For the stability of equilibria and Hopf bifurcation of system (1) at equilibria, we have the following conclusions:

(1) 

Equilibrium $E_k(k=1,2)$ is unstable, and system (1) has no fixed point bifurcation at $E_k(k=1,2)$ when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$.

(2) 

When (H3) and (H4) hold, we have the following conclusions for equilibrium $E_3$.

(a) 

When ${\tau }_1=0,{\tau }_2\ge 0$, the equilibrium $E_3$ is locally asymptotically stable.

(b) 

When ${\tau }_2={\tau }_2^{*}\in (0,+\infty )$, if F(${\omega }_2$) of Equation (14) has no positive roots, the equilibrium $E_3$ is locally asymptotically stable for ${\tau }_1\in [0,+\infty )$. If F(${\omega }_2$) of Equation (14) has positive roots and (H5) holds, system (1) undergoes Hopf bifurcation at $E_3$ when ${\tau }_1={\tau }_{1l}^{\left(j\right)}(j=1,2,\dots )$. The equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1\in [0,{\tau }_1^{*})$.

4. Parametric Analysis and Numerical Simulations

In this section, we first determine the reasonable parameter values based on official data. Then, we simulate the population dynamics of Larch and Betula platyphylla in various interaction modes. Combined with the simulation results, we analyze the evolution of a stand structure without interactions, elaborate on the interaction mechanism and propose suggestions for forest management.

4.1. Parametric Analysis

In this subsection, mathematical methods, such as hierarchical cluster analysis and model fitting, are performed to determine reasonable values of the model parameters.

(i)

Time delays ${\tau }_1,{\tau }_2$

Plants possess many age classes, and we need to estimate the mature time to determine time delays and the immature and mature populations. Therefore, we use hierarchical cluster analysis (HCA) to dimensionally reduce the age classes, which are finally input into two clusters representing the immature period and the mature period. First, we obtain five biological plant indices at different age classes, the number of plants, the carbon storage, the total increase in the diameter at breast height (DBH), the growth rate of the DBH, and the total increase in height. Then, we perform HCA on the five biological indices at different age classes and divide the age classes into two clusters. Finally, the critical age point of the two clusters is the mature time.

The paper selects the official Larch and Betula platyphylla data from the Daxing’an Mountains of Heilongjiang Province in China (Available online: www.forestdata.cn (accessed on 15 January 2023)). We also use the carbon storage data per hectare for different age classes of Larch and Betula platyphylla in the Daxing’an Mountains, Heilongjiang, China [32]. Moreover, we choose the square of the Euclidean metric to calculate the distances between individuals and adopt complete linkage as the classification standard. Finally, we obtain the dendrograms shown in Figure 1.

Figure 1 shows the HCA obtained for the age classes of Larch and Betula platyphylla based on the five indices, where blue lines represent the immature population and green lines represent the mature population. Larch with age classes of 20, 40, 60, and 80 years is included in blue cluster 1a. Furthermore, green cluster 2a consists of Larch with age classes exceeding 80 years. Thus, it is obvious that the mature time of Larch from birth to maturity is 80 years. Similarly, blue cluster 1b comprises Betula platyphylla with age classes of 10, 20, and 30 years. The remaining Betula platyphylla with age classes exceeding 30 years is included in green cluster 2b, which indicates that the mature time of Betula platyphylla is 30 years. Therefore, we determine the mature times ${\tau }_1=80$ years and ${\tau }_2=30$ years.

(ii)

Net growth rates ${\alpha }_1,{\alpha }_2$ and environmental carrying capacities $N_1,N_2$

First, we calculate the size of the population at different times by accumulating the number of plants in each age class before these times. As shown in Figure 2, we notice that the data points with t represent an ‘S’ shape, which is consistent with the logistic function. The classic logistic model is as follows

$$\begin{array}{c}\hfill y\left(t\right)=\frac{N}{1+c{e}^{-\alpha t}},\end{array}$$

where $y\left(t\right),t,N$, and $\alpha$ represent the population size, time, environmental carrying capacity, and net growth rate, respectively; c is a constant.

Therefore, we fit the classic logistic model to the population size by accumulating official data and use the non-linear least squares approach to estimate the parameters ${\alpha }_i(i=1,2)$ and $N_i(i=1,2)$ through MATLAB (The detailed codes are shown in Appendix A). The fitting results obtained for Larch and Betula platyphylla are illustrated in Figure 2.

In Figure 2, the black dots represent the total population sizes at different times based on the official data published by the Chinese government (Available online: www.forestdata.cn (accessed on 22 January 2023)). The blue solid line represents the best-fitting curve obtained by MATLAB by fitting the classic logistic model to the official data. The blue dotted line is the prediction bound under the 95% confidence level.

The results of the simulation show that at the 95% confidence level, ${\alpha }_1\in [0.04198,0.06488]$, ${\alpha }_2\in [0.05045,0.07924]$,$N_1\in [\mathrm{14,100},\mathrm{18,200}]$, and $N_2\in [\mathrm{16,720},\mathrm{19,700}]$. Then, we assess the model fitting quality by calculating $R^2$. The $R^2$ values for Larch and Betula platyphylla are 0.9975 (adjusted $R^2=0.9962$) and 0.9965 (adjusted $R^2=0.9947$), respectively, which indicates that the accuracy of the parameter estimation process is high. Facing severe global climate problems, the Chinese government attaches great importance to the restoration and development of the Daxing’an Mountains and carries out large-scale afforestation and forest protection projects. Considering the increase in the afforestation rate and the great development potential of the Daxing’an Mountains in China, we consider that ${\alpha }_1=0.06488,{\alpha }_2=0.07924,N_1=N_2=\mathrm{20,000}$.

(iii)

Mortalities $r_1,r_2,r_3,r_4$

For mortalities $r_1,r_2,r_3,r_4$, we first obtain the numbers of Larch and Betula platyphylla plants per hectare at different age classes from the official website (Available online: www.forestdata.cn (accessed on 28 January 2023)). Then, we calculate the mortality of each age class of Larch and Betula platyphylla with Formula (16) and Formula (17), respectively. $dat{a}_j$ represents the number of Larch plants in the age class of j years. $dat{a}_l$ represents the number of Betula platyphylla plants in the age class of l years.

$$r_a^j=\frac{dat{a}_j-dat{a}_{j+20}}{dat{a}_j}\frac{dat{a}_{120}}{dat{a}_j},j=20,40,60,80,100,120,$$

(16)

$$r_b^l=\frac{dat{a}_l-dat{a}_{l+10}}{dat{a}_l}\frac{dat{a}_{60}}{dat{a}_l},l=10,20,30,40,50,60.$$

(17)

Then, we average the mortalities of the age classes included in one cluster with the following formula.

$$r_1=\frac{r_a^{20}+r_a^{40}+r_a^{60}}{3},r_2=\frac{r_a^{80}+r_a^{100}+r_a^{120}}{3},r_3=\frac{r_b^{10}+r_b^{20}}{2},r_4=\frac{r_b^{30}+r_b^{40}+r_b^{50}+r_b^{60}}{4}.$$

(18)

Finally, the mortalities of immature Larch, mature Larch, immature Betula platyphylla, and mature Betula platyphylla, $r_1,r_2,r_3,r_4$, are obtained as follows:

$$\begin{array}{c}\hfill r_1\approx 0.07556,r_2\approx 0.06961,\\ \hfill r_3\approx 0.07508,r_4\approx 0.14375.\end{array}$$

(iv)

Transition factors $m_1,m_2$

We consider (H1) and (H2) with the above determined parameters to estimate the transition factors. (H1) and (H2) ensure that equilibria $E_1$ and $E_2$ are non-negative, which has biological meanings and conforms to reality. According to (H1), we calculate $m_1<0.064734$. According to (H2), we calculate $m_2<0.078791$. Considering the mature time differences between Larch and Betula platyphylla, we let $m_1=0.03$ and $m_2=0.045$.

(v)

Interaction factors $b_1,b_2$

To explore the effects of different interaction modes on the population, we consider five interaction modes expressed through parameters $b_1$ and $b_2$. First, we discuss the actual interaction mode between Larch and Betula platyphylla. As a pioneer species, Betula platyphylla improves ecological environments and benefits the growth of Larch trees. As Larch trees grow, they become increasingly competitive with Betula platyphylla. Therefore, we assume that the impact of Betula platyphylla on Larch is positive, and that of Larch on Betula platyphylla is negative. Then, we let $b_1=0.5$ and $b_2=-0.1$ represent the actual interaction mode. According to the above analysis, we take the following five groups of parameters:

Condition 1: $b_1=0$ and $b_2=0$ represent two coexisting populations without interactions.

Condition 2: $b_1=1$ and $b_2=1$ represent the mutualistic interaction mode between two populations with the maximum symmetry level.

Condition 3: $b_1=0.95$ and $b_2=-0.95$ represent the interaction mode in which the asymmetry reaches the maximum level while ensuring that all parameters are positive.

Condition 4: $b_1=-1$ and $b_2=-1$ represent the competitive interaction mode between two populations with the symmetry level reaching its maximum.

Condition 5: $b_1=0.5$ and $b_2=-0.1$ represent the actual interaction mode.

Based on the above discussion and calculation, we finally determine the biological parameters of Larch and Betula platyphylla as follows:

$$\begin{array}{cc}\hfill & N_1=2,{\alpha }_1=0.06488,r_1\approx 0.07556,r_2\approx 0.06961,m_1=0.03,{\tau }_1=80,\hfill \\ \hfill & N_2=2,{\alpha }_2=0.07924,r_3\approx 0.07508,r_4\approx 0.14375,m_2=0.045,{\tau }_2=30,\hfill \end{array}$$

under

$$\begin{array}{cc}\hfill & Condition1:b_1=0,b_2=0;\hfill \\ \hfill & Condition2:b_1=1,b_2=1;\hfill \\ \hfill & Condition3:b_1=0.95,b_2=-0.95;\hfill \\ \hfill & Condition4:b_1=-1,b_2=-1;\hfill \\ \hfill & Condition5:b_1=0.5,b_2=-0.1.\hfill \end{array}$$

4.2. Numerical Simulations

According to Theorem 1, the equilibria $E_1$ and $E_2$ are unstable, and system (1) has no fixed point bifurcation at $E_1$ and $E_2$ when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$. Thus, we are more concerned about the conditions of equilibrium $E_3$. We calculate the equilibrium $E_3$ with the obtained parameters and expressions of $E_3$ in Section 3, and we obtain:

$$\begin{array}{cc}\hfill & {E_3}^{\left(1\right)}=(0.1006,0.4310,0.0781,0.3130),undercondition1;\hfill \\ \hfill & {E_3}^{\left(2\right)}=(0.1751,0.4310,0.1641,0.3130),undercondition2;\hfill \\ \hfill & {E_3}^{\left(3\right)}=(0.1471,0.4310,0.0002878,0.3130),undercondition3;\hfill \\ \hfill & {E_3}^{\left(4\right)}=(0.0502,0.4310,0.0099,0.3130),undercondition4;\hfill \\ \hfill & {E_3}^{\left(5\right)}=(0.1305,0.4310,0.0702,0.3130),undercondition5.\hfill \end{array}$$

With the determined parameters, we find that (H3) and (H4) hold under five conditions. The assumption (H3) ensures that the equilibrium $E_3$ is positive, representing the fact that immature Larch, mature Larch, immature Betula platyphylla, and mature Betula platyphylla are all present. (H4) ensures that the equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$. Furthermore, we substitute the obtained parameters into Equation (14), which leads to $\tilde{\mathrm{F}}$(${\omega }_2$). We do not find that $\tilde{\mathrm{F}}$(${\omega }_2$) = 0 has a positive root. According to Theorem 1, with (H3) and (H4) holding and no positive of F(${\omega }_2$) in Equation (14), the equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$. System (1) has no fixed point bifurcation near $E_3$.

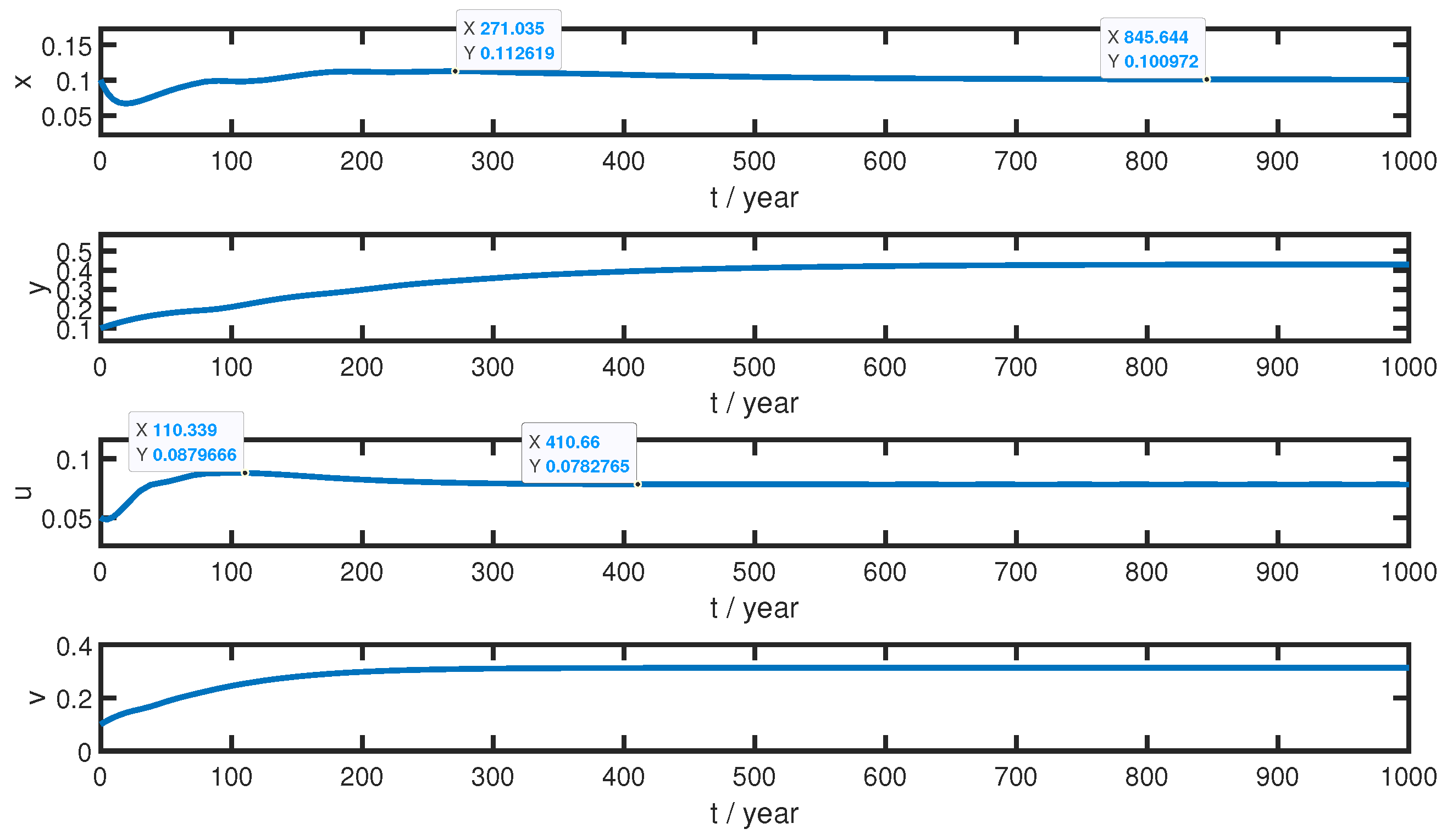
4.2.1. Exploration for the Evolution of Stand Structure

In this subsection, we conduct a simulation with the determined parameters under Condition 1:

$$\begin{array}{cc}\hfill & N_1=2,{\alpha }_1=0.06488,r_1\approx 0.07556,r_2\approx 0.06961,m_1=0.03,{\tau }_1=80,b_1=0\hfill \\ \hfill & N_2=2,{\alpha }_2=0.07924,r_3\approx 0.07508,r_4\approx 0.14375,m_2=0.045,{\tau }_2=30,b_2=0.\hfill \end{array}$$

This represents no interactions between two coexisting dependent populations. We calculate the equilibrium ${E_3}^{\left(1\right)}=(0.1006,0.4310,0.0781,0.3130)$. Under this group of parameters, assumptions (H3) and (H4) hold, and F(${\omega }_2$) of Equation (14) has no positive root. According to Theorem 1, the equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1\ge 0$ and ${\tau }_2\ge 0$, and system (1) has no fixed point bifurcation near $E_3$.

With $\left(x\right(t),y(t),u(t),v(t\left)\right)=(0.1,0.1,0.05,0.1),t\in [-\tau ,0)$ as the initial function and the above determined parameters, we solve system (1) and obtain solutions of $x,y,u,v$ at t (years) within $[0,1000]$ (years) through MATLAB’s dde23 function (The detailed codes are shown in Appendix B). Then, we plot the solutions of $x,y,u,v$ with t in the same figure. The equilibrium $E_3$ is locally asymptotically stable and, thus, consistent with Theorem 1, as shown in Figure 3.

Biological Interpretation for Larch The evolution of the stand structure of Larch: Overall, the numbers of immature Larch and mature Larch plants both increase. In part, we divide the population dynamics of Larch into three periods. The first period, 271 years ago, is the growing period. The second period is from 271 to 845 years, which is defined as the adjustment period. The third period occurs after 845 years, which is the stable period.

(a)

During the growing period, the number of immature Larch plants decreases and increases alternately, while the number of mature Larch plants continues to increase. The slopes of x and y with t are high at the beginning. Before 19 years, x drops rapidly. This indicates that the stand eliminates the uncompetitive immature Larch to ensure the quality of the stand. Next, after x drops to a minimum of 0.06675, x and y increase rapidly at $19<t<80$. The reason for this is that trees grow and propagate fast at low stand densities with abundant ecological resources and weak intraspecific competition. Furthermore, immature Larch gradually grows into mature Larch. With the increase in maturity, the reproductive capacity of the forest is strengthened, which promotes the growth of immature plants in turn. In 80 years, the number of Larch reaches a threshold. When $80<t<110$, x and the rising speed of y decrease significantly. This is because intraspecific competition forces the stand to adjust itself with the gradual occupation of ecological resources. Immature Larch, which has low competitiveness and avoids light, dies from intraspecific competition. Mature Larch is also slightly affected by intraspecific competition. Next, the number of immature Larch plants rises and falls alternately when $110<t<271$. The forest stand dynamically adjusts and develops itself continually.

(b)

At the beginning of the adjustment period, the number of Larch plants reaches a higher threshold. Then, the numbers of immature and mature plants decrease and increase slowly, respectively. This indicates that with high forest density and scarce ecological resources, competitive mature Larch has an advantage in the fierce intraspecific competition over immature Larch. Moreover, the slopes of x and y with time in the adjustment period are lower than those in the growth period. We suggest that mature Larch, with a large proportion in the population, enhances the stability of forests and makes adjustments of forests gentler. The stand structure is basically determined and gradually reaches stability.

(c)

During the stable period, the stand structure is determined and finally reaches its stable condition. At this time, the changing ranges of x and y with time are tiny. All curves become extraordinarily smooth.

Biological Interpretation for Betula platyphylla The evolution of the stand structure of Betula platyphylla: Overall, the numbers of both immature and mature Betula platyphylla plants increase. In part, the growth period, adjustment period, and stable period of Betula platyphylla are 110 years ago, 110 to 410 years, and 410 years later, respectively. In addition, Betula platyphylla’s growth period and adjustment period are shorter than the corresponding periods of Larch, and the population change rate is faster than that of Larch. During the growth period, the numbers of immature and mature Betula platyphylla plants both significantly increase with slight fluctuations. Similar to Larch, the amount of immature Betula platyphylla decreases rapidly at the beginning of the growth period, which indicates that the stand always selects competitive immature trees to ensure the quality of the stand. During the adjustment period, immature Betula platyphylla declines slowly, while mature Betula platyphylla changes from increasing to stable. During the stable period, the population remains stable.

Biological Interpretation for Larch and Betula platyphylla Based on the above analysis of Larch and Betula platyphylla, we believe that the evolution of the stand structure containing Larch and Betula platyphylla roughly experiences three periods: the growth period, the adjustment period and the stable period. During the growth period, the immature and mature populations spiral up and constantly adjust themselves with large and small fluctuations, respectively. At the beginning of the growth period, to ensure the quality of the forest stand, some immature trees with weak competitiveness may be eliminated. Then, as the population size and intraspecific competition level increase, the population changes from a rapid increase to alternating increases and declines. Then, when the population reaches a certain threshold, the stand enters the adjustment period. At this time, the stand structure is basically established and stable. Immature and mature populations have a slow rise or decline. Finally, the stand reaches the stable period, and the stand structure is completely established.

4.2.2. Exploration of the Interaction Mechanism

In this subsection, we vary the interaction modes and conduct numerical simulations under five conditions to analyze the interaction mechanisms and how stand characteristics affect the responses of the population to interactions.

$$\begin{array}{cc}\hfill & N_1=2,{\alpha }_1=0.06488,r_1\approx 0.07556,r_2\approx 0.06961,m_1=0.03,{\tau }_1=80,\hfill \\ \hfill & N_2=2,{\alpha }_2=0.07924,r_3\approx 0.07508,r_4\approx 0.14375,m_2=0.045,{\tau }_2=30,\hfill \end{array}$$

under

$$\begin{array}{cc}\hfill & Condition1:b_1=0,b_2=0;\hfill \\ \hfill & Condition2:b_1=1,b_2=1;\hfill \\ \hfill & Condition3:b_1=0.95,b_2=-0.95;\hfill \\ \hfill & Condition4:b_1=-1,b_2=-1;\hfill \\ \hfill & Condition5:b_1=0.5,b_2=-0.1.\hfill \end{array}$$

Similarly, we, respectively, calculate the equilibrium $E_3$ under five conditions and obtain ${E_3}^{\left(i\right)}(i=1,2,3,4,5)$. Based on previous calculations, assumptions (H3) and (H4) hold, and F(${\omega }_2$) of Equation (14) has no positive roots under the five conditions. According to Theorem 1, the equilibrium $E_3$ is locally asymptotically stable when ${\tau }_1\ge 0$, ${\tau }_2\ge 0$, and system (1) has no fixed point bifurcation near $E_3$ under the five conditions.

We also choose $\left(x\right(t),y(t),u(t),v(t\left)\right)=(0.1,0.1,0.05,0.1),t\in [-\tau ,0)$ as the initial function. Similarly, we solve system (1) with t in [0,1000] under five conditions and draw five population dynamics in one figure by MATLAB.

Figure 4 shows the different population dynamics that occur under five interaction modes. Comparing the population dynamics under these five conditions, we arrive at the following conclusions.

(a)

The effect of interactions is directly proportional to density. The x and u differences between condition 1 and other conditions are insignificant in the preperiod, but increase over time and eventually stabilize, similar to the changing trends of the population size. Thus, we assume that this phenomenon is related to the stand density. With the total population continuously increasing, the stand density increases, and the average distance between trees decreases, which contributes to more frequent interactions between trees.

(b)

The mutualistic interaction mode is more conducive to the population reproduction and survival than other interaction modes. Under condition 2, the populations of Larch and Betula platyphylla have the highest rises and sizes. Compared with those of condition 1, x and u both increase, which suggests that the effects of interactions can outweigh the decrease caused by intraspecies competition in the later period.

(c)

In contrast to mature plants, interactions have a larger influence on immature plants. our results show that differences in x and u are all greater than the differences in y and v as the immature population is more susceptible to environmental stress.

Comparing the population dynamics under condition 1 with those observed under condition 5, the interaction mechanism between Larch and Betula platyphylla is elaborated as follows.

During the initial stage, Betula platyphylla grows rapidly and occupies ecological resources as a pioneer tree species. Furthermore, Betula platyphylla improves soil productivity and accelerates the decomposition of Larch litter. However, the interaction effect is not obvious because of the low stand density. With stand densities increasing and interactions becoming more frequent and stronger over time, the negative impact of Larch on Betula platyphylla and the positive impact of Betula platyphylla on Larch gradually stand out. x and u apparently increase and decrease, respectively. The constant increase in the stand density intensifies interspecific competition, which limits the growth of Betula platyphylla. The number of immature Larch plants is reduced. Despite the facilitation gradually weakening, Larch still expands and has advantages in the competition depending on its high competitiveness. Eventually, Betula platyphylla gradually withdraws from the competition, and Larch becomes the dominant species.

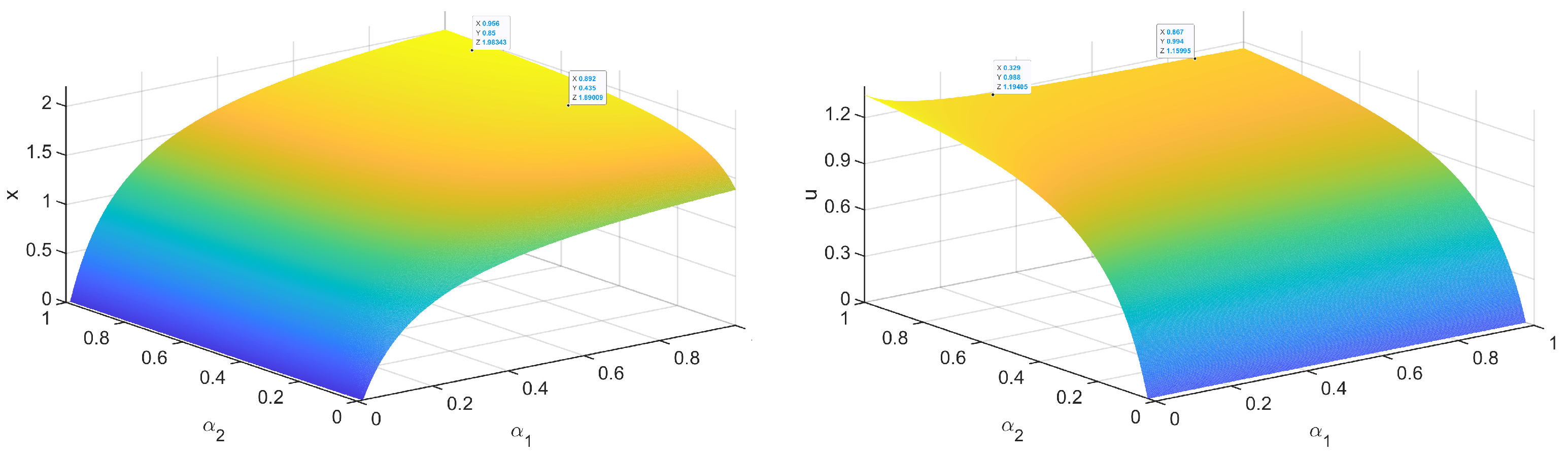
4.2.3. Study of the Influence of Each Parameter on Equilibrium $E_3$

(1)

To discuss the reasonable ranges of the important parameters ${\alpha }_1$ and ${\alpha }_2$ for scientific forest management, we pay more attention to the values of equilibrium $E_3$ under stability with varied ${\alpha }_1$ and ${\alpha }_2$, which contrasts with the simulation method used in Section 4.2.1 and Section 4.2.2.

First, we simultaneously vary ${\alpha }_1$ and ${\alpha }_2$ within (0, 1] and construct a $1000\times 1000$ grid matrix (${\alpha }_1\times {\alpha }_2$) with MATLAB’s meshgrid function. With determined parameters except ${\alpha }_1$ and ${\alpha }_2$ under condition 5, we obtain expressions for x and u with respect to ${\alpha }_1$ and ${\alpha }_2$. We calculate the values of x and u and plot 3-D grid surfaces, as shown in Figure 5.

It is shown that from Figure 5:

(a)

Immature Larch is significantly correlated with its growth rate ${\alpha }_1$ but weakly correlated with another population growth rate (${\alpha }_2$). Similarly, Betula platyphylla is significantly correlated with its growth rate ${\alpha }_2$ but weakly correlated with Larch’s growth rate.

(b)

The value changes observed with growth rate changes are apparent under certain thresholds but become insensitive to the parameters after the thresholds. When ${\alpha }_1$ exceeds 0.46, the fluctuation of immature Larch does not exceed 0.5% of the environmental carrying capacity with every 0.01 increase in ${\alpha }_1$. Similarly, the influence of ${\alpha }_2$ on immature Betula platyphylla decreases rapidly when ${\alpha }_2$ is greater than 0.41. This illustrates that when the growth rates ${\alpha }_1$ and ${\alpha }_2$ exceed certain thresholds, the ecological system restricts the reproduction of Larch and Betula platyphylla. In addition to thresholds, we consider biological meanings to control the growth rates within reasonable ranges. We let x and u be the positive population sizes of Larch and Betula platyphylla under the preset environmental carrying capacity, respectively. We finally obtain reasonable values for the growth rates as follows, $0.016<{\alpha }_1<0.366,0.032<{\alpha }_2<0.181$.

(2)

Since forest pests and diseases significantly hinder forestry developments, it is necessary to investigate their influences on populations and propose forest management strategies. For the Daxing’an Mountains, Larch and Betula platyphylla are both vulnerable to pests and disease during seedling growth. Therefore, we consider varying mortalities of immature populations $r_1$ and $r_3\in (0,1]$ and study the dynamic properties of system (1) at equilibrium $E_3$.

Similarly, we simultaneously vary $r_1$ and $r_3$ within (0, 1] and create a $1000\times 1000$ grid matrix ($r_1\times r_3$) with MATLAB’s meshgrid function. With the other determined parameters under Condition 5, we calculate values of x and u based on the expressions of the equilibrium $E_3$ in Section 3. The surfaces of x and u are shown in Figure 6.

It is shown that from Figure 6: The certain thresholds of mortality of the immature Larch and Betula platyphylla plants are 0.2 and 0.19, respectively. The number of the immature population decreases rapidly with increasing mortality when the mortality is below the threshold, and slowly when the mortality is above the threshold. This shows that 0.2 and 0.19 are reasonable threshold values of $r_1$ and $r_3$ for forest management. Moreover, the values of x and u are positive and satisfy the environmental carrying capacity constraints. Based on the above analysis, we determine that $0<r_1<0.2,0<r_3<0.19$.

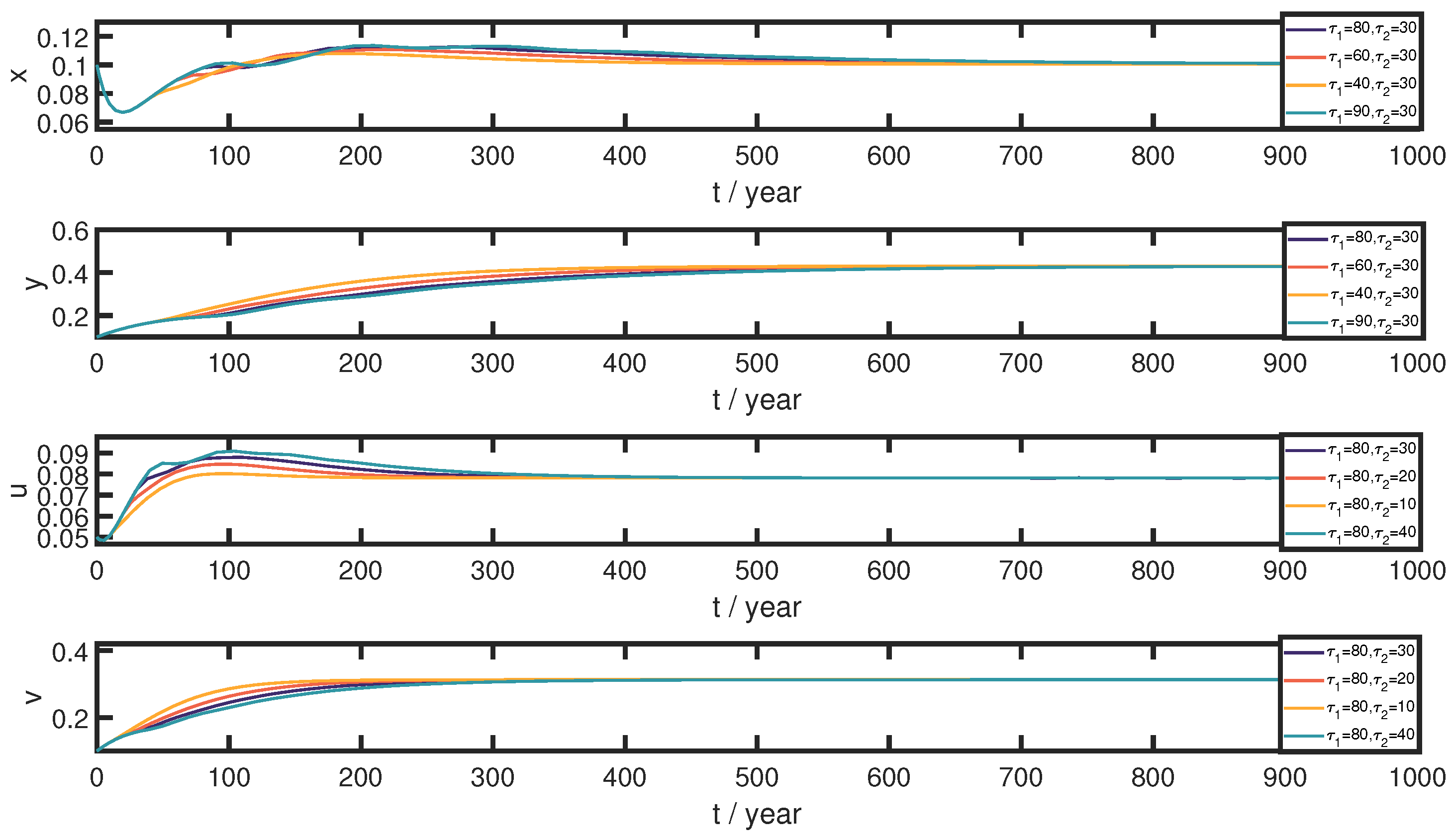
(3)

In this section, we explore the influence of time delays on the model. First, we select several sets of parameters, which are as follows:

$$\begin{array}{cc}\hfill & Group1:{\tau }_1=80,60,40,90,{\tau }_2=30;\hfill \\ \hfill & Group2:{\tau }_1=80,{\tau }_2=30,20,10,40.\hfill \end{array}$$

Then, we also choose $\left(x\right(t),y(t),u(t),v(t\left)\right)=(0.1,0.1,0.05,0.1),t\in [-\tau ,0)$ as the initial function. With Group 1 under condition 1, we solve x and y in system (1) and plot the solutions of x and y with t, as shown in Figure 7. With Group 2 under condition 1, we solve u and v in system (1) and plot the solutions of u and v with t, as shown in Figure 7.

Figure 7 suggests that time delays ${\tau }_1$ and ${\tau }_2$ have impacts on the speed at which $E_3$ tends toward stability. With smaller time delays, both Larch and Betula platyphylla can reach stability faster. Moreover, the simulations are in line with a study that suggested that the mature time could affect plant regeneration [31].

4.3. Recommendations for China

In view of the above basic conclusions, we put forward the following predictions for Larch-Betula platyphylla forests and provide suggestions for the collaborative forest management of the Daxing’an Mountains in China to assist with China’s double carbon goals.

(i)

Our results show that the populations of Larch and Betula platyphylla will both increase in the future, which indicates that the Larch-Betula platyphylla forest in the Daxing’an Mountains has enormous ecological value and carbon sink potential. Furthermore, when the structure of Larch-Betula platyphylla stands becomes stable, the proportion of Larch will be greater than that of Betula platyphylla and the mature population will account for a substantial part of the whole population. Thus, we predict that mature Larch will play a major role in the forest community organization and forest dynamics.

(ii)

The numbers of Larch and Betula platyphylla plants in mixed forests are greater than those in pure forests. We should develop mixed-species forests to achieve improved forest utilization efficiency and increase the capacity of forest carbon sinks.

(iii)

The increase in ${\alpha }_1$ and ${\alpha }_2$ increase the number of Larch and Betula platyphylla plants, respectively. However, when the net growth rate is higher than a certain threshold, the resulting population increase is not significant. Therefore, we should control the net growth rates of Larch and Betula platyphylla within $(0.016,0.366)$ and $(0.032,0.181)$, respectively, through intermediate cuttings, afforestation, and reforestation.

(iv)

The increase in $r_1$ and $r_3$ can cause a decrease in the number of Larch and Betula platyphylla plants, respectively. Moreover, when the mortality of immature plants is higher than a certain threshold, the population markedly decreases to a low level. Therefore, serious forest diseases and pests disturb forest ecosystems and hinder China’s green development. It is necessary to reduce the mortality of immature Larch and immature Betula platyphylla under 0.2 and 0.19, respectively, by regulating site conditions, resisting exotic forest insect pests, and developing mixed-species forests.

5. Conclusions

In this paper, we chose Larch and Betula platyphylla in the Daxing’an Mountains of China as the interacting species and constructed a two-species interaction model for different age populations with two-time delays. We analyzed the stability of equilibria and the existence of Hopf bifurcation. Next, we calculated reasonable parameter ranges using mathematical methods. Based on the determined parameters, we performed numerical simulations and obtained the following conclusions.

(i)

Without interactions, the evolution of a stand structure roughly experiences three periods, the growing period, the adjustment period, and the stable period. The characteristics of those periods are fluctuating rises, adjustments along one trend, and a stable stand structure. At the beginning of the growth period, the stand eliminates the uncompetitive immature Larch to ensure the quality of the stand. During the growth period, the population rises and fluctuates with frequent self-adjustments. Then, when the number of the population reaches a certain threshold, the stand enters the adjustment period. At this time, the stand structure is basically established and stable. The numbers of immature and mature plants rise or decline slowly with one trend. Finally, the stand reaches the stable period, and the stand structure is entirely established.

(ii)

With interactions, we find that age structure and density influence the responses of the population to interactions with magnitudes and patterns. First, the interaction effect is directly proportional to the stand density. Second, interactions have a larger influence on immature individuals than on mature individuals. Third, the mutualistic interaction mode is most conducive to the population reproduction across the five interaction modes. Furthermore, the interaction mechanism between Larch and Betula platyphylla is elaborated herein.

(iii)

Among the parameters under certain thresholds, the number of the population is more sensitive. Based on threshold control, we consider the biological meanings of these parameters and obtain that $0.016<{\alpha }_1<0.366,0.032<{\alpha }_2<0.181,0<r_1<0.2,0<r_3<0.19$.