A Novel “Finite Element-Meshfree” Triangular Element Based on Partition of Unity for Acoustic Propagation Problems
Abstract
:1. Introduction
2. Weak Form Formulation for Time-Harmonic Acoustics
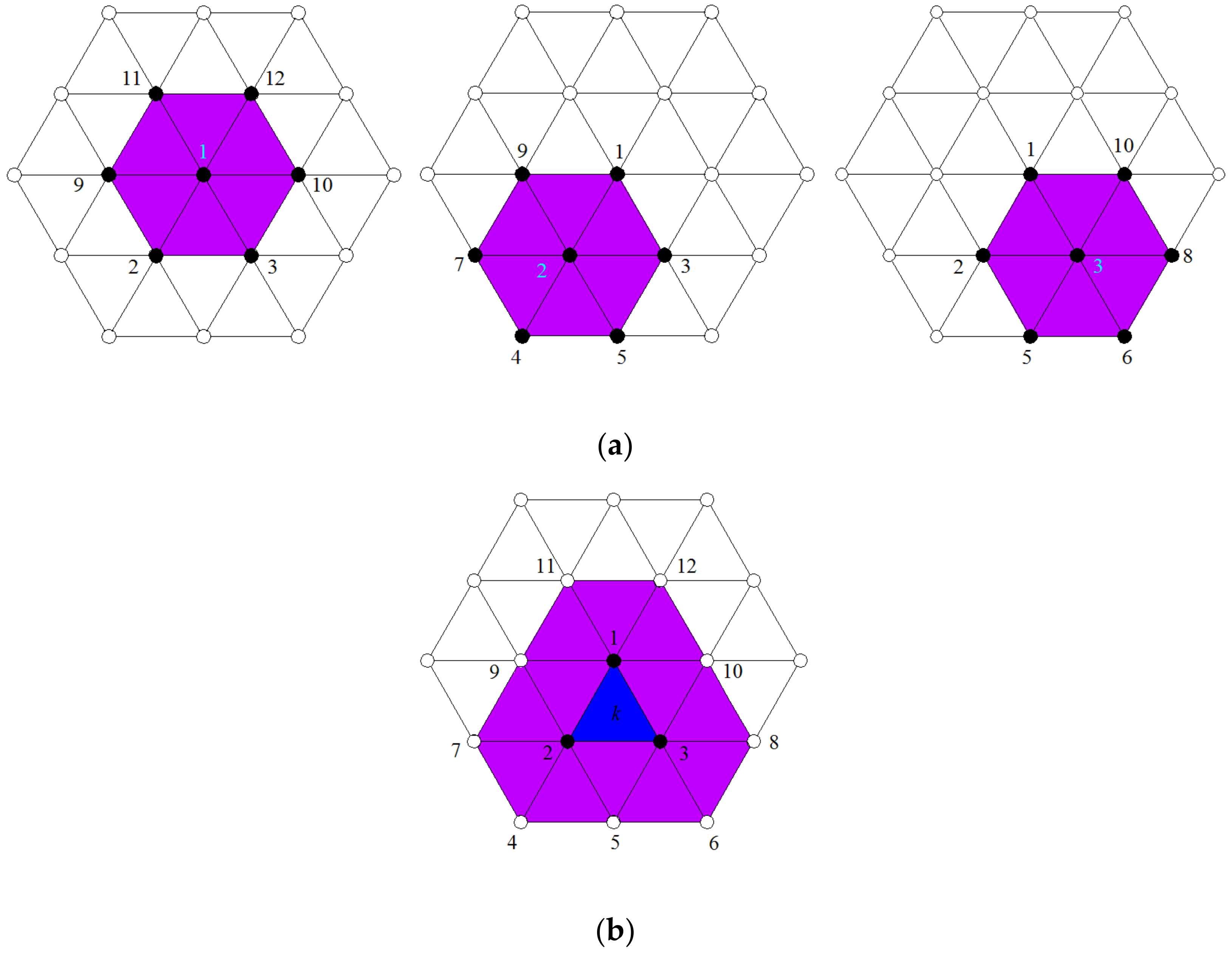
3. Construction of the Coupled “FE-Meshfree” Numerical Approximation
4. Numerical Examples
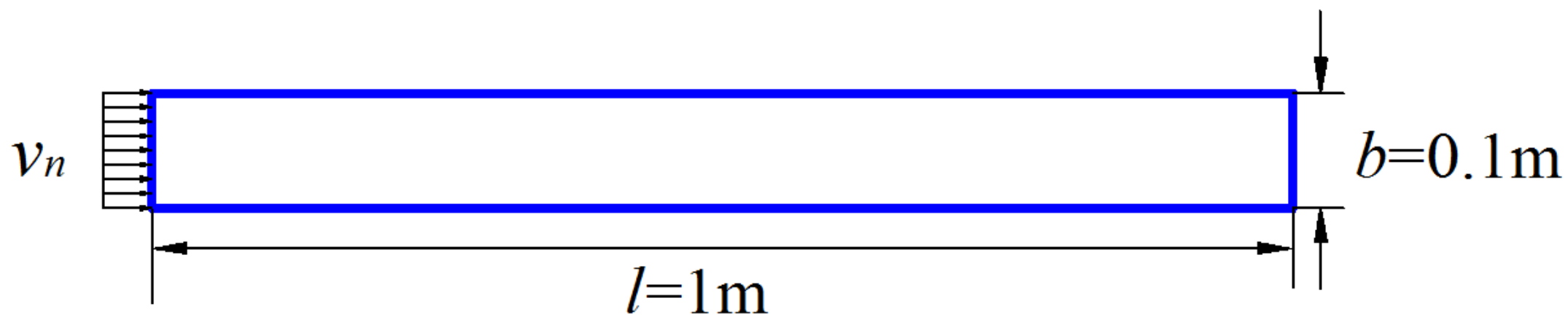
4.1. Acoustic Propagation in a 2D Tube
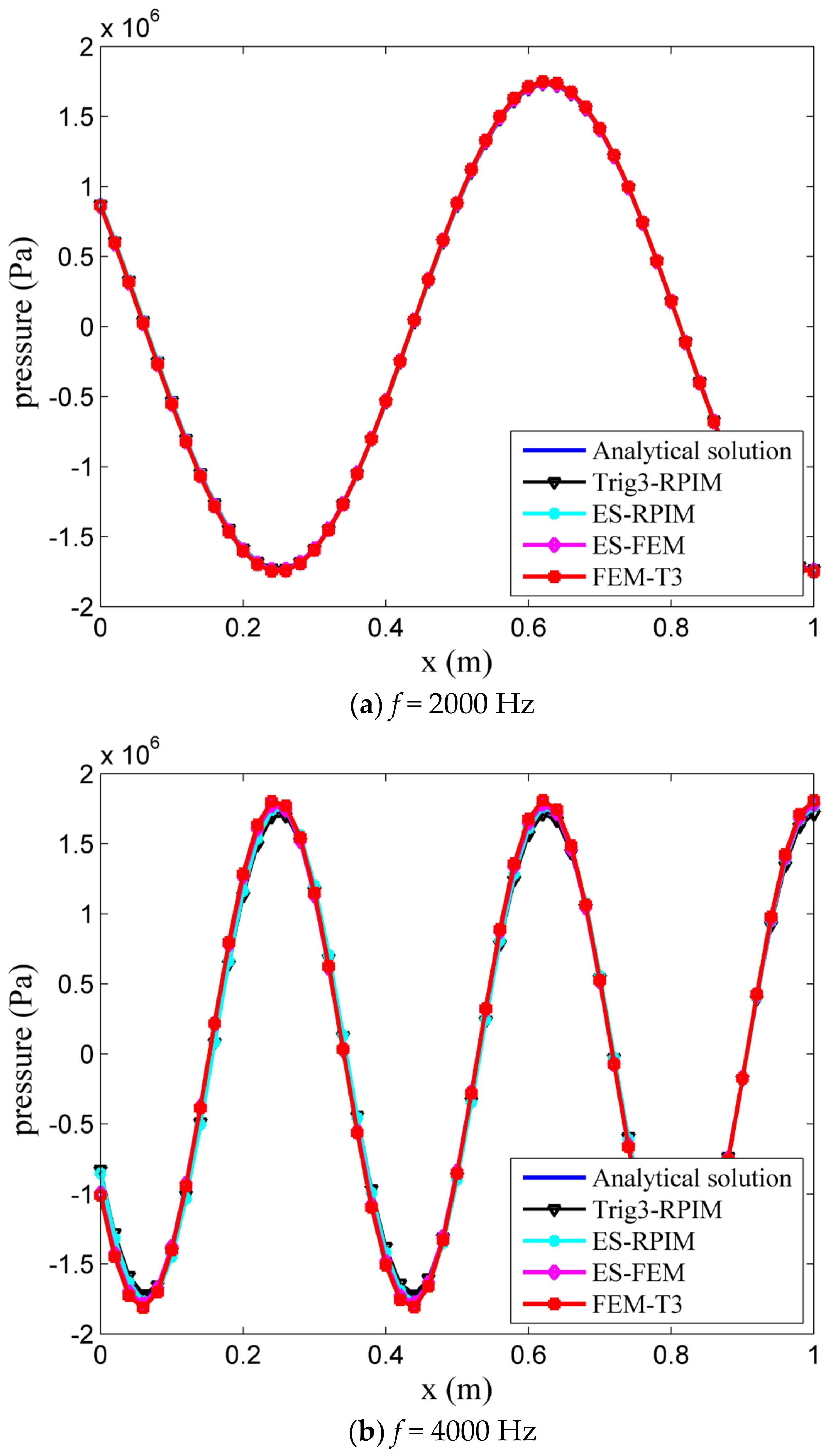
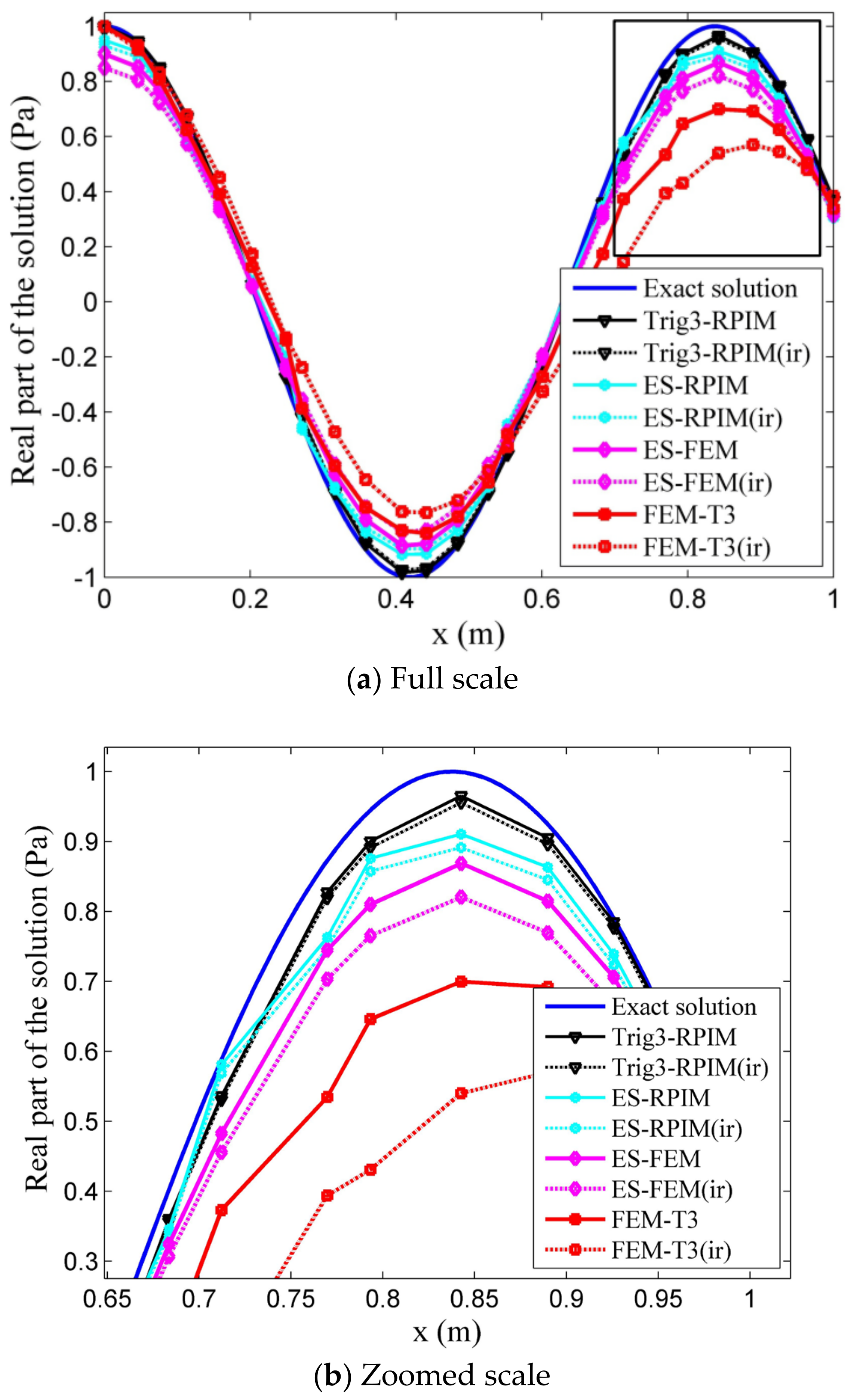
4.1.1. Computation Accuracy Study
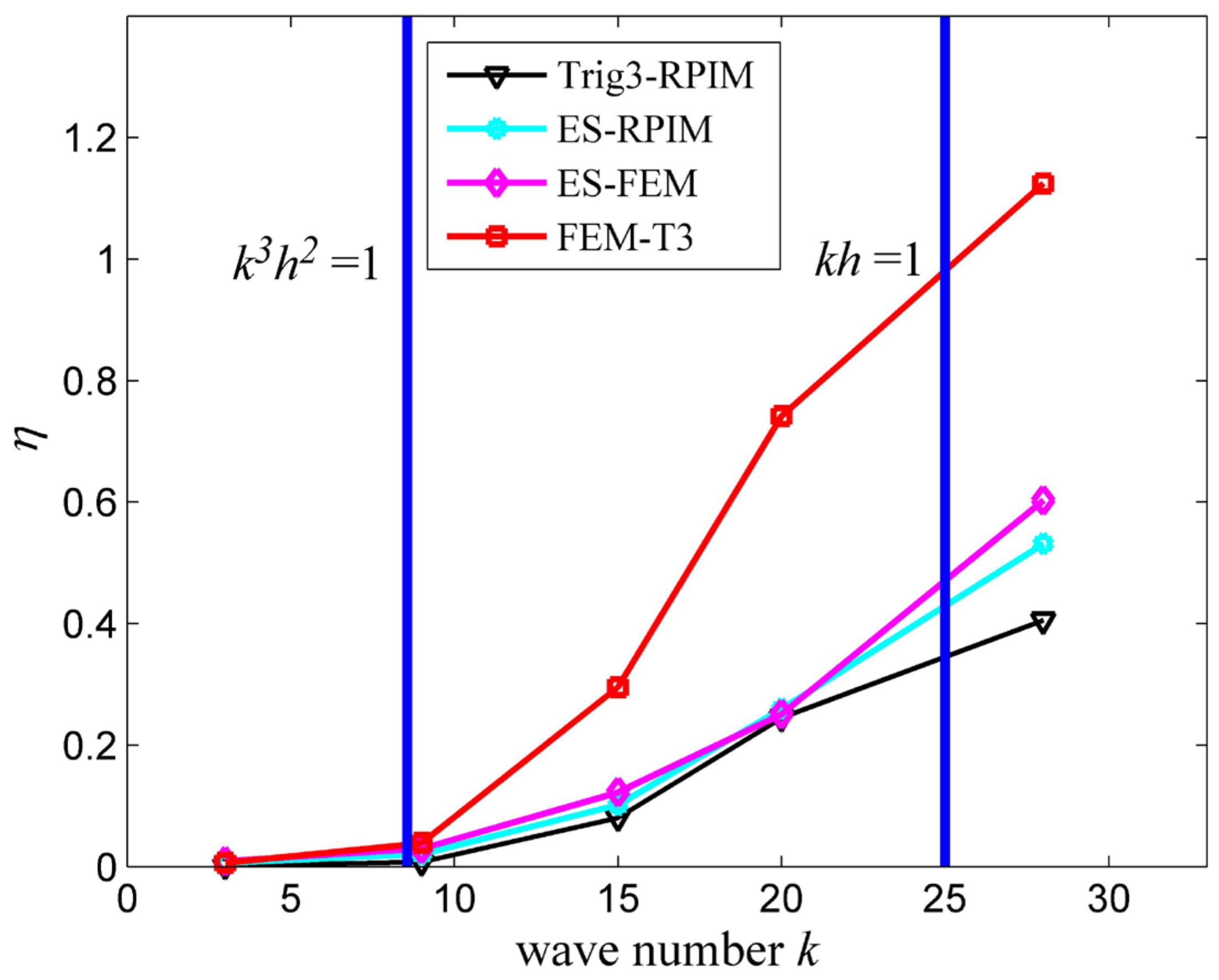
4.1.2. Convergence Rate Study
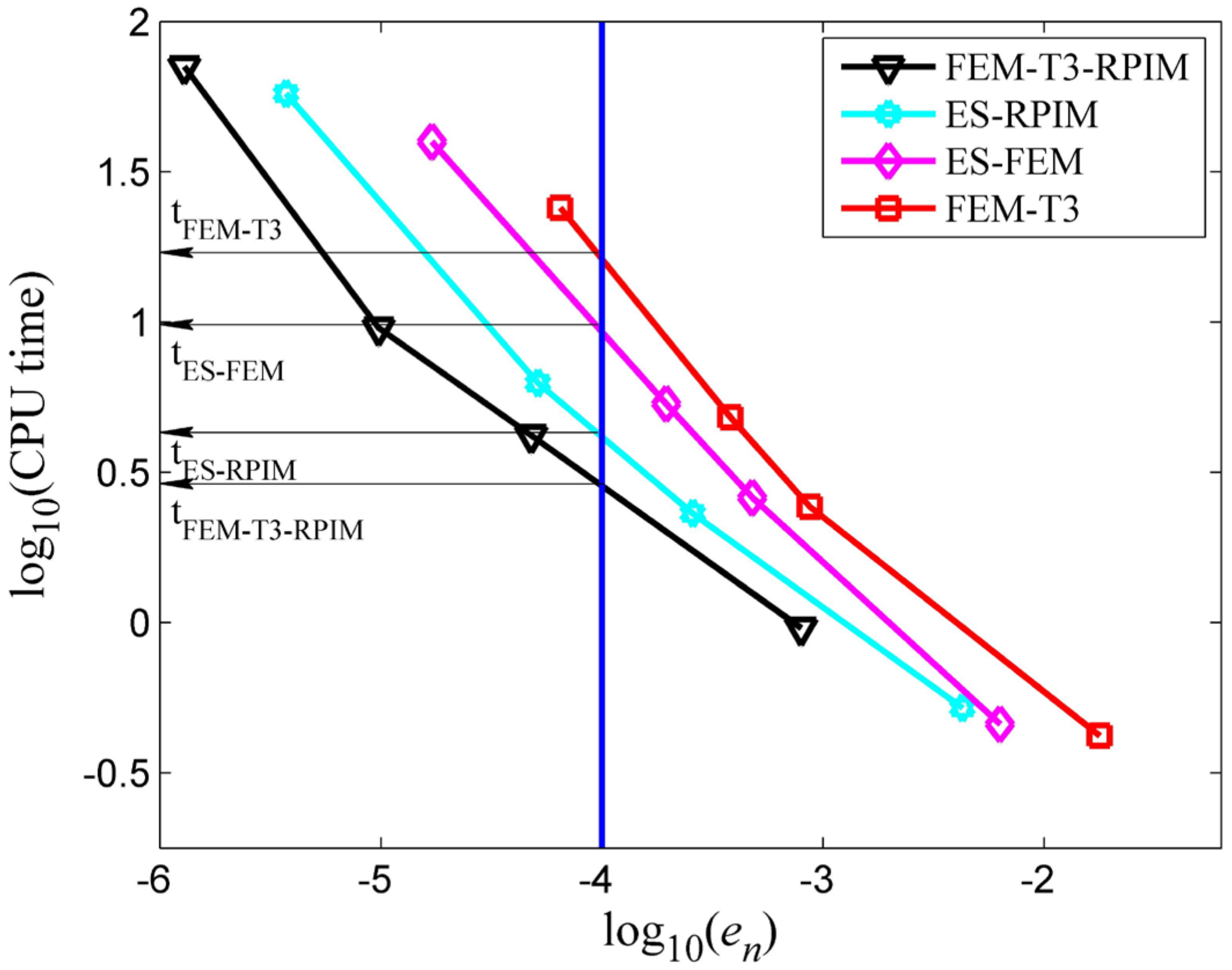
4.1.3. Computational Efficiency Study
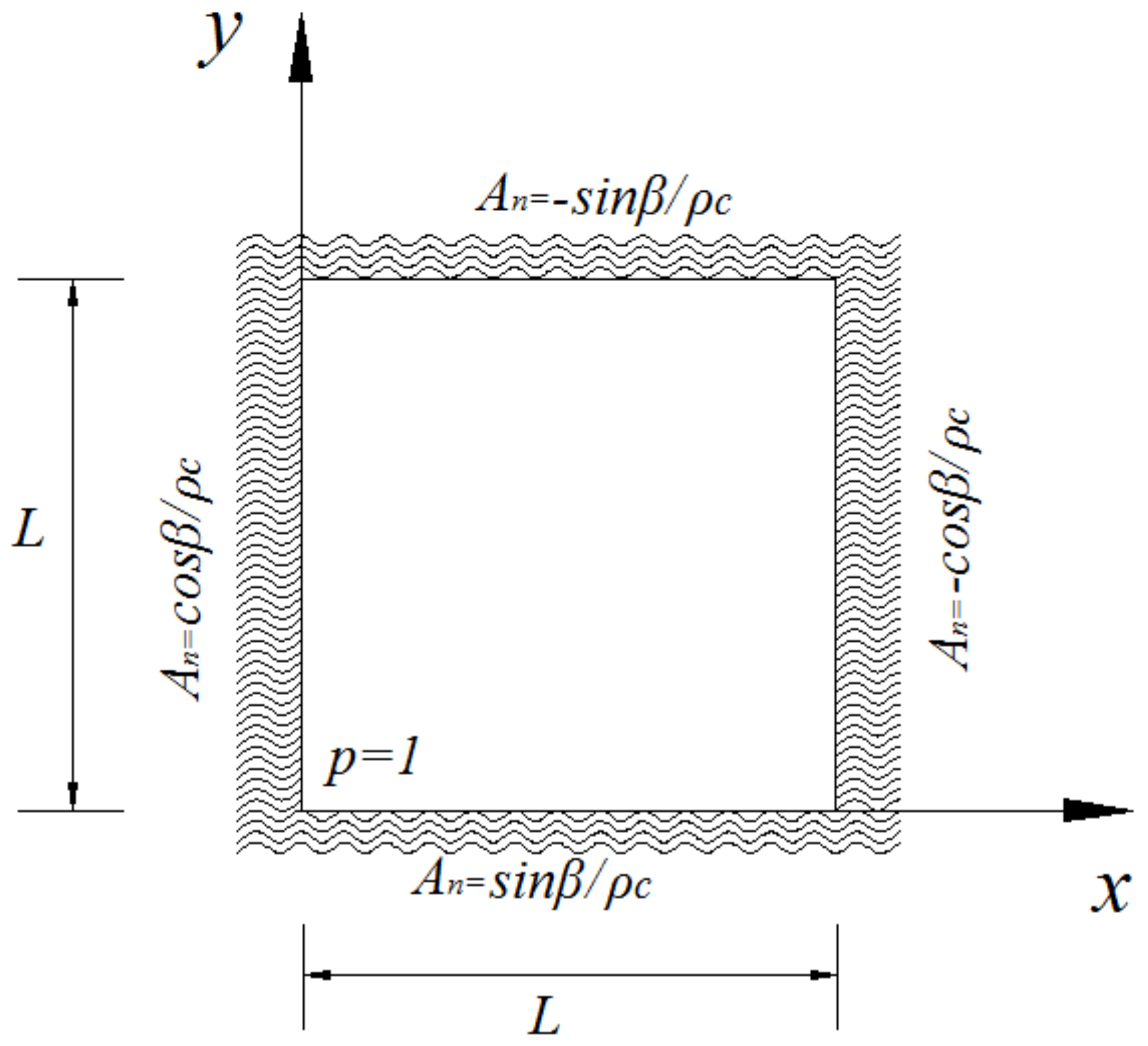
4.2. Acoustic Propagation in a Square Domain
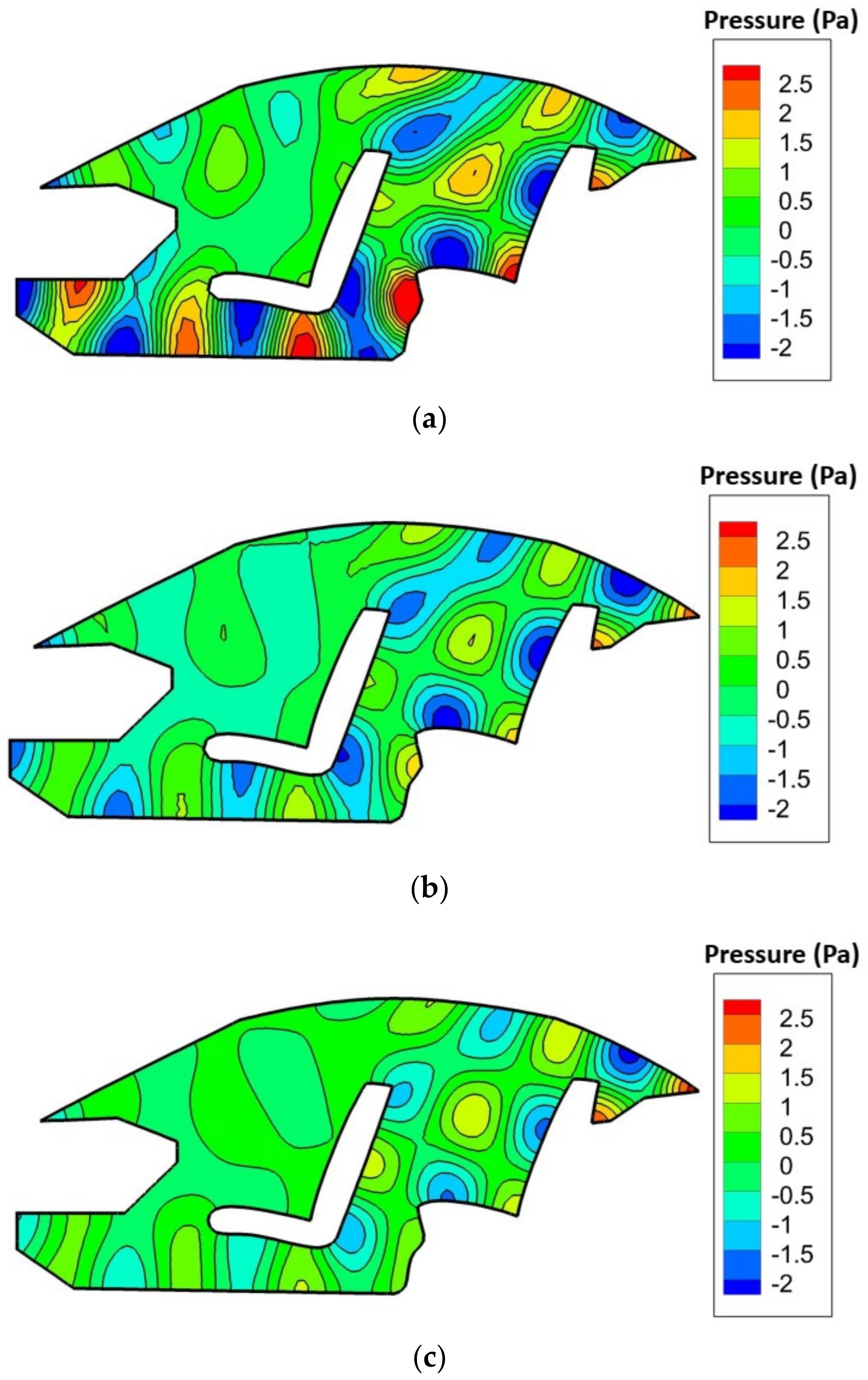
4.3. Acoustic Propagation in a 2D Car
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Harari, I. A survey of finite element methods for time-harmonic acoustics. Comput. Meth. Appl. Mech. Eng. 2006, 195, 1594–1607. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall: Watertown, MA, USA, 2014. [Google Scholar]
- Thompson, L.L. A review of finite-element methods for time-harmonic acoustics. J. Acoust. Soc. Am. 2006, 119, 1315–1330. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Li, X.L. Theoretical analysis of the generalized finite difference method. Comput. Math. Appl. 2022, 120, 1–14. [Google Scholar] [CrossRef]
- Ju, B.R.; Qu, W.Z. Three-dimensional application of the meshless generalized finite difference method for solving the extended Fisher-Kolmogorov equation. App. Math. Lett. 2023, 136, 108458. [Google Scholar] [CrossRef]
- Qu, W.Z.; He, H. A GFDM with supplementary nodes for thin elastic plate bending analysis under dynamic loading. Appl. Math. Lett. 2022, 124, 107664. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xie, Z.Y.; Ji, S.Y.; Tsai, C.C.; Li, A.L. Meshless generalized finite difference method for water wave interactions with multiple-bottom-seated-cylinder-array structures. Ocean Eng. 2020, 195, 106736. [Google Scholar] [CrossRef]
- Fogarty, T.R.; LeVeque, R.J. High-resolution finite-volume methods for acoustic waves in periodic and random media. J. Acoust. Soc. Am. 1999, 106, 17–28. [Google Scholar] [CrossRef]
- Fu, Z.J.; Tang, Z.C.; Xi, Q.; Liu, Q.G.; Gu, Y.; Wang, F.J. Localized collocation schemes and their applications. Acta. Mech. Sin. 2022, 38, 422167. [Google Scholar] [CrossRef]
- Fu, Z.J.; Yang, L.W.; Xi, Q.; Liu, C.S. A boundary collocation method for anomalous heat conduction analysis in functionally graded materials. Comput. Math. Appl. 2021, 88, 91–109. [Google Scholar] [CrossRef]
- Tang, Z.; Fu, Z.J.; Sun, H.; Liu, X. An efficient localized collocation solver for anomalous diffusion on surfaces. Fract. Calc. Appl. Anal. 2021, 24, 865–894. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.; Rabczuk, T.; Yin, D. A localized collocation scheme with fundamental solutions for long-time anomalous heat conduction analysis in functionally graded materials. Int. J. Heat Mass. Tran. 2021, 180, 121778. [Google Scholar] [CrossRef]
- Ihlenburg, F.; Babuška, I. Finite element solution of the Helmholtz equation with high wave number Part I: The h-version of the FEM. Comput. Math. Appl. 1995, 30, 9–37. [Google Scholar] [CrossRef]
- Bouillard, P.; Ihlenburg, F. Error estimation and adaptivity for the finite element method in acoustics: 2D and 3D applications. Comput. Meth. Appl. Mech. Eng. 1999, 176, 147–163. [Google Scholar] [CrossRef]
- Ihlenburg, F.; Babuška, I. Reliability of finite element methods for the numerical computation of waves. Adv. Eng. Softw. 1997, 28, 417–424. [Google Scholar] [CrossRef]
- Ihlenburg, F.; Babuška, I. Finite element solution of the Helmholtz equation with high wave number part II: The hp version of the FEM. SIAM J. Numer. Anal. 1997, 34, 315–358. [Google Scholar] [CrossRef]
- Steffens, L.M.; Parés, N.; Díez, P. Estimation of the dispersion error in the numerical wave number of standard and stabilized finite element approximations of the Helmholtz equation. Int. J. Numer. Methods Eng. 2011, 86, 1197–1224. [Google Scholar] [CrossRef]
- Chai, Y.B.; Gong, Z.X.; Li, W.; Li, T.Y.; Zhang, Q.F.; Zou, Z.H.; Sun, Y.B. Application of smoothed finite element method to two dimensional exterior problems of acoustic radiation. Int. J. Comput. Methods 2018, 15, 1850029. [Google Scholar] [CrossRef]
- Chai, Y.B.; Gong, Z.X.; Li, W.; Zhang, Y.O. Analysis of transient wave propagation in inhomogeneous media using edge-based gradient smoothing technique and bathe time integration method. Eng. Anal. Bound. Elem. 2020, 120, 211–222. [Google Scholar] [CrossRef]
- Li, W.; Gong, Z.X.; Chai, Y.B.; Cheng, C.; Li, T.Y.; Zhang, Q.F.; Wang, M.S. Hybrid gradient smoothing technique with discrete shear gap method for shell structures. Comput. Math. Appl. 2017, 74, 1826–1855. [Google Scholar] [CrossRef]
- Li, W.; You, X.Y.; Chai, Y.B.; Li, T.Y. Edge-Based Smoothed Three-Node Mindlin Plate Element. J. Eng. Mech. 2016, 142, 04016055. [Google Scholar] [CrossRef]
- Wang, T.T.; Zhou, G.; Jiang, C.; Shi, F.C.; Tian, X.D.; Gao, G.J. A coupled cell-based smoothed finite element method and discrete phase model for incompressible laminar flow with dilute solid particles. Eng. Anal. Bound. Elem. 2022, 143, 190–206. [Google Scholar] [CrossRef]
- Cui, X.; Liu, G.R.; Li, Z.R. A high-order edge-based smoothed finite element (ES-FEM) method with four-node triangular element for solid mechanics problems. Eng. Anal. Bound. Elem. 2023, 151, 490–502. [Google Scholar] [CrossRef]
- Li, W.; Chai, Y.B.; Lei, M.; Li, T.Y. Numerical investigation of the edge-based gradient smoothing technique for exterior Helmholtz equation in two dimensions. Comput. Struct. 2017, 182, 149–164. [Google Scholar] [CrossRef]
- Babuška, I.; Ihlenburg, F.; Paik, E.T.; Sauter, S.A. A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution. Comput. Methods Appl. Mech. Eng. 1995, 128, 325–359. [Google Scholar] [CrossRef]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Li, Y.C.; Dang, S.N.; Li, W.; Chai, Y.B. Free and Forced Vibration Analysis of Two-Dimensional Linear Elastic Solids Using the Finite Element Methods Enriched by Interpolation Cover Functions. Mathematics 2022, 10, 456. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Liu, Z.Y. Analysis of transient wave propagation dynamics using the enriched finite element method with interpolation cover functions. Appl. Math. Comput. 2022, 412, 126564. [Google Scholar] [CrossRef]
- Chai, Y.B.; Huang, K.Y.; Wang, S.P.; Xiang, Z.C.; Zhang, G.J. The Extrinsic Enriched Finite Element Method with Appropriate Enrichment Functions for the Helmholz Equation. Mathematics 2023, 11, 1664. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C. Achievements and some unsolved problems of the finite element method. Int. J. Numer. Methods Eng. 2000, 47, 9–28. [Google Scholar] [CrossRef]
- Chai, Y.B.; You, X.Y.; Li, W. Dispersion Reduction for the Wave Propagation Problems Using a Coupled “FE-Meshfree” Triangular Element. Int. J. Comput. Methods 2020, 17, 1950071. [Google Scholar] [CrossRef]
- Gui, Q.; Li, W.; Chai, Y.B. The enriched quadrilateral overlapping finite elements for time-harmonic acoustics. Appl. Math. Comput. 2023, 451, 128018. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Gong, Z.X.; Li, T.Y. Hybrid smoothed finite element method for two-dimensional underwater acoustic scattering problems. Ocean Eng. 2016, 116, 129–141. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Gong, Z.X.; Li, T.Y. Hybrid smoothed finite element method for two dimensional acoustic radiation problems. Appl. Acoust. 2016, 103, 90–101. [Google Scholar] [CrossRef]
- Preuss, S.; Gurbuz, C.; Jelich, C.; Baydoun, S.K.; Marburg, S. Recent Advances in Acoustic Boundary Element Methods. J. Theor. Comput. Acous. 2022, 30, 2240002. [Google Scholar] [CrossRef]
- Peake, M.J.; Trevelyan, J.; Coates, G. Extended isogeometric boundary element method (XIBEM) for two-dimensional Helmholtz problems. Comput. Meth. Appl. Mech. Eng. 2013, 259, 93–102. [Google Scholar] [CrossRef]
- Gu, Y.; Lei, J. Fracture mechanics analysis of two-dimensional cracked thin structures (from micro- to nano-scales) by an efficient boundary element analysis. Results Math. 2021, 11, 100172. [Google Scholar] [CrossRef]
- Chen, Z.T.; Wang, F.J. Localized Method of Fundamental Solutions for Acoustic Analysis Inside a Car Cavity with Sound-Absorbing Material. Adv. Appl. Math. Mech. 2023, 15, 182–201. [Google Scholar]
- Li, J.P.; Fu, Z.J.; Gu, Y.; Zhang, L. Rapid calculation of large-scale acoustic scattering from complex targets by a dual-level fast direct solver. Comput. Math. Appl. 2023, 130, 1–9. [Google Scholar] [CrossRef]
- Li, J.P.; Fu, Z.J.; Gu, Y.; Qin, Q.H. Recent advances and emerging applications of the singular boundary method for large-scale and high-frequency computational acoustics. Adv. Appl. Math. Mech. 2022, 14, 315–343. [Google Scholar] [CrossRef]
- Cheng, S.F.; Wang, F.J.; Wu, G.Z.; Zhang, C.X. Semi-analytical and boundary-type meshless method with adjoint variable formulation for acoustic design sensitivity analysis. Appl. Math. Lett. 2022, 131, 108068. [Google Scholar] [CrossRef]
- Fu, Z.J.; Xi, Q.; Gu, Y.; Li, J.P.; Qu, W.Z.; Sun, L.L.; Wei, X.; Wang, F.J.; Lin, J.; Li, W.W.; et al. Singular boundary method: A review and computer implementation aspects. Eng. Anal. Bound. Elem. 2023, 147, 231–266. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.J.; Li, P.W.; Qu, W. Singular boundary method for 2D and 3D acoustic design sensitivity analysis. Comput. Math. Appl. 2022, 119, 371–386. [Google Scholar] [CrossRef]
- Gu, Y.; Fan, C.M.; Fu, Z.J. Localized method of fundamental solutions for three-dimensional elasticity problems: Theory. Adv. Appl. Math. Mech. 2021, 13, 1520–1534. [Google Scholar]
- Fu, Z.J.; Xi, Q.; Li, Y.; Huang, H.; Rabczuk, T. Hybrid FEM–SBM solver for structural vibration induced underwater acoustic radiation in shallow marine environment. Comput. Methods Appl. Mech. Eng. 2020, 369, 113236. [Google Scholar] [CrossRef]
- Li, J.P.; Zhang, L.; Qin, Q.H. A regularized fast multipole method of moments for rapid calculation of three-dimensional time-harmonic electromagnetic scattering from complex targets. Eng. Anal. Bound. Elem. 2022, 142, 28–38. [Google Scholar] [CrossRef]
- Li, J.P.; Gu, Y.; Qin, Q.H.; Zhang, L. The rapid assessment for three-dimensional potential model of large-scale particle system by a modified multilevel fast multipole algorithm. Comput. Math. Appl. 2021, 89, 127–138. [Google Scholar] [CrossRef]
- Wei, X.; Rao, C.; Chen, S.; Luo, W. Numerical simulation of anti-plane wave propagation in heterogeneous media. App. Math. Lett. 2023, 135, 108436. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. An Introduction to Meshfree Methods and Their Programming; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Chen, Z.; Sun, L. A boundary meshless method for dynamic coupled thermoelasticity problems. App. Math. Lett. 2022, 134, 108305. [Google Scholar] [CrossRef]
- Li, Y.C.; Liu, C.; Li, W.; Chai, Y.B. Numerical investigation of the element-free Galerkin method (EFGM) with appropriate temporal discretization techniques for transient wave propagation problems. Appl. Math. Comput. 2023, 442, 127755. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 8, 1013–1024. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Huang, T.H.; Wei, H.; Chen, J.S.; Hillman, M.C. RKPM2D: An open-source implementation of nodally integrated reproducing kernel particle method for solving partial differential equations. Comput. Part. Mech. 2020, 7, 393–433. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, Y.H.; Reutskiy, S.; Feng, W.J. A novel meshless space-time backward substitution method and its application to nonhomogeneous advection-diffusion problems. Appl. Math. Comput. 2021, 398, 125964. [Google Scholar] [CrossRef]
- Li, X.; Li, S. A finite point method for the fractional cable equation using meshless smoothed gradients. Eng. Anal. Bound. Elem. 2022, 134, 453–465. [Google Scholar] [CrossRef]
- Suleau, S.; Bouillard, P. One-dimensional dispersion analysis for the element-free Galerkin method for the Helmholtz equation. Int. J. Numer. Methods Eng. 2000, 47, 1169–1188. [Google Scholar] [CrossRef]
- Suleaub, S.; Deraemaeker, A.; Bouillard, P. Dispersion and pollution of meshless solutions for the Helmholtz equation. Comput. Meth. Appl. Mech. Eng. 2000, 190, 639–657. [Google Scholar] [CrossRef]
- Wenterodt, C.; Estorff, O. Dispersion analysis of the meshfree radial point interpolation method for the Helmholtz equation. Int. J. Numer. Methods Eng. 2009, 77, 1670–1689. [Google Scholar] [CrossRef]
- Bouillard, P.; Sauter, S. Element-Free Galerkin solutions for Helmholtz problems: Formulation and numerical assessment of the pollution effect. Comput. Meth. Appl. Mech. Eng. 1998, 162, 317–335. [Google Scholar] [CrossRef]
- You, X.Y.; Li, W.; Chai, Y.B. A truly meshfree method for solving acoustic problems using local weak form and radial basis functions. Appl. Math. Comput. 2020, 365, 124694. [Google Scholar] [CrossRef]
- Liu, C.; Min, S.S.; Pang, Y.D.; Chai, Y.B. The Meshfree Radial Point Interpolation Method (RPIM) for Wave Propagation Dynamics in Non-Homogeneous Media. Mathematics 2023, 11, 523. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Gui, Q.; Chai, Y.B. A coupled FE-Meshfree triangular element for acoustic radiation problems. Int. J. Comput. Methods 2021, 18, 2041002. [Google Scholar] [CrossRef]
- He, Z.C.; Liu, G.R.; Zhong, Z.H.; Wu, S.C.; Zhang, G.Y.; Cheng, A.G. An edge-based smoothed finite element method (ES-FEM) for analyzing three-dimensional acoustic problems. Comput. Meth. Appl. Mech. Eng. 2009, 199, 20–33. [Google Scholar] [CrossRef]
- Sun, T.T.; Wang, P.; Zhang, G.J.; Chai, Y.B. Transient analyses of wave propagations in nonhomogeneous media employing the novel finite element method with the appropriate enrichment function. Comput. Math. Appl. 2023, 129, 90–112. [Google Scholar] [CrossRef]
- Yang, Y.T.; Chen, L.; Tang, X.H.; Zheng, H.; Liu, Q.S. A partition-of-unity based “FE-Meshfree” hexahedral element with continuous nodal stress. Comput. Struct. 2017, 178, 17–28. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Zheng, H. A partition-of-unity based “FE-Meshfree” triangular element with radial-polynomial basis functions for static and free vibration analysis. Eng. Anal. Bound. Elem. 2016, 65, 18–38. [Google Scholar] [CrossRef]
- Rajendran, S.; Zhang, B.R. A “FE-meshfree” QUAD4 element based on partition of unity. Comput. Meth. Appl. Mech. Eng. 2007, 197, 128–147. [Google Scholar] [CrossRef]
- Xu, J.P.; Rajendran, S. A partition-of-unity based “FE-Meshfree” QUAD4 element with radial-polynomial basis functions for static analyses. Comput. Meth. Appl. Mech. Eng. 2011, 200, 3309–3323. [Google Scholar] [CrossRef]
- Zhang, Y.O.; Dang, S.N.; Li, W.; Chai, Y.B. Performance of the radial point interpolation method (RPIM) with implicit time integration scheme for transient wave propagation dynamics. Comput. Math. Appl. 2022, 114, 95–111. [Google Scholar] [CrossRef]
- Nie, B.; Ren, S.H.; Li, W.Q.; Zhou, L.M.; Liu, C.Y. The hygro-thermo-electro-mechanical coupling edge-based smoothed point interpolation method for the response of functionally graded piezoelectric structure under hygrothermal environment. Eng. Anal. Bound. Elem. 2021, 130, 29–39. [Google Scholar] [CrossRef]






| Mode | Exact (Hz) | Trig3-RPIM (Hz) | Trig3-RPIM Error(%) | FEM-T3 (Hz) | FEM-T3 Error(%) | ES-FEM (Hz) | ES-FEM Error(%) |
|---|---|---|---|---|---|---|---|
| 1 | 750.00 | 749.99 | 0.00 | 750.12 | 0.02 | 750.06 | 0.01 |
| 2 | 1500.00 | 1499.77 | 0.02 | 1500.99 | 0.07 | 1500.74 | 0.05 |
| 3 | 2250.00 | 2249.23 | 0.03 | 2253.33 | 0.15 | 2252.69 | 0.12 |
| 4 | 3000.00 | 2998.18 | 0.06 | 3007.90 | 0.26 | 3006.53 | 0.22 |
| 5 | 3750.00 | 3746.49 | 0.09 | 3765.44 | 0.41 | 3762.87 | 0.34 |
| 6 | 4500.00 | 4494.02 | 0.13 | 4526.69 | 0.59 | 4522.28 | 0.50 |
| 7 | 5250.00 | 5240.67 | 0.18 | 5292.41 | 0.81 | 5285.36 | 0.67 |
| 8 | 6000.00 | 5986.34 | 0.23 | 6063.35 | 1.06 | 6052.65 | 0.88 |
| 9 | 6750.00 | 6730.99 | 0.28 | 6840.26 | 1.34 | 6824.65 | 1.11 |
| 10 | 7500.00 | 7474.57 | 0.34 | 7623.90 | 1.65 | 7601.81 | 1.36 |
| 11 | 7500.00 | 7547.38 | 0.63 | 7623.90 | 1.65 | 7622.74 | 1.64 |
| 12 | 7537.40 | 7584.21 | 0.62 | 7670.71 | 1.77 | 7663.63 | 1.67 |
| 13 | 7648.50 | 7693.12 | 0.58 | 7798.25 | 1.96 | 7786.83 | 1.81 |
| 14 | 7830.20 | 7871.27 | 0.52 | 7999.93 | 2.17 | 7988.40 | 2.02 |
| 15 | 8077.70 | 8113.91 | 0.45 | 8295.81 | 2.70 | 8263.10 | 2.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, S.; Wang, G.; Chai, Y. A Novel “Finite Element-Meshfree” Triangular Element Based on Partition of Unity for Acoustic Propagation Problems. Mathematics 2023, 11, 2475. https://doi.org/10.3390/math11112475
Dang S, Wang G, Chai Y. A Novel “Finite Element-Meshfree” Triangular Element Based on Partition of Unity for Acoustic Propagation Problems. Mathematics. 2023; 11(11):2475. https://doi.org/10.3390/math11112475
Chicago/Turabian StyleDang, Sina, Gang Wang, and Yingbin Chai. 2023. "A Novel “Finite Element-Meshfree” Triangular Element Based on Partition of Unity for Acoustic Propagation Problems" Mathematics 11, no. 11: 2475. https://doi.org/10.3390/math11112475
APA StyleDang, S., Wang, G., & Chai, Y. (2023). A Novel “Finite Element-Meshfree” Triangular Element Based on Partition of Unity for Acoustic Propagation Problems. Mathematics, 11(11), 2475. https://doi.org/10.3390/math11112475






