Stability Analysis for Digital Redesign of Discrete-Time Switched Systems Using H∞ Linear Matrix Inequality
Abstract
:1. Introduction
2. Systems Description and Preliminaries
3. The Prediction-Based Digital Redesign
3.1. Optimal Linearization
3.2. Linear-Quadratic Analogue Tracker Design
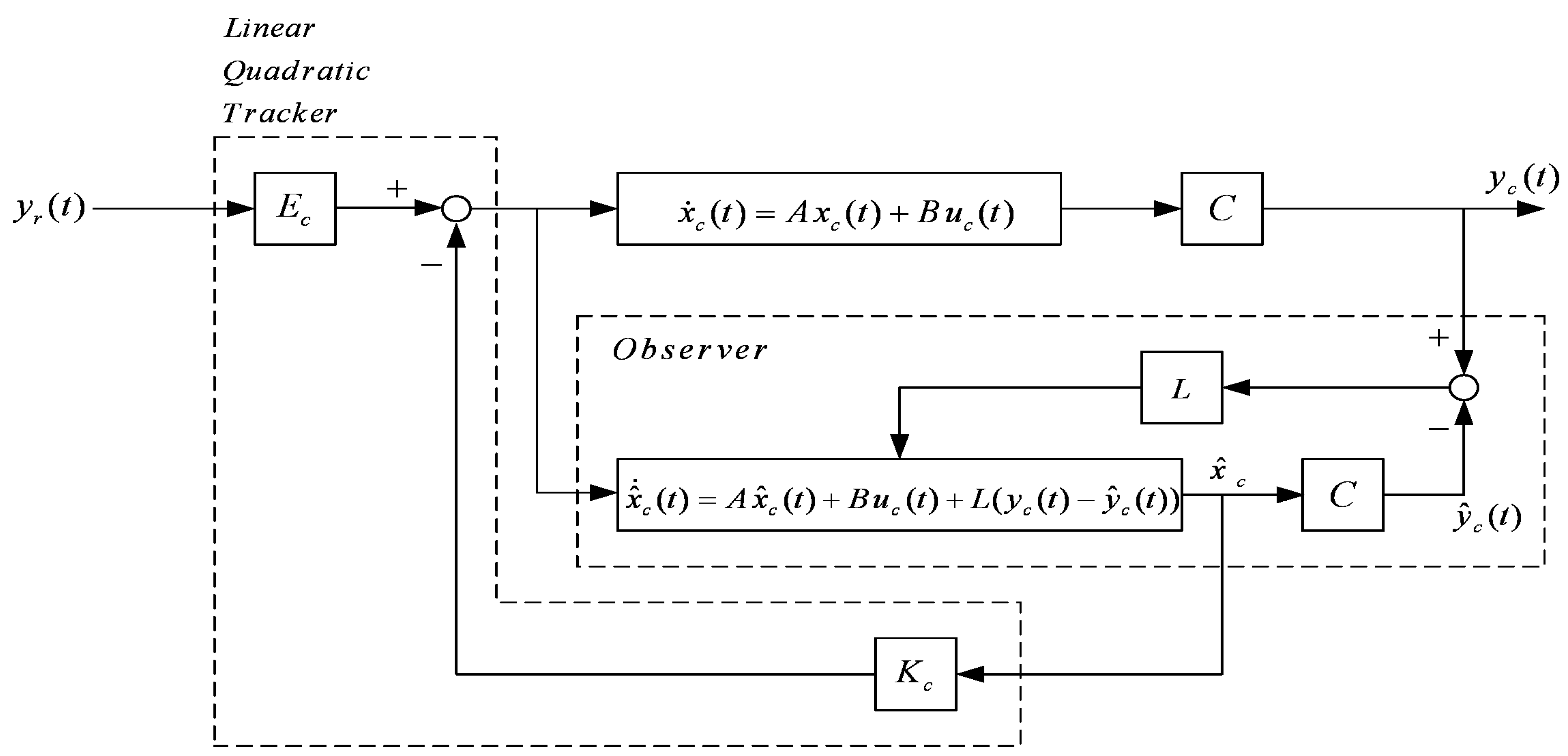
3.3. Observer-Based Linear-Quadratic Analogue Tracker Design
3.4. Digital Redesign of the Linear-Quadratic Analogue Tracker
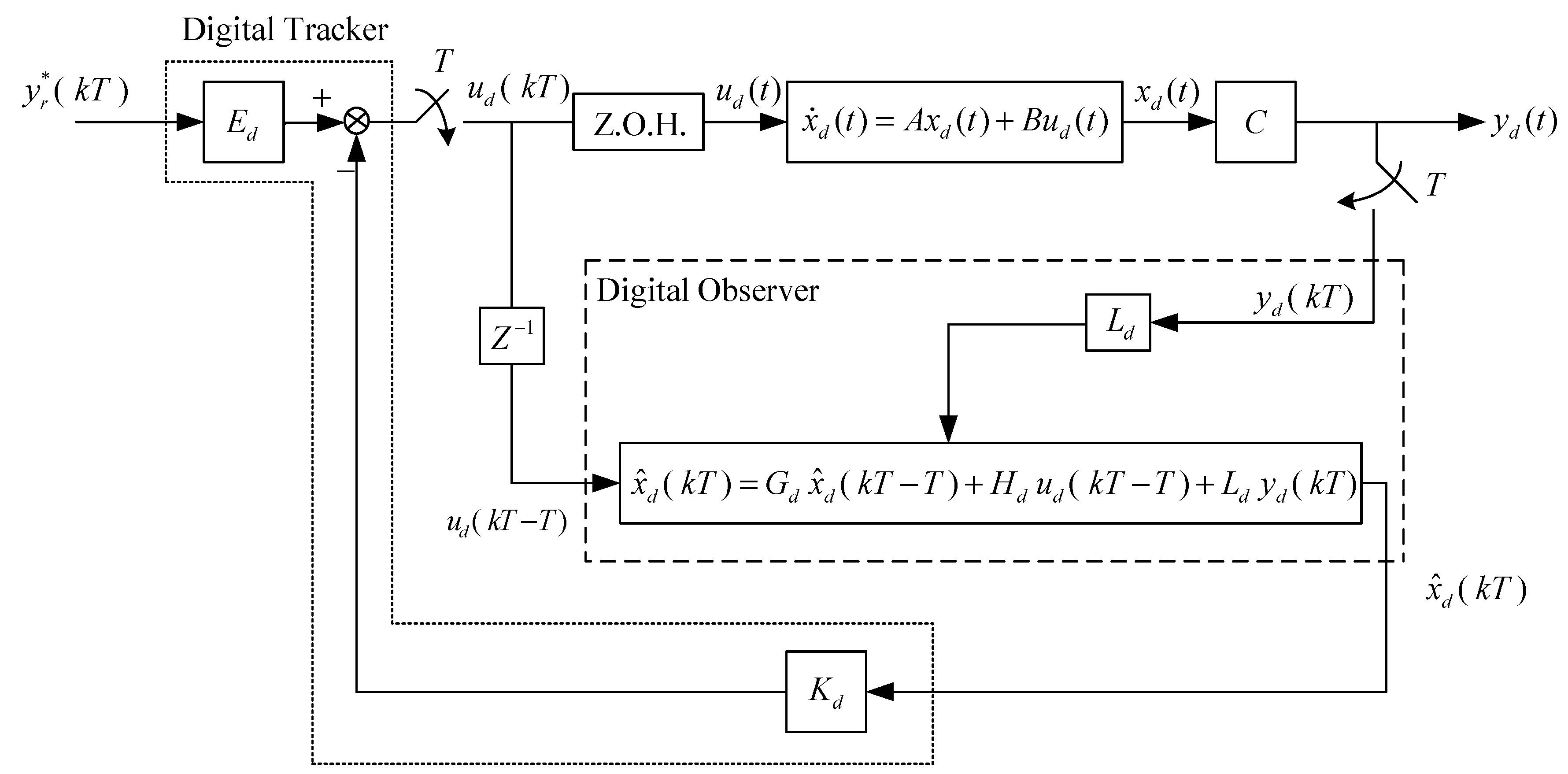
3.5. Digital Redesign of the Observer-Based Linear-Quadratic Analogue Tracker
4. Linear Matrix Inequality Constraint with An Unstable Discrete-Time System
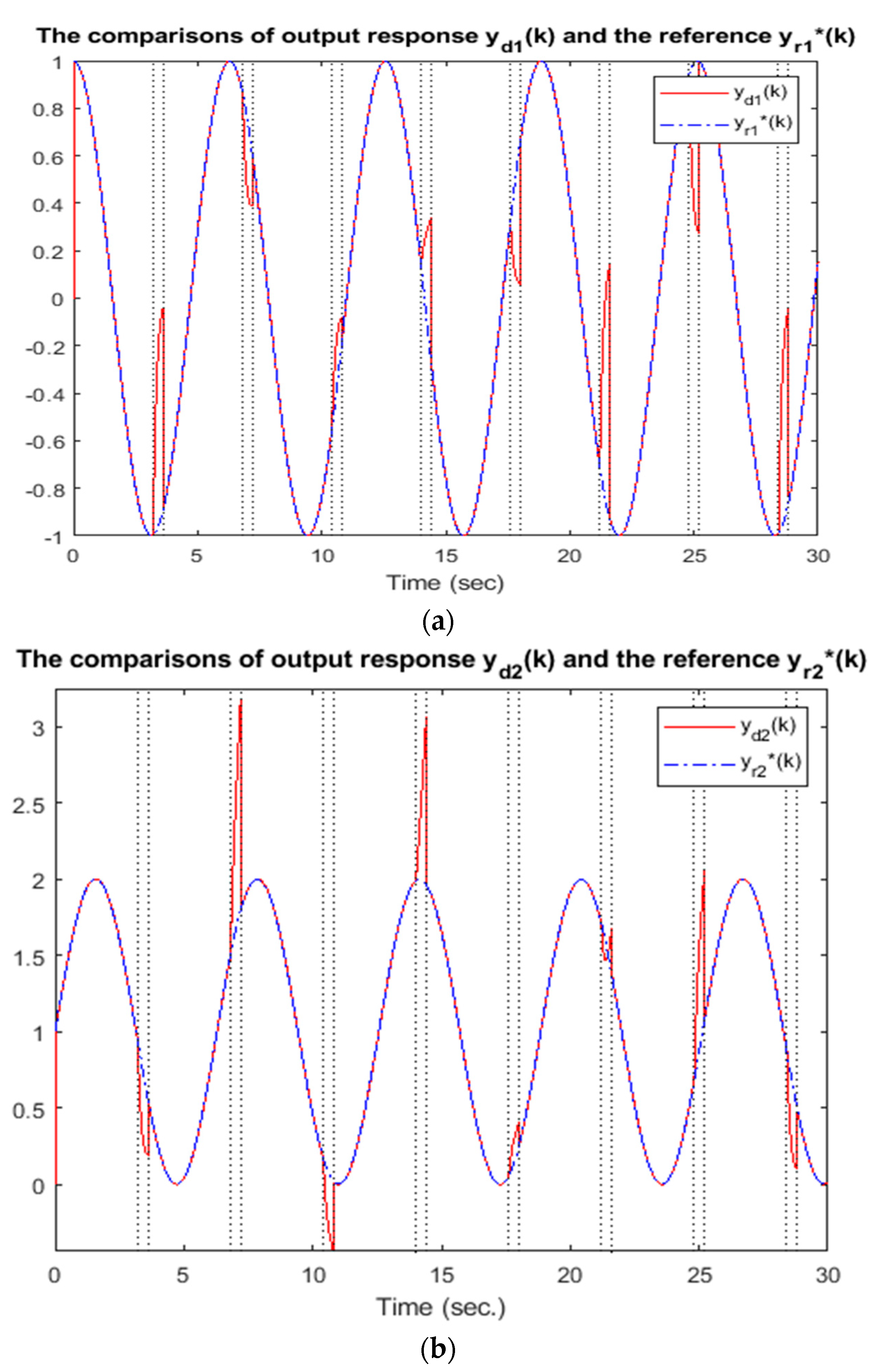
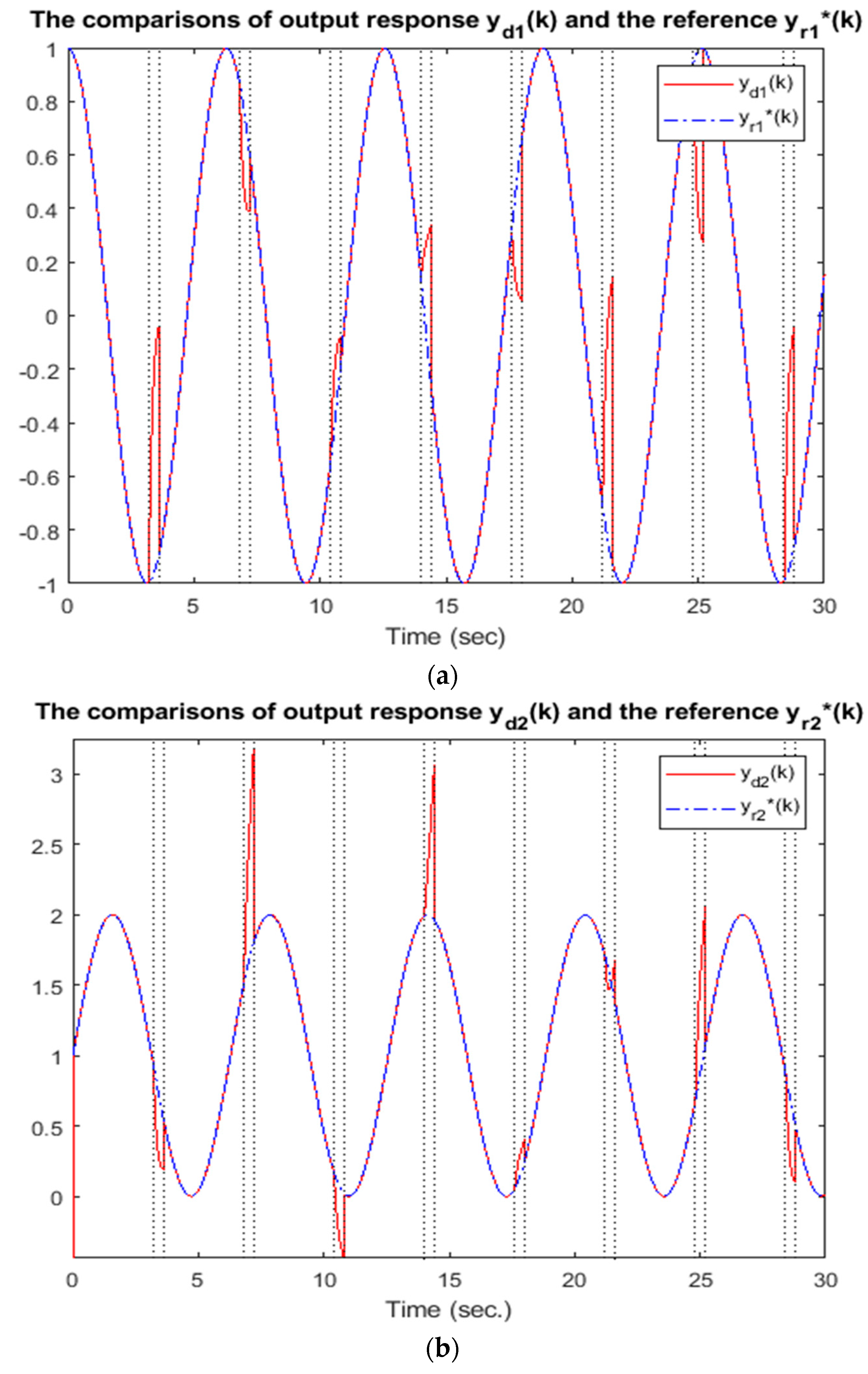
5. An Illustrative Example
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Xue, M.; Tang, Y.; Ren, W.; Qian, F. Stability of multi-dimensional switched systems with an application to open multi-agent systems. Automatica 2022, 146, 110644. [Google Scholar] [CrossRef]
- Li, F.P.; Wang, R.H.; Fei, S.M. Stability and controller design of discrete-time switched systems based on transferring-dependent lyapunov function approach. Int. J. Control Autom. Syst. 2022, 20, 1142–1153. [Google Scholar] [CrossRef]
- Qi, S.; Zhao, J.; Tang, L. Adaptive output feedback control for constrained switched systems with input quantization. Mathematics 2023, 11, 788. [Google Scholar] [CrossRef]
- Lin, X.; Huang, J.; Park, J. Finite-time non-smooth stabilization of cascade output-constrained switched systems. Int. J. Robust Nonlinear Control 2023, 33, 1407–2507. [Google Scholar] [CrossRef]
- Han, Y.; Zhao, Y.; Wang, P. Finite-time rate anti-bump switching control for switched systems. Appl. Math. Comput. 2021, 401, 126086. [Google Scholar] [CrossRef]
- Liberzon, D. Switching in Systems and Control, 1st ed.; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Sun, Z.; Ge, S.S. Switched Linear Systems: Control and Design, 1st ed.; Springer: London, UK, 2005. [Google Scholar]
- Liu, X.; Zhong, S.; Ding, X. A Razumikhin approach to exponential admissibility of switched descriptor delayed systems. Appl. Math. Model. 2014, 38, 1647–1659. [Google Scholar] [CrossRef]
- Lu, A.Y.; Yang, G.H. Stabilization of switched systems with all modes unstable via periodical switching laws. Automatica 2020, 122, 109150. [Google Scholar] [CrossRef]
- Yu, Q.; Lv, H. Stability analysis for discrete-time switched systems with stable and unstable modes based on a weighted average dwell time approach. Nonlinear Anal. Hybrid Syst. 2020, 38, 100949. [Google Scholar] [CrossRef]
- Sun, Z. Feedback stabilization of third-order switched linear control systems. IEEE Control Syst. Lett. 2020, 4, 857–861. [Google Scholar] [CrossRef]
- Kundu, A.; Chatterjee, D. On stability of discrete-time switched systems. Nonlinear Anal. Hybrid Syst. 2017, 23, 191–210. [Google Scholar] [CrossRef]
- Wang, R.H.; Jiao, T.C.; Zhang, T.; Fei, S.M. Improved stability results for discrete-time switched systems: A multiple piecewise convex Lyapunov function approach. Appl. Math. Comput. 2019, 353, 54–65. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, P.; Yin, Y.; Nguang, S.K. New results on stability of slowly switched systems: A multiple discontinuous Lyapunov function approach. IEEE Trans. Automat. Control 2016, 62, 3502–3509. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, L.; Li, J.; Zhang, W. Improved LVS guidance and path-following control for unmanned sailboat robot with the minimum triggered setting. Ocean Eng. 2023, 272, 113860. [Google Scholar] [CrossRef]
- Bertolin, A.L.J.; Oliveira, R.C.L.F.; Valmorbida, G.; Peres, P.L.D. An LMI approach for stability analysis and output-feedback stabilization of discrete-time Lur’e systems using Zames-Falb multipliers. IEEE Contr. Syst. Lett. 2022, 6, 710–715. [Google Scholar] [CrossRef]
- Li, X.; de Souza, C.E. Delay-dependent robust stability and stabilization of uncertain linear delay systems: A linear matrix inequality approach. IEEE Trans. Autom. Control 1997, 42, 1144–1148. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, P. Stability, L2—Gain and asynchronous H∞ control of discrete-time switched systems with average dwell time. IEEE Trans. Autom. Control 2009, 54, 2192–2199. [Google Scholar] [CrossRef]
- Zhao, X.D.; Zhang, L.X.; Shi, P.; Liu, M. Stability and stabilization of switched linear systems with mode-dependent average dwell time. IEEE Trans. Automat. Control 2012, 46, 1809–1815. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H. Dwell time stability and stabilization of interval discrete-time switched positive linear systems. Nonlinear Anal. Hybrid Syst. 2019, 33, 116–129. [Google Scholar] [CrossRef]
- Du, S.L.; Karimi, H.R.; Qiao, J.F.; Wu, D.; Feng, C. Stability analysis for a class of discrete-time switched systems with partial unstable subsystems. IEEE Trans. Circuit. Syst. II Express Briefs 2019, 66, 2017–2021. [Google Scholar] [CrossRef]
- Zhai, G.; Hu, B.; Yasuda, K.; Michel, A.N. Qualitative analysis of discrete-time switched systems. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002. [Google Scholar]
- Hespanha, J.P.; Morse, A.S. Stability of switched systems with average dwell-time. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999. [Google Scholar]
- Zhai, G.; Lin, H.; Xu, X.; Imae, J.; Kobayashi, T. Analysis of switched normal discrete-time systems. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Wicks, M.A.; Peleties, P.; DeCarlo, R.A. Construction of piecewise lyapunov functions for stabilizing switched systems. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994. [Google Scholar]
- Lee, L.; Chen, J.L. Strictly positive real lemma and absolute stability for discrete-time descriptor systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 788–794. [Google Scholar] [CrossRef]
- Peters, A.A.; Vargas, F.J.; Chen, J. An algebraic formula for performance bounds of a weighted H∞ optimal control problem. IEEE Trans. Automat. Control 2021, 66, 781–786. [Google Scholar] [CrossRef]
- Brogliato, B.; Lozano, R.; Maschke, B.; Egeland, O. Dissipative Systems Analysis and Control, 3rd ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Iwasaki, T.; Skelton, R.E.; Grigoriadis, K.M. A Unified Algebraic Approach to Linear Control Design; Taylor & Francis: London, UK, 1998. [Google Scholar]
- Guo, S.M.; Shieh, L.S.; Chen, G.; Lin, C.F. Effective chaotic orbit tracker: A prediction-based digital redesign approach. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 1557–1570. [Google Scholar]
- Tsai, J.S.H.; Chen, F.M.; Guo, S.M.; Chen, C.W.; Shieh, L.S. A novel tracker for a class of sampled-data nonlinear systems. J. Vib. Control 2011, 17, 81–101. [Google Scholar] [CrossRef]
- Shieh, L.S.; Wang, W.M.; Zheng, J.B. Robust control of sampled-data uncertain systems using digitally redesigned observer-based controller. Int. J. Control 1997, 66, 43–64. [Google Scholar] [CrossRef]
- Guo, S.M.; Shieh, L.S.; Lin, C.F.; Chandra, J. State-space self-tuning control for nonlinear stochastic and chaotic hybrid systems. Int. J. Birfurcation Chaos 2001, 11, 1079–1113. [Google Scholar] [CrossRef]
- Zhai, G.; Chen, X.; Takai, S.; Yasuda, K. Stability and H∞ disturbance attenuation analysis for LTI control systems with controller failures. Asian J. Control 2004, 6, 104–111. [Google Scholar]
- Xiang, W.; Tran, H.D.; Johnson, T.T. Nonconservative lifted convex conditions for stability of discrete-time switched systems under minimum dwell-time constraint. IEEE Trans. Autom. Control 2019, 64, 3407–3414. [Google Scholar] [CrossRef]
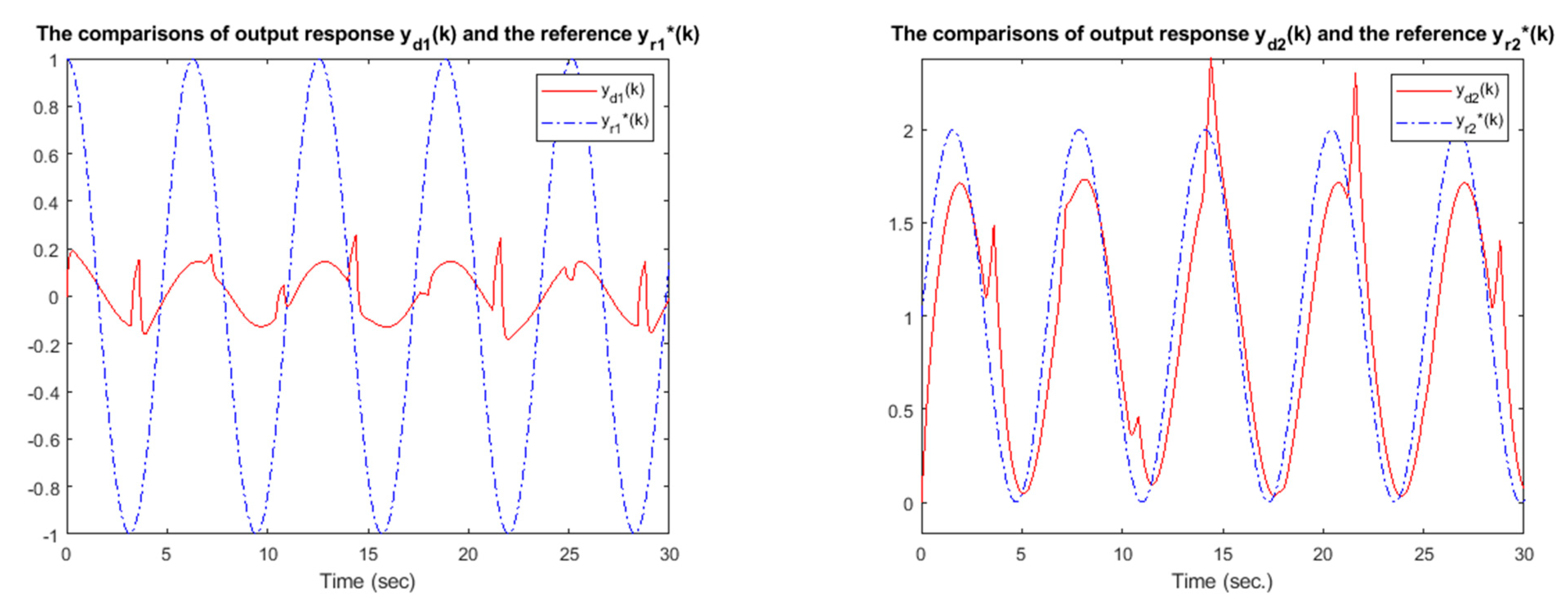
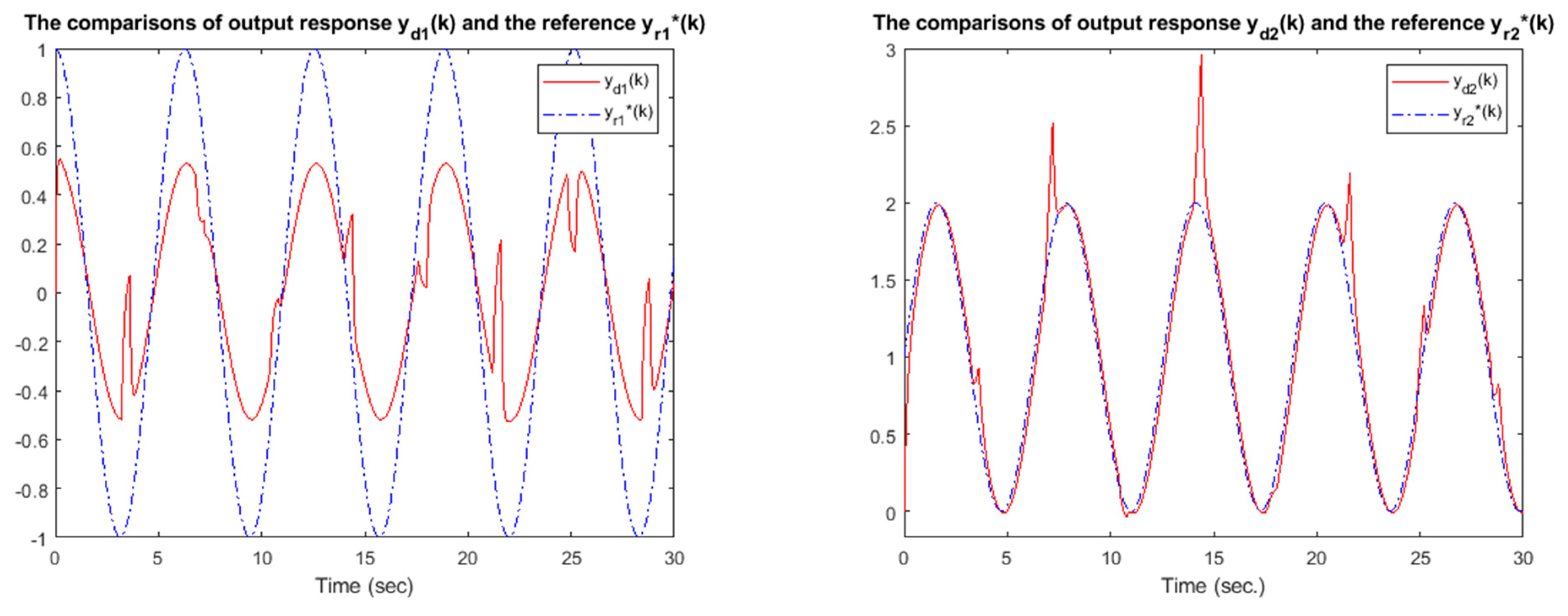
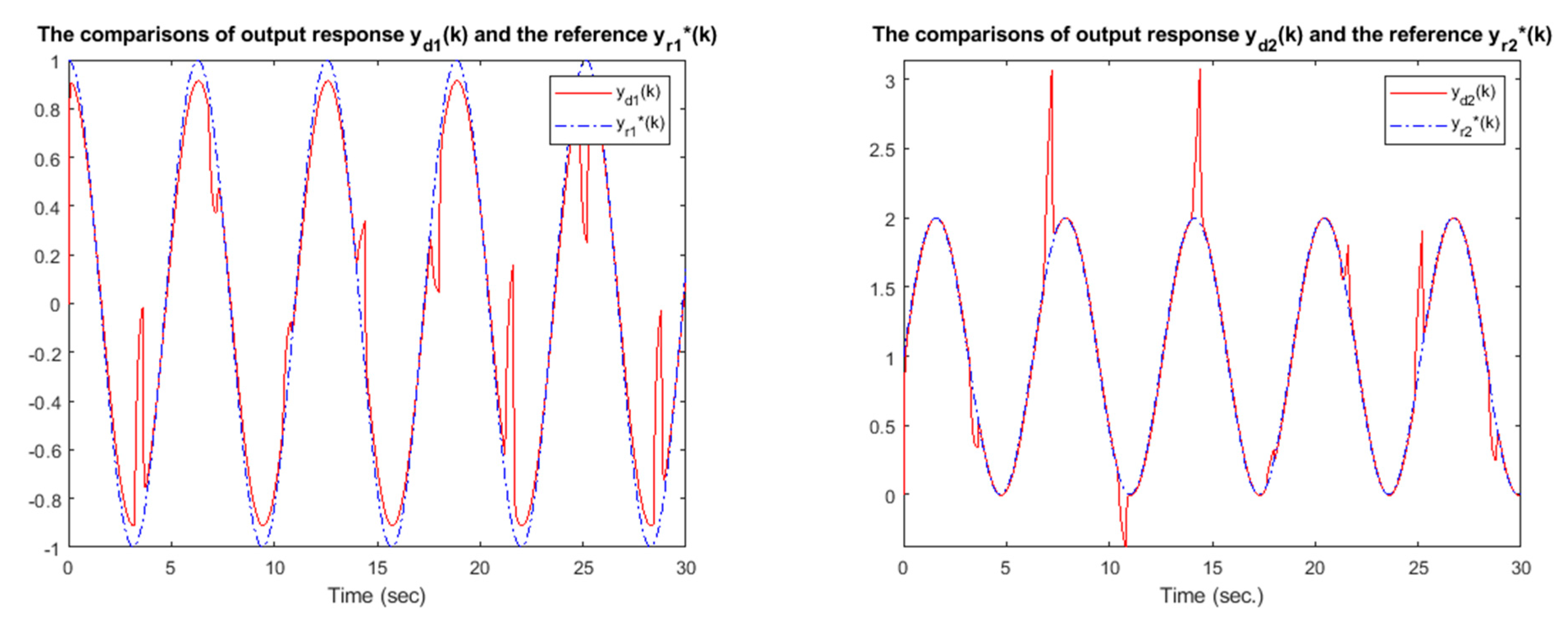
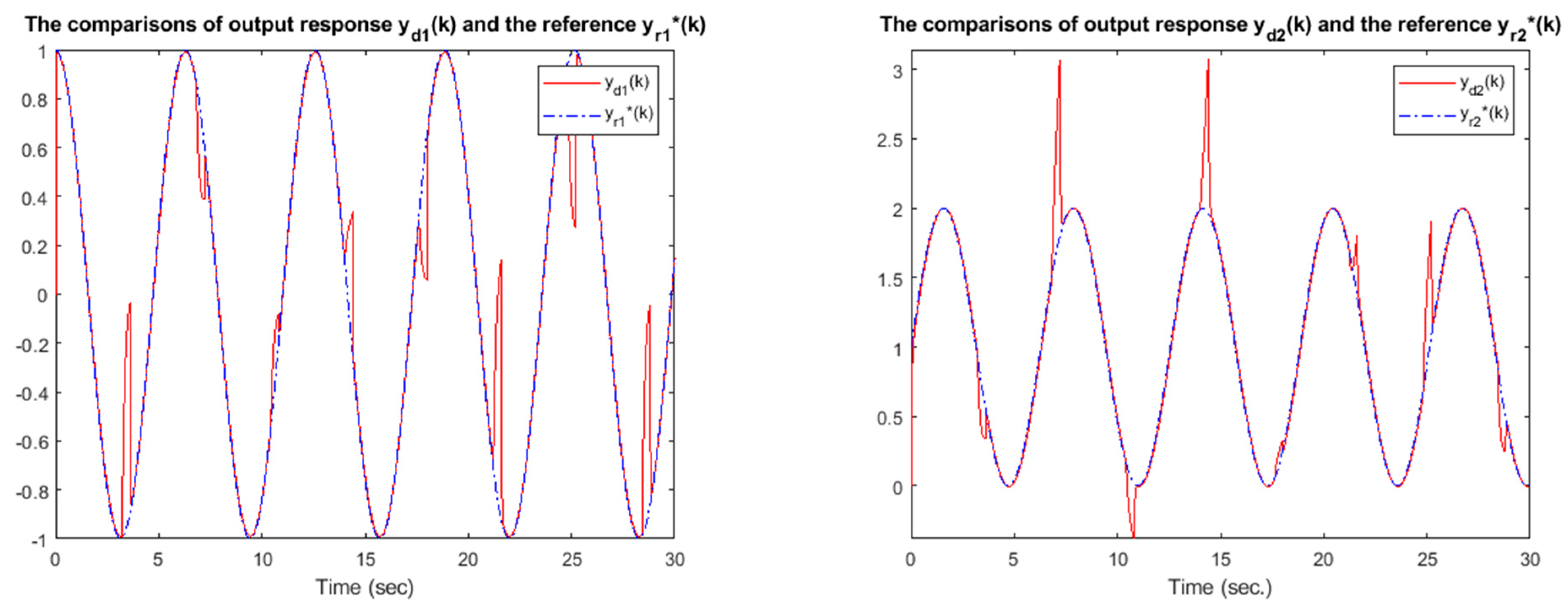
| Q | Bounded in the Intervals | Tracking Performance |
|---|---|---|
| poor | ||
| poor | ||
| acceptable | ||
| good | ||
| good |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, N.-T. Stability Analysis for Digital Redesign of Discrete-Time Switched Systems Using H∞ Linear Matrix Inequality. Mathematics 2023, 11, 2468. https://doi.org/10.3390/math11112468
Hu N-T. Stability Analysis for Digital Redesign of Discrete-Time Switched Systems Using H∞ Linear Matrix Inequality. Mathematics. 2023; 11(11):2468. https://doi.org/10.3390/math11112468
Chicago/Turabian StyleHu, Nien-Tsu. 2023. "Stability Analysis for Digital Redesign of Discrete-Time Switched Systems Using H∞ Linear Matrix Inequality" Mathematics 11, no. 11: 2468. https://doi.org/10.3390/math11112468
APA StyleHu, N.-T. (2023). Stability Analysis for Digital Redesign of Discrete-Time Switched Systems Using H∞ Linear Matrix Inequality. Mathematics, 11(11), 2468. https://doi.org/10.3390/math11112468






