Topological Properties and Entropy Calculations of Aluminophosphates
Abstract
:1. Introduction
2. Computational Theoretical Technique
- 1.
- 2.
- 3.
- 4.
3. Results and Discussion
3.1. Vertex Distance-Based Topological Indices
3.2. Vertex Degree-Based Topological Indices
3.3. Degree-Based Entropy
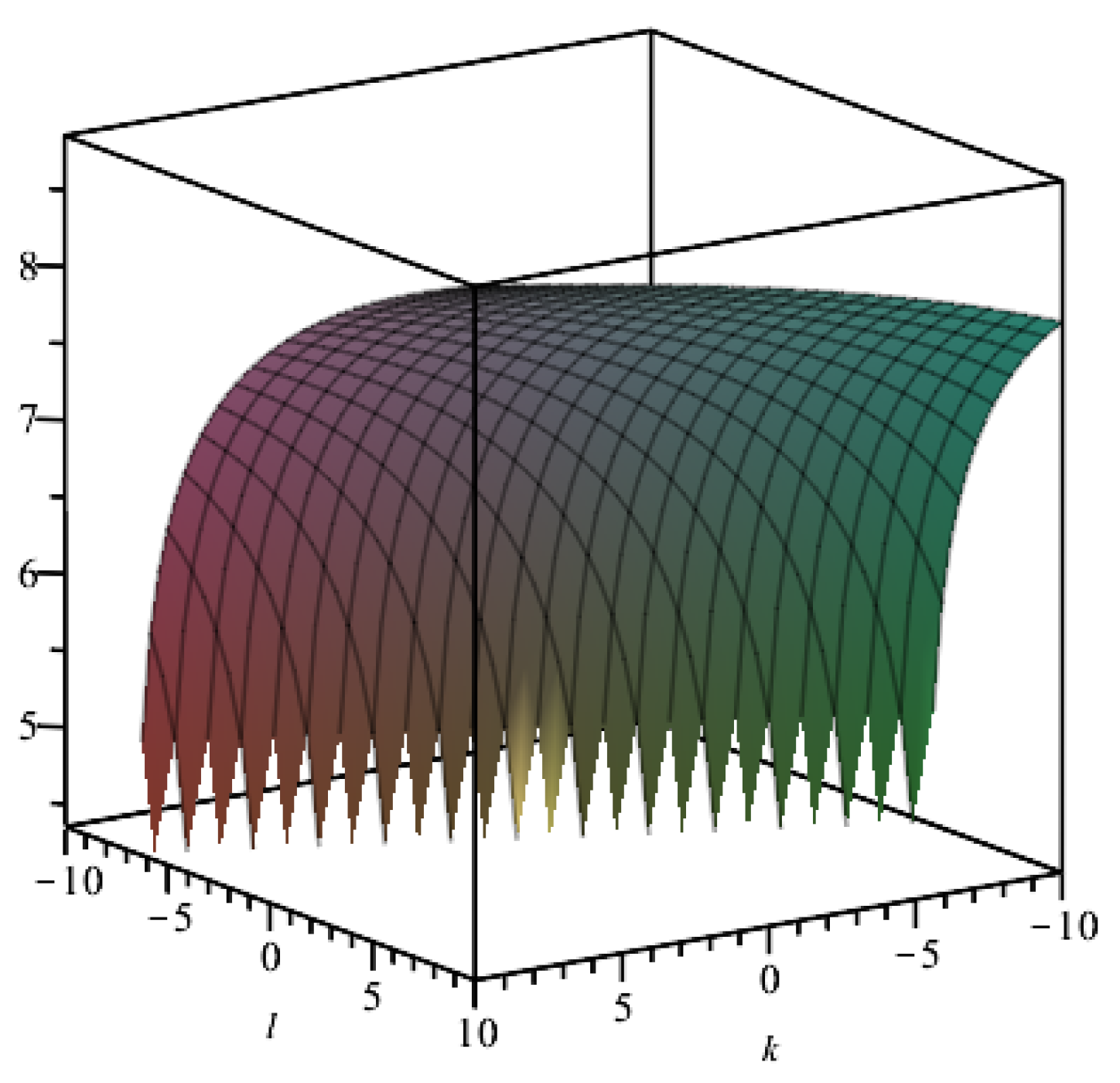
3.4. Numerical Results
3.5. Statistical Correlation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Zou, X.; Sun, L.; Rong, H.; Zhu, G. A zeolite-like aluminophosphate membrane with molecular-sieving property for water desalination. Chem. Sci. 2018, 9, 2533–2539. [Google Scholar] [CrossRef]
- Yang, M.; Fan, D.; Wei, Y.; Tian, P.; Liu, Z. Recent progress in methanol-to-olefins (MTO) catalysts. Adv. Mater. 2019, 31, 1902181. [Google Scholar] [CrossRef]
- Huang, Z.; Seo, S.; Shin, J.; Wang, B.; Bell, R.G.; Hong, S.B.; Zou, X. 3D-3D topotactic transformation in aluminophosphate molecular sieves and its implication in new zeolite structure generation. Nat. Commun. 2020, 11, 3762. [Google Scholar] [CrossRef]
- Yu, J.; Xu, R. Insight into the construction of open-framework aluminophosphates. Chem. Soc. Rev. 2006, 35, 593–604. [Google Scholar] [CrossRef]
- Cheetham, A.K.; Férey, G.; Loiseau, T. Open-framework inorganic materials. Angew. Chem. Int. Ed. 1999, 38, 3268–3292. [Google Scholar]
- Liu, Z.; Xu, J.; Xu, M.; Huang, C.; Wang, R.; Li, T.; Huai, X. Ultralow-temperature-driven water-based sorption refrigeration enabled by low-cost zeolite-like porous aluminophosphate. Nat. Commun. 2022, 13, 193. [Google Scholar] [CrossRef]
- Gozalbes, R.; Doucet, J.P.; Derouin, F. Application of topological descriptors in QSAR and drug design: History and new trends. Curr. Drug Targets-Infect. Disord. 2002, 2, 93–102. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Clement, J.; Tratnik, N.; Mushtaq, S.; Balasubramanian, K. Weighted Mostar indices as measures of molecular peripheral shapes with applications to graphene, graphyne and graphdiyne nanoribbons. SAR QSAR Environ. Res. 2020, 31, 187–208. [Google Scholar] [CrossRef]
- Gutman, I. A formula for the Wiener number of trees and its extension to graphs containing cycles. Graph Theory Notes NY 1994, 27, 9–15. [Google Scholar]
- Gutman, I.; Ashrafi, A.R. The edge version of the Szeged index. Croat. Chem. Acta 2008, 81, 263–266. [Google Scholar]
- Khadikar, P.V.; Karmarkar, S.; Agrawal, V.K. A novel PI index and its applications to QSPR/QSAR studies. J. Chem. Inf. Comput. Sci. 2001, 41, 934–949. [Google Scholar] [CrossRef] [PubMed]
- Khalifeh, M.H.; Yousefi-Azari, H.; Ashrafi, A.R.; Gutman, I. The edge Szeged index of product graphs. Croat. Chem. Acta 2008, 81, 277–281. [Google Scholar]
- Khalifeh, M.H.; Yousefi-Azari, H.; Ashrafi, A.R.; Wagner, S.G. Some new results on distance-based graph invariants. Eur. J. Comb. 2009, 30, 1149–1163. [Google Scholar] [CrossRef]
- Klein, D.J.; Lukovits, I.; Gutman, I. On the definition of the hyper-Wiener index for cycle-containing structures. J. Chem. Inf. Comput. Sci. 1995, 35, 50–52. [Google Scholar] [CrossRef]
- Schultz, H.P. Topological organic chemistry. 1. Graph theory and topological indices of alkanes. J. Chem. Inf. Comput. Sci. 1989, 29, 227–228. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Husin, M.N.; Ariffin, A. On the edge version of topological indices for certain networks. Ital. J. Pure Appl. Math. 2022, 47, 550–564. [Google Scholar]
- Liu, Y.; Rezaei, M.; Farahani, M.R.; Husin, M.N.; Imran, M. The Omega polynomial and the Cluj-Ilmenau index of an infinite class of the Titania Nanotubes Tio2 (m, n). J. Comput. Theor. Nanosci. 2017, 14, 3429–3432. [Google Scholar] [CrossRef]
- Husin, M.N.; Zafar, S.; Gobithaasan, R.U. Investigation of Atom-Bond Connectivity Indices of Line Graphs Using Subdivision Approach. Math. Probl. Eng. 2022, 2022, 6219155. [Google Scholar] [CrossRef]
- Modabish, A.; Husin, M.N.; Alameri, A.Q.; Ahmed, H.; Alaeiyan, M.; Farahani, M.R.; Cancan, M. Enumeration of spanning trees in a chain of diphenylene graphs. J. Discret. Math. Sci. Cryptogr. 2022, 25, 241–251. [Google Scholar] [CrossRef]
- Asif, F.; Zahid, Z.; Husin, M.N.; Cancan, M.; Taş, Z.; Alaeiyan, M.; Farahani, M.R. On Sombor indices of line graph of silicate carbide Si2C3 - I[p,q]. J. Discret. Math. Sci. Cryptogr. 2022, 25, 301–310. [Google Scholar] [CrossRef]
- Ghani, M.U.; Campena FJ, H.; Pattabiraman, K.; Ismail, R.; Karamti, H.; Husin, M.N. Valency-Based Indices for Some Succinct Drugs by Using M-Polynomial. Symmetry 2023, 15, 603. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Randić, M. Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Zhou, B.; Trinajstić, N. On a novel connectivity index. J. Math. Chem. 2009, 46, 1252–1270. [Google Scholar] [CrossRef]
- Vukičević, D.; Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 2009, 46, 1369–1376. [Google Scholar] [CrossRef]
- Albertson, M.O. The irregularity of a graph. Ars Comb. 1997, 46, 219–225. [Google Scholar]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverse problem for sigma index. MATCH Commun. Math. Comput. Chem. 2018, 79, 491e508. [Google Scholar]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Vasilyev, A. Upper and lower bounds of symmetric division deg index. Iran. J. Math. Chem. 2014, 5, 91–98. [Google Scholar]
- Hayat, S.; Imran, M.; Liu, J.B. An efficient computational technique for degree and distance based topological descriptors with applications. IEEE Access 2019, 7, 32276–32296. [Google Scholar] [CrossRef]
- Hayat, S.; Ahmad, S.; Umair, H.M.; Wang, S. Distance property of chemical graphs. Hacet. J. Math. Stat. 2018, 47, 1071–1093. [Google Scholar] [CrossRef]
- Hayat, S. Computing distance-based topological descriptors of complex chemical networks: New theoretical techniques. Chem. Phys. Lett. 2017, 688, 51–58. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Rezapour, H.; Sayadi, A.M. The hyper-Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rashevsky, N. Life, information theory and topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Dehmer, M.; Grabner, M. The discrimination power of molecular identification numbers revisited. MATCH Commun. Math. Comput. Chem. 2013, 69, 785–794. [Google Scholar]
- Ulanowicz, R.E. Quantitative methods for ecological network analysis. Comput. Biol. Chem. 2004, 28, 321–339. [Google Scholar] [CrossRef]
- Imran, M.; Hayat, S. On counting polynomials of certain polyomino chains. Bulg. Chem. Commun. 2016, 48, 332–337. [Google Scholar]
- Imran, M.; Hayat, S.; Shafiq, M.K. Computing omega and Sadhana polynomials of carbon nanotubes. Optoelectron. Adv. Mater. Rapid Commun. 2014, 8, 1218–1224. [Google Scholar]
- Hayat, S.; Khan, S.; Khan, A.; Imran, M. Distance-based topological descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications to carbon nanotubes. Math. Methods Appl. Sci. 2020; early View. [Google Scholar] [CrossRef]
- Morowitz, H.J. Some order-disorder considerations in living systems. Bull. Math. Biophys. 1955, 17, 81–86. [Google Scholar] [CrossRef]
- Manzoor, S.; Siddiqui, M.K.; Ahmad, S. On entropy measures of molecular graphs using topological indices. Arab. J. Chem. 2020, 13, 6285–6298. [Google Scholar] [CrossRef]
- Došlić, T.; Martinjak, I.; Škrekovski, R.; Tipurić Spužević, S.; Zubac, I. Mostar index. J. Math. Chem. 2018, 56, 2995–3013. [Google Scholar] [CrossRef]
- Djoković, D.Ž. Distance-preserving subgraphs of hypercubes. J. Comb. Theory Ser. B 1973, 14, 263–267. [Google Scholar] [CrossRef]
- Winkler, P.M. Isometric embedding in products of complete graphs. Discret. Appl. Math. 1984, 7, 221–225. [Google Scholar]
- Nadjafi-Arani, M.J.; Klavzar, S. Cut method and Djoković–Winkler’s relation. Electron. Notes Discret. Math. 2014, 45, 153–157. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Clement, J.; Paul, D.; Balasubramanian, K. Relativistic distance-based topological descriptors of Linde type A zeolites and their doped structures with very heavy elements. Mol. Phys. 2021, 119, e1798529. [Google Scholar] [CrossRef]
- Kavitha SR, J.; Abraham, J.; Arockiaraj, M.; Jency, J.; Balasubramanian, K. Topological characterization and graph entropies of tessellations of kekulene structures: Existence of isentropic structures and applications to thermochemistry, nuclear magnetic resonance and electron spin resonance. J. Phys. Chem. A 2021, 125, 8140–8158. [Google Scholar] [CrossRef]
- Martínez-Franco, R.; Moliner, M.; Yun, Y.; Sun, J.; Wan, W.; Zou, X.; Corma, A. Synthesis of an extra-large molecular sieve using proton sponges as organic structure-directing agents. Proc. Natl. Acad. Sci. USA 2013, 110, 3749–3754. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, K. Combinatorics, big data, neural network & AI for medicinal chemistry & drug administration. Lett. Drug Des. Discov. 2021, 18, 943–948. [Google Scholar]
- Sabirov, D.S.; Shepelevich, I.S. Information entropy in chemistry: An overview. Entropy 2021, 23, 1240. [Google Scholar] [CrossRef] [PubMed]
- Chaudhry, F.; Shoukat, I.; Afzal, D.; Park, C.; Cancan, M.; Farahani, M.R. M-polynomials and degree-based topological indices of the molecule copper (i) oxide. J. Chem. 2021, 2021, 6679819. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. Entropy and the complexity of graphs revisited. Entropy 2012, 14, 559–570. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Paul, D.; Klavžar, S.; Clement, J.; Tigga, S.; Balasubramanian, K. Relativistic distance based and bond additive topological descriptors of zeolite RHO materials. J. Mol. Struct. 2022, 1250, 131798. [Google Scholar] [CrossRef]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Arockiaraj, M.; Clement, J.; Tratnik, N. Mostar indices of carbon nanostructures and circumscribed donut benzenoid systems. Int. J. Quantum Chem. 2019, 119, e26043. [Google Scholar] [CrossRef]
- Augustine, T.; Roy, S. Topological Study on Triazine-Based Covalent-Organic Frameworks. Symmetry 2022, 14, 1590. [Google Scholar] [CrossRef]
- Sahaya Vijay, J.; Roy, S. Computation of Wiener Descriptor for Melamine Cyanuric Acid Structure. Polycycl. Aromat. Compd. 2023, 1–15. [Google Scholar] [CrossRef]
- Rahul, M.P.; Clement, J.; Junias, J.S.; Arockiaraj, M.; Balasubramanian, K. Degree-based entropies of graphene, graphyne and graphdiyne using Shannon’s approach. J. Mol. Struct. 2022, 1260, 132797. [Google Scholar] [CrossRef]
- Hussain, Z.; Ijaz, N.; Tahir, W.; Butt, M.T.; Talib, S. Calculating Degree Based Multiplicative Topological indices of Alcohol. Asian J. Appl. Sci. Technol. 2018, 2, 132–139. [Google Scholar] [CrossRef]
- Balasubramanian, K. Operator algebraic methods for NMR spectroscopy, I. Generation of NMR spin species. J. Chem. Phys. 1983, 78, 6358–6368. [Google Scholar] [CrossRef]
- Balasubramanian, K. Topological and group theoretical analysis in dynamic NMR spectroscopy. J. Phys. Chem. 1982, 86, 4668–4674. [Google Scholar] [CrossRef]
- Raza, Z.; Arockiaraj, M.; Maaran, A.; Kavitha SR, J.; Balasubramanian, K. Topological entropy characterization, NMR and ESR spectral patterns of coronene-based transition metal organic frameworks. ACS Omega 2023, 8, 13371–13383. [Google Scholar] [CrossRef] [PubMed]





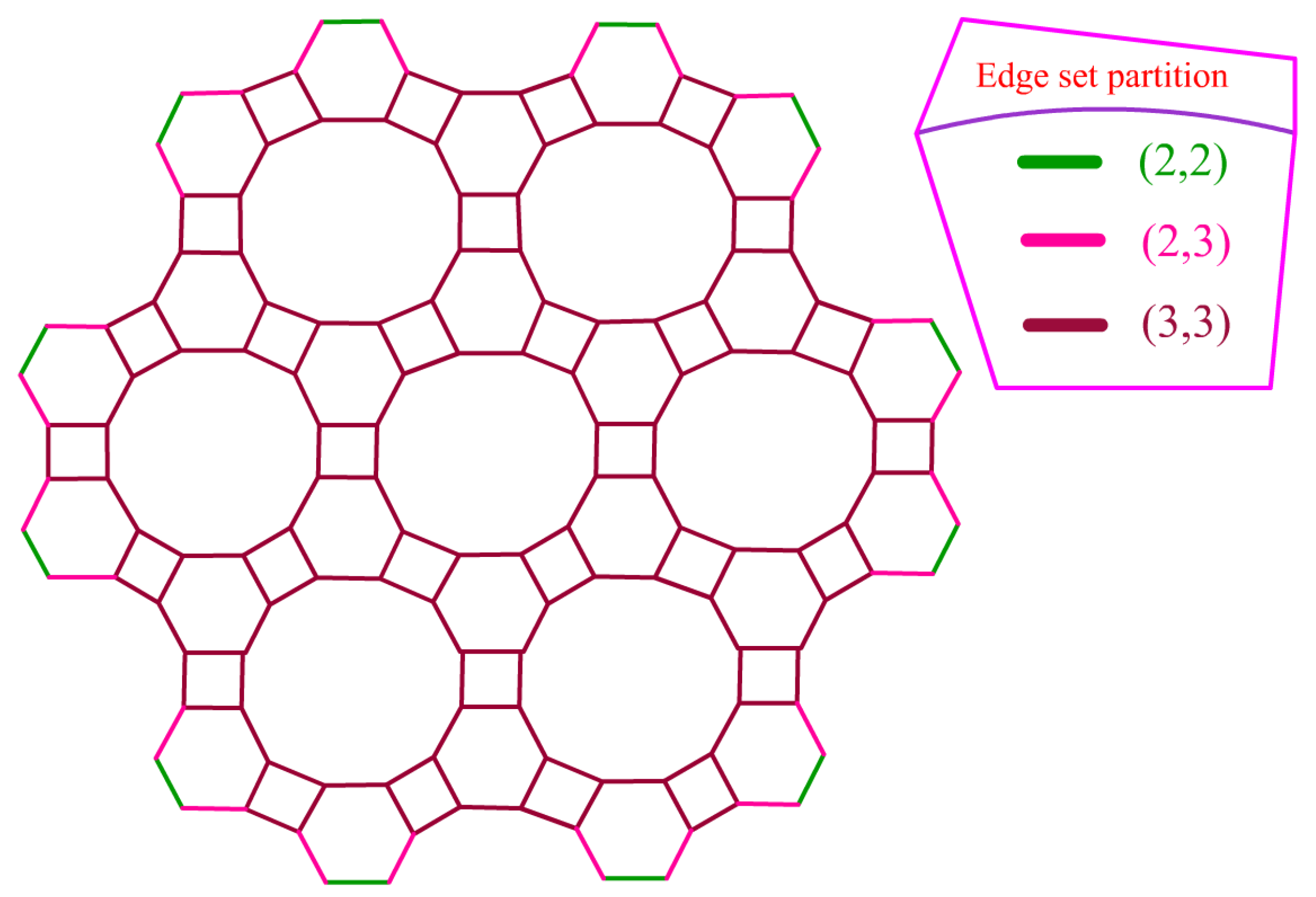



| Molecular Descriptors | Mathematical Formula |
|---|---|
| Wiener Index [16] | |
| Vertex–Szeged Index [9] | |
| Vertex–Padmakar–Ivan Index [11] | |
| Vertex–Mostar Index [45] |
| Molecular Descriptors | Mathematical Formula |
|---|---|
| First Zagreb Index | = |
| Second Zagreb Index | |
| Reduced Second Zagreb Index | |
| Hyper Zagreb Index | |
| Augmented Zagreb Index | |
| Randić Index | |
| Reciprocal Randić Index | |
| Reduced Reciprocal Randić Index | |
| Harmonic Index | |
| Sum Connectivity Index |
| 3024 | 270,000 | 4,668,072 | 37,920,768 | 198,934,944 | |
| 12,096 | 2,180,550 | 59,575,584 | 665,112,240 | 4,487,610,096 | |
| 1728 | 59,976 | 560,592 | 2,819,448 | 10,144,560 | |
| 576 | 27,684 | 265,776 | 1,385,064 | 4,916,352 | |
| 784,272,816 | 2,527,739,928 | 7,013,962,368 | 17,335,729,008 | 39,076,777,008 | |
| 21,585,912,126 | 82,522,470,576 | 264,389,591,088 | 743,053,567,968 | 1,873,931,558,022 | |
| 28,958,688 | 71,033,760 | 154,482,768 | 308,200,032 | 571,213,080 | |
| 14,290,380 | 34,549,680 | 76,122,576 | 149,955,648 | 280,858,740 |
| 264 | 1716 | 5328 | 12,072 | 22,920 | |
| 366 | 2514 | 7902 | 17,988 | 34,230 | |
| 150 | 1092 | 3474 | 7944 | 15,150 | |
| 1476 | 10,080 | 31,644 | 72,000 | 136,980 | |
| 485.71875 | 3226.78125 | 10,068.46875 | 22,856.0625 | 43,434.84375 | |
| 17.899 | 101.798 | 305.6969 | 683.5959 | 1290 | |
| 131.3939 | 856.7878 | 2662 | 6034 | 11,457 | |
| 82.9706 | 561.9411 | 1761 | 4004 | 7615 | |
| 13.66666667 | 71.33333333 | 209 | 462.6666667 | 868.3333333 | |
| 17.899 | 101.798 | 305.6969 | 683.5959 | 1290 | |
| 38,844 | 60,816 | 89,808 | 126,792 | 172,740 | |
| 58,086 | 91,014 | 134,472 | 189,918 | 258,810 | |
| 25,740 | 40,362 | 59,664 | 84,294 | 114,900 | |
| 232,416 | 364,140 | 537,984 | 759,780 | 1,035,360 | |
| 73,650.09375 | 115,347.0938 | 170,371.125 | 240,567.4688 | 327,781.4063 | |
| 2177 | 3401 | 5015 | 7073 | 9629 | |
| 19,418 | 30,404 | 44,899 | 63,391 | 86,364 | |
| 12,918 | 20,237 | 29,896 | 42,219 | 57,530 | |
| 1462 | 2279.666667 | 3357.333333 | 4731 | 6436.666667 | |
| 2177 | 3401 | 5015 | 7073 | 9629 |
| 3.8625 | 5.6801 | 6.8006 | 7.6137 | 8.2525 | 8.7787 | 9.2262 | 9.6155 | 9.96 | 10.269 | |
| 3.8383 | 5.6711 | 6.7961 | 7.6111 | 8.2507 | 8.7775 | 9.2253 | 9.6148 | 9.9594 | 10.2685 | |
| 3.7907 | 5.6552 | 6.7883 | 7.6064 | 8.2477 | 8.7753 | 9.2237 | 9.6135 | 9.9584 | 10.2677 | |
| 3.8404 | 5.6719 | 6.7965 | 7.6113 | 8.2509 | 8.7776 | 9.2254 | 9.6148 | 9.9595 | 10.2685 | |
| 3.8576 | 5.678 | 6.7995 | 7.6131 | 8.2521 | 8.7784 | 9.226 | 9.6153 | 9.9599 | 10.2689 | |
| 3.8599 | 5.6782 | 6.7995 | 7.6131 | 8.2521 | 8.7784 | 9.226 | 9.6153 | 9.9599 | 10.268 | |
| 3.862 | 5.6798 | 6.8005 | 7.6137 | 8.2525 | 8.7787 | 9.2262 | 9.6155 | 9.96 | 10.269 | |
| 3.8928 | 5.7735 | 6.9177 | 7.7412 | 8.3854 | 8.9147 | 9.3642 | 9.7548 | 10.1002 | 10.4098 | |
| 3.8552 | 5.6756 | 6.7976 | 7.6113 | 8.2504 | 8.7769 | 9.2245 | 9.6138 | 9.9584 | 10.2674 |
| 0.800895321 | 0.799930694 | 0.798222338 | 0.800014703 | 0.800664403 | |
| 0.822763752 | 0.80086312 | 0.800240768 | 0.798861487 | 0.801363561 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vijay, J.S.; Roy, S.; Beromeo, B.C.; Husin, M.N.; Augustine, T.; Gobithaasan, R.U.; Easuraja, M. Topological Properties and Entropy Calculations of Aluminophosphates. Mathematics 2023, 11, 2443. https://doi.org/10.3390/math11112443
Vijay JS, Roy S, Beromeo BC, Husin MN, Augustine T, Gobithaasan RU, Easuraja M. Topological Properties and Entropy Calculations of Aluminophosphates. Mathematics. 2023; 11(11):2443. https://doi.org/10.3390/math11112443
Chicago/Turabian StyleVijay, Jeyaraj Sahaya, Santiago Roy, Bheeter Charles Beromeo, Mohamad Nazri Husin, Tony Augustine, R.U. Gobithaasan, and Michael Easuraja. 2023. "Topological Properties and Entropy Calculations of Aluminophosphates" Mathematics 11, no. 11: 2443. https://doi.org/10.3390/math11112443
APA StyleVijay, J. S., Roy, S., Beromeo, B. C., Husin, M. N., Augustine, T., Gobithaasan, R. U., & Easuraja, M. (2023). Topological Properties and Entropy Calculations of Aluminophosphates. Mathematics, 11(11), 2443. https://doi.org/10.3390/math11112443






