Efficiency Index for Binary Classifiers: Concept, Extension, and Application

Abstract

Many metrics exist for the evaluation of binary classifiers, all with their particular advantages and shortcomings. Recently, an “Efficiency Index” (EI) for the evaluation of classifiers has been proposed, based on the consistency (or matching) and contradiction (or mismatching) of outcomes. This metric and its confidence intervals are easy to calculate from the base data in a 2 × 2 contingency table, and their values can be qualitatively and semi-quantitatively categorised. For medical tests, in which context the Efficiency Index was originally proposed, it facilitates the communication of risk (of the correct diagnosis versus misdiagnosis) to both clinicians and patients. Variants of the Efficiency Index (balanced, unbiased) which take into account disease prevalence and test cut-offs have also been described. The objectives of the current paper were firstly to extend the EI construct to other formulations (balanced level, quality), and secondly to explore the utility of the EI and all four of its variants when applied to the dataset of a large prospective test accuracy study of a cognitive screening instrument. This showed that the balanced level, quality, and unbiased formulations of the EI are more stringent measures.

1. Introduction

Diagnostic and screening tests used in clinical medicine may be evaluated by many metrics based on the use of test thresholds, and tabulated in a 2 × 2 contingency table comparing the index test to a reference standard (e.g., the diagnostic criteria) [1,2]. All of these metrics derived from binary classification have both advantages and shortcomings or limitations. For example, sensitivity (Sens) and specificity (Spec), probably the most commonly used test metrics (e.g., in Cochrane Study systematic evaluations) presuppose a known diagnosis, contrary to the typical clinical situation when such tests are administered, and hence these metrics are difficult to apply directly to the particular doctor–patient encounter. Moreover, these values will vary with the chosen test cut-off. Predictive values, positive (PPV) and negative (NPV), which are more patient-oriented measures than Sens and Spec, are dependent on the prevalence of the condition in the population under study. To try to address some of these shortcomings, a new metric called the Efficiency Index has been proposed and developed [3,4].

The basic concept of the EI is as follows. The 2 × 2 contingency table (Figure 1) categorises all the outcomes as per the standard theory of signal detection [5] as: true positives (TP) or hits; true negatives (TN) or correct rejections; false positives (FP) or false hits; and false negatives (FN) or misses. From these four cells, two conditions or relations between the index test and the reference standard may be distinguished: consistency, or matching, of outcomes (+/+ or True Positive and −/− or True Negative); and contradiction, or mismatching (+/− or False Positive and −/+ or False Negative).

From these two conditions, the paired complementary parameters of accuracy (Acc), or fraction correct, and inaccuracy (Inacc) or fraction incorrect or error rate, may be derived, as:

Acc = (TP + TN)/N = (a + d)/N

Inacc = (FP + FN)/N = (b + c)/N

Kraemer previously denoted the sum of (TP + TN) by the term “efficiency” [6]; accordingly, the sum of (FP + FN) may be termed “inefficiency”. Hence the ratio of efficiency to inefficiency may be denoted as the “Efficiency Index” (EI) [3,4], as:

 EI = Acc/Inacc
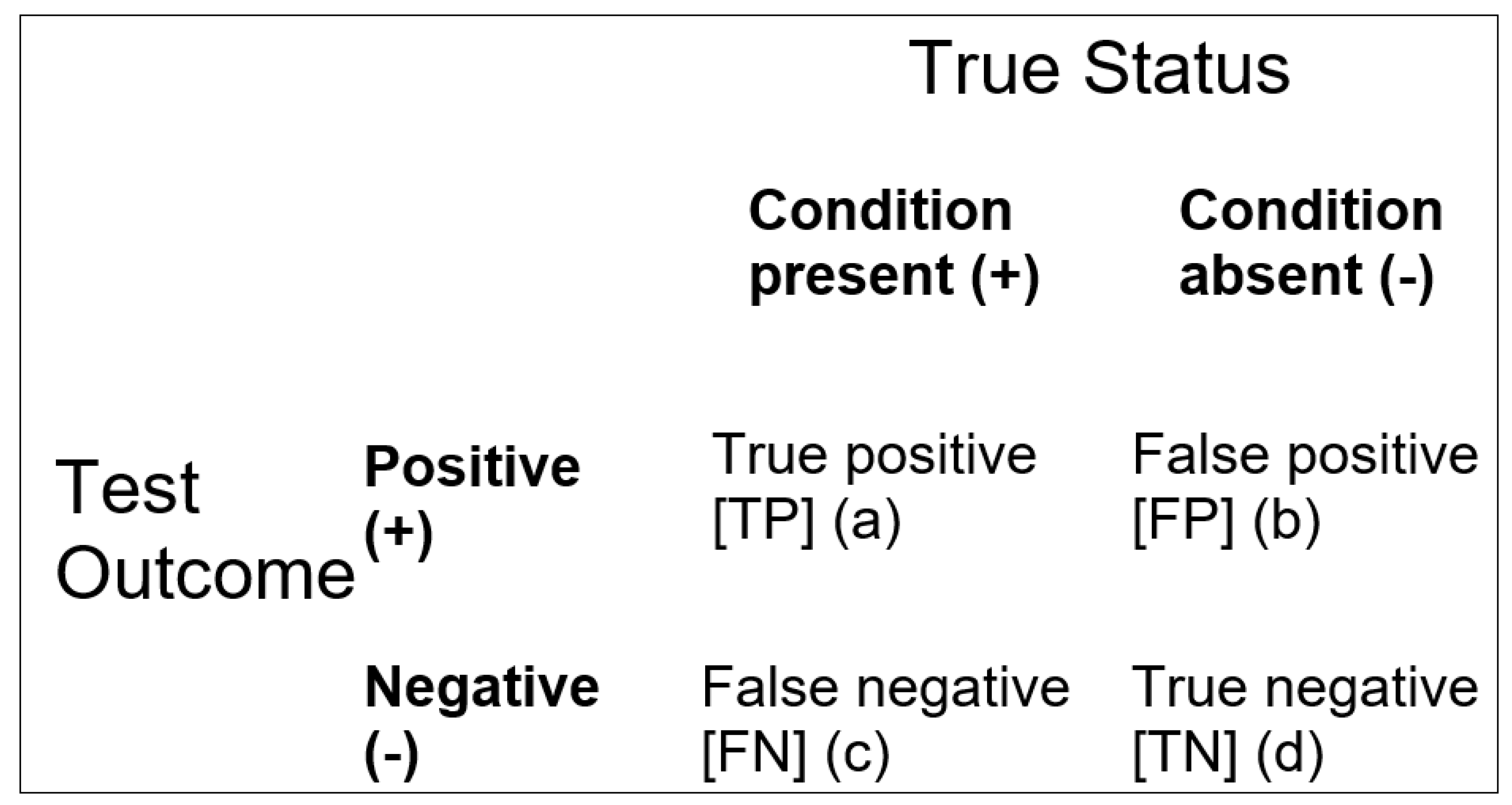
        = (TP + TN)/(FP + FN)
     = (a + d)/(b + c)

The boundary values of the EI are thus 0 (when Acc = 0; Inacc = 1) and ∞ (Acc = 1, Inacc = 0), denoting, respectively, a useless classifier and a perfect classifier. EI values have an inflection point at 1, whereby a value > 1 indicates correct classification and a value of <1 indicates incorrect classification, such that values >> 1 are desirable and a value of ∞ is an optimal classifier [3]. EI is of the form x/(1 − x) and hence is an odds ratio.

Because the “Efficiency Index” terminology is potentially ambiguous (there is a similarly named physical index of speed achieved in relation to power output, and various other efficiency indexes are described for energy efficiency or in business and finance), one might instead of EI use the term “selectivity” since the EI effectively selects true outcomes over false outcomes. Another possible way around any nomenclature issues is to calculate an “Inefficiency Index” (InI) defined as:

InI = Inacc/Acc
        = (FP + FN)/(TP + TN)
     = (b + c)/(a + d)

Similar to the EI, values of the InI have an inflection point at 1, but in this formulation an InI value < 1 indicates correct classification and a value of >1 indicates incorrect classification, such that InI values <<1 are desirable and a value of 0 is an optimal classifier (Inacc = 0, Acc = 1). The InI is of the form (1 − x)/x and hence is an odds against ratio.

The EI metric has a number of potential advantages. One is the simple calculation of confidence (or compatibility) intervals (CI) for the EI values by applying the log method [7] to the base data from the four cells of the 2 × 2 contingency table. For the 95% CI, the formula for the EI is [4]:

Loge(EI) +/− [1.96 × SE(logeEI)]

where:

SE(logeEI) = √[1/a − 1/(a + c) + 1/b − 1/(b + d)]

Classification of the EI values, both qualitatively and semi-quantitatively, is also possible. The boundary values of EI (0, ∞) are the same as those for likelihood ratios (LRs). LR values may be categorised qualitatively, as slight, moderate, large, or very large [8]. It has been shown that this qualitative classification may also be applicable to EI values [3] (Table 1).

The EI is a form of odds ratio; its boundary values (0, ∞) are the same as those for another outcome parameter derived from the 2 × 2 contingency table, the diagnostic odds ratio (DOR) or cross-product ratio [9]. DORs may be categorised qualitatively, as small, medium, large, or very large [10]. The suggested qualitative classification scheme for DORs might therefore also be applicable to EI values (Table 1). Additionally, just as the log(DOR) is sometimes used to compensate for small values in one or more cells of the 2 × 2 contingency table, one may calculate the log(EI) in similar circumstances from the Acc and Inacc, specifically from their logit, where:

  log(EI) = log(Acc) − log(Inacc)
     = log[Acc/(1 − Acc)]
= logit(Acc)

A more quantitative classification of EI values may also be applied, based on the system for LRs derived by McGee [11] which calculates the (approximate) difference in pre- and post-test odds, since post-test odds = pre-test odds × LR. McGee showed that the LR values of 2, 5, and 10 increased the probability of diagnosis by approximately 15%, 30%, and 45%, respectively, whereas the LR values of 0.5, 0.2, and 0.1 decreased the probability of diagnosis by approximately 15%, 30%, and 45%, respectively. These figures derive from the almost linear relationship of probability and the natural logarithm of odds over the range 0.1–0.9. With the appropriate modification, the percentage change in the probability of diagnosis may be calculated for the EI values independent of pre-test probability [3], as:

Change in probability = 0.19 × loge(EI)

The EI construct may be extended to other formulations. Although Sens and Spec, as strictly columnar ratios in the 2 × 2 contingency table, are mathematically independent of prevalence, P, Acc, and Inacc as diagonal ratios are dependent on P and its complement P′ (= 1 − P):

Acc = (Sens.P) + (Spec.P′)
        Inacc = (1 − Sens).P + (1 − Spec).P′

The EI is thus dependent on the disease prevalence [4]. Both Sens and Spec, and hence Acc and Inacc, are also dependent on the level of the test, Q [6], or the threshold. Balanced and unbiased EI measures were previously introduced to try to take into account the values of P and Q [4]. In these and other studies, the EI values have found application in the assessment of cognitive screening instruments used in the assessment of patients with memory complaints [3,4,12].

Table 1. Suggested classifications of EI values (extended from [3]).

EI Value	Qualitative Classification: Change in Probability of Diagnosis (after Jaeschke et al. [8])	Qualitative Classification: “Effect Size” (after Rosenthal [10])	Semi-Quantitative Classification: Approximate % Change in Probability of Diagnosis (after McGee [11])
≤0.1	Very large decrease	-	-
0.1	Large decrease	-	−45
0.2	Large decrease	-	−30
0.5	Moderate decrease	-	−15
1.0			0
~1.5	-	Small	-
2.0	Moderate increase	-	+15
~2.5	-	Medium	-
~4	-	Large	-
5.0	Moderate increase	-	+30
10.0	Large increase	-	+45
≥10.0	Very large increase	Very large	-

Table 1. Suggested classifications of EI values (extended from [3]).

EI Value	Qualitative Classification: Change in Probability of Diagnosis (after Jaeschke et al. [8])	Qualitative Classification: “Effect Size” (after Rosenthal [10])	Semi-Quantitative Classification: Approximate % Change in Probability of Diagnosis (after McGee [11])
≤0.1	Very large decrease	-	-
0.1	Large decrease	-	−45
0.2	Large decrease	-	−30
0.5	Moderate decrease	-	−15
1.0			0
~1.5	-	Small	-
2.0	Moderate increase	-	+15
~2.5	-	Medium	-
~4	-	Large	-
5.0	Moderate increase	-	+30
10.0	Large increase	-	+45
≥10.0	Very large increase	Very large	-

The aims of the current paper were twofold: firstly, to extend the EI construct to other formulations, namely “balanced level” and “quality” variants; and secondly, to apply all the described EI variants, both previously described (standard, balanced, unbiased [3,4]) and new (balanced level, quality) to the dataset of a large prospective test accuracy study of a cognitive screening instrument, the Mini-Addenbrooke’s Cognitive Examination.

2. Methods

2.1. Participants

The dataset from a screening test accuracy study of a cognitive screening instrument, the Mini-Addenbrooke’s Cognitive Examination (MACE) [13], was examined. In this study, which observed the STARDdem guidelines for reporting diagnostic test accuracy studies in dementia [14], the MACE was administered to consecutive new outpatient referrals (N = 755) at a dedicated cognitive disorders clinic, of whom 114 received a final criterial diagnosis of dementia [15]. The MACE scores were not used in making the reference diagnosis to avoid review bias. The optimal MACE cut-off was calculated from the maximal value for the Youden index [15].

2.2. Analyses

2.2.1. Balanced Efficiency Index

In the particular case of a balanced dataset, where P = P′ = 0.5, one may calculate the balanced accuracy (BAcc) and balanced inaccuracy (BInacc) [16]:

   BAcc = (Sens + Spec)/2
 BInacc =1 − BAcc
                BInacc = [(1 − Sens) + (1 − Spec)]/2

Balanced Efficiency Index (BEI) is thus [4]:

BEI = BAcc/BInacc
                = (Sens + Spec)/[(1 − Sens) + (1 − Spec)]

BEI in this formulation is thus independent of P. The BEI values “pull back” the EI values towards those anticipated with a balanced dataset and may be of particular value when there is marked class imbalance in test datasets.

2.2.2. Balanced Level Efficiency Index

The Balanced EI formulation is not independent of Q since both Sens and Spec, and hence Acc and Inacc, are dependent on Q. Another formulation of a “balanced” EI may be derived to accommodate this variable, based around positive and negative predictive values (PPV, NPV), since Sens and Spec may be expressed in terms of PPV, NPV, P, and Q, thus:

 Sens = PPV.Q/P
  Spec = NPV.Q′/P′

Since:

 Acc = (Sens.P) + (Spec.P′)
     Inacc = (1 − Sens).P + (1 − Spec).P′

then substituting:

 Acc = (PPV.Q) + (NPV.Q′)
     Inacc = (1 − PPV).Q + (1 − NPV).Q′

In the particular case where Q = Q′ = 0.5, one may calculate another form of “balanced accuracy” and “balanced inaccuracy”. Since these terms have already been used (Section 2.2.1) and since balanced accuracy as (Sens + Spec)/2 is familiar, a different terminology is desirable here, so it is suggested that “balanced level accuracy” (BLAcc) and “balanced level inaccuracy” (BLInacc) are used, where:

  BLAcc = (PPV + NPV)/2
BLInacc = 1 − BLAcc
         BLInacc = [(1 − PPV) + (1 − NPV)]/2

It follows that Balanced Level Efficiency index (BEI) is given by:

BLEI = BLAcc/BLInacc
              = (PPV + NPV)/[(1 − PPV) + (1 − NPV)]

2.2.3. Quality Efficiency Index

As shown in the previous section, Sens and Spec are dependent on the level or bias of the test, Q, determined by the test cut-off. One way to accommodate this dependency is to rescale Sens and Spec according to Q, following the method of Kraemer [6], as QSens and QSpec:

QSens = (Sens − Q)/Q′

QSpec = (Spec − Q′)/Q

This permits the calculation of various other “quality” measures [17]. For example, quality accuracy (QAcc) and quality inaccuracy (QInacc) may be calculated:

        QAcc = (QSens.P) + (QSpec.P′)
QInacc = 1 − QAcc
             QInacc = (1 − QSens).P + (1 − QSpec).P′

Quality Efficiency index (QEI) is thus:

QEI = QAcc/QInacc
                    = (QSens + QSpec)/[(1 − QSens) + (1 − QSpec)]

2.2.4. Unbiased Efficiency Index

As Sens and Spec are unscaled measures, so is Acc. As an unscaled measure, Acc gives no direct measure of the degree to which diagnostic uncertainty is reduced. This can be addressed by calculating the unbiased accuracy (UAcc) and unbiased inaccuracy (Uinacc) which take into account both the values of P and Q, thus removing the biasing effects of random associations between the test result and disease prevalence ([18], p. 470), such that [16]:

    UAcc = (Sens.P + Spec. P′) − (P.Q + P′.Q′)/1 − (P.Q + P′.Q′)
= Acc − (P.Q + P′.Q′)/1 − (P.Q + P′.Q′)

UInacc = 1 − UAcc

Unbiased Efficiency index (UEI) is thus [4]:

UEI = UAcc/UInacc
       = UAcc/(1 − UAcc)

3. Results

In the MACE study dataset, at the optimal MACE cut-off of ≤20/30, the outcomes were TP = 104, FP = 188, FN = 10, and TN = 453. Hence:

   Acc = 0.738 (95% CI = 0.722 − 0.754)

   Inac = 0.262 (95% CI = 0.231 − 0.294)

  EI = 2.81 (95% CI = 2.46 − 3.21)

   InI = 0.355 (95% CI = 0.321 − 0.390)

The dataset was used to calculate the values for EI, BEI, BLEI, QEI, and UEI across the range of meaningful MACE cut-offs (

Table 2. Diagnosis of dementia: comparing EI, BEI, BLEI, QEI, and UEI metrics at various MACE cut-offs (fixed value of P = 0.151).

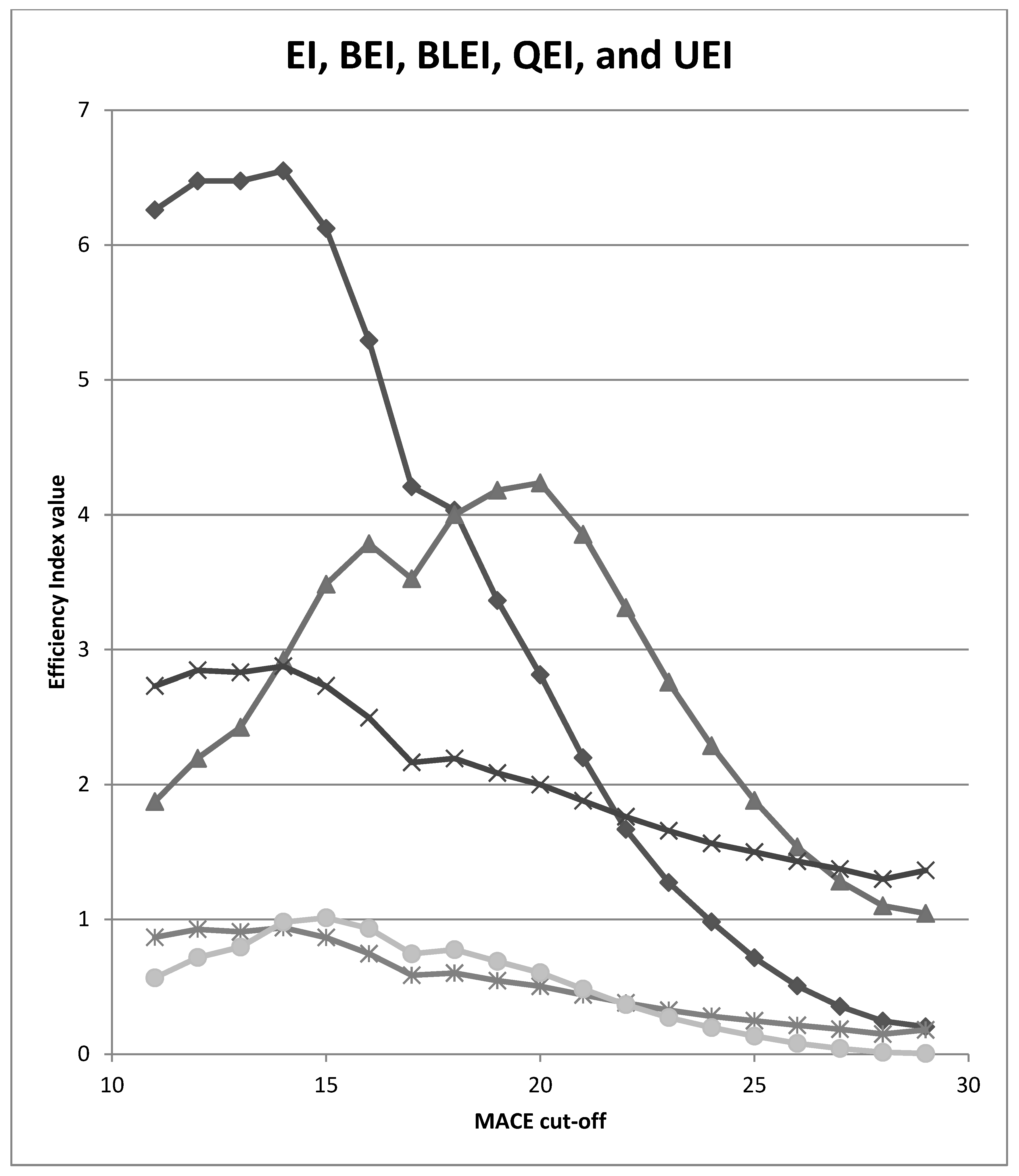
MACE Cut-Off	EI	BEI	BLEI	QEI	UEI
≤29/30	0.204	1.045	1.364	0.181	0.006
≤28/30	0.246	1.101	1.299	0.150	0.015
≤27/30	0.355	1.283	1.374	0.186	0.043
≤26/30	0.507	1.538	1.432	0.215	0.081
≤25/30	0.716	1.882	1.500	0.249	0.135
≤24/30	0.982	2.289	1.564	0.282	0.198
≤23/30	1.274	2.759	1.658	0.327	0.272
≤22/30	1.668	3.310	1.762	0.381	0.368
≤21/30	2.199	3.854	1.880	0.440	0.484
≤20/30	2.813	4.236	2.000	0.504	0.605
≤19/30	3.364	4.181	2.086	0.546	0.689
≤18/30	4.033	4.000	2.194	0.602	0.776
≤17/30	4.207	3.525	2.165	0.586	0.745
≤16/30	5.292	3.785	2.497	0.746	0.934
≤15/30	6.123	3.484	2.731	0.866	1.012
≤14/30	6.550	2.922	2.876	0.939	0.980
≤13/30	6.475	2.425	2.831	0.908	0.795
≤12/30	6.475	2.195	2.846	0.927	0.718
≤11/30	6.260	1.874	2.731	0.868	0.567

Abbreviations: EI = efficiency index, BEI = balanced efficiency index, BLEI = balanced level efficiency index, MACE = Mini-Addenbrooke’s Cognitive Examination, QEI = quality efficiency index, UEI = unbiased efficiency index.

) and these were displayed graphically (Figure 2).

4. Discussion

Reanalysis of the dataset from the MACE study has shown the feasibility of calculating the different EI formulations. All these variants are based on different formulations of Acc and its complement Inacc, and the extended forms try to take into account the values of base rate or prevalence, P, and/or the level or bias of the test, Q. Similar to the EI, they all have boundary values of 0 and ∞.

The data presented in Table 2 and Figure 2 show that those measures which do not take into account the value of Q, specifically the EI and BEI, have higher maximal values and may therefore give a more optimistic view of the test outcomes [4]. Conversely, the measures taking into account Q, specifically the BLEI, QEI, and UEI, are more stringent measures which give a more pessimistic view of the test outcomes. The QEI and UEI give relatively stable values across the range of the MACE cut-offs.

In what circumstances might the EI or its extended formulations prove useful in clinical practice? It has been suggested [3,4] that the EI may effectively communicate risk to both clinicians and patients and their families, specifically the risk of correct diagnosis versus misdiagnosis for a particular test, in a way that is more transparent than for sensitivity, specificity, predictive values, and likelihood ratios. The EI values have been calculated for various cognitive screening instruments [3,4,12]. This measure may be of particular value when the administration of invasive tests or tests associated with morbidity and even mortality are being proposed.

5. Limitations

The EI as a measure for the evaluation of classifiers has hitherto been applied only to medical classifiers. More widespread application will therefore be required to assess the utility of the EI and its various extensions.

Comparison with other frequently used measures of classifier evaluation, such as the area under the receiver operating characteristic (ROC) curve [19] or the F measure [20], as well as other odds ratios and logit transform, might also help to define the place of EI in the catalogue of measures available for these purposes [1,2].

Further refinements of the EI and its variants may also be explored, for example, to address its application to imbalanced datasets [21] (although in the current examples there was class imbalance in the dataset, with a prevalence of dementia P = 0.15 [15]).

For example, high EI values could result from very high numbers of TN alone even if the numbers of TP were modest, as long as the numbers of FP and FN were few, a situation which may be encountered, for example, when handling administrative health datasets [22] and polygenic hazard scores [23]. Addressing the class imbalance problem using methods which oversample the minority class (the TP cases in the current example), such as variants of the synthetic majority oversampling technique, SMOTE [21], or which undersample the majority class (the TN in the current example), might be applicable. Comparisons of the EI with measures such as the F measure [2,20] or the critical success index [2,24] which eschew the TN values might be particularly pertinent in this class imbalance situation.

As well as statistical tests, data semantics may be crucial in applied research, such that a new semantics may need to be identified to improve the classifier [25]. In the particular case of cognitive screening instruments, as examined here, it is known that the test performance may be influenced by factors other than cognitive ability alone, such as the level of fatigue, mood disorder, and primary visual or hearing difficulty. Restriction of the dataset to take into account such confounding factors might be one strategy when further examining EI and its variants. Another might be to introduce a time element, with repeat testing or sequential testing to ensure intra-test reliability as a criterion for data semantics.

6. Conclusions

EI has been characterised as the ratio of Accuracy to Inaccuracy, and hence the ratio of consistency or matching of outcomes in the 2 × 2 contingency table to contradiction or mismatching. Extensions of the EI concept, such as BEI, BLEI, QEI, and UEI, are new metrics for the evaluation of binary classifiers which may be easily calculated from the base data cells of a 2 × 2 contingency table. All are based on different formulations of Accuracy and its complement Inaccuracy and aim to take into account values of prevalence and/or the level of the test. EI values may be classified qualitatively and semi-quantitatively. In the clinical context, these metrics may prove to be of particular use in the communication of risk to both clinicians and patients. Their application in other fields of binary classification is awaited.