The Poisson–Lindley Distribution: Some Characteristics, with Its Application to SPC
Abstract
:1. Introduction
- Integration with industry technologies: As more and more factories become digitized and automated, there is a need for SPC methodologies to be integrated with these new technologies. For example, using sensors to collect data in real time and feeding that data into statistical models to identify process variations and anomalies.
- Multivariate SPC: Traditional SPC techniques focus on monitoring single variables at a time, but many manufacturing processes involve multiple interconnected variables. Researchers are working on developing multivariate SPC methods that can handle these complex relationships.
- Adaptive SPC: Another area of active research is the development of adaptive SPC methods that can automatically adjust control limits in response to changes in the process.
2. Some of the Characteristics of the
2.1. Moments
2.2. Moment Generating Function and Probability Generating Function
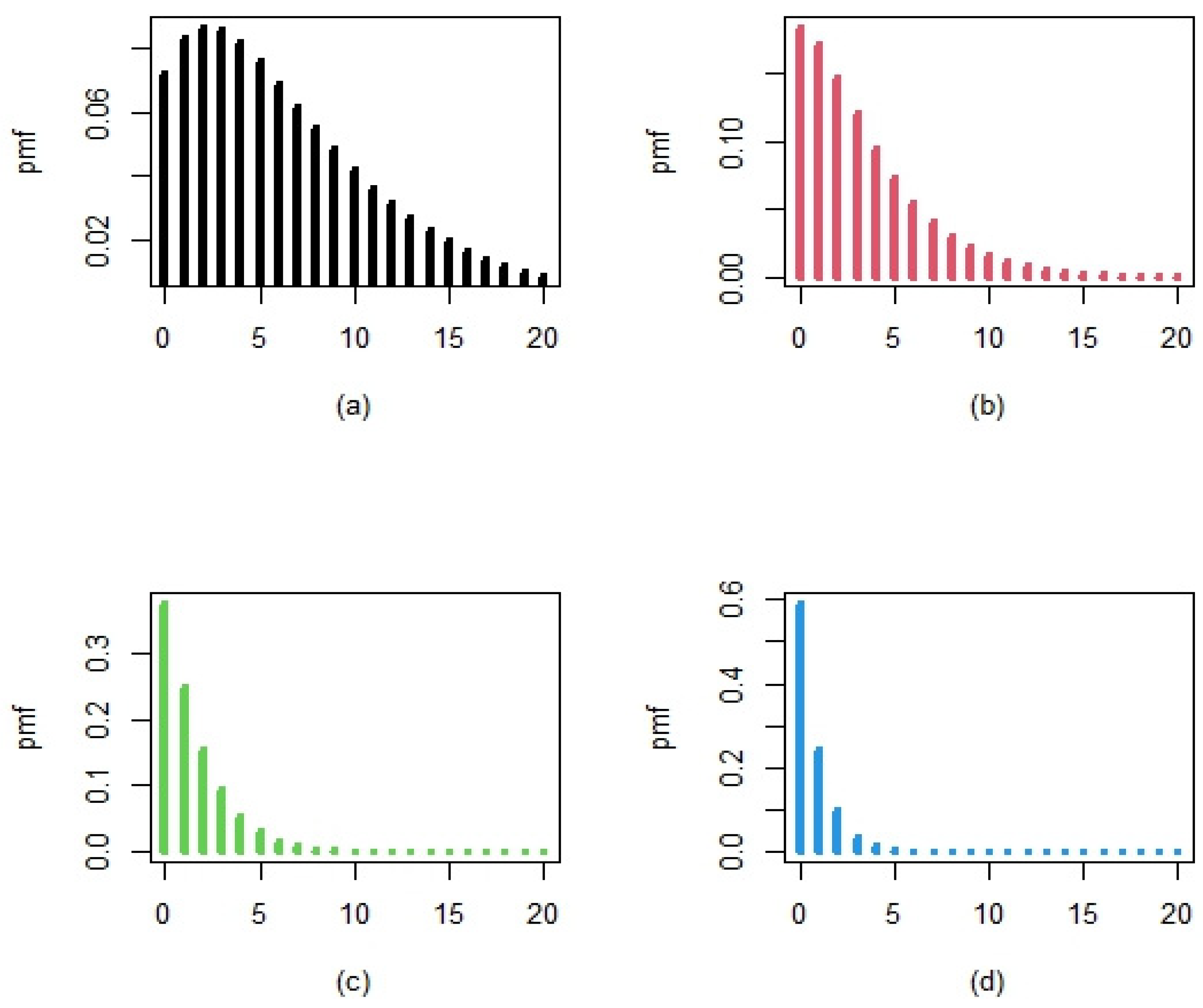
2.3. Generating Random Numbers from PLD
| Algorithm 1: Generating a random number from the |
| Step 1: Generate from a Lindley distribution with parameter as follows: |
| (i) Generate from a distribution. |
| (ii) If , let ; otherwise, let , where and are random numbers generated from an distribution. |
| Step 2: Generate from a Poisson distribution with parameter . |
2.4. Estimation of the Parameter of the
2.4.1. Method of Moment Estimation
2.4.2. Maximum Likelihood Estimation
3. Control Charts for Poisson–Lindley Processes
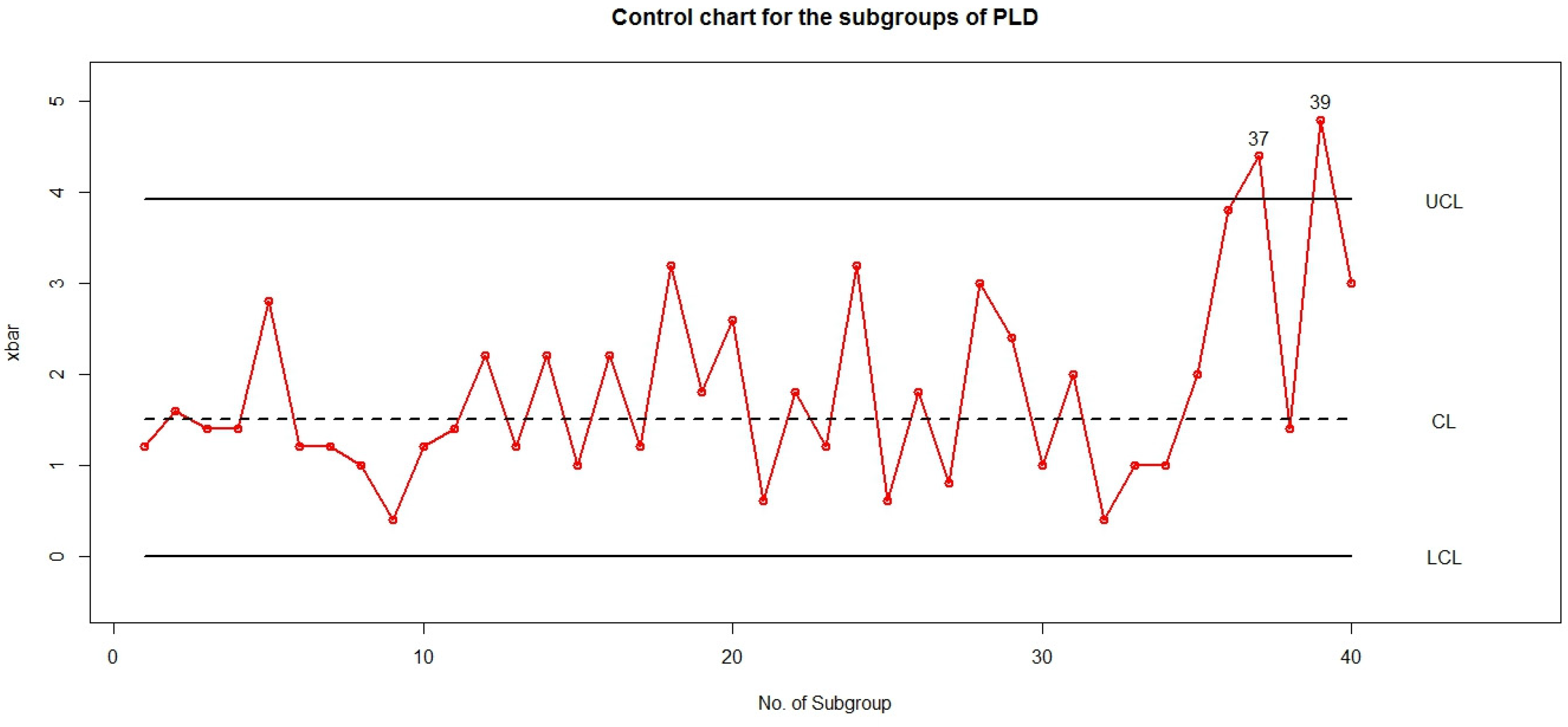
3.1. Control Charts When the Parameter Is Known
3.2. Control Charts When the Parameter Is Unknown
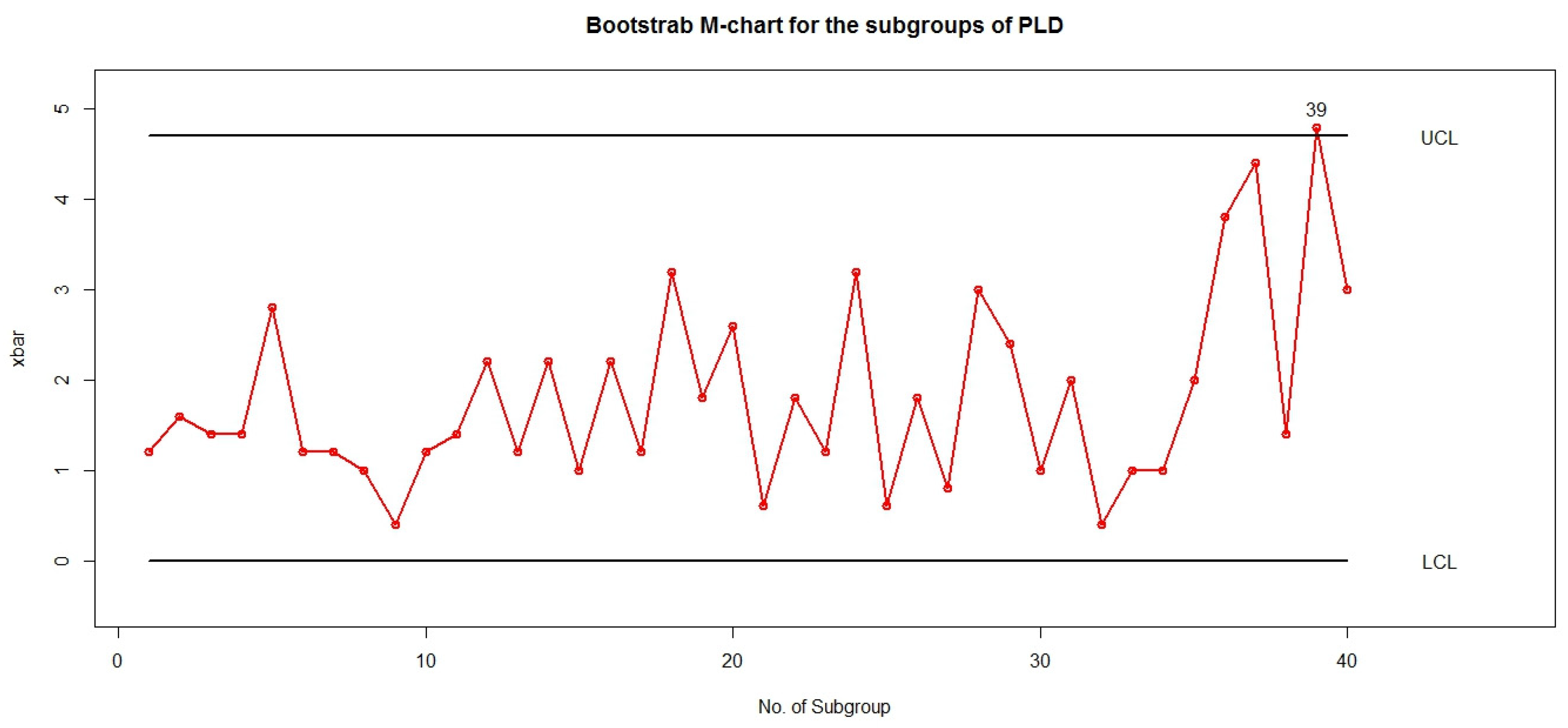
3.3. Bootstrap Control Charts
| Algorithm 2: Computing the Bootstrap M and S control charts |
| Phase I: Estimation and computation of the control limits |
|
| Phase II: Monitoring of process |
|
3.4. Process Capability Analysis Using the Proposed Control Charts
- and values less than 1 indicate that the process is not capable of meeting customer requirements.
- values greater than 1 indicate that the process has the potential to meet customer requirements, but may not be doing so consistently.
- values greater than 1 indicate that the process is capable of meeting customer requirements with a low defect rate.
4. Numerical Results and Simulation
4.1. Simulated Example
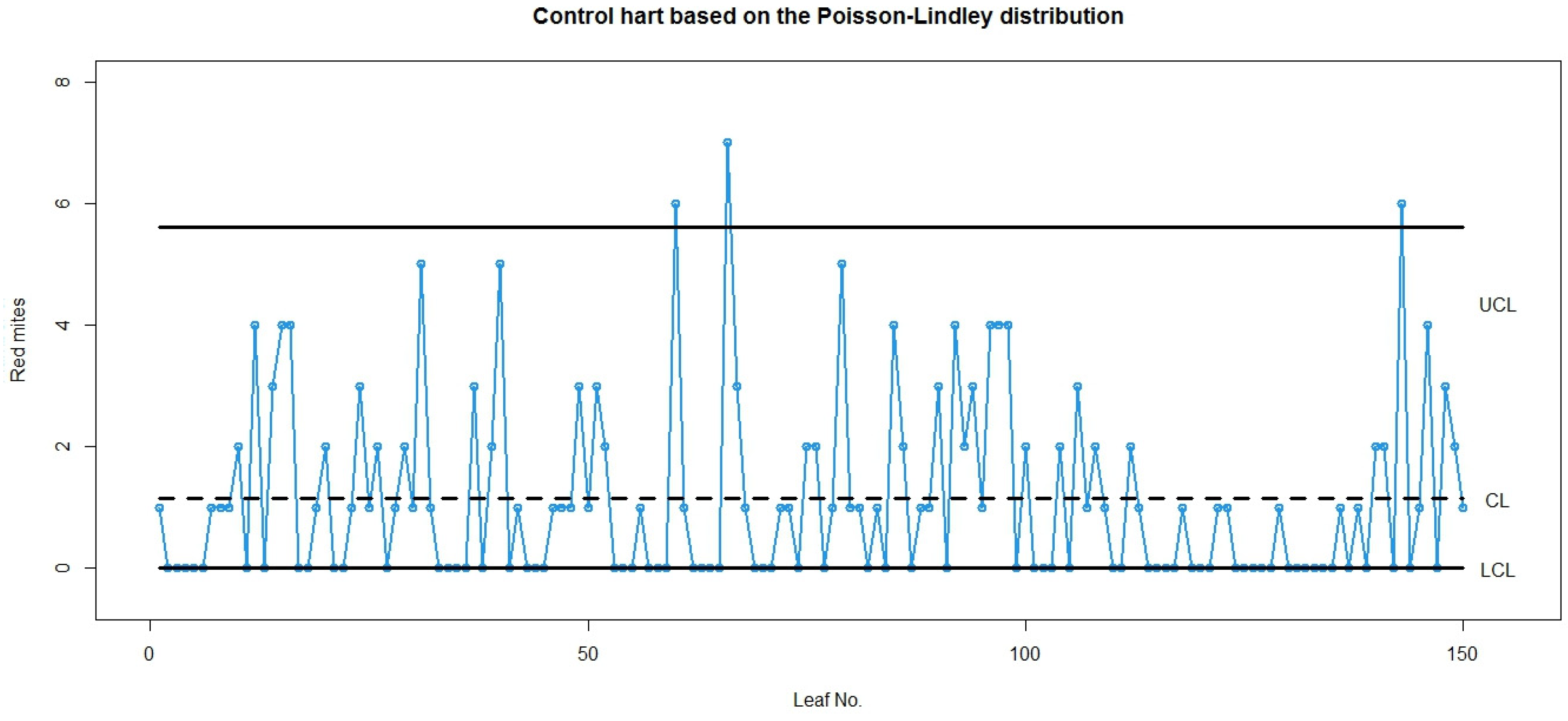
4.2. A Real Data Set Example
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramos, M.; Ascencio, J.; Hinojosa, M.V.; Vera, F.; Ruiz, O.; Jimenez-Feijoó, M.I.; Galindo, P. Multivariate statistical process control methods for batch production: A review focused on applications. Prod. Manuf. Res. 2021, 9, 33–55. [Google Scholar] [CrossRef]
- Apsemidis, A.; Psarakis, S.; Moguerza, J.M. A review of machine learning kernel methods in statistical process monitoring. Comput. Ind. Eng. 2020, 142, 106376. [Google Scholar] [CrossRef]
- Zhang, C.; Niu, S. Adaptive industrial control data analysis based on deep learning. Evol. Intell. 2023, 20, 1–9. [Google Scholar] [CrossRef]
- Vellaisamy, P.; Upadhye, N.; Cekanavicius, V. On negative binomial approximation. Theory Probab. Its Appl. 2013, 57, 97–109. [Google Scholar] [CrossRef]
- Sengar, A.S.; Upadhye, N.S. Subordinated compound Poisson processes of order k. Mod. Stoch. Theory Appl. 2020, 7, 395–413. [Google Scholar] [CrossRef]
- Kumar, A.N.; Upadhye, N.S. On discrete Gibbs measure approximation to runs. Commun. Stat.-Theory Methods 2022, 51, 1488–1513. [Google Scholar] [CrossRef]
- Sankaran, M. 275. note: The discrete poisson-lindley distribution. Biometrics 1970, 26, 145–149. [Google Scholar] [CrossRef]
- Lindley, D.V. Fiducial distributions and Bayes’ theorem. J. R. Stat. Soc. Ser. B 1958, 20, 102–107. [Google Scholar] [CrossRef]
- Mahmoudi, E.; Zakerzadeh, H. Generalized poisson–lindley distribution. Commun. Stat.-Theory Methods 2010, 39, 1785–1798. [Google Scholar] [CrossRef]
- Shanker, R.; Mishra, A. A two-parameter Poisson-Lindley distribution. Int. J. Stat. Syst. 2014, 9, 79–85. [Google Scholar]
- Hassan, A.S.; Assar, S.M.; Ali, K.A. The complementary Poisson-Lindley class of distributions. Int. J. Adv. Stat. Probab. 2015, 3, 146–160. [Google Scholar] [CrossRef]
- Zamani, H.; Faroughi, P.; Ismail, N. Bivariate Poisson-Lindley distribution with application. J. Math. Stat. 2015, 11, 1. [Google Scholar] [CrossRef]
- Shanker, R.; Mishra, A. On size-biased two parameter Poisson-Lindley distribution and its applications. Am. J. Math. Stat. 2017, 7, 99–107. [Google Scholar]
- Das, K.K.; Ahmed, I.; Bhattacharjee, S. A new three-parameter Poisson-Lindley distribution for modelling over-dispersed count data. Int. J. Appl. Eng. Res. 2018, 13, 16468–16477. [Google Scholar]
- Ghitany, M.; Al-Mutairi, D. Estimation methods for the discrete Poisson–Lindley distribution. J. Stat. Comput. Simul. 2009, 79, 1–9. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Bai, D.; Choi, I. X and R control charts for skewed populations. J. Qual. Technol. 1995, 27, 120–131. [Google Scholar] [CrossRef]
- Nichols, M.D.; Padgett, W. A bootstrap control chart for Weibull percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]
- Lio, Y.; Park, C. A bootstrap control chart for inverse Gaussian percentiles. J. Stat. Comput. Simul. 2010, 80, 287–299. [Google Scholar] [CrossRef]
- Lio, Y.L.; Park, C. A bootstrap control chart for Birnbaum–Saunders percentiles. Qual. Reliab. Eng. Int. 2008, 24, 585–600. [Google Scholar] [CrossRef]
- Chiang, J.-Y.; Lio, Y.; Ng, H.; Tsai, T.-R.; Li, T. Robust bootstrap control charts for percentiles based on model selection approaches. Comput. Ind. Eng. 2018, 123, 119–133. [Google Scholar] [CrossRef]
- Saeed, N.; Kamal, S.; Aslam, M. Percentile bootstrap control chart for monitoring process variability under non-normal processes. Sci. Iran. 2021, in press. [CrossRef]
- Ma, Z.; Park, C.; Wang, M. A Robust Bootstrap Control Chart for the Log-Logistic Percentiles. J. Stat. Theory Pract. 2022, 16, 3. [Google Scholar] [CrossRef]
- Seppala, T.; Moskowitz, H.; Plante, R.; Tang, J. Statistical process control via the subgroup bootstrap. J. Qual. Technol. 1995, 27, 139–153. [Google Scholar] [CrossRef]
- Liu, R.Y.; Tang, J. Control charts for dependent and independent measurements based on bootstrap methods. J. Am. Stat. Assoc. 1996, 91, 1694–1700. [Google Scholar] [CrossRef]
- Jones, L.A.; Woodall, W.H. The performance of bootstrap control charts. J. Qual. Technol. 1998, 30, 362–375. [Google Scholar] [CrossRef]
- Bliss, C.I.; Fisher, R.A. Fitting the negative binomial distribution to biological data. Biometrics 1953, 9, 176–200. [Google Scholar] [CrossRef]


| M-Chart | S-Chart | ||||
|---|---|---|---|---|---|
| δ | ξ | ||||
| 0 | 370.61 | 371.72 | 1 | 370.71 | 369.83 |
| 0.25 | 182.43 | 185.64 | 1.1 | 156.78 | 162.49 |
| 0.5 | 51.31 | 58.42 | 1.2 | 52.36 | 55.74 |
| 0.75 | 18.67 | 22.96 | 1.3 | 26.35 | 28.47 |
| 1 | 8.23 | 7.32 | 1.4 | 14.18 | 14.93 |
| 1.25 | 4.15 | 3.97 | 1.5 | 8.32 | 7.64 |
| 1.5 | 2.34 | 1.83 | 1.6 | 5.92 | 5.76 |
| 1.75 | 1.76 | 1.28 | 1.7 | 4.56 | 3.97 |
| 2 | 1.22 | 0.63 | 1.8 | 3.47 | 3.16 |
| 2.25 | 1.14 | 0.42 | 1.9 | 2.95 | 2.48 |
| 2.5 | 1.03 | 0.24 | 2 | 2.52 | 2.23 |
| −0.2 | 132.4 | 136.3 | 2.25 | 2.18 | 1.34 |
| −0.4 | 43.6 | 44.7 | 2.5 | 1.50 | 1.12 |
| −0.6 | 8.8 | 8.2 | |||
| −0.8 | 2.2 | 1.9 | |||
| Number of European Red Mites per Leaf | Observed Frequency | Expected Frequency | |
|---|---|---|---|
| Poisson Distribution | Poisson–Lindley Distribution | ||
| 0 | 70 | 47.6 | 67.2 |
| 1 | 38 | 54.6 | 38.9 |
| 2 | 17 | 31.3 | 21.2 |
| 3 | 10 | 11.9 | 11.1 |
| 4 | 9 | 3.4 | 5.7 |
| 5 | 3 | 0.8 | 2.8 |
| 6 | 2 | 0.2 | 1.4 |
| 7 | 1 | 0.1 | 0.9 |
| 8 | 0 | 0.1 | 0.8 |
| Total | 150 | 150 | 150 |
| ML Estimate | |||
| Standard Error | 0.08743245 | 0.1139965 | |
| Chi-square Statistic | 49.15817 | 1.251797 | |
| Chi-square d.f | 3 | 3 | |
| Chi-square p-value | 1.207139 × 10−10 | 0.7406099 | |
| 487.6199 | 447.0218 | ||
| 490.6305 | 450.0324 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Nuaami, W.A.H.; Heydari, A.A.; Khamnei, H.J. The Poisson–Lindley Distribution: Some Characteristics, with Its Application to SPC. Mathematics 2023, 11, 2428. https://doi.org/10.3390/math11112428
Al-Nuaami WAH, Heydari AA, Khamnei HJ. The Poisson–Lindley Distribution: Some Characteristics, with Its Application to SPC. Mathematics. 2023; 11(11):2428. https://doi.org/10.3390/math11112428
Chicago/Turabian StyleAl-Nuaami, Waleed Ahmed Hassen, Ali Akbar Heydari, and Hossein Jabbari Khamnei. 2023. "The Poisson–Lindley Distribution: Some Characteristics, with Its Application to SPC" Mathematics 11, no. 11: 2428. https://doi.org/10.3390/math11112428
APA StyleAl-Nuaami, W. A. H., Heydari, A. A., & Khamnei, H. J. (2023). The Poisson–Lindley Distribution: Some Characteristics, with Its Application to SPC. Mathematics, 11(11), 2428. https://doi.org/10.3390/math11112428








