Mathematical Physics of Time Dilation through Curved Trajectories with Applications

Abstract

In special relativity, the time dilation formula has been obtained by particles propagation in a straight line trajectory relative to an observer in motion. Up to now, there are no available formulas for other possible trajectories of particles. However, this paper obtains formulas of time dilation for several trajectories of particle such as parabolic, elliptic, and circular and finds a relatively accurate trajectory. The obtained formulas are employed in order to analyze the time dilation of the muon particles decay. In this paper, it is found that the time dilation of the parabolic and the elliptical trajectories exceed the corresponding results utilizing the standard Lorentz-Einstein time dilation formula. Consequently, if we are able to control the trajectory of unstable particles by some external forces, then their life-times might be increased. Probably, the increase in lifetime via a curved trajectory occurs at lower relative velocity & acceleration energy if compared to the straight line trajectory. In addition, the circular trajectory leads to multiple values of time dilation at certain velocities of an observer in motion, which may give an interpretation of fluctuations of time dilation in quantum mechanics. The result arises from the present relatively accurate formula of time dilation that is very close to the experimental data of muon decay (CERN experiment) when it is compared to the result obtained by the Lorentz-Einstein formula. Finally, it may be concluded that the time dilation not only depends on relative velocity and acceleration energy of particles but also on curved trajectories. The present work may attract other researchers to study different trajectories.

1. Introduction

In this paper, the time dilation formulas in several trajectories are considered along with examining their accuracy. At the advent of the last century, Lorentz published his transformations [1,2] based on the ether theory. After that, Einstein developed his special theory of relativity based on a couple of fundamental assumptions [3]. Then, Lorentz combined his transformations with Einstein’s formula and produced the well-known Lorentz-Einstein theory [4]. Einstein’s geometrical derivation of time dilation was based on an observer in motion that notices the light propagation relatively in a straight line trajectory [5,6]. However, when such trajectory is changed to a curved trajectory, this observer will notice an enhancement in prolonging the lifetime of relativistic particles as fermions [7]. Time dilation depends on acceleration energy and velocity of an object. The basic equation, Total energy (E_T) = kinetic energy (E_K) + potential energy (E_P), leads to the relativisitc factor $\gamma =\frac{E_K+m_0{c}^2}{m_0{c}^2}$ [8], where m₀ is the rest mass and c is the speed of light. According to Blokhintsev [9] and Rédei [10], it is suggested that the special relativity not only breaks down at very large distances due to gravitational effects, but also there may also be a breakdown below some fundamental distance $\alpha$. Thus, the effect of such a breakdown on the muon lifetime in flight has been calculated by Rédei [11] using a correction to the Einstein’s formula, given by $t=\gamma t_0\left(1+2.5\times {10}^{24}{\left(\frac{E_{\mu }}{m_{\mu }{c}^2}\right)}^2{\alpha }^2\right)$ where $\alpha$ is the distance in centimeters such that $\alpha >7\times {10}^{-14}\left(\frac{m_{\mu }{c}^2}{E_{\mu }}\right)$ cm (95% confidence level). Lazanu [12] concluded some elementary remarks about the time, mass and relativistic dynamics of quantum systems, while Budriga et al. [13] simulated the protons and electrons acceleration. Tsipenyuk and Belayev [14] discussed the photon dynamics in the gravitational field. Additionally, Mocanu [15] investigated the trajectories of charged particles undergoing Brownian motion in a time variable magnetic field. Based on the CERN experiment [16] for time dilation of muons, the authors declared that there is a fundamental difference between the theoretical and the experimental values, especially at velocities relatively close to the speed of light. They attributed the reason for such drawbacks to the particle trajectory, as it should follow a curved trajectory [16]. However, the exact form of such a trajectory was not addressed. So, searching for an accurate equation for the particle trajectory has become a challenge. Especially, in quantum mechanics, the change of particle mass during the motion was not taken into account.

Actually, the mass increases as the velocity increases, and the mass reaches a very large value as the velocity of the particle approaches the speed of light. This increase in mass will inevitably lead to the effect of gravity on it. Consequently, a curved trajectory is expected, such as a projectile due to the gravitational effect on its mass [17,18]. The main reason for searching for other trajectories, different from the straight line, is simply to find an accurate description for particle trajectory as the authors in CERN experiment referred to. This is the main motivation of the current work. In addition, the authors of [16] pointed out that the difference between the experimental results and Einstein’s time dilation formula becomes substantial, especially when the velocity approaches the speed of light. As far as we know, the CERN experiment in 1977 [16] was the last practical experiment in that framework, while the maximum energy used, at that time, was 3 GeV.

It should be noted here that the energy of the CERN accelerator has reached 7 TeV in recent years. However, scientists never investigated this experiment again to conduct the time dilation of the muon particle under such high energy level (7 TeV). Reconducting the CERN experiment has become necessary in order to specify the reason for the fundamental difference between the experimental results and Einstein’s time dilation formula, especially because the higher energy (7 TeV) allows the particle to reach a velocity so close to the speed of light. This will contribute in specifying the fundamental breakdown in Einstein’s equation at very large velocities, as well as the exact form of the particle trajectory. In this study, we showed that the experimental values in ref. [16] are closer to our results when the parabolic trajectory is considered. Perhaps this leads to a possible link between quantum mechanics and general relativity as a result of the increase in mass. This paper is an attempt to overcome the difficulties raised above. Determining a more liable formula for time dilation is the main target of this paper via considering several curved trajectories.

2. Basic Concepts and Equations

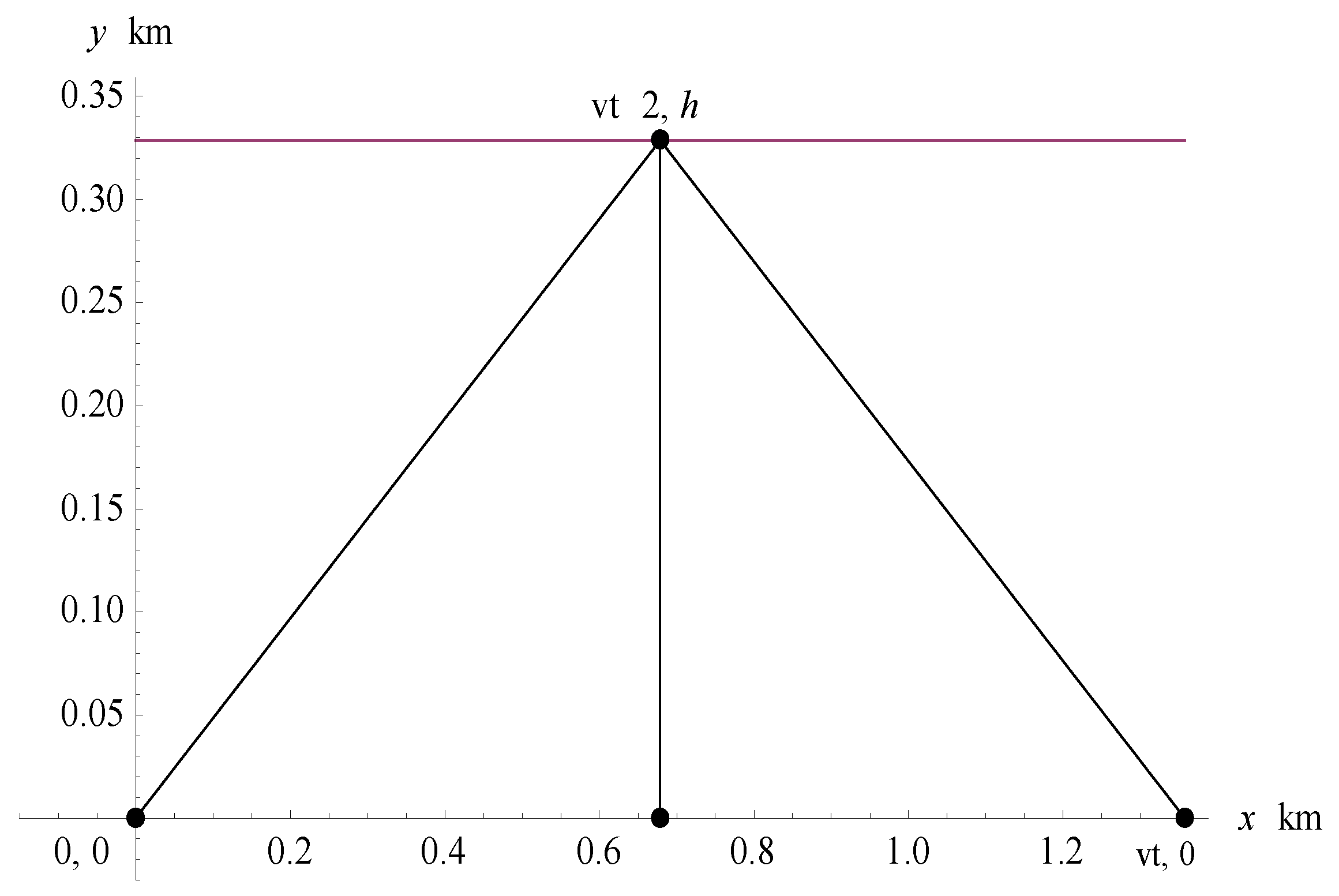
In the first part of this section, we address Einstein’s geometrical derivation of time dilation. Later in this section, we will introduce basic equations to reproduce the time dilation formula when a curved trajectory of a particle is considered. Einstein gave an example using a flashing light through the vertical axis $y$ inside a train. In this case, an observer at rest ($v=0$) but in motion relative to an observer in horizontal pathway axis $x$, the vertical straight line trajectory of light turns into diagonal straight line trajectory, which is in the final Einstein’s formula of time dilation given as $t=\frac{t_0}{\sqrt{1-\frac{v^2}{c^2}}}$. As an example, we give in Figure 1 a representation of the obsereved straight line trajectory when $v=0.9c$ and $t_0=2.2\mu \mathrm{s}$.

In this paper, we consider curved trajectories instead of the straight line trajectory followed by Einstein. In our case, light appears in a curved trajectory (as a portion of a parabola, an ellipse, and a circle) relative to observer in motion. As a result, we expect an increase in the time dilation of the particles. By the observer at rest ($v=0$), a beam of light cuts the distance $2h$ in a time $t_0$ where

$$h=\frac{c{t}_0}{2},$$

(1)

and the horizontal distance is

$$x=vt.$$

(2)

Based on the physical grounds, the possible curved trajectories of light should pass through the three points $(0,0)$, $(\frac{vt}{2},h)$, and $(vt,0)$, where $v$ and $t$ are the velocity and the time of the moving observer, respectively. Consequently, $t$ is given by

$$t=\frac{2l}{c}.$$

(3)

In trder to find the extended Lorentz fahis section, we search for several possible types of curved trajectories and study their effects on the time dilation. It should be noted that the total distance traveled by light in a time $t$ is $2l$, where $l$ is the length of the arc, defined by

$$l={\displaystyle {\int }_0^{\frac{vt}{2}}}\sqrt{1+{\left(y^{\prime }(x)\right)}^2}dx,$$

(4)

where $y(x)$ describes the curve, whether parabolic, elliptic, circular, or any another trajectory. In the following section, we will determine the time dilation formula corresponding to the parabolic trajectory. Furthermore, the time dilation formulas corresponding to the elliptic and the circular trajectories will be obtained in subsequent sections.

2.1. Parabolic Path

The path of the parabolic type is in the form

$${\left(x-p\right)}^2={\alpha }_1\left(y-q\right),$$

(5)

where $p$, $q$, and ${\alpha }_1$ are defined by

$$p=\frac{vt}{2},q=h,{\alpha }_1=-\frac{v^2{t}^2}{4h},$$

(6)

respectively. Accordingly, for the parabolic trajectory, $y(x)$ is expressed as

$$y(x)=h\left(1-\frac{4}{v^2{t}^2}{\left(x-\frac{vt}{2}\right)}^2\right).$$

(7)

Applying the integral Formula (4) on the parabolic path (7), yields

$$l=\frac{c{t}_0}{2}\sqrt{1+{\left(\frac{\mu \Gamma }{2}\right)}^2}+{\left(\frac{\mu \Gamma }{2}\right)}^2{\sinh }^{-1}\left(\frac{2}{\mu \Gamma }\right),$$

(8)

where

$$\mu =\frac{v}{c},\hspace{1em}\Gamma =\frac{t}{t_0}.$$

(9)

Finally, substituting (8) in (3) and rearranging yields the following expression:

$$\Gamma =\sqrt{1+{\left(\frac{\mu \Gamma }{2}\right)}^2}+{\left(\frac{\mu \Gamma }{2}\right)}^2{\sinh }^{-1}\left(\frac{2}{\mu \Gamma }\right),\hspace{1em}\mathrm{where}\hspace{1em}t=\Gamma t_0.$$

(10)

This equation is to be solved to obtain the extended Lorentz factor, $\Gamma$. In a subsequent section, comparisons between $\Gamma$ and the standard Lorentz factor γ ($\gamma =1/\sqrt{1-v^2/c^2}$) will be performed as $v$ varies.

2.2. Elliptic Path

Suppose that the path is an ellipse with semi-minor and semi-major axes given by $(vt)/2$ and $h$, respectively, and consequently, the equation of the ellipse takes the form of

$$\frac{{\left(x-\frac{vt}{2}\right)}^2}{{\left(\frac{vt}{2}\right)}^2}+\frac{y^2}{h^2}=1.$$

(11)

Hence

$$y\left(x\right)=h{(1-\frac{4}{v^2{t}^2}{(x-\frac{vt}{2})}^2)}^{\frac{1}{2}}.$$

(12)

In order to find the extended Lorentz factor $\Gamma$ for the elliptic path, we substitute Equation (12) in (4); this gives

$$l=\frac{vt}{2}E\left(1-\frac{4h^2}{v^2{t}^2}\right),$$

(13)

where $E(\nu )$ is the elliptic integral, which is given by

$$E(\nu )={\displaystyle {\int }_0^{\pi /2}}\sqrt{1-\nu {\sin }^2\theta }d\theta .$$

(14)

Applying (13) in (3) gives

$$\mu E\left(1-\frac{1}{{\mu }^2{\Gamma }^2}\right)=1,$$

(15)

where $\mu$ and $\Gamma$ are already defined in Equation (9).

3. Circular Path

Here, the arc is considered as a portion of a circular path. In this case, we have

$$y(x)=\rho +\sqrt{r^2-{\left(x-p\right)}^2}.$$

(16)

The quantities $\rho$ and $r$ are obtained by

$$\rho =\frac{h^2-p^2}{2h},\hspace{1em}r=\sqrt{p^2+{\rho }^2}=\frac{h^2+p^2}{2h},\hspace{1em}h<p,$$

(17)

where $h$ and $p$ are defined in (1) and (6), respectively. Similarly, applying (4) in (16) yields the following expression:

$$l=r{\tan }^{-1}\left(\frac{p}{\sqrt{r^2-p^2}}\right)=r{\tan }^{-1}\left(\frac{p}{\left|\rho \right|}\right).$$

(18)

By substituting this arc length into Equation (3) and employing the quantities $\rho$ and $r$ in (17), we obtain the transcendental equation

$$2\Gamma =\left(1+{\mu }^2{\Gamma }^2\right){\tan }^{-1}\left(\frac{2\mu \Gamma }{|1-{\mu }^2{\Gamma }^2|}\right),$$

(19)

or equivalently,

$$\tan \left(\frac{2\mu \Gamma }{1+{\mu }^2{\Gamma }^2}\right)=\frac{\mu \Gamma }{|1-{\mu }^2{\Gamma }^2|}.$$

(20)

4. Accurate Relativity Path

The arithmetic mean between the arc lengths of parabolic and straight line cases are used to find a relatively accurate trajectory, which corresponds to the experiment lifetime value of the accelerated muon particles. Sequential arithmetic averages between $l=\sqrt{a^2+4h^2}+{\left(\frac{2h}{a}\right)}^2{\sinh }^{-1}\left(\frac{2h}{a}\right)$ and $l=2\sqrt{{\left(\frac{vt}{2}\right)}^2+{\left(\frac{c{t}_0}{2}\right)}^2}$ leads to the following equation of time dilation:

$$\Gamma =\frac{116\sqrt{1+{\left(\mu \Gamma \right)}^2}+6\sqrt{4+{\left(\mu \Gamma \right)}^2}+3{\left(\mu \Gamma \right)}^2{\sinh }^{-1}\left(\frac{2}{\mu \Gamma }\right)}{128},$$

(21)

which agrees with the experimental value processed in CERN, as will be discussed later.

5. Results & Discussion

First of all, as $v\to 0$ (i.e., $\mu \to 0$), we observe from Equtaion (10) that

$$\underset{\mu \to 0}{\lim }\left({\left(\frac{\mu \Gamma }{2}\right)}^2{\sinh }^{-1}\left(\frac{2}{\mu \Gamma }\right)\right)=0,$$

(22)

and accordingly, Equation (10), as ($\mu \to 0$), leads to $\Gamma =1$, i.e., $t=t_0$. Although the analytical solution of Equation (10) is not available, the numerical solution can be evaluated at any given velocity of the moving observer. For example, the extended Lorentz factor $\Gamma$ has been numerically calculated at different values of v, utilizing the command ‘NSolve’ in MATHEMATICA and also comparing it to the standard Lorentz factor $\gamma =1/\sqrt{1-v^2/c^2}$, and the results are presented in

Table 1. The comparison between the extended Lorentz factor, $\Gamma$, and the standard Lorentz factor $\gamma$ for the parabolic path as $v$ varies.

$\mathit{v}$	$\mathbf{The}\mathbf{Extended}\mathbf{Lorentz}\mathbf{Factor}\mathbf{\Gamma }\mathbf{\left(}\mathbf{Present}\mathbf{\right)}$	$\mathbf{The}\mathbf{Standard}\mathbf{Lorentz}\mathbf{Factor}\mathit{\gamma }$ [16]
$0.1c$	1.01067	1.00504
$0.2c$	1.03723	1.02062
$0.3c$	1.07905	1.04828
$0.4c$	1.13902	1.09109
$0.5c$	1.22354	1.15470
$0.6c$	1.34535	1.25000
$0.7c$	1.53179	1.40028
$0.8c$	1.85443	1.66667
$0.9c$	2.59874	2.29416
$0.9994c$	33.3343	28.7818

. The results reveal that the values of $\Gamma$ (the extended Lorentz factor) are always greater than the values of $\gamma$ (the standard Lorentz factor) for the all cases. This means that the lifetime of unstable particles may be increased through the parabolic trajectory. In addition, in the experimental works of those in [16,19], t₀ (lifetimes of ${\mu }^{+}$ and ${\mu }^{-}$ were 2.1966 $\mu$s and 2.1948 $\mu$s, respectively) and $t$ (lifetimes in flight of ${\mu }^{+}$ and ${\mu }^{-}$ were 64.419 $\mu$s and 64.368 $\mu$s, respectively, at $0.9994c$) with an average $\gamma =29.327$ for the ${\mu }^{+}$ and ${\mu }^{-}$ unstable particles. However, with the expected lifetime 63.3939 $\mu$s, the expected value of $\gamma$ was 28.8718. It is found that, both of the expected lifetime (63.3939 $\mu$s) and the experimental lifetime average (64.3935 $\mu$s) are less than the present lifetime of the parabolic trajectory (73.1921 $\mu$s), where $\Gamma =33.3343$.

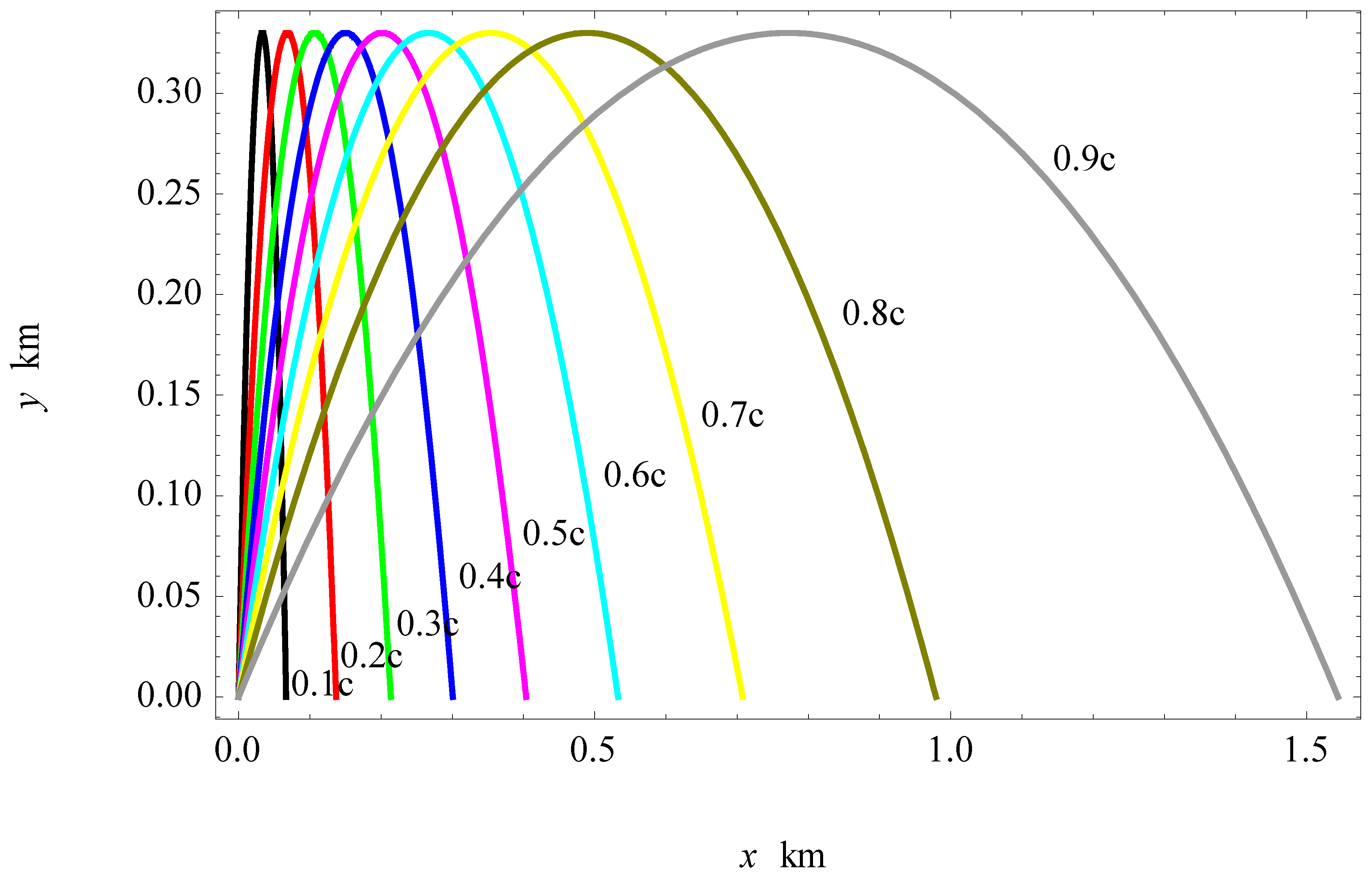
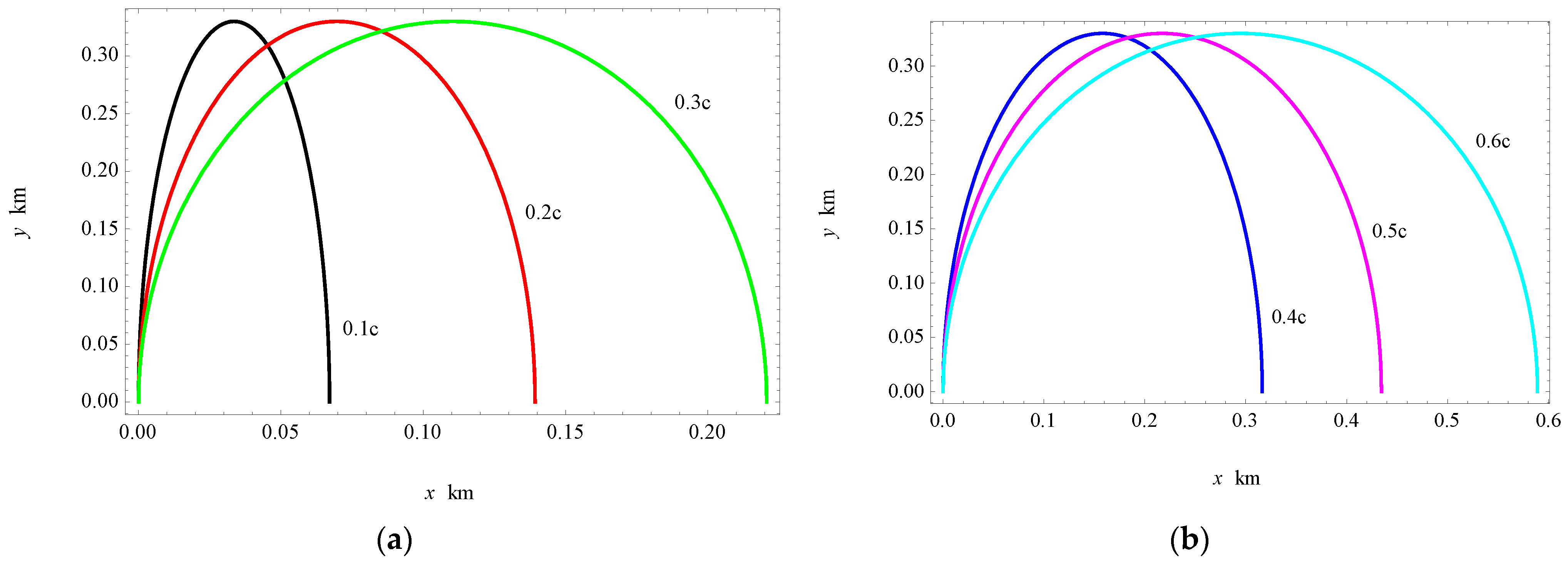
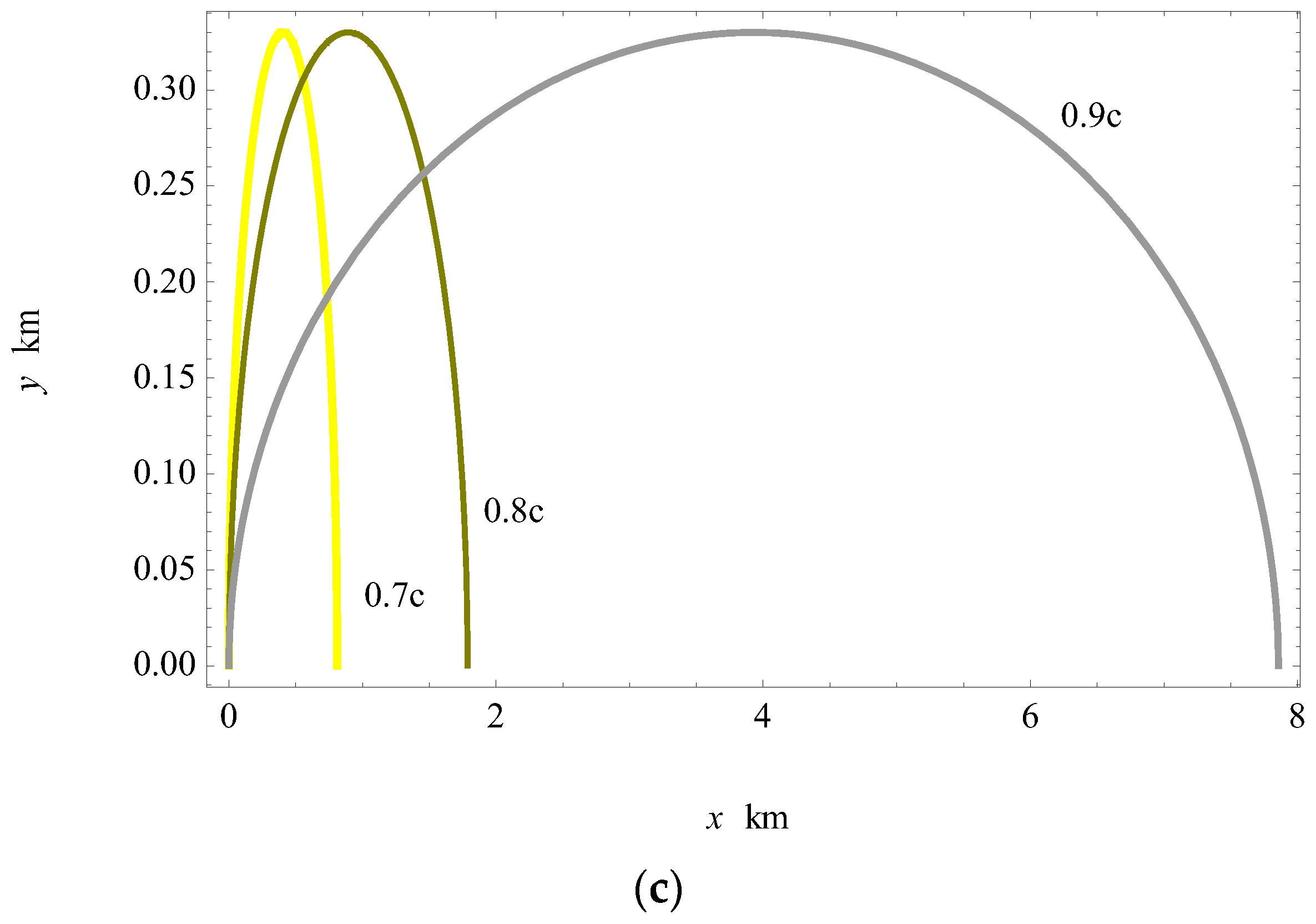
Graphically, the parabolic trajectories are shown in Figure 2 at different velocities $v$ when $t_0=2.2\mu \mathrm{s}$. It can be seen in Figure 2 that the curvature of the parabolic trajectory becomes significant as the velocity increases. For a declaration, the parabolic trajectory is closer to the straight line one at relatively lower velocities, such as $v<0.1c$. For $v>0.1c$, the difference between the curved trajectory and the straight line is clear and obvious. From this figure, it is also clear that the particle travels a longer horizontal distance than the corresponding one in a straight line due to the increase in the lifetime. This is because $\Gamma >\gamma$, as shown in Table 1. The difference in the value of the horizontal distance ($\Delta x$) can be calculated from the relationship $\Delta x=\left(\Gamma -\gamma \right)v{t}_0$. Accordingly, such a difference increases as $v$ increases. For the elliptic trajectory, the limit of (15) as $\mu \to 0$ gives

$$\underset{\mu \to 0}{\lim }\left(\mu E\left(1-\frac{1}{{\mu }^2{\Gamma }^2}\right)\right)=1,$$

(23)

and this yields

$$\frac{1}{\Gamma }=1.$$

(24)

It is clear from Equation (24) that $t=t_0$ when $v\to 0$. Although Equation (15) is an implicit transcendental equation in the extended Lorentz factor $\Gamma$, this equation can be accurately solved by any advanced software such as MATHEMATICA; in this regard,

Table 2. The comparison between the extended Lorentz factor $\Gamma$ and the standard Lorentz factor $\gamma$ for the elliptic path as $v$ varies.

$\mathit{v}$	$\mathbf{The}\mathbf{Extended}\mathbf{Lorentz}\mathbf{Factor}\mathbf{\Gamma }\mathbf{\left(}\mathbf{Present}\mathbf{\right)}$	$\mathbf{The}\mathbf{Standard}\mathbf{Lorentz}\mathbf{Factor}\mathit{\gamma }$ [16]
$0.1c$	1.01644	1.00504
$0.2c$	1.05508	1.02062
$0.3c$	1.11424	1.04828
$0.4c$	1.19807	1.09109
$0.5c$	1.31612	1.1547
$0.6c$	1.48762	1.25
$0.7c$	1.75468	1.40028
$0.8c$	2.2304	1.66667
$0.9c$	3.38383	2.29416
$0.9994c$	64.9539	28.7818

presents the numerical values of $\Gamma$ for different values of $v$ and compares them with the values of standard Lorentz factor $\gamma$. The corresponding elliptic trajectories are displayed in Figure 3a–c when $t_0=2.2\mu \mathrm{s}$. It is seen that the time dilation of the elliptic trajectory and present parabolic trajectory has been increased over the straight line (the standard path of special theory of relativity), especially at $v=0.9994c$, where $\Gamma =64.9539$, and the lifetime of the muon particle equals 142.899 $\mu$s.

Regarding a circular trajectory, the solution of Equation (19) or Equation (20) is not unique at some given values of $v$. For example, when $v=0.1c$, then Equation (19) or Equation (20) has multiple roots, such as Γ = 1.80664, 4.13974, 24.1561, and 55.3515. Similarly, when $v=0.2c$, we obtain two roots given as $\Gamma =2.61268$ and $\Gamma =9.56872$. Additionally, for muons particles; i.e., for $v=0.9994c$, there exist two possible values for the extended Lorentz factor given by $\Gamma =0.03003$ and $\Gamma =33.3403$. Although the value $\Gamma =33.3403$ is too close to the unique value obtained by the parabolic trajectory, the other value $\Gamma =0.03003$ is unacceptable because $t<t_0$. Certainly, we can exclude values for $\Gamma$ that are smaller than one for the muons particles with velocity $v=0.9994c$. However, on the other hand, it is important to note that all values of $\Gamma$ are greater than one if muons particles take lower velocities, such as $v=0.1c$ and $v=0.2c$. It is indicated above that all values of $\Gamma$ are greater than one when $v=0.1c$ and $v=0.2c$. It may be concluded that the cricular trajectory is still unique at the higher velocity $v=0.9994c$. Therefore, the present circular trajectory is acceptable for mouns moving with higher velocities (comparable to speed of light). Additionally, the circular trajectory may be useful in another case, such as the interpretation of time dilation as expected in quantum mechanics. The time dilation equation of Lorentz-Einstein cannot be utilized to explain the decay of unstable particles in quantum mechanics due to the occurance of fluctuations in time dilation, where $t>t_0$ (acceptable) and, at the same velocity, $t<t_0$ (unacceptable). Probable fluctuations occur in unstable particles due to a special trajectory of unstable particles as a reason for fluctuations in quantum mechanics [20,21]. Using the arithmetic mean method, we can find many curves formulas and obligate any particles to move in any path. Our new formula, which describes the relatively accurate trajectory corresponding to time dilation of muon particle, is closer to the CERNexperimental results [16].

Table 3. The comparison between the extended Lorentz factor $\Gamma$ and the standard Lorentz factor $\gamma$ for the experimentally path as $v$ varies.

$\mathit{v}$	$\mathbf{The}\mathbf{Extended}\mathbf{Lorentz}\mathbf{Factor}\mathbf{\Gamma }\mathbf{\left(}\mathbf{Present}\mathbf{\right)}$	$\mathbf{The}\mathbf{Standard}\mathbf{Lorentz}\mathbf{Factor}\mathit{\gamma }$ [16]
$0.1c$	1.00556	1.00504
$0.2c$	1.02215	1.02062
$0.3c$	1.05108	1.04828
$0.4c$	1.09540	1.09109
$0.5c$	1.16087	1.1547
$0.6c$	1.25855	1.25
$0.7c$	1.41217	1.40028
$0.8c$	1.68395	1.66667
$0.9c$	2.32308	2.29416
$0.9994c$	29.3189	28.7818

shows numerical values of $\Gamma$ for different values of $v$ and compares them with the standard Lorentz factor $\gamma$.

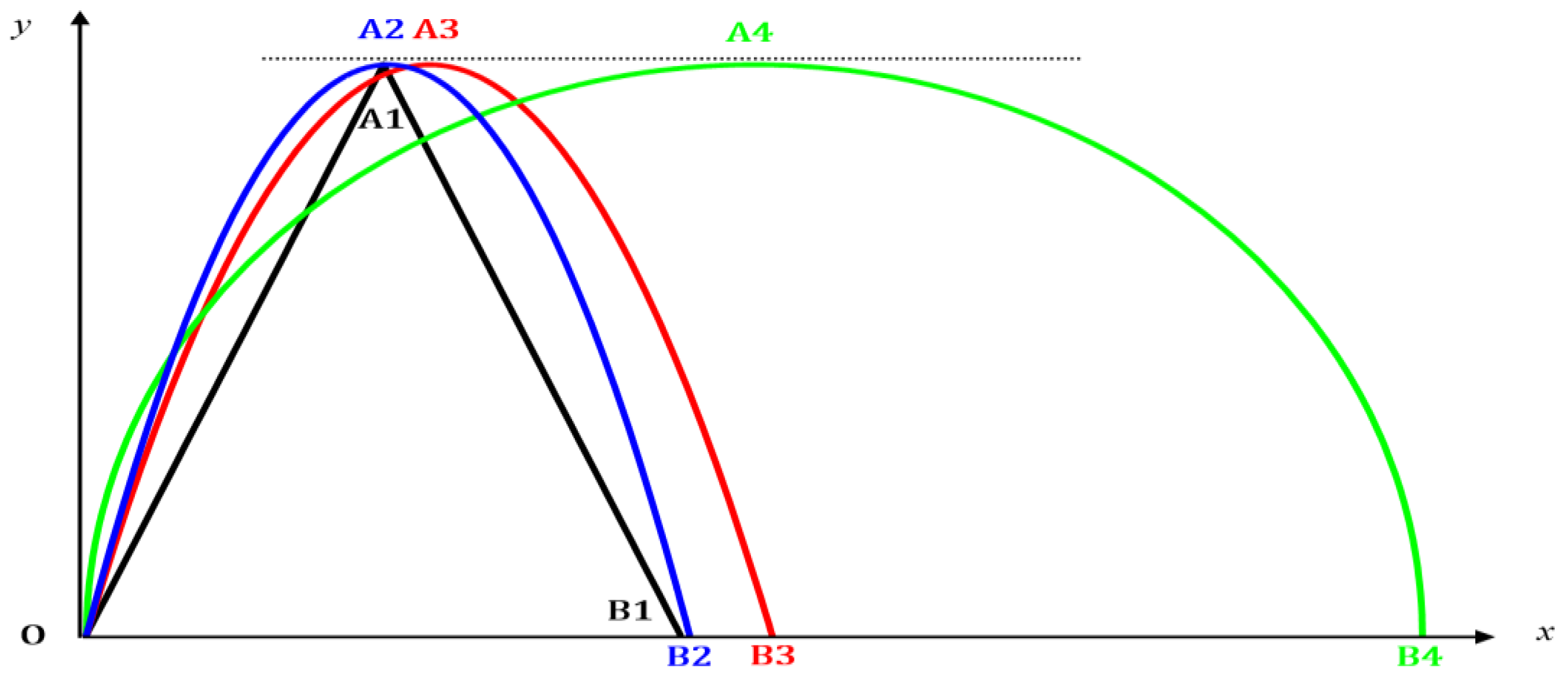
As a result, it can be concluded that the particles move relativity in a curved, not in a straight, trajectory, and it is restricted by Equation (21). Figure 4 shows the geometrical difference between the trajectories of the standard straight line (black curve OA${}_1$B${}_1$), the current accurate trajectory (blue curve OA${}_2$B${}_2$), parabolic trajectory (red curve OA${}_3$B${}_3$), and the elliptic trajectory (green curve OA${}_4$B${}_4$) at $v=0.9994c$.

It is observed that the black straight line in special theory of relativity and the blue curve of the current study, resulting from Equation (21), pass (approximately) through the same three points with shifting amount in horizontal distance $x=vt=352.6102$ m. However, the horizontal and vertical points, which are shifted by some amounts for the parabolic and the elliptical trajectories, are equal to 2988.7506 m, 23,747.2564 m, respectively.

This means that the horizontal distance, traveled by unstable particles, mainly depends on the trajectory. Moreover, the elliptical trajectory gains the greatest value of lifetime and distance. Therefore, the lifetime of unstable particles can be enhanced by controlling their trajectories (if it is experimentally possible). The current results give some light on expanding the time dilation concept by considering different curved trajectories.

6. Conclusions

In this paper, several time dilation formulas have been obtained for various probable trajectories of light. Both the parabolic and the elliptic trajectories gave a unique value for the extended Lorentz factor $\Gamma$, while the circular trajectory gave multiple values. The obtained numerical values of time dilation are greater than the standard Lorentz-Einstein using straight line in the special theory of relativity. In view of the current results, the present authors believe that the time dilation of unstable particles can be increased at the same velocity and acceleration energy by any curved trajectory different than the straight line. This certainly will motivate us and other researchers in the field to investigate other trajectories in the near future. The circular trajectory may be useful to interpret fluctuations of the unstable particles decaying in quantum mechanics. In addition, in our point of view, the relative motion of an object is actually in a curved trajectory (i.e., not in straight path) due to gravity or a new behavior in the object itself that occurs during the relative motion. It seems that the reason for the relative curvature of the movement of objects is not only due to the influence of the gravity on the mass of objects but may also be due to an another property that impact the objects during the motion. Additionaly, a proposed accurate curved trajectory of the muon particle was obtained through the values implemented in the CERN experiment. It turns out that it is a curved path, i.e., not a straight line path. Accordingly, we encourage that the CERN-experiment be reconducted with the new 7 TeV acceleration energy, especially because the greater the acceleration energy, the greater both the particle’s velocity and the curvature of the particle’s trajectory. This explains why there is a difference between the results of the CERN experiment and the Einstein time dilation equation when the velocities become more close to the speed of light.