Coexistence and Replacement of Two Different Maturation Strategies Adopted by a Stage-Structured Population

Abstract

Maturation strategies play a key role in the survival and development of populations. In response to changes in the external environment and human interventions, populations adopt appropriate maturation strategies. Different maturation strategies can lead to different birth and mortality rates. In this paper, we develop and analyze a stage-structured population model with two maturation strategies to obtain conditions for the coexistence of two maturation strategies and conditions for competitive exclusion. Our results also show that equality of fitness—represented by basic reproductive numbers being greater than 1 under different maturation strategies—promotes the coexistence of the two strategies. The reason why a strategy is replaced by another one is that the population adopting this strategy has weak fitness, which is measured by the basic reproductive number.

1. Introduction

Maturation, which means the onset of reproduction, is a key life-history transition for an individual [1]. Maturation strategy plays a crucial role in determining fitness, which is usually represented by the basic reproductive number (or net reproductive rate), that is, the expected number of newborn offspring per female per lifetime [2,3,4]. Different life-history strategies of individual organisms cause species to display great differences in their behavior patterns, such as their reproductive development, fecundity, maximum life span and so on. The dynamics of populations have been studied extensively; however, few prior studies have considered the strategies of life history in a mathematical model.

Over the last few decades, it has been realized that changes to life-history strategies have be incorporated among competing populations. Fujiwara et al. [5] analyzed the mechanism of different but coexisting populations with different life-history strategies by using two-stage Beverton–Holt models [6]. They showed how demographic biodiversity can equalize the fitness of two species, thereby promoting their coexistence. A two-stage Ricker model [7] was analyzed on the assumption that only individuals in the same stage can compete with each other, but this did not interpret the biological processes for the outcomes. Recently, Tian and Liu [8] established a competitive model with two populations who display different life-history strategies in a seasonal environment in order to study the evolution of maturation time. However, few of studies focus on the coexistence and replacement of two maturation strategies for the same population. Here, we show how the life-history strategies influence the fitness so that the same population with two maturation strategies can coexist or can replace each other.

Fitness is a function of life-history parameters assuming no individual heterogeneity besides stage difference. Adjusting individuals’ life-history strategies makes the fitness equalize, hence promoting coexistence. We denote the basic reproductive number by $R_0$, which can be considered as a measure of Darwinian fitness [9,10] because natural selection prompts the optimal life history to maximize the number of surviving offspring. Sometimes, rates of increase can also be considered as a measure of fitness [11]. Life-history strategies are the major components of fitness and can vary in response to seasonal environmental conditions [8], such as temperature, sunlight and so on, or human interventions, such as harvest, fishing and so on. Seasonality may affect the decision of organism life-history strategies. Further, harvesting leads to evolutionary responses, in particular, changes to maturation strategies [12,13,14,15]. For example, the phenomenon of age at maturity of Atlantic cods advancing after over-harvesting has been observed [12]. Hence, not all individuals employ the same strategies in response to competition [16]. Therefore, in this paper, we analyze the effect of two different maturation strategies adopted by same population on the population dynamics and use the adaptive dynamics theory to study the evolution of maturation strategy. Same populations compete for shared resources, thereby causing strong competition between the two. Hence, we establish a competitive model to study the dynamics of populations with different maturation strategies, as shown in Section 2.

2. Two-Strategy Two-Stage Model

In this study, we consider two different maturation strategies adopted by the same population with a two-stage structure (juveniles and adults). The two maturation strategies $S_1,S_2$ can be adopted by juveniles. Different maturation strategies of juveniles lead to different birth rates and mortality rates of juveniles and adults. Same populations compete for shared resources. K is the carrying capacity. Without each other, the adult development follows logistical growth. The per capita birth rate $B\left(S_1\right)$ (or $B\left(S_2\right)$) denotes the average newborn juveniles per adult individual under maturation strategy $S_1$ (or $S_2$) per unit of time. The death rate $D_J\left(S_i\right)$ or $D_A\left(S_i\right)$ denotes the average death number of juveniles or adults under maturation strategy $S_i,i=1,2$ per unit of time. We denote by $J_i$, $A_i,i=1,2$ the number of juveniles and adults that adopt maturation strategy $S_i$, respectively, at time t. The flow chart is shown in Figure 1. Then, we consider the following stage-structured model with two different maturation strategies:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{J}_1}{dt}}& =B\left(S_1\right)A_1(1-{\displaystyle \frac{A_1+A_2}{K}})-S_1{J}_1-D_J\left(S_1\right)J_1,\hfill \\ \hfill {\displaystyle \frac{d{A}_1}{dt}}& =S_1{J}_1-D_A\left(S_1\right)A_1,\hfill \\ \hfill {\displaystyle \frac{d{J}_2}{dt}}& =B\left(S_2\right)A_2(1-{\displaystyle \frac{A_1+A_2}{K}})-S_2{J}_2-D_J\left(S_2\right)J_2,\hfill \\ \hfill {\displaystyle \frac{d{A}_2}{dt}}& =S_2{J}_2-D_A\left(S_2\right)A_2,\hfill \end{array}$$

(1)

where $B\left(S_i\right)$, $D_J\left(S_i\right)$, $D_A\left(S_i\right)$ are continuous non-negative functions of maturation strategy $S_i$, $i=1,2$. Natural death and mortality due to capture are respectively embodied in the death terms $D_J\left(S_i\right)$ and $D_A\left(S_i\right)$, $i=1,2.$

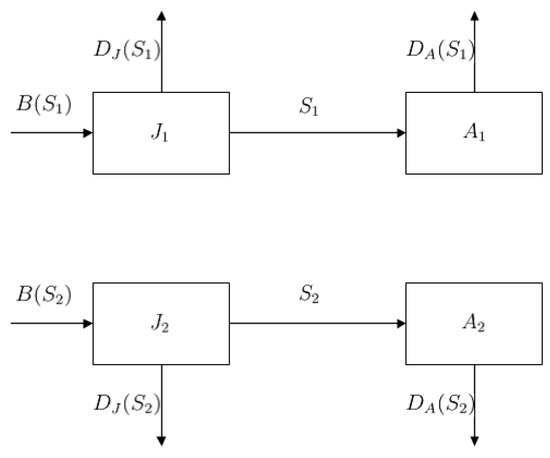
Figure 1. Flow chart of two-strategy two-stage model. Juveniles $J_i$ mature into adults $A_i$ at maturity rate $S_i$, $i=1,2$. Adults $A_i$ reproduce new offspring in the juvenile stage at per capita birth rate $B\left(S_i\right)$. The death rates of juveniles and adults are $D_J\left(S_i\right)$ and $D_A\left(S_i\right)$, respectively.

Define the basic reproductive number of the species that adopts maturation strategy i by

$$R_{S_i}={\displaystyle \frac{S_{i}B\left(S_i\right)}{D_A\left(S_i\right)(S_i+D_J\left(S_i\right))}},i=1,2.$$

(2)

For convenience, we also define a related number $R_0$ by $R_0=R_{S_1}/R_{S_2}$.

2.1. Existence of the Equilibria

System (1) has four equilibria: one trivial equilibrium, two single-strategy boundary equilibria and one coexisting two-strategy equilibrium. The single-strategy boundary equilibrium means that only one of two strategies can survive to the end. The coexisting two-strategy equilibrium means that two strategies can eventually coexist.

Clearly, model (1) has a trivial equilibrium denoted by $E_0=(0,0,0,0)$.

Furthermore, the two single-strategy boundary equilibria are given by

$$E_1=(J_1^{*},A_1^{*},0,0)=(D_A\left(S_1\right)A_1^{*}/S_1,K(1-1/R_{S_1}),0,0)$$

with $R_{S_1}>1$ and

$$E_2=(0,0,J_2^{*},A_2^{*})=(0,0,D_A\left(S_2\right)A_2^{*}/S_2,K(1-1/R_{S_2}))$$

with $R_{S_2}>1$.

The positive equilibrium $E_p=(J_1^{*},A_1^{*},J_2^{*},A_2^{*})$, where $J_1^{*}>0,A_1^{*}>0,J_2^{*}>0,A_2^{*}>0$ must satisfy

$$\begin{array}{cc}\hfill B\left(S_1\right)A_1(1-{\displaystyle \frac{A_1+A_2}{K}})-S_1{J}_1-D_J\left(S_1\right)J_1& =0,\hfill \\ \hfill S_1{J}_1-D_A\left(S_1\right)A_1& =0,\hfill \\ \hfill B\left(S_2\right)A_2(1-{\displaystyle \frac{A_1+A_2}{K}})-S_2{J}_2-D_J\left(S_2\right)J_2& =0,\hfill \\ \hfill S_2{J}_2-D_A\left(S_2\right)A_2& =0,\hfill \end{array}$$

or

$$\begin{array}{cc}\hfill A_1^{*}+A_2^{*}& =K(1-1/R_{S_1}),\hfill \\ \hfill J_1^{*}& =D_A\left(S_1\right)A_1^{*}/S_1,\hfill \\ \hfill A_1^{*}+A_2^{*}& =K(1-1/R_{S_2}),\hfill \\ \hfill J_2^{*}& =D_A\left(S_2\right)A_2^{*}/S_2.\hfill \end{array}$$

(3)

Obviously, a positive solution of the above equations is possible only if the following condition

$$R_{S_1}=R_{S_2}>1$$

(4)

holds.

Notice that for any positive constant $c>0$, we have

$$A_1^{*}+A_2^{*}=K(1-1/R_{S_1})=\left(\frac{1}{1+c}+\frac{c}{1+c}\right)K(1-1/R_{S_1}).$$

Thus, set

$$A_1^{*}={\displaystyle \frac{K}{1+c}}(1-1/R_{S_1})>0,A_2^{*}={\displaystyle \frac{cK}{1+c}}(1-1/R_{S_2})>0$$

is the positive general solution of the following equation

$$A_1^{*}+A_2^{*}=K(1-1/R_{S_1})=K(1-1/R_{S_2}).$$

Then, it follows from (3), that System (1) has a cluster of positive equilibria

$$E_p=(J_1^{*},A_1^{*},J_2^{*},A_2^{*})=\left({\displaystyle \frac{D_A\left(S_1\right)A_1^{*}}{S_1}},{\displaystyle \frac{K(1-1/R_{S_1})}{1+c}},{\displaystyle \frac{D_A\left(S_2\right)A_2^{*}}{S_2}},{\displaystyle \frac{cK(1-1/R_{S_2})}{1+c}}\right)$$

(5)

where $c>0$ is an arbitrary constant, if condition (4) holds. The coexisting equilibrium can be biologically meaningful if the two strategies can achieve equal fitness greater than one at the same time.

Hence, we summarize the existence of the equilibria for System (1) as follows.

Theorem 1.

For System (1), when $R_{S_i}$, $(i=1,2)$ are as given by (2), we have some results in the following:

1. 

There is always a trivial equilibrium $E_0=(0,0,0,0)$ in any situation.

2. 

If $R_{S_1}>1$, there exists a single-strategy boundary equilibrium

$$E_1=(D_A\left(S_1\right)A_1^{*}/S_1,K(1-1/R_{S_1}),0,0).$$

3. 

If $R_{S_2}>1$, there exists a single-strategy boundary equilibrium

$$E_2=(0,0,D_A\left(S_2\right)A_2^{*}/S_2,K(1-1/R_{S_2})).$$

4. 

If the condition $R_{S_1}=R_{S_2}>1$ holds, there exists a cluster of positive equilibria

$$E_p=\left(J_1^{*},A_1^{*},J_2^{*},A_2^{*}\left)=\right({\displaystyle \frac{D_A\left(S_1\right)A_1^{*}}{S_1}},{\displaystyle \frac{K(1-1/R_{S_1})}{1+c}},{\displaystyle \frac{D_A\left(S_2\right)A_2^{*}}{S_2}},{\displaystyle \frac{cK(1-1/R_{S_2})}{1+c}}\right).$$

2.2. Linear Stability Analysis of the Four Equilibria

A linear stability analysis is made in order to determine the behavior of the solution of System (1) near the equilibrium. The Jacobian matrix at the equilibrium $E=(J_1,A_1,J_2,A_2)$ for System (1) is given by the general form

$${J|}_E=\left(\begin{array}{cccc}-(S_1+D_J\left(S_1\right))& B\left(S_1\right)(1-{\displaystyle \frac{2A_1+A_2}{K}})& 0& -B\left(S_1\right)A_1/K\\ S_1& -D_A\left(S_1\right)& 0& 0\\ 0& -B\left(S_2\right)A_2/K& -(S_2+D_J\left(S_2\right))& B\left(S_2\right)(1-{\displaystyle \frac{A_1+2A_2}{K}})\\ 0& 0& S_2& -D_A\left(S_2\right)\end{array}\right).$$

The eigenvalues of the Jacobian matrix at the trivial equilibrium $E_0=(0,0,0,0)$ are $(S_1+D_J\left(S_1\right))(R_{S_1}-1),-D_A\left(S_1\right),(S_2+D_J\left(S_2\right))(R_{S_2}-1),-D_A\left(S_2\right),$ where $R_{S_i},i=1,2$ are given by (2). Hence, if $R_{S_1}<1$ and $R_{S_2}<1$, $E_0$ is locally asymptotically stable; otherwise, $(0,0,0,0)$ is unstable if $R_{S_1}>1$ or $R_{S_2}>1$.

We apply the Routh–Hurwitz criteria [17,18,19] to determine the stability of the equilibrium. In order to analyze the stability of the equilibrium, it is useful to consider the characteristic equation for the eigenvalue $\lambda$. Herein, $P_{E_1}\left(\lambda \right),P_{E_2}\left(\lambda \right),P_{E_p}\left(\lambda \right)$ are denoted as the characteristic polynomials of the Jacobian matrix J at equilibria $E_1$, $E_2$, $E_p$, respectively.

The Jacobian matrix at $E_1=(J_1^{*},A_1^{*},0,0)$ has the form

$${J|}_{E_1}:=\left(\begin{array}{cccc}-(S_1+D_J\left(S_1\right))& B\left(S_1\right)(1-2{\displaystyle \frac{A_1^{*}}{K}})& 0& -B\left(S_1\right)A_1^{*}/K)\\ S_1& -D_A\left(S_1\right)& 0& 0\\ 0& 0& -(S_2+D_J\left(S_2\right))& B\left(S_2\right)(1-{\displaystyle \frac{A_1^{*}}{K}})\\ 0& 0& S_2& -D_A\left(S_2\right)\end{array}\right).$$

The characteristic polynomial equation $P_{E_1}\left(\lambda \right)=\det (J{|}_{E_1}-\lambda I)=0$ can be regrouped into the form of two factors $H_{S_1}\left(\lambda \right)H_{S_2}\left(\lambda \right)=0$, where

$$\begin{array}{cc}\hfill H_{S_1}\left(\lambda \right)& =(\lambda +S_1+D_J\left(S_1\right))(\lambda +D_A\left(S_1\right))-S_{1}B\left(S_1\right)(1-2{\displaystyle \frac{A_1^{*}}{K}})\hfill \\ \hfill & ={\lambda }^2+(S_1+D_J\left(S_1\right)+D_A\left(S_1\right))\lambda +S_{1}B\left(S_1\right)A_1^{*}/K,\hfill \end{array}$$

(6)

and

$$\begin{array}{cc}\hfill H_{S_2}\left(\lambda \right)& =(\lambda +S_2+D_J\left(S_2\right))(\lambda +D_A\left(S_2\right))-S_{2}B\left(S_2\right)(1-{\displaystyle \frac{A_1^{*}}{K}})\hfill \\ \hfill & ={\lambda }^2+(S_2+D_J\left(S_2\right)+D_A\left(S_2\right))\lambda +(S_2+D_J\left(S_2\right))D_A\left(S_2\right)(1-1/R_0),\hfill \end{array}$$

(7)

according to the equation

$$1-{\displaystyle \frac{A_1^{*}}{K}}={\displaystyle \frac{(S_1+D_J\left(S_1\right))D_A\left(S_1\right)}{S_{1}B\left(S_1\right)}}=1/R_{S_1}.$$

(8)

The second factor $H_{S_2}\left(\lambda \right)$ provides two negative eigenvalues or two eigenvalues with a negative real part when $R_0>1$. The first factor $H_{S_1}\left(\lambda \right)$ always provides two negative eigenvalues or two eigenvalues with a negative real part. Based on the polynomial equation ${\lambda }^2+a_1\lambda +a_2=0$ and according to the Routh–Hurwitz criteria, the sufficient and necessary conditions for the eigenvalue or the real part of the eigenvalue to be negative are $a_1>0$ and $a_2>0$. Therefore, if $R_0>1$, the coefficients are positive; that is, all the eigenvalues or the real part of the eigenvalues are negative. Thus, $E_1=(J_1^{*},A_1^{*},0,0)$ is locally asymptotically stable. However, if $R_0<1$, then one eigenvalue or the real part of the eigenvalue is positive; thus, $E_1=(J_1^{*},A_1^{*},0,0)$ is unstable. Analysis of the factors $H_{S_1}$ and $H_{S_2}$ reveals that the equilibrium $E_1$ cannot undergo a Hopf bifurcation because of the positive coefficients of the linear terms, thus preventing the eigenvalue from being purely imaginary.

To examine the stability of the equilibrium $E_2$, we obtain the eigenvalues from the characteristic polynomial equation $P_{E_2}\left(\lambda \right)=\det (J{|}_{E_2}-\lambda I)=0$, where the Jacobian matrix at $E_2=(0,0,J_2^{*},A_2^{*})$ has the form

$${J|}_{E_2}:=\left(\begin{array}{cccc}-(S_1+D_J\left(S_1\right))& B\left(S_1\right)(1-{\displaystyle \frac{A_2^{*}}{K}})& 0& 0\\ S_1& -D_A\left(S_1\right)& 0& 0\\ 0& -B\left(S_2\right)A_2^{*}/K& -(S_2+D_J\left(S_2\right))& B\left(S_2\right)(1-2{\displaystyle \frac{A_2^{*}}{K}})\\ 0& 0& S_2& -D_A\left(S_2\right)\end{array}\right).$$

This equation can be factorized and rewritten as $P_{E_2}\left(\lambda \right)=L_{S_1}\left(\lambda \right)L_{S_2}\left(\lambda \right)=0$, where

$$\begin{array}{cc}\hfill L_{S_1}\left(\lambda \right)& =(\lambda +S_1+D_J\left(S_1\right))(\lambda +D_A\left(S_1\right))-S_{1}B\left(S_1\right)(1-{\displaystyle \frac{A_2^{*}}{K}})\hfill \\ \hfill & ={\lambda }^2+(S_1+D_J\left(S_1\right)+D_A\left(S_1\right))\lambda +(S_1+D_J\left(S_1\right))D_A\left(S_1\right)(1-R_0),\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill L_{S_2}\left(\lambda \right)& =(\lambda +S_2+D_J\left(S_2\right))(\lambda +D_A\left(S_2\right))-S_{2}B\left(S_2\right)(1-2{\displaystyle \frac{A_2^{*}}{K}}))\hfill \\ \hfill & ={\lambda }^2+(S_2+D_J\left(S_2\right)+D_A\left(S_2\right))\lambda +S_{2}B\left(S_2\right)A_2^{*}/K,\hfill \end{array}$$

(10)

according the equation

$$1-{\displaystyle \frac{A_2^{*}}{K}}={\displaystyle \frac{(S_2+D_J\left(S_2\right))D_A\left(S_2\right)}{S_{2}B\left(S_2\right)}}=1/R_{S_2}.$$

(11)

Following the analysis scheme discussed earlier, we can obtain that the second factor $L_{S_2}$ always has two negative eigenvalues or two eigenvalues with a negative real part but the first factor $L_{S_1}$ has two negative eigenvalues or two eigenvalues with a negative real part if the condition $R_0<1$ holds. However, if $R_0>1$, the first factor $L_{S_1}$ has two eigenvalues, for which one is positive and the other is negative. Hence, the equilibrium $E_2$ is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$. Obviously, the two factors provide no possibility for a Hopf bifurcation due to the strictly positive linear coefficient in the quadratic polynomial.

In summary, we have the following results on the boundary equilibria.

Theorem 2.

Define the basic reproductive number $R_{S_i},i=1,2$, given by (2) under the maturation strategy $S_i$ for System (1); then,

1. 

If $R_{S_1}<1$ and $R_{S_2}<1$, $E_0=(0,0,0,0)$ is always locally asymptotically stable;

2. 

If $R_{S_1}>1,R_0>1$, the boundary equilibrium $E_1=(J_1^{*},A_1^{*},0,0)$ is locally asymptotically stable;

3. 

If $R_{S_2}>1,R_0<1$, the boundary equilibrium $E_2=(0,0,J_2^{*},A_2^{*})$ is locally asymptotically stable.

For the positive equilibrium $E_p$, the Jacobian matrix J at the equilibrium $E_p=(J_1^{*},A_1^{*},J_2^{*},A_2^{*})$ has the form

$${J|}_{E_p}:=\left(\begin{array}{cccc}-(S_1+D_J\left(S_1\right))& B\left(S_1\right)(1-{\displaystyle \frac{2A_1^{*}+A_2^{*}}{K}})& 0& -B\left(S_1\right)A_1^{*}/K\\ S_1& -D_A\left(S_1\right)& 0& 0\\ 0& -B\left(S_2\right)A_2^{*}/K& -(S_2+D_J\left(S_2\right))& B\left(S_2\right)(1-{\displaystyle \frac{A_1^{*}+2A_2^{*}}{K}})\\ 0& 0& S_2& -D_A\left(S_2\right)\end{array}\right).$$

Then, the characteristic equation at the equilibrium $E_p$ is

$$\begin{array}{c}\hfill P_{E_p}\left(\lambda \right)=L_p\left(S_1\right)L_p\left(S_2\right)-S_1{S}_{2}B\left(S_1\right)B\left(S_2\right)A_1^{*}{A}_2^{*}/K^2=0,\end{array}$$

(12)

where

$$\begin{array}{cc}\hfill L_p\left(S_1\right)& =(\lambda +S_1+D_J\left(S_1\right))(\lambda +D_A\left(S_1\right))-S_{1}B\left(S_1\right)(1-{\displaystyle \frac{2A_1^{*}+A_2^{*}}{K}})\hfill \\ \hfill & ={\lambda }^2+(S_1+D_J\left(S_1\right)+D_A\left(S_1\right))\lambda +S_{1}B\left(S_1\right)A_1^{*}/K,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill L_p\left(S_2\right)& =(\lambda +S_2+D_J\left(S_2\right))(\lambda +D_A\left(S_2\right))-S_{2}B\left(S_2\right)(1-{\displaystyle \frac{A_1^{*}+2A_2^{*}}{K}}))\hfill \\ \hfill & ={\lambda }^2+(S_2+D_J\left(S_2\right)+D_A\left(S_2\right))\lambda +S_{2}B\left(S_2\right)A_2^{*}/K,\hfill \end{array}$$

according to the equation

$$1-{\displaystyle \frac{A_1^{*}+A_2^{*}}{K}}={\displaystyle \frac{(S_1+D_J\left(S_1\right))D_A\left(S_1\right)}{S_{1}B\left(S_1\right)}}={\displaystyle \frac{(S_2+D_J\left(S_2\right))D_A\left(S_2\right)}{S_{2}B\left(S_2\right)}},$$

Equation (12) can be written as

$$\begin{array}{c}\hfill P_{E_p}\left(\lambda \right)=\lambda ({\lambda }^3+c_1{\lambda }^2+c_2\lambda +c_3)=0,\end{array}$$

(13)

where

$$\begin{array}{cc}\hfill c_1& =S_1+D_J\left(S_1\right)+D_A\left(S_1\right)+S_2+D_J\left(S_2\right)+D_A\left(S_2\right),\hfill \\ \hfill c_2& =(S_1+D_J\left(S_1\right)+D_A\left(S_1\right))(S_2+D_J\left(S_2\right)+D_A\left(S_2\right))+S_{1}B\left(S_1\right)A_1^{*}/K+S_{2}B\left(S_2\right)A_2^{*}/K,\hfill \\ \hfill c_3& =S_{1}B\left(S_1\right)A_1^{*}/K(S_2+D_J\left(S_2\right)+D_A\left(S_2\right))+S_{2}B\left(S_2\right)A_2^{*}/K(S_1+D_J\left(S_1\right)+D_A\left(S_1\right)).\hfill \end{array}$$

From Equation (13), we have ${\lambda }_1=0$. According to the Routh–Hurwitz criteria [17,18], the real parts of these eigenvalues ${\lambda }_i,i=2,3,4,$ are negative. Because of the existence of a zero eigenvalue, the stability of positive equilibria cannot be decided by the above linearized system. Therefore, to determine the stability of the positive equilibrium $E_p$, one should further calculate the corresponding center manifold and normal form [20].

2.3. The Global Stability of the Boundary Equilibria

For System (1), there are two boundary equilibria: $E_1$ and $E_2$. We have obtained the local stability of these two boundary equilibria. In this subsection, we analyze the global stability of the boundary equilibria using the Lyapunov method.

Now, we analyze the global stability of the boundary equilibrium $E_1=(J_1^{*},A_1^{*},0,0)$.

Let

$$V=J_2+{\displaystyle \frac{S_2+D_J\left(S_2\right)}{S_2}}{A}_2.$$

Obviously, $V>0$ for $J_2>0,A_2>0$ and $J_1\ge 0,A_1\ge 0$, and $V\equiv 0$ for $J_2=A_2=0$.

Differentiating V along (1) gives

$$\begin{array}{cc}\hfill \dot{V}& =B\left(S_2\right)A_2(1-{\displaystyle \frac{A_1+A_2}{K}})-S_2{J}_2-D_J\left(S_2\right)J_2+{\displaystyle \frac{S_2+D_J\left(S_2\right)}{S_2}}(S_2{J}_2-D_A\left(S_2\right)A_2)\hfill \\ \hfill & =B\left(S_2\right)A_2(1-{\displaystyle \frac{A_1+A_2}{K}})-{\displaystyle \frac{S_2+D_J\left(S_2\right)}{S_2}}{D}_A\left(S_2\right)A_2\hfill \\ \hfill & <B\left(S_2\right)A_2(1-{\displaystyle \frac{A_2}{K}})-{\displaystyle \frac{S_2+D_J\left(S_2\right)}{S_2}}{D}_A\left(S_2\right)A_2\hfill \\ \hfill & =B\left(S_2\right)A_2-{\displaystyle \frac{S_2+D_J\left(S_2\right)}{S_2}}{D}_A\left(S_2\right)A_2-B\left(S_2\right)A_2^2/K\hfill \\ \hfill & =B\left(S_2\right)A_2(1-{\displaystyle \frac{(S_2+D_J\left(S_2\right))D_A\left(S_2\right)}{S_{2}B\left(S_2\right)}})-B\left(S_2\right)A_2^2/K\hfill \\ \hfill & =B\left(S_2\right)A_2(1-1/R_{S_2})-B\left(S_2\right)A_2^2/K.\hfill \end{array}$$

(14)

It follows from (14) that $\dot{V}<0$ provided that $R_{S_2}<1$. Therefore, by the idea of a Lyapunov function, the solution starting from initial values $\left(J_1\left(0\right),A_1\left(0\right),J_2\left(0\right),A_2\left(0\right)\right)$ with $J_1\left(0\right)\ge 0$, $A_1\left(0\right)\ge 0,J_2\left(0\right)>0,A_2\left(0\right)>0$ finally approaches the point in the $J_1-A_1$ plane. Notice that when $J_2=A_2=0$, System (1) becomes a single-strategy model:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{J}_1}{dt}}& =B\left(S_1\right)A_1(1-{\displaystyle \frac{A_1}{K}})-S_1{J}_1-D_J\left(S_1\right)J_1=f,\hfill \\ \hfill {\displaystyle \frac{d{A}_1}{dt}}& =S_1{J}_1-D_A\left(S_1\right)A_1=g.\hfill \end{array}$$

(15)

The single-strategy model has a zero equilibrium $(0,0)$ and a unique positive equilibrium $(J_1^{*},A_1^{*})$. If $R_{S_1}>1$, then $(0,0)$ is unstable, and $(J_1^{*},A_1^{*})$ is locally asymptotically stable since $tr\left(J{|}_{(J_1^{*},A_1^{*})}\right)<0$ and $det\left(J{|}_{(J_1^{*},A_1^{*})}\right)={\displaystyle \frac{B\left(S_1\right)A_1}{K}}>0$. Further, let Dulac function D = 1; we have

$${\displaystyle \frac{\partial Df}{\partial J_1}}+{\displaystyle \frac{\partial Dg}{\partial A_1}}=-S_1-D_J\left(S_1\right)-D_A\left(S_1\right)<0.$$

According to the Bendixson–Dulac theorem, there exists no closed orbit. Thus, the unique positive equilibrium $(J_1^{*},A_1^{*})$ is globally asymptotically stable for two-dimensional subsystem (15). This, together with the conclusion that the solution of the four-dimensional system (1) starting from initial values $\left(J_1\left(0\right),A_1\left(0\right),J_2\left(0\right),A_2\left(0\right)\right)$ with $J_1\left(0\right)\ge 0$, $A_1\left(0\right)\ge 0$, $J_2\left(0\right)>0,A_2\left(0\right)>0$ finally approaches the point in the $J_1-A_1$ plane, implies that the boundary equilibrium $(J_1^{*},A_1^{*},0,0)$ is globally asymptotically stable for $R_{S_2}<1<R_{S_1}$.

Next, we analyze the global stability of the boundary equilibrium $E_2=(0,0,J_2,A_2)$. Let

$$V=J_1+{\displaystyle \frac{S_1+D_J\left(S_1\right)}{S_1}}{A}_1.$$

Similar to the above analysis, we also have $\dot{V}<0$ with the condition $R_{S_1}<1$. Hence, System (1) has a globally asymptotically stable boundary equilibrium $E_2$ if the condition $R_{S_1}<1<R_{S_2}$ holds.

In summary, we have the following results.

Theorem 3.

Define the basic reproductive number $R_{S_i},i=1,2$, given by (2) under the maturation strategy $S_i$ for System (1); then,

1. 

If $R_{S_1}>1>R_{S_2}$, the boundary equilibrium $E_1=(J_1^{*},A_1^{*},0,0)$ is globally asymptotically stable;

2. 

If $R_{S_2}>1>R_{S_1}$, the boundary equilibrium $E_2=(0,0,J_2^{*},A_2^{*})$ is globally asymptotically stable.

2.4. Numerical Results

In this section, we use numerical methods to verify our theoretical results. We show concrete functions $B\left(S_1\right)$, $B\left(S_2\right)$, $D_J\left(S_1\right)$, $D_J\left(S_2\right)$, $D_A\left(S_1\right)$, $D_A\left(S_2\right)$ as follows: $B\left(S_1\right)=c_1{e}^{-S_1}$, $B\left(S_2\right)=c_2{e}^{-S_2}$, $D_J\left(S_1\right)=D_A\left(S_1\right)=e^{S_1}$, $D_J\left(S_2\right)=D_A\left(S_2\right)=e^{S_2}$, where $S_1$ and $S_2$ are one-dimensional variables. The parameters are given in four imaginary cases:

(1) The extinction of the two strategies: Let $S_1=0.141$, $S_2=0.3799$, $c_1=0.6$, $c_2=0.5118$, $k=10$; hence, we have $R_{S_1}=0.0494<1$ and $R_{S_2}=0.0494<1$. The numerical result is shown in the upper left part of Figure 2.

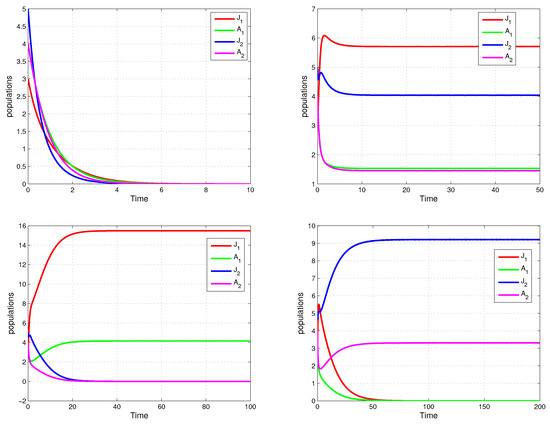
Figure 2. Time plots of population dynamics.

(2) The coexistence of the two strategies: Let $S_1=0.4$, $S_2=0.8$, $c_1=15$, $c_2=26.694$, $k=10$; hence, we have $R_{S_1}=1.425>1$ and $R_{S_2}=1.425>1$. The numerical result is shown in the upper right part of Figure 2.

(3) The strategy $S_1$ over $S_2$: Let $S_1=0.4$, $S_2=0.8$, $c_1=18$, $c_2=26.694$, $k=10$; hence, we have $R_{S_1}=1.7101>1$, $R_{S_2}=1.425>1$ and $R_0=R_{S_1}/R_{S_2}=1.2>1$. The numerical result is shown in the lower left part of Figure 2.

(4) The strategy $S_2$ over $S_1$: Let $S_1=0.4$, $S_2=0.8$, $c_1=14$, $c_2=28$, $k=10$; hence, we have $R_{S_1}=1.3301>1$, $R_{S_2}=1.4948>1$ and $R_0=R_{S_1}/R_{S_2}=0.8898<1$. The numerical result is shown in the lower right part of Figure 2.

3. The Adaptive Dynamical System

In this section, we analyze the evolution of maturation strategies for successful invasion of invasive populations. As mentioned in Section 2, the invasive population with an invasion strategy $S_2$ can invade the resident population with a resident strategy $S_1$ if and only if $R_0=R_{S_1}/R_{S_2}<1$ or $R_{S_2}>R_{S_1}$. Thus, the fitness function of the invasion strategy $S_2$ can be defined as

$$W(S_2,S_1)=S_{2}B\left(S_2\right)D_A\left(S_1\right)(S_1+D_J\left(S_1\right)-S_{1}B\left(S_1\right)D_A\left(S_2\right)(S_2+D_J\left(S_2\right)).$$

(16)

With the assumption of small mutation steps, the derivation of invasion fitness $W(S_2,S_1)$ with respect to invasion strategy $S_2$ can be obtained as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial W(S_2,S_1)}{\partial S_2}}{|}_{S_2=S_1}& =[B\left(S_1\right)+S_1{B}^{\prime }\left(S_1\right)]D_A\left(S_1\right)(S_1+D_J\left(S_1\right))-S_{1}B\left(S_1\right)[D_A^{\prime }\left(S_1\right)\hfill \\ \hfill & (S_1+D_J\left(S_1\right))+D_A\left(S_1\right)(1+D_J^{\prime }\left(S_1\right))].\hfill \end{array}$$

(17)

Furthermore, the second-order derivation of invasion fitness $W(S_2,S_1)$ with respect to invasion strategy $S_2$ can be obtained as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}W(S_2,S_1)}{\partial S_2^2}}& =[2B^{\prime }\left(S_1\right)+S_1{B}^{″}\left(S_1\right)]D_A\left(S_1\right)(S_1+D_J\left(S_1\right))-S_{1}B\left(S_1\right)[D_A^{″}\left(S_1\right)\hfill \\ \hfill & (S_1+D_J\left(S_1\right))+2D_A^{\prime }\left(S_1\right)(1+D_J^{\prime }\left(S_1\right))+D_A\left(S_1\right)D_J^{″}\left(S_1\right)].\hfill \end{array}$$

(18)

The assumption $H_1$: The existence condition for a single species that adopts maturation strategy $S_1$ is $R_{S_1}>1$. We assume that $R_{S_1}-1>0$ when $S_1\in ({\tau }_1,{\tau }_2)$, where ${\tau }_1$ and ${\tau }_2$ are two solutions of the equation $R_{S_1}-1=0$.

A singular strategy $S^{*}$ is a local ESS, meaning that no nearby strategy can invade [21]. Thus, in other words, once the strategy has been established in a population, no further evolutionary change is possible by small mutations. A strategy $S^{*}$ is a local ESS if and only if the following conditions hold:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial W(S_2,S_1)}{\partial S_2}}{|}_{S_2=S_1=S^{*}}& =& 0\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}W(S_2,S_1)}{\partial S_2^2}}{|}_{S_2=S_1=S^{*}}& <& 0.\hfill \end{array}$$

The above two conditions of (19) can easily be achieved since there exists a local strategy $S^{*}$, where $S^{*}\in ({\tau }_1,{\tau }_2)$, such that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{d{S}_1}}{R}_{S_1}{|}_{S_1=S^{*}}& =& 0.\hfill \\ \hfill {\displaystyle \frac{d^2}{d{S}_1^2}}{R}_{S_1}{|}_{S_1=S^{*}}& <& 0.\hfill \end{array}$$

Hence, there exists a local ESS $S^{*}$ located in the interval $({\tau }_1,{\tau }_2)$ if the assumption $H_1$ holds.

Next, we show the proof of the uniqueness of the ESS $S^{*}$. Along the line $l:S_1=S_2$, the directional derivative function $\partial W/\partial S_2$ at the point $(S_1,S_2)=(S^{*},S^{*})$ is provided as follows:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial {\displaystyle \frac{\partial W(S_2,S_1)}{\partial S_2}}}{\partial l}}{|}_{(S^{*},S^{*})}\hfill \\ \hfill & =\{[B\left(S_2\right)+S_2{B}^{\prime }\left(S_2\right)][D_A^{\prime }\left(S_1\right)(S_1+D_J\left(S_1\right))+D_A\left(S_1\right)(1+D_J^{\prime }\left(S_1\right))]\hfill \\ \hfill & -[B\left(S_1\right)+S_1{B}^{\prime }\left(S_1\right)][D_A^{\prime }\left(S_2\right)(S_2+D_J\left(S_2\right))+D_A\left(S_2\right)(1+D_J^{\prime }\left(S_2\right))]{\}cos\alpha |}_{(S^{*},S^{*})}\hfill \\ \hfill & +\{[2B^{\prime }\left(S_2\right)+S_2{B}^{″}\left(S_2\right)]D_A\left(S_1\right)(S_1+D_J\left(S_1\right))-S_{1}B\left(S_1\right)[D_A^{″}\left(S_2\right)(S_2+D_J\left(S_2\right))\hfill \\ \hfill & +2D_A^{\prime }\left(S_2\right)(1+D_J^{\prime }\left(S_2\right))+D_A\left(S_2\right)D_J^{″}\left(S_2\right){\left]\right\}sin\alpha |}_{(S^{*},S^{*})},\hfill \end{array}$$

where $\alpha$ is the direction angle of the line, and thus, $cos\alpha =sin\alpha =\sqrt{2}/2.$

It is easy to see that the difference between the two terms in the first curly bracket is 0; hence, the above equation is simplified as follows:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial {\displaystyle \frac{\partial W(S_2,S_1)}{\partial S_2}}}{\partial l}}{|}_{(S^{*},S^{*})}\hfill \\ \hfill & =\{[2B^{\prime }\left(S_2\right)+S_2{B}^{″}\left(S_2\right)]D_A\left(S_1\right)(S_1+D_J\left(S_1\right))-S_{1}B\left(S_1\right)[D_A^{″}\left(S_2\right)(S_2+D_J\left(S_2\right))\hfill \\ \hfill & +2D_A^{\prime }\left(S_2\right)(1+D_J^{\prime }\left(S_2\right))+D_A\left(S_2\right)D_J^{″}\left(S_2\right){\left]\right\}sin\alpha |}_{(S^{*},S^{*})}.\hfill \end{array}$$

Since in the assumptions for $H_1$, we mention that $R_{S_1}>1$ or $S_{1}B\left(S_1\right)-D_A\left(S_1\right)(S_1+D_J\left(S_1\right))>0$, thus

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial {\displaystyle \frac{\partial W(S_2,S_1)}{\partial S_2}}}{\partial l}}{|}_{(S^{*},S^{*})}\hfill \\ \hfill & =\{[2B^{\prime }\left(S_2\right)+S_2{B}^{″}\left(S_2\right)]D_A\left(S_1\right)(S_1+D_J\left(S_1\right))-S_{1}B\left(S_1\right)[D_A^{″}\left(S_2\right)(S_2+D_J\left(S_2\right))\hfill \\ \hfill & +2D_A^{\prime }\left(S_2\right)(1+D_J^{\prime }\left(S_2\right))+D_A\left(S_2\right)D_J^{″}\left(S_2\right){\left]\right\}sin\alpha |}_{(S^{*},S^{*})}\hfill \\ \hfill & <D_A\left(S^{*}\right)(S^{*}+D_J\left(S^{*}\right))\{[2B^{\prime }\left(S_2\right)+S_2{B}^{″}\left(S_2\right)]-[D_A^{″}\left(S_2\right)(S_2+D_J\left(S_2\right))\hfill \\ \hfill & +2D_A^{\prime }\left(S_2\right)(1+D_J^{\prime }\left(S_2\right))+D_A\left(S_2\right)D_J^{″}\left(S_2\right){\left]\right\}sin\alpha |}_{(S^{*},S^{*})}\hfill \\ \hfill & <0.\hfill \end{array}$$

Therefore, when $S_1=S_2=S^{*}$, the function $\partial W/\partial S_2=0$ has a unique strategy $S^{*}$.

In fact, the ESS $S^{*}$ is also convergence stable [22]. A singular strategy $S^{*}$ that is convergence stable is an evolutionary attractor, which means that a population that adopts a nearby strategy can be invaded by those strategies that are even closer to $S^{*}$.

According to the results of Geritz et al. [23], a sufficient condition ${\partial }^{2}W(S^{*},S^{*})/\partial S_1^2>{\partial }^{2}W(S^{*},S^{*})/\partial S_2^2$ is needed to make a strategy $S^{*}$ convergence stable.

Obviously, we have

$$\partial W(S^{*},S^{*})/\partial S_1=-\partial W(S^{*},S^{*})/\partial S_2$$

and

$${\partial }^{2}W(S^{*},S^{*})/\partial S_1^2=-{\partial }^{2}W(S^{*},S^{*})/\partial S_2^2.$$

Hence,

$${\displaystyle \frac{{\partial }^{2}W(S^{*},S^{*})}{\partial S_1^2}}-{\displaystyle \frac{{\partial }^{2}W(S^{*},S^{*})}{\partial S_2^2}}=-2{\displaystyle \frac{{\partial }^{2}W(S^{*},S^{*})}{\partial S_2^2}}>0.$$

(19)

A strategy is called continuously stable if it is both ESS and convergence stable [24]. As above, we have shown that there exists an ESS $S^{*}$, and it is also continuously stable under the assumption $H_1$.

In conclusion, we summarize these results in the following theorem.

Theorem 4.

If assumption $H_1$ holds, there exists a unique local ESS $S^{*}$ that belongs to the interval $({\tau }_1,{\tau }_2)$ and is both convergence stable and, thus, continuously stable.

4. Conclusions

Due to environmental changes such as climate, temperature, and, in particular, harvesting and so on, life-history strategies change accordingly. Maturation strategy plays a crucial role in life-history evolution since it affects the reproduction and survival of the population. Therefore, in order to analyze the effect of the maturation strategy on population dynamics, two different maturation strategies are considered in our research. Juveniles adopt either a fast maturation strategy or a delayed maturation strategy in response to the change to the environment. These two different maturation strategy may result in changes to the birth rate and the death rate of the population due to the tradeoffs. In this paper, we establish a two-strategy evolutionary model with a two-stage structure (juveniles and adults). From this model, we analyze the existence and stability of the coexistence equilibrium and single-strategy equilibrium for the same population with two different maturation strategies and summarize them as following:

(1) Extinction of two strategies: The fitness is represented by the basic reproductive number in this paper. The existence and extinction of the strategy only depend on its fitness. If the basic reproductive number is greater than 1 without competition, the population that adopts this strategy will persist; otherwise, this population will go to extinction. For example, in Figure 3, Region I means that both strategies would be extinct.

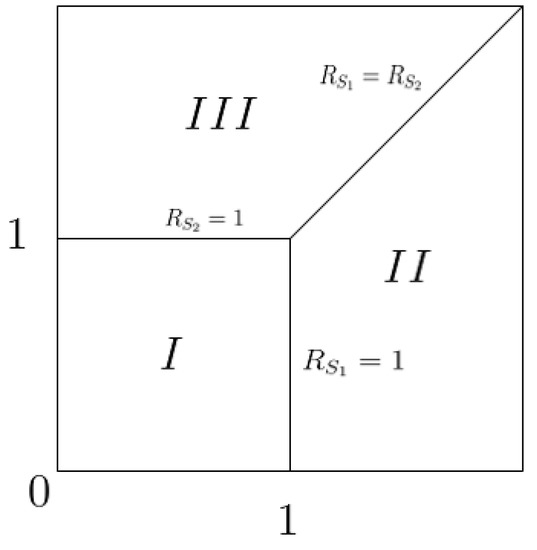
Figure 3. Partition area according to the stability conditions of the equilibrium. I Region: only $E_0$ exists and is globally asymptotically stable; II Region: only $E_1$ is locally asymptotically stable; III Region: only $E_2$ is locally asymptotically stable; The solid line between II Region and III Region: only $E_p$ exist, but the stability is unclear because of the existence of a zero eigenvalue.

(2) Competitive exclusion of the two strategies: If competition between two strategies occurs, one will be dominant and the other one will go to extinction, which means competitive exclusion of the two strategies. For example, in Figure 3, Region II describes the situation in which the population that adopts strategy $S_1$ wins the competition, and the population that adopts strategy $S_2$ is excluded. Similarly, Region III is the competition exclusion region where $S_2$ wins and $S_1$ vanishes.

(3) Two-strategy coexistence: In order to achieve the coexistence of populations with different strategies, the basic reproductive numbers $R_{S_1}$ and $R_{S_2}$ must be equal and be greater than 1. In a biological sense, if two different mature strategies achieve the same level of benefits for the same population, then both of the populations with the two strategies can coexist at the same time or both populations with the two strategies can become extinct. In other words, when two strategies have equal fitness with the basic condition of the fitness being greater than 1, coexistence occurs. For example, in Figure 3, the solid line between Region II and III is the coexistence of two strategies.

By adjusting the life-history parameters, for example, the maturation rate, the population can change competitive strength and maximize its fitness.

Seasonality plays a crucial role in the maturation strategy [8]. In future research, we will consider a seasonality factor to formulate a mathematical model of maturation strategies. More-realistic complex factors can also be included in the model.