Construction of Local-Shape-Controlled Quartic Generalized Said-Ball Model
Abstract
1. Introduction
- The QGS-Ball basis functions are proposed by introducing three shape parameters.
- The QGS-Ball curves and surfaces are proposed, and the impact of shape parameters on the curves and surfaces is discussed.
- The CQGS-Ball curves are defined based on the novel QGS-Ball curves, and the continuity conditions of G1 and G2 smooth joining of QGS-Bal curves are derived.
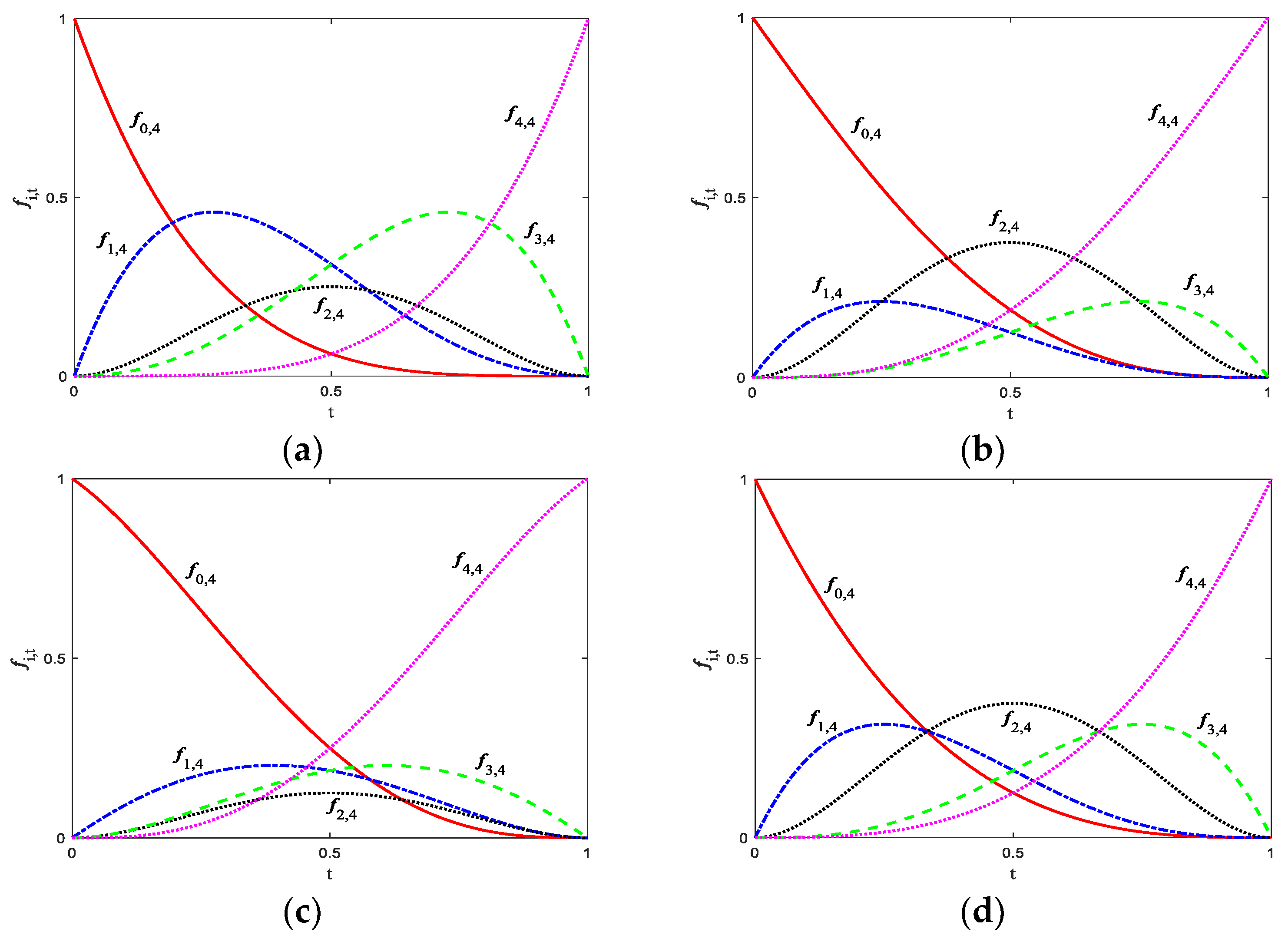
2. Quartic Generalized Said-Ball Basis Functions
2.1. Definition of QGS-Ball Basis Functions
2.2. Properties of QGS-Ball Basis Functions
- (1)
- Non-negativity: For , there are , where .
- (2)
- Normality: .
- (3)
- Symmetry under the particular case: When , the QGS-Ball basis functions are symmetric, that is, and .
- (4)
- Endpoint properties:
- (5)
- Unimodal property: The QGS-Ball basis functions have only one maximum value on .
- (6)
- Monotonicity of parameters: Consider as a constant, is a decreasing function about , is an increasing function about and a decreasing function about , is an increasing function about , is a decreasing function about and an increasing function about , and is a decreasing function about .
- (7)
- Degeneracy: The QGS-Ball basis functions reduce into the traditional quartic Said-Ball basis functions when . It reduces into the quartic Bernstein basis functions when . It reduces into the cubic Bernstein basis functions when .
- (1)
- Because of , and , there are
- (2)
- According to Equation (1), there are
- (3)
- When , Equation (1) can be written as
- (4)
- The endpoint properties can be obtained by simple calculation of .
- (5)
- The unimodality of QGS-Ball basis functions can be verified by derivation. and have unimodality according to the property (3), so it is only necessary to prove that and have unimodality.
- (6)
- If is regarded as a constant, is a decreasing function about , is an increasing function about and a decreasing function about , is an increasing function about , is a decreasing function about and an increasing function about , and is a decreasing function about , property (6) is proved.
- (7)
- When , then the QGS-Ball basis functions can be written aswhich are the traditional quartic Said-Ball basis functions.When , then the QGS-Ball basis functions can be written aswhich are the traditional quartic Bernstein basis functions.When , then the QGS-Ball basis functions can be written aswhich are the traditional cubic Bernstein basis functions. □
3. Quartic Generalized Said-Ball Curve
3.1. Definition and Properties of QGS-Ball Curve
- (1)
- Endpoint properties: For and , the QGS-Ball curve at the endpoints satisfyThe first and second derivatives of the curve at the endpoints satisfy
- (2)
- Symmetry under the particular case: When , the shape of the QGS-Ball curve with as the control polygon and the shape of the QGS-Ball curve with as the control polygon are the same, but the direction is opposite, i.e.,
- (3)
- Convexity: The QGS-Ball curve is involved in the convex hull of the control polygon.
- (4)
- Geometric invariability and affine invariability: Because the QGS-Ball basis functions satisfy the normalization, the affine transformation is performed on the QGS-Ball curve , the new curve is obtained by using the linear transformation and the translation , that is,It is the QGS-Ball curve corresponding to the new control points , which is obtained by the same affine transformation for .
- (5)
- Shape adjustability: The global and local shape of the QGS-Ball curve can be modified via the parameters.
- When five control points are given, only one unique quartic Bézier curve can be generated, while the QGS-Ball curve containing multiple shape parameters defines a family of curves.
- Because the QGS-Ball curve contains multiple shape parameters, the curves can be modified flexibly via the parameters while keeping the control points unchanged.
- Since the QGS-Ball curve contains shape parameters, shape optimization can be performed on the curves.
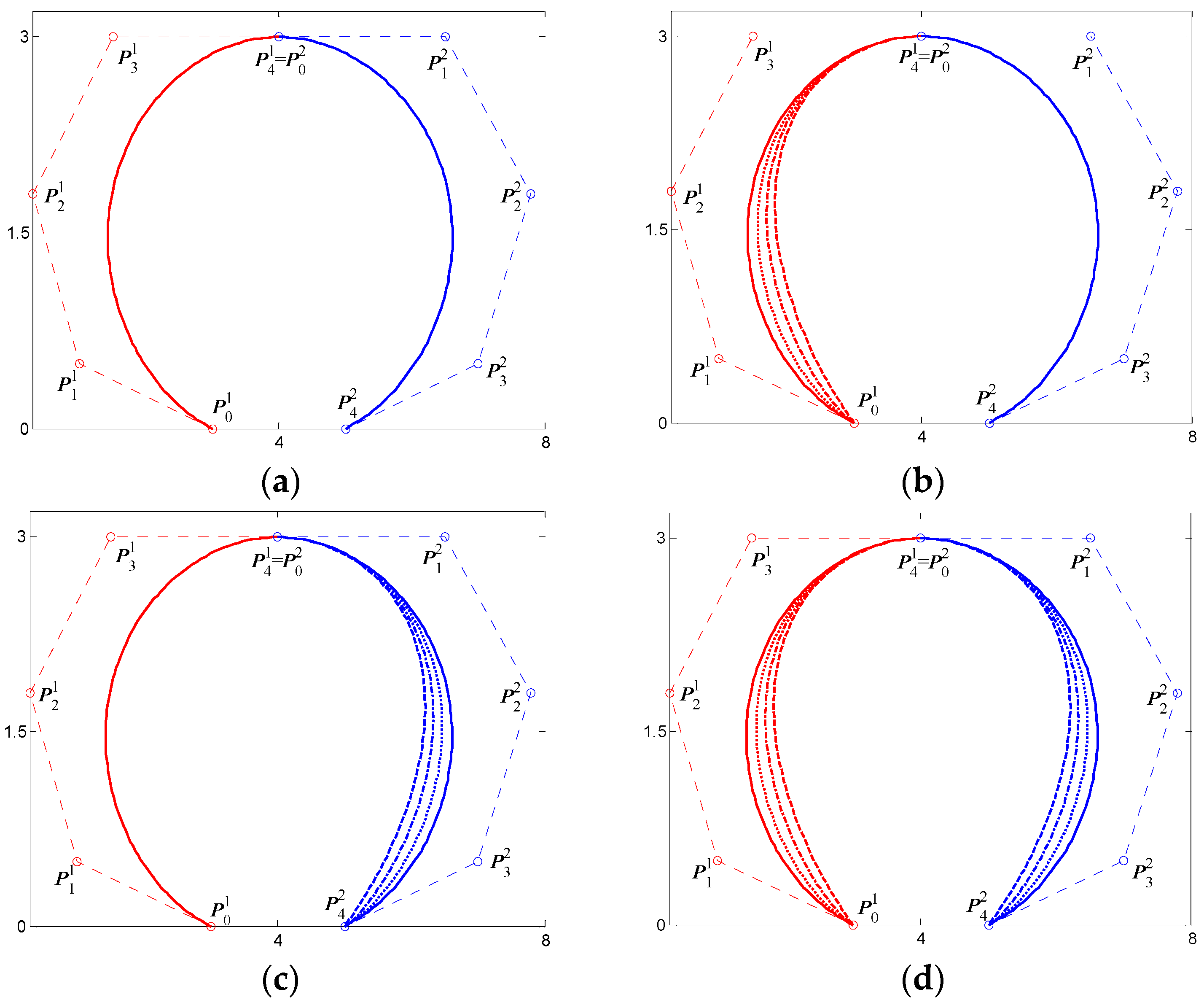
3.2. Impact of Shape Parameters on the QGS-Ball Curve
3.3. Performance Comparison of QGS-Ball Curves and Other Ball Curves
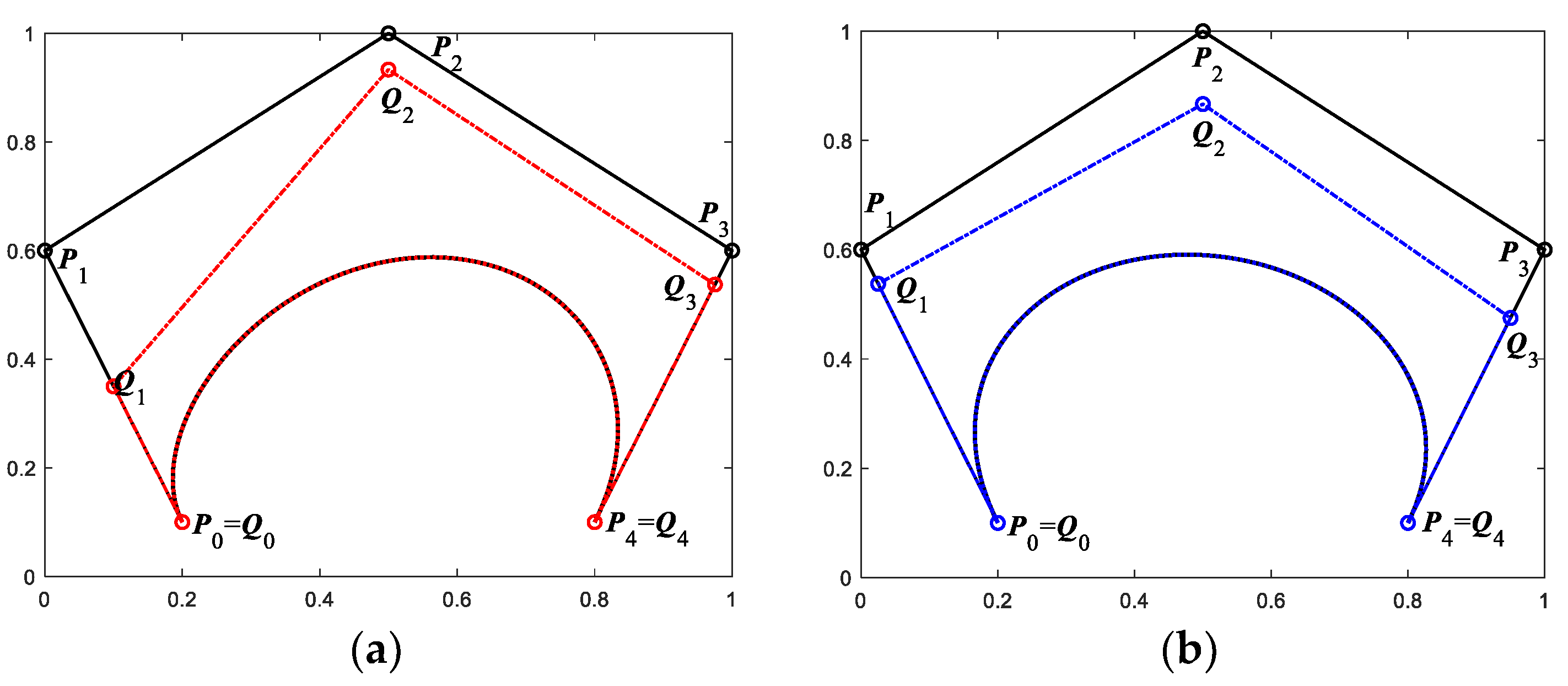
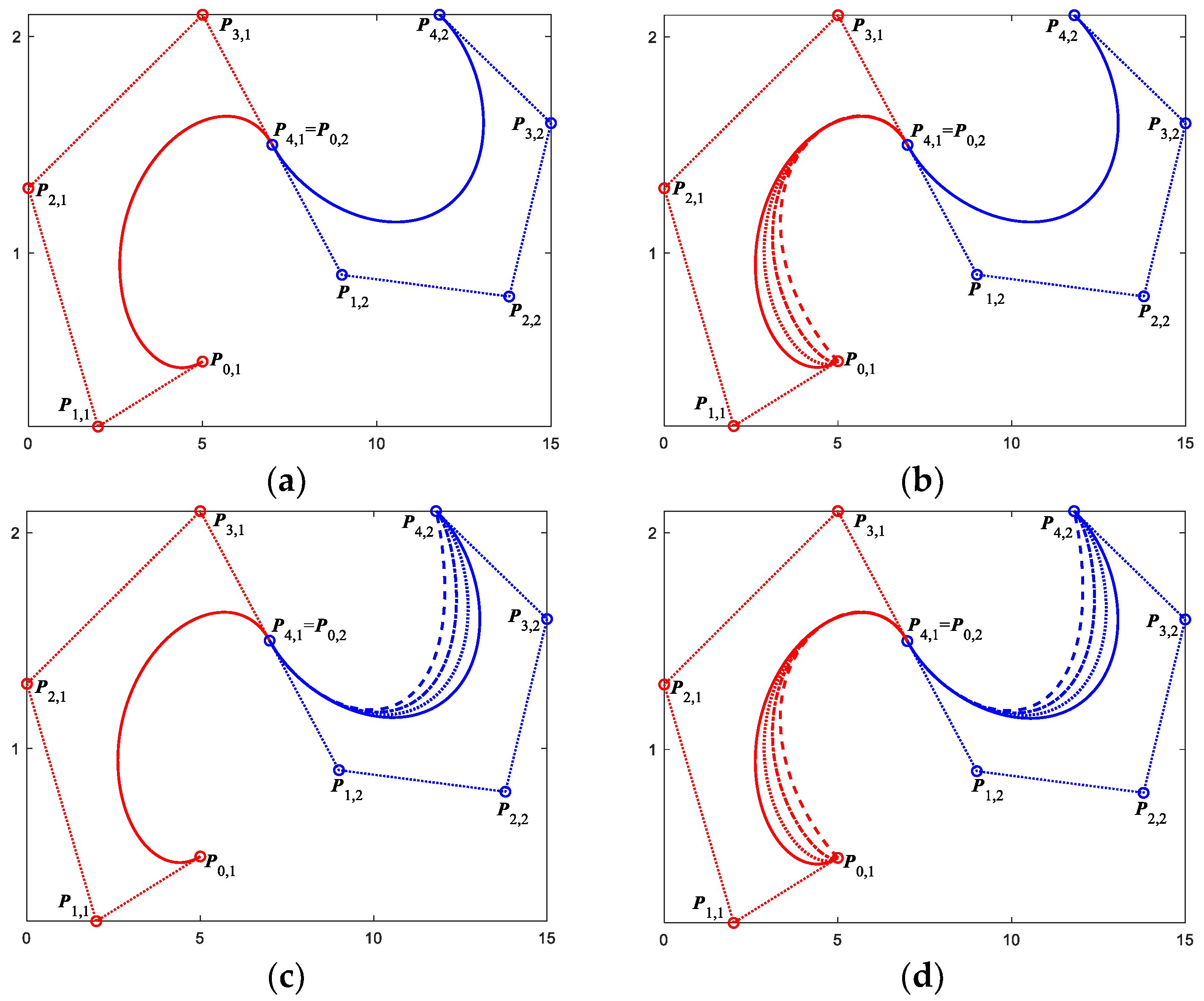
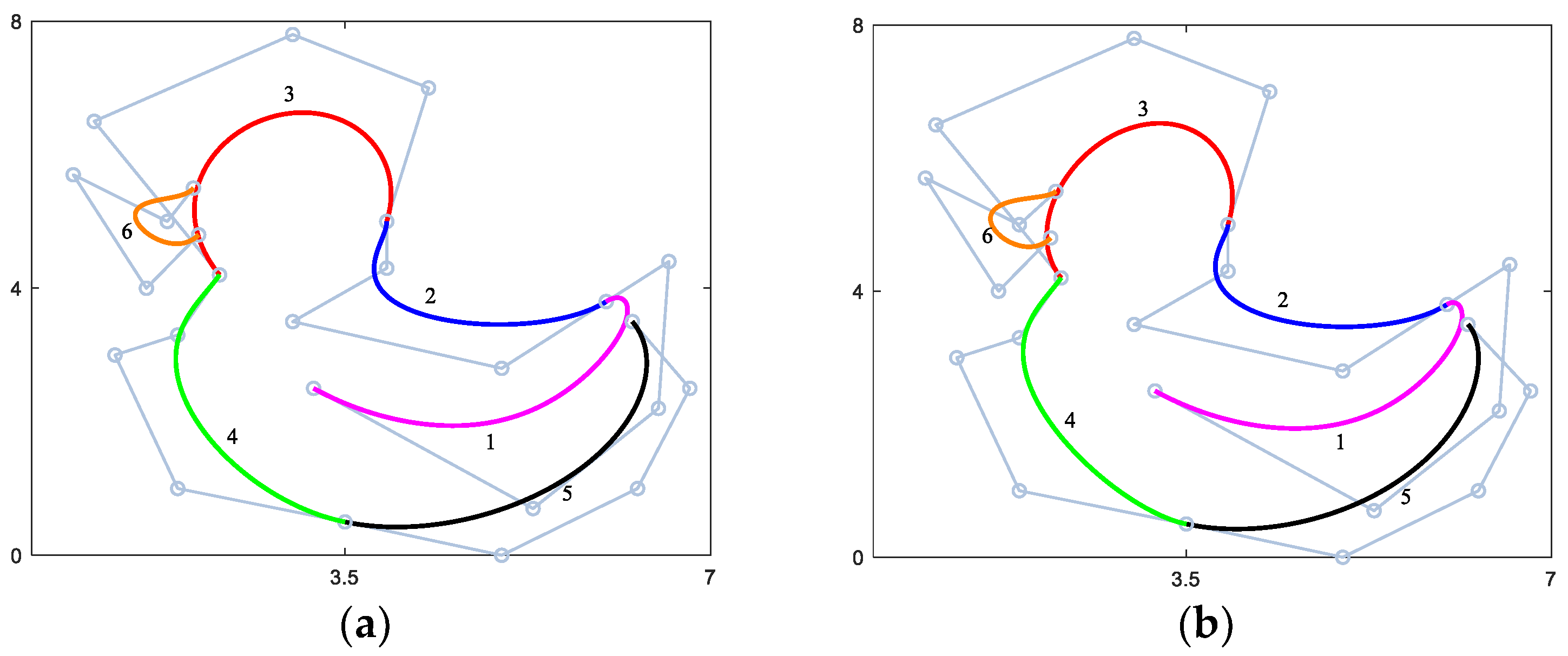
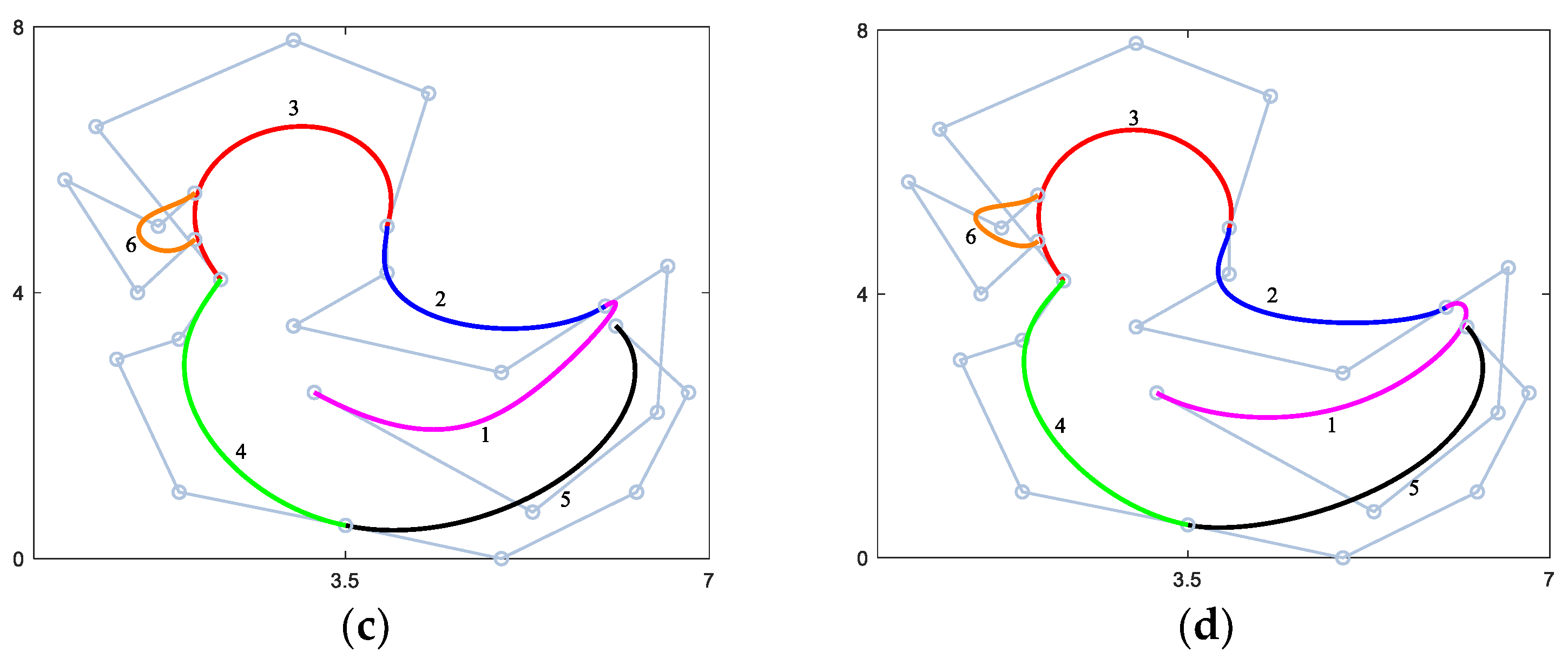
4. Smooth Joining of Combined Quartic Generalized Said-Ball Curves
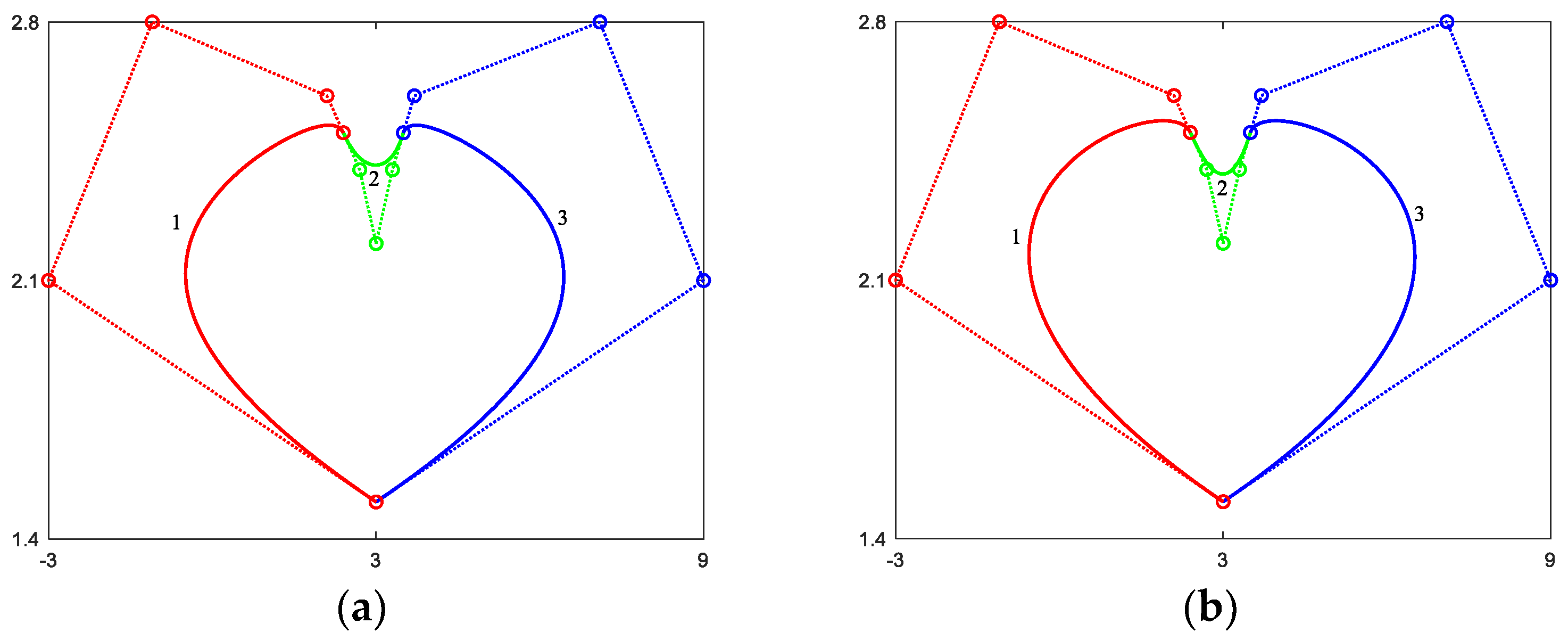
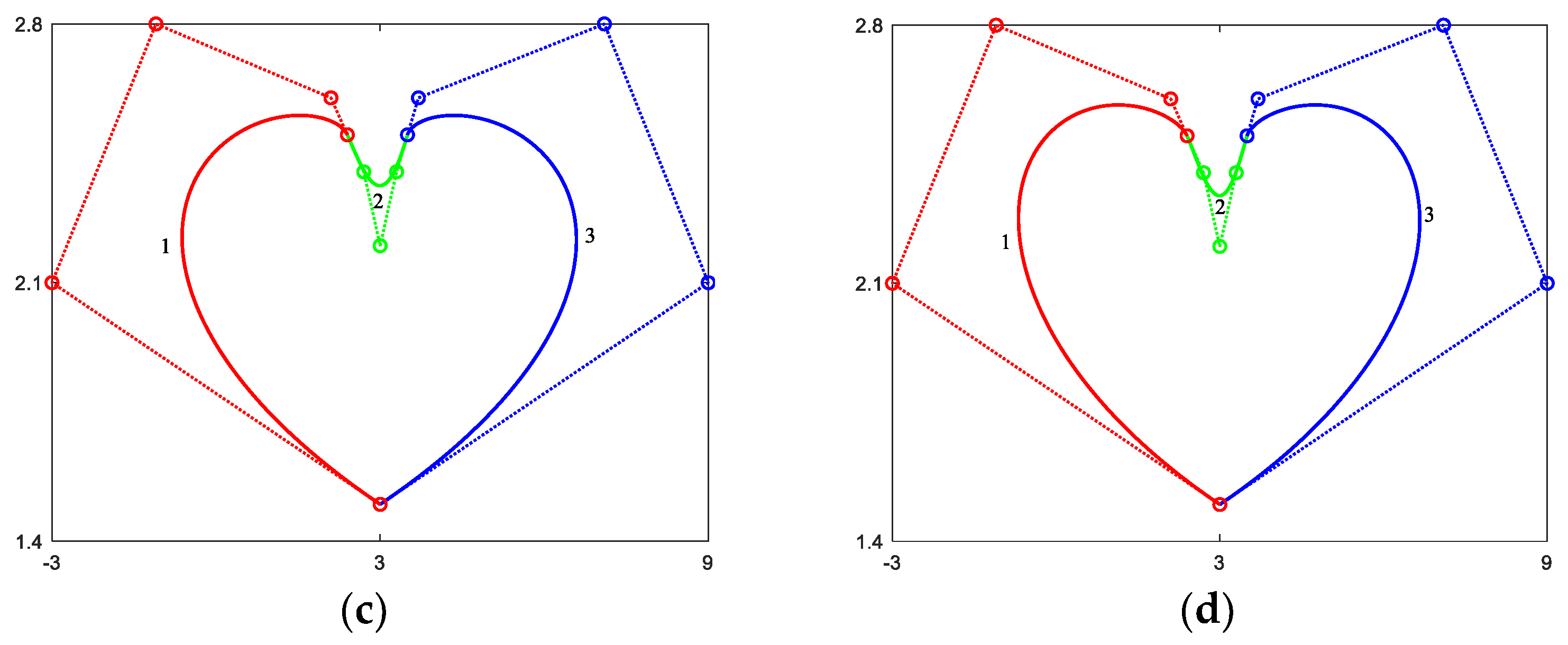
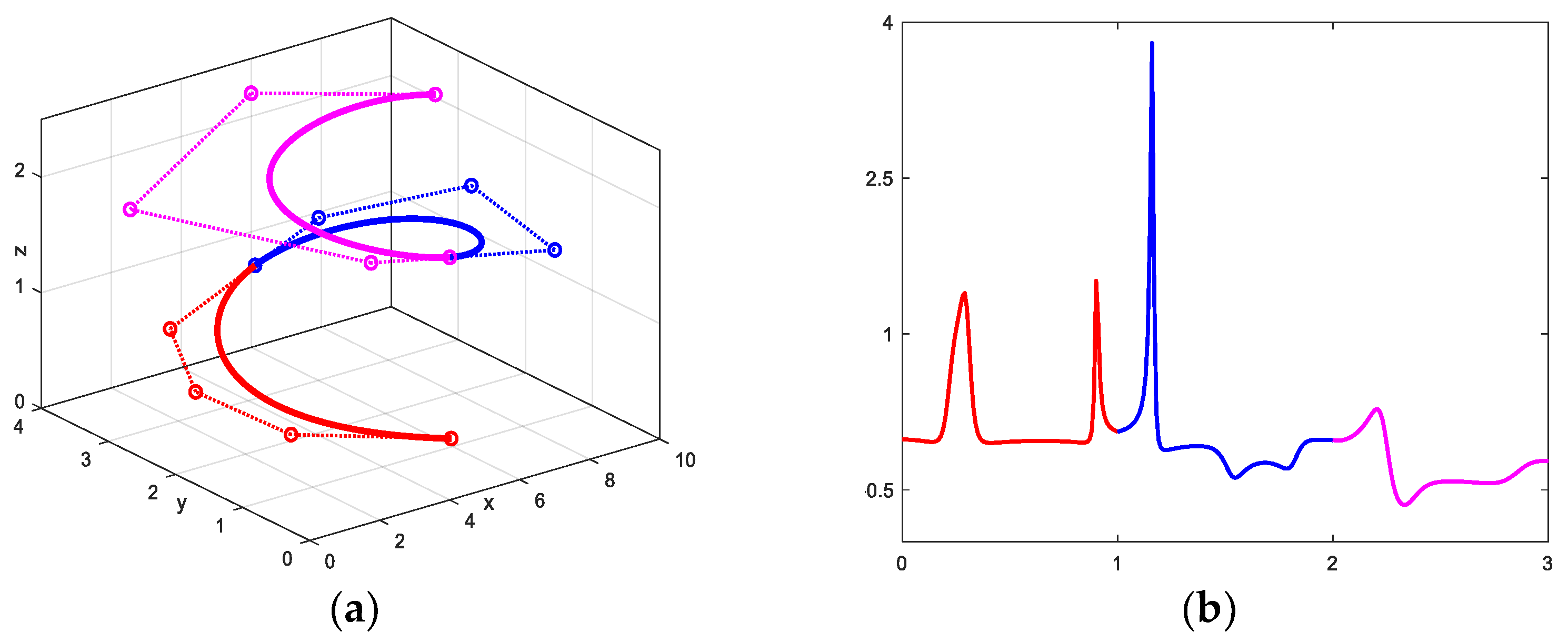
4.1. Continuity Conditions of G1 Smooth Joining of QGS-Ball Curves
4.2. Continuity Conditions of G2 Smooth Joining of QGS-Ball Curves
4.3. Examples of CQGS-Ball Curves
5. Quartic Generalized Said-Ball Surface
5.1. Definition and Properties of the QGS-Ball Surface
- (1)
- Corner interpolation: The four corners of the QGS-Ball surfaces are interpolated to the four corners of the surface’s control mesh, that are
- (2)
- Boundary property: For the QGS-Ball surfaces , four boundary curves are the QGS-Ball curves generated by their corresponding outermost control points, respectively, that are
- (3)
- Tangent planarity of corners: For the QGS-Ball surfaces , the tangent planes at the four corners are determined by , , , and , respectively.
- (4)
- Symmetry: If the given control mesh vertices are symmetric, the QGS-Ball surfaces are also symmetric.
- (5)
- Convexity: The QGS-Ball surface is located in the convex hull of its control mesh.
- (6)
- Geometric invariability and affine invariability: Given the shape parameters and , the QGS-Ball surfaces are only related to the control vertices .
- (7)
- Shape adjustability: Given the control vertices , the global and local shape of QGS-Ball surfaces can be modified via the parameters and .
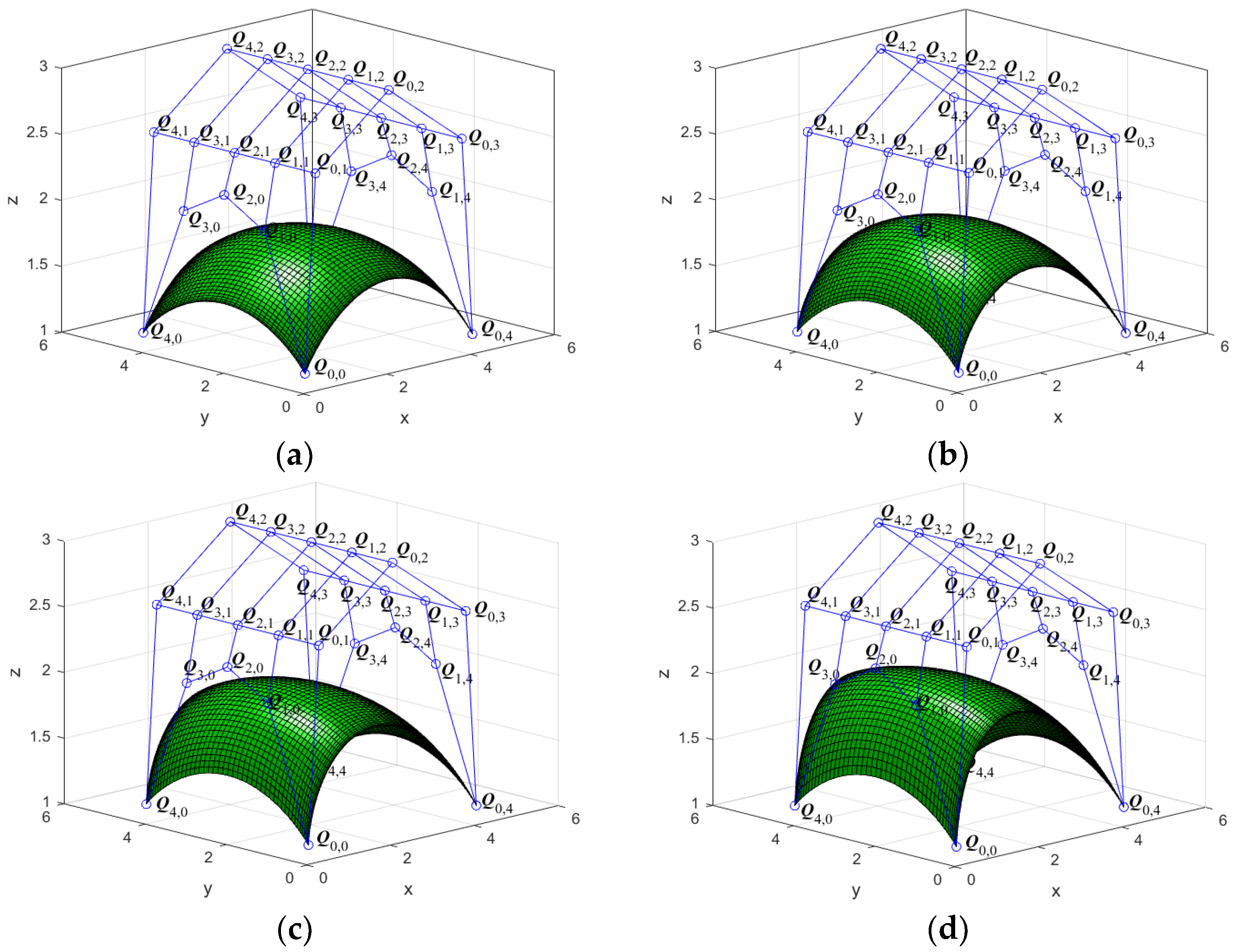
5.2. Impact of Shape Parameters on the QGS-Ball Surfaces
- (1)
- Given the control vertices and the shape parameters , the QGS-Ball surfaces move in the same direction as the control vertices by altering the shape parameters , that is, the shape parameters affect the local surface shape around the control vertices . In addition, the shape of borderline curves and is changed, while the shape of borderline curves and is not changed (see Figure 10).
- (2)
- Given the control vertices and the shape parameters , the QGS-Ball surfaces move in the same direction as the control vertices by altering the shape parameters , that is, the shape parameters affect the local surface shape around the control vertices . In addition, the shape of borderline curves and is changed, while the shape of borderline curves and is not changed (see Figure 11).
- (3)
- Given the control vertices , if the shape parameters and are increased (or decreased) at the same time, the QGS-Ball surfaces will approach (or move far from) its control mesh.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barnhill, R.E.; Riesenfeld, R.F. Computer Aided Geometric Design; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Ball, A.A. CONSURF, Part 1: Introduction to the conic lofting title. Comput. Aided Des. 1974, 6, 243–249. [Google Scholar] [CrossRef]
- Ball, A.A. CONSURF, Part 2: Description of the algorithms. Comput. Aided Des. 1975, 7, 237–242. [Google Scholar] [CrossRef]
- Ball, A.A. CONSURF, Part 3: How the program is used. Comput. Aided Des. 1977, 9, 9–12. [Google Scholar] [CrossRef]
- Wang, G.J. Ball curve of high degree and its geometric properties. Appl. Math. J. Chin. Univ. 1987, 2, 126–140. [Google Scholar]
- Said, H.B. A generalized Ball curve and its recursive algorithm. ACM Trans. Graph. 1989, 8, 360–371. [Google Scholar] [CrossRef]
- Hu, S.M.; Wang, G.Z.; Jin, T.G. Properties of two types of generalized Ball curves. Comput. Aided Des. 1996, 28, 125–133. [Google Scholar] [CrossRef]
- Othman, W.A.M.; Goldman, R.N. The dual basis functions for the generalized Ball basis of odd degree. Comput. Aided Geom. Des. 1997, 14, 571–582. [Google Scholar] [CrossRef]
- Hu, Q.; Wang, G. Rational cubic/quartic Said-Ball conics. Appl. Math. J. Chin. Univ. 2011, 26, 198–212. [Google Scholar] [CrossRef]
- Wu, H.Y. Two new classes of generalized Ball curves. Acta Math. Appl. Sin. 2000, 23, 196–205. [Google Scholar]
- Wu, H.Y. Dual bases for a new family of generalized Ball bases. J. Comput. Math. 2004, 22, 79–88. [Google Scholar]
- Wang, C.W. Extension of cubic Ball curve. J. Eng. Graph. 2008, 29, 1003–1058. [Google Scholar]
- Yan, L.L.; Wu, G.G.; Liang, J.F. Generalized Ball curves of ninth degree. In Proceedings of the 2009 International Conference on Environmental Science and Information Application Technology, Wuhan, China, 4–5 July 2009; Volume 1, pp. 557–560. [Google Scholar]
- Wu, X.Q.; Han, X.L. Shape analysis of quartic Ball curve with shape parameter. Acta Math. Appl. Sin. 2011, 34, 671–682. [Google Scholar]
- Xiong, J.; Guo, Q.W. Generalized Said-Ball curves. J. Numer. Methods Comput. Appl. 2012, 33, 58–67. [Google Scholar]
- Xiong, J.; Guo, Q.W. Generalized Wang-Ball curves. J. Numer. Methods Comput. Appl. 2013, 34, 187–195. [Google Scholar]
- Cao, H.X.; Zheng, H.C.; Hu, G. Adjusting the energy of Ball surfaces by modifying unfixed control balls. Numer. Algorithms 2022, 89, 749–768. [Google Scholar] [CrossRef]
- Liu, H.Y.; Li, L.; Zhang, D.M. Quartic Ball curve with multiple shape parameters. J. Shandong Univ. 2011, 41, 23–28. [Google Scholar]
- Huang, C.L.; Huang, Y.D. Quartic Wang-Ball type curves and surfaces with two parameters. J. Hefei Univ. Tech. 2012, 35, 1436–1440. [Google Scholar]
- Wang, C.W.; Chen, H. Extension of quartic Said-Ball curve with two parameters. In Mechanics and Mechanical Engineering: Proceedings of the 2015 International Conference (MME2015); World Scientific: Singapore, 2016; pp. 543–552. [Google Scholar]
- Hu, G.; Luo, L.; Li, R.; Yang, C. Quartic generalized Ball surfaces with shape parameters and its continuity conditions. In Proceedings of the International Conference on Computer Science and Network Technology, Dalian, China, 21–22 October 2017; pp. 5–10. [Google Scholar]
- Hu, G.; Du, B. Ball Said-Ball curve: Construction and its geometric algorithms. Adv. Eng. Softw. 2022, 174, 103334. [Google Scholar] [CrossRef]
- Hu, G.; Zhu, X.N.; Wei, G.; Chang, C. An improved marine predators algorithm for shape optimization of developable Ball surfaces. Eng. Appl. Artif. Intel. 2021, 105, 104417. [Google Scholar] [CrossRef]
- Hu, G.S.; Wang, D.; Yu, A.M.; Zhou, Q.T. 2m+2 order Ball curve construction and its applications with shape parameters. J. Eng. Graph. 2009, 30, 69–79. [Google Scholar]
- Hu, G.; Li, M.; Wang, X.F.; Wei, G.; Chang, C.T. An enhanced manta ray foraging optimization algorithm for shape optimization of complex CCG-Ball curves. Knowl.-Based Syst. 2022, 240, 108071. [Google Scholar] [CrossRef]
- Ghomanjani, F.; Noeiaghdam, S. Application of Said Ball Curve for Solving Fractional Differential-Algebraic Equations. Mathematics 2021, 9, 1926. [Google Scholar] [CrossRef]
- Debnath, P.; Srivastava, H.M.; Chakraborty, K.; Kumam, P. Advances in Number Theory and Applied Analysis; World Scientific: Singapore, 2023. [Google Scholar]
- Hu, G.; Yang, R.; Qin, X.Q.; Wei, G. MCSA: Multi-strategy boosted chameleon-inspired optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2023, 403, 115676. [Google Scholar] [CrossRef]
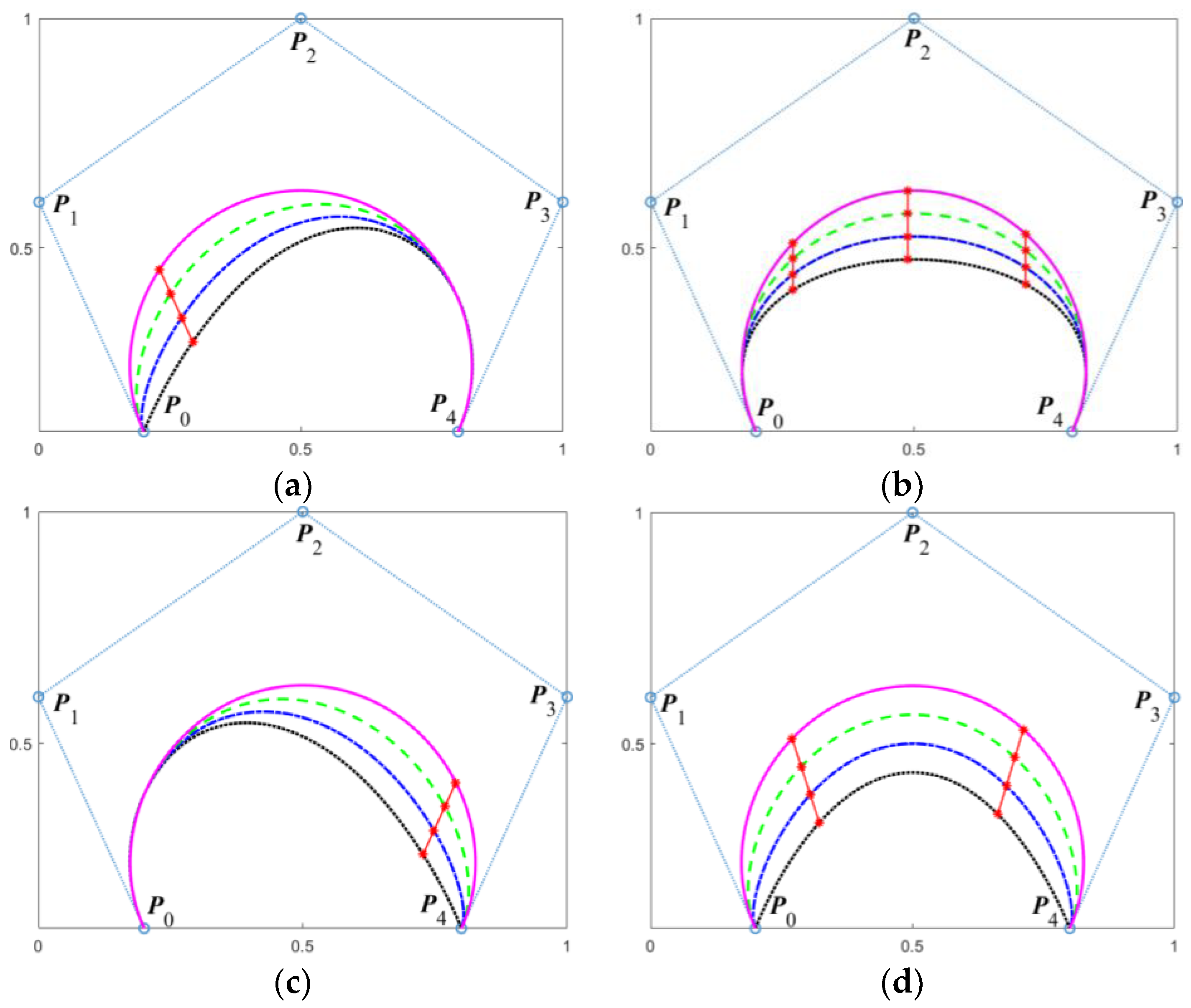


| Property | QGS-Ball Curves | Rational Cubic/Quartic Said-Ball Conics [9] | Generalized Ball Curves [10] | Said-Ball Curves [15] | Generalized Said-Ball Curves [20] | |
|---|---|---|---|---|---|---|
| Same | End-point properties | √ | √ | √ | √ | √ |
| Convex hull property | √ | √ | √ | √ | √ | |
| Symmetry | √ | √ | √ | √ | √ | |
| Affine invariability | √ | √ | √ | √ | √ | |
| Different | Computational complexity | Low | High | Low | Low | Low |
| Number of shape parameters | 3 | * | 0 | 2 | 2 | |
| Shape adjustability | Global and local | Global | × | Global | Global | |
| Extra degree of freedom | √ | √ | × | √ | √ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Ji, X.; Ma, Z.; Hu, G. Construction of Local-Shape-Controlled Quartic Generalized Said-Ball Model. Mathematics 2023, 11, 2369. https://doi.org/10.3390/math11102369
Zheng J, Ji X, Ma Z, Hu G. Construction of Local-Shape-Controlled Quartic Generalized Said-Ball Model. Mathematics. 2023; 11(10):2369. https://doi.org/10.3390/math11102369
Chicago/Turabian StyleZheng, Jiaoyue, Xiaomin Ji, Zhaozhao Ma, and Gang Hu. 2023. "Construction of Local-Shape-Controlled Quartic Generalized Said-Ball Model" Mathematics 11, no. 10: 2369. https://doi.org/10.3390/math11102369
APA StyleZheng, J., Ji, X., Ma, Z., & Hu, G. (2023). Construction of Local-Shape-Controlled Quartic Generalized Said-Ball Model. Mathematics, 11(10), 2369. https://doi.org/10.3390/math11102369






