Abstract
Hessenberg differential algebraic equations (Hessenberg-DAEs) with a high index play a critical role in the modeling of mechanical systems and multibody dynamics. Motivated by the widely used Lie-group differential algebraic equation (LGDAE) method, which handles index-2 systems, we first propose a modified extended Lie-group differential algebraic equation (MELGDAE) method for solving index-3 Hessenberg-DAEs and then provide a theoretical analysis to deepen the foundation of the MELGDAE method. Moreover, the performance of the MELGDAE method is compared with the standard methods RADAU and MEBDF on index-2 and -3 DAE systems, and it is demonstrated that the MELGDAE integrator exhibits a competitive performance in terms of high accuracy and the preservation of algebraic constraints. In particular, all differential variables in index-3 Hessenberg-DAEs achieve second-order convergence using the MELGDAE method, which suggests the potential for extension to Hessenberg-DAEs with an index of 4 or higher.
MSC:
65L80; 70G65
1. Introduction
Differential algebraic equations (DAEs) are a class of mathematical models that arise in various fields, such as multibody dynamics [1], electrical circuits [2], fluid mechanics [3], optimal control [4], and chemical reactions [5]. DAEs are a natural extension of ordinary differential equations that also involve algebraic equations. As such, they offer a convenient way to model complex systems that involve both dynamic and algebraic components. The study of DAEs has been an active area of research for many years, and numerous numerical methods have been developed to solve these DAEs, particularly for low-index systems. These methods include the well-known Runge–Kutta methods [6,7,8], backward differentiation formulas [9,10], and others. However, the efficient solution of DAEs remains a challenging problem due to the presence of algebraic equations that may be nonlinear, implicit, and of high index. In general, the index of DAEs refers to the number of differentiations required to convert them into the corresponding ordinary differential equations (ODEs), and the higher the index of a DAE, the more challenging it is to find numerical solutions.
Hessenberg differential algebraic equations (Hessenberg-DAEs) are an important type of differential equation that are also commonly used in the modeling of mechanical systems and electrical circuits. Because of their unique structure, the numerical methods for solving Hessenberg-DAEs can differ significantly from those used for other types of differential equations. Over the years, some approaches have been proposed for the numerical solution of Hessenberg-DAEs, including the variational iteration method [11], the Adomian decomposition method [12], and exponential integrators [13]. These methods either lack a rigorous theoretical analysis or are only suitable for low-index systems.
One promising approach is the Lie-group method, whose several variations have been developed specifically for solving (Hessenberg) DAEs with a high index in recent years. The Lie-group methods mostly constitute one-step extensions of classical methods, including Runge–Kutta type formulas [14]. In mechanical engineering, BDF methods, which have traditionally been used, have been extended to Lie groups as well [15]. Despite their usefulness, these methods suffer from a numerical disadvantage. Various numerical techniques can be used to compute the matrix exponential, but the properties of these methods, such as stability, accuracy, and efficiency, can impact the results of the Lie-group methods. Based on the structural information of Hessenberg-DAEs, C.S. Liu [16,17,18] proposed a Lie-group differential algebraic equation (LGDAE) method. By converting the canonical representation of the governing equations for nonholonomic systems, the LGDAE method expresses them in the form of DAE systems, comprising nonlinear ordinary differential equations and nonlinear algebraic equations. The method is composed of two components: The first component pertains to the Lie-group structure and concerns the numerical solution of nonlinear ordinary differential equations. The second component, the Newton iterative scheme, is used to solve the nonlinear algebraic equations. The LGDAE method has been successfully employed to solve various practical problems such as the heat source recovery problem [19,20], sliding mode control problem [21], and inverse nonlinear vibration problems [22]. However, it is noteworthy that the LGDAE method is only applicable to systems with index 2.
The main focus of this paper is to investigate Lie-group methods for Hessenberg-DAEs with an index of 3 or higher. We present a modified extended Lie-group method that incorporates the benefits of Liu’s original method, along with the structural characteristics of Hessenberg-DAEs. Our proposed method enables the accurate solution of high-index Hessenberg-DAEs and effectively captures the behavior of solutions to algebraic constraints. We demonstrate the effectiveness of our method through numerical experiments on some benchmark problems.
The structure of this paper is as follows. Section 2 presents a brief introduction to Hessenberg-DAEs and Lie-group methods. In Section 3, we present our novel modified extended Lie-group DAE method for Hessenberg-DAEs with an index of 3 and provide a theoretical justification for the proposed method. Section 4 presents the results of numerical experiments on several benchmark problems. Finally, we conclude with a discussion of our results and directions for future research in Section 5.
2. Preliminaries
In this section, we provide a concise overview of Hessenberg-DAEs and an implicit Lie-group method.
2.1. Hessenberg-DAEs
The general form of a system of ODEs with algebraic constraints which can be expressed as
is called a DAE, where may be singular, and the rank and structure of the Jacobian matrix can be dependent on the solution . A significant particular case of (1) is the semi-explicit DAE in the following form
whose index is 1 if the Jacobian matrix function is assumed to be nonsingular for all t. A semi-explicit index-1 system is also commonly known as Hessenberg Index-1.
Definition 1.
Hessenberg Index-2
where are sufficiently differentiable, the variable of the algebraic part is absent from the constraint and the product of Jacobians is nonsingular. Therefore, all algebraic variables act as index-2 variables, indicating that this system is a pure index-2 DAE.
Definition 2.
Hessenberg Index-3
In this case the product of three matrix functions is nonsingular, where , , and are , , and dimensions, respectively. To determine the index of a Hessenberg-DAE, the differentiation method is used, just as in the general case. However, in this case, only the algebraic constraints are differentiated.
Definition 3.
Hessenberg Index-r
In this case the product of three matrix functions is nonsingular.
2.2. Lie-Group Structure of ODEs
A Lie group is a differentiable manifold that possesses a group structure consistent with the manifold’s underlying topology. The general linear group is an example of a Lie group, where its manifold is an open subset denoted as . Therefore, is also an -dimensional manifold. The group composition is determined by matrix multiplication.
From the general linear group , a unique real Lie algebra is obtained. Let be a one-parameter subgroup of for . This subgroup is a curve that passes through the group identity at , i.e., . When the subgroup acts on the n-dimensional Euclidean space through left action, it results in a congruence of curves in , which can be expressed as:
Due to the closure property of the Lie group, also belongs to . When is sufficiently close to t, becomes very close to the identity . Furthermore, the derivative of with respect to t, denoted as , evaluated at , can be expressed as:
This expression (7) defines a sequence of tangent vectors in the tangent space at the group identity of the group manifold. Specifically, it represents a continuously parameterized series of one-dimensional sub-algebras within the real Lie algebra .
Solving system (8) generates the flow that corresponds to the vector field, which produces the congruence of curves. It is crucial to note that establishing a local coordinate on a smooth manifold that is acted upon by a finite-dimensional Lie group of transformations requires solving the system of differential equations.
The Lie-group method has an advantage over other numerical methods because of its Lie-group structure, making it a powerful technique for solving ODEs. In this context, we present a new formulation of the dynamics given by Equation (4a) or (4b) using the Lie-group structure. In order to fit the format in Equation (8), the vector field on the right-hand side of Equation (4a) or (4b) can be written as
where is the coefficient matrix and denotes the dyadic operation of a and b, i.e., . Here we suppose that .
2.3. An Implicit Lie-Group Method
The Equation (9) provides a new starting point for constructing the Lie-group approach. In order to develop a numerical scheme, we suppose that the coefficient matrix is constant with
which can be obtained by taking the values of and at a suitable mid-point of , where and h is a small timestep size.
By introducing the new variable , we obtain an augmented dynamical system
Because the state matrix in Equation (11) can be decomposed as
the solution of the linear dynamical system can be written analytically as follows
where , . We reduce the augmented system to the system, obtaining
and . Note that is indeed an element in the Lie group . Therefore, by introducing the auxiliary variable and the augmented system, we are able to derive an explicit expression for the components of a one-parameter group .
3. MELGDAE Method for Index-3 Hessenberg-DAEs
In this section, we present a novel modified extended Lie-group DAE (MELGDAE) method for Hessenberg-DAEs with an index of 3 and provide a theoretical justification for the proposed method.
We first calculate the solution with the given variables and , then obtain the solution via the given variables , , and . Moreover, we compute the solution by the resulting value of and . Hereafter, we denote the loop that solves for the variable as the -loop. The MELGDAE method, which is presented in detail below, utilizes the notation .
For the -loop:
- S1:
- Give , , .
- S2:
- Estimate via the Euler method as follows,
- S3:
- Let .
- S4:
- Compute :
- S5:
- If convergers according to a given stopping criterionthen let ; otherwise, let and go to S4.
For the -loop:
- S1:
- Give , , , resulting from the -loop.
- S2:
- Estimate via the Euler method as follows,
- S3:
- Let .
- S4:
- Compute :
- S5:
- If convergers according to a given stopping criterionthen let ; otherwise, let and go to S4.
For the -loop:
- S1:
- Let , .
- S2:
- Compute via the Newton iterative method:where , , , which is proven to be nonsingular in Theorem 1. We can obtain , from Equation (14).
- S3:
- If convergers according to a given stopping criterionthen let ; otherwise, letand go to S2.
To prove the nonsingularity of in the MELGDAE method, we first present the following lemmas.
Lemma 1.
([23]). Let be an matrix and be an matrix. Then
where λ is any scalar and denotes the identity matrix.
Lemma 2.
Let be an matrix, be an matrix, and and be non-zero vectors. Define the matrix for . If is nonsingular and , where , then UEV is nonsingular.
Proof.
To prove that is nonsingular, we need to show that its determinant () is nonzero.
To begin with, is nonsingluar, which implies . Further, it is noted that ; then .
For case , we obtain
and using Lemma 1, we have
where .
Since both and are nonzero, then is also nonzero. Therefore is nonsingular.
For case , using Lemma 1, we obtain
Moreover, ; then , which means that is nonsingular from Equation (28). □
Lemma 3.
Let be an matrix, be an matrix, and be an matrix. Let and be nonzero vectors, and let and be nonzero vectors. Define the matrices and , where . Suppose that is nonsingular and that h satisfies
where , , and . Then, the matrix is nonsingular.
Proof.
Firstly, is nonsingular, which implies and .
Let
that is, is nonsingular. Moreover, and , where . By Lemma 2, is nonsingular, which means is nonsingular.
Then, let
and is nonsingular. In addition, , if , where . By Lemma 2, is nonsingular, which means is nonsingular.
Now, we need proof that
It is noted that
where . Moreover, we are able to obtain and .
Then, we obtain
For , then we obtain the inequality (29). □
Theorem 1.
For the -loop of Hessenberg-DAEs with index 3, if h is sufficiently small, then the Jacobian matrix is nonsingular.
Proof.
Futhermore, we are able to obtain
where (), and ) is nonsingular.
From Lemma 1, it is noted that
For small , .
Moreover, by using Lemma 3, if
where , and , then is nonsingular. Therefore, satisfying for small h with
we are able to obtain that is nonsingular. □
4. Numerical Examples
In this section, we perform numerical simulation experiments to illustrate the performance of the MELGDAE. All code is written in a Windows 10 system and run on a personal computer with an Intel(R) Core(TM) i5-3570 CPU @ 3.40 GHz, 4.00 GB RAM, and a 64-bit operating system.
We consider a Hessenberg-DAE system with index 3 as follows, which can be found in [24].
Let , , and , , , then .
To obtain DAEs with index 2, we differentiate the constraint to obtain the following equation.
Then, we are able to obtain the index-2 DAEs below.
We compared the numerical results of the MELGDAE method with those of RADAU, a code based on implicit Runge–Kutta methods, and MEBDFI, a code based on the MEBDF method, which has better theoretical properties than BDF methods, to demonstrate the capability of the MELGDAE method. The comparison was made using the Hessenberg-DAEs with index 2 or 3 mentioned above.
Without loss of generality, we assume the absolute error (,,) is , the relative error is , the (initial) step size is , . Based on Figure 1 and Figure 2, the MELGDAE method showed comparable accuracy with the RADAU method for the differential variables and for both index-2 and index-3 Hessenberg-DAEs. In contrast, the MEBDFI method was less accurate for these variables. For the algebraic variable , both the RADAU and MEBDFI methods provided more accurate results than the MELGDAE method. However, for the algebraic constraints and , the MELGDAE method exhibited a significantly higher accuracy compared to the RADAU and MEBDFI methods.
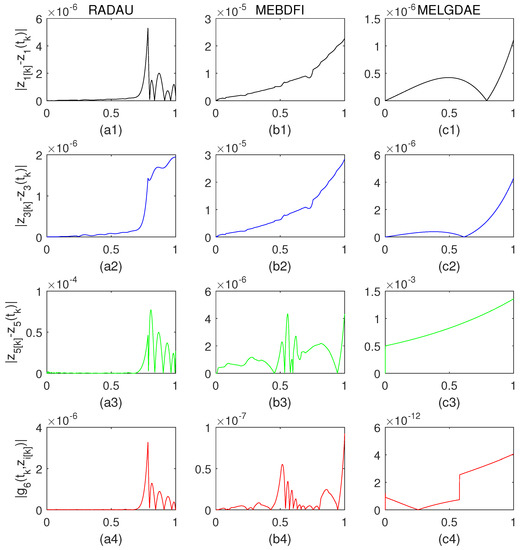
Figure 1.
The absolute errors of three methods for index-2 DAEs. (a1–a4) are the absolute errors of , , , and of RADAU, respectively; (b1–b4) are the absolute errors of MEBDFI; (c1–c4) are the absolute errors of MELGDAE.
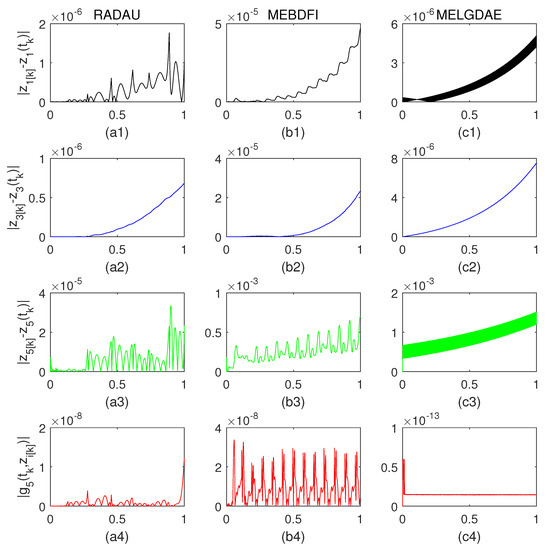
Figure 2.
The absolute errors of three methods for index-3 DAEs. (a1–a4) are the absolute errors of , , , and of RADAU, respectively; (b1–b4) are the absolute errors of MEBDFI; (c1–c4) are the absolute errors of MELGDAE.
Upon observing Figure 1 and Figure 2, it is clear that all three methods exhibit a reduction in the absolute errors of , , and as the index increases from 2 to 3. This reduction is not significant for the MELGDAE and RADAU methods. Therefore, we can conclude that the MELGDAE method has the potential to be extended to computing DAE systems with an index higher than 3.
Furthermore, we conducted numerical experiments to verify the convergence accuracy of the MELGDAE method for index-3 DAEs. We assumed and calculated their constants in () and , which represents and , using the standard least-squares method. The results are presented in Figure 3, which indicate that the MELGDAE method exhibits second-order convergence for , , , and (all differential variables) and (the algebraic constraints) and first-order convergence for (algebraic variable). Thus, this method may be extended to compute systems with an index of 4 or higher and is suitable for DAE systems that cannot be directly solved using other classical methods.
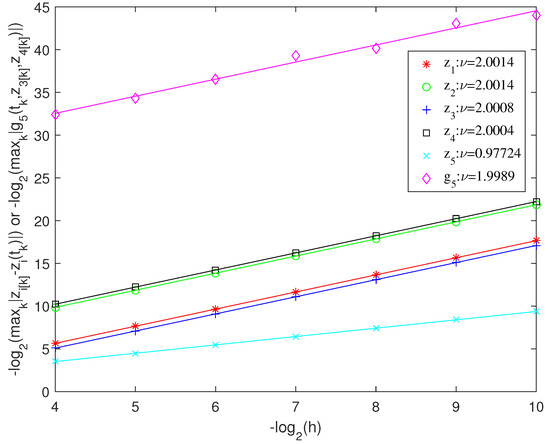
Figure 3.
The convergence order of MELGDAE for index-3 DAEs.
5. Conclusions
The modified extended Lie-group differential algebraic equation (MELGDAE) method was developed in this paper to solve Hessenberg-DAEs with index 3. While the LGDAE method presented in [18] is only capable of handling index-2 systems, the MELGDAE method can solve higher-index systems by taking into account the differential equation components with respect to the index in Hessenberg form. It is worth mentioning that the MELGDAE method demonstrates superior theoretical properties compared to the LGDAEs, as illustrated in Theorem 1.
We conducted a comparison of the MELGDAE method with the standard methods RADAU and MEBDFI on index-2 and -3 DAE systems. The MELGDAE method demonstrated promising results in terms of solution errors when compared to RADAU and MEBDFI, which are known to be powerful on different DAE systems. However, the MELGDAE method excelled in preserving the algebraic constraints. Moreover, all differential variables in index-3 Hessenberg-DAEs exhibited order-2 convergence with the MELGDAE method, whereas MEBDFI in [10] and RADAU in [7,25] demonstrated order reduction. Although the MELGDAE method has a high stability and accuracy when solving strong nonlinear Hessenberg-DAEs with index 3, there are still some theoretical gaps that need to be addressed in the future. Additionally, the MELGDAE method can be further extended to solve DAEs with an index of 4 or higher, which cannot be directly solved using standard methods.
Author Contributions
J.T. contributed to supervision, methodology, validation, funding acquisition, and project administration. J.L. contributed to investigation, computations, funding acquisition, and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the NSF of China (No: 12201144), the Science and Technology Program of Guangzhou (No: 202002030138), the GuangDong Basic and Applied Basic Research Foundation (No: 2020A1515110554), the Science and Technology Foundation of Guizhou Province (No: QKHJC-ZK[2021]YB015), and the University–Industry Collaborative Education Program of the Ministry of Education (No: 220606429152043), China.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank the referee for his or her very helpful comments and useful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schiehlen, W. Multibody system dynamics: Roots and perspectives. Multibody Syst. Dyn. 1997, 1, 149–188. [Google Scholar] [CrossRef]
- Winkler, R. Stochastic differential algebraic equations of index 1 and applications in circuit simulation. J. Comput. Appl. Math. 2003, 157, 477–505. [Google Scholar] [CrossRef]
- Coffey, T.S.; Kelley, C.T.; Keyes, D.E. Pseudotransient continuation and differential-algebraic equations. SIAM J. Sci. Comput. 2003, 25, 553–569. [Google Scholar] [CrossRef]
- Peng, H.J.; Li, F.; Liu, J.G.; Ju, Z.J. A symplectic instantaneous optimal control for robot trajectory tracking with differential-algebraic equation models. IEEE Trans. Ind. Electron. 2019, 67, 3819–3829. [Google Scholar] [CrossRef]
- Çelik, E.; Karaduman, E.; Bayram, M. Numerical solutions of chemical differential-algebraic equations. Appl. Math. Comput. 2003, 139, 259–264. [Google Scholar] [CrossRef]
- Ascher, U.M.; Petzold, L.R. Projected implicit Runge–Kutta methods for differential-algebraic equations. SIAM J. Numer. Anal. 1991, 28, 1097–1120. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Stiff differential equations solved by radau methods. J. Comput. Appl. Math. 1999, 111, 93–111. [Google Scholar] [CrossRef]
- Skvortsov, L.M. Diagonally implicit Runge—Kutta methods for differential algebraic equations of indices two and three. Comput. Math. Math. Phys. 2010, 50, 993–1005. [Google Scholar] [CrossRef]
- Cash, J.; Considine, S. An mebdf code for stiff initial value problems. ACM Trans. Math. Softw. 1992, 18, 142–158. [Google Scholar] [CrossRef]
- Cash, J.R. Modified extended backward differentiation formulae for the numerical solution of stiff initial value problems in ODEs and DAEs. J. Comput. Appl. Math. 2000, 125, 117–130. [Google Scholar] [CrossRef]
- Karta, M.; Celik, E. On the numerical solution of differential-algebraic equations with Hessenberg Index-3. Discret. Dyn. Nat. Soc. 2012, 2012, 12. [Google Scholar] [CrossRef]
- Benhammouda, B. A novel technique to solve nonlinear higher-index Hessenberg differential-algebraic equations by Adomian decomposition method. SpringerPlus 2016, 5, 590. [Google Scholar] [CrossRef] [PubMed]
- Celledoni, E.; Kometa, B.K. Semi-Lagrangian multistep exponential integrators for index 2 differential–algebraic systems. J. Comput. Phys. 2011, 230, 3413–3429. [Google Scholar] [CrossRef]
- Iserles, A.; Zanna, A. Preserving algebraic invariants with Runge–Kutta methods. J. Comput. Appl. Math. 2000, 125, 69–81. [Google Scholar] [CrossRef]
- Wieloch, V.; Arnold, M. BDF integrators for constrained mechanical systems on Lie groups. J. Comput. Appl. Math. 2021, 387, 112517. [Google Scholar] [CrossRef]
- Liu, C.S. Preserving constraints of differential equations by numerical methods based on integrating factors. Comput. Model. Eng. Sci. 2006, 12, 83–107. [Google Scholar]
- Liu, C.S. Finding unknown heat source in a nonlinear Cauchy problem by the Lie-group differential algebraic equations method. Eng. Anal. Bound. Elem. 2015, 50, 148–156. [Google Scholar] [CrossRef]
- Liu, C.S.; Chen, L.; Liu, L.W. Solving mechanical systems with nonholonomic constraints by a Lie-group differential algebraic equations method. J. Eng. Mech. 2017, 143, 04017097. [Google Scholar] [CrossRef]
- Liu, C.S. Lie-group differential algebraic equations method to recover heat source in a Cauchy problem with analytic continuation data. Int. J. Heat Mass Transf. 2014, 78, 538–547. [Google Scholar] [CrossRef]
- Liu, C.S.; Kuo, C.L.; Chang, J.R. Recovering a heat source and initial value by a Lie-group differential algebraic equations method. Numer. Heat Transf. Part B Fundam. 2015, 67, 231–254. [Google Scholar] [CrossRef]
- Liu, C.S. A new sliding control strategy for nonlinear system solved by the Lie-group differential algebraic equation method. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2012–2038. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, C.W. A real-time Lie-group differential algebraic equations method to solve the inverse nonlinear vibration problems. Inverse Probl. Sci. Eng. 2016, 24, 1569–1586. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012; pp. 66–67. [Google Scholar]
- Jay, L. Convergence of Runge-Kutta methods for differential-algebraic systems of index 3. Appl. Numer. Math. 1995, 17, 97–118. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Roche, M. The Numerical Solution of Differential-Algebraic Systems by Runge-Kutta Methods; Springer: Berlin/Heidelberg, Germany, 1989; pp. 19–20. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).