Coexisting Attractors in a Heterogeneous Agent Model in Discrete Time
Abstract
1. Introduction
2. The Model
- 1.
- Fundamentalists:
- 2.
- Absolute momentum investors:
- 3.
- Cross-sectional momentum investors:
- The left-hand side of the ODE is discretized in the following way:where h is the step size and
- has the following formwith real constant.
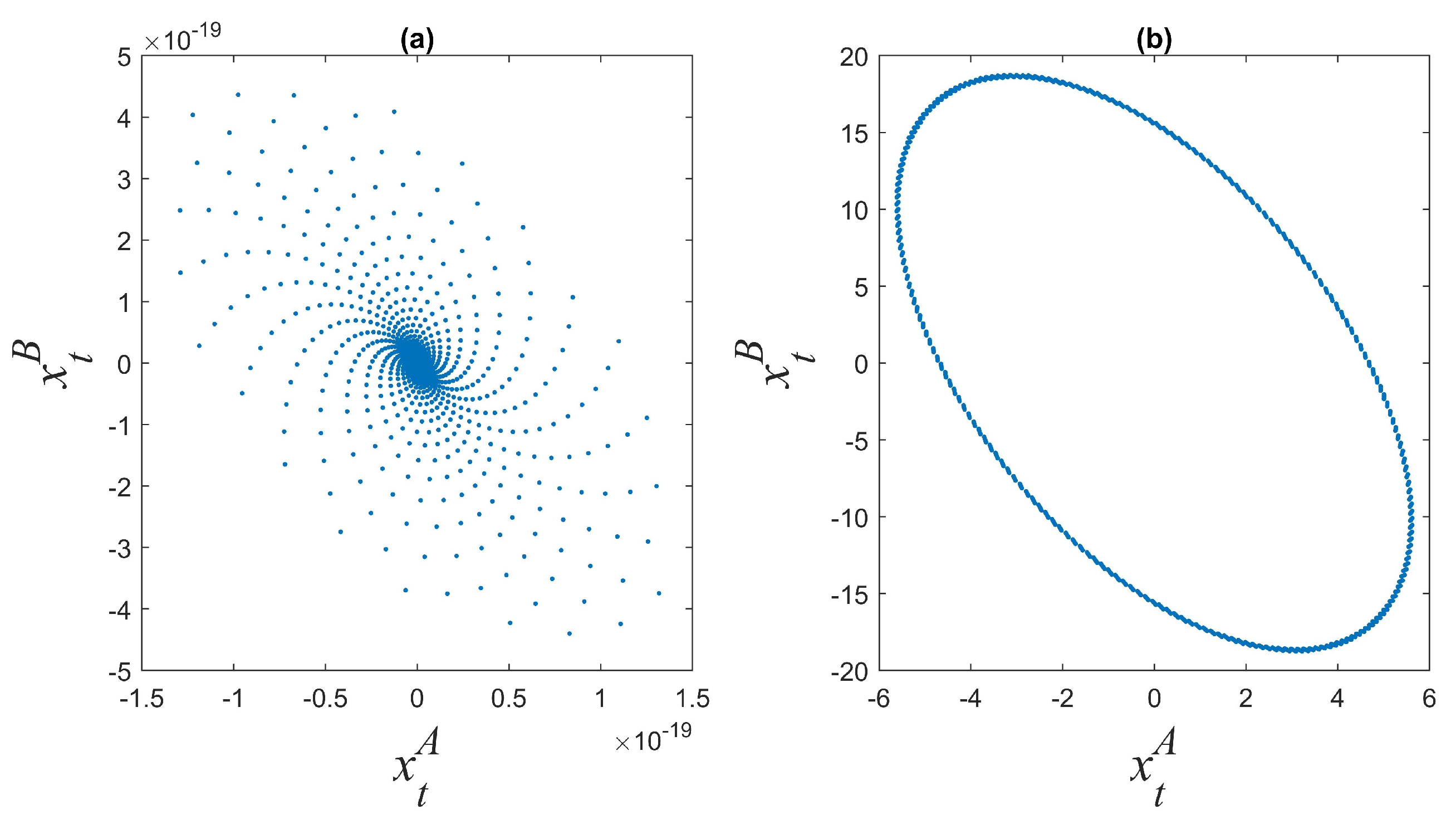
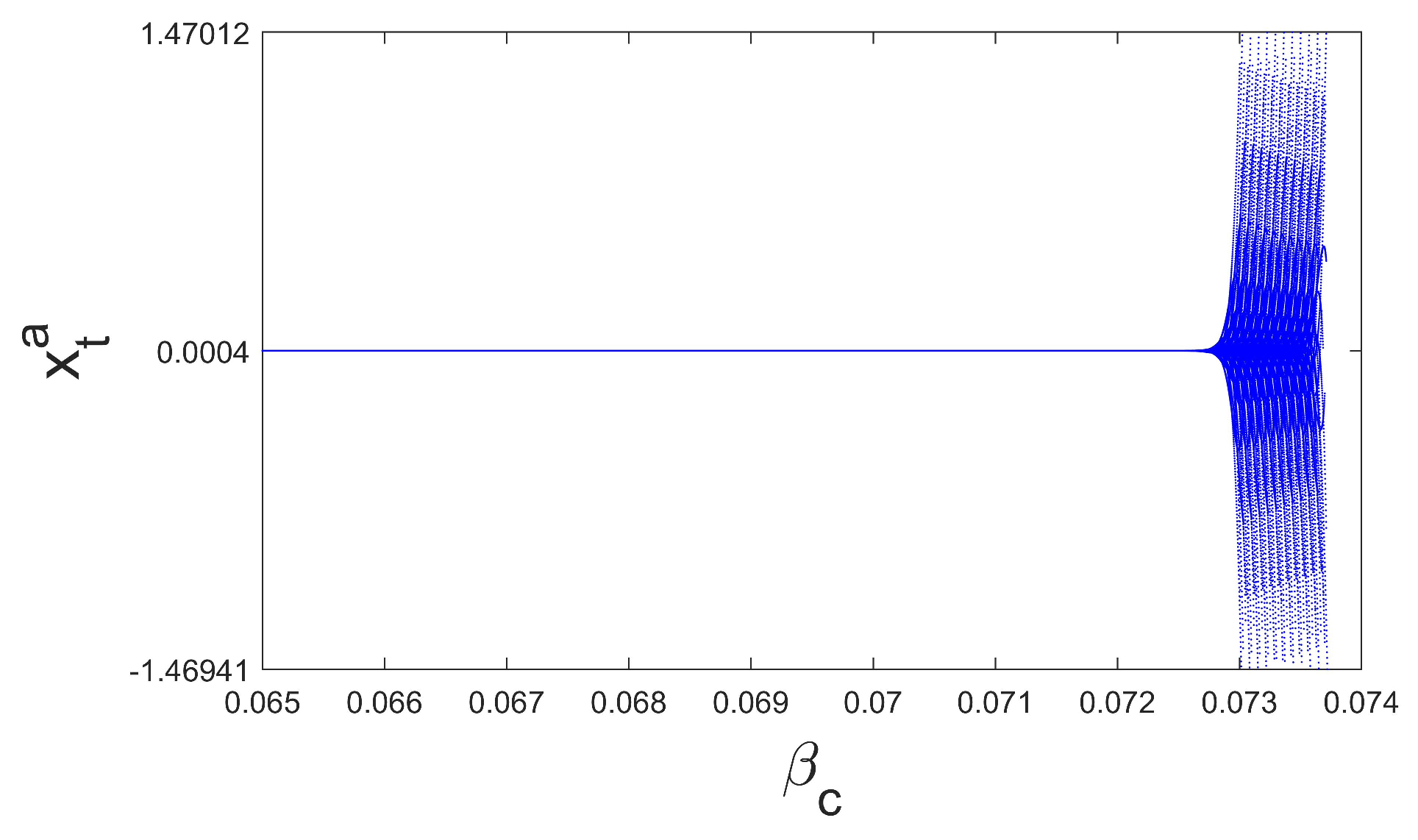
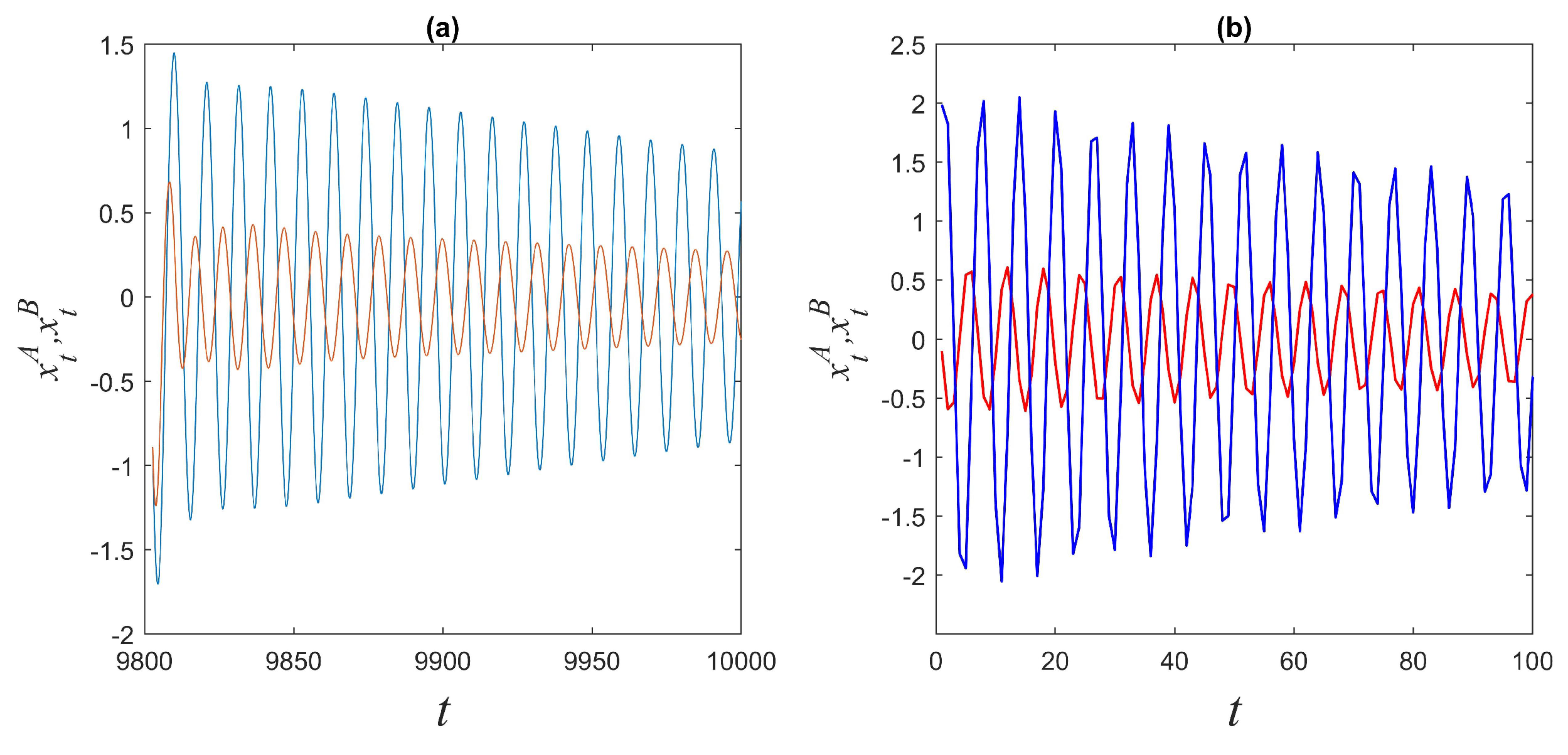
3. Local Dynamics
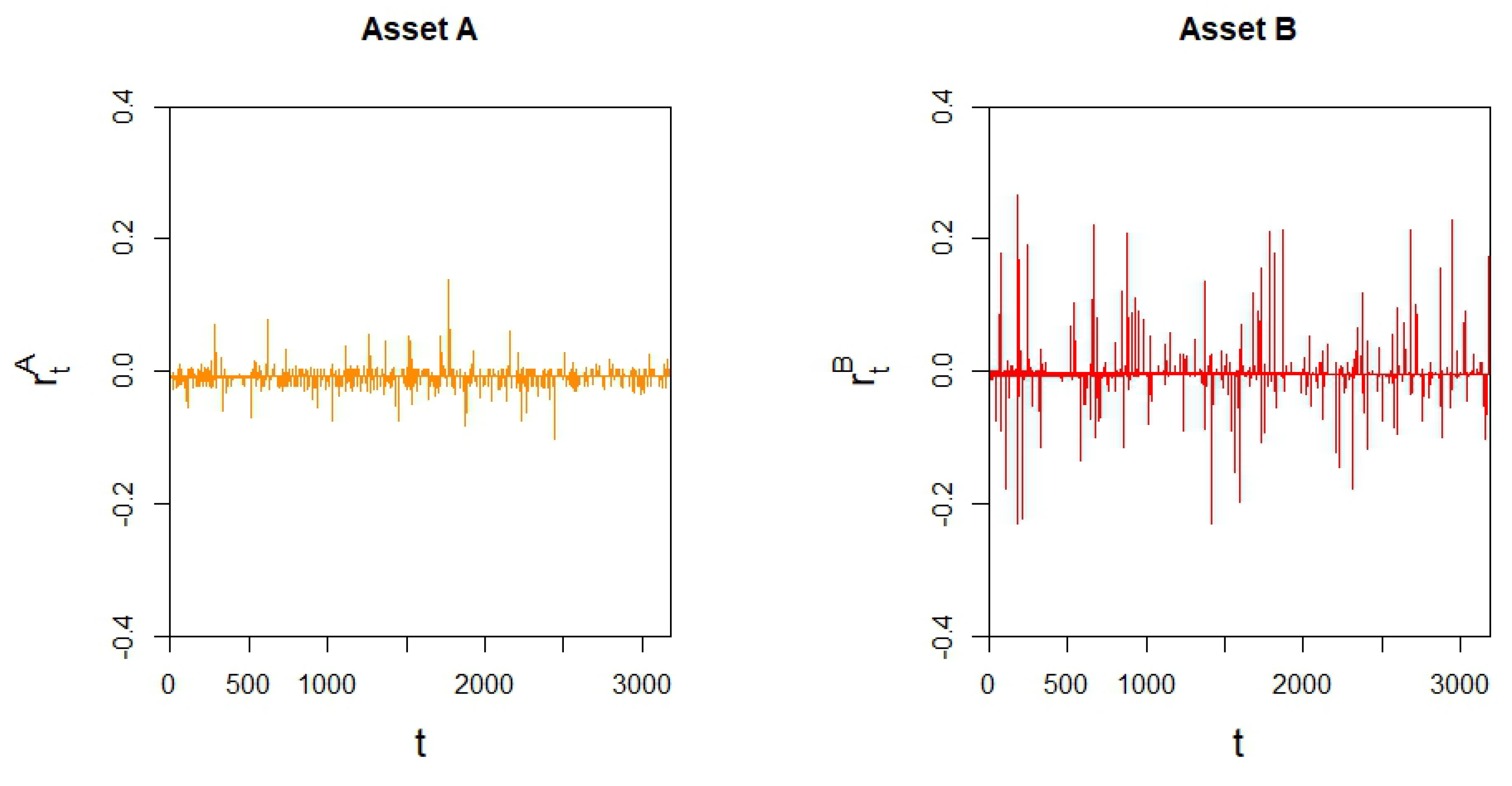
4. Empirical Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Day, R.H.; Huang, W. Bulls, bears and market sheep. J. Econ. Behav. Organ. 1990, 14, 299–329. [Google Scholar] [CrossRef]
- Brock, W.A.; Hommes, C.H. Heterogeneous beliefs and routes to chaos in a simple asset pricing model. J. Econ. Dyn. Control 1998, 22, 1235–1274. [Google Scholar] [CrossRef]
- Bischi, G.I.; Gallegati, M.; Gardini, L.; Leombruni, R.; Palestrini, A. Herd behavior and nonfundamental asset price fluctuations in financial markets. Macroecon. Dyn. 2006, 10, 502–528. [Google Scholar] [CrossRef]
- Tramontana, F.; Gardini, L.; Dieci, R.; Westerhoff, F. The emergence of bull and bear dynamics in a nonlinear model of interacting markets. Discret. Dyn. Nat. Soc. 2009, 2009, 310471. [Google Scholar]
- Brianzoni, S.; Mammana, C.; Michetti, E. Updating wealth in an asset pricing model with heterogeneous agents. Discret. Dyn. Nat. Soc. 2010, 2010, 676317. [Google Scholar] [CrossRef]
- Dieci, R.; He, X.Z. Cross-section instability in financial markets: Impatience, extrapolation, and switching. Decis. Econ. Financ. 2021, 44, 727–754. [Google Scholar] [CrossRef]
- He, X.Z.; Li, K.; Wang, C. Time-varying economic dominance in financial markets: A bistable dynamics approach. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 055903. [Google Scholar] [CrossRef] [PubMed]
- Kwessi, E.; Elaydi, S.; Dennis, B.; Livadiotis, G. Nearly exact discretization of single species population models. Nat. Resour. Model. 2018, 31, e12167. [Google Scholar] [CrossRef]
- Grassetti, F.; Guzowska, M.; Michetti, E. A dynamically consistent discretization method for Goodwin model. Chaos Solitons Fractals 2020, 130, 109420. [Google Scholar] [CrossRef]
- He, X.Z.; Zheng, H. Trading heterogeneity under information uncertainty. J. Econ. Behav. Organ. 2016, 130, 64–80. [Google Scholar] [CrossRef]
- Campisi, G.; Muzzioli, S.; Zaffaroni, A. Nonlinear dynamics in asset pricing: The role of a sentiment index. Nonlinear Dyn. 2021, 105, 2509–2523. [Google Scholar] [CrossRef]
- Medio, A.; Lines, M. Nonlinear Dynamics: A Primer; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Lux, T. The socio-economic dynamics of speculative markets: Interacting agents, chaos, and the fat tails of return distributions. J. Econ. Behav. Organ. 1998, 33, 143–165. [Google Scholar] [CrossRef]
- Chiarella, C.; Iori, G. A simulation analysis of the microstructure of double auction markets. Quant. Financ. 2002, 2, 346. [Google Scholar] [CrossRef]
- Gilbert, N. Agent-Based Models; Sage Publications: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Weisberg, M. Simulation and Similarity: Using Models to Understand the World; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Westerhoff, F.H.; Dieci, R. The effectiveness of Keynes–Tobin transaction taxes when heterogeneous agents can trade in different markets: A behavioral finance approach. J. Econ. Dyn. Control 2006, 30, 293–322. [Google Scholar] [CrossRef]
- Franke, R.; Westerhoff, F. Why a simple herding model may generate the stylized facts of daily returns: Explanation and estimation. J. Econ. Interact. Coord. 2016, 11, 1–34. [Google Scholar] [CrossRef]
- Kukacka, J.; Barunik, J. Estimation of financial agent-based models with simulated maximum likelihood. J. Econ. Dyn. Control 2017, 85, 21–45. [Google Scholar] [CrossRef]


| Asset | Mean | sd | Min | Max |
|---|---|---|---|---|
| Amazon | 0.0009 | 0.0205 | −0.1514 | 0.1462 |
| Apple | 0.0008 | 0.0179 | −0.1377 | 0.1132 |
| Tesla | 0.0016 | 0.0354 | −0.2365 | 0.2183 |
| Netflix | 0.0009 | 0.0327 | −0.4326 | 0.3522 |
| Exxon | −0.0002 | 0.0162 | −0.1194 | 0.1304 |
| Intel | −0.0001 | 0.0188 | −0.1783 | 0.1990 |
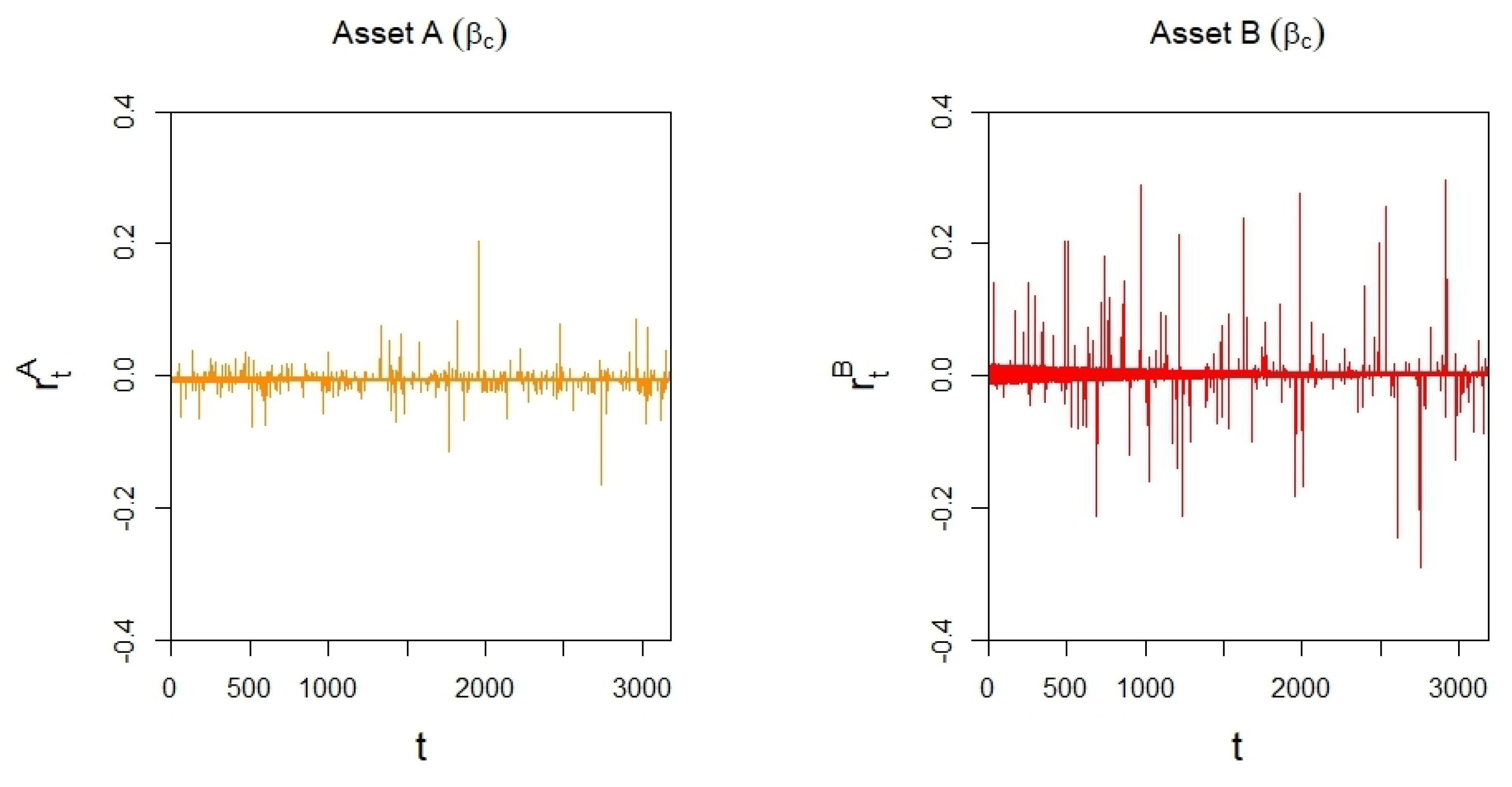
| A | 0.0084 | 0.0183 | −0.1040 | 0.1376 |
| B | −0.0039 | 0.0210 | −0.2314 | 0.2662 |
| Asset | Mean | sd | Min | Max | |
|---|---|---|---|---|---|
| 0.2001 | A | −0.0006 | 0.0081 | −0.1074 | 0.1391 |
| B | 0.0030 | 0.0232 | −0.2898 | 0.2794 | |
| 0.2003 | A | −0.0007 | 0.0199 | −0.1158 | 0.1448 |
| B | 0.0029 | 0.0638 | −0.2979 | 0.2960 | |
| 0.2004 | A | −0.0009 | 0.0685 | −0.1442 | 0.1589 |
| B | 0.0023 | 0.2220 | −0.3219 | 0.3130 | |
| 0.20044 | A | −0.0101 | 0.1185 | −0.2509 | 0.2150 |
| B | 0.0004 | 0.3886 | −0.6522 | 0.6488 |
| Asset | Mean | sd | Min | Max | |
|---|---|---|---|---|---|
| 0.0301 | A | −0.0008 | 0.0089 | −0.1067 | 0.1382 |
| B | −0.0039 | 0.0233 | −0.2435 | 0.2719 | |
| 0.03018 | A | −0.0006 | 0.0092 | −0.1647 | 0.2038 |
| B | 0.0020 | 0.0221 | −0.2916 | 0.2967 | |
| 0.03025 | A | 0.0007 | 0.0096 | −0.1349 | 0.1109 |
| B | 0.0005 | 0.0248 | −0.2971 | 0.2617 | |
| 0.0305 | A | 0.0203 | 0.0277 | −0.1445 | 0.1765 |
| B | 0.0004 | 0.0843 | −0.3041 | 0.2875 |
| d | N | |||
|---|---|---|---|---|
| amzn | *** | *** | 60 | |
| aapl | *** | *** | 60 | |
| nflx | *** | *** | 60 | |
| tsla | *** | *** | 60 | |
| exxon | *** | *** | 60 | |
| intel | *** | *** | 60 | |
| Asset A | ** | * | 60 | |
| Asset B | *** | *** | 60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brianzoni, S.; Campisi, G.; Pacelli, G. Coexisting Attractors in a Heterogeneous Agent Model in Discrete Time. Mathematics 2023, 11, 2348. https://doi.org/10.3390/math11102348
Brianzoni S, Campisi G, Pacelli G. Coexisting Attractors in a Heterogeneous Agent Model in Discrete Time. Mathematics. 2023; 11(10):2348. https://doi.org/10.3390/math11102348
Chicago/Turabian StyleBrianzoni, Serena, Giovanni Campisi, and Graziella Pacelli. 2023. "Coexisting Attractors in a Heterogeneous Agent Model in Discrete Time" Mathematics 11, no. 10: 2348. https://doi.org/10.3390/math11102348
APA StyleBrianzoni, S., Campisi, G., & Pacelli, G. (2023). Coexisting Attractors in a Heterogeneous Agent Model in Discrete Time. Mathematics, 11(10), 2348. https://doi.org/10.3390/math11102348






