Methodology to Obtain Universal Solutions for Systems of Coupled Ordinary Differential Equations: Examples of a Continuous Flow Chemical Reactor and a Coupled Oscillator
Abstract
1. Introduction
2. Basis of Discriminated Nondimensionalization
- i)
- Choice of appropriate references
- ii)
- Definition of dimensionless variables and formation of dimensionless governing equations
- iii)
- Obtaining the dimensionless groups
- iv)
- Existence of m groups with a different unknown each (πu), and n groups without unknowns (πw)
3. Network Simulation Method
4. Nondimensionalization of Systems of Coupled Ordinary Differential Equations
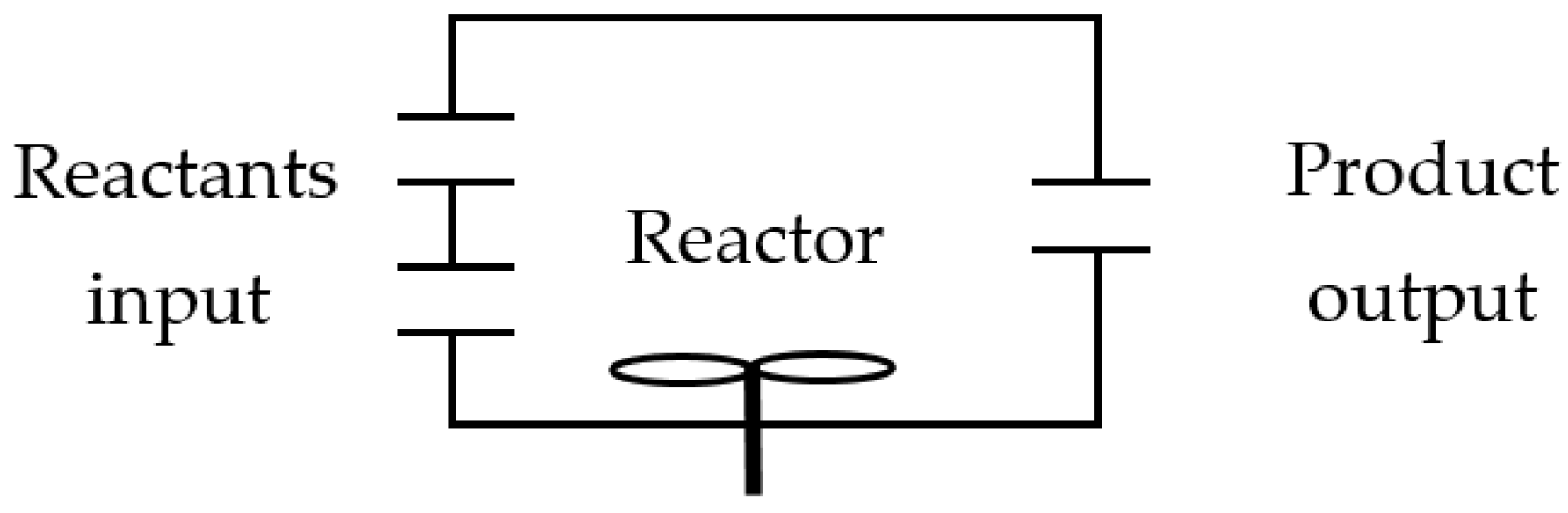
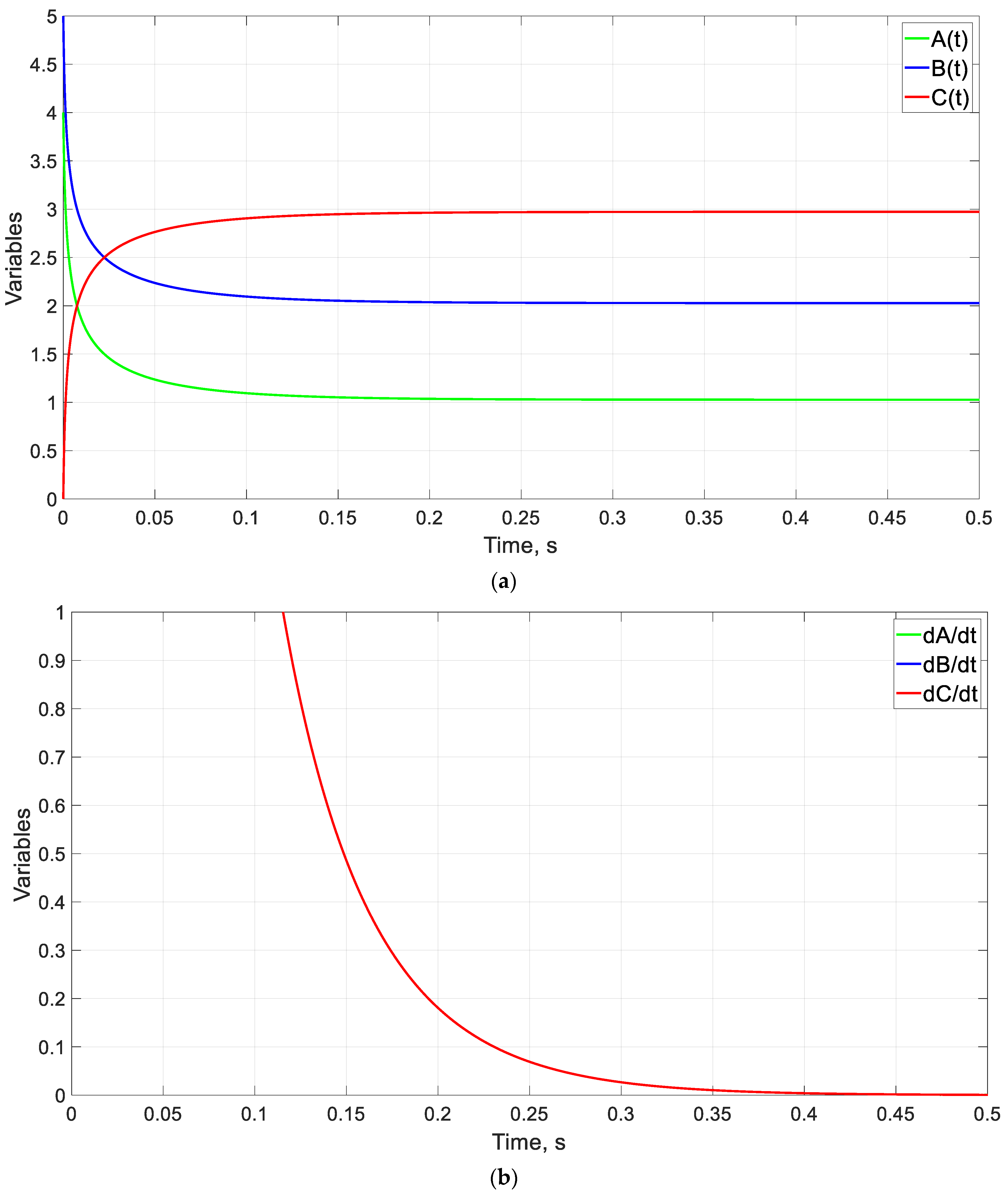
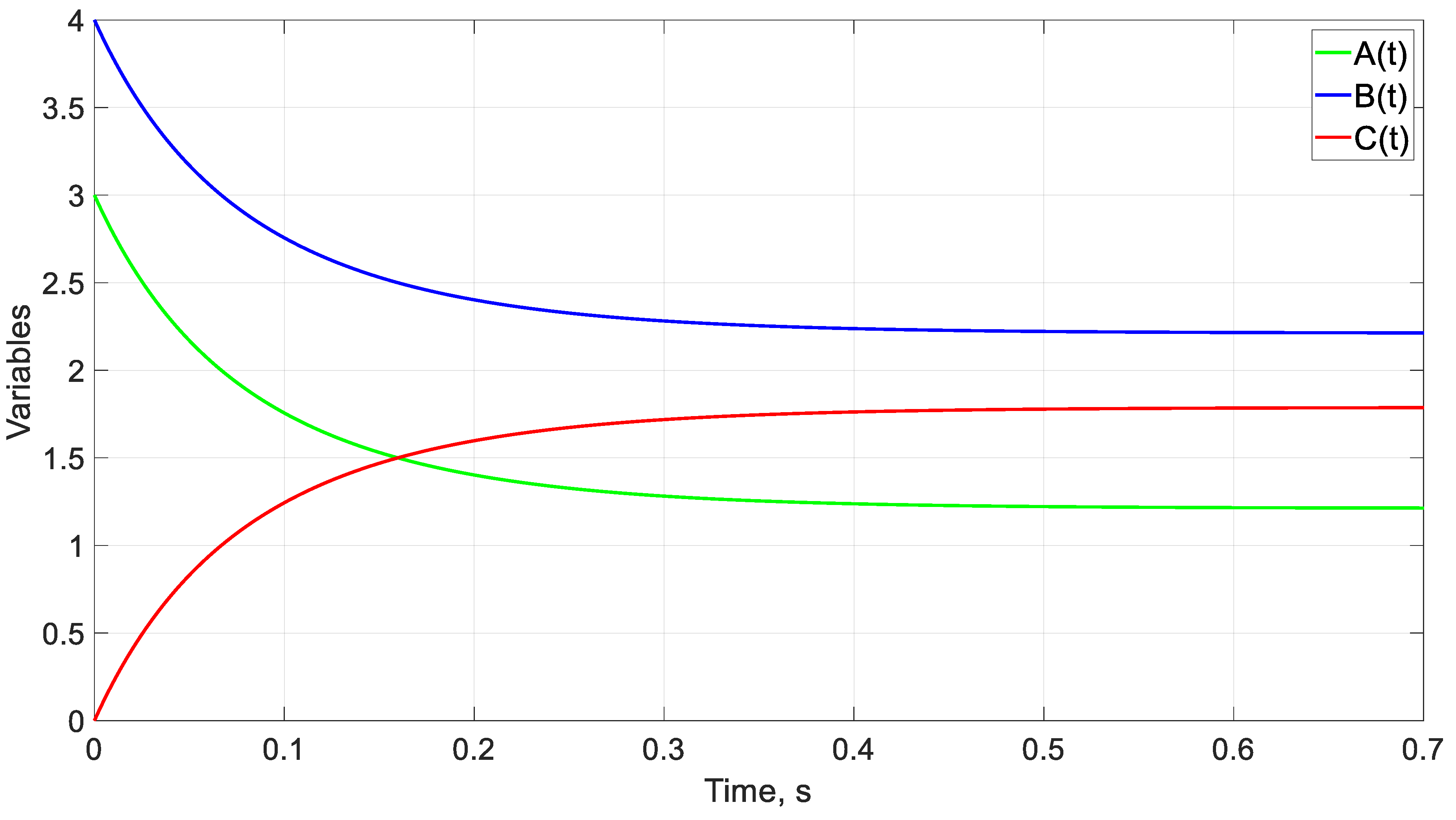
4.1. Example of a Continuous Flow Chemical Reactor
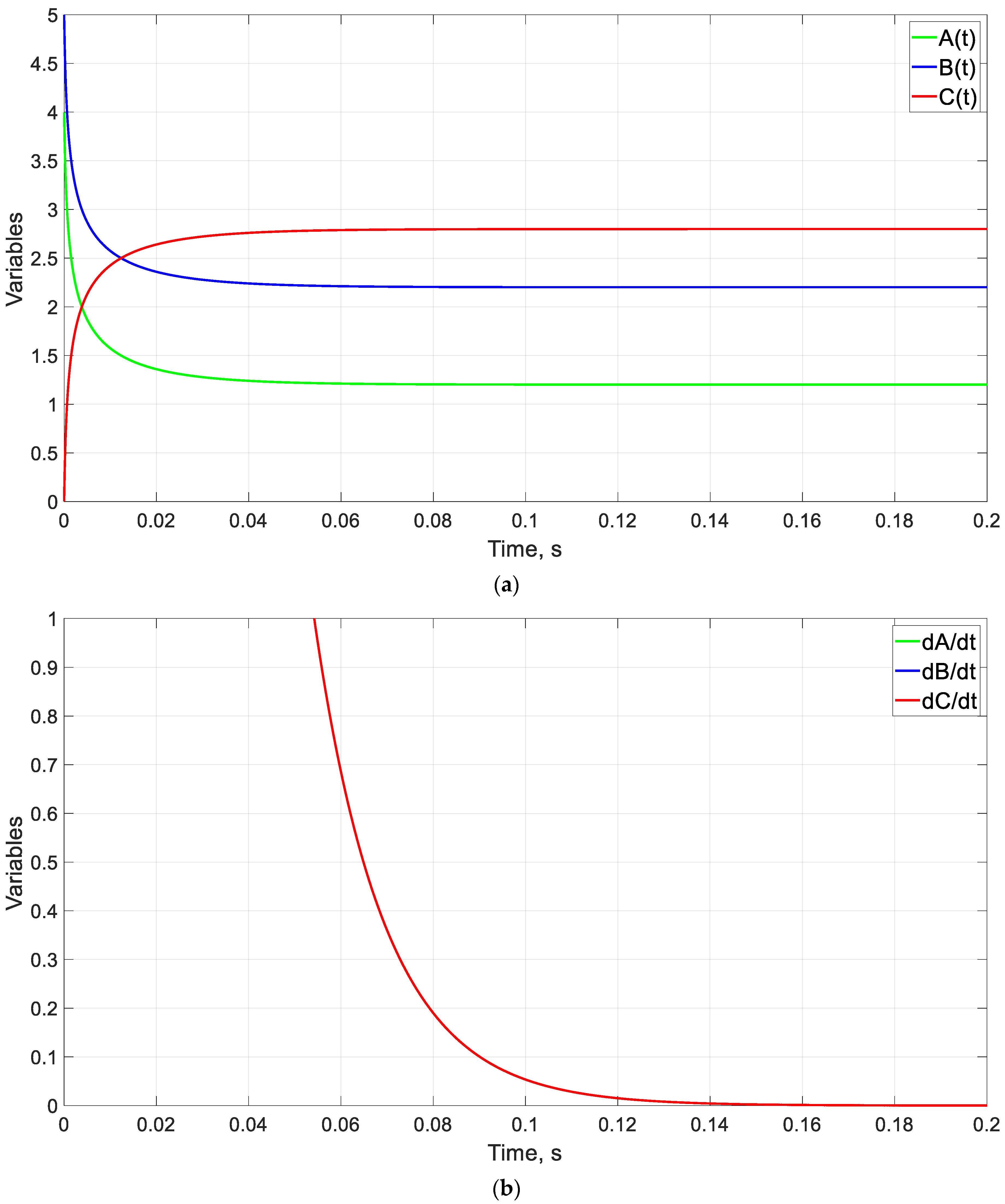
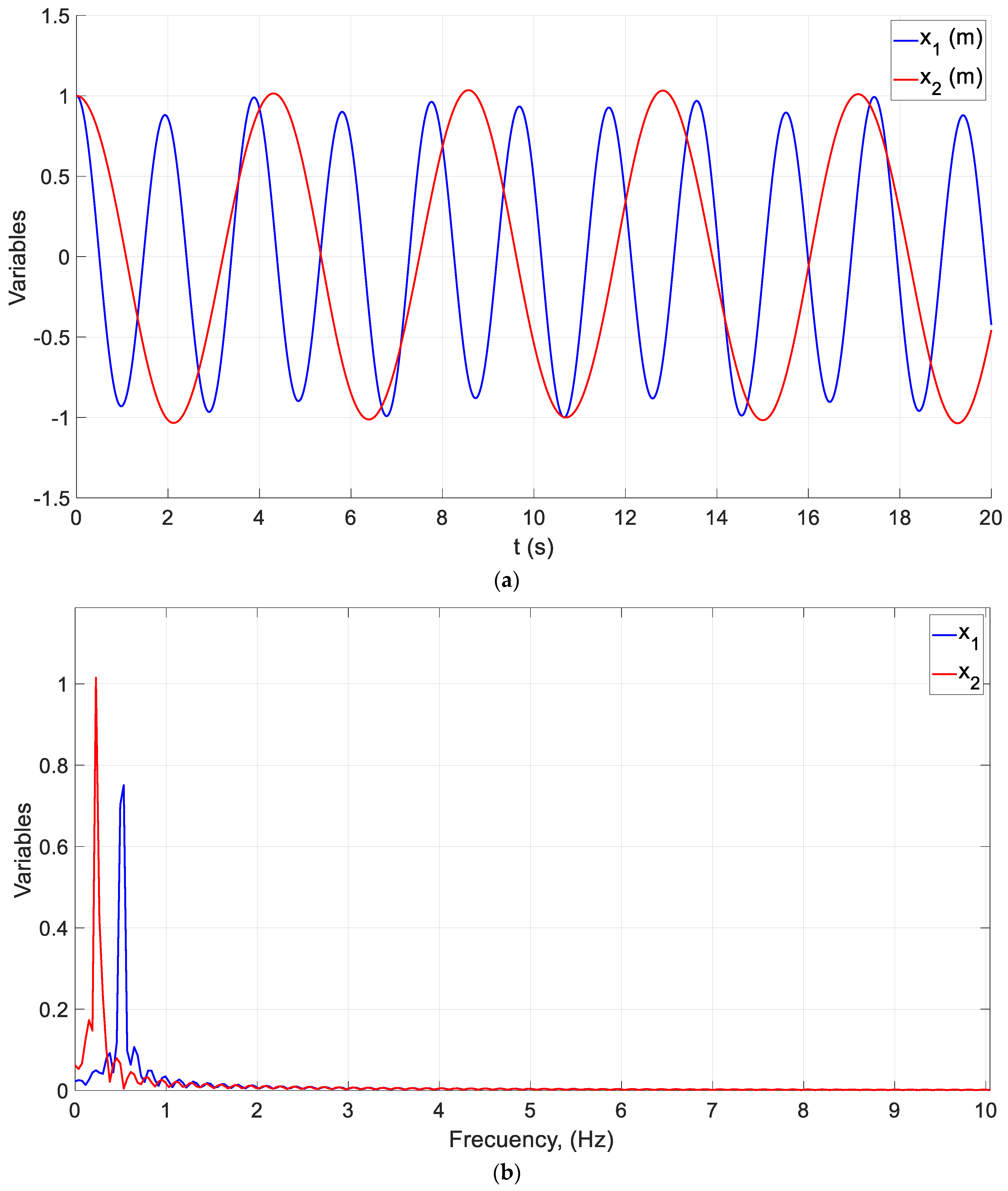
4.2. Example of a Coupled Oscillator
5. Functionals Adjustment: Universal Curves
- v)
- Obtaining the functionals
- vi)
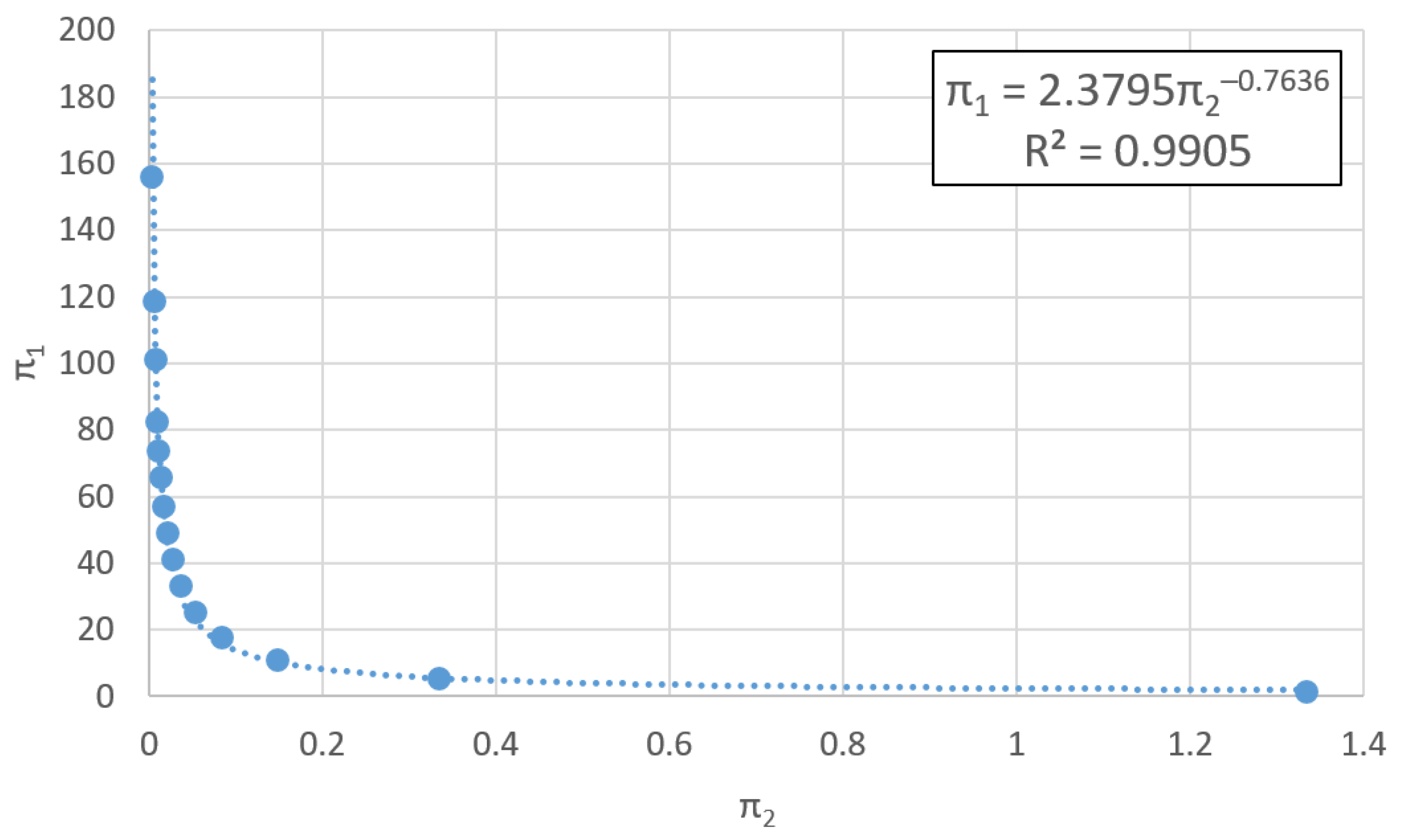
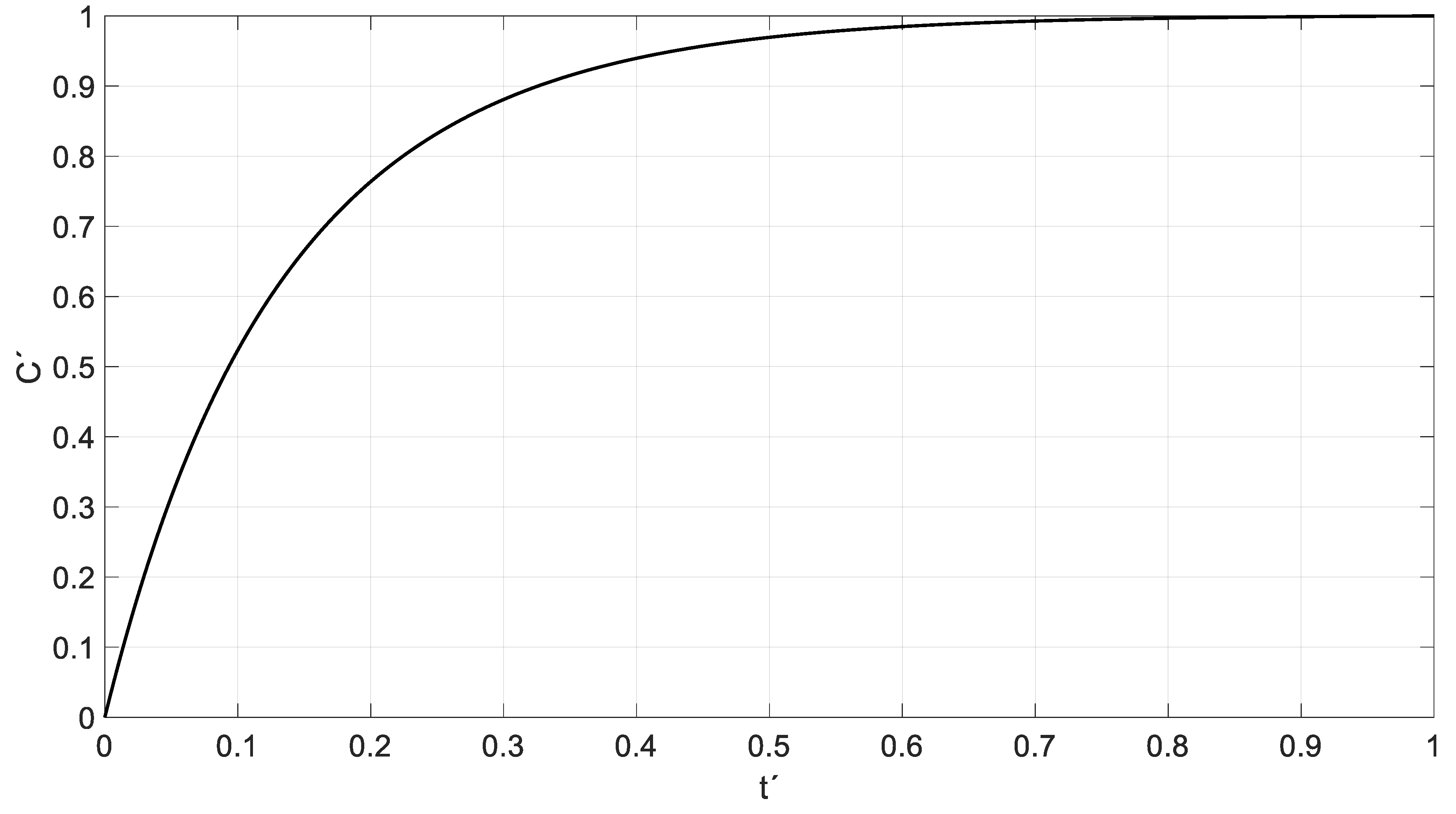
- Obtaining universal curves or universal solutions
5.1. Example of a Continuous Flow Chemical Reactor
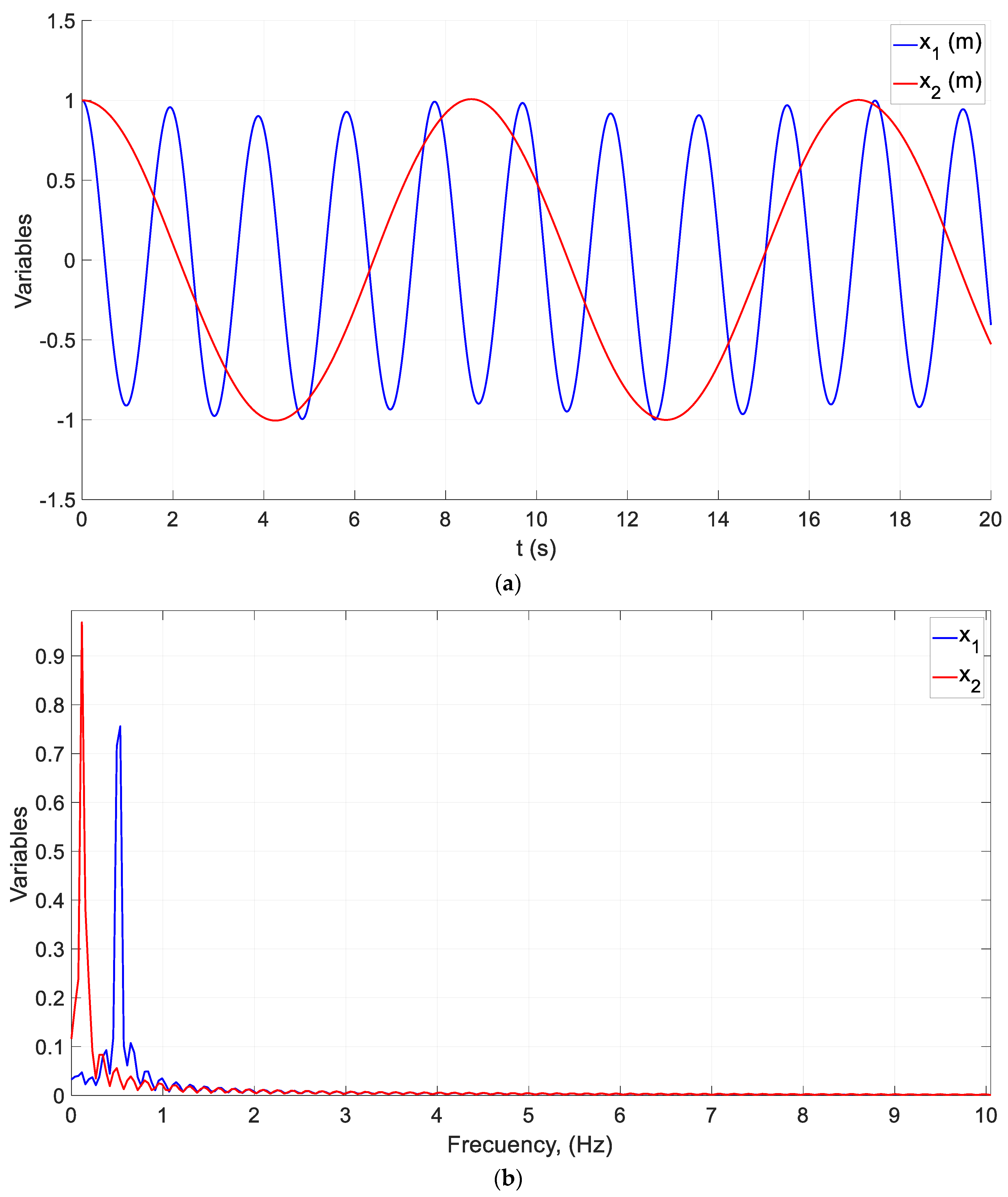
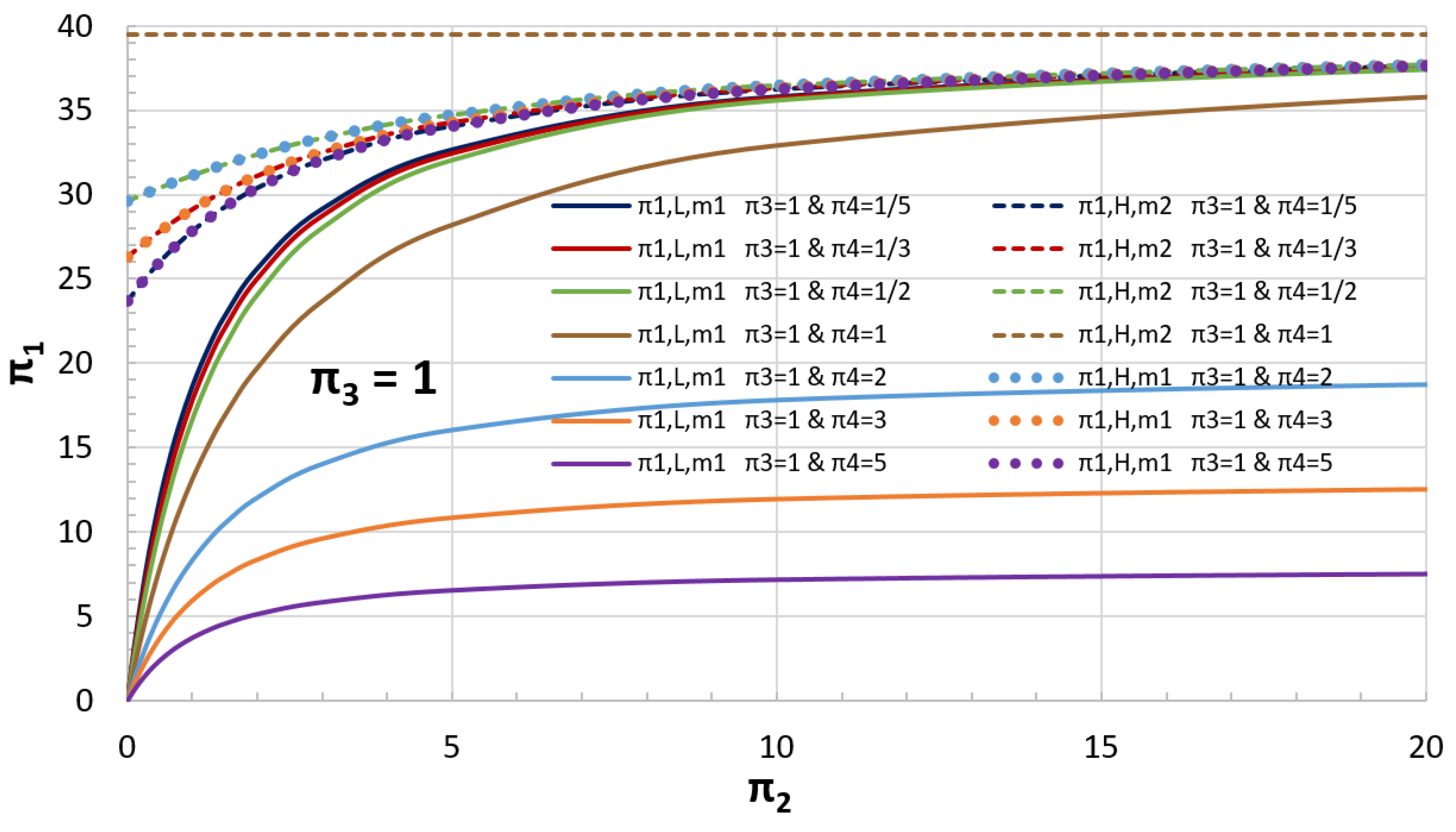
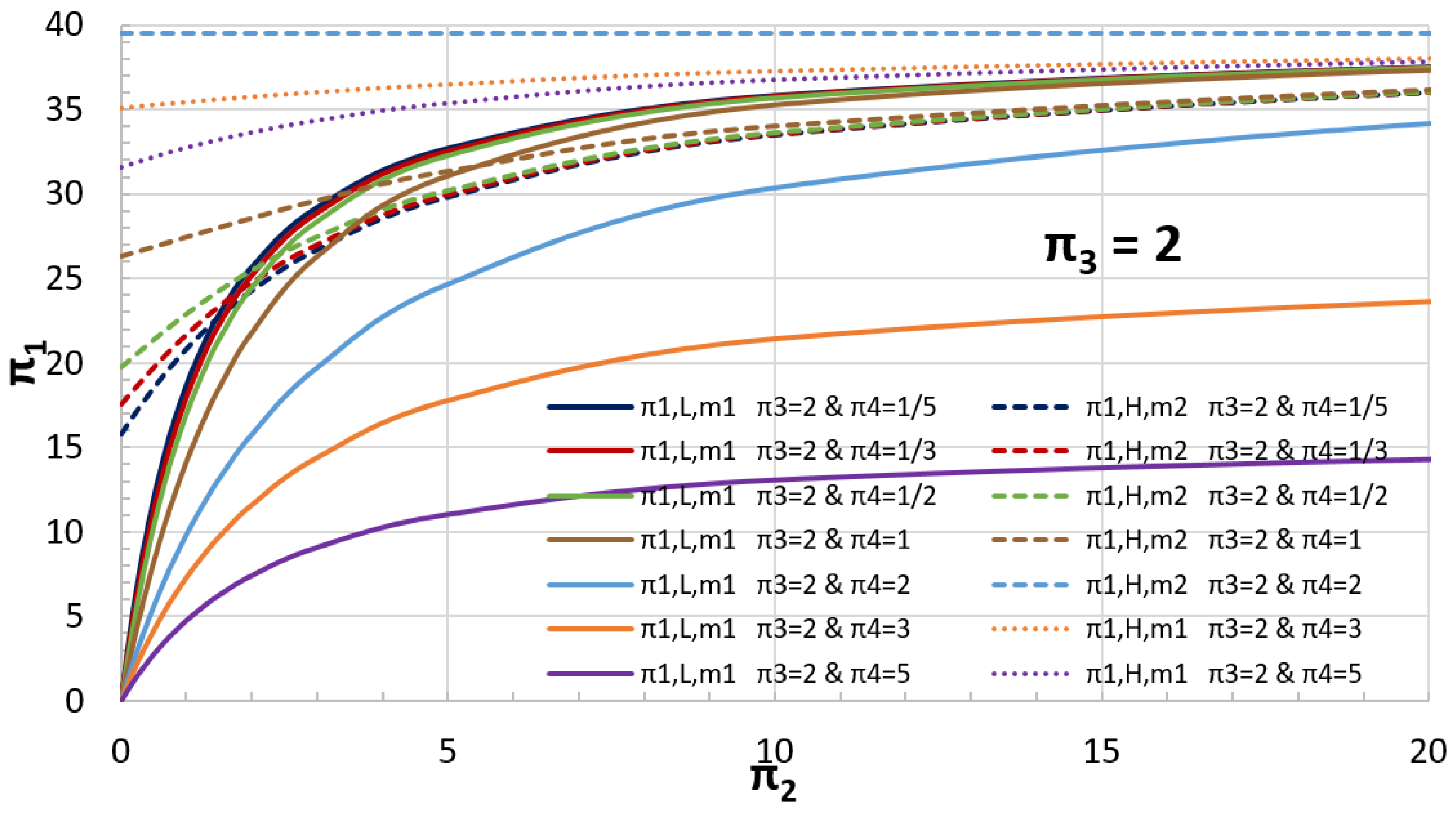
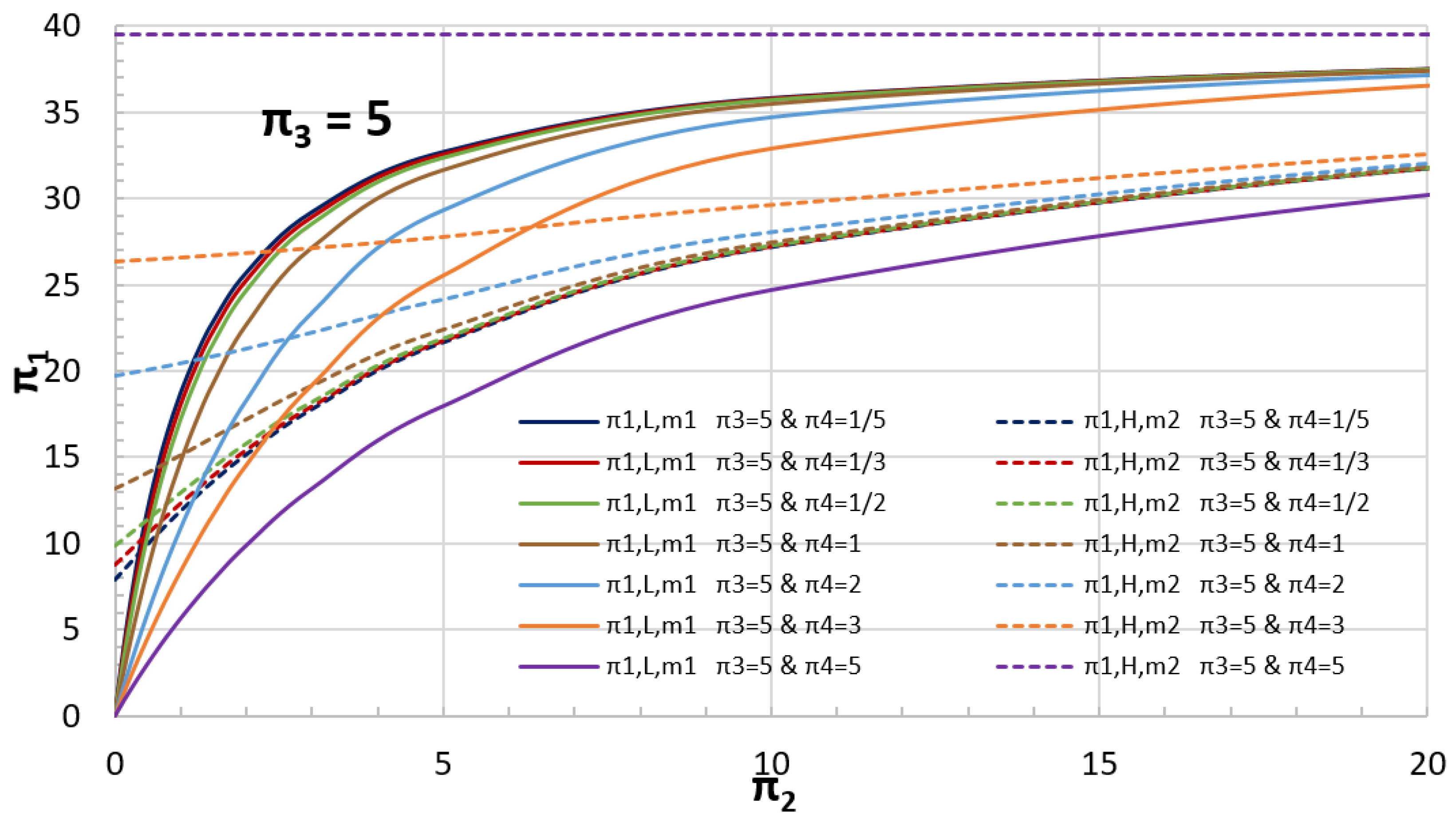
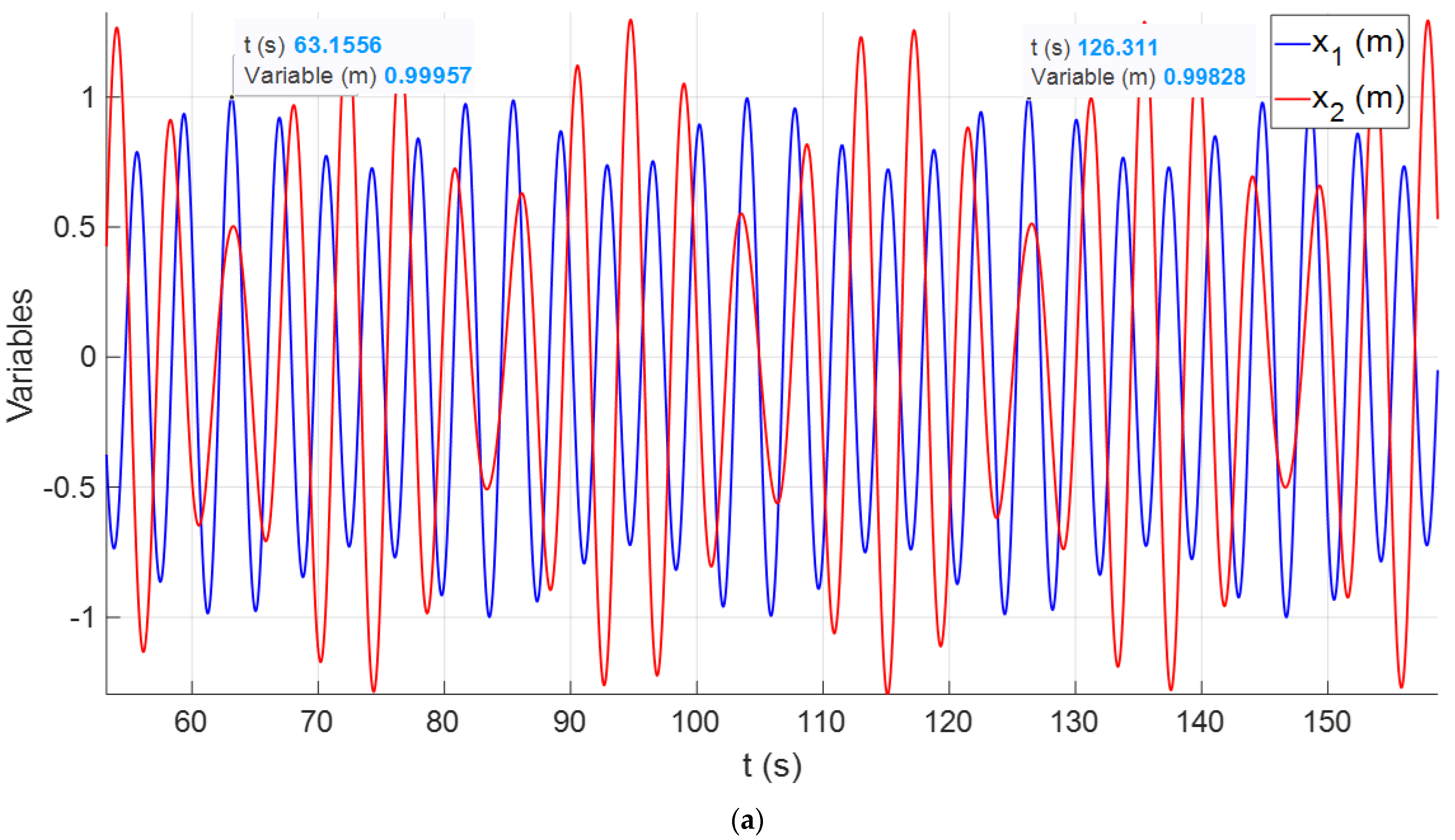
5.2. Example of a Coupled Oscillator
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gibbings, J.C. A logic of dimensional analysis. J. Phys. A Math. Gen. 1982, 15, 1991–2002. [Google Scholar] [CrossRef]
- Gibbings, J.C. On dimensional analysis. J. Phys. A Math. Gen. 1980, 13, 75–89. [Google Scholar] [CrossRef]
- Gibbings, J.; Hignett, E. Dimensional analysis of electrostatic streaming current. Electrochim. Acta 1966, 11, 815–826. [Google Scholar] [CrossRef]
- Sonin, A.A. The Physical Basis of Dimensional Analysis; Department of Mechanical Engineering, MIT: Cambridge, MA, USA, 2001. [Google Scholar]
- Potter, M.C.; Wiggert, D.C.; Ramadan, B.H. Mechanics of Fluids SI Version; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Capobianchi, M.; Aziz, A. A scale analysis for natural convective flows over vertical surfaces. Int. J. Therm. Sci. 2012, 54, 82–88. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Sharp, J. On J. C. Gibbings’ discussion of paper by J. J. Sharp et al. ‘application of matrix manipulation in dimensional analysis involving large numbers of variables’. Vol. 5, no. 4, 1992, 333–348. Mar. Struct. 1994, 7, 113–119. [Google Scholar] [CrossRef]
- Gibbings, J.C. The Pi-Theorem. In Dimensional Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Hristov, J. Magnetic field assisted fluidization—A unified approach. Part 8. Mass transfer: Magnetically assisted bioprocesses. Rev. Chem. Eng. 2010, 26, 55–128. [Google Scholar] [CrossRef]
- Kreith, F.; Bohn, M.; Kirkpatrick, A. Principles of Heat Transfer; Cengage Learning: Boston, MA, USA, 2011; Volume 2. [Google Scholar]
- Madrid, C.; Alhama, F. Análisis Dimensional Discriminado en Mecánica de Fluidos y Transferencia de Calor; Editorial Reverté: Barcelona, Spain, 2012. [Google Scholar]
- Langhaar, L. Dimensional Analysis and Theory of Models; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1951. [Google Scholar]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Conesa, M.; Alhama, I.; Cánovas, M. Study of Lotka–Volterra Biological or Chemical Oscillator Problem Using the Normalization Technique: Prediction of Time and Concentrations. Mathematics 2020, 8, 1324. [Google Scholar] [CrossRef]
- Sánchez Pérez, J.F.; Conesa, M.; Alhama, I.; Alhama, F.; Cánovas, M. Searching fundamental information in ordinary differential equations. Nondimensionalization technique. PLoS ONE 2017, 12, e0185477. [Google Scholar] [CrossRef]
- Conesa, M.; Pérez, J.F.S.; Alhama, I.; Alhama, F. On the nondimensionalization of coupled, nonlinear ordinary differential equations. Nonlinear Dyn. 2015, 84, 91–105. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Alhama, I. Universal curves for the solution of chlorides penetration in reinforced concrete, water-saturated structures with bound chloride. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105201. [Google Scholar] [CrossRef]
- García-Ros, G.; Alhama, I.; Cánovas, M. Use of discriminated nondimensionalization in the search of universal solutions for 2-D rectangular and cylindrical consolidation problems. Open Geosci. 2018, 10, 209–221. [Google Scholar] [CrossRef]
- García-Ros, G.; Alhama, I.; Cánovas, M.; Alhama, F. Derivation of Universal Curves for Nonlinear Soil Consolidation with Potential Constitutive Dependences. Math. Probl. Eng. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Manteca, I.A.; García-Ros, G.; López, F.A. Universal solution for the characteristic time and the degree of settlement in nonlinear soil consolidation scenarios. A deduction based on nondimensionalization. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 186–201. [Google Scholar] [CrossRef]
- García-Ros, G.; Alhama, I. Method to Determine the Constitutive Permeability Parameters of Non-linear Consolidation Models by Means of the Oedometer Test. Mathematics 2020, 8, 2237. [Google Scholar] [CrossRef]
- Alhama, F.; Madrid, C. Discriminated Dimensional Analysis Versus Classical Dimensional Analysis and Applications to Heat Transfer and Fluid Dynamics. Chin. J. Chem. Eng. 2007, 15, 626–631. [Google Scholar] [CrossRef]
- Madrid, C.; Alhama, F. Discrimination: A fundamental and necessary extension of classical dimensional analysis theory. Int. Commun. Heat Mass Transf. 2006, 33, 287–294. [Google Scholar] [CrossRef]
- Madrid, C.; Alhama, F. Discriminated dimensional analysis of the energy equation: Application to laminar forced convection along a flat plate. Int. J. Therm. Sci. 2005, 44, 333–341. [Google Scholar] [CrossRef]
- Conesa, M. Sobre la Adimensionalización Discriminada de Ecuaciones y Sistemas de Ecuaciones Diferenciales Ordinarias, No Lineales y Solución Numérica Mediante el Método de Redes: Aplicación a Problemas Mecánicos. Ph.D. Thesis, Universidad Politécnica de Cartagena, Cartagena, Spain, 2016. [Google Scholar]
- Perez, J.F.S.; Conesa, M.; Alhama, I. Solving ordinary differential equations by electrical analogy: A multidisciplinary teaching tool. Eur. J. Phys. 2016, 37, 065703. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.F.; Marin, F.; Morales, J.L.; Cánovas, M.; Alhama, F. Modeling and simulation of different and representative engineering problems using Network Simulation Method. PLoS ONE 2018, 13, e0193828. [Google Scholar] [CrossRef]
- Nagel, L.W.; Pederson, D.O. SPICE (Simulation Program with Integrated Circuit Emphasis); EECS Department: Berkeley, CA, USA, 1973. [Google Scholar]
- Vogt, H.; Atkinson, G.; Nenzi, P.; Warning, D.; Ngspice User’s Manual Version 40 Plus. NgSpice 2023. Available online: https://ngspice.sourceforge.io/docs/ngspice-html-manual/manual.xhtml (accessed on 15 April 2023).
- MicroSim Corporation Fairbanks PSPICE. Irvine, 1994. Available online: http://www.it.uom.gr/project/digital/appnts.pdf (accessed on 15 April 2023).
- Nagel, L.W. SPICE2: A Computer Program to Simulate Semiconductor Circuits; University of California: Berkeley, CA, USA, 1975. [Google Scholar]
- Gear, C.W. The automatic integration of ordinary differential equations. Commun. ACM 1971, 14, 176–179. [Google Scholar] [CrossRef]
- Sankar, C.P.; Thumba, D.A.; Ramamohan, T.; Chandra, S.V.; Kumar, K.S. Agent-based multi-edge network simulation model for knowledge diffusion through board interlocks. Expert Syst. Appl. 2019, 141, 112962. [Google Scholar] [CrossRef]
- Hu, D.; Zhao, J.L.; Hua, Z.; Wong, M.C. Network-Based Modeling and Analysis of Systemic Risk in Banking Systems. MIS Q. 2012, 36, 1269. [Google Scholar] [CrossRef]
- Campuzano-Bolarín, F.; Marín-García, F.; Moreno-Nicolás, J.A.; Bogataj, M.; Bogataj, D. Network Simulation Method for the evaluation of perturbed supply chains on a finite horizon. Cent. Eur. J. Oper. Res. 2021, 29, 823–839. [Google Scholar] [CrossRef]
- Siregar, E.; Mawengkang, H.; Nababan, E.B.; Wanto, A. Analysis of Backpropagation Method with Sigmoid Bipolar and Linear Function in Prediction of Population Growth. J. Phys. Conf. Ser. 2019, 1255, 012023. [Google Scholar] [CrossRef]
- Peixoto, P.S.; Marcondes, D.; Peixoto, C.; Oliva, S.M. Modeling future spread of infections via mobile geolocation data and population dynamics. An application to COVID-19 in Brazil. PLoS ONE 2020, 15, e0235732. [Google Scholar] [CrossRef]
- Alarcón, M.; Alhama, F.; González-Fernández, C.F. Transient Conduction in a Fin-Wall Assembly with Harmonic Excitation--Network Thermal Admittance. Heat Transf. Eng. 2002, 23, 31–43. [Google Scholar] [CrossRef]
- Horno, J.; García-Hernández, M.; González-Fernández, C. Digital simulation of electrochemical processes by the network approach. J. Electroanal. Chem. 1993, 352, 83–97. [Google Scholar] [CrossRef]
- Moya, A.A. Influence of dc electric current on the electrochemical impedance of ion-exchange membrane systems. Electrochim. Acta 2011, 56, 3015–3022. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Alhama, F.; Moreno, J.; Cánovas, M. Study of main parameters affecting pitting corrosion in a basic medium using the network method. Results Phys. 2018, 12, 1015–1025. [Google Scholar] [CrossRef]
- Horno, J.; Caballero, F.G.; Hayas, A.; González-Fern’Andez, C. The effect of previous convective flux on the nonstationary diffusion through membranes. Network simulation. J. Membr. Sci. 1990, 48, 67–77. [Google Scholar] [CrossRef]



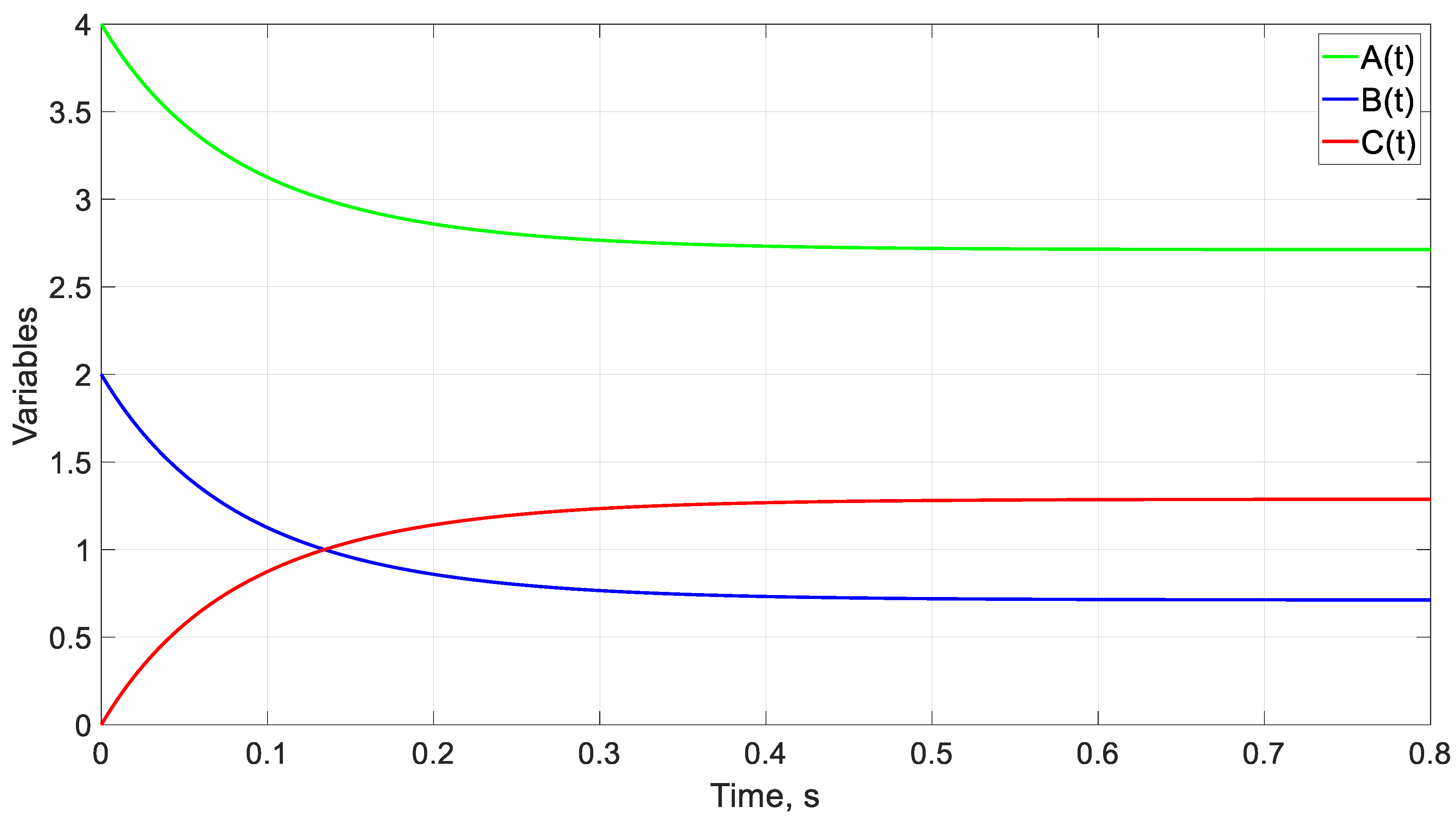
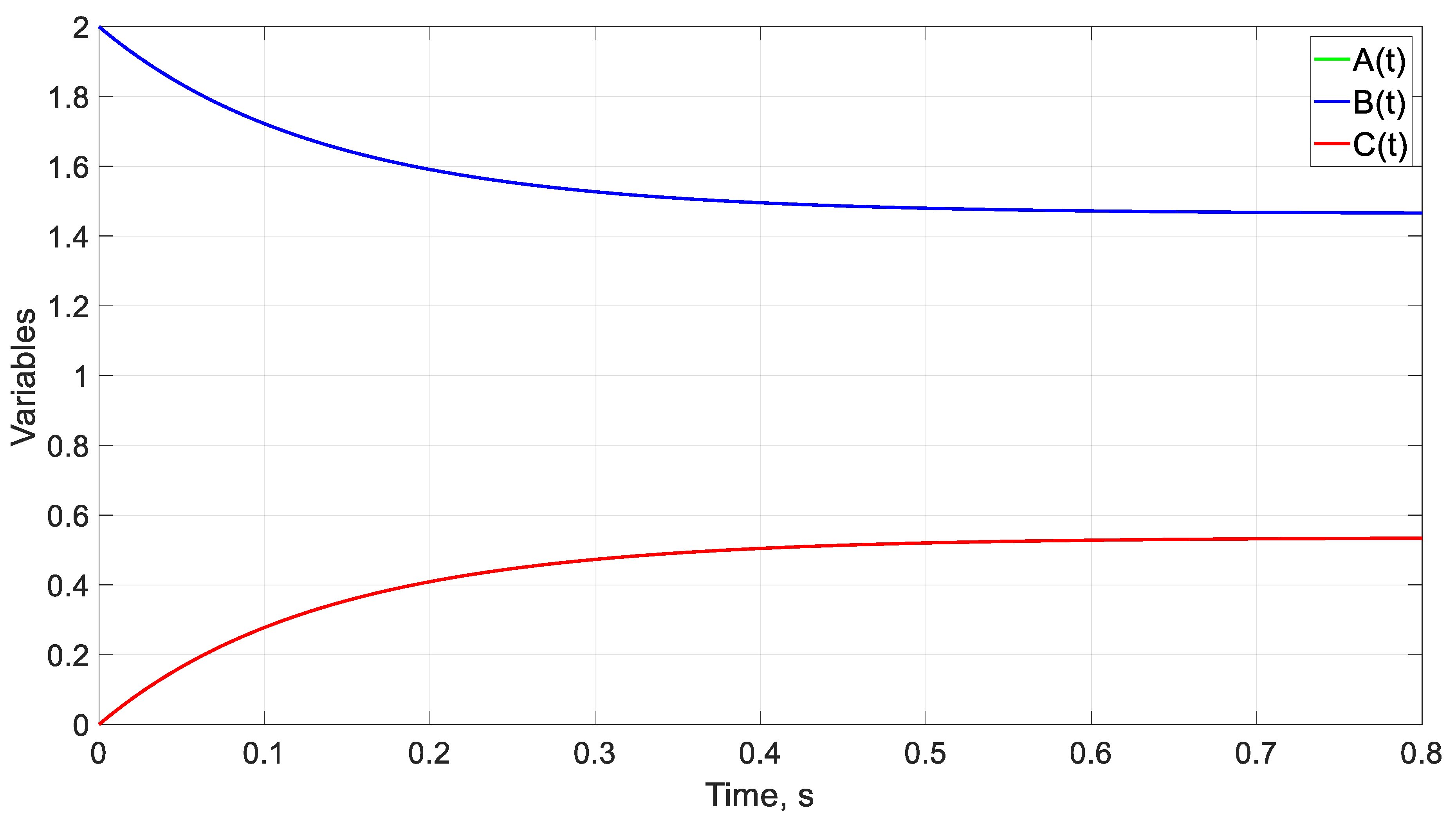
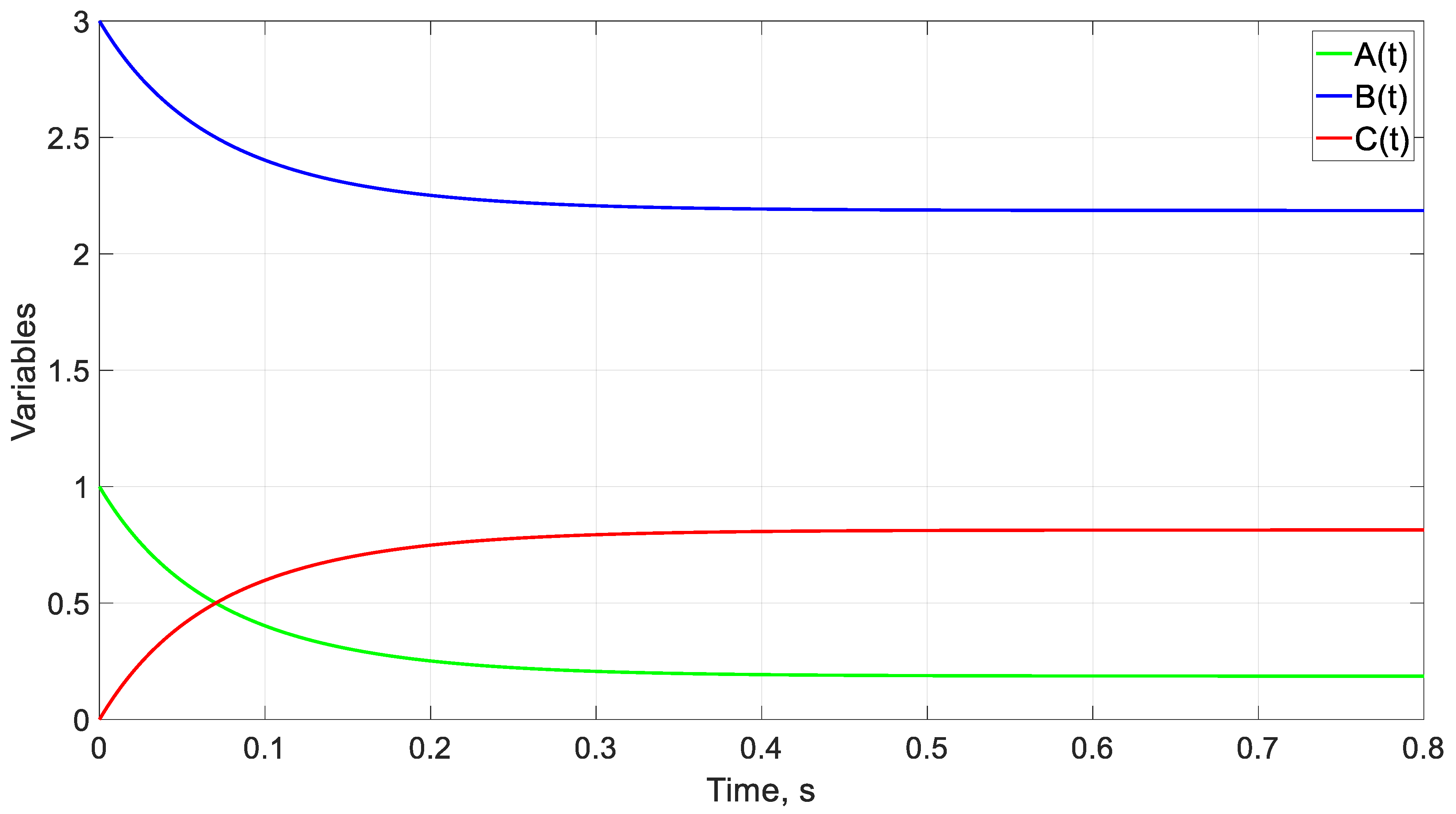
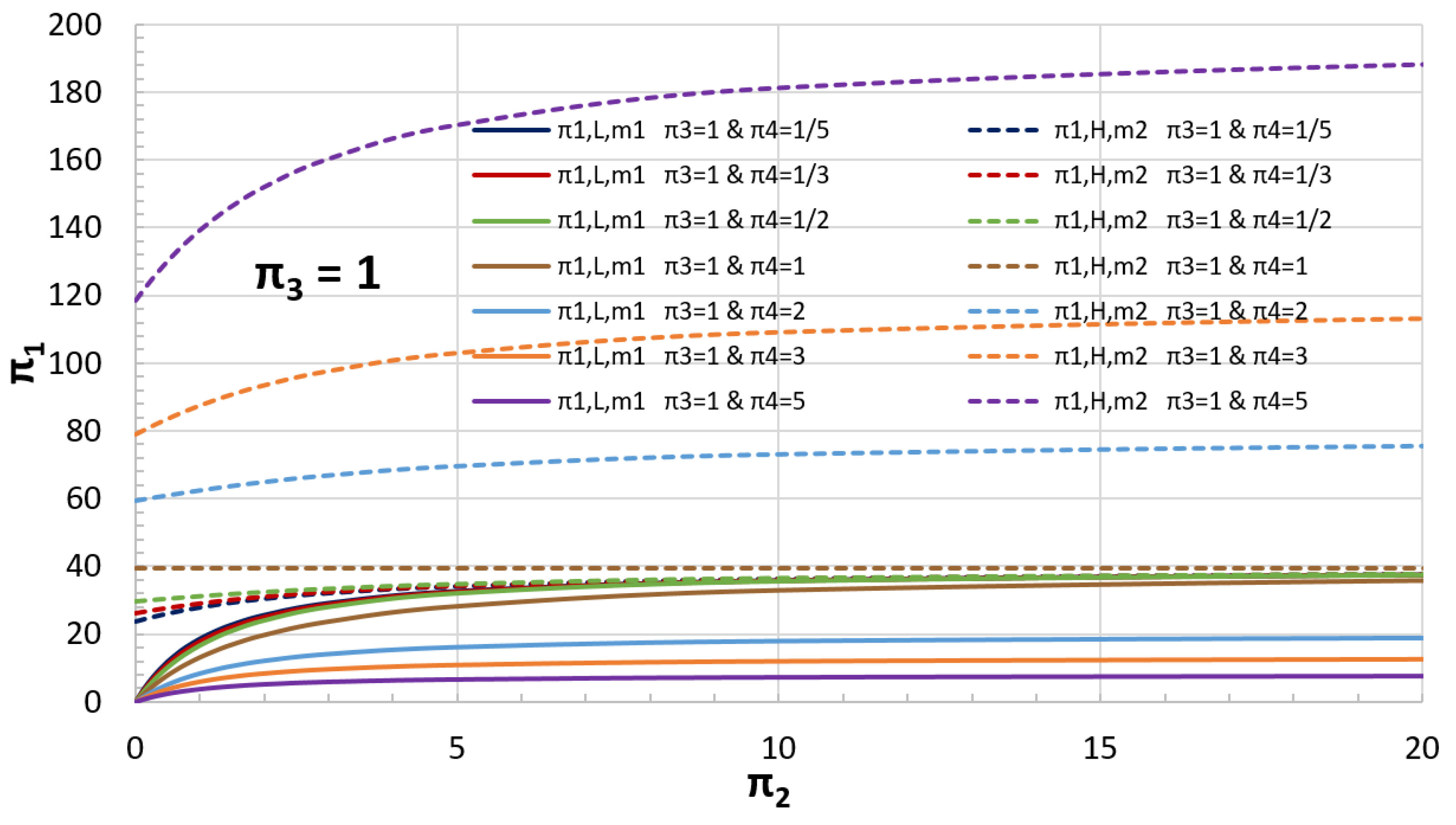
| Case | α | β | kF | r | to (s) | ||
|---|---|---|---|---|---|---|---|
| 1 | 4 | 5 | 3 | 2 | 2 | 3 | 0.26 |
| 2 | 4 | 5 | 3 | 2 | 4 | 6 | 0.14 |
| 3 | 4 | 5 | 3 | 2 | 1 | 1.5 | 0.48 |
| 4 | 4 | 5 | 3 | 2 | 2 | 6 | 0.16 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 10 | 10 | 10 | 10 | 20 | 10 | 20 | 5 | 5 | 5 | |
| 0.5 | 0.5 | 0.5 | 1 | 4 | 0.5 | 0.5 | 0.5 | 10 | 10 | 10 | |
| 6 | 6 | 6 | 6 | 6 | 6 | 12 | 12 | 5 | 10 | 5 | |
| 1 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 3 | 3 | 12 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 0.5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 1 | 1 | |
| 1.9390 | 3.8551 | 1.9391 | 1.8886 | 1.6507 | 1.3885 | 1.9391 | 1.3885 | 1.2555 | 1.1916 | 1.0130 | |
| 4.2827 | 4.3122 | 8.5106 | 4.1477 | 3.7230 | 4.2827 | 3.0769 | 3.0769 | 2.8121 | 2.3408 | 2.4637 | |
| Ψ1 | 6.1315 | 6.0954 | 6.1320 | 5.9722 | 5.2200 | 6.2096 | 6.1320 | 6.2096 | 2.8074 | 2.6645 | 2.2651 |
| Ψ2 | 1.2363 | 1.2448 | 2.4694 | 1.6933 | 3.0398 | 1.2363 | 0.6281 | 0.6281 | 3.9770 | 2.3408 | 3.4841 |
| Simulated | Unviversal Curves | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | KF | r | t (s) | A | to (s) | |||||||
| 1 | 3 | 4 | 2 | 3 | 0.1 | 1.75 | 2.75 | 1.24 | 1.77 | 2.77 | 1.23 | 0.63 |
| 2 | 4 | 2 | 2 | 3 | 0.2 | 2.85 | 0.86 | 1.14 | 2.90 | 0.90 | 1.10 | 0.74 |
| 3 | 2 | 2 | 1 | 4 | 0.3 | 1.53 | 1.53 | 0.47 | 1.49 | 1.49 | 0.51 | 0.70 |
| 4 | 1 | 3 | 4 | 2 | 0.4 | 0.19 | 2.19 | 0.81 | 0.21 | 2.21 | 0.79 | 0.78 |
| Universal Curves | Simulated | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | k1 | kc | k2 | m1 | m2 | x1,0 | x2,0 | π2 | π3 | π4 | π1,L | π1,H | t0,L | t0,H | t0,L | t0,H |
| 1 | 12 | 0.6 | 2.4 | 4.5 | 1.5 | 1 | 1/2 | 20 | 5 | 3 | 36.8 | 32.6 | 3.7148 | 4.5139 | 3.7141 | 4.5132 |
| 2 | 1/4 | 1/20 | 1/8 | 3 | 6 | 3/4 | 3/4 | 5 | 2 | 0.5 | 32.4 | 30.2 | 19.7180 | 38.0736 | 19.6822 | 38.0574 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Pérez, J.F.; García-Ros, G.; Conesa, M.; Castro, E.; Cánovas, M. Methodology to Obtain Universal Solutions for Systems of Coupled Ordinary Differential Equations: Examples of a Continuous Flow Chemical Reactor and a Coupled Oscillator. Mathematics 2023, 11, 2303. https://doi.org/10.3390/math11102303
Sánchez-Pérez JF, García-Ros G, Conesa M, Castro E, Cánovas M. Methodology to Obtain Universal Solutions for Systems of Coupled Ordinary Differential Equations: Examples of a Continuous Flow Chemical Reactor and a Coupled Oscillator. Mathematics. 2023; 11(10):2303. https://doi.org/10.3390/math11102303
Chicago/Turabian StyleSánchez-Pérez, Juan Francisco, Gonzalo García-Ros, Manuel Conesa, Enrique Castro, and Manuel Cánovas. 2023. "Methodology to Obtain Universal Solutions for Systems of Coupled Ordinary Differential Equations: Examples of a Continuous Flow Chemical Reactor and a Coupled Oscillator" Mathematics 11, no. 10: 2303. https://doi.org/10.3390/math11102303
APA StyleSánchez-Pérez, J. F., García-Ros, G., Conesa, M., Castro, E., & Cánovas, M. (2023). Methodology to Obtain Universal Solutions for Systems of Coupled Ordinary Differential Equations: Examples of a Continuous Flow Chemical Reactor and a Coupled Oscillator. Mathematics, 11(10), 2303. https://doi.org/10.3390/math11102303










