Bounds for the Error in Approximating a Fractional Integral by Simpson’s Rule

Abstract

Simpson’s rule is a numerical method used for approximating the definite integral of a function. In this paper, by utilizing mappings whose second derivatives are bounded, we acquire the upper and lower bounds for the Simpson-type inequalities by means of Riemann–Liouville fractional integral operators. We also study special cases of our main results. Furthermore, we give some examples with graphs to illustrate the main results. This study on fractional Simpson’s inequalities is the first paper in the literature as a method.

1. Introduction

The classical Simpson’s inequality for four times continuously differentiable functions is the following.

Theorem 1

([1]). Let $f:\left[a,b\right]\to \mathbb{R}$ be a four times continuously differentiable function on $\left(a,b\right)$, and let us consider ${∥f^{\left(4\right)}∥}_{\infty }={\displaystyle \underset{x\in \left(a,b\right)}{sup}}\left|f^{\left(4\right)}\left(x\right)\right|<\infty .$ Then, the following inequality holds:

$$\left|\frac{1}{3}\left[\frac{f\left(a\right)+f\left(b\right)}{2}+2f\left(\frac{a+b}{2}\right)\right]-\frac{1}{b-a}{\int }_a^{b}f\left(x\right)dx\right|\le \frac{1}{2880}{∥f^{\left(4\right)}∥}_{\infty }{\left(b-a\right)}^4.$$

Since the theory of convex functions is an effective and useful way to solve a large number of problems from different branches of mathematics, many mathematicians have investigated the Simpson-type inequalities for convex functions. More precisely, in [1], some Simpson-type inequalities via s-convex mappings are established by utilizing differentiable mappings. Furthermore, new versions of the Simpson-type inequalities for differentiable convex mappings were established in [2,3]. The reader is referred to [4,5,6,7,8,9,10] and the references therein for more information and unexplained aspects regarding Simpson-type inequalities for various convex classes.

Many mathematicians have investigated the twice differentiable convex functions to obtain significant inequalities. For example, Sarikaya et al. proved some inequalities of Simpson’s type by using twice differentiable mappings in [11]. In addition, some Simpson-type inequalities are given for differentiable convex mappings in [12]. Moreover, the authors provide new estimates on the generalization of Hadamard, Ostrowski, and Simpson inequalities in the case of functions whose second derivatives in absolute values at certain powers are convex and quasi-convex functions in [13]. Furthermore, Simpson-type inequalities are established for $P-$convex functions in [14]. The reader may refer to [15,16,17,18] for further pieces of information and unexplained aspects regarding these types of inequalities, including twice differentiable functions.

Mathematical preliminaries in fractional calculus theory, which will be used throughout this paper, are given as follows.

Definition 1

([19]). Let us consider $f\in L_1[\rho ,\mu ].$ The Riemann–Liouville integrals $J_{\rho +}^{\alpha }f$ and $J_{\mu -}^{\alpha }f$ of order $\alpha >0$ are defined by

$$J_{\rho +}^{\alpha }f\left(\xi \right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{\rho }^{\xi }{\left(\xi -t\right)}^{\alpha -1}f\left(t\right)dt,\xi >\rho$$

and

$$J_{\mu -}^{\alpha }f\left(\xi \right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{\xi }^{\mu }{\left(t-\xi \right)}^{\alpha -1}f\left(t\right)dt,\xi <\mu ,$$

respectively. Here, $\Gamma \left(\alpha \right)$ is the Gamma function and is described as follows:

$$\Gamma \left(\alpha \right)={\int }_0^{\infty }{e}^{-u}{u}^{\alpha -1}du.$$

Let us also note that $J_{\rho +}^{0}f\left(\xi \right)=J_{\mu -}^{0}f\left(\xi \right)=f\left(\xi \right).$

Remark 1.

If we choose $\alpha =1$ in Definition 1, then the fractional integral reduces to the classical integral.

In [20], the Simpson inequalities for differentiable functions are extended to Riemann–Liouville fractional integrals. In addition to these, several papers are focused on fractional Simpson inequalities [21,22,23,24,25,26,27]. For further similar results and properties of Riemann–Liouville fractional integrals, see [19,28,29,30,31].

In [32], the authors proved some new inequalities of Simpson’s type based on $s-$convexity by fractional integrals. If we choose $s=1$ as in ([32], Theorem 2.3), we obtain the following.

Theorem 2

([32]). Let $f:I\subset [0,\infty )\to \mathbb{R}$ be a function such that f is differentiable on $I^0$. Let $a,b\in I$ with $a<b.$ Suppose that $f^{\prime }\in L_1[a,b]$ and $\left|f^{\prime }\right|$ is convex on $[a,b].$ Then, the following inequality for Riemann–Liouville fractional integrals holds:

$$\begin{array}{cc}\hfill & \frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{b-a}{2}\phi \left(\alpha \right)\left(\left|f^{\prime }\left(a\right)\right|+\left|f^{\prime }\left(b\right)\right|\right).\hfill \end{array}$$

Here,

$$\phi \left(\alpha \right)={\left(\frac{2}{3}\right)}^{\frac{1}{\alpha }+1}\left(\frac{\alpha }{1+\alpha }\right)+\frac{1}{2\left(1+\alpha \right)}-\frac{1}{3}.$$

Theorem 3

([33]). Suppose that the assumptions of Theorem 2 hold. Then, the following inequalities hold:

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\frac{a+b}{2}+}^{\alpha }f\left(b\right)+J_{\frac{a+b}{2}-}^{\alpha }f\left(a\right)\right]\right|\hfill \\ \hfill & \\ \hfill & \le \frac{b-a}{12}\left[C_2\left(\alpha \right)\left(\left|f^{\prime }\left(b\right)\right|+\left|f^{\prime }\left(a\right)\right|\right)+2C_1\left(\alpha \right)\left|f^{\prime }\left(\frac{a+b}{2}\right)\right|\right]\hfill \\ \hfill & \\ \hfill & \le \frac{b-a}{12}\left(C_1\left(\alpha \right)+C_2\left(\alpha \right)\right)\left(\left|f^{\prime }\left(a\right)\right|+\left|f^{\prime }\left(b\right)\right|\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill C_1\left(\alpha \right)& =2{\left(\frac{1}{3}\right)}^{\frac{2}{\alpha }}\left[\frac{1}{2}-\frac{1}{\alpha +2}\right]+\frac{3}{\alpha +2}-\frac{1}{2},\hfill \\ \hfill & \\ \hfill C_2\left(\alpha \right)& =2{\left(\frac{1}{3}\right)}^{\frac{1}{\alpha }}\left[1-\frac{1}{\alpha +1}\right]-2{\left(\frac{1}{3}\right)}^{\frac{2}{\alpha }}\left[\frac{1}{2}-\frac{1}{\alpha +2}\right]+\frac{3}{\left(\alpha +1\right)\left(\alpha +2\right)}-\frac{1}{2}.\hfill \end{array}$$

Iqbal et al. [20] established new Simpson-type inequalities for Riemann–Liouville fractional integrals using the convexity for the class of functions whose derivatives in absolute value at certain powers are convex functions, as proposed in the following theorem.

Theorem 4

([20]). Suppose that the assumptions of Theorem 2 are valid. Then, the inequality

$$\begin{array}{cc}\hfill & \left[\frac{1}{6}f\left(a\right)+\frac{2}{3}f\left(\frac{a+b}{2}\right)+\frac{1}{6}f\left(b\right)\right]-\frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{b-a}{2^{\alpha }}\left(K_1+K_2\right)\left(\left|f^{\prime }\left(a\right)\right|+\left|f^{\prime }\left(b\right)\right|\right)\hfill \end{array}$$

is valid. Here, $d^{\alpha }=\frac{2\left(2^{\alpha }-1\right)}{3}+1$ and

$$\begin{array}{c}{K}_1=\frac{1}{6}-\frac{1}{3}\left(1-{\left(\frac{1}{3}\right)}^{\frac{1}{\alpha }}\right)-\frac{1}{\left(\alpha +1\right)}{\left(\frac{1}{3}\right)}^{1+\frac{1}{\alpha }}+\frac{1}{2\left(\alpha +1\right)},\hfill \\ \\ K_2=2\left[\frac{1}{3}+\frac{1}{2\left(2^{\alpha }-1\right)}\right]\left(d-1\right)+\frac{1+2^{\alpha +1}-2d^{\alpha +1}}{2\left(2^{\alpha }-1\right)\left(\alpha +1\right)}-\left(\frac{1}{3}+\frac{1}{2\left(2^{\alpha }-1\right)}\right).\hfill \end{array}$$

The purpose of this paper is to prove some Simpson-type inequalities for Riemann–Liouville fractional integrals. The general structure of the paper consists of three sections, including the Introduction. The remaining parts of the paper are as follows. In Section 2, we will establish some upper and lower bounds for Simpson’s rule for Riemann–Liouville fractional integral operators by using functions whose second derivatives are bounded. Moreover, we also show a Simpson-type inequality for Riemann integrals by using a special case of our main results. Furthermore, we will give some examples to illustrate the main results. In the last section, some conclusions and further directions of research will be presented.

2. Main Results of Simpson-Type Inequalities for Bounded Functions

In this section, we establish the following inequalities, which give the upper and lower bounds for the Simpson-type inequalities for Riemann–Liouville fractional integral operators. Here, fractional Simpson-type inequalities are applied to the functions that have the conditions $m\le f^{″}\left(t\right)\le M$ for all $t\in \left[a,b\right]$ instead of convexity. Throughout this paper, we will refer to Theorems 2–4 as the Simpson-type inequalities of the first sense, second sense, and third sense, respectively.

2.1. Simpson-Type Inequalities of the First Sense

Theorem 5.

Let $f:\left[a,b\right]\to \mathbb{R}$ be a positive, twice differentiable function, and $f\in L_1\left[a,b\right].$ If $f^{″}$ is bounded, i.e., $m\le f^{″}\left(t\right)\le M$ for all $t\in \left[a,b\right]$ with $m,M\in \mathbb{R}$ and $\alpha >0,$ then the following inequalities hold:

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{12(\alpha +2)}\left[m\alpha -M\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{{(b-a)}^2}{12(\alpha +2)}\left[M\alpha -m\right].\hfill \end{array}$$

(1)

Proof. 

By using the change of variables, we have

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\left[\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^{\alpha -1}f\left(x\right)dx+\underset{\frac{a+b}{2}}{\overset{b}{\int }}{\left(x-\frac{a+b}{2}\right)}^{\alpha -1}f\left(x\right)dx\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\left[\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^{\alpha -1}f\left(x\right)dx+\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^{\alpha -1}f(a+b-x)dx\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^{\alpha -1}\left[f\left(x\right)+f(a+b-x)\right]dx.\hfill \end{array}$$

(2)

By the equality (2), we obtain

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^{\alpha -1}\left[f\left(x\right)+f(a+b-x)\right]dx-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^{\alpha -1}\left[3f\left(x\right)+3f(a+b-x)-\left(f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right)\right]dx.\hfill \end{array}$$

(3)

We can write easily that

$$f\left(x\right)-f\left(a\right)=\underset{a}{\overset{x}{\int }}{f}^{\prime }\left(t\right)dt,$$

(4)

$$f\left(a+b-x\right)-f\left(b\right)=-\underset{a+b-x}{\overset{b}{\int }}{f}^{\prime }\left(t\right)dt=-\underset{a}{\overset{x}{\int }}{f}^{\prime }(a+b-t)dt,$$

(5)

$$f\left(x\right)-f\left(\frac{a+b}{2}\right)=-\underset{x}{\overset{\frac{a+b}{2}}{\int }}{f}^{\prime }\left(t\right)dt,$$

(6)

and

$$f\left(a+b-x\right)-f\left(\frac{a+b}{2}\right)=\underset{\frac{a+b}{2}}{\overset{a+b-x}{\int }}{f}^{\prime }\left(t\right)dt=\underset{x}{\overset{\frac{a+b}{2}}{\int }}{f}^{\prime }(a+b-t)dt.$$

(7)

By using the equalities (4) and (5), we have

$$f\left(x\right)+f\left(a+b-x\right)-f\left(a\right)-f\left(b\right)=\underset{a}{\overset{x}{\int }}\left[f^{\prime }\left(t\right)-f^{\prime }(a+b-t)\right]dt.$$

(8)

From (6) and (7), we obtain

$$f\left(x\right)-2f\left(\frac{a+b}{2}\right)+f\left(a+b-x\right)=\underset{x}{\overset{\frac{a+b}{2}}{\int }}\left[f^{\prime }(a+b-t)-f^{\prime }\left(t\right)\right]dt.$$

(9)

We also have

$$f^{\prime }(a+b-t)-f^{\prime }\left(t\right)=\underset{t}{\overset{a+b-t}{\int }}{f}^{″}\left(u\right)du.$$

(10)

By using the equality (10) and $m<f^{″}\left(u\right)<M,$$u\in \left[a,b\right],$ we obtain

$$m\underset{t}{\overset{a+b-t}{\int }}du\le \underset{t}{\overset{a+b-t}{\int }}{f}^{″}\left(u\right)du\le M\underset{t}{\overset{a+b-t}{\int }}du$$

i.e.,

$$m\left(a+b-2t\right)\le f^{\prime }(a+b-t)-f^{\prime }\left(t\right)\le M\left(a+b-2t\right).$$

(11)

Integrating the inequality (11) with respect to t on $\left[a,x\right]$, we obtain

$$M\left(b-x\right)\left(a-x\right)\le \underset{a}{\overset{x}{\int }}\left[f^{\prime }\left(t\right)-f^{\prime }(a+b-t)\right]dt\le m\left(b-x\right)\left(a-x\right).$$

With the help of the equality (8), it follows that

$$M\left(b-x\right)\left(a-x\right)\le f\left(x\right)+f(a+b-x)-f\left(a\right)-f\left(b\right)\le m\left(b-x\right)\left(a-x\right).$$

(12)

Integrating the inequality (11) with respect to t on $\left[x,\frac{a+b}{2}\right]$, we obtain

$$m{\left(\frac{a+b}{2}-x\right)}^2\le \underset{x}{\overset{\frac{a+b}{2}}{\int }}\left[f^{\prime }\left(t\right)-f^{\prime }(a+b-t)\right]dt\le M{\left(\frac{a+b}{2}-x\right)}^2.$$

By using the equality (9), it follows that

$$2m{\left(\frac{a+b}{2}-x\right)}^2\le 2\left[f\left(x\right)-2f\left(\frac{a+b}{2}\right)+f\left(a+b-x\right)\right]\le 2M{\left(\frac{a+b}{2}-x\right)}^2.$$

(13)

From (12) and (13), we obtain

$$\begin{array}{cc}\hfill & M\left(b-x\right)\left(a-x\right)+2m{\left(\frac{a+b}{2}-x\right)}^2\hfill \\ \hfill & \hfill \\ \hfill & \le 3f\left(x\right)+3f(a+b-x)-f\left(a\right)-4f\left(\frac{a+b}{2}\right)-f\left(b\right)\hfill \\ \hfill & \hfill \\ \hfill & \le m\left(b-x\right)\left(a-x\right)+2M{\left(\frac{a+b}{2}-x\right)}^2.\hfill \end{array}$$

(14)

Multiplying the inequalities (14) by $\frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}{\left(\frac{a+b}{2}-x\right)}^2$ and integrating the resultant inequality with respect to x on $\left[a,\frac{a+b}{2}\right]$, we have

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^2\left(M\left(b-x\right)\left(a-x\right)+2m{\left(\frac{a+b}{2}-x\right)}^2\right)dx\hfill \\ \hfill & \le \frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^2\left[3f\left(x\right)+3f(a+b-x)-f\left(a\right)-4f\left(\frac{a+b}{2}\right)-f\left(b\right)\right]dx\hfill \\ \hfill & \le \frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^2\left(m\left(b-x\right)\left(a-x\right)+2M{\left(\frac{a+b}{2}-x\right)}^2\right)dx.\hfill \end{array}$$

By using the equalities (3) and the equality

$$\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^2\left(M\left(b-x\right)\left(a-x\right)+2m{\left(\frac{a+b}{2}-x\right)}^2\right)dx=\frac{2}{\alpha +2}\left[m-\frac{M}{\alpha }\right]{\left(\frac{b-a}{2}\right)}^{\alpha +2},$$

then we obtain

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{12(\alpha +2)}\left[m\alpha -M\right]\hfill \\ \hfill & \\ \hfill & \le \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{{(b-a)}^2}{12(\alpha +2)}\left[M\alpha -m\right].\hfill \end{array}$$

This completes the proof of Theorem 5. □

Corollary 1.

Let us consider $\alpha =1$ in Theorem 5. Then, we obtain

$$\frac{{(b-a)}^2}{36}\left[m-M\right]\le \frac{1}{b-a}\underset{a}{\overset{b}{\int }}f\left(t\right)dt-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\le \frac{{(b-a)}^2}{36}\left[M-m\right].$$

Equivalently, we have

$$\left|\frac{1}{b-a}\underset{a}{\overset{b}{\int }}f\left(t\right)dt-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\right|\le \frac{{(b-a)}^2}{36}\left[M-m\right].$$

Example 1.

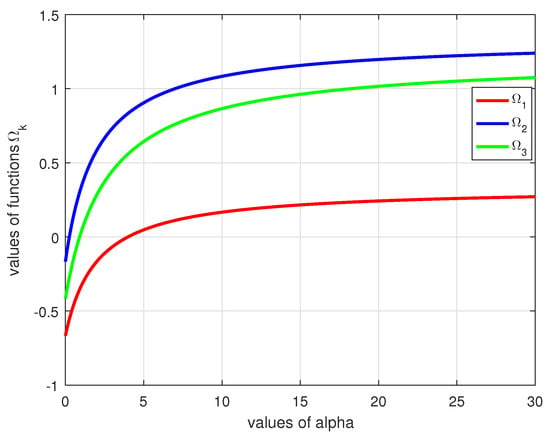
If we define a function $f:[a,b]=[0,1]\to \mathbb{R}$ by $f\left(x\right)=x^3+x^2$, then we obtain $m=2$ and $M=8$. Let us consider the left and right sides of the inequalities (1) as follows:

$$\frac{{(b-a)}^2}{12(\alpha +2)}\left[m\alpha -M\right]=\frac{\alpha -4}{6(\alpha +2)}:={\Omega }_1$$

and

$$\frac{{(b-a)}^2}{12(\alpha +2)}\left[M\alpha -m\right]=\frac{4\alpha -1}{6(\alpha +2)}:={\Omega }_2.$$

The middle parts of the inequalities (1) are as follows:

$$\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]=\frac{1}{6}\left[f\left(0\right)+4f\left(\frac{1}{2}\right)+f\left(1\right)\right]=\frac{7}{12},$$

(15)

$$\begin{array}{cc}\hfill J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)& =J_{0+}^{\alpha }f\left(\frac{1}{2}\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{0}{\overset{\frac{1}{2}}{\int }}\left(\frac{1}{2}-x\right)\left(x^3+x^2\right)dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{1}{\Gamma \left(\alpha \right)}\left[-\frac{1}{2^{\alpha +3}\left(\alpha +3\right)}+\frac{5}{2\left(\alpha +2\right)}-\frac{7}{4\left(\alpha +1\right)}+\frac{3}{2^{\alpha +3}\alpha }\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{3{\alpha }^3+3{\alpha }^2+4\alpha +18}{2^{\alpha +3}\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)},\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)& =J_{1-}^{\alpha }f\left(\frac{1}{2}\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{\frac{1}{2}}{\overset{1}{\int }}\left(\frac{1}{2}-x\right)\left(x^3+x^2\right)dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{16{\alpha }^3+76{\alpha }^2+92\alpha +18}{2^{\alpha +3}\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}.\hfill \end{array}$$

(17)

With the help of the equalities (15)–(17), we have

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{19{\alpha }^3+79{\alpha }^2+96\alpha +36}{16\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}-\frac{7}{12}:={\Omega }_3.\hfill \end{array}$$

As one can see in Figure 1, the result of our appropriate choices in Example 1 is provided in the double inequality (1).

2.2. Simpson’s Type Inequalities of the Second Sense

Theorem 6.

Under the assumptions of Theorem 5, we have the following double inequality:

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4m-\alpha \left(\alpha +3\right)M\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}f\left[\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4M-\alpha \left(\alpha +3\right)m\right].\hfill \end{array}$$

(18)

Proof. 

By using the change of variables, we have

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\left[\underset{\frac{a+b}{2}}{\overset{b}{\int }}{\left(b-x\right)}^{\alpha -1}f\left(x\right)dx+\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(x-a\right)}^{\alpha -1}f\left(x\right)dx\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\left[\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(x-a\right)}^{\alpha -1}f\left(a+b-x\right)dx+\underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(x-a\right)}^{\alpha -1}f\left(x\right)dx\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[f\left(x\right)+f(a+b-x)\right]{\left(x-a\right)}^{\alpha -1}dx.\hfill \end{array}$$

(19)

By the equalities (19), we obtain

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[f\left(x\right)+f(a+b-x)\right]{\left(x-a\right)}^{\alpha -1}dx-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[3f\left(x\right)+3f(a+b-x)-f\left(a\right)-4f\left(\frac{a+b}{2}\right)-f\left(b\right)\right]{\left(x-a\right)}^{\alpha -1}dx.\hfill \end{array}$$

Multiplying the inequality (14) by $\frac{2^{\alpha -1}\alpha {\left(x-a\right)}^{\alpha -1}}{3{\left(b-a\right)}^{\alpha }}$ and integrating the resultant inequality with respect to x on $\left[a,\frac{a+b}{2}\right]$, we obtain

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left(2{\left(\frac{a+b}{2}-x\right)}^{2}m-M(b-x)(x-a)\right){\left(x-a\right)}^{\alpha -1}dx\hfill \\ \hfill & \\ \hfill & \le \frac{2^{\alpha -1}\alpha }{{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[3f\left(x\right)-f\left(a\right)-f\left(b\right)-4f\left(\frac{a+b}{2}\right)+3f(a+b-x)\right]{\left(x-a\right)}^{\alpha -1}dx\hfill \\ \hfill & \\ \hfill & \le \frac{2^{\alpha -1}\alpha }{3{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left(2{\left(\frac{a+b}{2}-x\right)}^{2}M-m(b-x)(x-a)\right){\left(x-a\right)}^{\alpha -1}dx.\hfill \end{array}$$

If we consider the equalities

$$\begin{array}{cc}\hfill \underset{a}{\overset{\frac{a+b}{2}}{\int }}{\left(\frac{a+b}{2}-x\right)}^2{\left(x-a\right)}^{\alpha -1}dx& =\frac{{\left(b-a\right)}^{\alpha +2}}{2^{\alpha +1}\alpha (\alpha +1)(\alpha +2)}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \underset{a}{\overset{\frac{a+b}{2}}{\int }}\left(b-x\right){\left(x-a\right)}^{\alpha }dx& =\frac{2{\left(b-a\right)}^{\alpha +2}\left(\alpha +3\right)}{2^{\alpha +2}(\alpha +1)(\alpha +2)},\hfill \end{array}$$

then we obtain

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4m-\alpha \left(\alpha +3\right)M\right]\hfill \\ \hfill & \\ \hfill & \le \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{{\left(\frac{a+b}{2}\right)}^{+}}^{\alpha }f\left(b\right)+J_{{\left(\frac{a+b}{2}\right)}^{-}}^{\alpha }f\left(a\right)\right]-\frac{1}{6}f\left[\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4M-\alpha \left(\alpha +3\right)m\right].\hfill \end{array}$$

This concludes the proof of the inequalities (18). □

Remark 2.

If we choose $\alpha =1$ in Theorem 6, then Theorem 6 reduces to Corollary 1.

Example 2.

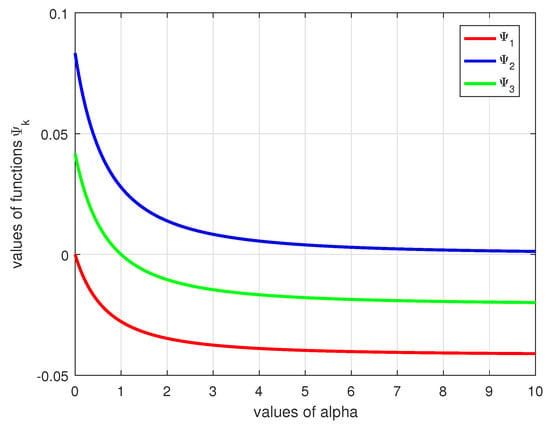
If we describe a function $f:[a,b]=[0,1]\to \mathbb{R}$ by $f\left(x\right)=\frac{x^3}{6}$, then we have $m=0$ and $M=1$. The left and right sides of the inequalities (18) are as follows:

$$\frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4m-\alpha \left(\alpha +3\right)M\right]=\frac{-\alpha \left(\alpha +3\right)}{24(\alpha +1)(\alpha +2)}:={\Psi }_1$$

and

$$\frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4M-\alpha \left(\alpha +3\right)m\right]=\frac{1}{6(\alpha +1)(\alpha +2)}:={\Psi }_2.$$

The middle parts of inequalities (18) are as follows:

$$\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]=\frac{1}{6}\left[0+\frac{1}{12}+\frac{1}{6}\right]=\frac{1}{24},$$

(20)

$$\begin{array}{cc}\hfill J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)& =J_{\left(\frac{1}{2}\right)+}^{\alpha }f\left(1\right)=\frac{1}{6\Gamma \left(\alpha \right)}\underset{\frac{1}{2}}{\overset{1}{\int }}{\left(1-x\right)}^{\alpha -1}{x}^{3}dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{1}{6\Gamma \left(\alpha \right)}\left[-\frac{1}{2^{\alpha +3}\left(\alpha +3\right)}+\frac{3}{2^{\alpha +2}\left(\alpha +2\right)}-\frac{3}{2^{\alpha +1}\left(\alpha +1\right)}+\frac{1}{2^{\alpha }\alpha }\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{{\alpha }^3+9{\alpha }^2+32\alpha +48}{3·2^{\alpha }\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)},\hfill \end{array}$$

(21)

and

$$\begin{array}{cc}\hfill J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)& =J_{\left(\frac{1}{2}\right)-}^{\alpha }f\left(0\right)=\frac{1}{6\Gamma \left(\alpha \right)}\underset{0}{\overset{\frac{1}{2}}{\int }}{x}^{\alpha +2}dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{1}{3·2^{\alpha +4}\Gamma \left(\alpha \right)\left(\alpha +3\right)}.\hfill \end{array}$$

(22)

By using equalities (20)–(22), it follows that

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}f\left[\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{-{\alpha }^3-6{\alpha }^2-5\alpha +12}{48\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}:={\Psi }_3.\hfill \end{array}$$

As one can see in Figure 2, the result of Example 2 is satisfied in the inequality (18).

2.3. Simpson’s Type Inequalities of the Third Sense

Theorem 7.

Under the assumptions of Theorem 5, we have the inequalities

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[m\frac{{\alpha }^2-\alpha +2}{2\alpha }-M\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{{(b-a)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[M\frac{{\alpha }^2-\alpha +2}{2\alpha }-m\right].\hfill \end{array}$$

(23)

Proof. 

With the help of the change of variables, we have

$$\begin{array}{cc}\hfill & \frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{2{\left(b-a\right)}^{\alpha }}\left[\underset{a}{\overset{b}{\int }}{\left(b-x\right)}^{\alpha -1}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}{\left(x-a\right)}^{\alpha -1}f\left(x\right)dx\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{2{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{b}{\int }}\left[{\left(b-x\right)}^{\alpha -1}+{\left(x-a\right)}^{\alpha -1}\right]f\left(x\right)dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{2{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{b}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]f(a+b-x)dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{b}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left[f\left(x\right)+f(a+b-x)\right]dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{2{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left[f\left(x\right)+f(a+b-x)\right]dx.\hfill \end{array}$$

(24)

By the equality (24), we obtain

$$\begin{array}{cc}\hfill & \frac{\Gamma (\alpha +1)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{2{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left[f\left(x\right)+f(a+b-x)\right]dx-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{\alpha }{6{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left[3f\left(x\right)+3f(a+b-x)-\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\right]dx.\hfill \end{array}$$

(25)

Multiplying the inequalities (14) by $\frac{\alpha }{6{\left(b-a\right)}^{\alpha }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]$ and integrating the resultant inequality with respect to x on $\left[a,\frac{a+b}{2}\right]$, it follows that

$$\begin{array}{cc}\hfill & \frac{\alpha }{6{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left(M\left(b-x\right)\left(a-x\right)+2m{\left(\frac{a+b}{2}-x\right)}^2\right)dx\hfill \\ \hfill & \\ \hfill & \le \frac{\alpha }{6{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left(3f\left(x\right)+3f(a+b-x)-f\left(a\right)-4f\left(\frac{a+b}{2}\right)-f\left(b\right)\right)dx\hfill \\ \hfill & \\ \hfill & \le \frac{\alpha }{6{\left(b-a\right)}^{\alpha }}\underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left(m\left(b-x\right)\left(a-x\right)+2M{\left(\frac{a+b}{2}-x\right)}^2\right)dx.\hfill \end{array}$$

From (25) and the equality

$$\begin{array}{cc}\hfill & \underset{a}{\overset{\frac{a+b}{2}}{\int }}\left[{\left(x-a\right)}^{\alpha -1}+{\left(b-x\right)}^{\alpha -1}\right]\left(M\left(b-x\right)\left(a-x\right)+2m{\left(\frac{a+b}{2}-x\right)}^2\right)dx\hfill \\ \hfill & \\ \hfill & =\frac{{\left(b-a\right)}^{\alpha +2}}{\left(\alpha +1\right)\left(\alpha +2\right)}\left[\frac{{\alpha }^2-\alpha +2}{2\alpha }m-M\right],\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill & \frac{{\left(b-a\right)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[\frac{{\alpha }^2-\alpha +2}{2\alpha }m-M\right]\hfill \\ \hfill & \\ \hfill & \le \frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{{\left(b-a\right)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[\frac{{\alpha }^2-\alpha +2}{2\alpha }M-m\right].\hfill \end{array}$$

This completes the proof of Theorem 7. □

Remark 3.

Let us consider $\alpha =1$ in Theorem 7. Then, Theorem 7 becomes Corollary 1.

Example 3.

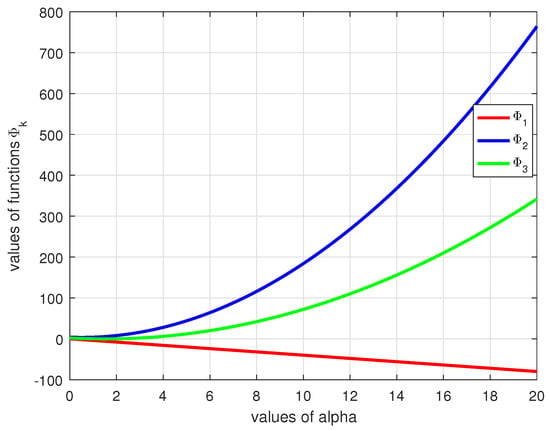
If we choose a function $f:[a,b]=[0,2]\to \mathbb{R}$ by $f\left(x\right)=x^3+1,$ then we obtain $m=0$ and $M=12$. Let us consider the left and right sides of the double inequality (23). Then, the following equalities hold:

$$\frac{{(b-a)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[m\frac{{\alpha }^2-\alpha +2}{2\alpha }-M\right]=\frac{-8\alpha }{(\alpha +1)(\alpha +2)}:={\Phi }_1$$

and

$$\frac{{(b-a)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[M\frac{{\alpha }^2-\alpha +2}{2\alpha }-m\right]=\frac{4\left({\alpha }^2-\alpha +2\right)}{(\alpha +1)(\alpha +2)}:={\Phi }_2.$$

The middle parts of inequalities (23) are as follows:

$$\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]=\frac{1}{6}\left[f\left(0\right)+4f\left(1\right)+f\left(2\right)\right]=3,$$

(26)

$$\begin{array}{cc}\hfill J_{a+}^{\alpha }f\left(b\right)& =J_{0+}^{\alpha }f\left(2\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{0}{\overset{2}{\int }}{\left(2-x\right)}^{\alpha -1}\left(x^3+1\right)dx\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha +3}}{\Gamma \left(\alpha \right)}\left[\frac{3}{\alpha +2}-\frac{1}{\alpha +3}+\frac{9}{8\alpha }-\frac{2}{\alpha +1}\right]\hfill \\ \hfill & \hfill \\ \hfill & =\frac{2^{\alpha }\left({\alpha }^3+6{\alpha }^2+11\alpha +54\right)}{\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}.\hfill \end{array}$$

(27)

Similarly, we can also obtain

$$\begin{array}{cc}\hfill J_{b-}^{\alpha }f\left(a\right)& =J_{2-}^{\alpha }f\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}\underset{0}{\overset{2}{\int }}{x}^{\alpha -1}\left(x^3+1\right)dx=\frac{2^{\alpha }\left(9\alpha +3\right)}{\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}.\hfill \end{array}$$

(28)

By utilizing equalities (26)–(28), the following equality arises:

$$\begin{array}{cc}\hfill & \frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{2{\alpha }^3-14\alpha +12}{\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}:={\Phi }_3.\hfill \end{array}$$

As one can see in Figure 3, the result of our appropriate choices in Example 3 is provided in the double inequality (23).

3. Conclusions

In the present paper, we prove some Simpson-type inequalities for Riemann–Liouville fractional integral operators by utilizing the functions whose second derivatives are bounded. Some examples that give a graphical illustration of our main results are presented. With reference to our paper, other authors can try to find better bounds using functions with conditions $m\le f^{″}\left(t\right)\le M$ for all $t\in \left[a,b\right]$ instead of convexity in future studies. Moreover, by applying these results, researchers can obtain some new approaches in the theory of optimization.