An Improved Mixture Model of Gaussian Processes and Its Classification Expectation–Maximization Algorithm
Abstract
1. Introduction
2. Related Works
3. Model Construction
3.1. The GP
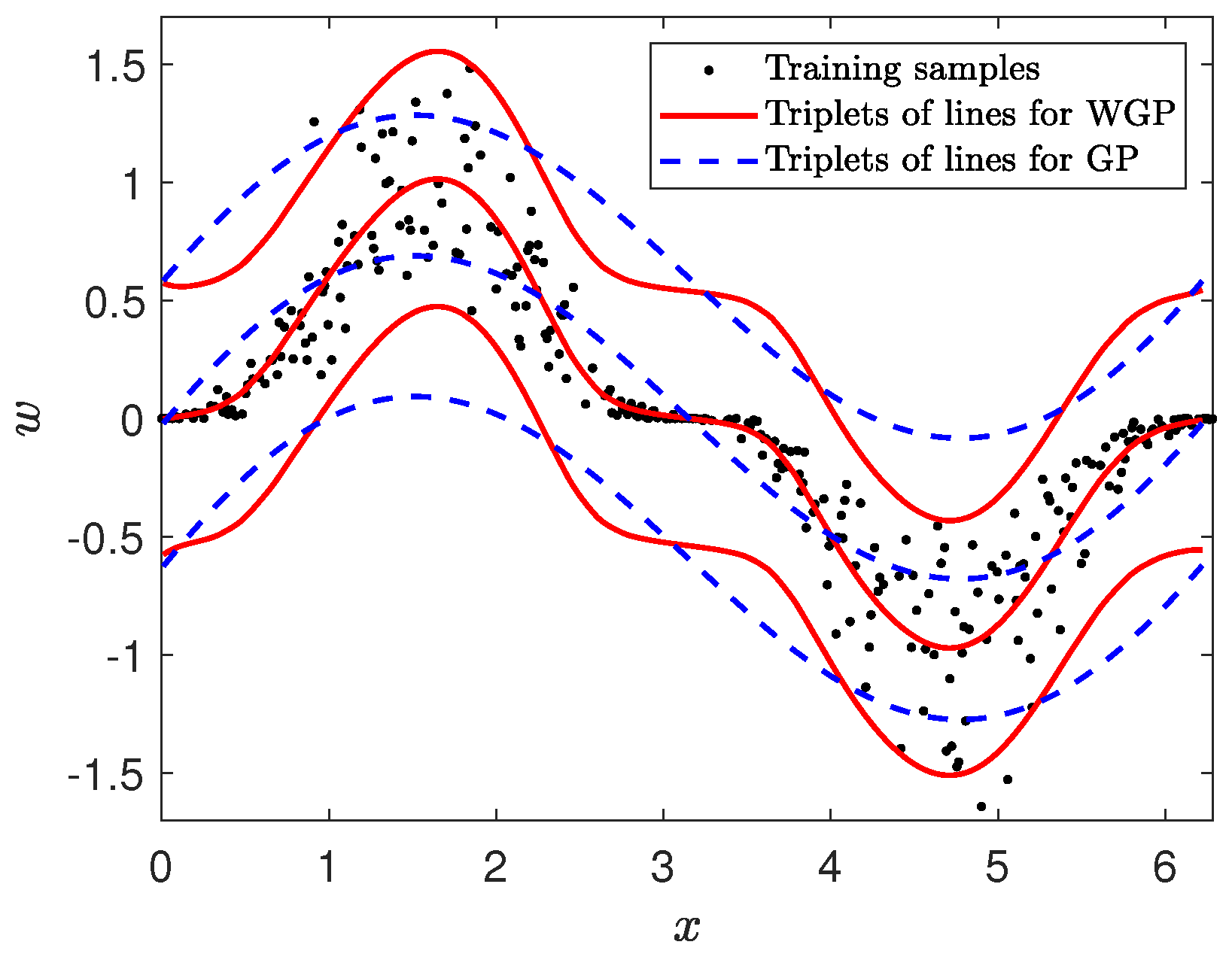
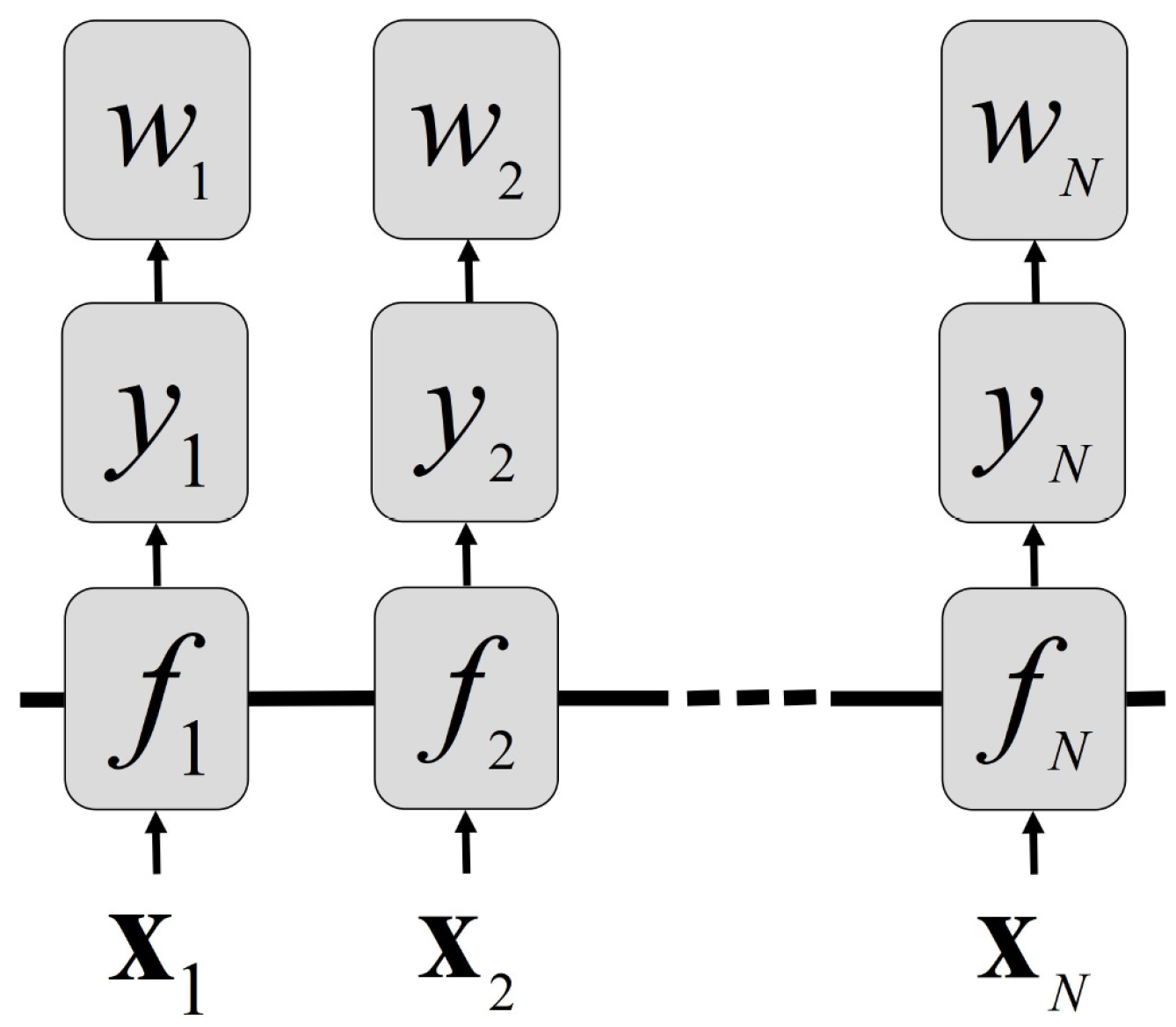
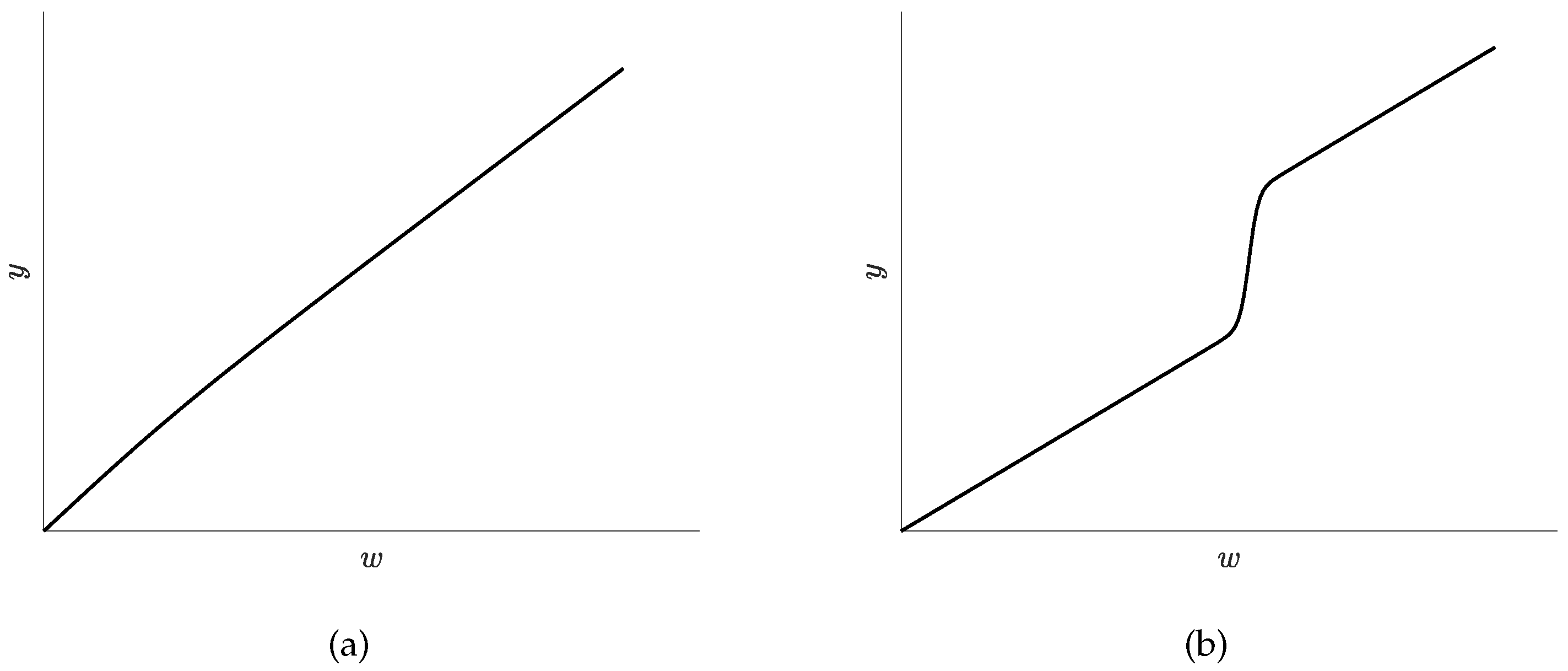
3.2. The WGP Model
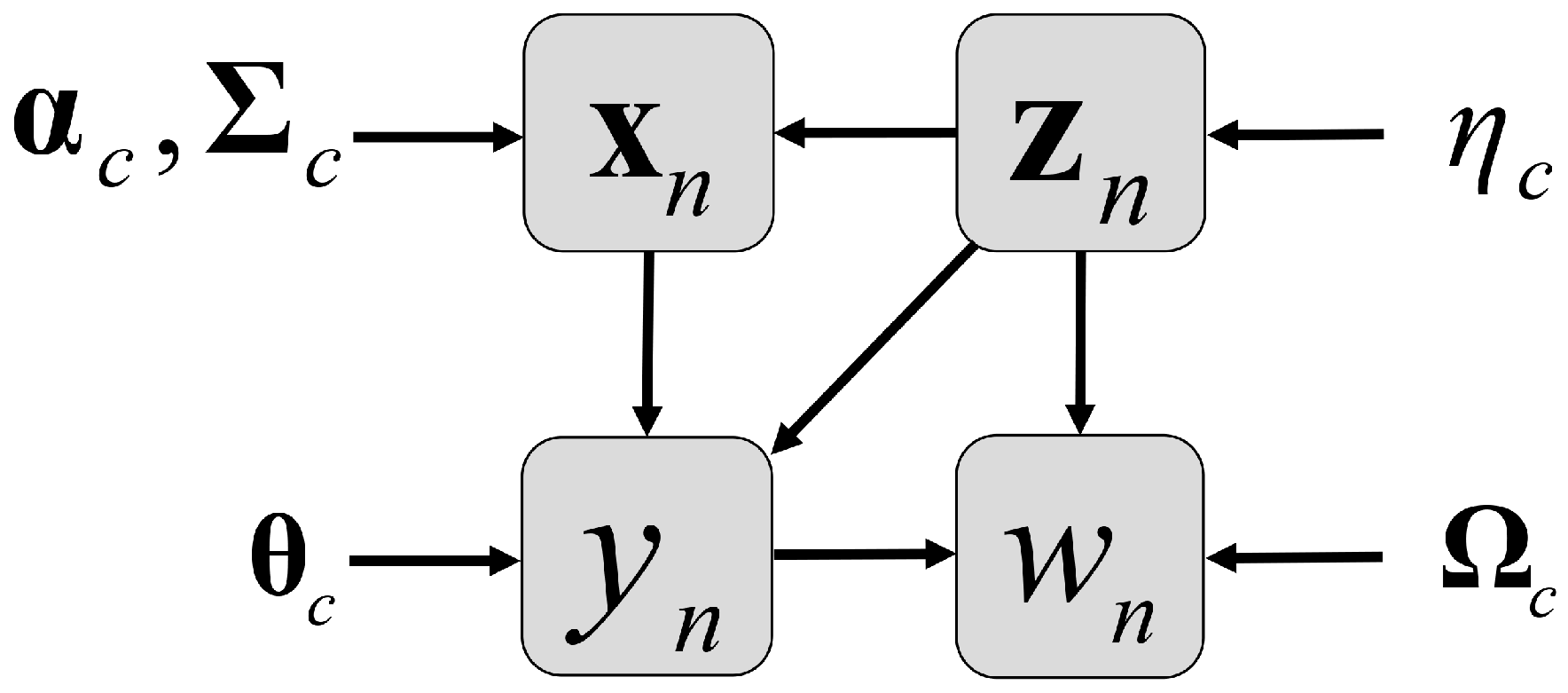
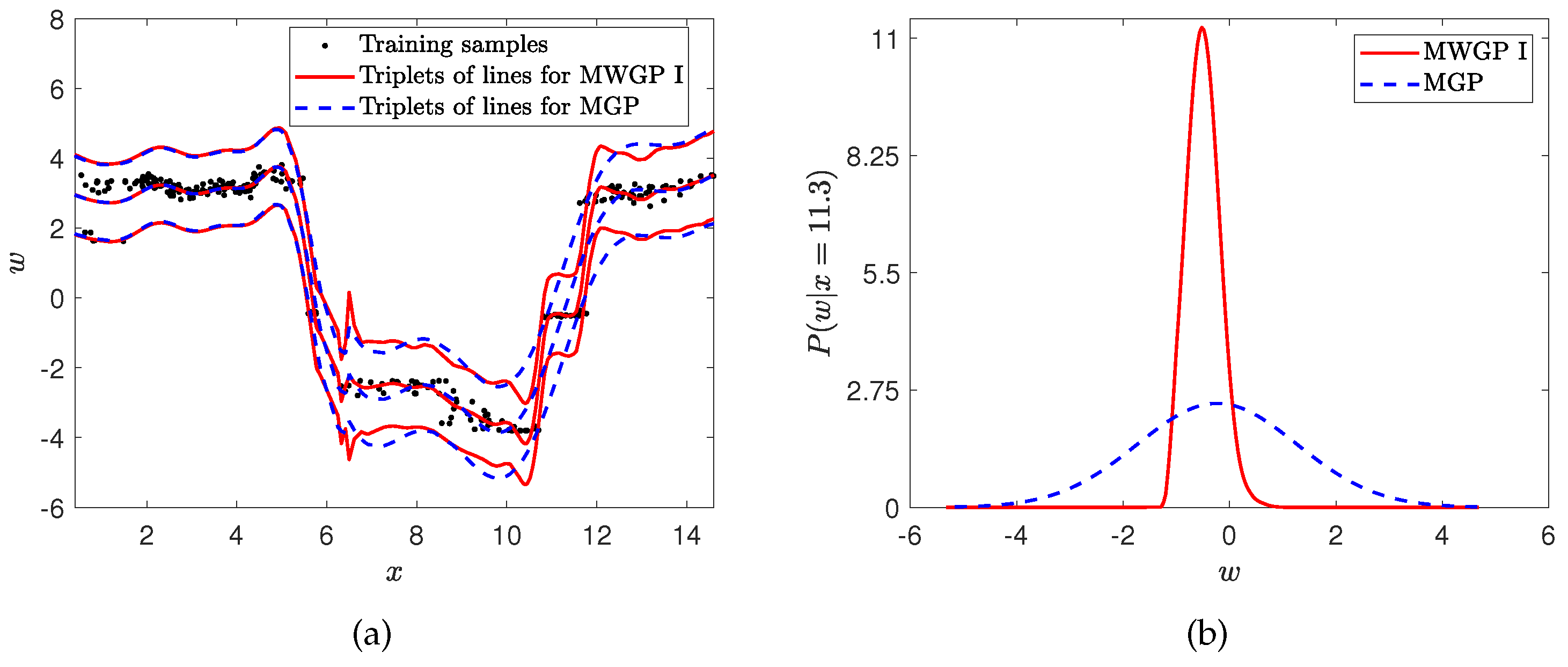
3.3. The MWGP Model
4. Algorithm Design
4.1. Procedures of the Proposed Algorithms
| Algorithm 1 The SMCEM algorithm for MWGP |
| Input: Output:
|
| Algorithm 2 The CEM algorithm for MWGP |
| Input: Output:
|
| Algorithm 3 The partial CEM algorithm for MWGP. |
| Input: Output:
|
4.2. Prediction Strategy
5. Experimental Results
5.1. Comparative Models
5.2. Synthetic Datasets of MWGP I
- (a low noise dataset): .
- (a high noise dataset): .
- , .
- , .
- (a short length-scale dataset): , .
- (a long length-scale dataset): , .
- (a medium overlapping dataset): , .
- (a large overlapping dataset): , .
- (an unbalanced dataset): , .
5.3. Synthetic Datasets of MWGP II
- (a noise dataset): , and .
- , , , , and .
- (a length-scale dataset): , , , , and .
- (an overlapping dataset):
- (an unbalanced dataset): , , , and , .
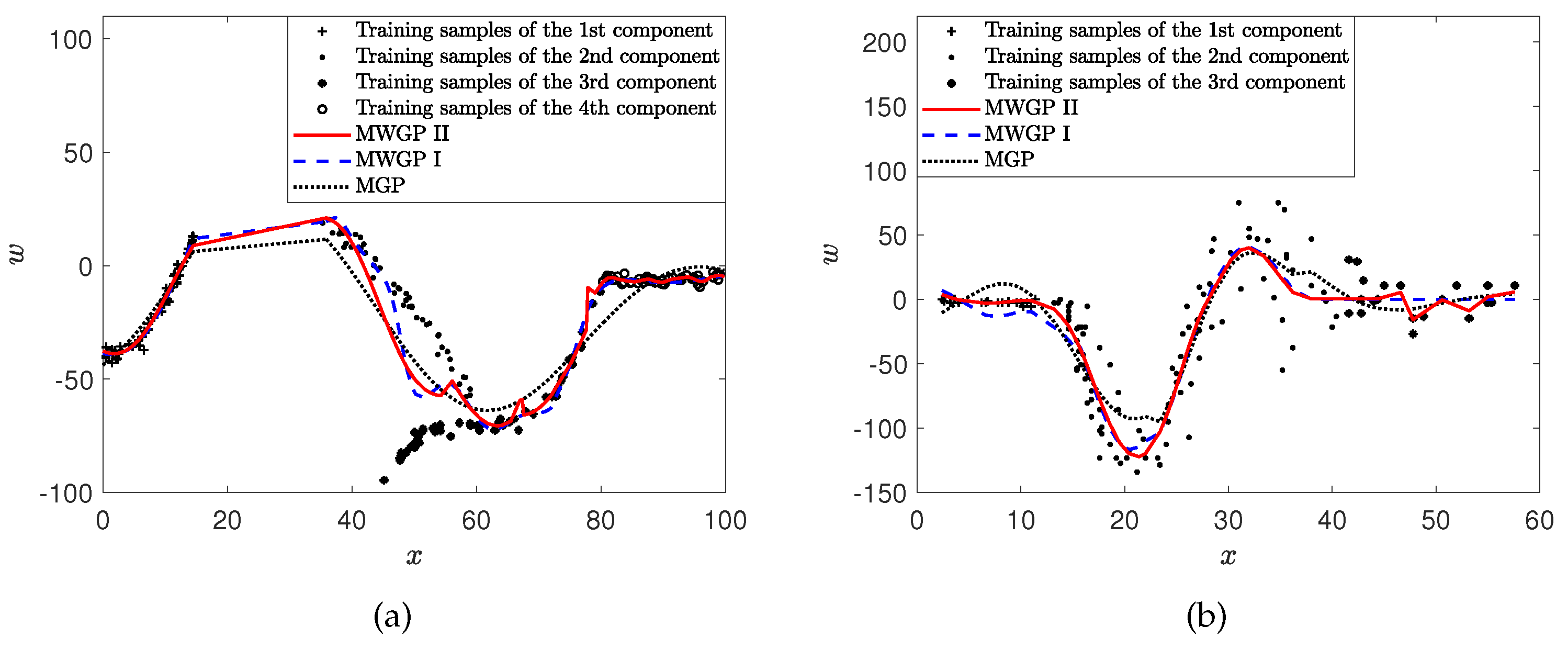
5.4. Toy and Motorcycle Datasets
5.5. River-flow Datasets
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AEP | Average estimated parameter |
| ALLF | Approximated log-likelihood function |
| CEM | Classification expectation–maximization (also called hard-cut expectation–maximization or hard expectation–maximization) |
| EM | Expectation–maximization |
| FNN | Feedforward neural network |
| GP | Gaussian process |
| LOOCV | Leave-one-out cross-validation |
| MAE | Mean absolute error |
| MAP | Maximum a posteriori |
| MCMC | Markov chain Monte Carlo |
| ME | Mixture of experts |
| MGP | Mixture of Gaussian processes |
| MLE | Maximum likelihood estimation |
| MWGP | Mixture of warped Gaussian processes |
| RMSE | Root mean square error |
| RP | Real parameter |
| SDEP | Standard deviation of the estimated parameter |
| SD | Standard deviation |
| SMCEM | Split and merge classification expectation–maximization |
| SVM | Support vector machine |
| VB | Variational Bayesian |
| WGP | Warped Gaussian process |
Appendix A. Details of the CEM Algorithm
Appendix A.1. The Derivation of the Q-Function and Details of the Approximated MAP Principle
Appendix A.2. Details for Maximizing the Approximated Q-Function
Appendix B. Details of the Partial CEM Algorithm
Appendix B.1. Details of Maximizing the Approximated Q-Function of the Partial CEM Algorithm
Appendix B.2. Details of the Approximated MAP Principle of the Partial CEM Algorithm
Appendix C. Split and Merge Criteria
References
- Yuksel, S.E.; Wilson, J.N.; Gader, P.D. Twenty years of mixture of experts. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1177–1193. [Google Scholar] [CrossRef]
- Jordan, M.I.; Jacobs, R.A. Hierarchies mixtures of experts and the EM algorithm. Neural Comput. 1994, 6, 181–214. [Google Scholar] [CrossRef]
- Lima, C.A.M.; Coelho, A.L.V.; Zuben, F.J.V. Hybridizing mixtures of experts with support vector machines: Investigation into nonlinear dynamic systems identification. Inf. Sci. 2007, 177, 2049–2074. [Google Scholar] [CrossRef]
- Tresp, V. Mixtures of Gaussian processes. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Denver, CO, USA, 1 January 2000; Volume 13, pp. 654–660. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar]
- Rasmussen, C.E.; Ghahramani, Z. Infinite mixture of Gaussian process experts. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 9–14 December 2002; Volume 2, pp. 881–888. [Google Scholar]
- Meeds, E.; Osindero, S. An alternative infinite mixture of Gaussian process experts. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 4–7 December 2005; Volume 18, pp. 883–896. [Google Scholar]
- Yuan, C.; Neubauer, C. Variational mixture of Gaussian process experts. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–11 December 2008; Volume 21, pp. 1897–1904. [Google Scholar]
- Brahim-Belhouari, S.; Bermak, A. Gaussian process for nonstationary time series prediction. Comput. Stat. Data Anal. 2004, 47, 705–712. [Google Scholar] [CrossRef]
- Pérez-Cruz, F.; Vaerenbergh, S.V.; Murillo-Fuentes, J.J.; Lázaro-Gredilla, M.; Santamaría, I. Gaussian processes for nonlinear signal processing: An overview of recent advances. IEEE Signal Process. Mag. 2013, 30, 40–50. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Process for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Chapter 2. [Google Scholar]
- MacKay, D.J.C. Introduction to Gaussian processes. NATO ASI Ser. F Comput. Syst. Sci. 1998, 168, 133–166. [Google Scholar]
- Xu, Z.; Guo, Y.; Saleh, J.H. VisPro: A prognostic SqueezeNet and non-stationary Gaussian process approach for remaining useful life prediction with uncertainty quantification. Neural Comput. Appl. 2022, 34, 14683–14698. [Google Scholar] [CrossRef]
- Heinonen, M.; Mannerström, H.; Rousu, J.; Kaski, S.; Lähdesmäki, H. Non-stationary Gaussian process regression with hamiltonian monte carlo. In Proceedings of the Machine Learning Research, Cadiz, Spain, 9–11 May 2016; Volume 51, pp. 732–740. [Google Scholar]
- Wang, Y.; Chaib-draa, B. Bayesian inference for time-varying applications: Particle-based Gaussian process approaches. Neurocomputing 2017, 238, 351–364. [Google Scholar] [CrossRef]
- Rhode, S. Non-stationary Gaussian process regression applied in validation of vehicle dynamics models. Eng. Appl. Artif. Intell. 2020, 93, 103716. [Google Scholar] [CrossRef]
- Sun, S.; Xu, X. Variational inference for infinite mixtures of Gaussian processes with applications to traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2010, 12, 466–475. [Google Scholar] [CrossRef]
- Jeon, Y.; Hwang, G. Bayesian mixture of gaussian processes for data association problem. Pattern Recognit. 2022, 127, 108592. [Google Scholar] [CrossRef]
- Li, T.; Ma, J. Attention mechanism based mixture of Gaussian processes. Pattern Recognit. Lett. 2022, 161, 130–136. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J. Efficient clustering for continuous occupancy mapping using a mixture of Gaussian processes. Sensors 2022, 22, 6832. [Google Scholar] [CrossRef]
- Tayal, A.; Poupart, P.; Li, Y. Hierarchical double Dirichlet process mixture of Gaussian processes. In Proceedings of the 26th AAAI Conference on Artificial Intelligence (AAAI), Toronto, ON, Canada, 22–26 July 2012; pp. 1126–1133. [Google Scholar]
- Sun, S. Infinite mixtures of multivariate Gaussian processes. In Proceedings of the International Conference on Machine Learning and Cybernetics (ICMLC), Tianjin, China, 14–17 July 2013; pp. 1011–1016. [Google Scholar]
- Kastner, M. Monte Carlo methods in statistical physics: Mathematical foundations and strategies. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1589–1602. [Google Scholar] [CrossRef]
- Khodadadian, A.; Parvizi, M.; Teshnehlab, M.; Heitzinger, C. Rational design of field-effect sensors using partial differential equations, Bayesian inversion, and artificial neural networks. Sensors 2022, 22, 4785. [Google Scholar] [CrossRef] [PubMed]
- Noii, N.; Khodadadian, A.; Ulloa, J.; Aldakheel, F.; Wick, T.; François, S.; Wriggers, P. Bayesian inversion with open-source codes for various one-dimensional model problems in computational mechanics. Arch. Comput. Methods Eng. 2022, 29, 4285–4318. [Google Scholar] [CrossRef]
- Ross, J.C.; Dy, J.G. Nonparametric mixture of Gaussian processes with constraints. In Proceedings of the 30th International Conference on Machine Learning (ICML), Atlanta, GA, USA, 17–19 June 2013; pp. 1346–1354. [Google Scholar]
- Yang, Y.; Ma, J. An efficient EM approach to parameter learning of the mixture of Gaussian processes. In Proceedings of the Advances in International Symposium on Neural Networks (ISNN), Guilin, China, 29 May–1 June 2011; Volume 6676, pp. 165–174. [Google Scholar]
- Chen, Z.; Ma, J.; Zhou, Y. A precise hard-cut EM algorithm for mixtures of Gaussian processes. In Proceedings of the 10th International Conference on Intelligent Computing (ICIC), Taiyuan, China, 3–6 August 2014; Volume 8589, pp. 68–75. [Google Scholar]
- Celeux, G.; Govaert, G. A classification EM algorithm for clustering and two stochastic versions. Comput. Stat. Data Anal. 1992, 14, 315–332. [Google Scholar] [CrossRef]
- Wu, D.; Chen, Z.; Ma, J. An MCMC based EM algorithm for mixtures of Gaussian processes. In Proceedings of the Advances in International Symposium on Neural Networks (ISNN), Jeju, Republic of Korea, 15–18 October 2015; Volume 9377, pp. 327–334. [Google Scholar]
- Wu, D.; Ma, J. An effective EM algorithm for mixtures of Gaussian processes via the MCMC sampling and approximation. Neurocomputing 2019, 331, 366–374. [Google Scholar] [CrossRef]
- Ma, J.; Xu, L.; Jordan, M.I. Asymptotic convergence rate of the EM algorithm for Gaussian mixtures. Neural Comput. 2000, 12, 2881–2907. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, Z.; Ma, J. An effective model selection criterion for mixtures of Gaussian processes. In Proceedings of the Advances in Neural Networks-ISNN, Jeju, Republic of Korea, 15–18 October 2015; Volume 9377, pp. 345–354. [Google Scholar]
- Ueda, N.; Nakano, R.; Ghahramani, Z.; Hinton, G.E. SMEM algorithm for mixture models. Adv. Neural Inf. Process. Syst. 1998, 11, 599–605. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, L. A novel split and merge EM algorithm for Gaussian mixture model. In Proceedings of the International Conference on Natural Computation (ICNC), Tianjin, China, 14–16 August 2009; pp. 479–483. [Google Scholar]
- Zhang, Z.; Chen, C.; Sun, J.; Chan, K.L. EM algorithms for Gaussian mixtures with split-and-merge operation. Pattern Recognit. 2003, 36, 1973–1983. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, J. A dynamic model selection algorithm for mixtures of Gaussian processes. In Proceedings of the IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1095–1099. [Google Scholar]
- Li, T.; Wu, D.; Ma, J. Mixture of robust Gaussian processes and its hard-cut EM algorithm with variational bounding approximation. Neurocomputing 2021, 452, 224–238. [Google Scholar] [CrossRef]
- Snelson, E.; Rasmussen, C.E.; Ghahramani, Z. Warped Gaussian processes. Adv. Neural Inf. Process. Syst. 2003, 16, 337–344. [Google Scholar]
- Schmidt, M.N. Function factorization using warped Gaussian processes. In Proceedings of the 26th International Conference on Machine Learning (ICML), Montreal, QC, Canada, 14–18 June 2009; pp. 921–928. [Google Scholar]
- Lázaro-Gredilla, M. Bayesian warped Gaussian processes. Adv. Neural Inf. Process. Syst. 2012, 25, 6995–7004. [Google Scholar]
- Rios, G.; Tobar, F. Compositionally-warped Gaussian processes. Neural Netw. 2019, 118, 235–246. [Google Scholar] [CrossRef]
- Zhang, Y.; Yeung, D.Y. Multi-task warped Gaussian process for personalized age estimation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 2622–2629. [Google Scholar]
- Wiebe, J.; Cecílio, I.; Dunlop, J.; Misener, R. A robust approach to warped Gaussian process-constrained optimization. Math. Program. 2022, 196, 805–839. [Google Scholar] [CrossRef]
- Mateo-Sanchis, A.; Muñoz-Marí, J.; Pérez-Suay, A.; Camps-Valls, G. Warped Gaussian processes in remote sensing parameter estimation and causal inference. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1647–1651. [Google Scholar] [CrossRef]
- Jadidi, M.G.; Miró, J.V.; Dissanayake, G. Warped Gaussian processes occupancy mapping with uncertain inputs. IEEE Robot. Autom. Lett. 2017, 2, 680–687. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Gao, F.; Gao, L. Probabilistic wind power forecasting with online model selection and warped Gaussian process. Energy Convers. Manag. 2014, 84, 649–663. [Google Scholar] [CrossRef]
- Gonçalves, I.G.; Echer, E.; Frigo, E. Sunspot cycle prediction using warped Gaussian process regression. Adv. Space Res. 2020, 65, 677–683. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Nickisch, H. Gaussian processes for machine learning (GPML) toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feedforward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Mcleod, A.I. Parsimony, model adequacy and periodic correlation in forecasting time series. Int. Stat. Rev. 1993, 61, 387–393. [Google Scholar] [CrossRef]

| Symbol | Model | Algorithm |
|---|---|---|
| MWGP II | MWGP | SMCEM |
| MWGP I | CEM | |
| MGP [28] | MGP | CEM |
| WGP [39] | WGP | MLE |
| GP [49] | GP | |
| [50] | FNN | Levenberg–Marquardt |
| [51] | SVM | Sequential minimal optimization |
| RP | 0.5000 | 3.0000 | 1.8974 | 0.1414 | 0.1414 | 0.2887 | |
| AEP | 0.4944 | 3.1380 | 1.9185 | 0.1449 | 0.1584 | 0.2708 | |
| SDEP | |||||||
| RP | 0.5000 | 10.500 | 2.8460 | 0.1414 | 1.0000 | 2.2361 | |
| AEP | 0.5056 | 10.688 | 2.9122 | 0.1477 | 1.2247 | 2.0492 | |
| SDEP |
| Model | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Time | RMSE | Time | RMSE | Time | RMSE | Time | RMSE | Time | |||||||||||
| Average | SD | p-Value | Average | SD | p-Value | Average | SD | p-Value | Average | SD | p-Value | Average | SD | p-Value | ||||||
| MWGP I | 0.0312 | − | 0.0641 | − | 0.0543 | − | 0.0394 | − | 0.5077 | 0.0346 | − | 2.5261 | ||||||||
| MGP | 0.0217 | 0.0000 | 0.0638 | 0.0000 | 0.0473 | 0.1319 | 0.0418 | 0.0000 | 0.0415 | 0.0571 | ||||||||||
| WGP | 0.0242 | 0.0000 | 0.0505 | 0.0000 | 0.0096 | 0.0000 | 0.0437 | 0.0000 | 0.0310 | 0.0000 | ||||||||||
| GP | 0.0605 | 0.0000 | 0.0471 | 0.0000 | 0.0261 | 0.0000 | 0.0624 | 0.0000 | 0.0113 | 0.0000 | ||||||||||
| FNN | 0.3715 | 0.1330 | 0.0000 | 1.9095 | 0.2695 | 0.0143 | 0.0000 | 1.6244 | 0.7014 | 0.1307 | 0.0000 | 1.7249 | 0.2928 | 0.0514 | 0.0000 | 2.4233 | 0.6749 | 0.1753 | 0.0000 | 2.1344 |
| SVM | 0.4605 | 0.1942 | 0.0000 | 45.236 | 0.3561 | 0.0139 | 0.0000 | 52.126 | 0.7901 | 0.1889 | 0.0000 | 39.451 | 0.3051 | 0.0539 | 0.0000 | 52.089 | 0.7295 | 0.2657 | 0.0000 | 58.141 |
| Model | ||||||||||||||||||||
| RMSE | Time | RMSE | Time | RMSE | Time | RMSE | Time | RMSE | Time | |||||||||||
| average | SD | p-value | average | SD | p-value | average | SD | p-value | average | SD | p-value | average | SD | p-value | ||||||
| MWGP I | 0.0196 | − | 0.0318 | − | 0.2582 | 0.0316 | − | 2.8099 | 0.4858 | 0.0296 | − | 2.7052 | 0.0273 | − | ||||||
| MGP | 0.0197 | 0.0000 | 0.0528 | 0.0000 | 0.2719 | 0.0372 | 0.0000 | 2.2128 | 0.5105 | 0.0343 | 0.0000 | 2.1638 | 0.0337 | 0.0000 | ||||||
| WGP | 0.0527 | 0.0000 | 0.0492 | 0.0000 | 0.3069 | 0.1058 | 0.0000 | 0.2342 | 0.5492 | 0.1279 | 0.0000 | 0.2958 | 0.0581 | 0.0000 | ||||||
| GP | 0.0828 | 0.0000 | 0.0836 | 0.0000 | 0.4352 | 0.1304 | 0.0000 | 0.1680 | 0.5596 | 0.1336 | 0.0000 | 0.2086 | 0.0977 | 0.0000 | ||||||
| FNN | 0.3230 | 0.0907 | 0.0000 | 2.0654 | 0.3720 | 0.1551 | 0.0000 | 1.8096 | 0.4527 | 0.1316 | 0.0000 | 2.2110 | 0.5496 | 0.1561 | 0.0000 | 2.1758 | 0.3768 | 0.1409 | 0.0000 | 1.6346 |
| SVM | 0.4915 | 0.1544 | 0.0000 | 51.590 | 0.5443 | 0.2024 | 0.0000 | 43.145 | 0.4958 | 0.1672 | 0.0000 | 55.062 | 0.5578 | 0.1736 | 0.0000 | 55.242 | 0.4675 | 0.1632 | 0.0000 | 48.347 |
| 0.2000 | 3.0000 | 3.0000 | 1.8974 | 1.5000 | 1.5000 | 1.8974 | 0.1414 | 0.1414 | 0.2887 | 1.2910 | |
| 0.2000 | 10.500 | 10.500 | 2.8460 | −2.1000 | −2.1000 | 2.8460 | 0.0200 | 1.0000 | 2.2361 | 0.5000 | |
| 0.2000 | 18.000 | 18.000 | 1.8974 | 0.0000 | 0.0000 | 1.8974 | 0.1414 | 0.4472 | 1.8257 | 1.5811 | |
| 0.2000 | 25.500 | 25.500 | 2.8460 | −2.1000 | −2.1000 | 2.8460 | 0.0200 | 0.5000 | 0.7071 | 0.7071 | |
| 0.2000 | 33.000 | 33.000 | 1.8974 | 1.5000 | 1.5000 | 1.8974 | 0.1414 | 0.2739 | 2.2361 | 1.2910 |
| Model | ||||||
|---|---|---|---|---|---|---|
| ALLF | Time | ALLF | Time | ALLF | Time | |
| MWGP II | 11.438 | 10.584 | 11.478 | |||
| MWGP I | 5.4443 | 3.9803 | 5.4065 | |||
| Model | ||||||
| ALLF | Time | ALLF | Time | ALLF | Time | |
| MWGP II | 10.315 | 11.527 | 12.130 | |||
| MWGP I | 3.9889 | 5.5424 | 5.7286 | |||
| Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | Time | RMSE | MAE | Time | RMSE | MAE | Time | RMSE | MAE | Time | |
| MWGP II | 13.481 | 7.7561 | 6.9812 | 24.153 | 13.297 | 15.671 | 47.896 | 29.157 | 2.3341 | 10.425 | 5.5228 | 2.2285 |
| MWGP I | 8.1550 | 14.309 | 29.316 | 5.7159 | ||||||||
| MGP | 14.714 | 8.4912 | 1.6331 | 26.370 | 14.351 | 4.4129 | 49.060 | 30.075 | 0.7358 | 11.071 | 6.0772 | 0.6139 |
| WGP | 8.4834 | 16.579 | 30.391 | 6.5137 | ||||||||
| GP | 13.322 | 14.725 | 35.323 | 8.7933 | ||||||||
| FNN | 18.004 | 11.974 | 1.6293 | 30.359 | 17.213 | 16.433 | 49.588 | 30.514 | 1.2033 | 11.669 | 6.5154 | 1.1592 |
| SVM | 17.267 | 11.445 | 46.223 | 29.782 | 16.885 | 182.67 | 54.627 | 34.917 | 25.333 | 12.780 | 7.4816 | 23.858 |
| Model | ||||||||||||
| RMSE | MAE | Time | RMSE | MAE | Time | RMSE | MAE | Time | RMSE | MAE | Time | |
| MWGP II | 4.5938 | 3.7556 | 2.2943 | 14.266 | 8.6631 | 2.4118 | 16.617 | 10.885 | 2.2389 | 31.171 | 22.483 | 2.2581 |
| MWGP I | 4.6721 | 3.8321 | 1.0644 | 14.570 | 8.9534 | 1.1831 | 16.727 | 10.988 | 1.1016 | 22.814 | ||
| MGP | 5.1759 | 4.3327 | 0.5734 | 14.924 | 9.2859 | 0.5911 | 16.814 | 11.067 | 0.7345 | 34.575 | 26.257 | 0.7646 |
| WGP | 4.7084 | 3.8626 | 0.0673 | 15.318 | 9.6578 | 0.0939 | 16.728 | 10.990 | 0.0886 | 23.877 | ||
| GP | 5.6274 | 4.6852 | 0.0587 | 16.161 | 10.527 | 0.0718 | 17.043 | 11.302 | 0.0711 | 26.416 | ||
| FNN | 4.7079 | 3.8629 | 1.1525 | 15.599 | 9.9261 | 1.3947 | 16.738 | 10.996 | 1.1650 | 32.666 | 24.093 | 1.1725 |
| SVM | 4.8446 | 3.9841 | 19.240 | 16.353 | 10.673 | 26.039 | 17.415 | 11.579 | 23.659 | 33.163 | 24.552 | 23.745 |
| Model | ||||||||||||
| RMSE | MAE | Time | RMSE | MAE | Time | RMSE | MAE | Time | RMSE | MAE | Time | |
| MWGP II | 27.736 | 19.675 | 2.4640 | 30.696 | 22.095 | 2.4040 | 50.497 | 31.265 | 2.2823 | 33.789 | 24.613 | 2.2461 |
| MWGP I | 19.702 | 30.708 | 22.121 | 1.1113 | 50.502 | 31.283 | 1.1090 | 33.792 | 24.624 | 1.0795 | ||
| MGP | 28.053 | 20.015 | 0.7480 | 32.061 | 23.216 | 0.7923 | 52.317 | 32.837 | 0.7065 | 34.529 | 25.277 | 0.7084 |
| WGP | 19.719 | 30.712 | 22.128 | 0.0909 | 50.712 | 31.415 | 0.0857 | 34.004 | 24.858 | 0.0826 | ||
| GP | 20.263 | 32.803 | 23.871 | 0.0756 | 52.994 | 33.478 | 0.0745 | 35.276 | 26.064 | 0.0738 | ||
| FNN | 27.921 | 19.998 | 1.1907 | 30.727 | 22.141 | 1.1980 | 50.603 | 31.357 | 1.1813 | 34.163 | 25.040 | 1.1099 |
| SVM | 28.098 | 20.068 | 24.062 | 31.812 | 22.844 | 27.023 | 52.920 | 33.432 | 26.387 | 35.072 | 25.821 | 20.228 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Wu, D.; Qiang, Z. An Improved Mixture Model of Gaussian Processes and Its Classification Expectation–Maximization Algorithm. Mathematics 2023, 11, 2251. https://doi.org/10.3390/math11102251
Xie Y, Wu D, Qiang Z. An Improved Mixture Model of Gaussian Processes and Its Classification Expectation–Maximization Algorithm. Mathematics. 2023; 11(10):2251. https://doi.org/10.3390/math11102251
Chicago/Turabian StyleXie, Yurong, Di Wu, and Zhe Qiang. 2023. "An Improved Mixture Model of Gaussian Processes and Its Classification Expectation–Maximization Algorithm" Mathematics 11, no. 10: 2251. https://doi.org/10.3390/math11102251
APA StyleXie, Y., Wu, D., & Qiang, Z. (2023). An Improved Mixture Model of Gaussian Processes and Its Classification Expectation–Maximization Algorithm. Mathematics, 11(10), 2251. https://doi.org/10.3390/math11102251






