An Efficient Legendre–Galerkin Approximation for Fourth-Order Elliptic Problems with SSP Boundary Conditions and Variable Coefficients
Abstract
1. Introduction
2. Sobolev Spaces and Equivalent Variational Formulation
3. Existence and Uniqueness of Solutions and Error Estimates
4. Algorithm Design
5. Extension of the Algorithm
5.1. Three-Dimensional Resource Problems
5.1.1. Case of Constant Coefficients
5.1.2. Case of Variable Coefficients
5.2. Two-Dimensional Fourth-Order Eigenvalue Problem
6. Numerical Tests
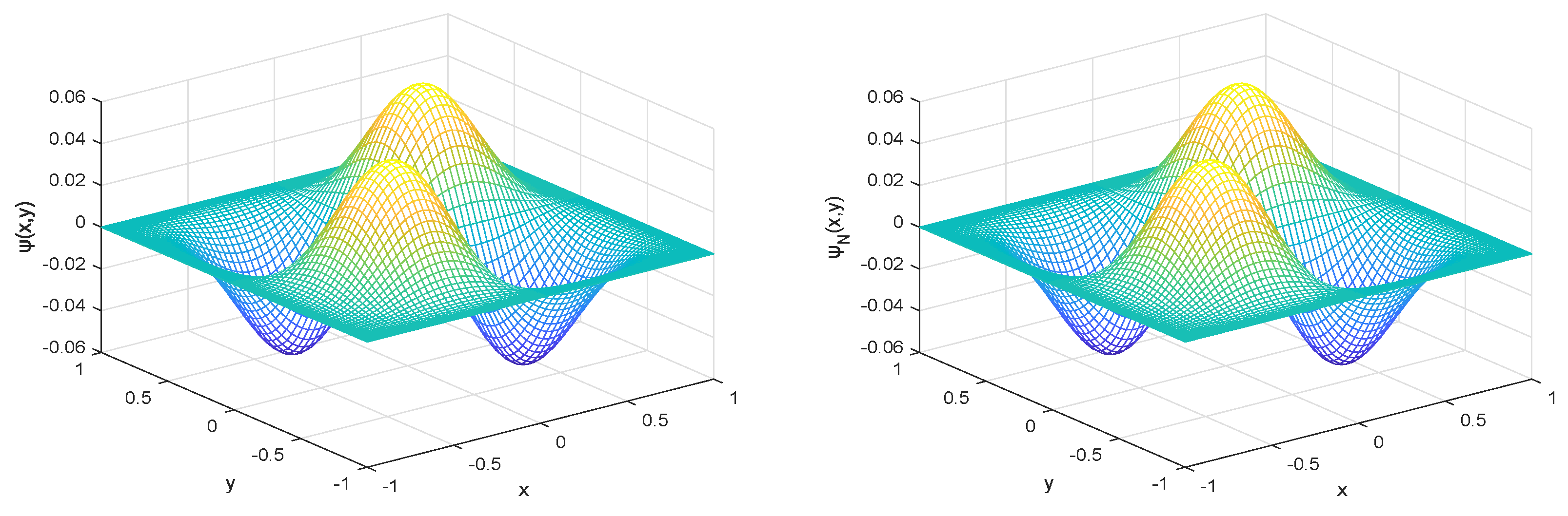
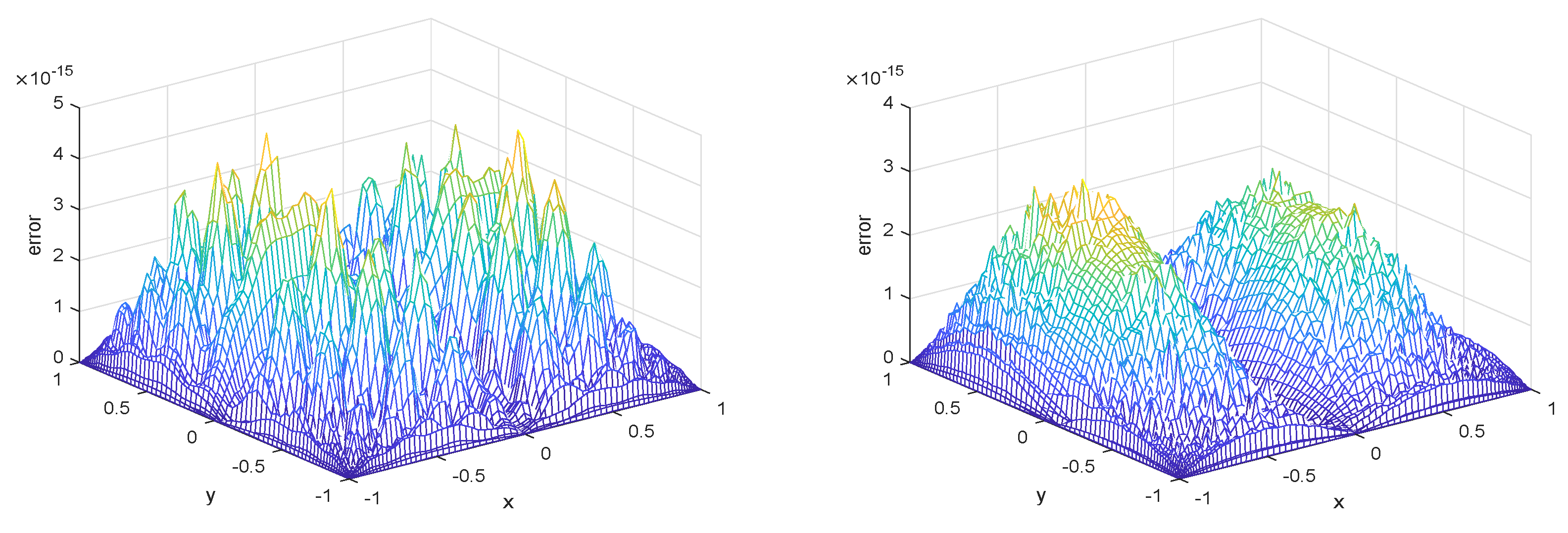
6.1. Two-Dimensional Resource Problem
6.2. Three-Dimensional Resource Problem
6.3. Two-Dimensional Eigenvalue Problem
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Qiao, Z. On the stabilization size of semi-implicit Fourier-spectral methods for 3D Cahn–Hilliard equations. Commun. Math. Sci. 2017, 15, 1489–1506. [Google Scholar] [CrossRef]
- Liu, F.; Shen, J. Stabilized semi-implicit spectral deferred correction methods for Allen-Cahn and Cahn-Hilliard equations. Math. Methods Appl. Sci. 2015, 38, 4564–4575. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X. Numerical approximations of Allen-Cahn and Cahn-Hilliard equations. Discret. Contin. Dyn. Syst. 2010, 28, 1669–1691. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Michelson, D.M.; Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames-II. Numerical experiments. Acta Astronaut. 1977, 4, 1207–1221. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames-I. Derivation of basic equations. Acta Astronaut. 1977, 4, 1177–1206. [Google Scholar] [CrossRef]
- Canuto, C. Eigenvalue approximations by mixed methods. RAIRO. Anal. Numrique 1978, 12, 27–50. [Google Scholar] [CrossRef]
- Rappaz, J.; Mercier, B.; Osborn, J.; Raviart, P.A. Eigenvalue approximation by mixed and hybrid methods. Math. Comput. 1981, 36, 427–453. [Google Scholar]
- Chen, W.; Lin, Q. Approximation of an eigenvalue problem associated with the stokes problem by the stream function-vorticity-pressure method. Appl. Math. 2006, 51, 73–88. [Google Scholar] [CrossRef]
- Yang, Y.D.; Jiang, W. Upper spectral bounds and a posteriori error analysis of several mixed finite element approximations for the stokes eigenvalue problem. Sci. China Math. 2013, 56, 1313–1330. [Google Scholar] [CrossRef]
- Sousa, E. An explicit high order method for fractional advection diffusion equations. J. Comput. Phys. 2014, 278, 257–274. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Li, H.; He, S.; Gao, W. Finite difference/finite element method for a nonlinear time-fractional fourth-order reaction-diffusion problem. Comput. Math. Appl. 2015, 70, 573–591. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Guo, B.Y.; Jia, H.L. Spectral method on quadrilaterals. Math. Comput. 2010, 79, 2237–2264. [Google Scholar]
- Guo, B.Y.; Wang, L.L. Error analysis of spectral method on a triangle. Adv. Comput. Math. 2007, 26, 473–496. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Chelmsford, MA, USA, 2001. [Google Scholar]
- Bialecki, B.; Karageorghis, A. A Legendre spectral Galerkin method for the biharmonic Dirichlet problem. SIAM J. Sci. Comput. 2001, 22, 1549–1569. [Google Scholar] [CrossRef]
- Zhuang, Q. A Legendre spectral-element method for the one-dimensional fourth-order equations. Appl. Math. Comput. 2011, 218, 3587–3595. [Google Scholar] [CrossRef]
- Li, L.; An, J. An efficient spectral method and rigorous error analysis based on dimension reduction scheme for fourth order problems. Numer. Methods Partial Differ. Equ. 2021, 37, 152–171. [Google Scholar] [CrossRef]
- Shen, J. Efficient spectral-Galerkin method I. Direct solvers of second-and fourth-order equations using Legendre polynomials. SIAM J. Sci. Comput. 1994, 15, 1489–1505. [Google Scholar] [CrossRef]
- Shen, J. Efficient spectral-Galerkin method II. Direct solvers of second-and fourth-order equations using Chebyshev polynomials. SIAM J. Sci. Comput. 1995, 16, 74–87. [Google Scholar] [CrossRef]
- Eftekhari, T.; Rashidinia, J. A new operational vector approach for time-fractional subdiffusion equations of distributed order based on hybrid functions. Math. Methods Appl. Sci. 2023, 46, 388–407. [Google Scholar] [CrossRef]
- Chen, L.; An, J.; Zhuang, Q. Direct solvers for the biharmonic eigenvalue problems using Legendre polynomials. J. Sci. Comput. 2017, 70, 1030–1041. [Google Scholar] [CrossRef]
- Aslefallah, M.; Shivanian, E. Nonlinear fractional integro-differential reaction-diffusion equation via radial basis functions. Eur. Phys. J. Plus 2015, 130, 47. [Google Scholar] [CrossRef]
- Shivanian, E.; Aslefallah, M. Stability and convergence of spectral radial point interpolation method locally applied on two-dimensional pseudoparabolic equation. Numer. Methods Partial Differ. Equ. 2017, 33, 724–741. [Google Scholar] [CrossRef]
- Aslefallah, M.; Abbasbandy, S.; Shivanian, E. Numerical solution of a modified anomalous diffusion equation with nonlinear source term through meshless singular boundary method. Eng. Anal. Bound. Elem. 2019, 107, 198–207. [Google Scholar] [CrossRef]
- Aslefallah, M.; Yüzbaşi, Ş.; Abbasbandy, S. A Numerical Investigation Based on Exponential Collocation Method for Nonlinear SITR Model of COVID-19. CMES-Comput. Model. Eng. Sci. 2023, 136, 1687–1706. [Google Scholar] [CrossRef]
- Bernardi, C.; Maday, Y. Spectral methods. Handb. Numer. Anal. 1997, 5, 209–485. [Google Scholar]





| N | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|
| N | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|
| 0.0033 |
| N | 10 | 12 | 14 | 16 | 18 |
|---|---|---|---|---|---|
| 0.0047 |
| N | 10 | 12 | 14 | 16 | 18 |
|---|---|---|---|---|---|
| N | ||||
|---|---|---|---|---|
| 5 | 35.2544775663993164 | 126.33914595504443 | 177.793597223306051 | 427.801015793001625 |
| 10 | 35.2460676597821418 | 126.34139750648265 | 178.093277397853029 | 430.41218968297477 |
| 15 | 35.2460676594985998 | 126.341393331936359 | 178.093272608351242 | 430.412179313580339 |
| 20 | 35.2460676594985713 | 126.341393331936658 | 178.093272608351157 | 430.412179313579088 |
| 25 | 35.2460676594986495 | 126.341393331936516 | 178.093272608351043 | 430.412179313579827 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yang, X.; Jin, J.; Zhang, X.; Zhang, J. An Efficient Legendre–Galerkin Approximation for Fourth-Order Elliptic Problems with SSP Boundary Conditions and Variable Coefficients. Mathematics 2023, 11, 2236. https://doi.org/10.3390/math11102236
Zhang H, Yang X, Jin J, Zhang X, Zhang J. An Efficient Legendre–Galerkin Approximation for Fourth-Order Elliptic Problems with SSP Boundary Conditions and Variable Coefficients. Mathematics. 2023; 11(10):2236. https://doi.org/10.3390/math11102236
Chicago/Turabian StyleZhang, Hui, Xingrong Yang, Jiulin Jin, Xu Zhang, and Jun Zhang. 2023. "An Efficient Legendre–Galerkin Approximation for Fourth-Order Elliptic Problems with SSP Boundary Conditions and Variable Coefficients" Mathematics 11, no. 10: 2236. https://doi.org/10.3390/math11102236
APA StyleZhang, H., Yang, X., Jin, J., Zhang, X., & Zhang, J. (2023). An Efficient Legendre–Galerkin Approximation for Fourth-Order Elliptic Problems with SSP Boundary Conditions and Variable Coefficients. Mathematics, 11(10), 2236. https://doi.org/10.3390/math11102236






