Dependence Structure Analysis and Its Application in Human Microbiome

Abstract

The human microbiome has been recently shown to be associated with disease risks and has important implications in risk stratification and precision medicine. Due to abundant taxa in the human body, microbiome data are high-dimensional and compositional. Dirichlet distributions and their generalization are used to characterize the dependence structures of microbial data. Another existing method for fitting microbiome data employed Gaussian graphical model using the centered log-transformation (CLR). However, Dirichlet distributions are not able to infer networks or to estimate some extremely rare probabilities. On the other hand, it is hard to interpret the network analysis results using CLR. Furthermore, the data analysis showed that there is a lack of efficient multivariate distributions for fitting microbiome data, which results in inadequate statistical inferences. In this paper, we propose new multivariate distributions for modeling the dependence structures of the high dimensional and compositional microbiome data using inverse gamma distributions and copula techniques. The data analysis in the American gut project shows our proposed methods perform well.

1. Introduction

The human microbiome is a gathering of microbes that inhabit different sites of the human body, including bacteria, archaea, and fung. The research on low-price high-throughput sequencing analyses has substantially facilitated the characterization of the compositions and diversities of the human microbiome. It provides a chance to carry out large-scale population-based microbiome studies to identify novel risk factors and to improve the risk prediction of diseases. Over the past two decades, increased research has focused on studying the structure, function, and dynamics of microbiome data, referring to all of the taxa and their genes in a well-defined environment [1]. Technical advancements and reduced costs in sequencing have led to large-scale studies such as the human microbiome project (HMP) and the American gut project (AGP), which characterize the microbiome of largely healthy individuals [2,3]. Most of the early research focused on microbial diversity and taxonomic classification. More recently, research has focused on differential abundance analysis and understanding how the host environment is associated with the microbiome [4,5,6,7]. The human microbiome is known to be associated with complex diseases, such as obesity, inflammatory bowel disease, and rheumatoid arthritis [8,9,10].

Despite these advances, little is known about inter-microbial interactions. Much of the lack of information on microbial interactions comes from the fact that most standard statistical methods for correlation or network analysis cannot be directly applied to such high-dimensional, compositional, and sparse data. To analyze microbiome data, there are two methods in the literature for modeling the distributions of the relative abundance data of many taxa. One method is utilizing multivariate normal distributions to model correlation structures of taxa by means of the centred log ratio transformation (CLR) or alternative log ratio transformations (ALR), and the other is using Dirichlet multinomial distribution to model taxa counts [11,12]. Dirichlet distributions are not quite flexible enough to fit many real data sets in microbiome studies. Moreover, the lack of dependence structure analysis hinders further statistical inferences in microbiome studies [13].

For modeling microbial dependence structures with multivariate normal distributions, two of the most common methods, SparCC and SPIEC-EASI, are used. SparCC uses the additive log-ratio transformations and assumes that the underlying unobserved counts are correlated through log-ratio [14]. In contrast, SPIEC-EASI uses the CLR and assumes that the network of interactions is generated from a precision matrix [15]. 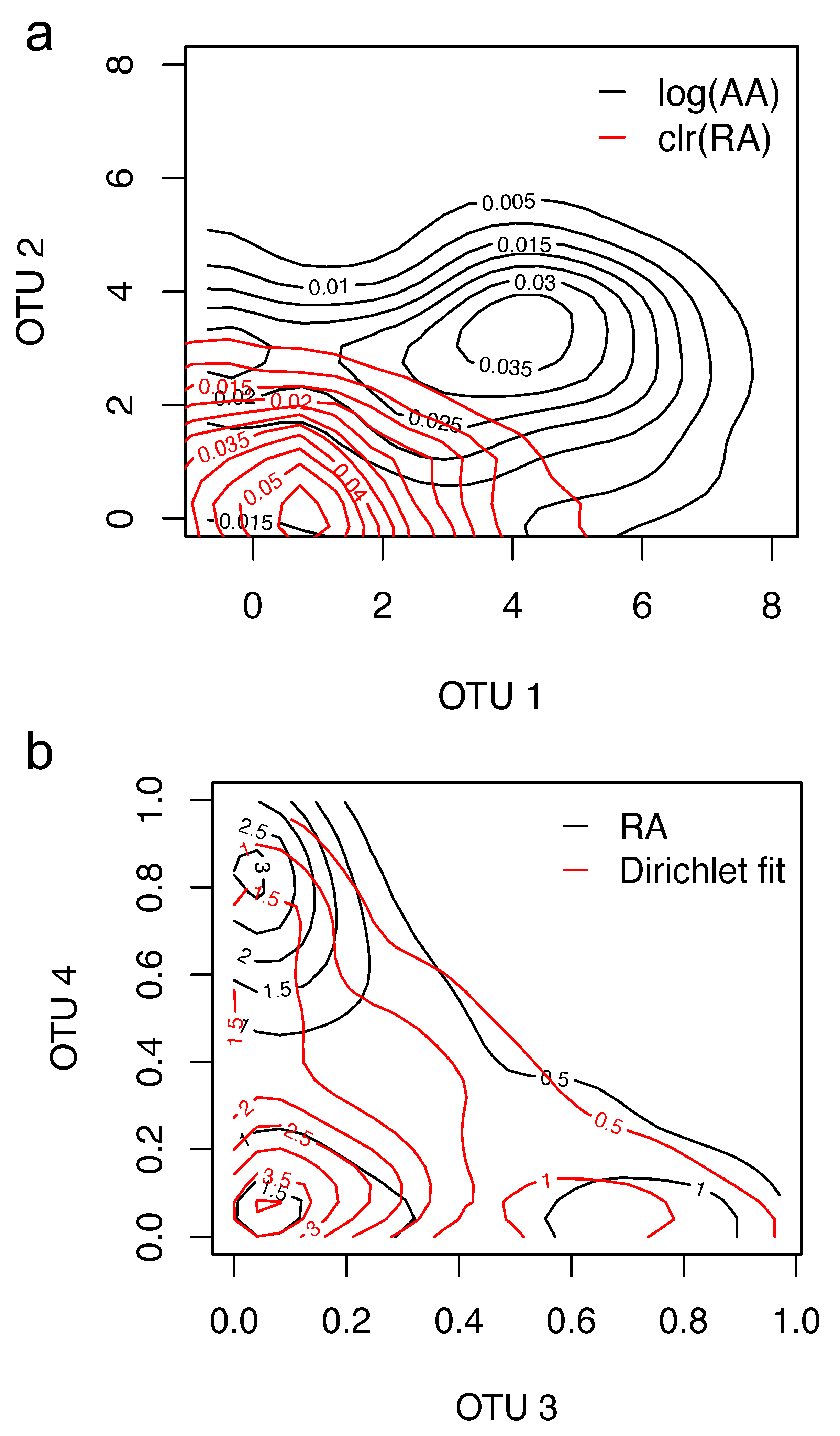While the log-ratio transformations are common in compositional data analysis, they are not particularly fitting for data with excessive zeros [16], as is the case with microbial sequencing data. The normality assumption of such data often does not hold (see, e.g., Figure 1a below), and they require the use of pseudo-counts, thus forcing the assumption that the true absolute abundance (AA) for every taxa is non-zero in each sample. Figure 1 shows that there are large departures between the estimated contour plots of samples and the contour plots based on the estimated normal distribution with CLR or the estimated Dirichlet distribution. Furthermore, the corresponding results from such transformations are difficult to interpret and are sensitive to the choice of reference groups; as Feng et al. [17] pointed out, the results of standard statistical tests performed on log-transformed data are often not relevant for the original, non-transformed data.

To model the high-dimensional and compositional data in microbiome studies, we propose two classes of multivariate distributions on a simplex. A new class of multivariate distributions on a simplex is composed of variable transformation of inverse gamma distributions since most datasets show that a single taxonomy can be characterized by an inverse Gamma distribution. Another new class of multivariate distributions on simplex is constructed by means of copula techniques. Copulas are functions that join univariate uniform distribution functions to form multivariate distributions and are powerful for characterizing the dependence structures of random variables [18].

Furthermore, human microbiota can be influenced by environment changes and life-style changes. Microbiome data are compositional and sparse. A few taxa are abundant, most taxa are rare (present in <10% subjects), and there are zero counts for some taxa. This could be caused by sampling zero (low sequence depth) or structural zeros (absent taxa). To deal with sampling zeros, we could enlarge the sequencing depth. However, in our settings, we ignore sampling zeros and only deal with structural zeros by zero-inflated distributions.

The remainder of this paper is organized as follows. Section 2 constructs the new class of multivariate distributions on a simplex by variable transformation of inverse gamma distributions. In Section 3, using the copula techniques, we propose a new class of multivariate distributions on a simplex with a Gaussian copula and a Farlie–Gumbel–Morgenstern copula. The real data from the American gut project (AGP) is analyzed to demonstrate the effectiveness of the proposed new multivariate distributions in Section 4, and some conclusions are given in Section 5.

2. Multivariate Distributions on Simplex via Inverse Gamma Distributions

Suppose there are $k+1$ microbial taxa, and denote $\mathbf{Y}={(Y_1,\dots ,Y_{k+1})}^T$ as the true relative abundance (RA) of microbial taxa. The RA has a compositional structure with ${\sum }_{j=1}^{k+1}{Y}_j=1$, and the vector $\mathbf{Y}$ lies on the k-dimensional simplex ${\mathcal{S}}^k$,

$${\mathcal{S}}^k:=\left\{{(y_1,\dots ,y_k)}^T:y_i>0,i=1,\dots ,k,\sum _{i=1}^k{y}_i\le 1\right\}$$

(1)

To construct the distributions of $\mathbf{Y}$, the inverse Gamma distributions on $(0,\infty )$ are employed since most datasets show that a single taxonomy can be characterized by an inverse Gamma distribution (IG). Let $X_1,\dots ,X_{k+1}$ be independent random variables on $(0,\infty )$ and have the inverse Gamma distributions $X_j\sim IG(\alpha ,{\beta }_j)$ with its density function

$$f(x;\alpha ,{\beta }_j)=\frac{{\beta }_j^{\alpha }}{\Gamma \left(\alpha \right)}{x}^{-\alpha -1}exp\left(\frac{-{\beta }_j}{x}\right),\mathrm{for}x>0,$$

(2)

where $\alpha >0$ is the shape parameter and ${\beta }_j>0$ are the scale parameters for $j=1,\dots ,k+1$. For a given subject, we assume that the k taxa have the same shape parameter $\alpha$, but the scale parameters ${\beta }_j$ vary. With the following transformation,

$$Y_j=\frac{X_j}{{\sum }_{j=1}^{k+1}{X}_j},Y_{k+1}=1-\sum _{j=1}^k{Y}_j,\mathrm{for}j=1,\dots ,k,$$

(3)

The RA of microbial taxa $\mathbf{Y}$ has the multivariate distribution on the k-dimensional simplex ${\mathcal{S}}^k$ with its density function as

$$f(\mathbf{y};\alpha ,{\beta }_1,\dots ,{\beta }_{k+1})=\frac{\Gamma \left(\right(k+1\left)\alpha \right)}{\Gamma {\left(\alpha \right)}^{k+1}}\prod _{j=1}^{k+1}{\beta }_j^{\alpha }\prod _{j=1}^{k+1}{y}_j^{-\alpha -1}{\left(\sum _{j=1}^{k+1}\frac{{\beta }_j}{y_j}\right)}^{-(k+1)\alpha },$$

(4)

for $\mathbf{y}={(y_1,\dots ,y_{k+1})}^T$ and $0<y_j<1$, ${\sum }_{j=1}^{k+1}{y}_j=1$ for $j=1,\dots ,k+1$. We denote $\mathbf{Y}={(Y_1,\dots ,Y_{k+1})}^T\sim MSIG(\alpha ;{\beta }_1,\dots ,{\beta }_{k+1})$. The special case of this multivariate distribution when $\alpha =\frac{1}{2}$ was first introduced by Carlton [19] and further discussed in Favaro et al. [20].

For the density function (4), the marginal density functions are

$$f(y_j;\alpha ;{\beta }_1,\dots ,{\beta }_{k+1})=\frac{{\beta }_j^{\alpha }}{\Gamma \left(\alpha \right)}\frac{{(1-y_j)}^{\alpha +3}}{y_j^{\alpha +1}}\underset{0}{\overset{\infty }{\int }}\cdots \underset{0}{\overset{\infty }{\int }}\frac{exp\left[\frac{-{\beta }_j(1-y_j)}{y_j\left({\displaystyle \sum _{i\ne j}}{x}_i\right)}-{\displaystyle \sum _{i\ne j}}\frac{{\beta }_i}{x_i}\right]}{{\left({\displaystyle \sum _{i\ne j}}{x}_i\right)}^{\alpha }{\displaystyle \prod _{i\ne j}}{x}_i^{\alpha +1}}{\displaystyle \prod _{i\ne j}}d{x}_i,$$

(5)

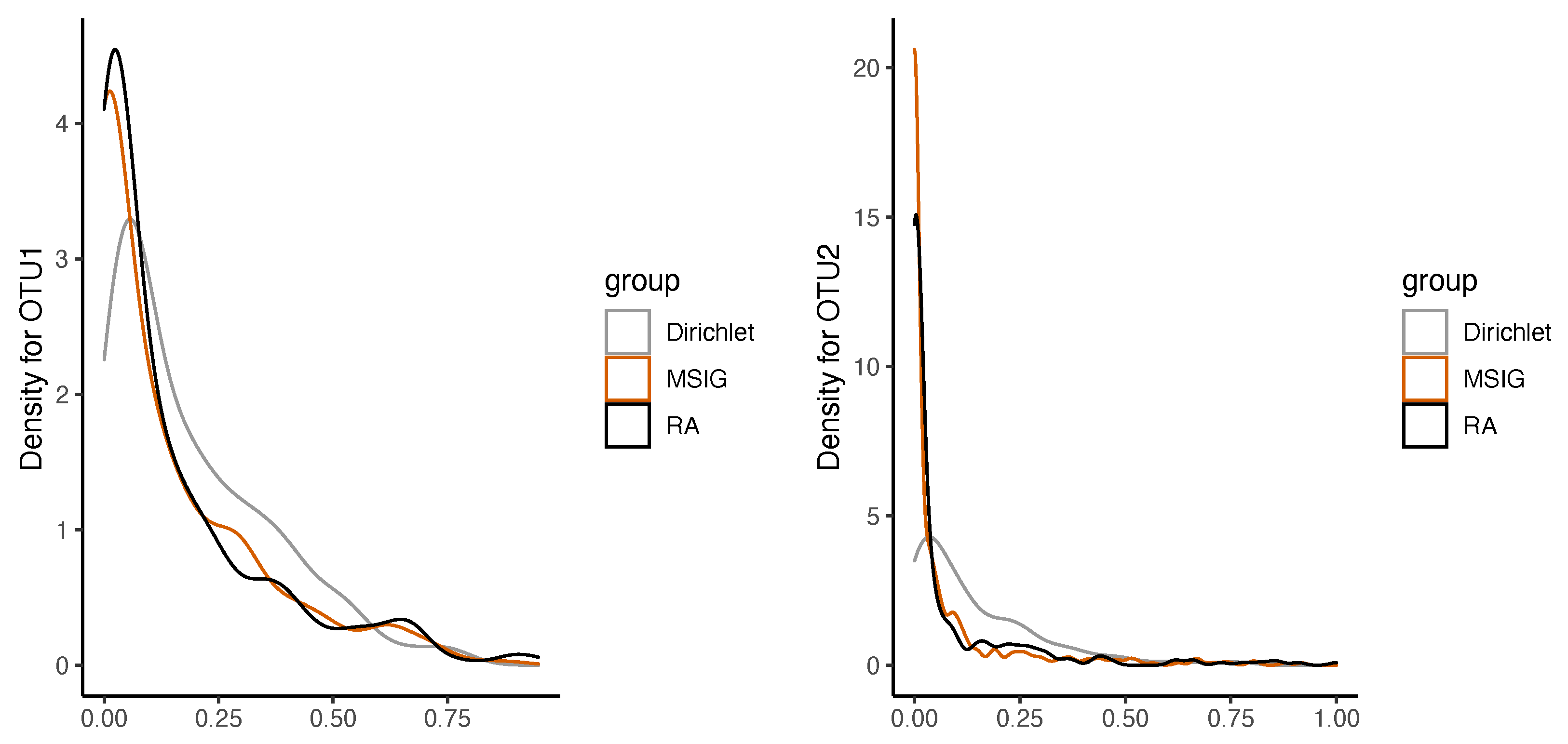
for $j=1,\dots ,k+1$. Figure 2 shows the estimated marginal density functions by (5) are fitting well for the sample density functions of Faecalibacterium (OTU1) and Bacteroides (OTU2) from AGP.

In the studies of the human microbiome, it is more expedient to consider the average total positivity [21] (and reverse regularity) of order two microbial taxa. Kendall’s correlation coefficient is a measure of the difference between the probabilities of concordance and discordance for two independent and identically distributed pairs of random variables. It is the difference between the probabilities of concordance and discordance for two independent and identically distributed pairs of random variables [22,23]. Let $\mathbf{Y}={(Y_1,\dots ,Y_{k+1})}^T\sim MSIG(\alpha ;{\beta }_1,\dots ,{\beta }_{k+1})$ with the density given in (4). Because of the transformation (3), the corresponding Kendall correlation coefficient of $Y_i$ and $Y_j$ is given by

$$\tau (Y_i,Y_j)=E\left(sign(Y_i-Y_{i^{\prime }})sign(Y_j-Y_{j^{\prime }})\right)=E\left(sign(X_i-X_{i^{\prime }})sign(X_j-X_{j^{\prime }})\right)$$

(6)

where $(Y_{i^{\prime }},Y_{j^{\prime }})$ is an independent copy of $(Y_i,Y_j)$ and $(X_{i^{\prime }},X_{j^{\prime }})$ is an independent copy of $(X_i,X_j)$ for $i\ne j$, $i,j=1,\dots ,k+1$. Since

$$P(X_i-X_{i^{\prime }}<0)={\int }_0^{\infty }{\int }_x^{\infty }\frac{{\beta }_i^{\alpha }}{\Gamma \left(\alpha \right)}{x}^{-\alpha -1}exp\left(\frac{-{\beta }_i}{x}\right)\frac{{\beta }_i^{\alpha }}{\Gamma \left(\alpha \right)}{y}^{-\alpha -1}exp\left(\frac{-{\beta }_i}{y}\right)dydx,$$

(7)

then, the Kendall correlation coefficient of $Y_i$ and $Y_j$ is the same as that of two independent IG random variables $X_i$ and $X_j$, and we have that

$$\begin{array}{ccc}\hfill \tau (Y_i,Y_j)& =& P(X_i>X_{i^{\prime }})P(X_j>X_{j^{\prime }})+P(X_i<X_{i^{\prime }})P(X_j<X_{j^{\prime }})\hfill \\ \hfill & & -P(X_i>X_{i^{\prime }})P(X_j<X_{j^{\prime }})-P(X_i<X_{i^{\prime }})P(X_j>X_{j^{\prime }})\hfill \\ \\ \hfill & =& {\displaystyle 2\left(1-\frac{2^{-2\alpha }}{\Gamma \left(\alpha \right)}\sum _{l=0}^{\infty }\frac{\Gamma (2\alpha +l)}{2^l\Gamma (\alpha +l+1)}\right)\left(1-\frac{2^{-2\alpha +1}}{\Gamma \left(\alpha \right)}\sum _{l=0}^{\infty }\frac{\Gamma (2\alpha +l)}{2^l\Gamma (\alpha +l+1)}\right),}\hfill \end{array}$$

(8)

which is only dependent on the parameter $\alpha$, for $i\ne j$, $i,j=1,\dots ,k+1$.

2.1. Paramter Estimation

Let ${\mathbf{y}}^{\left(1\right)},\dots ,{\mathbf{y}}^{\left(n\right)}$ be i.i.d samples from $\mathbf{Y}\sim MSIG(\alpha ;{\beta }_1,\dots ,{\beta }_{k+1})$. The log-likelihood function of parameters $\Theta =(\alpha ;{\beta }_1,\dots ,{\beta }_{k+1})$ is given by

$$\begin{array}{ccc}\hfill \ell (\Theta |{\mathbf{y}}^{\left(1\right)},\dots ,{\mathbf{y}}^{\left(n\right)})& \propto & n\alpha {\displaystyle \sum _{j=1}^{k+1}}log{\beta }_j+nlog(\Gamma \left((k+1)\alpha \right))-n(k+1)log(\Gamma \left(\alpha \right))\hfill \\ & & -{\displaystyle \sum _{i=1}^n}\left[(\alpha +1){\displaystyle \sum _{j=1}^{k+1}}log{y}_j^{\left(i\right)}+(k+1)\alpha log\left({\displaystyle \sum _{j=1}^{k+1}}\frac{{\beta }_j}{y_j^{\left(i\right)}}\right)\right],\hfill \end{array}$$

and we obtain the score functions

$$\begin{array}{c}{\displaystyle k{\beta }_h=\sum _{i=1}^n\left(\frac{{\sum }_{j\ne h}^{k+1}\frac{{\beta }_j}{y_j^{\left(i\right)}}}{{\beta }_h+{\sum }_{j\ne h}^{k+1}\frac{{\beta }_j}{y_j^{\left(i\right)}}}\right){\left[\sum _{i=1}^n\frac{1}{{\beta }_h+{\sum }_{j\ne h}^{k+1}\frac{{\beta }_j}{y_j^{\left(i\right)}}}\right]}^{-1},h=1,\dots ,k+1;}\hfill \\ \\ n(k+1)\left(\frac{{\Gamma }^{\prime }\left((k+1)\alpha \right)}{\Gamma \left(\right(k+1\left)\alpha \right)}-\frac{{\Gamma }^{\prime }\left(\alpha \right)}{\Gamma \left(\alpha \right)}\right)={\displaystyle \sum _{i=1}^n}\left[{\displaystyle \sum _{j=1}^{k+1}}log{y}_j^{\left(i\right)}+log\left({\displaystyle \sum _{j=1}^{k+1}}\frac{{\beta }_j}{y_j^{\left(i\right)}}\right)(k+1)\right]-n{\displaystyle \sum _{j=1}^{k+1}}log{\beta }_j,\hfill \end{array}$$

(9)

where ${\Gamma }^{\prime }(·)$ is the derivative function of $\Gamma (·)$. The maximum likelihood estimation (MLE) of $\Theta =(\alpha ;{\beta }_1,\dots ,{\beta }_{k+1})$ can be obtained by an iterative algorithm.

2.2. Multivariate Goodness–of–Fit Testing

For given n samples ${\mathbf{y}}^{\left(1\right)},\dots ,{\mathbf{y}}^{\left(n\right)}$ in the k-dimensional simplex ${\mathcal{S}}^k$, we can obtain the estimated parameters $\widehat{\Theta }=(\widehat{\alpha };{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})$. A goodness-of-testing procedure is necessary to test the hypothesis that the samples ${\left\{{\mathbf{y}}^{\left(i\right)}\right\}}_{i=1}^n$ come from the distribution $\mathbf{Y}\sim MSIG(\widehat{\alpha };{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})$. For one-dimensional or low-dimensional data, there are a wide variety of useful and powerful goodness-of-fit and two-sample testing procedures, such as Kolmogorov–Smirnov (K-S) test. However, for high-dimensional ($k>3$) data, those tests rapidly lose statistical power because all finite samples are sparse in high-dimensional settings owing to the “curse of dimensionality” [24]. In this paper, a machine learning method for two-sample testing is employed, which was proposed by Friedman [24] and further developed by Gretton et al. [25]. For the given observed samples ${\left\{{\mathbf{y}}^{\left(i\right)}\right\}}_{i=1}^n$, we can obtain a set of score values ${\left\{v_i=F\left({\mathbf{y}}^{\left(i\right)}\right)\right\}}_{i=1}^n$, where $F\left(\mathbf{y}\right)$ is the cdf of $MSIG(\widehat{\alpha };{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})$. At same time, with the “Monte Carlo” samples ${\left\{{\mathbf{z}}^{\left(i\right)}\right\}}_{i=1}^n$ from the distribution $MSIG(\widehat{\alpha };{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})$, we can obtain another set of score values ${\left\{w_i=F\left({\mathbf{z}}^{\left(i\right)}\right)\right\}}_{i=1}^n$. Then, a univariate two-sample test, such as the K-S test, chi–squared test, or Mann–Whitney test, can be used to test the goodness of fit based on the scores. The testing procedure is as follows:

Step 1.

Generating n samples ${\left\{x_{ij}\right\}}_{i=1}^n$ from the distribution $IG(\widehat{\alpha },{\widehat{\beta }}_j)$ for $j=1,\dots ,k+1$. With the transform (3), we can obtain n samples ${\left\{{\mathbf{z}}^{\left(i\right)}\right\}}_{i=1}^n$ from the distribution $MSIG(\widehat{\alpha };{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})$ such that ${\mathbf{z}}^{\left(i\right)}={(z_{i1},\dots ,z_{i,k+1})}^T$, $z_{ij}=\frac{x_{ij}}{{\sum }_{j=1}^{k+1}{x}_{ij}}$, $z_{i,k+1}=1-{\sum }_{j=1}^k{z}_{ij}$, for $j=1,\dots ,k$, and $i=1,\dots ,n$.

Step 2.

By denoting $F\left(\mathbf{y}\right)$ the cumulative distribution function (cdf) of $MSIG(\widehat{\alpha };{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})$, we obtain two samples ${\left\{w_i=F\left({\mathbf{z}}^{\left(i\right)}\right)\right\}}_{i=1}^n$ and ${\left\{v_i=F\left({\mathbf{y}}^{\left(i\right)}\right)\right\}}_{i=1}^n$.

Step 3.

Using the one-dimensional two-sample test, such as the K-S test, chi–squared test, or Mann–Whitney test, to test the hypothesis that the two samples ${\left\{w_i\right\}}_{i=1}^n$ and ${\left\{v_i\right\}}_{i=1}^n$ have the same distribution.

Step 4.

Repeating N (for example, $N=5000$) times of Steps 1–3, we cannot reject the null hypothesis if the percent of rejecting times of testing in Step 3 (i.e., the p-value < 0.05) is less than 5%.

Friedman showed that the power of this testing procedurecan be highly sensitive to the learning machine methods that are employed [24].

2.3. Zero-Inflated Distribution with Zero Counts for Absent Taxa

The above multivariate distribution assumes that all taxa have positive proportions. However, for a given taxonomy j, they may be absent in some subjects. To consider the zero-inflated structures, we introduce the zero-inflated inverse Gamma distributions [26]. Let $X_1^{*},\dots ,X_{k+1}^{*}$ be independent random variables on $[0,\infty )$ and $X_j^{*}=(1-{\Delta }_j)+{\Delta }_j{X}_j$, where ${\Delta }_j$ follows a Bernoulli distribution ${\Delta }_j\sim Bernoulli\left({\pi }_j\right)$ with $P({\Delta }_j=1)={\pi }_j$ and $P({\Delta }_j=0)=1-{\pi }_j$, and $X_j$ follows a inverse Gamma distribution $X_j\sim IG(\alpha ,{\beta }_j)$ for $j=1,\dots ,k+1$. Then, $X_j^{*}$ has a zero-inflated inverse Gamma distribution $X_j^{*}\sim ZIIG({\pi }_j,\alpha ,{\beta }_j)$ with the probability density

$$f\left(x\right|{\pi }_j,\alpha ,{\beta }_j)={\pi }_j^{\delta }{\left((1-\pi )\frac{{\beta }_j^{\alpha }}{\Gamma \left(\alpha \right)}{x}^{-\alpha -1}exp\left(\frac{-{\beta }_j}{x}\right)\right)}^{1-\delta },\delta =I\{x=0\},$$

(10)

for $x\in [0,\infty )$. With the transformation

$$Y_j=\frac{X_j^{*}}{{\sum }_{j=1}^{k+1}{X}_j^{*}},Y_{k+1}=1-\sum _{j=1}^k{Y}_j,\mathrm{for}j=1,\dots ,k,$$

(11)

The RA of microbial taxa $\mathbf{Y}$ has the multivariate distribution on the k-dimensional simplex ${\mathcal{S}}^k$ with its density function as

$$\begin{array}{cc}\hfill f(\mathbf{y};\alpha ,{\beta }_1,\dots ,{\beta }_{k+1})=& {\displaystyle \prod _{j=1}^{k+1}}{\pi }_j^{{\delta }_j}{(1-{\pi }_j)}^{1-{\delta }_j}\frac{\Gamma \left({\displaystyle \sum _{j=1}^{k+1}}(1-{\delta }_j)\alpha \right)}{\Gamma {\left(\alpha \right)}^{{\sum }_{j=1}^{k+1}(1-{\delta }_j)}}\hfill \\ \\ \hfill & {\displaystyle \prod _{j=1}^{k+1}}{\beta }_j^{(1-{\delta }_j)\alpha }{\displaystyle \prod _{j=1}^{k+1}}{y}_j^{(-\alpha -1)(1-{\delta }_j)}{\left({\displaystyle \sum _{j=1}^{k+1}}\frac{(1-{\delta }_j){\beta }_j}{y_j}\right)}^{-{\sum }_{j=1}^{k+1}(1-{\delta }_j)\alpha },\hfill \end{array}$$

(12)

where ${\delta }_j=I\{y_j=0\}$ for $\mathbf{y}={(y_1,\dots ,y_{k+1})}^T$ and $0\le y_j<1$, ${\sum }_{j=1}^{k+1}{y}_j=1$ for $j=1,\dots ,k+1$.

3. Multivariate Distributions on Simplex Using Copula Dependence Structures

Since the $k+1$ microbial taxa $\mathbf{Y}={(Y_1,\cdots ,Y_{k+1})}^T$ lie on the k-dimensional simplex ${\mathcal{S}}^k$ defined in (1), $\mathbf{Y}$ is a k-dimensional random vector. To characterize the dependence structure of the k-dimensional random vector, copula techniques are usually employed [18,23]. Copulas are multivariate distributions with uniformly distributed marginals on $[0,1]$. Utilizing copulas, the density function of a multivariate distribution can be decomposed into the density weighting function and the product of marginal densities [27]. For a d-variate random vector $\mathbf{X}=(X_1,\dots ,X_d)$ with joint cdf $F(·)$ and marginal strictly increasing cdf $F_i(·)$ ($i=1,\dots ,d$), Sklars’s Theorem [28] states that there a d-variate copula cdf $C(·)$ on ${[0,1]}^d$ exists such that

$$\begin{array}{ccc}\hfill F(x_1,\dots ,x_d)& =& C(F_1\left(x_1\right),\dots ,F_d\left(x_d\right)),\hfill \\ \\ \hfill C(u_1,\dots ,u_d)& =& F(F_1^{-1}\left(u_1\right),\dots ,F_d^{-1}\left(u_d\right)),\hfill \end{array}$$

(13)

for all $\mathbf{x}={(x_1,\dots ,x_d)}^T\in {\mathbb{R}}^d$ and $\mathbf{u}={(u_1,\dots ,u_d)}^T\in {[0,1]}^d$, where $F^{-1}(·)$ is the inverse function of $F(·)$. Let $f(x_1,\dots ,x_d)$ and $f_i\left(x_i\right)$$(i=1,\dots ,d)$ be the density function and the marginal density functions of $\mathbf{X}=(X_1,\dots ,X_d)$, respectively. The corresponding copula density and the density function of $\mathbf{X}$ have the following relationships:

$$\begin{array}{ccc}\hfill c(u_1,\dots ,u_d)& =& {\displaystyle \frac{{\partial }^{d}C(u_1,\dots ,u_d)}{\partial u_1,\dots ,\partial u_d}=\frac{f(F_1^{-1}\left(u_1\right),\dots ,F_d^{-1}\left(u_d\right))}{f_1\left(F_1^{-1}\left(u_1\right)\right),\dots ,f_d\left(F_d^{-1}\left(u_d\right)\right)},}\hfill \\ \\ \hfill f(x_1,\dots ,x_d)& =& c(F_1\left(x_1\right),\dots ,F_d\left(x_d\right))\prod _{j=1}^d{f}_j\left(x_j\right).\hfill \end{array}$$

(14)

The distributions of individual taxonomy are easily estimated, for example, Qiu et al. [13] proposed two-parametric simplex distribution with its density function,

$$f\left(y\right)={\left(2\pi s{\left(y(1-y)\right)}^3\right)}^{-1/2}exp(-\frac{{(y-m)}^2}{2m{(1-m)}^{2}y(1-y)s}))$$

where $(s,m)$ are shaping parameters for $0<y<1$. In this paper, we propose two families of copulas, Gaussian and Farlie–Gumbel–Morgenstern copulas, to characterize the dependence structures of microbial taxa such that the corresponding multivariate distributions are good-of-fit for a given microbial data.

3.1. Gaussian Copula

Many new multivariate distributions are constructed based on the dependence structures of multivariate normal distributions, which are called Gaussian copulas. Let $\mathbf{Z}={(Z_1,\cdots ,Z_k)}^T\sim N(\mathbf{0},R)$ with mean vector $\mathbf{0}$ and the $k\times k$ covariance matrix R,

$$R=\left\{{\rho }_{ij}:{\rho }_{ii}=1,-1<{\rho }_{ij}<1\mathrm{for}i\ne j,{\rho }_{ij}={\rho }_{ji};i,j=1,\dots ,k\right\}.$$

(15)

Denote the cdf of $\mathbf{Z}$ by $F_{\mathbf{Z}}(z_1,\dots ,z_k)$; the corresponding copula of $\mathbf{Z}$ is given by

$$C_{\mathbf{Z}}(u_1,\dots ,u_k)=F_{\mathbf{Z}}({\Phi }^{-1}\left(u_1\right),\dots ,{\Phi }^{-1}\left(u_k\right)),$$

(16)

for ${(u_1,\dots ,u_k)}^T\in {(0,1)}^k$, where $\Phi (·)$ is the cdf of standard normal distribution $N(0,1)$.

Suppose that the marginal distributions of the $k+1$ microbial taxa $\mathbf{Y}={(Y_1,\cdots ,Y_{k+1})}^T$ are $F_j\left(y_j\right)$ the cdf of $Y_j$ for $j=1,\dots ,k$, and $Y_{k+1}=1-{\sum }_{j=1}^k{Y}_j$, the distribution function of $\mathbf{Y}$ can be constructed with the copula (16) to be

$$\begin{array}{ccc}\hfill F_{\mathbf{Y}}(y_1,\dots ,y_k;R)& =& P\left\{Y_1\le y_1,\dots ,Y_k\le y_k\right\}\hfill \\ \hfill & =& F_{\mathbf{Z}}({\Phi }^{-1}\left(F_1\left(y_1\right)\right),\dots ,{\Phi }^{-1}\left(F_k\left(y_k\right)\right)).\hfill \end{array}$$

(17)

Fang et al. [18] show that Kendall’s correlation coefficient $\tau (Y_i,Y_j)$ of $Y_i$ and $Y_j$ is given by

$$\tau (Y_i,Y_j)=\frac{2}{\pi }arcsin\left({\rho }_{ij}\right),\mathrm{for}i\ne j,i,j=1,\dots ,k,$$

(18)

which depends only on ${\rho }_{ij}$. Thus, the estimates of ${\rho }_{ij}$ can be obtained by the estimators of Kendall’s correlation coefficient $\tau (Y_i,Y_j)$ of $Y_i$ and $Y_j$.

3.2. Farlie–Gumbel–Morgenstern (FGM) Copula

As an alternative to a multivariate normal distribution, the FGM copula has been widely studied and applied to statistical modeling in various research fields [29,30,31]. Let $\mathbf{U}={(U_1,\dots ,U_k)}^T$ be a random vector that follows a k-dimensional FGM copula with its cdf $C_{FGM}(u_1,\dots ,u_k;\Theta )$,

$$\begin{array}{ccc}\hfill C_{FGM}(u_1,\dots ,u_k;\Theta )& =& P\left(U_1\le u_1,\dots ,U_k\le u_k\right)\hfill \\ \\ \hfill & =& {\displaystyle \prod _{j=1}^k}{u}_j\left(1+{\displaystyle \sum _{i=2}^k}{\displaystyle \sum _{1\le j_1<\cdots <j_i\le k}}{\theta }_{j_1\cdots j_i}(1-u_{j_1})\cdots (1-u_{j_i})\right),\hfill \end{array}$$

(19)

where ${(u_1,\dots ,u_k)}^T\in {[0,1]}^k$ and $\Theta =\{{\theta }_{j_1\cdots j_i}:1\le j_1<\cdots <j_i\le k,i=2,\dots ,k\}$ are dependence parameters since $\Theta \equiv 0$ means that the random variables $U_1,\dots ,U_k$ are obviously independent. According to Johnson and Kotz [30], the $2^k-k-1$ parameters $\Theta$ have the following constraints:

$$1+\sum _{i=2}^k\sum _{1\le j_1<\cdots <j_i\le k}{\theta }_{j_1\cdots j_i}{\delta }_{j_1}\cdots {\delta }_{j_i}\ge 0,{\delta }_j=\pm 1,$$

(20)

for $j=1,\dots ,k$. With the cdf (19), we have the joint-density function of $\mathbf{U}$ given by

$$\begin{array}{ccc}\hfill c_{FGM}(u_1,\dots ,u_k;\Theta )& =& {\displaystyle \frac{{\partial }^k}{\partial u_1\cdots \partial u_k}{C}_{FGM}(u_1,\dots ,u_k;\Theta )}\hfill \\ \\ \hfill & =& 1+{\displaystyle \sum _{i=2}^k}{\displaystyle \sum _{1\le j_1<\cdots <j_i\le k}}{\theta }_{j_1\cdots j_i}(1-2u_{j_1})\cdots (1-2u_{j_i}).\hfill \end{array}$$

(21)

For the given marginal distributions $F_j\left(y_j\right)$ of the cdf of $Y_j$ for $j=1,\dots ,k$, the distribution function of microbial taxa $\mathbf{Y}={(Y_1,\cdots ,Y_{k+1})}^T$ can be constructed with the copula (19) to be

$$\begin{array}{ccc}\hfill F_{\mathbf{Y}}(y_1,\dots ,y_k;\Theta )& =& P\left\{Y_1\le y_1,\dots ,Y_k\le y_k\right\}\hfill \\ \hfill & =& {\displaystyle \prod _{j=1}^k}{F}_j\left(y_j\right)\left(1+{\displaystyle \sum _{i=2}^k}{\displaystyle \sum _{1\le j_1<\cdots <j_i\le k}}{\theta }_{j_1\cdots j_i}(1-F_{j_1}\left(y_{j_1}\right))\cdots (1-F_{j_i}\left(y_{j_i}\right))\right),\hfill \end{array}$$

(22)

where $0<y_j<1$ for $j=1,\dots ,k$, and $y_{k+1}=1-{\sum }_{j=1}^k{y}_j$. The Kendall’s correlation coefficient $\tau (Y_i,Y_j)$ of $Y_i$ and $Y_j$ is given by

$$\begin{array}{cc}\hfill \tau (Y_i,Y_j)=& {\displaystyle 4\underset{{[0,1]}^2}{\int \int }C(u_i,u_j)dC(u_i,u_j)-1}\hfill \\ \\ \hfill =& {\displaystyle \frac{{\theta }_{ij}}{9}({\theta }_{ij}-8),\mathrm{for}i\ne j,i,j=1,\dots ,k,}\hfill \\ \hfill \end{array}$$

(23)

which depends only on ${\theta }_{ij}$.

Thus, the estimates of ${\theta }_{ij}$ can be obtained by the estimators of Kendall’s correlation coefficient $\tau (Y_i,Y_j)$ of $Y_i$ and $Y_j$, but all of the parameters $\Theta =\{{\theta }_{j_1\cdots j_i}:1\le j_1<\cdots <j_i\le k,i=2,\dots ,k\}$ should satisfy the constraints in (20). Shih et al. [32,33] provided the maximum likelihood estimates of $\Theta$ with the constrains in (20).

3.3. Multivariate Distributions with Zero-Inflated Marginal Distributions

Let the $k+1$ microbial taxa $\mathbf{Y}={(Y_1,\cdots ,Y_{k+1})}^T$ lie on the k-dimensional simplex ${\mathcal{S}}^k$ defined in (1). When there are proportions with zero counts for absent taxa, the zero and the non-zero responses are assumed to occur from two different processes; then, we could use two-part models to characterize the marginal distributions. Define that ${\Delta }_j=I\{Y_j=0\}$ and $Y_j^{*}=Y_j|(Y_j>0)$. Let $f_j^{*}(y,{\omega }_j)$ and $F_j^{*}(y,{\omega }_j)$ be the pdf and cdf of $Y_j^{*}$, respectively, where ${\omega }_j$ is a parameter (or a parametric vector). Assume that ${\Delta }_j\sim Bernoulli\left({\pi }_j\right)$ with $P({\Delta }_j=1)={\pi }_j$ and $P({\Delta }_j=0)=1-{\pi }_j$. Then, the marginal random variable $Y_j$ has the probability density,

$$f_j\left(y\right)={\pi }_j^{{\delta }_j}{\left((1-{\pi }_j)f_j^{*}(y,{\omega }_j)\right)}^{1-{\delta }_j},{\delta }_j=I\{y=0\},$$

(24)

for $j=1,\dots ,k$. To construct the multivariate distribution of $\mathbf{Y}$, we assume that ${\Delta }_1,\dots ,{\Delta }_k$ have the multinomial distribution with its probability mass function

$$\begin{array}{ccc}\hfill g({\delta }_1,\dots ,{\delta }_k;{\pi }_1,\dots ,{\pi }_k)& =& P\{{\Delta }_1={\delta }_1,\dots ,{\Delta }_k={\delta }_k\}\hfill \\ \hfill & =& \prod _{j=1}^k{\pi }_j^{{\delta }_j}\times \prod _{j=1}^k{(1-{\pi }_j)}^{1-{\delta }_j},\hfill \end{array}$$

(25)

and the joint cdf of $(Y_1^{*},\dots ,Y_k^{*})$ is given by

$$f_{{\mathbf{Y}}^{*}}(y_1,\dots ,y_k;{\omega }_1,\dots ,{\omega }_k)=c(F_1^{*}(y_1,{\omega }_1),\dots ,F_k^{*}(y_k,{\omega }_k))\prod _{j=1}^k{f}_j^{*}(y_j,{\omega }_j),$$

(26)

where $c(u_1,\dots ,u_k)$ is the density function of a copula $C(u_1,\dots ,u_k)$. Denote ${\rm Y}=({\pi }_1,\dots ,{\pi }_k;$${\omega }_1,\dots ,{\omega }_k;\Theta )$ or ${\rm Y}=({\pi }_1,\dots ,{\pi }_k;{\omega }_1,\dots ,{\omega }_k;R)$, where $\Theta$ and R are the parameters in the given copula function. Thus, the joint probability function of $\mathbf{Y}$ is given by

$$\begin{array}{c}{f}_{\mathbf{Y}}(y_1,\cdots ,y_k;{\rm Y})=\hfill \\ \prod _{j=1}^k{\pi }_j^{{\delta }_j}+\prod _{j=1}^k{(1-{\pi }_j)}^{1-{\delta }_j}\prod _{j=1}^k{f}_j^{*}{(y_j,{\omega }_j)}^{1-{\delta }_j}\tilde{c}\left({\left[F_1^{*}(y_1,{\omega }_1)\right]}^{1-{\delta }_1},\cdots ,{\left[F_k^{*}(y_k,{\omega }_k)\right]}^{1-{\delta }_k}\right),\hfill \end{array}$$

(27)

where ${\delta }_j=I\{y_j=0\}$ for $j=1,\dots ,k$, $\tilde{c}\left({\left[F_1^{*}(y_1,{\omega }_1)\right]}^{1-{\delta }_1},\dots ,{\left[F_k^{*}(y_k,{\omega }_k)\right]}^{1-{\delta }_k}\right)$ is the density function of $C(u_1^{1-{\delta }_1},\dots ,u_k^{1-{\delta }_k})$ at $u_j=F_j^{*}(y_j,{\omega }_j)$ for ${\delta }_j=0$ and $j=1,\dots ,k$. Note that $a^0=1$ and the marginal cdf $C(u_1^{1-{\delta }_1},\dots ,u_k^{1-{\delta }_k})$ are also a copula.

3.4. Parameter Estimation and Goodness–of–Fit Testing

Let ${\mathbf{y}}^{\left(1\right)},\dots ,{\mathbf{y}}^{\left(n\right)}$ be i.i.d samples from the multivariate distribution with its pdf in (27). To obtain the maximum likelihood estimates of parameters ${\rm Y}$, a two-stage approach is employed [34]. The marginal distributions are first estimated based on partial maximum likelihood methods. Given these marginal fits, the estimated cumulative distribution functions are then obtained using the estimates of the parameters in copula. Denote ${\delta }_{ij}=I\{y_j^{\left(i\right)}=0\}$ for $j=1,\dots ,k$, $i=1,\dots ,n$. The estimates of $\pi$’s can be obtained by

$${\widehat{\pi }}_j=\sum _{i=1}^n{\delta }_{ij}/n,j=1,\dots ,k,$$

(28)

and the estimates of $\omega$’s maximize the log-likelihood functions.

$$\ell \left({\omega }_j\right)=\sum _{i=1}^n(1-{\delta }_{ij})log\left(f_j^{*}(y_j^{\left(i\right)},{\omega }_j)\right),j=1,\dots ,k.$$

(29)

Then, the estimates of the parameters in copula can be obtained by maximizing the likelihood function

$$Lik\left({\rm Y}\right)=\prod _{i=1}^n\tilde{c}\left({\left[F_1^{*}(y_1^{\left(i\right)},{\widehat{\omega }}_1)\right]}^{1-{\delta }_{i1}},\dots ,{\left[F_k^{*}(y_k^{\left(i\right)},{\widehat{\omega }}_k)\right]}^{1-{\delta }_{ik}}\right).$$

(30)

When $C(u_1,\dots ,u_k)$ is an FGM copula, Shih et al. [33] provides the maximum likelihood estimates of $\Theta$. If $C(u_1,\dots ,u_k)$ is a Gaussian copula, the parameters $R=\left({\rho }_{ij}\right)$ can be estimated by the corresponding estimates of Kendall’s correlation coefficient $\tau (Y_i^{*},Y_j^{*})$ based on (23).

When we obtain the estimates of parameters ${\rm Y}$, the machine learning method given in Section 2.1 can be used for goodness-of-fit testing of the proposed multivariate distributions. Shih et al. [33] provides a procedure of generating samples from FGM copulas, and Fang et al. [18] gives a procedure of generating samples from Gaussian copulas.

4. Real Data Analysis

Now we apply our proposed methods to the datasets from AGP, a self-selected, open-platform cohort [2]. The cohort consists of individuals mostly from the United States, with some from the United Kingdom and Australia, who opted into the study by providing informed consent and paying a fee to offset the cost of processing and sequencing. The data, both 16S rRNA gene sequencing and self-reported meta-data, are publicly available in The European Bioinformatics Institute repository under the accession ERP012803.

We focus on the fecal microbiome samples and restrict our samples to individuals who reported not having inflammatory bowel disease or diabetes. We filtered data that showed that OTUs were removed if present in fewer than 37% of samples. Samples were removed if total sequencing depth fell below 10,800 sequence reads [15]. After filtering, there were 127 OTUs and 289 samples remaining in our dataset.

To illustrate our methods, the analysis results of two OTUs are shown only in this section. As shown in Figure 2, the sample density functions of Faecalibacterium (OTU1) and Bacteroides (OTU2) from AGP are fitted well by the marginal distributions of MSIG distribution, where the parameters $(\alpha ,{\beta }_1,{\beta }_2)$ are estimated to be $(\widehat{\alpha },{\widehat{\beta }}_1,{\widehat{\beta }}_2))=(0.351,0.089,0.036)$. The parameters for the fitted Dirichlet distribution are estimated to be $({\widehat{\alpha }}_1,{\widehat{\alpha }}_2)=(0.0791$, $0.0562)$. 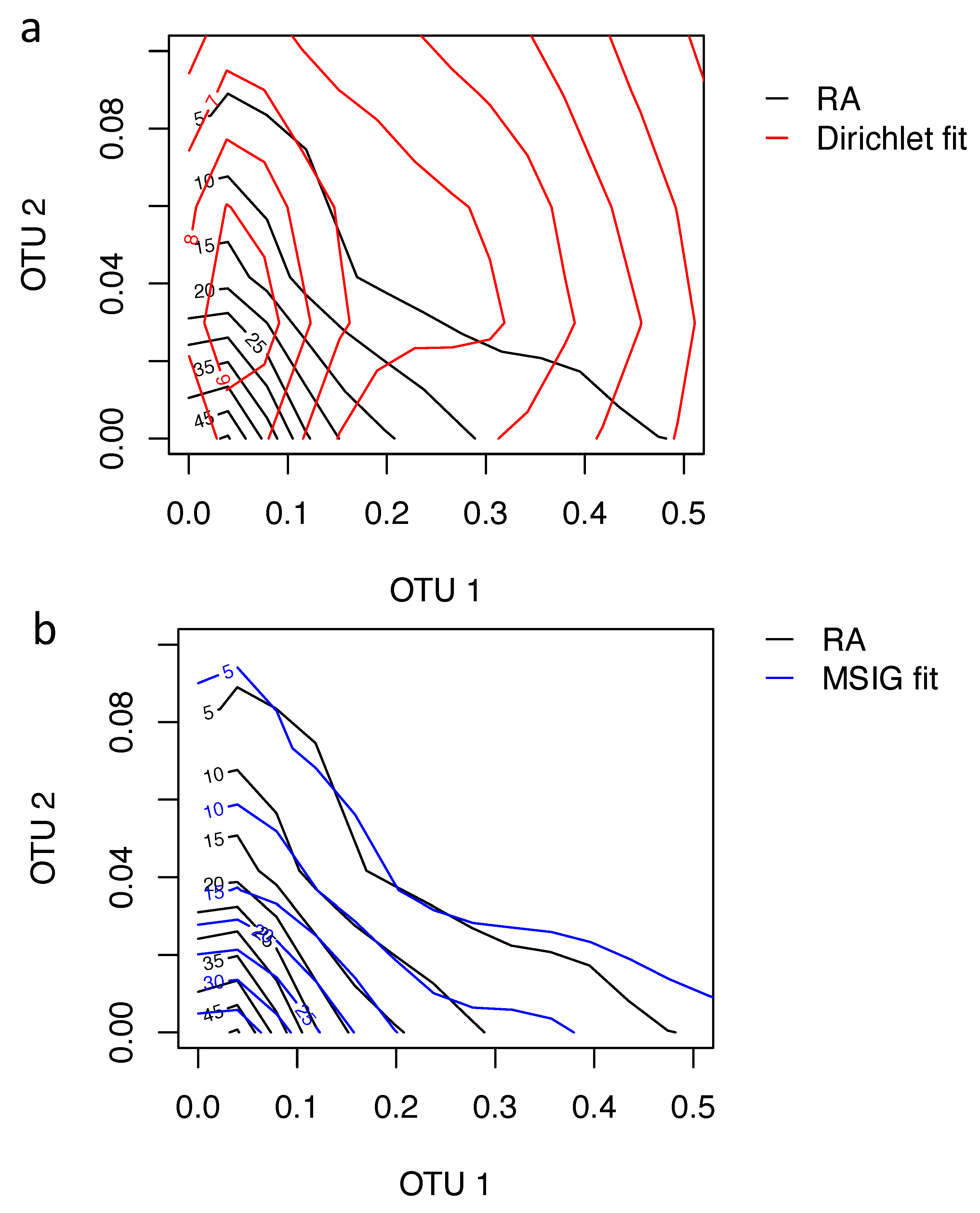Figure 3 shows the contour plots from the estimated Dirichlet distribution (DD) and MSIG, respectively. The p-values for the GOF test are 0.001 versus 0.567 between DD and MSIG, which show that the proposed MSIG is goodness-of-fitting the data. Furthermore, the Kendall’s correlation coefficient between OTU1 and OTU2 is estimated to be $\tau =-0.061$ based on the samples, but the corresponding Kendall’s $\tau$ are calculated to be $-0.102$ with DD and $-0.057$ with MSIG, respectively.

Black lines in both panels are the estimated contour plots for samples. Red lines in the left panel are the contour plots of the estimated Dirichlet distribution. Blue lines in the right panel are the contour plots of the estimated MSIG. These figures show that MSIG is a goodness-of-fit for the data.

Some individual taxa can not be fitted by the marginal distribution of MSIG. Figure 4a,b shows that taxa Clostridium (OTU3) and Escherichia (OTU4) are fitted by the two-parametric simplex distributions [13], where the corresponding parameters are estimated to be $({\widehat{m}}_1,{\widehat{s}}_1)=(0.249,5.801)$ and $({\widehat{m}}_2,{\widehat{s}}_2)=(0.125,8.610)$. The Kendall’s correlation coefficient between OTU3 and OTU4 is estimated to be $\tau =0.448$ based on the samples. We use the Gaussian copula (GC) to fit the joint distribution of OTU3 and OTU4 with $\widehat{\rho }=0.071$. The contour plots in Figure 4c show that the proposed multivariate distribution via Gaussian copula fitted the joint distribution of OTU3 and OTU4 well, and the p-value for GOF test is 0.647. However, Figure 1 (the right panel) shows that the contour plots of samples are a departure from that of the Dirichlet distribution, of which the corresponding parameters are estimated to be $({\widehat{\alpha }}_1,{\widehat{\alpha }}_2)=(0.444,0.556)$; the Kendall’s $\tau =-0.407$, and the p-value for the GOF test is 0.001.

5. Discussions

The human microbiome has been recently shown to be associated with disease risks and has important implications in risk stratification and precision medicine. The existing methods for modeling microbiome dynamics focus on abundant taxa and ignore rare taxa. Modeling both will be crucial to provide information about microbial causal interactions and information for designing effective large-scale epidemiology. In this paper, we propose two classes of multivariate distributions to characterize the dependence structures among taxa in microbiome studies. Multivariate distributions on simplex via inverse Gamma distributions (MSIG) are useful in regression analysis due to the close-form of their density functions, but all of the Kendall’s correlation coefficients between two taxa are assumed to be the same. The copula techniques are very useful to characterize the dependence structures of random variables. We proposed two most popular copulas, Gaussian and Farlie–Gumbel–Morgenstern copulas, to construct the multivariate distributions of taxa. The data analysis shows that our methods perform well.

In this paper, we consider only the dependence structures of taxa at the fixed time points. Some new methodologies for longitudinal observations to study the dynamics of the microbiome community have to be developed, which will investigated in the future.