Abstract
We hope this work allows one to calculate large prime numbers directly, not by trial-and-error, but following a physical law. We report—contrary to conventional assumptions—that differentiation of discontinuous functions (DDF) exists in the set Q, which becomes central to algorithms for quantum computation. DDF have been thought to exist not in the classical sense, but using distributions. However, DDF using distributions still is defined in terms of mathematical real-numbers (MRN), and do not address the Problem of Closure, here investigated. These facts lead to contradictions using MRN, solved by this work, providing a new unbounded class of physical solutions using physical numbers in quantum mechanics (QM), that were always there (just hidden), allowing DDF without distributions, or MRN. It is worthwhile to see this only in mathematics, to avoid the prejudices found in physics, as this reforms both general relativity and QM. This confirms the opinions of Nicolas Gisin that MRN are non-computable with probability 1, and Niels Bohr that physics is not reality, it is a fitting story about reality. Mathematics can get closer to reality, surprisingly. We just have to base mathematics on nature, not on how it defines nature.
Keywords:
communication; tri-state+; nature; physical numbers; algebraic; quantum mechanics; general relativity; classical; coherence; law of the excluded middle; laser; wave–particle duality MSC:
11T71; 11Y05
1. Introduction
The analog, continuous signal on Figure 1 provides a generic, continuous function x(t), representing what researchers used to want to measure in the 17/18/19th centuries, in calculating area.
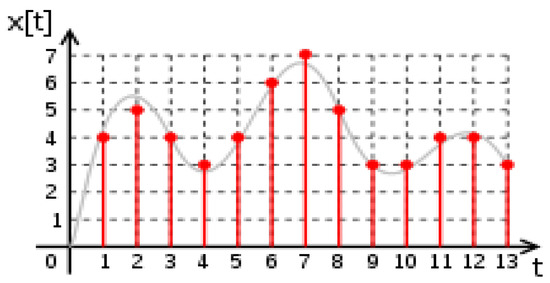
Figure 1.
Example of analog and digital signals.
Now, in the 21st century, the interest is in the discrete signal in red color (also represented in Figure 1). The red lines in Figure 1 represent what actually should be measured or reproduced, where some points in the red lines in Figure 1 fall short of reaching the classically supposed continuous wave, and other points exceed.
One recognizes that the discrete signal in red color in Figure 1 is the actual cause of the measured/reproduced interpolated analog signal, which seems continuous in Figure 1.
The utility of the method is to now recognize the analog signal as mythical, including measurement errors in the x-axis and in the y-axis, and taking into account the recipient as well as the environment, while the discrete signal in red color is more likely what is produced, and what should be reproduced.
The discrete signal represents a digital signal, now familiar in CD music and text/videos on the Internet, consisting of a sequence of samples as digital packets, which are integer values. They could also be rationals, at rational values.
However, since the 17/19th centuries, “the differential and integral calculus is based upon two concepts of outstanding importance, apart from the concept of number, namely, the concept of function and the concept of limit”, according to the well-known textbook by R. Courant in Germany and worldwide [1].
Without including any philosophical opinions, the system of rational and irrational numbers builds a continuum of numbers [1] such that each point on an axis corresponds to just one number, and each number corresponds to just one point on the axis, called the system of mathematical real-numbers (MRN), or set , according to P. J. Nahin [2].
Therefore, every MRN in the number line is in one of two sets—the rationals (expressible as the ratio of two integers) and the irrationals (all the remaining MRN). Every MRN is one of either [2]. This construction is often credited to Richard Dedekind in ETH Zurich, in 1888 [3], writing, “Numbers are free creations of the human mind; they serve as a means of apprehending more easily and more sharply the difference of things”.
Because uncountably infinite sets are always larger than countably infinite sets, one can conclude that there are more irrational numbers than rational ones. It is worth mentioning that the rationals and the irrationals are both dense, but unlike the rationals, the irrationals are not “sparse”, and do not have a zero measure mathematically. This fact emphasizes that rationals and irrationals are really quite different, even though one can find a rational between any two irrationals, actually an infinite number of them, and an irrational between any two rationals.
For example, regarding the well-known Fermat’s last theorem (FLT) (Which can be considered first proven by the well-known Descartes coordinate construction, at Fermat’s time.), the FLT is a Diophantine equation, using only the set Z. Here, one can think that the irrationals have a “more complicated” structure than the rationals, and avoid them. If , then where q is in the set , and one avoids the irrationals.
Now, here is the Problem of Closure: how can one calculate the sum/difference between a rational and an irrational? Such a result is non-computable with probability one [4].
The difference appears in the numerator () and in the denominator ( of the derivative [1], and the sum in the FLT (if using irrationals). This Problem of Closure has not been solved by Courant [1], Dedekind [3], Apostol [5], and others.
According to Apostol [5], he points out that “There seems to be no general agreement as to what should constitute a first course in calculus and analytic geometry.” [5]. Although Apostol recognizes that calculus is a deductive science and a branch of pure mathematics, “At the same time it is very important to remember that calculus has strong roots in physical problems and that it derives much of its power and beauty from the variety of its applications” [5].
The Problem of Closure has been solved constructively in physics, for example, by Ozhigov [6], by considering only what happens in nature as filtered by a physical Hamiltonian—which “cuts off” irrationals (one can only physically measure rationals). Recently, and according to Nicolas Gisin in physics [4], “More precisely, the set of computable numbers is countably-infinite, like the integers, while the set of [mathematical] real numbers is continuously-infinite, like the mathematical points on a line. Consequently, [mathematical] real numbers are non-computable with probability one.” This poses the Problem of Closure as non-computable by humans or machines. Or, equivalently, the set of computable numbers has [mathematical] measure zero among the set of all [mathematical] real numbers. [4].
While other related works could be added in mathematics, such as in neural networks, Hopf bifurcation, and in the bifurcation theory of fractional order delayed differential equations [7,8,9], they do not relate directly to the Problem of Closure.
Therefore, the Problem of Closure remains open in mathematics, and this work solves it by connecting physics in quantum mechanics (QM) with number theory (NT) in pure mathematics as a “wormhole”.
This work, then, proposes a novel solution in mathematics for the Problem of Closure, which may also be applied to the bifurcation theory of fractional-order delayed differential equations. The novelty and main contribution of this article is to hopefully lead one to calculate large prime numbers directly, not by trial-and-error, but following a physical law in QM.
This work also opens new theoretical space for computer science (CS) and new applications of calculus in QM, including DDF and deprecating the mean value theorem (that incorrectly connects the average rate of change of a function to its derivative)—both against [1,3,5], and other conventional textbooks in calculus. This also opens new results in physics, contrary to [10].
2. The Problem of Closure
Apostol provides us with an insightful answer as to the solution of the Problem of Closure in mathematical terms, and the potential hidden in calculus and physical numbers (PN), based on physical applications, while giving us a guide to the problems in mathematical numbers (MN).
Following the well-known principles of semiotics, a PN is hereafter considered as a 1:1 mapping between a symbol and a value, with no philosophical opinions, and contrary to Dedekind [3] and the concept of MN. This is valid for all PN, including natural numbers, infinite decimal numbers, and complex numbers using them, but not for MRN.
The symbol can be arbitrary, subjective, even with no sound. While in MN, the values can also be arbitrary (according to Dedekind), in PN all values must be rational (one can only physically measure rationals) and objective. Many different persons looking at our physical star, the Sun, may refer to it by different names qua symbols, but all agree on 1 physical value: there is 1 star, in English called the Sun, no matter where it sets or rises at each time of the year, or how it is called.
This eliminates problems with MN, MRN, and “mathematical measure”, by restricting those concepts to algebra, which solves the mathematical Problem of Closure. The number , e.g., even though is irrational and a MRN.
In this view, the value of a number must exist in nature, and be objective so as to be unique for all observers, humans and non-humans, friends or foes, also computers.
Our definitions of numbers as values must be objective, and must be measurable in a physical sense—this happens when following PN, not MN and not the notion of a mathematical measure. One means, then, objective values when one talks, even generally, about PN. This allows results calculated by computers to be “real” in an interchangeable, physical way—not when using MRN that are subjective in value.
Nature or reality cannot be defined by mathematics or by any science, because one does not know their limits or parts. In that, the derivative is still given by the same expression, of .
Differentiation of discontinuous functions (DDF) may be thought to have been introduced by Laurent Schwartz, with his Distribution Theory [11]. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense, giving a well-defined meaning to objects such as the well-known Dirac delta function. However, DDF still uses the set , and do not address the Problem of Closure, here investigated. There is no “differentiable in a sense” for functions—there is only one sense, the one mathematical sense that has made sense physically, for ages. We did not feel free to change it.
The definition of PN begins in this work with integer numbers (set ), that can be chosen by the well-known definition by Kronecker, and includes 0. The definition of natural numbers (set ) follows from integers, and excludes 0. A rational number (set ) is defined as a ratio of integers, excluding 0 in the denominator.
The complex numbers, as a double PN and called the set (for Gauss), are defined by where are in the set , and i is a number called “iota”, and is representable physically as the counterclockwise rotation by 90 degrees of 1, in the set . The value of , is a number in the set . A root of unity is a complex number that, when raised to a positive integer power, results in 1. Roots of unity have connections to many areas of mathematics, including the geometry of regular polygons, group theory, and number theory, as well as in physics, and engineering. For example, is a complex number, where 2 is a PN (called Re) and is also a PN (called Im). The different types of PN are seen as value types, and follow the Martin–Löf-type theory, called TT. Hereafter, “numbers” mean PN, and obey TT.
3. Quantum Computing
Paradoxically, apparently, experimental successes must be highly valued in the math community, said Alexei Borodin [12]. What makes it so? Not math as a human invention, but math as a human discovery—based on nature.
Not nature as definable in math, but nature as that which is known for 13.8 billion years.
Starting from this “natural” basis on numbers as this work suggests, the periodicity in numbers can provide prime number factoring, as famously treated by Peter Shor in 1994 [13] in terms of quantum computing. This is very inspiring to solve an otherwise difficult problem in number theory. A prime number in the star Betelgeuse (with no humans) must be the same as on Earth.
This connects physics in quantum mechanics (QM) with number theory (NT) in pure mathematics, using a “wormhole” to connect these different universe sets. The numbers in those two distinct universe sets possess only one common physical reality, connected by the “wormhole”: the natural numbers (the set N).
The laws that work for N are common to all uses of N. Using TT, reality, or nature itself, wins over any logically assumed or theoretical result, such as MRN as imagined by Dedekind, with Courant [1], Apostol [5], and other conventional textbooks. We will use the above connection between QM and NT, as a “wormhole” to present in this work a physical and absolutely exact formulation of calculus, using the sets , , and , benefiting from the experimental laws in QM to provide corresponding proven relations in theoretical NT and theoretical physics [10], while discarding unproven assumptions.
Then, applications of calculus can teach us that there are no problems to define velocity or density of a fluid, with the set , being the ratio of two rationals, and the denominator is not 0 by construction. Gravity is not considered a force that would impose transmission, and not a continuous force either. We find that the third law of Newton is not mandated by a contrarian demon, but by the stimulated emission of radiation. Special relativity will demand that E and B have the same units, which is called gauss. In classical physics or mathematics, it then becomes strange to mandate what does not exist in nature: continuity. Here, continuity is meant as defined in Courant [1], Apostol [5].
Discontinuity is clarified the same way. This also clarifies the topology regarding which that continuity/discontinuity is considered. The same happens with the term ‘derivative’ as used in this work. Mathematically, to define differentiability of a function at a point we initially define as in Courant [1] and Apostol [5], where one clarifies beforehand the following: (1) the metric regarding which the derivation is considered and; (2) the algebraic structure (e.g., ring, field, and group) equipped with that metric that the function in question is defined. Conversely, this work does not consider any metric in calculating the differentiability of a function at a point, and uses the algebraic structure of a field in the set . The set is a prime field, and is the smallest field with a characteristic of zero. All the other definitions needed are inherited verbatim from Courant [1] and Apostol [5].
Discrete or quantum behavior must be allowed in the orbits of objects, and values of numbers according to theoretical physics [10] and all experiments performed to date, with zero exception. If we accept experiments, they already provide such proof of quantum behavior, but the theoretical picture in QM [10] still uses MRN, and proposes a non-observed conservation of the number of particles [10]. In that, one does obtain discrete energy values for energy, but the eigenfunctions are hopelessly continuous. The same reasoning applies in other areas of physics, so the existence of continuity besets all solutions, including the well-known general relativity equations (GR), the Dirac equations (DE), and the Navier–Stokes (NS) equations. This, we advance, has prevented GR to meet QM, and to solve the NS, as we discuss forthwith.
There are still many physicists who find it easier to think in terms of Maxwell’s equations than in terms of the curl and divergence of a four tensor, in special relativity (SR). However, as Feynman states, physicists should always be willing to keep several different formulations of the same physical laws in mind, as there seems to be no rule that tells us which form is the best when the necessity of generalizations arises due to more precise experiments or some other reason breaking the old laws.
This work proposes one such law: one must use the set . Further, the SR and QM are exceptions to this cautious behavior, being widely demonstrated physically. Thus, calculus, SR, and QM, must use . There is also a clear need for the Lagrangian or Hamiltonian formulations of mechanics, because essentially, they can go beyond Newton’s laws and have on-ramps to SR, QM and the Noether theorems, in publication. It is also much easier to find the Schrödinger equation for bound states or Feynman’s path integrals if one knows Hamiltonian and Lagrangian mechanics.
This work defines the sets , , , and as “natural”. With this work, one does not need to use irrationals, or MRN, which can be used in algebra, however. Algebra deals well with unknown quantities. Conversely, when the digital result, as a concrete number value, is the only reality to consider, one can resort to arithmetic and calculus. This is further explained in our book, Quickest Calculus [14].
These are, in the 21st century, other models besides continuity, as considered in Figure 1, with better predictions and fewer contradictions, using this work and [14]. The model of continuity is correctly based on mathematics but fails in physics.
This work will challenge the heretofore conventional classical concepts of limit, irrational numbers, “mathematical measure”, MRN, etc., as given by Courant and Apostol [1,5] in mathematics, and in physics of a “continuous” spacetime and probabilistic quantum mechanics [10], changing GR and QM to accept quantum behavior as unknown but not uncertain. This is based on 21st century knowledge of discrete properties, as provided by CS and current quantum physics (QP), in new applications, as discussed forthwith.
4. “Mathematical Paint”
We follow the metaphors of a “mathematical paint” versus a “physical paint” to explain the situation of MRN, as introduced by P. J. Nahin [2].
The reason for the Problem of Closure can be visualized as one who simultaneously holds two conflicting ideas about numbers that cannot ever be reconciled in Boolean logic [2]. “Mathematical paint” has no atoms. That is not physical. Numbers in a physical reality, however, have a discrete structure, while mathematical numbers are infinitely divisible. Consistently using either one of these two conceptions of numbers removes the Problem of Closure in this view [2]. Here is how.
For mathematical numbers, one can consistently consider numbers as 0-dimensional and, using a “mathematical measure”, as close to one another as desired, achieving “continuity”. It is akin to a “mathematical paint” in the metaphor of P. J. Nahin [2], that has no molecular structure. This can be used to represent the mathematical idea of an “induced topological space”. Given a topological space X and a subspace , the induced topology on S is defined to be the topology in which the open sets are of form , where U is open in X, the (the n-sphere) with its induced topology is a manifold. One can consider an n-sphere as a subset of a (n + 1)-dimensional Euclidean space. It is also often called the subspace topology.
For example, one can “mathematically measure” the quality of rational approximations to any irrational, by applying the Hurwitz theorem [15], which converges more quickly, the finer the separation:
Hurwitz Theorem: Every irrational number has infinitely many rational approximations p/q, where the approximation p/q has an error less than . Thus, can be approximated by the infinite sequence of rational numbers:
where [15], providing a physical representation of , an irrational, as closely as desired, with an exponential convergence.
For the infinitely approximating fractions of rational approximations of an irrational, it does not follow, however, that it takes an infinite amount of “mathematical paint” to cover an infinite space. The thickness of a “mathematical paint” is zero. That is, zero thickness times an infinite length is zero. The Problem of Closure has vanished.
With “physical paint”: It takes an infinite volume of real paint to paint an infinite space because the physical paint has nonzero thickness. Additionally, at some point, the separation between the infinitely, ever-narrowing, approximating fractions using Hurwitz theorem becomes less than a molecule of paint. The paint will not fit.
This means that we simply cannot compare the two different methods of painting since covering with the physical paint cannot even be done for two reasons—it would require an infinite volume of real paint, and the atoms of the real paint will not fit. The “mathematical measure” corresponds to a “mathematical paint”.
5. Discrete Properties
Another view of the Problem of Closure, in which there is nothing to differentiate according to Courant [1], Apostol [5], and others, (by the very nature of of a “mathematical paint”), comes from discrete probability theory, using an explanation provided by P. J. Nahin [2].
Then, the independent variable does not vary continuously but, rather, in discontinuous jumps. In such cases, taking a derivative simply has no meaning, in the formalism of Courant [1], Apostol [5], and others that require “continuity” before differentiation.
The irrationals far outweigh the rationals in the MRN used in calculus by Courant [1], Apostol [5], and others (that use MRN), making the Problem of Closure overwhelmingly likely, and making such calculus to be indeterminate, due to the use of “mathematical paint”.
Both views are accretive, where the Problem of Closure becomes more pronounced as the number of digits increases, where one is more likely to hit an irrational the longer the number of digits. So, the Problem of Closure is not soluble mathematically except by restricting the irrationals to algebra, which solves the mathematical Problem of Closure.
This was used mathematically in [14] to provide the same known calculus formulas as given by Courant and Apostol [1,5], but with absolute precision, less work, and with no illusions that are unphysical, or added assumptions, by using the set .
6. “Continuous” Signal
The well-known conclusion, from experience with all physical measurements, such as in Figure 1, is that one can only measure rationals, which has been confirmed, for example, by Andre Gontijo Campos [16], such that irrational numbers cannot be physically measured (the only alternative). However, according to Ahmadieh Khanesar, et al. [17], XOR operations can give appropriate response to continuous design changes.
Notwithstanding [17], that result requires the use of “mathematical paint". This work, however, does not consider any metric in calculating the differentiability of a function at a point, because the set is a prime field (Because is a prime field, that means that does not posses any proper subfield. This is well-known.).
According to the author, and as seen when investigating [18] the derivative of the XOR function, binary numbers are discontinuous. This is important to computer programs that must use 2-adic numbers, which are then discontinuous and cannot follow a continuous design change with an appropriate response. The discontinuity is valid for any base number, not just 2-adic numbers, decimal, or base 20, also for p-adic numbers.
MRN cannot be computed, according to Nicolas Gisin [4], so they would not be continuous either, although infinite. As this work shows, MRN is non-computable in arithmetic and calculus, and should be restricted to algebra, the same for irrational numbers. This is also described by Nahin [2]. One can also only produce rationals [14].
These several references all indicate that irrationals and MRN can be restricted to algebra, which deals with unknown quantities.
Figure 1 above and considerations on MRN mean that the “mean value theorem” has a flaw, as it does not allow discontinuous jumps. It is true in universality [14], when continuity with MRN can be assumed as a mythical interpolation. We do not need to use the mean value theorem in calculus, according to [14].
7. New Family of Solutions to the Schrödinger Equation for Bound States
In 1977 to 1982, Ed Gerck, J. A. C. Gallas, and A. B. d’Oliveira proved [19] that a new family of solutions exists for the Schrödinger equation for bound states:
with the boundary conditions , where is not continuous, but piece-wise continuous in the set . In 1983, they applied this result to find new scaling laws for Rydberg states in magnetic fields [20]. Both results were easily be extended in [21,22], considering that is also the coherent superposition of the solutions and , that can exist at the same time:
which creates an algebraic bridge from the set to quantum computing (QC). This was expanded in [22], and was preceded by successful attempts to use continued fractions to overcome the non-computable nature of MRN [23].
If the second derivative is to be included in quantum mechanics (QM) by the well-known Schrödinger equation, even though the second derivative only exists if the solution is continuous [1,5], this is—by itself—contradictory, as stated in [21,22].
The standard justification for using derivatives with , describing a discrete behavior on/off that lacks continuity, is that would represent an average behavior, in the Bohr interpretation, following [1,5]. However, a wave is an illusion, a collective effect visible in the macrocosm, while physically one only has particles that are discrete.
This leaves out many behaviors that are not continuous, and they do not have to be continuous for to be an average, even as a continuous function interpolating isolated data points, or piece-wise continuous as [19,20]. A number of contradictions also arise from the use of infinitesimal analysis [24], including infinities and the concept of renormalization [25]. In particular, for the Schrödinger equation, the very applicability of which turns out also to be limited by non-compliance with the conservation of the number of particles, as [10] assumes incorrectly.
To overcome these contradictions, [26] in 1978 replaced the Schrödinger equation by an exact difference scheme in the set of functions U of Equation (3). This results [21,22] in a curvature representation, that does not use continuity explicitly. The second-derivative is represented exactly [26] in any function spanned by linear combinations in the set U:
with [19,20], all values in the set , where linear combinations in the set U already obey the known boundary conditions. As explained further in [19,20], the hypothesis of continuity between the two points was not assumed nor used, and the set was used by context.
This then reveals a remarkable behavior of all energy levels that they all scale as = an + b + c/n + , where n is the quantum number. The values of n are in the set , and all others in the set . This allows scaling laws to be calculated, even for very complicated potentials, such as for Rydberg states in magnetic fields [20].
A continuous solution, even as the average , cannot be digitally calculated in CS, so any digital code in CS must be seen necessarily as an approximation of some expected (although mythical, or an illusion) “analog”, continuous code.
These two contradictions and more, directly impact QC and have diverse manifestations. With the book “Quickest Calculus”, all functions are discontinuous (because they are all defined in the set ), and can be differentiated if the derivative is measurable in the set , which satisfies the concerns of this work, allowing the integral to be calculated by the second theorem of calculus [14], and all such functions providing examples for this work. This motivates one to find new extensions beyond [21,22]. This is systematically provided by the set , according to this work.
Nature is considered in this work a primitive object, incapable of mathematical or physical a priori definitions. The “mathematical paint” is not physical. This motivates us to consider a more general approach to the Schrödinger equation, where DDF are directly considered in the set , using the algebraic approach in [14], which promises to be important to QC. Serendipity appears, in that the rational numbers are given by the set called that is both quantum in behavior [14] and yet may seem continuous.
We hope to satisfy the behavior of systems described by the Niels Bohr interpretation of QM, that do not support the Copenhagen interpretation [27,28], and is against [10], but supports our experience, where the coherent superposition breaks the law of the excluded middle (LEM), as observed by the author in [22].
8. Mathematical Applications
On many problems becoming solvable with this work, this includes some in mathematics. E.g., the area and volume of the revolution of 1/x is a well-known paradox, called “Torricelli’s paradoxical funnel” [2]. It is the apparent discovery in mathematics of a surface of revolution that, even infinite in extent, nevertheless bounds a finite volume. This method solves that paradox, that exists since 1648, in print.
All 4 arithmetic operations work fine either way, but one cannot mix the two approaches. In cryptography, one cannot use MRN (albeit infinite), and has to use modular arithmetic with finite integers, in the set , achieving absolute exactness. Also, distributions are out in our approach and many problems become solvable, including the one above.
9. Discussion
In 2021, to provide a context, in trying to open the “black box” in the quantum state for QC, we hoped [21,22] to better understand the limitations about quantum processes, and provide a new complete extension of these results.
Now in 2022, to clarity the new definition of differentiability given in [14], Chapter 6, we introduce the concept of a measurable function. According to Apostol [5], every rectangle is a measurable function in the 2D plane; every step function is measurable, and its total area is the sum of areas of its rectangular pieces (i.e., the Linearity Property).
Working backwards in a compatible way, the first fundamental theorem of calculus defines the new definition of differentiability as capable of providing a primitive by integration [5,14], where the integral must be a measurable function, and one can observe that continuity is not required. Here, to “measure” is always intended to mean “of some physical, real-world quantity”, as stated in Chapter 1 of [14]. One cannot also demand continuity before one starts to measure what must represent a lack of continuity, a change.
Next, we provide two examples of the new definition of differentiability, besides every point of the set itself, and not necessarily linked to QM.
The function (module of x) seems to create a problem in conventional mathematics, with Courant [1], Apostol [5], using the set . Its differential is discontinuous at x = 0, and cannot be differentiated twice. However, the discontinuity is a change, and creates no problem in this formulation, using the set and not using distributions:
- every function is discontinuous at every point and differentiable; and
- step functions are naturally differentiable.
As a first example, in addition to (1), let us consider (2). The second theorem of calculus connects the integral of the second derivative of , with the first differential equation of , as it must.
The second example is the step-wise function, which further explains the result above, in more generality:
First, this is a measurable function (see definition in [14], Chapter 6) and can be integrated easily. The integral is :
integrated by parts, using the Linearity Property in [14], Chapter 6. By the second theorem of calculus (shown in [14], Chapter 6), the primitive and its first derivative are:
while its second derivative of is:
+ an impulse delta function of value 6 when .
Integrating this to check, this returns to , where c is a constant, which is calculated to be equal to 1, reproducing y(x):
Thus, an impulse delta function (not a distribution) of value 6 when . This conforms to the second theorem of calculus.
Therefore, discontinuous functions can be differentiated. The condition is no longer continuity, but that the result be measurable. Ignoring this infinite class of solutions is a current problem in physics and mathematics, and deprecates MRN.
To the current insistence on using bits and qubits, Einstein, in 1917 [29], proved that a binary signal is not enough—by reproducing the law of radiation found in 1900 by Max Planck. That required a third, coherent channel to exist, invalidating qubits before their concept started. It was a historical mistake by Shannon [30] with difficult consequences to this day, highlighting the importance of correct technical work, some 50 years later. This has now led to bits and qubits being seriously considered and spilling lots of ink on them, with reputations and careers being lost. However, facts cannot be swayed by will.
This work is in print: the mistake was first that information could be treated as a fluid, which can only be blocked or let pass, as a relay, not considering network encoding. This was also against the theory of line formation, from Max Planck and Einstein, that required three processes—so-called “spontaneous” emission, “spontaneous” absorption, and stimulated emission (today, all three processes are viewed as stimulated emission, in different energy ranges). That led Shannon to consider Boolean logic for information, with the LEM [22]. This second mistake led people to qubits, the third mistake in treating information. One must use tri-state+ to represent information, classically or quantically, as [21,22].
QM shows in physics that continuity does not exist, and now this can be represented in mathematics, solving the Problem of Closure.
This work shows that continuity can indeed exist mathematically, although it leads to non-physical results. Thus, MRN need to be abandoned in calculus. Either way is logically correct, but only the non-existence of MRN leads one to obtain physical results.
The way one learns in conventional mathematics does not lead one to obtain physical results in all applications, only to obtain mathematical results. One cannot find all solutions to the Schrödinger equation, nor to the GR, DE, and NS equations. The book by Apostol gives a good clue: abandon irrationals in arithmetic and calculus. One can consider them algebraically but not in arithmetic nor in calculus; they are non-computable numerically, with probability 1.
This work shows an unbounded class of valid solutions to the Schrödinger equation, using DDF. Quantum computing seems to need that in order to calculate prime numbers, which are essentially discontinuous “lumps”. We hope that this work provides tools to calculate large prime numbers directly, using algebra and calculus, not by trial-and-error using arithmetic in computers as tried today using qubits.
Funding
This research received external funding from DCTA/ITA, DCTA/IEAv, CAPES/CNPq, CNEN, Fapesp, Network Manifold Associates, Inc. (NMA), Planalto Research, the Max-Planck Institut für Quantenoptik, the Bundesministerium fúr Forschung und Technologie, and Euratom.
Acknowledgments
The author is indebted to RAS Peter Jackson, André Gerck, Ann Gerck Planalto Research, Edgardo V. Gerck, and two anonymous reviewers. ResearchGate discussions and private messages were also used, for “live” feedback, important due to the physical isolation caused by COVID.
Conflicts of Interest
The author declares no conflict of interest.
References
- Courant, R. Differential and Integral Calculus, Volume 1; First Published in Germany in 1930 as Vorlesungen über Differential-und Integralrechnung; Ishi Press: New York, NY, USA, 2011. [Google Scholar]
- Nahin, P. When Least is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Dedekind, R. Was sind und was sollen die Zahlen. In From Kant to Hilbert; Ewald, W.B., Ed.; Oxford University Press: Oxford, UK, 1999; Volume 2, pp. 787–832. [Google Scholar]
- Gisin, N. Indeterminism in Physics, Classical Chaos and Bohmian Mechanics: Are Real Numbers Really Real; Springer Nature: Berlin/Heidelberg, Germany, 2021; pp. 1469–1481. [Google Scholar] [CrossRef]
- Apostol, T.M. Calculus, Volume I; John Wiley and Sons: New York, NY, USA, 2005. [Google Scholar]
- Ozhigov, Y.I. Constructive Physics (Physics Research and Technology); Nova Science Pub Inc.: Hauppauge, NY, USA, 2011; ISBN 1612095534. [Google Scholar]
- Huang, C.; Nie, X.; Zhao, X.; Song, Q.; Tu, Z.; Xiao, M.; Cao, J. Novel bifurcation results for a delayed fractional-order quaternion-valued neural network. Neural Netw. 2019, 117, 67–93. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Hayat, T. Effects of time delays on stability and Hopf bifurcation in a fractional ring-structured network with arbitrary neurons. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 1–13. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P.; Guo, Y.; Liu, Z. Bifurcation Properties for Fractional Order Delayed BAM Neural Networks. Cogn. Comput. 2021, 13, 322–356. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Ekert, A.; Zeilinger, A. (Eds.) The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation; Springer Publishing Company: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Schwartz, L. THÉORIE DES NOYAUX. In Proceedings of the International Congress of Mathematicians, Cambridge, Massachusetts, USA, 1950; Volume 1. pp. 220–230.
- Lerner, E. Penn Physicists Help Show Math behind Growth of ’Coffee Rings’. PennToday. 2013. Available online: https://penntoday.upenn.edu/news/penn-physicists-help-show-math-behind-growth-coffee-rings (accessed on 18 December 2022).
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Gerck, E. Quickest Calculus. Planalto Research. 2023. Available online: https://www.researchgate.net/publication/365130122/ (accessed on 18 December 2022).
- Hurwitz, A. Über die angenäherte Darstellung der Irrationalzahlen durch rationale Brüche. Math. Ann. 1891, 39, 279–284. [Google Scholar] [CrossRef]
- Campos, A.G. Do Irrational Numbers Exist in Nature. 2021. Available online: https://www.researchgate.net/post/Do-irrational-numbers-exist-in-nature (accessed on 18 December 2022).
- Ahmadieh Khanesar, M.; Bansal, R.; Martínez-Arellano, G.; Branson, D.T. XOR Binary Gravitational Search Algorithm with Repository: Industry 4.0 Applications. Appl. Sci. 2020, 10, 6451. [Google Scholar] [CrossRef]
- Gerck, E. Private Communication. ResearchGate. 2021. Available online: https://www.researchgate.net (accessed on 18 December 2022).
- Gerck, E.; Gallas, J.A.C.; d’Oliveira, A.B. Solution of the Schrödinger equation for bound states in closed form. Phys. Rev. A 1982, 26, 662. [Google Scholar] [CrossRef]
- Gerck, E.; d’Oliveira, A.B.; Gallas, J.A.C. New Approach to Calculate Bound State Eigenvalues. Rev. Bras. Ensino FíSica 1983, 13, 183–300. [Google Scholar]
- Gerck, E. On The Physical Representation Of Quantum Systems. Comput. Nanotechnol. 2021, 8, 13–18. [Google Scholar] [CrossRef]
- Gerck, E. Tri-state (or more...) quantum information model. Comput. Nanotechnol. 2021, 8, 29–35. [Google Scholar] [CrossRef]
- Gerck, E.; d’Oliveira, A.B. Continued fraction calculation of the eigenvalues of tridiagonal matrices arising from the Schrödinger equation. J. Comput. Appl. Math. 1980, 6, 81–82. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Wilson, K.G. The renormalization group: Critical phenomena and the Kondo problem. Rev. Mod. Phys. 1975, 47, 773. [Google Scholar] [CrossRef]
- Gerck, E. The Exponential Difference; Private communication, cited in report number: EAV-12/78; Laboratorio de Estudos Avan cados, IAE, CTA: Sao Jose dos Campos, Brazil, 1978. [Google Scholar]
- Grib, A.; Rodrigues, W.A., Jr. Copenhagen Interpretation. In Nonlocality in Quantum Physics; Springer: Boston, MA, USA, 1999. [Google Scholar]
- Howard, D. Who Invented the “Copenhagen Interpretation”? A Study in Mythology. Philos. Sci. 2004, 71, 669–682. [Google Scholar] [CrossRef]
- Einstein, A. Zur Quantentheorie der Strahlung. Dtsch. Phys. Z. 1917, 18, 121–128. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).