Abstract
In this article, a nonlinear autocatalytic chemical reaction glycolysis model with the appearance of advection and diffusion is proposed. The occurrence and unicity of the solutions in Banach spaces are investigated. The solutions to these types of models are obtained by the optimization of the closed and convex subsets of the function space. Explicit estimates of the solutions for the admissible auxiliary data are formulated. An elegant numerical scheme is designed for an autocatalytic chemical reaction model, that is, the glycolysis model. The fundamental traits of the prescribed numerical method, for instance, the positivity, consistency, stability, etc., are also verified. The authenticity of the proposed scheme is ensured by comparing it with two extensively used numerical techniques. A numerical example is presented to observe the graphical behavior of the continuous system by constructing the numerical algorithm. The comparison depicts that the projected numerical design is more productive as compared to the other two schemes, as it holds all the important properties of the continuous model.
Keywords:
optimal solution; auxiliary data; advection; equilibrium point; glycolysis; diffusion; structure preserving MSC:
49J30; 34A12
1. Introduction
Glycolysis reaction behavior arises in biological sciences, chemistry, biochemical sciences, open chemical reactors, etc. This type of reaction reflects the pattern behavior of the solutions. So, the solution of the underlying reaction model exhibits oscillatory behavior when the steady state of the model is unstable. Hess and Boiteux [1] investigated the metabolic oscillations in various cellular systems. Initially, glycolytic traveling waves were observed in yeast cells. Afterward, the oscillatory wave solutions were observed in many phenomena, such as an open spatial reactor [2] and the glycolysis reaction for the uptake of glucose in cones [3]. The dynamical systems are generally associated with the real-world problems, represented by the mathematical systems involving the partial or ordinary differential equations. Mostly, these differential equations contain the space and time derivatives of the unknown quantities which represent the dynamics of the physical model. In the system of differential equations, the space derivatives of a different order have a strong impact on the behavior of the dynamical system. These types of mathematical models with the time derivatives have vast applications in the various fields of the real world, for instance, chemistry, physics, biological sciences and engineering [4,5,6,7,8,9,10,11,12,13]. Physical chemistry also has a verity of applications in mathematics. There are several chemical reaction models in the form of differential equations that represent the different properties of the chemical substances. Glycolysis is a fundamental chemical reaction which appears in the cytosol of cells’ cytoplasm. It is actually a metabolic pathway for the energy of cells in an organism [14,15]. This pathway concerns the oxidative disruption of one glucose molecule into two pyruvate with the addition of energy in the form of adenosine triphosphate (ATP) and nicotinamide adenine dinucleotide (NAD) [16]. Glycolysis plays a significant role in the body cells as glucose is a major source of propellant for the tissues in the body. For instance, the only mean of energy for the brain is the glucose. The body must carry a sufficient quantity of glucose in the blood to guarantee the brain functioning naturally. So, glycolysis appears in almost all living organisms.
To study the advection–diffusion systems, the applications of the derivatives, ultimately the differential equations in the mathematical models of the underlying systems, have a significant role. The governing equations involved in the phenomenon provide an easy understanding for investigating the model. For the numerical solution of the glycolysis model, it is of great significance to verify the important properties such as the existence, uniqueness and convergence toward the true steady states. To explore the numerical solution of the set of equations representing the system, the awareness of the existence and uniqueness of the solution is an important thing. Moreover, the study of the convergence behavior of the solution plays a vital role in the numerical analysis [17]. Before computing an approximate solution, it is more beneficial to ensure the existence of the solution. When the solution is guaranteed, then it is a further challenging task to find how many solutions are possible. Then, a feasible solution is traced, which is in accordance with the constraints of the system. The solutions of differential equations generally lie in the function spaces called Banach spaces. Generally, the desired values of the state variables involved in the system of differential equations cannot have a global bound, so it is obviously attractive to consider a closed ball in the space of continuous functions. The advantage of considering such subsets is that explicit estimates can be obtained. In the first stage, the problems are reduced to the operator having a fixed-point property for which the solutions are guaranteed in the closed balls of these spaces of the functions that lead to the limitations on the radius of the closed balls for an available interval or boundary conditions. Likewise, the same radius chosen in the same problem can also lead to the limitations for admissible auxiliary data. The closed ball for which the limitation or restriction is placed is called the optimal ball. Tutschke, in 2005, gave the idea about explicit estimates for the general equations of operators [18]. Numerical schemes are immensely applied to approximate the solutions of the system of differential equations. So, it is necessarily required to establish such numerical schemes that carry all the fundamental traits of the model, namely the positivity, boundedness and convergence toward the fixed point. In recent years, a number of researchers studied the glycolysis models [19,20] which are nonlinear in nature. Due to the nonlinearity, to find the analytical solutions for these models is a strenuous job, so most of the researchers found the numerical solutions of these types of mathematical models [21,22].
In 1968, Selkov [23] constructed a simple model of glycolysis that represents the qualitative behavior of most experimental data for a single-frequency oscillation in glycolysis. Selkov’s model is described as
Mickens, in [24], analyzed the above Selkov model numerically and obtained the approximate solution by using a finite difference scheme in a nonstandard way (NSFD), which possesses the property of positivity preserving naturally. In the abovementioned model, and represent the concentrations of the chemical substances, so they must be positive. The systems of first-order partial differential equations have been considered within the framework of the Clifford analysis, where the components of the Clifford algebra-valued functions are the solutions of the diffusion equations [25]. Verveyko and Verisikin demonstrated the computational analysis of the glycolysis reaction model in an open spatial reactor [26]. In [27], Nauman et al. considered a one-dimensional coupled autocatalytic glycolysis model and solved it numerically by an efficient finite difference explicit numerical scheme, which preserves the positivity of the unknown quantities used in the model. Now, we convert the model, mentioned above, into the advection–reaction–diffusion model as follows:
With the inclusion of the advection and diffusion terms in the mathematical model concerning population dynamics and an autocatalytic chemical reaction system, it represents more realistic behavior as advection describes the directed movements and the random movements are represented by the diffusion process. So, the extended models thoroughly explain the relevant physical phenomena [28,29,30,31,32,33,34,35]. In this paper, we dealt with a one-dimensional glycolysis model with advection–diffusion.
with initial and boundary conditions
and
where f and g are the unknown quantities representing the concentration of chemical substances, and and represent the diffusion coefficients. In the above proposed model, and exhibit the diffusion (random movement) and , show the advection (directed movement) of f and g, respectively.
The remainder of this article consists of the following sections. In Section 2, the general form of the advection–reaction–diffusion system is considered for the analysis. The existence of the optimal solution of this system in an optimal ball of a Banach space with explicit estimates is discussed. A result about the uniqueness of the solution of the proposed system is also established. Section 3 is devoted to the numerical study of the autocatalytic glycolysis model. A reliable and efficient numerical scheme, which is known as a nonstandard finite difference technique, is designed which preserves the traits of the physical system. The consistency and stability of the proposed scheme are also discussed in this section. In order to show the efficiency of the proposed scheme, its comparison with the other well-known numerical schemes is necessary. So, to compare our results, two other existing methods are also applied on the same problem, and the results are compared in this section. A numerical example with complete numerical simulations is illustrated in Section 4. In Section 5, some concluding remarks are given.
2. Existence of Optimal Solutions
In this section, we find some optimality conditions in Banach spaces for some quantities used in the existence of optimal solutions to glycolysis model and . This system can be expressed in a more general form as
In the above form, and showing in the right sides of Equations and may be linear or nonlinear functions in which nonlinearity of and may depend on f and g as well as on their first- and second-order apace derivatives [36]. The equivalent form for the solution of the above system can be written as follows
Combining these two equations, we obtain
In the light of the theory of operators, the integral equation showing above to evaluate the solution to Equations and can be written in operator form, which becomes a fixed-point problem as follows
For any real number , let be a Banach space in which we will optimize the proposed problem. Optimization can be performed by choosing a closed and convex subset, called closed ball, in the solution space X. To choose this closed and convex subset in X, two possibilities arise as follows:
- 1.
- Consider a closed ball in the Banach space X whose center is at which is usually known as the zero of the space X.
The fixed point results from the literature of a nonlinear analysis can be helpful to ensure the existence of the solution. In this regard, Schauder fixed-point theorem is applied to guarantee the existence result for the system and . First, it is important to consider that the fixed-point operator J maps continuously the ball in to itself.
Now, consider a mapping
defined as
Suppose that
is a real-valued continuous function.
Take
To fulfill the first condition of Schauder’s fixed-point theorem, J is needed to be a self-map. So,
If we choose the initial condition and , length of the interval for continuity, we can optimize r, that is, the optimal ball. Then,
If we fix r and , then
To obtain the highest value of , we have to find the maximum value of . Let be the value of optimized radius r, then it satisfies the equation
This implies
Again, if is chosen first, the value of can be optimized from , that is,
For the greatest value of , we have the maximum value of . The optimized value of r satisfies the equation
- 2.
- If we consider an optimal ball with center at the initial condition .
By Schauder’s fixed-point theorem, existence of the solutions to Equations and require the self-mapping first for defined as
Let us take , where is a real-valued continuous function. Take
where . For J to be self-mapping, we have
For the largest possible value of , maximization technique can be applied from applied calculus on in which is considered as a differentiable function. Suppose that be the value of optimal radius, then it should be the root of the equation
If and
If we suppose is positive for all values of r, then has a maximum value at every value which satisfies Equation . Because between two maximum values there exists at least one minimum value, the assumption of implies that Equation has at most one solution.
With the help of the above discussion, we can develop a result.
Theorem 1.
Suppose that for a real-valued continuously differentiable function , the optimal value of radius is the root of Equation . Moreover, and positive. Then, at most, one value of optimal radius of a closed ball exists in which the solutions of Equations and exist.
Numerical solutions have a key role in the applied study of mathematics. Along with the approximate solutions, numerical simulations help us to understand the behavior of the solutions as well as the numerical scheme [37,38,39]. In the following section, we use a suitable and reliable Mickem’s technique, named the nonstandard finite difference (NSFD) scheme, to obtain the solution of the prescribed model, and to show the strong reasonings to use this scheme, we will find the solution to the same problem by some well-known numerical schemes for the comparison.
3. Numerical Solutions of Glycolysis Model with Analysis
In the literature of numerical analysis, the finite difference schemes have a pivotal role to find the numerical solution of differential equations that may be linear or nonlinear. The use of such kind of techniques makes the numerical calculations very easy as compared to the other existing methods because this technique converts the continuous model into a discrete formulation by taking some finite number of values of the function defined on the corresponding finite number of points in the given domain which is easy to handle [40,41,42,43,44]. The Taylor’s series expansion is the best tool to obtain the numerical approximations.
In the remaining part of this paper, assume that m, n are two positive integers and , a positive real number. For finding the values of the state variables involved in Equations and , we proceed as follows: the intervals and are discretized as given below and of and , respectively, with the norm and
Let and be the approximate values of the function and , respectively, at a grid point . The fixed point (point of equilibria) of Equations and is . Strogatz discussed the stability of the fixed point of the glycolysis model in [45]. According to Strogatz, the fixed point of glycolysis is stable if and unstable if .
As for some nonlinear systems, it is difficult to investigate the analytical solutions to Equations (1) and (2). So, we adopt some numerical techniques to approximate them. A numerical scheme is called reliable if it sustains the fundamental traits of the system. In particular, it should preserve the structure of the continuous system. Mickens established the criteria for constructing the structure-preserving nonstandard numerical scheme [46]. Here, we apply the scheme which was established by Charpentier [47]. This scheme retains the positivity property for the underlying system. The efficiency of the proposed scheme is elucidated by comparing it with other existing schemes in the literature.
There are many implicit and explicit schemes in the literature proposed by various researchers. In the explicit scheme, the dependent quantities are expressed in terms of some already known quantities for the previous step of time, while for the implicit schemes, both dependent and independent variables (the value of functions at a future time step) are used in one equation, so they can be represented in the matrix notation. We can discretize our proposed model and by using the formulas
Substituting these formulas in Equations and ( and applying the rules defined by Mickens [46], we obtain
After some simplifications, we obtain
where , , .
3.1. Order of Accuracy
For the accuracy of the numerical solution, it is very important that is achieved by the numerical design. The accuracy of the proposed scheme is obtained by using Taylor’s expansions. From Equation , let
Take
Similarly, after finding the values of , by using Taylor’s series, we obtain
So, as and .
Now, for Equation , let
By applying Taylor’s expansion series formulas on and after some simple calculations, we obtain as and . Hence, the proposed scheme is consistent with order 1.
3.2. Stability of Proposed Scheme
From Equation ,
After linearization, we have
Put
which is less than 1.
Again, from Equation (15), after linearization, we obtain
Similarly, we obtain
which is also less than 1.
Hence, the proposed scheme is von Nuemann stable.
3.3. Positivity of Proposed Scheme
M-matrix theory [48] is quite useful for proving the positivity of a large number of mathematical models regarding population dynamics, economy, engineering, autocatalytic chemical reactions, etc.
M-matrix over R is a square matrix if all the entries in off-diagonal position are non-positive.
Remark 1.
It is evident that M-matrix obeys the diagonal dominance property and all the entries of the inverse of M-matrix are always positive.
Theorem 2.
For any and , the discretized system and has positive solutions. That is, and for all .
Proof.
The system and can be expressed as
where K and L are square matrices, while U and V represent the column matrices of the system and .
The diagonal elements of the matrix K represented by , where , are . On the other hand, the elements in K other than diagonal elements represented by , where are , and , in which , . The diagonal elements of matrix L defined as , where are . While the off-diagonal entries in L represented by , and are , and , where , . Column matrix entries in both the matrices L and M are and , respectively.
Again,
Because , and clearly, the diagonal elements of both above matrices K and L, and , respectively, are non-negative. Moreover, and , all are negative in both the above matrices.
In the presence of all the abovementioned properties, both the matrices K and L are M-matrices. This implies that K and L are non-singular matrices. So, the Equations (18) and (19) can be represented by
Assume that and , K and L are M-matrices. This implies that all the entries of and are positive. So, we obtain and . Hence, by induction, the system and is positive. □
3.4. The Upwind Implicit Scheme
In upwind scheme, both time and space derivatives are developed in the following manner:
Substitute the above approximations in Equations and , we obtain
where , and .
The upwind scheme is implicit in nature, and it constructs a diagonally dominant system of algebraic equations. The von Neumann criteria are applied in describing the stability of the model.
3.5. The Classical Crank Nicolson Scheme
In this famous numerical classical method, the partial derivatives with respect to time and space are replaced by using the classical central difference concept at , which represents the average of the two consecutive points of the time coordinate, while keeping the space coordinates fixed, i.e., and . Then,
The corresponding difference equations are determined by Equations and , and after substituting the above approximations, we have
4. Numerical Experiment
In this section, we discuss a numerical experiment. Consider the system (1) and (2) with the following initial and no-flux boundary conditions:
Figure 1 and Figure 2 indicate the graphical solutions of the state variables f and g which represent the concentration of the chemical substances with the help of the popular Crank Nicolson technique. The graphs in Figure 1 show the negative solution of g, which is worthless, while this scheme is mathematically stable and unconditionally consistent. Moreover, the graphs in Figure 2 point out that this technique is divergent for various step sizes. So, we can conclude that the Crank Nicolson method is not applicable to the proposed model.
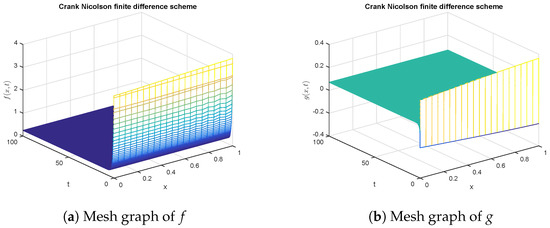
Figure 1.
Graphical solution of (concentration of substances) using Crank Nicolson method at .
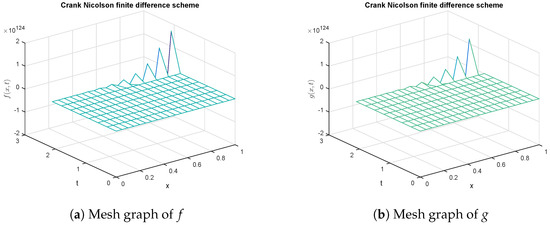
Figure 2.
Graphical solution of (concentration of substances) using Crank Nicolson method at .
The simulations in Figure 3 and Figure 4 for the upwind implicit method are similar to the Crank Nicolson method. The upwind implicit scheme exhibits the non-physical behavior in these graphs. Therefore, this method also fails to sustain the structure of the glycolysis model.
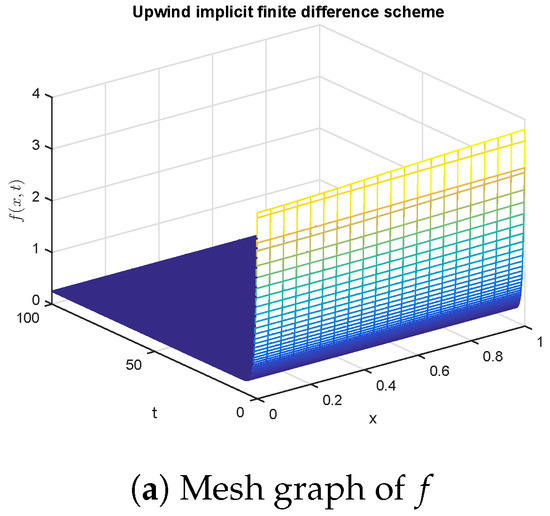
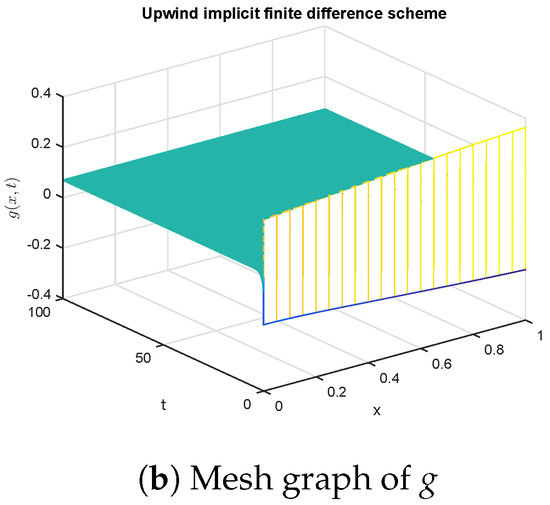
Figure 3.
Graphical solution of (concentration of substances) using upwind implicit method at .
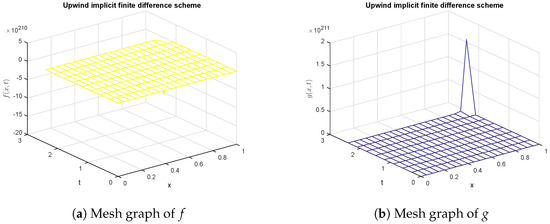
Figure 4.
Graphical solution of (concentration of substances) using upwind implicit method at .
The graphical approach of the suggested NSFD implicit technique is performed in Figure 5 and Figure 6. All the important attributes of the state variables involved in the system and are contained by the proposed technique. This technique achieves the convergent solutions for all the step sizes and also holds the positive solution. In Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, we select the values of a and b in such a way that the condition is satisfied, so the fixed point of the glycolysis model is stable. It is clear from Figure 2, Figure 4, Figure 5 and Figure 6 that the designed NSFD implicit technique retains the stability of the fixed point while the upwind and Crank Nicolson schemes fail in this regard.
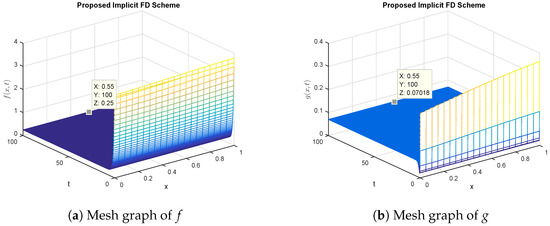
Figure 5.
Graphical solution of (concentration of substances) using designed NSFD implicit method at .
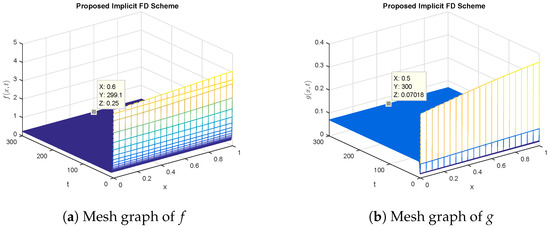
Figure 6.
Graphical solution of (concentration of substances) using NSFD implicit method at .
It is evident from the above figures that the underlying system and is unstable at the fixed point , if the expression is less than zero. Figure 7 validates that the proposed technique demonstrates the same behavior as possessed by the model and . In the graphs of Figure 7, we take the values of a and b in such a way that the expression is less than zero. Clearly, the graphical solution exhibits unstable behavior.
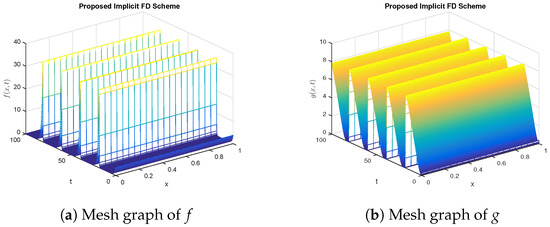
Figure 7.
Graphical solution of (concentration of substances) using designed NSFD implicit method at .
5. Conclusions
In the current article, the existence of the solution for a chemical reaction system, known as a glycolysis model, is described by using a renowned result of the fixed-point theory. Firstly, we considered a function space (solution space) of the continuous functions and optimized the solution by a closed ball which is a subset of the function space. In the framework of optimization, we constructed a result with suitable conditions. The uniqueness of the solution in this regard was also discussed. After acquiring the existence and uniqueness of the values of the state variables, we constructed a scheme for the numerical approximation of the solutions of the system which holds the unconditional positivity of the required solutions. We also proved that our proposed numerical scheme is consistent with the model and . The comparison of the current scheme with the existing schemes verified that our proposed scheme is more efficient. The upwind and Crank Nicolson schemes were selected for the comparison. Moreover, these schemes did not preserve the structure of the continuous model. Because the elements of the function space are not globally bounded, it is better to choose the optimal balls for handling the issue. These balls provide the explicit estimates for the approximate solutions to the system. In the future, numerical solutions can be optimized in this manner. Our proposed scheme may be used as a significant tool for solving the different nonlinear systems.
Author Contributions
Conceptualization, M.D.l.S.; data curation, M.S.I.; investigation, T.S.S. and N.A.; resources, N.S.; visualization, M.R.; writing—original draft, M.A.-u.R. and N.A.; writing—review & editing, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
Basque Government, Grant IT1555-22 and Grant KK-2022/00090 MCIN/AEI 269.10.13039/ 501100011033, Grant PID2021-1235430B-C21/C22.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hess, B.; Boiteux, A.; Krüger, J. Cooperation of glycolytic enzymes. Biol. Chem. 1968, 349, 1567–1574. [Google Scholar] [CrossRef] [PubMed]
- Bagyan, S.; Mair, T.; Dulos, E.; Boissonade, J.; De-Kepper, P.; Miller, S.C. Glycolytic oscillations and waves in an open spatial reactor: Impact of feedback regulation of phosphofructokinase. Biophys. Chem. 2005, 116, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Camacho, E.T.; Brager, D.; Elachouri, G.; Korneyeva, T.; Millet-Puel, G.; Sahel, J.; Léveillard, T. Mathematical Analysis of Aerobic Glycolysis Triggered by Glucose Uptake in Cones. Sci. Rep. 2019, 9, 4162. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, B.; Wazwaz, A.M. Rational and Semi-Rational Solutions to the Nonlocal Mel’nikov Equation via Determinants. Rom. J. Phys. 2020, 65, 109. [Google Scholar]
- Cristescu, I.A. Finite Element Approximation for the Coupled Two-Dimensional Burgers’ Equation. Rom. J. Phys. 2018, 63, 105. [Google Scholar]
- Youssri, Y.H.; Abd-Elhameed, W.M. Numerical Spectral Legendre-Galerkin Algorithm for Solving Time Fractional Telegraph Equation. Rom. J. Phys. 2018, 63, 107. [Google Scholar]
- Baleanua, D.; Yusuf, M.I.A.; Aliyu, A.I. Time Fractional Third-Order Evolution Equation: Symmetry Analysis, Explicit Solutions, and Conservation Laws. J. Comput. Nonlinear Dynam. 2017, 13, 021011. [Google Scholar] [CrossRef]
- Baleanua, D.; Inc, M.; Yusuf, A.; Aliyu, A.I. Dark optical solitons and conservation laws to the resonance nonlinear Shrödinger’s equation with Kerr law nonlinearity. Optik 2017, 147, 248–255. [Google Scholar] [CrossRef]
- Ahmed, N.; Rafiq, M.; Baleanu, D.; Rehman, M.A. Spatio-Temporal Numerical Modeling of Auto-Catalytic Brusselator Model. Rom. J. Phys. 2019, 64, 110. [Google Scholar]
- Hafez, R.M.; Doha, E.H.; Bhrawy, A.H.; Baleanu, D. Numerical solutions of two-dimensional mixed volterra-fredholm integral equations via bernoulli collocation method. Rom. J. Phys. 2017, 62, 111. [Google Scholar]
- Younis, M.; Ali, S. Solitary wave and shock wave solutions of (1+1)-dimensional perturbed Klein-Gordon,(1+1)-dimensional Kaup-Keperschmidt and (2+1)-dimensional ZK-BBM equations. Open Eng. 2015, 5, 124–130. [Google Scholar] [CrossRef]
- Ali, K.; Rizvi, S.T.R.; Nawaz, B.; Younis, M. Optical solitons for paraxial wave equation in Kerr media. Mod. Phys. Lett. B 2019, 33, 1950020. [Google Scholar] [CrossRef]
- Younis, M.; Shahid, I.; Anbreen, S.; Rizvi, S.T.R. Exact optical solitons in (n+1)-dimensions with anti-cubic nonlinearity. Mod. Phys. Lett. B 2018, 32, 1850071. [Google Scholar] [CrossRef]
- Dai, Z.; Locasale, J.W. Metabolic pattern formation in the tumor microenvironment. Mol. Syst. Biol. 2017, 13, 915. [Google Scholar] [CrossRef]
- Romano, A.H.; Conway, T. Evolution of carbohydrate metabolic pathways. Res. Microbiol. 1996, 147, 448–455. [Google Scholar] [CrossRef]
- Lane, A.N.; Fan, T.W.M.; Higashi, R.M. Metabolic acidosis and the importance of balanced equations. Metabolomics 2009, 5, 163–165. [Google Scholar] [CrossRef]
- Shah, K.; Wang, J.; Khalil, H.; Khan, R.A. Existence and numerical solutions of a coupled system of integral BVP for fractional differential equations. Adv. Differ. Equ. 2018, 2018, 149. [Google Scholar] [CrossRef]
- Tutschke, W. Optimal balls for the application of the Schauder Fixed-Point Theorem. Complex Var. Theory Appl. Int. J. 2005, 50, 697–705. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, J. Pattern formation in a general glycolysis reaction–diffusion system. IMA J. Appl. Math. 2015, 80, 1703–1738. [Google Scholar] [CrossRef][Green Version]
- Meihua, W.; Yanling, L.; Xi, W. Stability and bifurcation with singularity for a glycolysis model under no-flux boundary condition. Discrete Cont. DYN-B 2019, 24, 5203–5224. [Google Scholar]
- Dehghana, M.; Saadatmandi, A. The numerical solution of a nonlinear system of second-order boundary value problems using the sinc-collocation method. Math. Comput. Model. 2007, 46, 1434–1441. [Google Scholar] [CrossRef]
- Malik, Z.U.; Soleymani, F.; Al-Fhaid, A.S. Numerical solution of nonlinear systems by a general class of iterative methods with application to nonlinear PDEs. Numer. Algor. 2014, 67, 223–242. [Google Scholar]
- Sel’Kov, E.E. Self-Oscillations in Glycolysis 1. A Simple Kinetic Model. Eur. J. Biochem. 1968, 4, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Mickens, R.E. Positivity preserving discrete model for the coupled ODES modeling glycolysis. In Proceedings of the Fourth International Conference on Dynamical Systems and Differential Equations, Wilmington, NC, USA, 24–27 May 2002; pp. 623–629. [Google Scholar]
- Iqbal, M.S. Boundary Value Problems for Non-linear First Order Systems of Partial Differential Equations in Higher Dimensions, Especially in Three Dimensions. Adv. Appl. Clifford Algebras 2019, 29, 98. [Google Scholar] [CrossRef]
- Verveyko, D.V.; Verisokin, A.Y. Computational analysis of glycolytic reaction in open spatial reactor. Appl. Math. Model. 2014, 38, 4796–4803. [Google Scholar] [CrossRef]
- Ahmed, N.; Tahira, S.S.; Imran, M.; Rafiq, M.; Rehman, M.A.; Younis, M. Numerical analysis of auto-catalytic glycolysis model. AIP Adv. 2019, 9, 085213. [Google Scholar] [CrossRef]
- Twizell, E.H.; Gumel, A.B.; Cao, Q. A second-order scheme for the “Brusselator” reaction–diffusion system. J. Math. Chem. 1999, 26, 297–316. [Google Scholar] [CrossRef]
- Zhou, P.; Xiao, D. Global dynamics of a classical Lotka–Volterra competition–diffusion–advection system. J. Funct. Anal. 2018, 275, 356–380. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Zhou, P. On a Lotka–Volterra competition model: The effects of advection and spatial variation. Calc. Var. 2016, 55, 73. [Google Scholar] [CrossRef]
- Peng, R.; Zhao, X.Q. A nonlocal and periodic reaction-diffusion-advection model of a single phytoplankton species. J. Math. Biol. 2016, 72, 755–791. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, X.Q. Propagation Phenomena for A Reaction–Advection–Diffusion Competition Model in A Periodic Habitat. J. Dyn. Diff. Equat. 2017, 29, 41–66. [Google Scholar] [CrossRef]
- Zhang, L.; Wanga, Z.C.; Zhao, X.Q. Threshold dynamics of a time periodic reaction–diffusion epidemic model with latent period. J. Differ. Equ. 2015, 258, 3011–3036. [Google Scholar] [CrossRef]
- He, X.; Ni, W.M. The effects of diffusion and spatial variation in Lotka–Volterra competition–diffusion system II: The general case. J. Differ. Equ. 2013, 254, 4088–4108. [Google Scholar] [CrossRef]
- Dockery, J.; Hutson, V.; Mischaikow, K.; Pernarowski, M. The evolution of slow dispersal rates: A reaction diffusion model. J. Math. Biol. 1998, 37, 61–83. [Google Scholar] [CrossRef]
- Kostic, M. Abstract Volterra Integro-Differential Equations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Ahmed, N.; Wei, Z.; Baleanu, D.; Rafiq, M.; Rehman, M.A. Spatio-temporal numerical modeling of reaction-diffusion measles epidemic system. Chaos 2019, 29, 103101. [Google Scholar] [CrossRef]
- Ahmed, N.; Rafiq, M.; Rehman, M.A.; Iqbal, M.S.; Ali, M. Numerical modeling of three dimensional Brusselator reaction diffusion system. AIP Adv. 2019, 9, 015205. [Google Scholar] [CrossRef]
- Fatima, U.; Ali, M.; Ahmed, N.; Rafiq, M. Numerical modeling of susceptible latent breaking-out quarantine computer virus epidemic dynamics. Heliyon 2018, 4, 00631. [Google Scholar] [CrossRef]
- Arson, D.G. A Comparison Method for Stability Analysis of Nonlinear Parabolic Problems. SIAM Rev. 1978, 20, 245–264. [Google Scholar] [CrossRef]
- Bebernes, J.W.; Schmitt, K. On the existence of maximal and minimal solutions for parabolic partial differential equations. Proc. Am. Math. Soc. 1979, 73, 211–218. [Google Scholar] [CrossRef]
- Escobedo, M.; Herrero, M.A. Boundedness and blow up for a semilinear reaction-diffusion system. J. Differ. Equ. 1991, 89, 176–202. [Google Scholar] [CrossRef]
- Liu, B.C.; Dong, M.Z.; Li, F.J. Asymptotic properties of blow-up solutions in reaction–diffusion equations with nonlocal boundary flux. Z. Angew. Math. Phys. 2018, 69, 27. [Google Scholar] [CrossRef]
- Lin, H.; Wang, F. On a reaction–diffusion system modeling the dengue transmission with nonlocal infections and crowding effects. Appl. Math. Comput. 2014, 248, 184–194. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering; Adisson-Wesley: New York, NY, USA, 1994; pp. 205–209. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Chen-Charpentier, B.M.; Kojouharov, H.V. An unconditionally positivity preserving scheme for advection–diffusion reaction equations. Math. Comput. Model. 2013, 57, 2177–2185. [Google Scholar] [CrossRef]
- Fujimoto, T.; Ranade, R. Two characterizations of inverse-positive matrices: The Hawkins-Simon condition and the Le Chatelier-Braun principle. Electron. J. Linear Algebra 2004, 11, 59–65. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).